A Study of Fuel Economy Improvement in a Plug-in Hybrid Electric Vehicle using Engine on/off and Battery Charging Power Control Based on Driver Characteristics
Abstract
:1. Introduction
2. Development of the Powertrain System and Performance Simulator
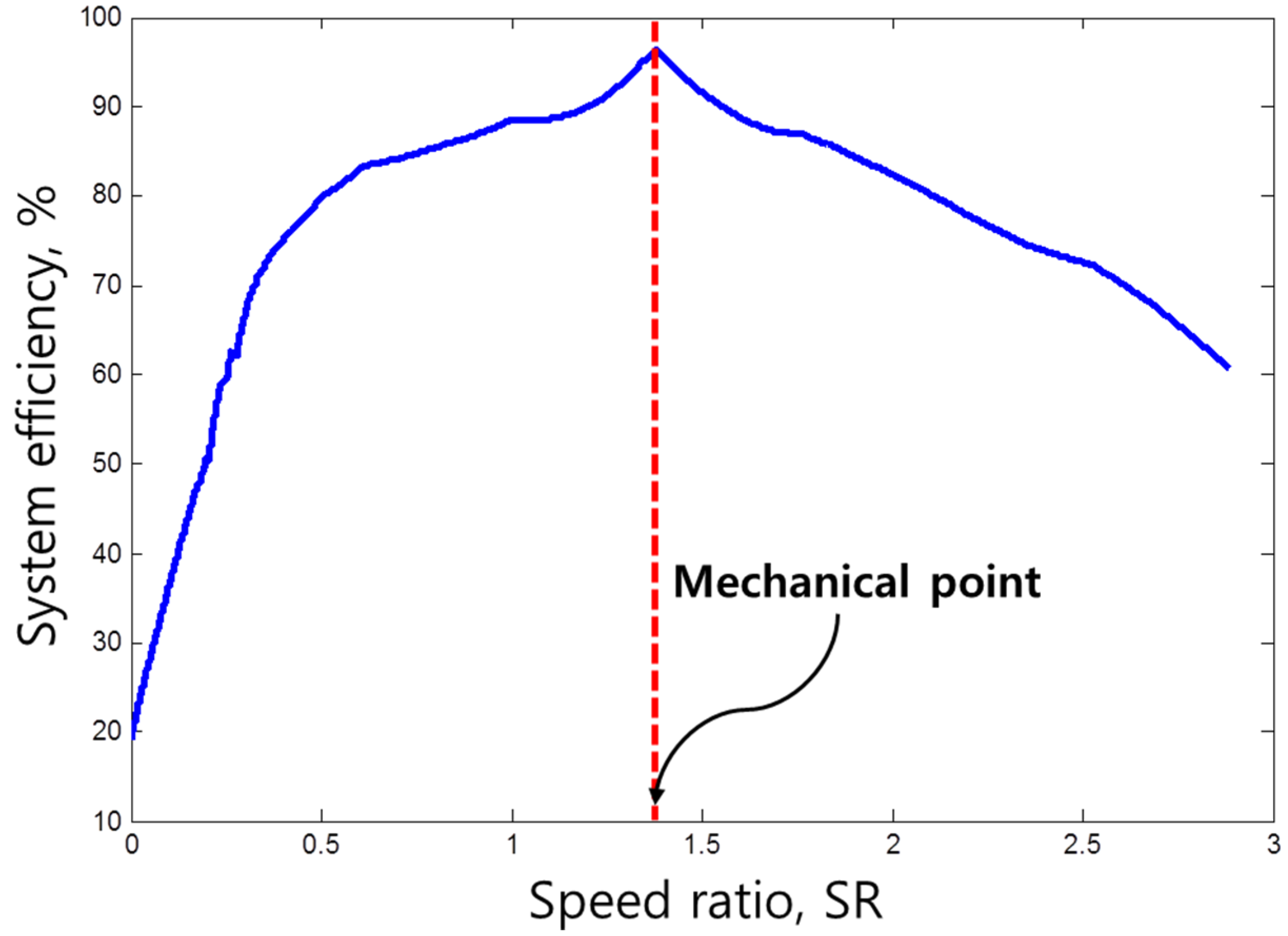
2.1. Powertrain System Modeling of the PHEV
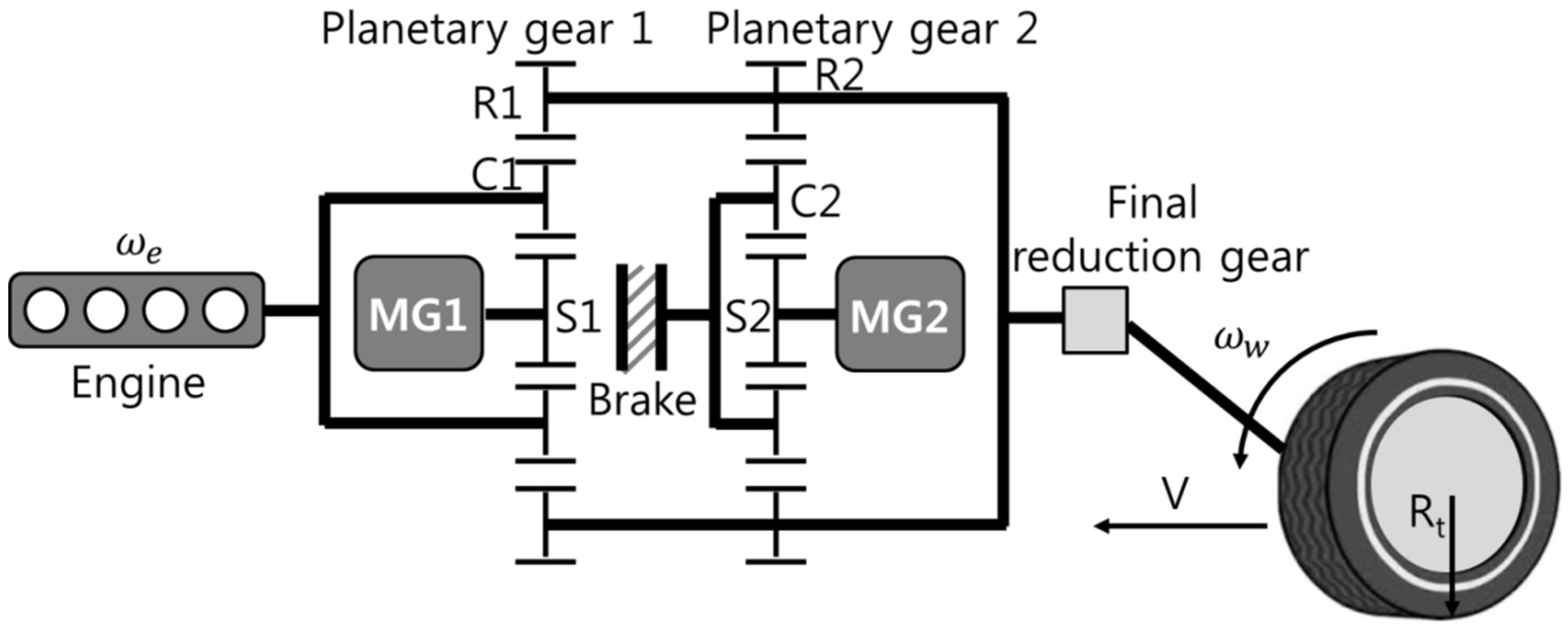
| Components | Type | Specifications | |
|---|---|---|---|
| Engine | 1.8 L gasoline 4-cylinder Atkinson engine | Max engine torque | 142 Nm |
| Max engine output | 73 kW | ||
| Motor | Synchronous AC motor | Max output | 60 kW |
| Max torque | 207 Nm | ||
| Max speed | 13,900 rpm | ||
| Max current | 170 Arms | ||
| Battery | Lithium-ion | Capacity | 4.4 kWh |
| Max output | 27 kW | ||
| Voltage | 201.6 V | ||
| Curb weight | 1420 kg | ||
| Motor reduction gear ratio (planetary gear ratio ZR2/ZS2) | 2.636 | ||
| Final reduction gear ratio | 3.267 | ||
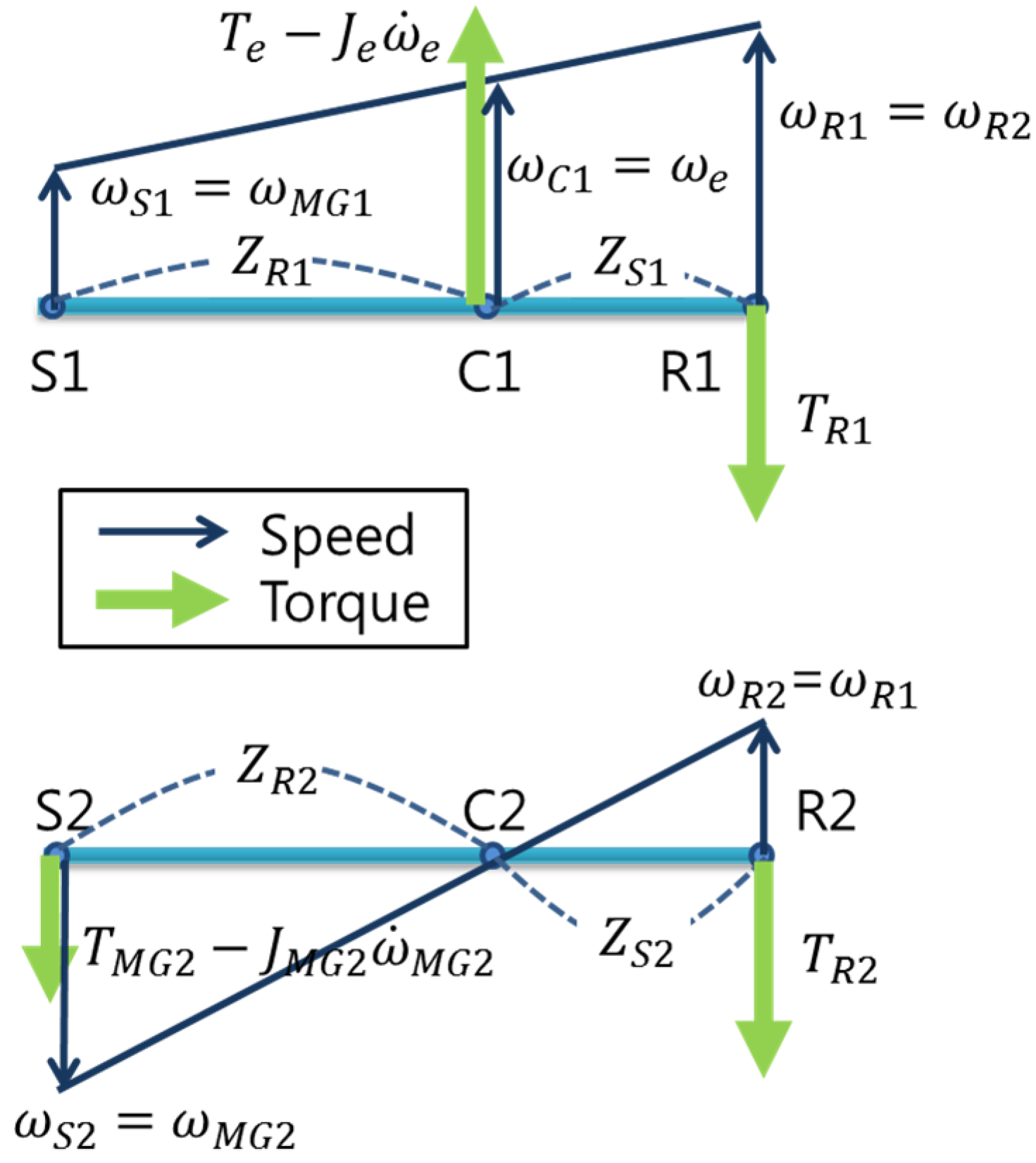
2.2. Development of the Target PHEV Simulator
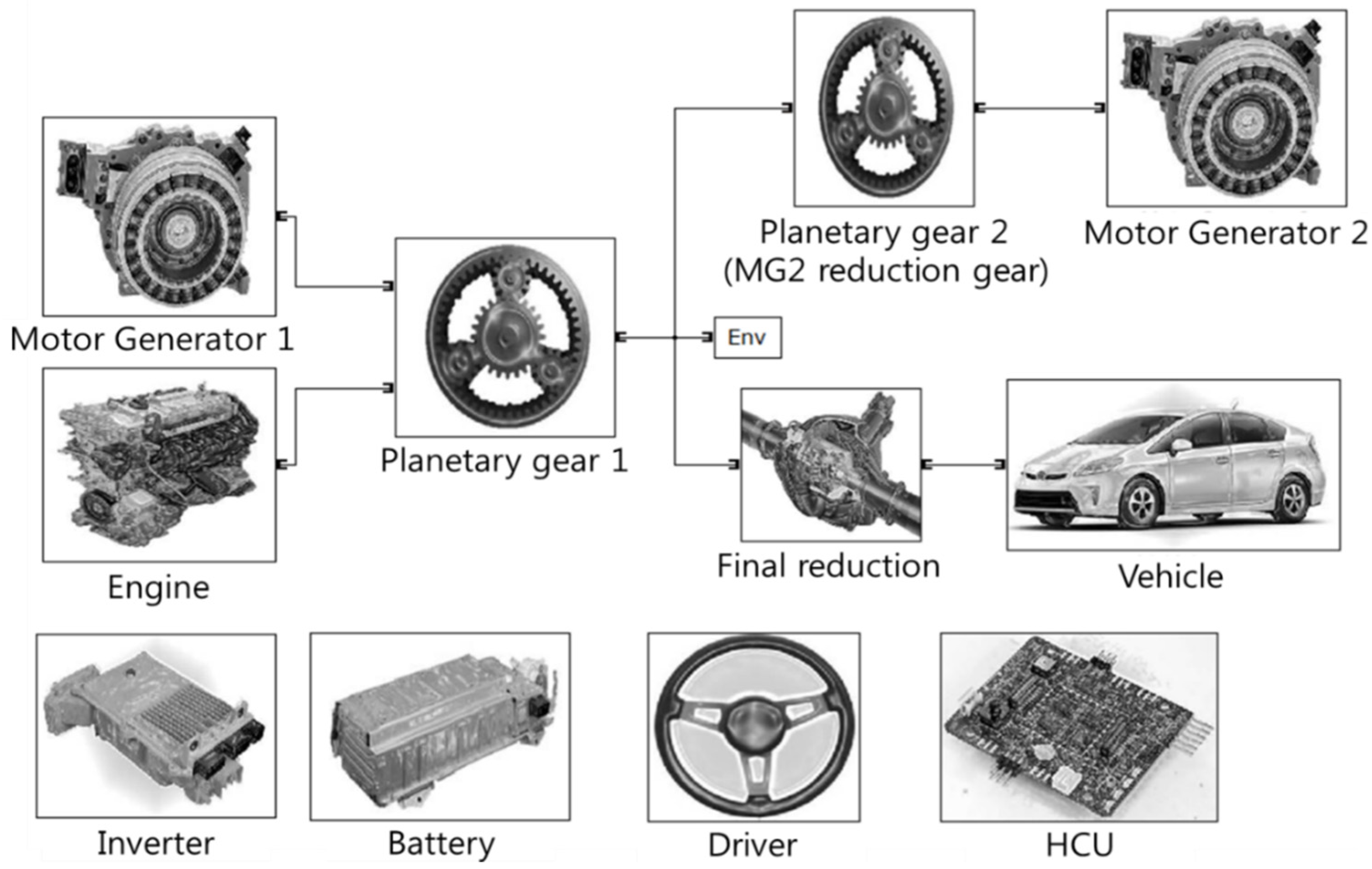
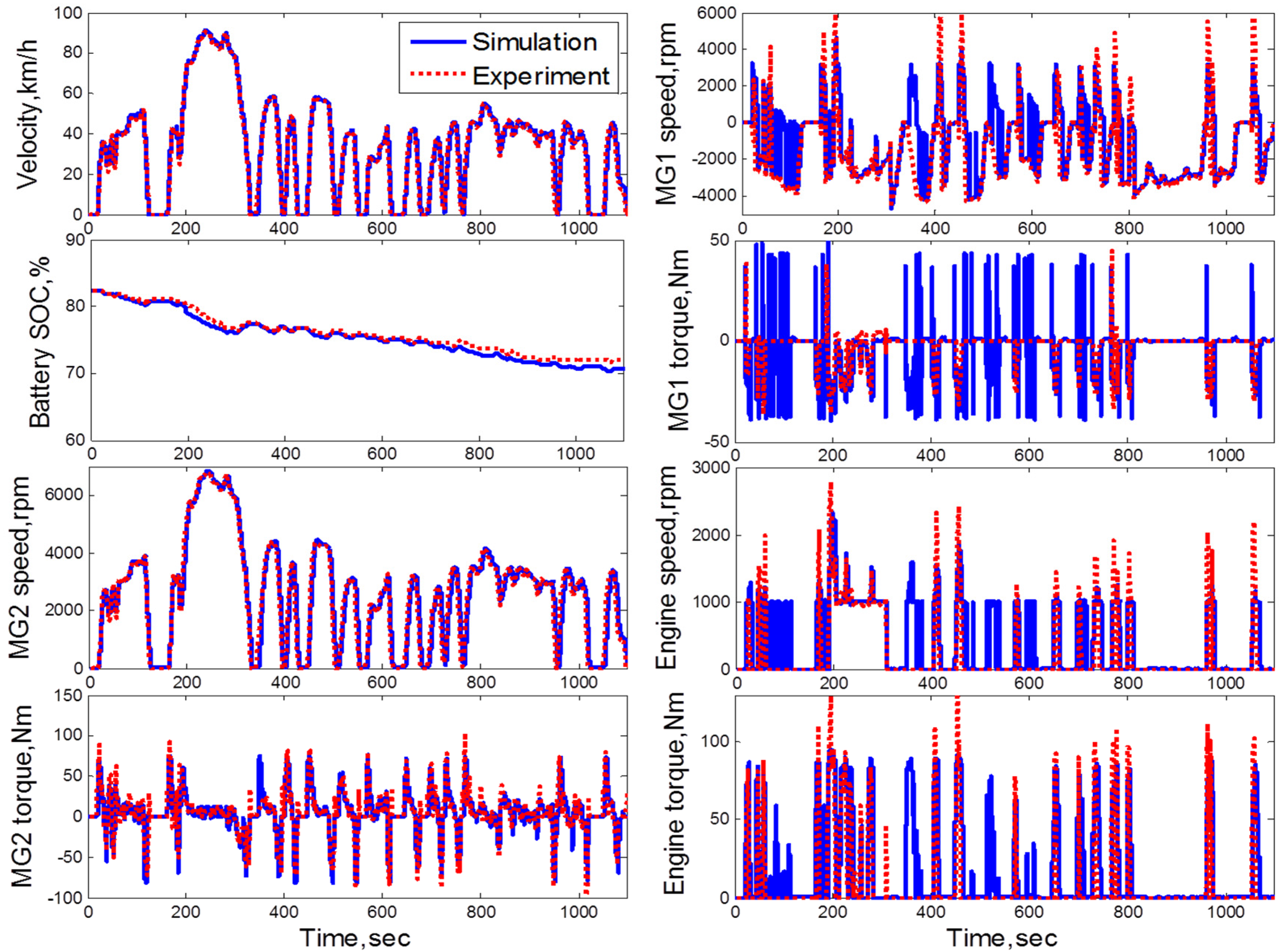
2.3. Verification of the Target PHEV Simulator
3. Driver Model and Tendency of the Driver
3.1. Development of the Driver Model

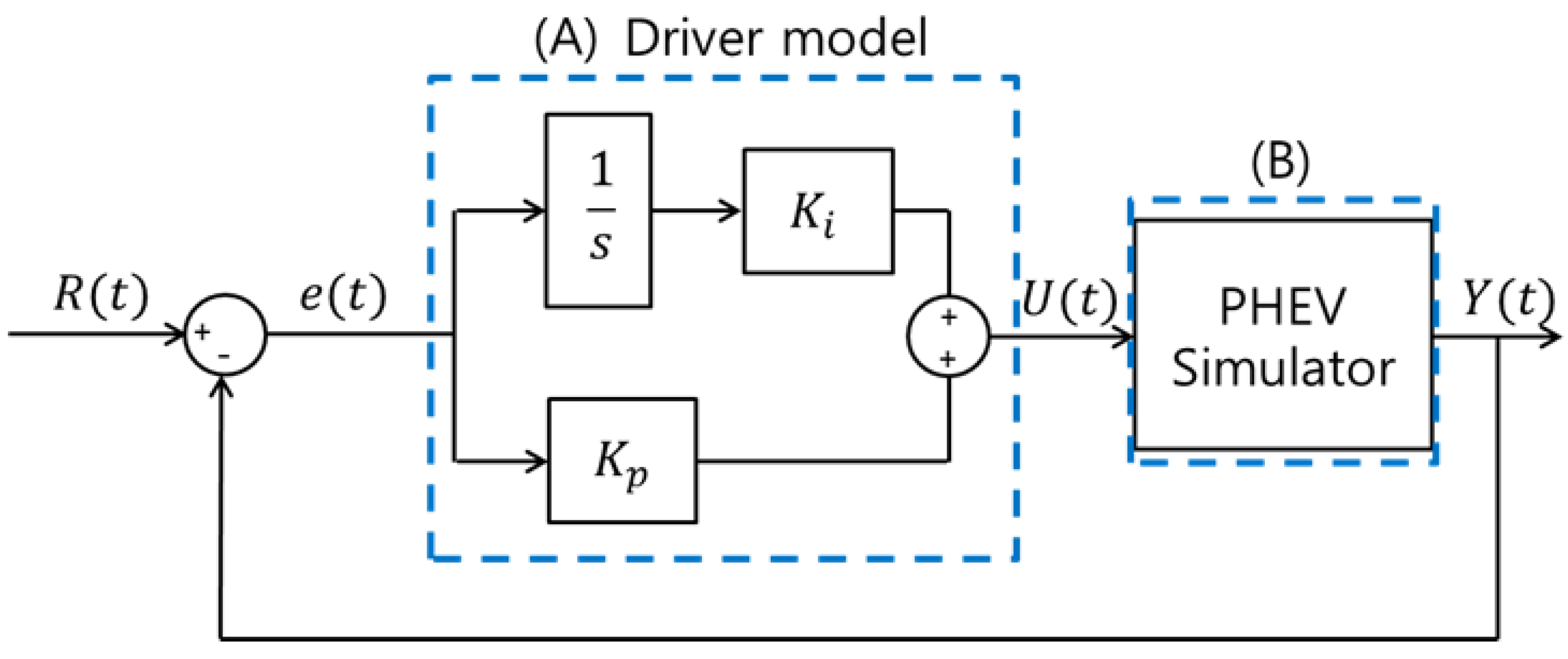
| Driver No. | Mean Value of | Number of Crossing between Ap and Bp | NCCP |
|---|---|---|---|
| Driver 1 | 0.0137 | 95 | 0.98916 |
| Driver 2 | 0.2059 | 659 | 0.99748 |
| Driver 3 | 0.0280 | 173 | 0.99102 |
| Driver 4 | 0.0315 | 185 | 0.99661 |
| Driver 5 | 0.1211 | 511 | 0.9972 |
| Driver 6 | 0.0593 | 297 | 0.99669 |
| Driver 7 | 0.0148 | 101 | 0.99249 |
| Driver 8 | 0.0726 | 379 | 0.99782 |
| Driver 9 | 0.0401 | 233 | 0.99663 |
| Driver 10 | 0.0625 | 325 | 0.99682 |
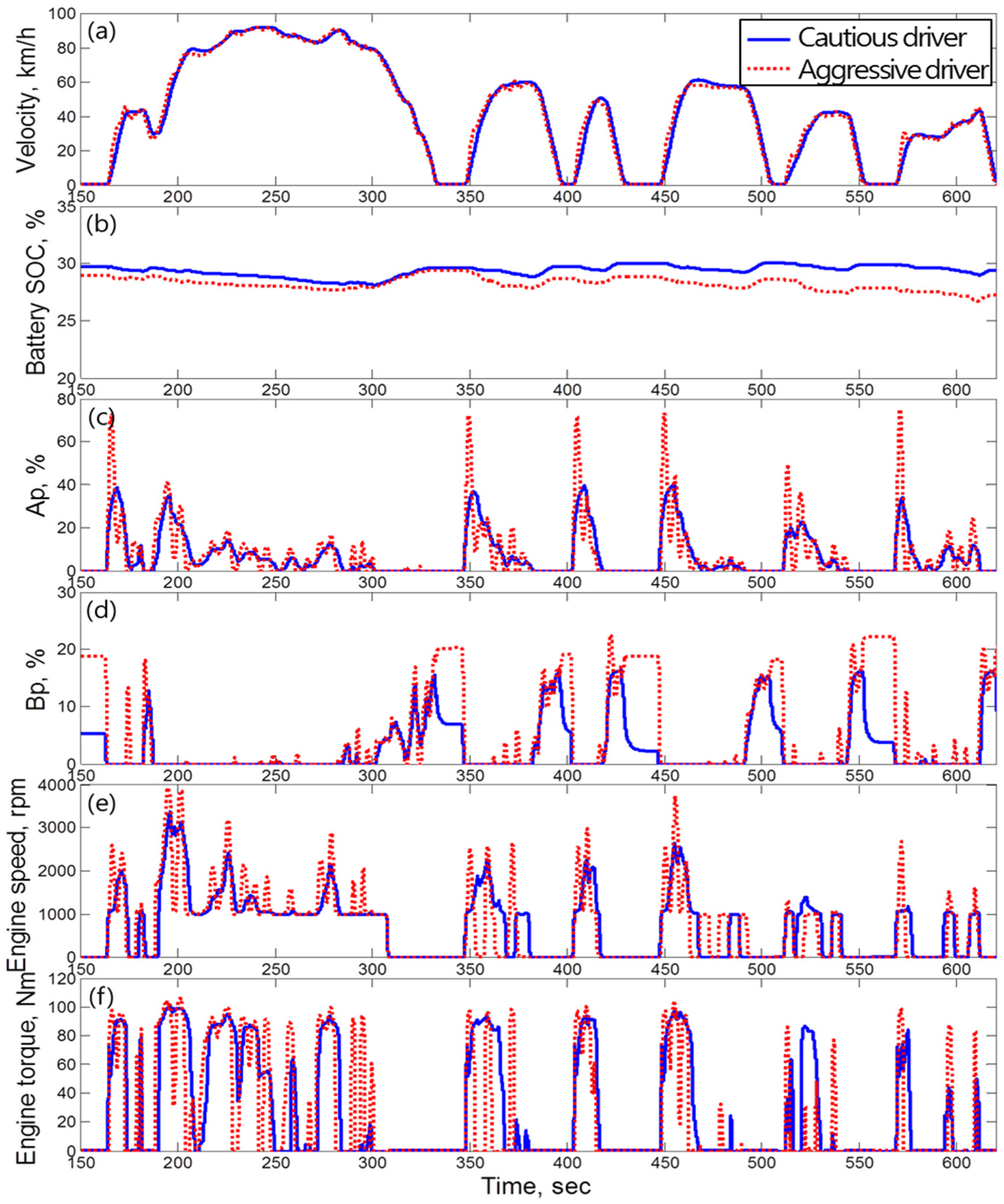
3.2. Fuel Economy Analysis According to Driver Characteristics
| Driver No. | Fuel Economy (km/L) |
|---|---|
| Driver 1 | 28.16 |
| Driver 7 | 27.17 |
| Driver 8 | 13.26 |
| Driver 9 | 16.03 |
| Driver 10 | 13.56 |
4. Categorizing Drivers with an Appropriate Algorithm
4.1. Driver Tendency Determination
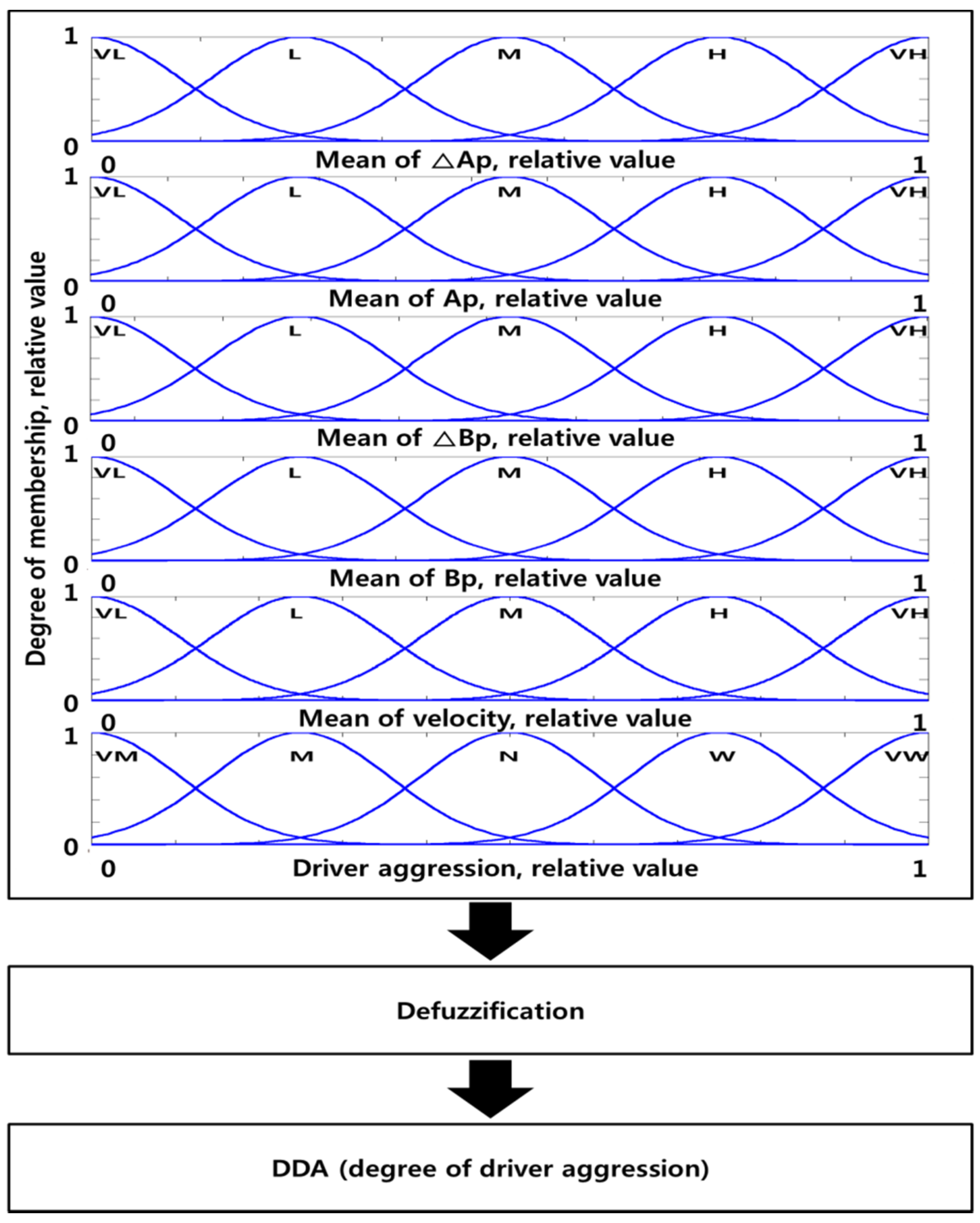
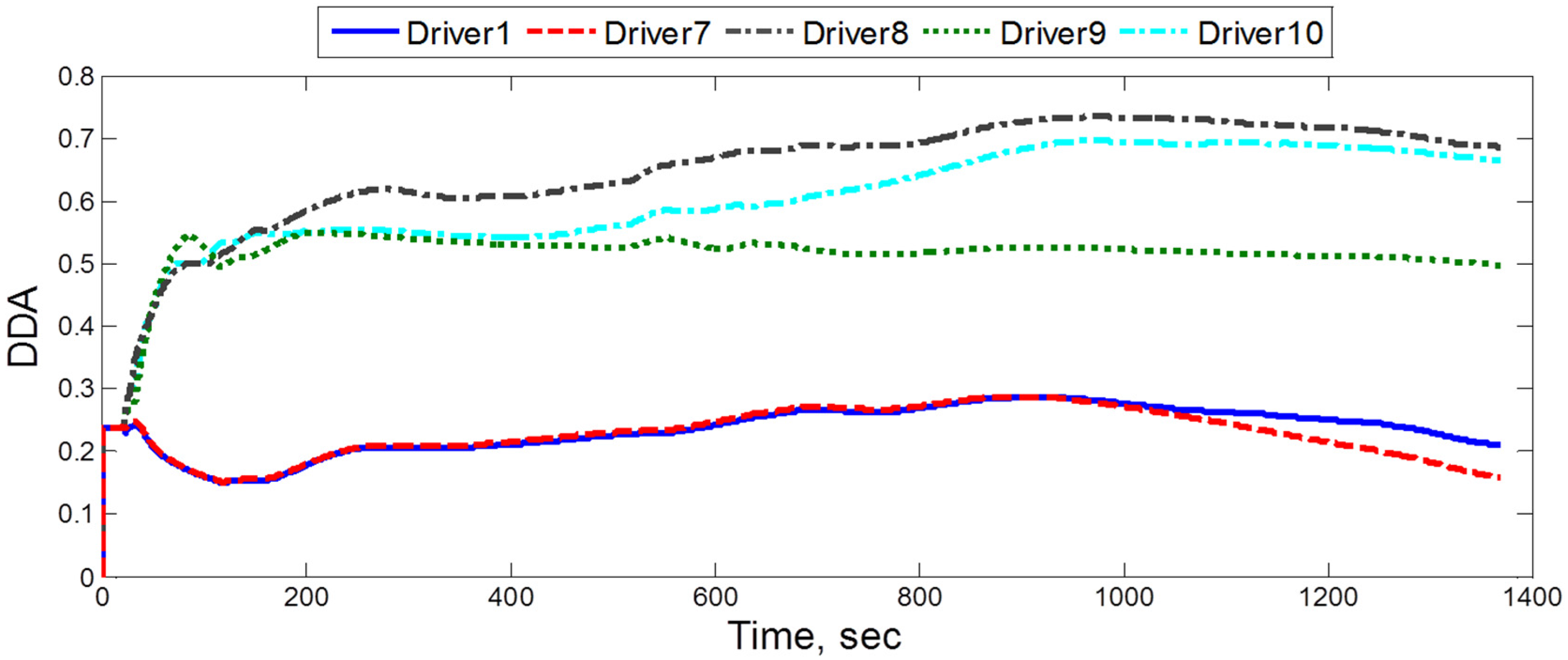
4.2. Engine on/off Control Algorithm Using DDA
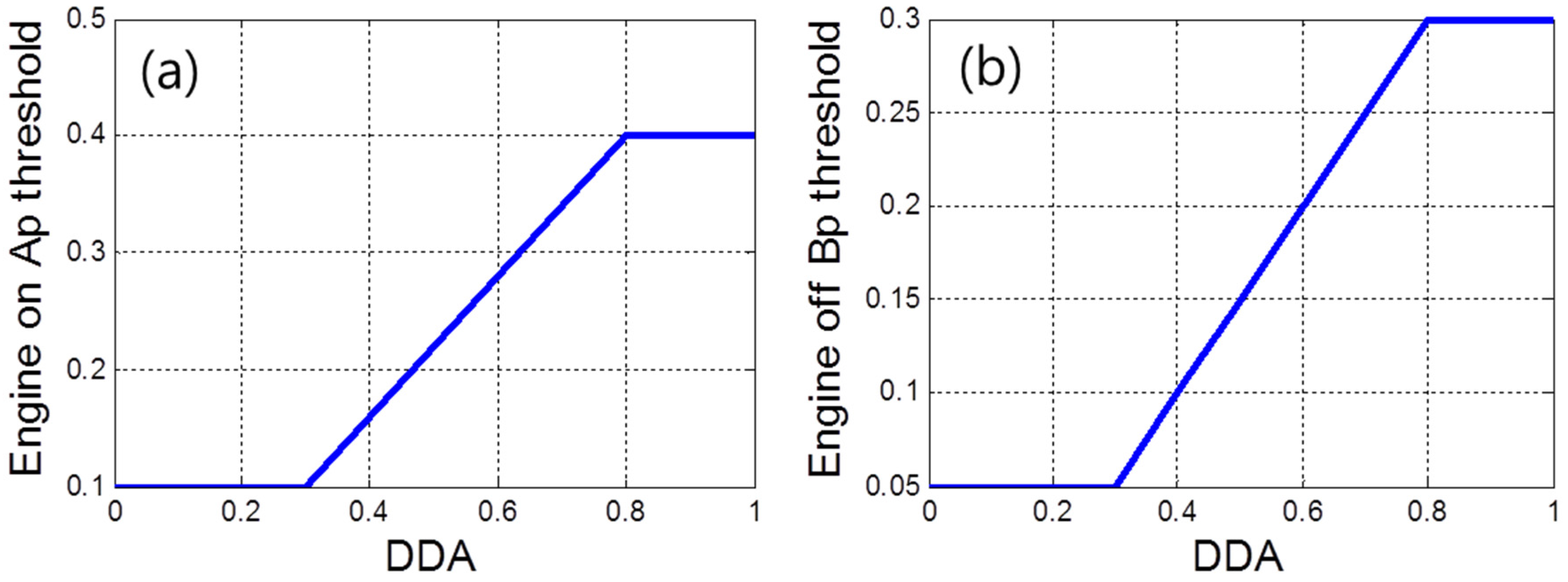


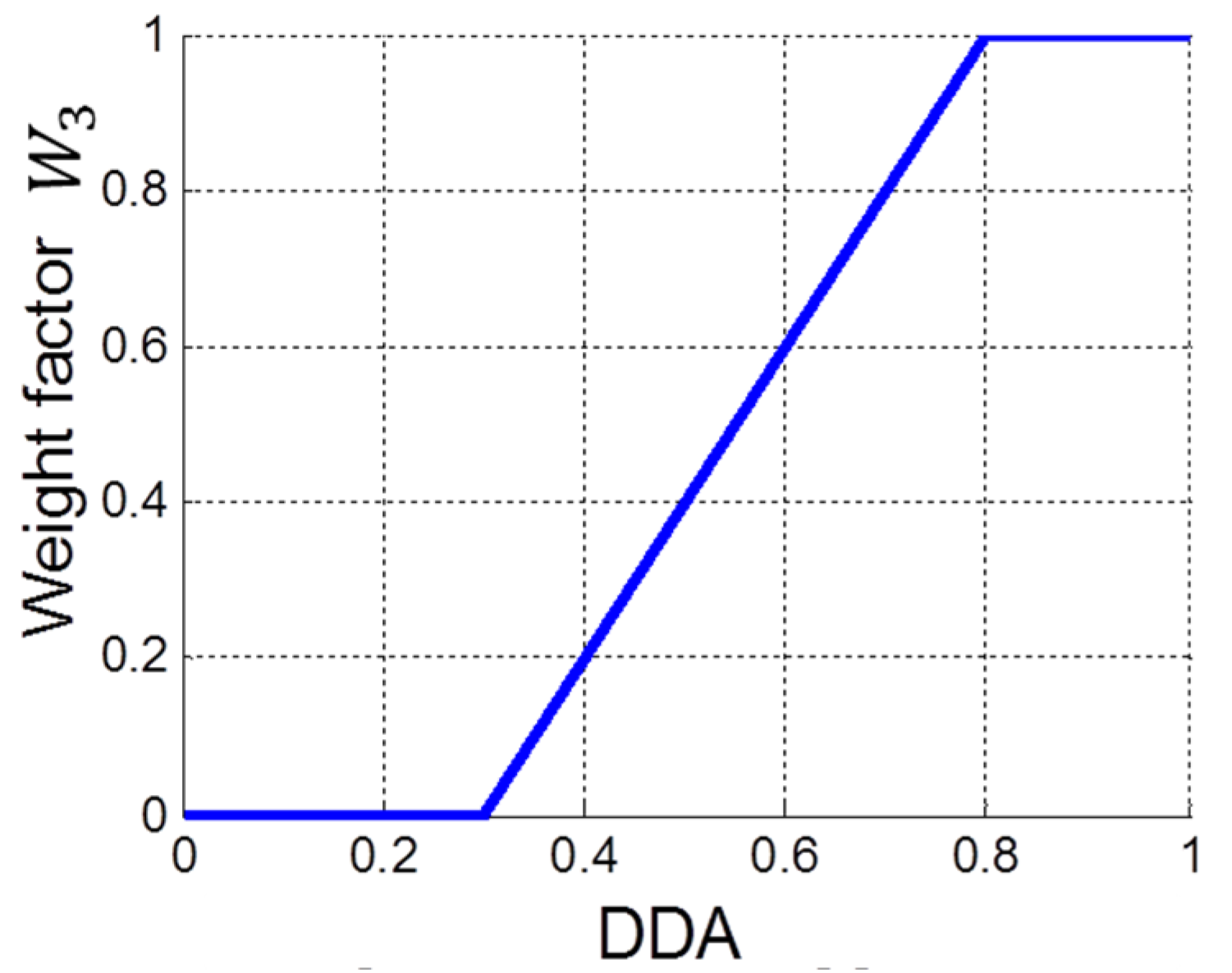
4.3. Battery Charging Power Control

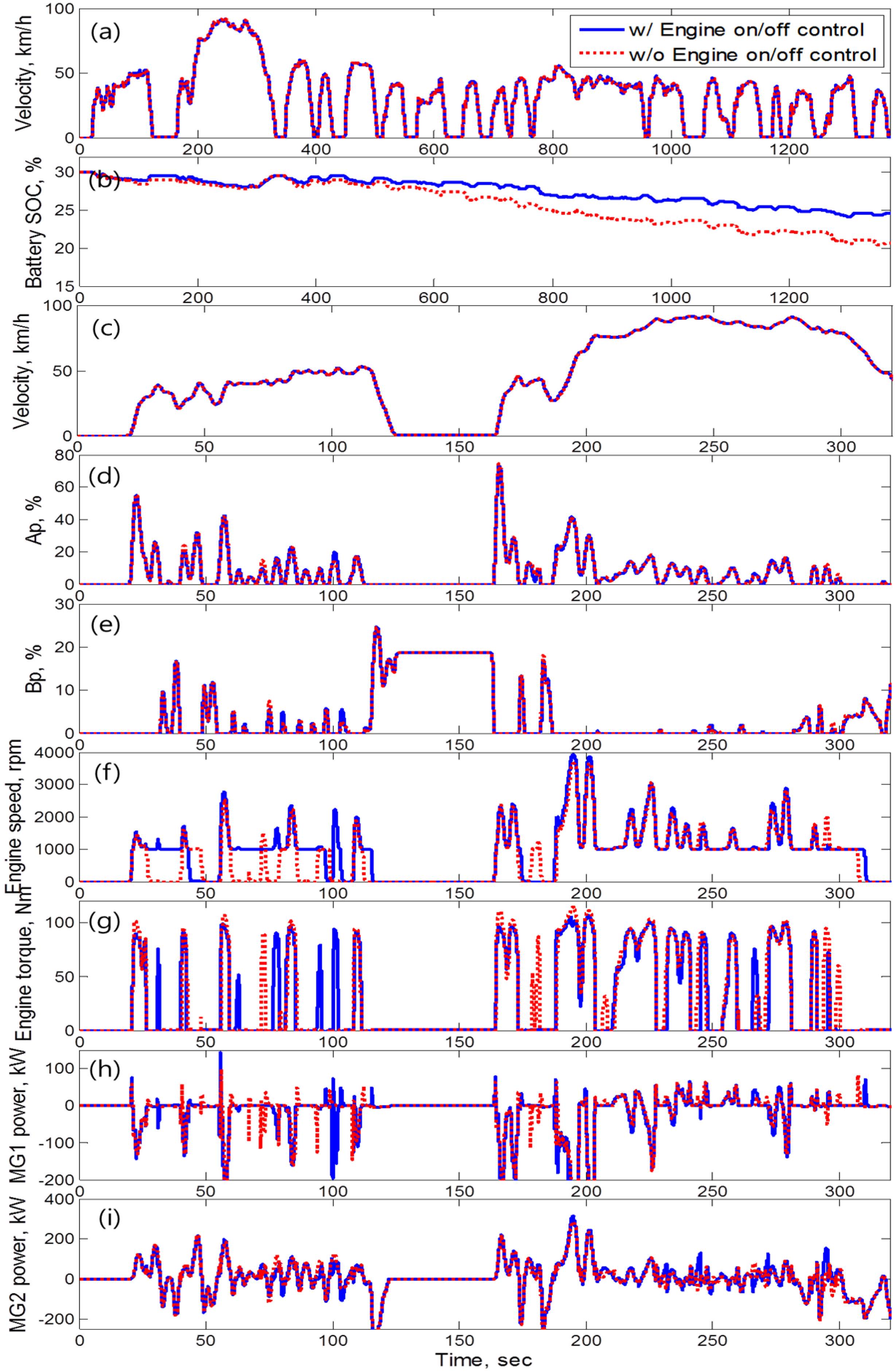
5. Performance Evaluation of the Control Algorithm Considering Driver Tendency for Fuel Economy Improvement
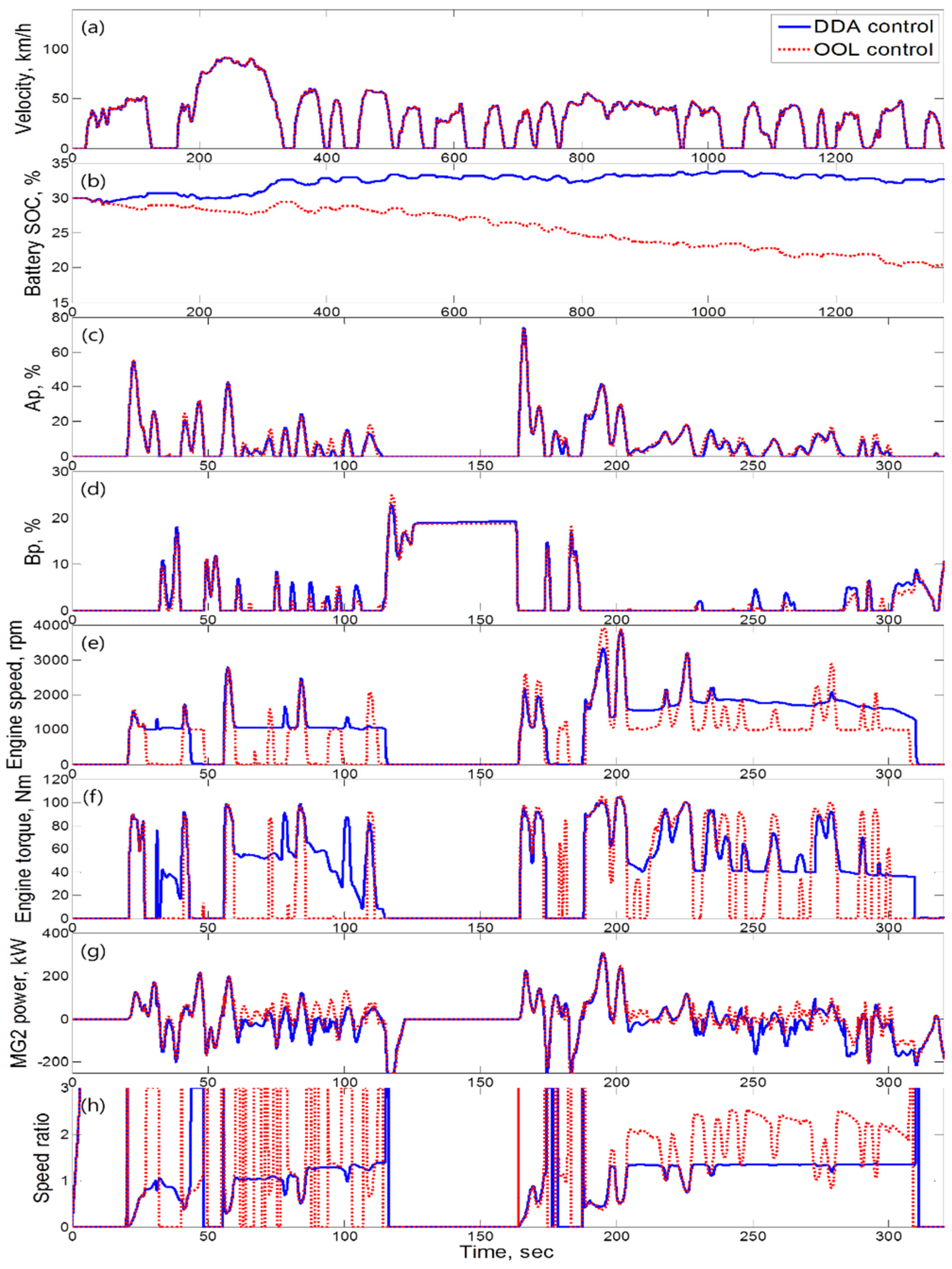
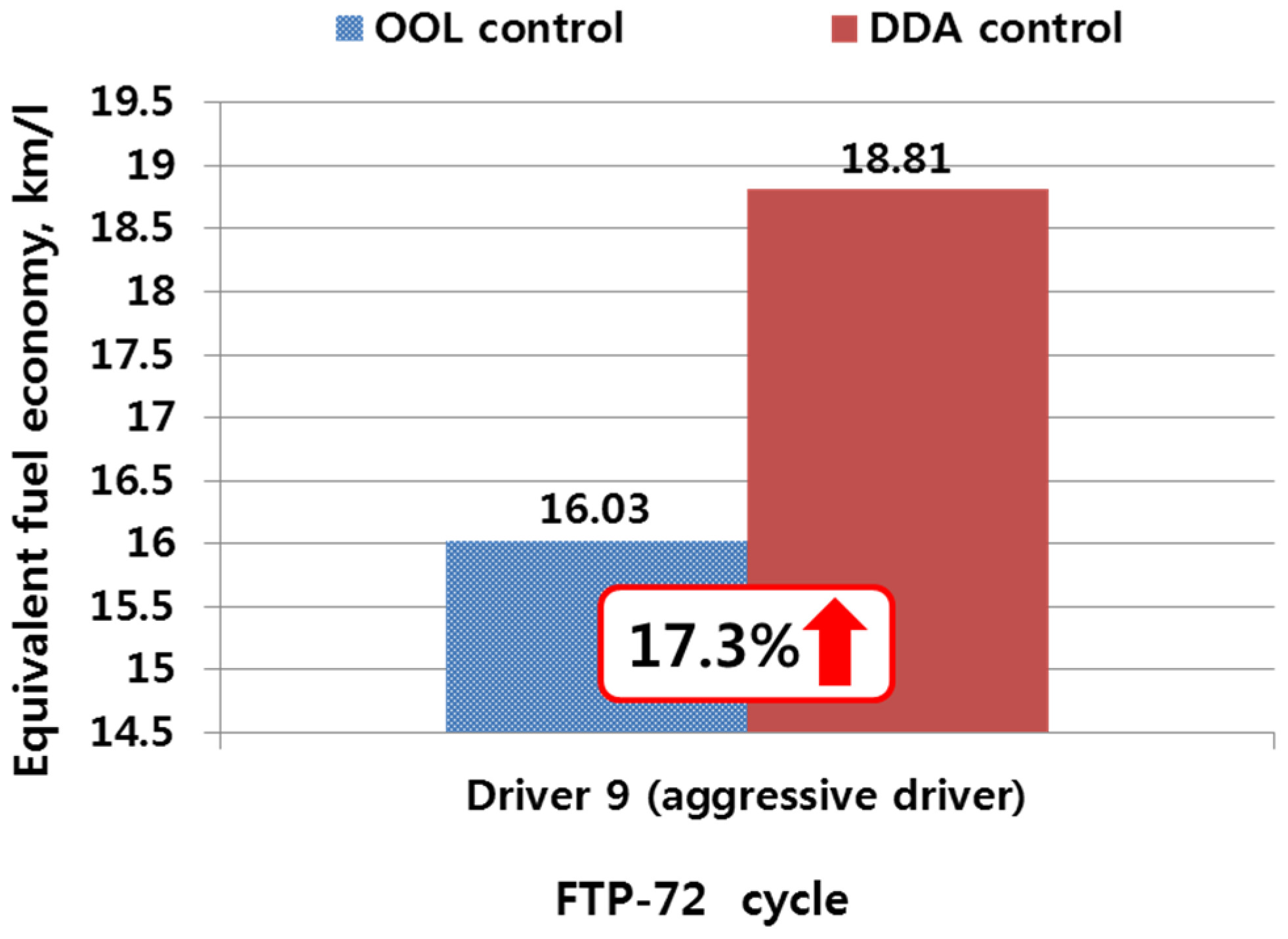
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- PwC. Shale Oil: The Next Energy Revolution. Available online: http://www.pwc.com/en_GX/gx/oil-gas-energy/publications/pdfs/pwc-shale-oil.pdf (accessed on 27 August 2015).
- Climate Works Fundation. Policies That Work: How Vehicle Standards and Fuel Fees Can Cut CO2 Emissions and Boost the Economy; Climate Works Foundation: San Francisco, CA, USA, 13 December 2012. [Google Scholar]
- Wirasingha, S.G.; Schofield, N.; Emadi, A. Plug-in Hybrid Electric Vehicle Developments in the US: Trends, Barriers, and Economic Feasibility. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Harbin, China, 3–5 September 2008; pp. 1–8.
- Murphey, Y.; Milton, R.; Kiliaris, L. Driver’s Style Classification Using Jerk Analysis. In Proceedings of the IEEE Computational Intelligence in Vehicles and Vehicular Systems, Nashville, TN, USA, 30 March–2 April 2009; pp. 23–28.
- Lee, S.; Choi, J.; Park, S.; Pi, J.; Shin, H.; Jeong, K.; Kim, H. Development of a Control Algorithm to Improve Fuel Economy for PHEV considering Driver Tendency. In Proceedings of the 10th International Conference on Ecological Vehicles and Renewable Energies, Monte-Carlo, Monaco, 31 March–2 April 2015.
- Kamichi, K.; Yamamoto, M.; Fushiki, S.; Yoda, T.; Kurachi, S.; Kojima, K. Development of Plug-In Hybrid System for Midsize Car; Society of Automotive Engineers: Detroit, MI, USA, 16 April 2012. [Google Scholar]
- Zhang, D.; Luo, Y.; Luo, W.; Bao, Y.; Peng, W.; Li, S. Investigation of Novel Ultraviolet Detecting System Used in Aero Magneto Ignition Energy Monitoring. In Proceedings of the 9th International Conference on Electronic Measurement & Instruments (ICEMI), Beijing, China, 16–19 August 2009; pp. 164–167.
- Kim, J.; Sim, H.; Oh, J. The Flexible EV/HEV and SOC Band Control Corresponding to Driving Mode, Driver’s Driving Style and Environmental Circumstances; Society of Automotive Engineers: Detroit, MI, USA, 16 April 2012. [Google Scholar]
- Takasaki, A.; Mizutani, T.; Kitagawa, K.; Yamahana, T.; Odaka, K.; Kuzuya, T.; Mizuno, Y.; Nishikawa, Y. Development of New Hybrid Transmission for 2009 Prius. In Proceedings of the International Battery, Hybrid Fuel Cell Electric Vehicle Symposium (EVS24), Stavanger, Norway, 1 June 2009.
- Matsubara, T.; Yaguchi, H.; Takaoka, T.; Jinno, K. Development of New Hybrid System for Compact Class Vehicles; Society of Automotive Engineers: Detroit, MI, USA, 4 April 2009. [Google Scholar]
- Toyota Prius Plug-In Hybrid. Available online: http://en.wikipedia.org/wiki/Toyota_Prius_Plug-in_Hybrid (accessed on 27 August 2015).
- Li, S.; Ke, B. Study of Battery Modeling using Mathematical and Circuit Oriented Approaches. In Proceedings of the IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 24–29 July 2011; pp. 1–8.
- Ma, C.; Kang, J.; Choi, W.; Song, M.; Ji, J.; Kim, H. Comparative Study on Power Characteristics and Control Strategies for Plug-in Hybrid Electric Vehicle. Int. J. Automot. Technol. 2012, 12, 505–516. [Google Scholar] [CrossRef]
- Lee, S.; Choi, J.; Park, S.; Pi, J.; Shin, H.; Jeong, K.; Kim, H. Control Strategy to Improve Fuel Economy for Plug-in Hybrid Electric Vehicle considering Degree of Driver Aggression. In Proceedings of the 28th International Electric Vehicle Symposium and Exhibition, Ilsan, Korea, 3–6 May 2015.
- Lee, S.; Park, T.; Son, J.; Won, K.; Lee, H. Development of a Driver Model for the Analysis of Fuel Economy; Korea Society of Automotive Engineers: Ilsan, Korea, 21 November 2012; pp. 2284–2292. [Google Scholar]
- Meng, Y.; Jennings, M.; Tsou, P.; Brigham, D.; Bell, D.; Soto, C. Test Correlation Framework for Hybrid Electric Vehicle System Mode; Society of Automotive Engineers: Detroit, MI, USA, 12 April 2011. [Google Scholar]
- U.S. Department of Energy. Electric and Hybrid Vehicle Research, Development, and Demonstration Program; Petroleum-Equivalent Fuel Economy Calculation; U.S. Department of Energy: Washington, DC, USA, 12 June 2000.
- Fesefeldt, T.; Müller, S. Optimization and Comparison of Quick and Hybrid Start. Society of Automotive Engineers: Detroit, MI, USA, 20 April 2009. [Google Scholar]
- Kang, J.; Choi, W.; Kim, H. Development of a control strategy based on the transmission efficiency with mechanical loss for a dual mode power split-type hybrid electric vehicle. Int. J. Automot. Technol. 2012, 13, 825–833. [Google Scholar] [CrossRef]
- Liu, J.; Peng, H. Control Optimization for a Power-Split Hybrid Vehicle. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006.
- Kim, N.; Carlson, R.; Jehlik, F.; Rousseau, A. Tahoe HEV Model Development in PSAT; Society of Automotive Engineers: Detroit, MI, USA, 2009. [Google Scholar]
- Ahn, K.; Papalambros, P.Y. Engine optimal operation lines for power-split hybrid electric vehicles. J. Automob. Eng. 2009, 223, 1149–1162. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Choi, J.; Jeong, K.; Kim, H. A Study of Fuel Economy Improvement in a Plug-in Hybrid Electric Vehicle using Engine on/off and Battery Charging Power Control Based on Driver Characteristics. Energies 2015, 8, 10106-10126. https://doi.org/10.3390/en80910106
Lee S, Choi J, Jeong K, Kim H. A Study of Fuel Economy Improvement in a Plug-in Hybrid Electric Vehicle using Engine on/off and Battery Charging Power Control Based on Driver Characteristics. Energies. 2015; 8(9):10106-10126. https://doi.org/10.3390/en80910106
Chicago/Turabian StyleLee, Seulgi, Jingyu Choi, Kiyun Jeong, and Hyunsoo Kim. 2015. "A Study of Fuel Economy Improvement in a Plug-in Hybrid Electric Vehicle using Engine on/off and Battery Charging Power Control Based on Driver Characteristics" Energies 8, no. 9: 10106-10126. https://doi.org/10.3390/en80910106






