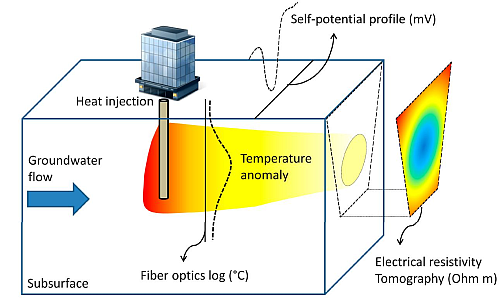
Geophysical Methods for Monitoring Temperature Changes in Shallow Low Enthalpy Geothermal Systems
Abstract
:1. Introduction

2. Electrical Resistivity Tomography
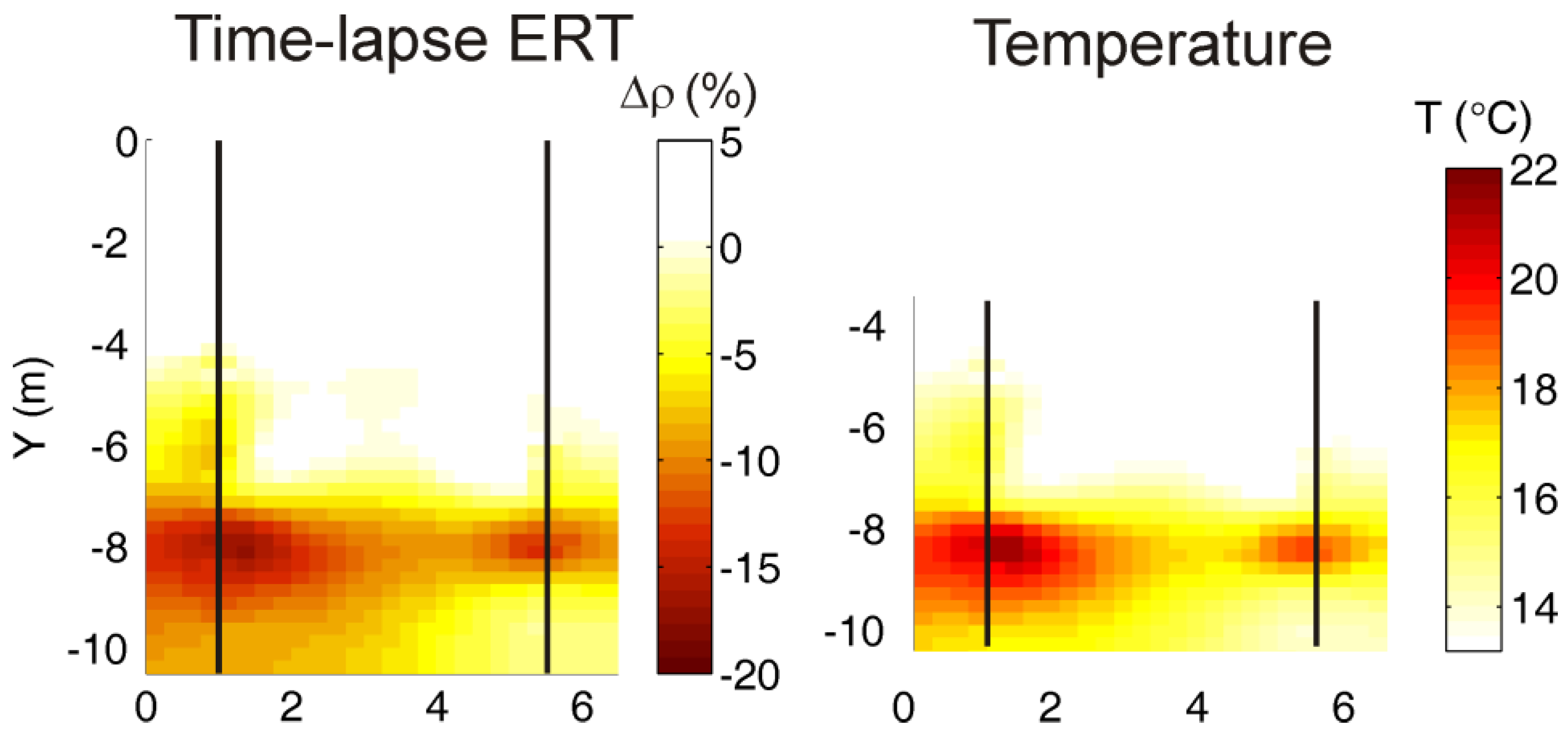
2.1. Time-Lapse ERT
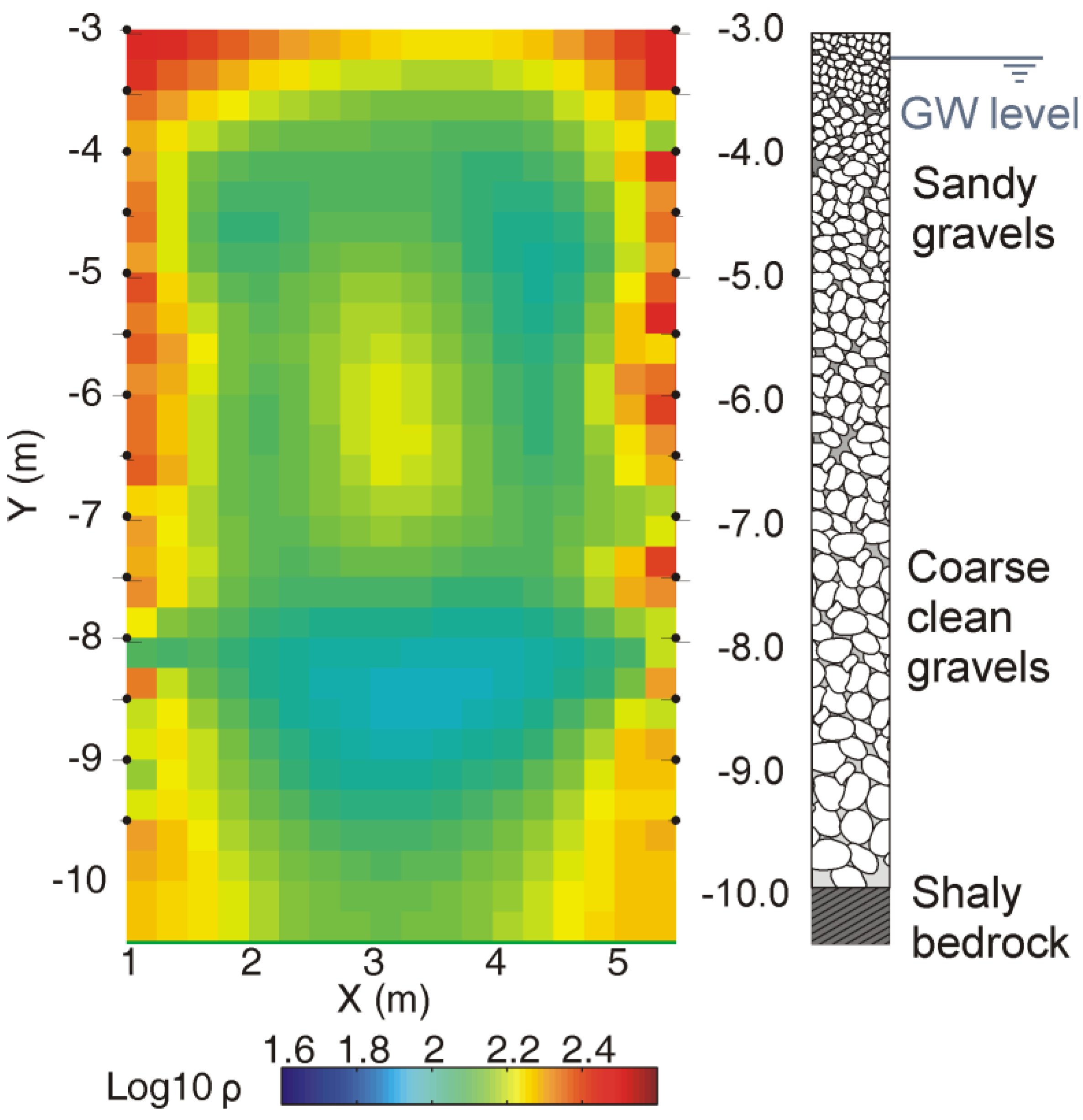
2.2. Petrophysical Considerations
3. Self-Potential Method
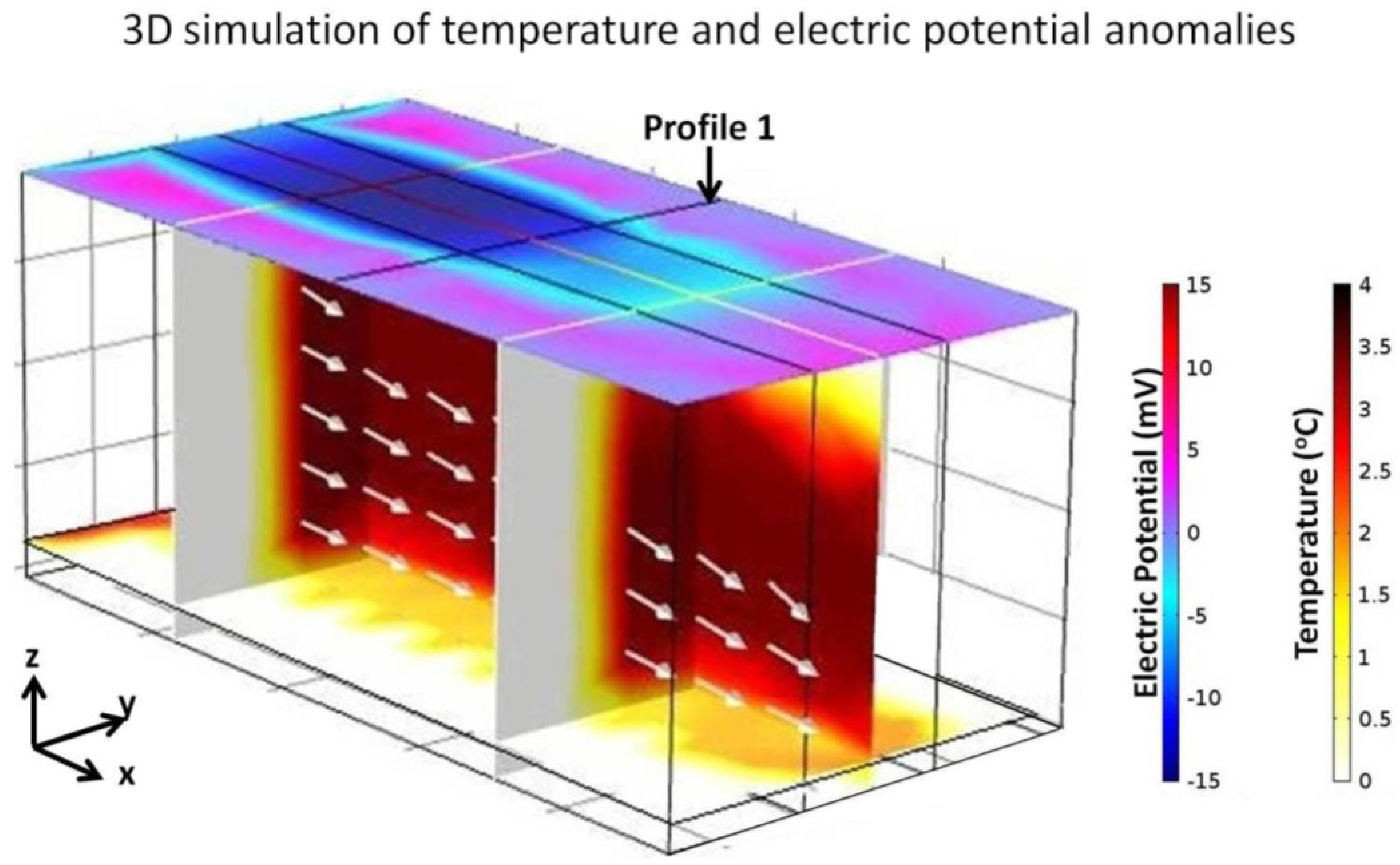

4. Distributed Temperature Sensing
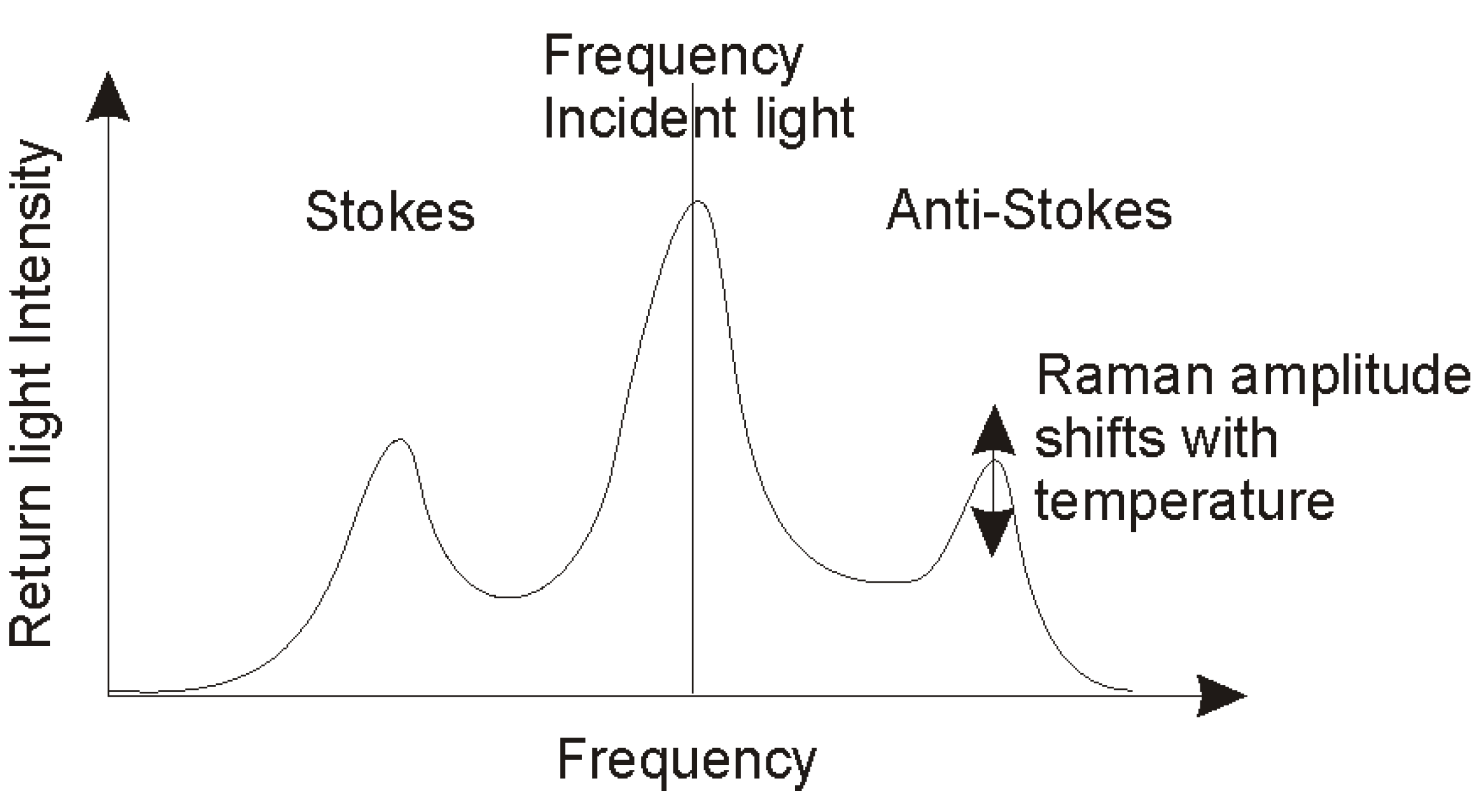
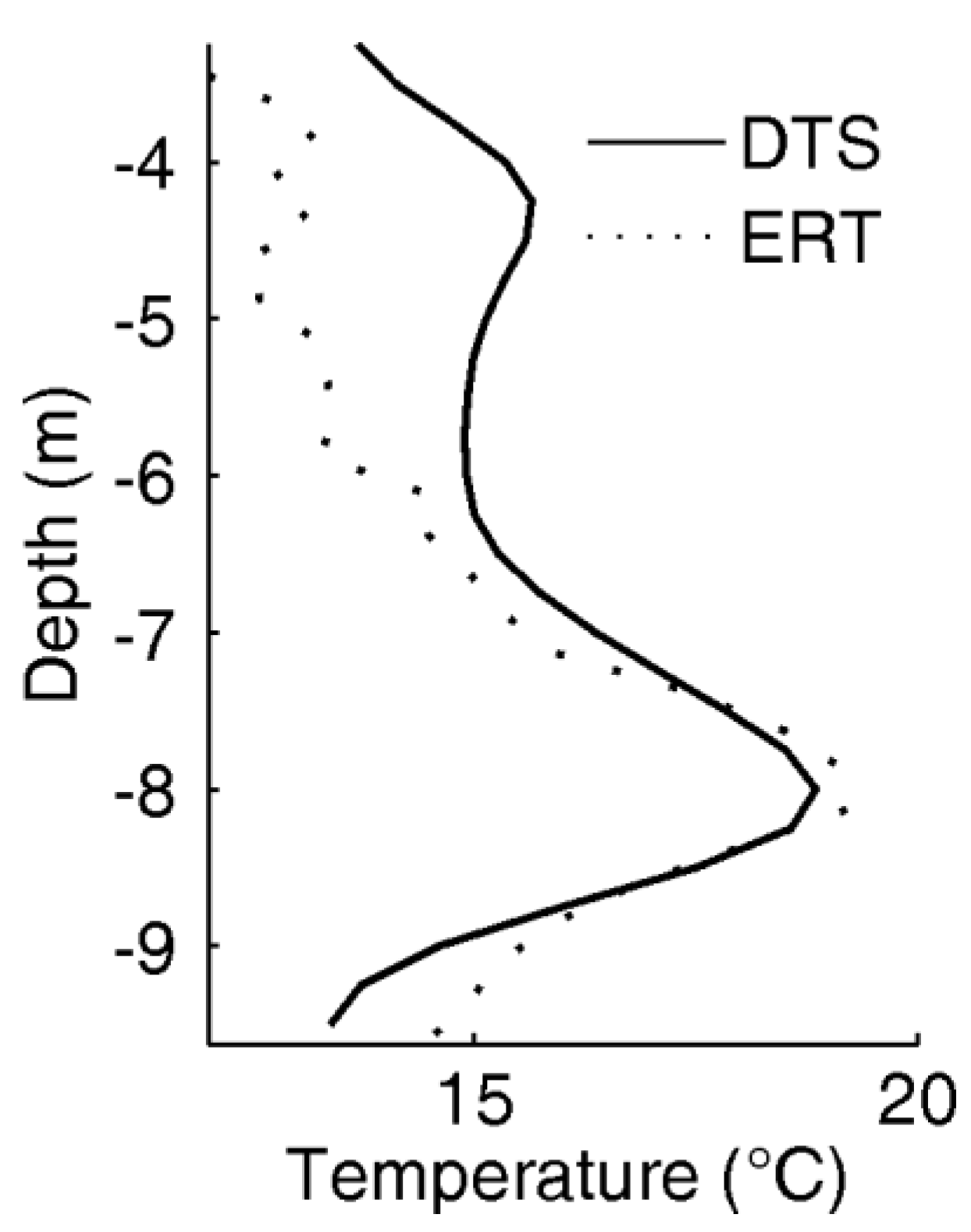
5. Previous Works
5.1. Using ERT to Monitor Temperature Changes
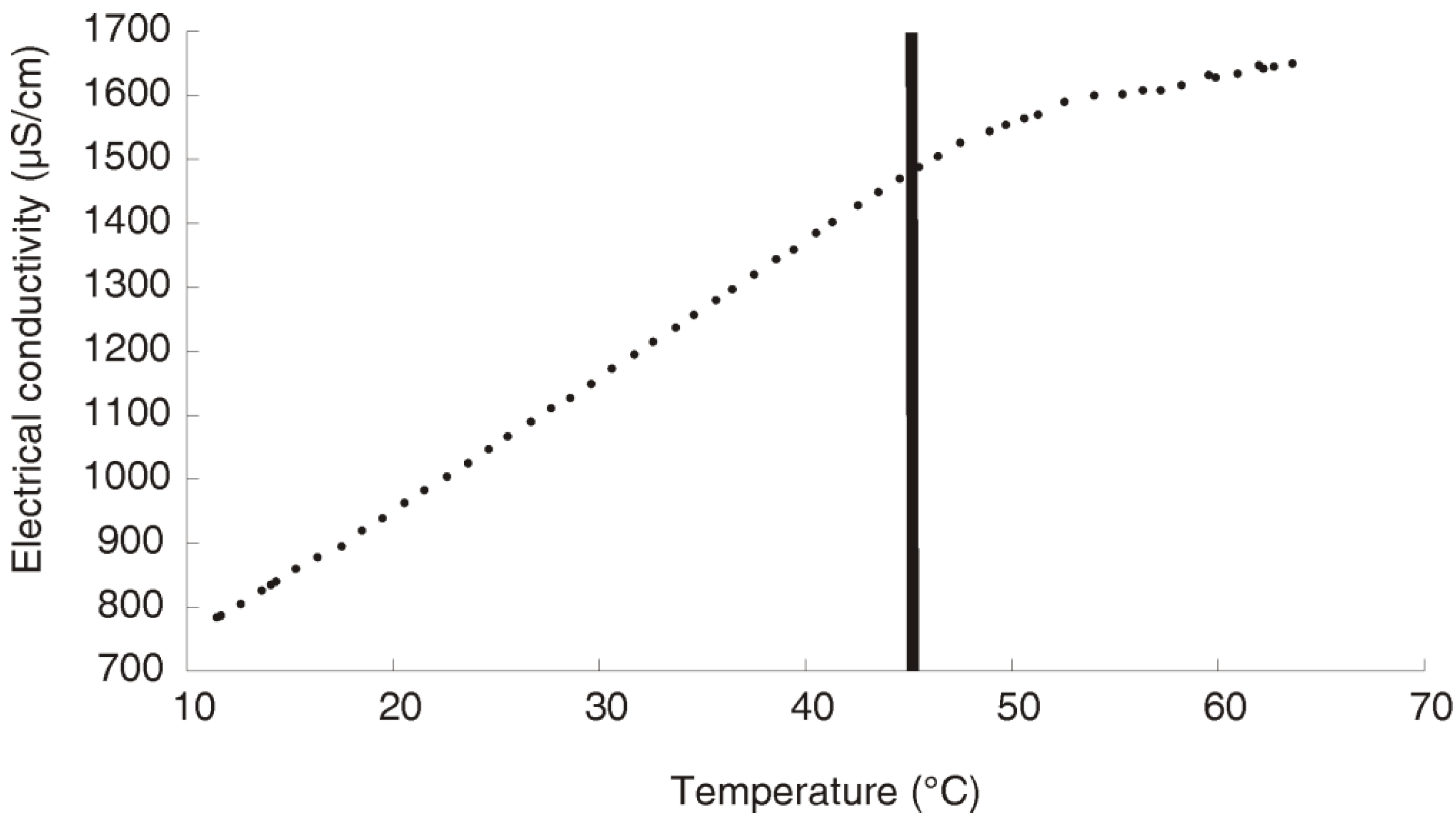
5.2. Petrophysical Considerations Regarding Electrical Conductivity

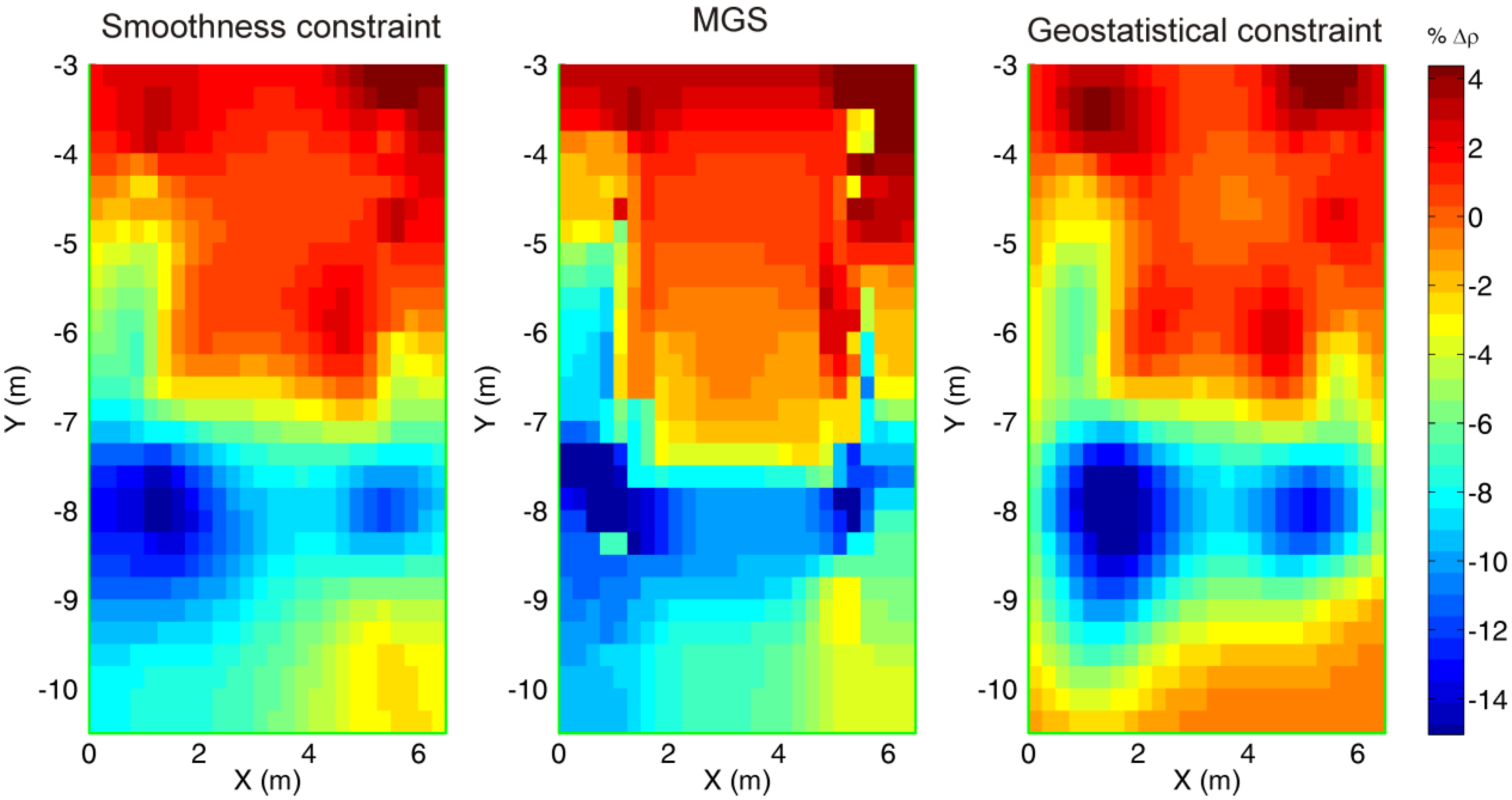
5.3. ERT Survey Design
5.4. Sensitivity of Self-Potential Signals to Temperature
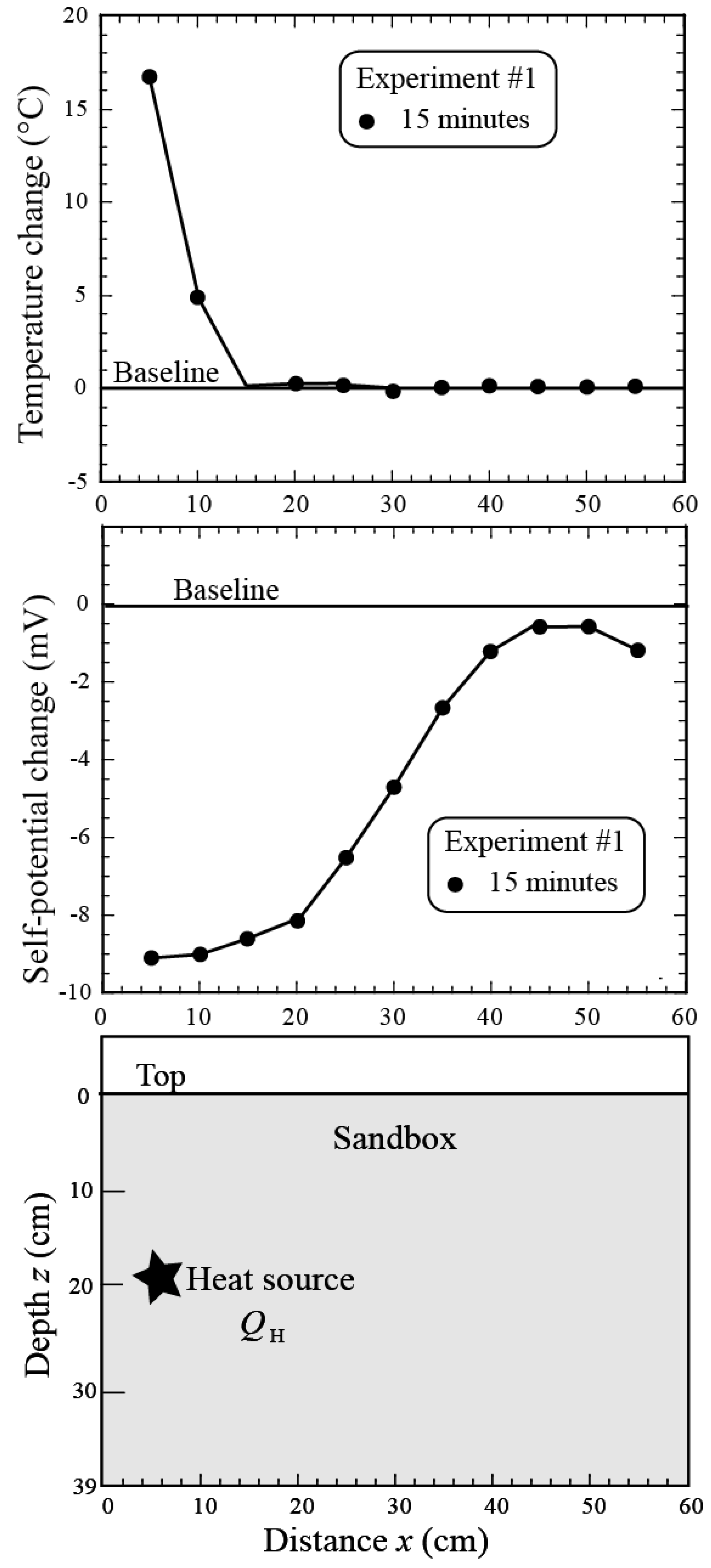

5.5. Using DTS to Measure Temperature
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bayer, P.; Rybach, L.; Blum, P.; Brauchler, R. Review on life cycle environmental effects of geothermal power generation. Renew. Sustain. Energy Rev. 2013, 26, 446–463. [Google Scholar] [CrossRef]
- Saner, D.; Juraske, R.; Kübert, M.; Blum, P.; Hellweg, S.; Bayer, P. Is it only CO2 that matters? A life cycle perspective on shallow geothermal systems. Renew. Sustain. Energy Rev. 2010, 14, 1798–1813. [Google Scholar] [CrossRef]
- Andersson, O. ATES utilization in Sweden—An overview. In Proceedings of the MEGASTOCK’97 7th International Conference on Thermal Energy Storage, Sapporo, Japan, 18–20 June 1997; pp. 925–930.
- Vanhoudt, D.; Desmedt, J.; van Bael, J.; Robeyn, N.; Hoes, H. An aquifer thermal storage system in a Belgian hospital: Long-term experimental evaluation of energy and cost savings. Energy Build. 2011, 43, 3657–3665. [Google Scholar] [CrossRef]
- Blum, P.; Campillo, G.; Kölbel, T. Techno-economic and spatial analysis of vertical ground source heat pump systems in Germany. Energy 2011, 36, 3002–3011. [Google Scholar] [CrossRef]
- b>Haehnlein, S.; Bayer, P.; Ferguson, G.; Blum, P. Sustainability and policy for the thermal use of shallow geothermal energy. Energy Policy 2013, 59, 914–925. [Google Scholar] [CrossRef]
- Lund, J.W. Direct utilization of geothermal energy. Energies 2010, 3, 1443–1471. [Google Scholar] [CrossRef]
- European Commission. Horizon 2020: The EU Framework Programme for Research and Innovation. Secure, Clean and Efficient Energy. Available online: http://ec.europa.eu/programmes/horizon2020/en/h2020-section/secure-clean-and-efficient-energy (accessed on 11 August 2014).
- Lund, J.W.; Freeston, D.H.; Boyd, T.L. Direct application of geothermal energy: 2005 worldwide review. Geothermics 2005, 34, 691–727. [Google Scholar] [CrossRef]
- Allen, A.; Milenic, D. Low-enthalpy geothermal energy resources from groundwater in fluvioglacial gravels of buried valleys. Appl. Energy 2003, 74, 9–19. [Google Scholar] [CrossRef]
- b>Haehnlein, S.; Bayer, P.; Blum, P. International legal status of the use of shallow geothermal energy. Renew. Sustain. Energy Rev. 2010, 14, 2611–2625. [Google Scholar] [CrossRef]
- Mattsson, N.; Steinmann, G.; Laloui, L. Advanced compact device for the in situ determination of geothermal characteristics of soils. Energy Build. 2008, 40, 1344–1352. [Google Scholar] [CrossRef]
- Raymond, J.; Therrien, R.; Gosselin, L.; Lefebvre, R. A review of thermal response test analysis using pumping test concepts. Groundwater 2011, 49, 932–945. [Google Scholar] [CrossRef]
- Haffen, S.; Geraud, Y.; Diraison, M.; Dezayes, C. Determination of fluid-flow zones in a geothermal sandstone reservoir using thermal conductivity and temperature logs. Geothermics 2013, 46, 32–41. [Google Scholar] [CrossRef]
- Busby, J.; Lewis, M.; Reeves, H.; Lawley, R. Initial geological considerations before installing ground source heat pump systems. Q. J. Eng. Geol. Hydrogeol. 2009, 42, 295–306. [Google Scholar]
- De Paly, M.; Hecht-Méndez, J.; Beck, M.; Blum, P.; Zell, A.; Bayer, P. Optimization of energy extraction for closed shallow geothermal systems using linear programming. Geothermics 2012, 43, 57–65. [Google Scholar]
- Liang, J.; Yang, Q.; Liu, L.; Li, X. Modeling and performance evaluation of shallow ground water heat pumps in Beijing plain, China. Energy Build. 2011, 43, 3131–3138. [Google Scholar] [CrossRef]
- Lo Russo, S.; Civita, M.V. Open-loop groundwater heat pumps development for large buildings: A case study. Geothermics 2009, 38, 335–345. [Google Scholar]
- Molson, J.W.; Frind, E.O.; Palmer, C.D. Thermal energy storage in an unconfined aquifer: 2. Model development, validation and application. Water Resour. Res. 1992, 28, 2857–2867. [Google Scholar]
- Palmer, C.D.; Blowes, D.W.; Frind, E.O.; Molson, J.W. Thermal energy storage in an unconfined aquifer: 1. Field injection experiment. Water Resour. Res. 1992, 28, 2845–2866. [Google Scholar] [CrossRef]
- Warner, D.L.; Algan, U. Thermal impact of residential ground-water heat pumps. Groundwater 1984, 22, 6–12. [Google Scholar] [CrossRef]
- Bonte, M. Impacts of Shallow Geothermal Energy Storage on Groundwater Quality—A Hydrochemical and Hydromicrobial Study of the Effects of Ground Source Heat Pumps and Aquifer Thermal Storage. Ph.D. Thesis, VU University Amsterdam, Amsterdam, The Netherlands, 2013. [Google Scholar]
- Garnier, F. Contribution à l’évaluation Biogéochimique des Impacts liés à l’exploitation Géothermique des Aquifères Superficiels: Expérimentations et Simulations à l’échelle d’un Pilote et d’installations Réelles. Ph.D. Thesis, Bureau de Recherche Géologique et Minière¡ªInstitut des Sciences de la Terre d’Orléans, Université d’Orléans, Orléans, France, 2012. [Google Scholar]
- Jesuβek, A.; Grandel, S.; Dahmke, A. Impacts of subsurface heat storage on aquifer hydrogeochemistry. Environ. Earth Sci. 2013, 69, 1999–2012. [Google Scholar]
- Brielmann, H.; Griebler, C.; Schmidt, S.I.; Michel, R.; Lueders, T. Effects of thermal energy discharge on shallow groundwater ecosystems. FEMS Microbiol. Ecol. 2009, 68, 273–286. [Google Scholar] [CrossRef] [PubMed]
- Lerm, S.; Westphal, A.; Miethling-Graff, R.; Alawi, M.; Seibt, A.; Wolfgramm, M.; Würdemann, H. Thermal effects on microbial composition and microbiologically induced corrosion and mineral precipitation affecting operation of a geothermal plant in a deep saline aquifer. Extremophiles 2013, 17, 311–327. [Google Scholar] [CrossRef] [PubMed]
- Vetter, A.; Mangelsdorf, K.; Wolfgramm, M.; Rauppach, K.; Schettler, G.; Vieth-Hillebrand, A. Variations in fluid chemistry and membrane phospholipid fatty acid composition of the bacterial community in a cold storage groundwater system during clogging events. Appl. Geochem. 2012, 27, 1278–1290. [Google Scholar] [CrossRef]
- Lo Russo, S.; Gnavia, L.; Roccia, E.; Taddia, G.; Verda, V. Groundwater Heat Pump (GWHP) system modeling and Thermal Affected Zone (TAZ) prediction reliability: Influence of temporal variations in flow discharge and injection temperature. Geothermics 2014, 51, 103–112. [Google Scholar]
- Lo Russo, S.; Taddia, G.; Verda, V. Development of the thermally affected zone (TAZ) around a groundwater heat pump (GWHP) system: A sensitivity analysis. Geothermics 2012, 43, 66–74. [Google Scholar]
- Gao, Q.; Zhou, X.-Z.; Jiang, Y.; Chen, X.-L.; Yan, Y.-Y. Numerical simulation of the thermal interaction between pumping and injecting well groups. Appl. Therm. Eng. 2013, 51, 10–19. [Google Scholar] [CrossRef]
- Milnes, E.; Perrochet, P. Assessing the impact of thermal feedback and recycling in open-loop groundwater heat pump (GWHP) systems: A complementary design tool. Hydrogeol. J. 2013, 21, 505–514. [Google Scholar]
- Anderson, M.P. Heat as a ground water tracer. Groundwater 2005, 43, 951–968. [Google Scholar] [CrossRef]
- Wikdemeersch, S.; Jamin, P.; Orban, P.; Hermans, T.; Nguyen, F.; Brouyère, S.; Dassargues, A. Coupling heat and chemical tracer experiments for estimating heat transfer parameters in shallow alluvial aquifers. J. Contam. Hydrol. 2014. submitted. [Google Scholar]
- Saar, M.O. Review: Geothermal heat as a tracer of large-scale groundwater flow and as a means to determine permeability fields. Hydrogeol. J. 2011, 19, 31–52. [Google Scholar] [CrossRef]
- Giambastiani, B.M.S.; Colombanii, N.; Mastrocicco, M. Limitation of using heat as a groundwater tracer to define aquifer properties: Experiment in a large tank model. Environ. Earth Sci. 2013, 70, 719–728. [Google Scholar] [CrossRef]
- Vandenbohede, A.; Hermans, T.; Nguyen, F.; Lebbe, L. Shallow heat injection and storage experiment: Heat transport simulation and sensitivity analysis. J. Hydrol. 2011, 409, 262–272. [Google Scholar] [CrossRef]
- Vandenbohede, A.; Louwyck, A.; Lebbe, L. Conservative solute versus heat transport in porous media during push-pull tests. Transp. Porous Med. 2009, 76, 265–287. [Google Scholar] [CrossRef]
- Brouyère, S. Etude et Modélisation du Transport et du Piégeage des Solutés en Milieu Souterrain Variablement Saturé. Ph.D. Thesis, University of Liege, Liege, Belgium, 2001. [Google Scholar]
- b>Jardani, A.; Revil, A.; Dupont, J.P. Stochastic joint inversion of hydrogeophysical data for salt tracer test monitoring and hydraulic conductivity imaging. Adv. Water Resour. 2013, 52, 62–77. [Google Scholar] [CrossRef]
- b>Hayley, K.; Bentley, L.R.; Gharibi, M.; Nightingale, M. Low temperature dependence of electrical resistivity: Implications for near surface geophysical monitoring. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Revil, A.; Cathles, L.M.; Losh, S.; Nunn, J.A. Electrical conductivity in shaly sands with geophysical applications. J. Geophys. Res. 1998, 103, 23925–23936. [Google Scholar] [CrossRef]
- Waxman, M.H.; Smits, L.J.M. Electrical conductivities in oil-bearing shaly sands. Soc. Pet. Eng. J. 1968, 8, 107–122. [Google Scholar] [CrossRef]
- Vereecken, H.; Binley, A.; Cassiani, G.; Revil, A.; Titov, K. Applied Hydrogeophysics. NATO Science Series: IV Earth and Environmental Sciences; Springer: Berlin, Germany, 2006. [Google Scholar]
- Hermans, T.; Vandenbohede, A.; Lebbe, L.; Martin, R.; Kemna, A.; Beaujean, J.; Nguyen, F. Imaging artificial salt water infiltration using electrical resistivity tomography constrained by geostatistical data. J. Hydrol. 2012, 438–439, 168–180. [Google Scholar]
- Nguyen, F.; Kemna, A.; Antonsson, A.; Engesgaard, P.; Kuras, O.; Ogilvy, R.; Gisbert, J.; Jorreto, S.; Pulido-Bosch, A. Characterization of seawater intrusion using 2D electrical imaging. Near Surf. Geophys. 2009, 7, 377–390. [Google Scholar] [CrossRef]
- Binley, A.; Winship, P.; West, L.J.; Pokar, M.; Middleton, R. Seasonal variation of moisture content in unsaturated sandstone inferred from borehole radar and resistivity profiles. J. Hydrol. 2002, 267, 160–172. [Google Scholar] [CrossRef]
- Chambers, J.E.; Gunn, D.A.; Wilkinson, P.B.; Meldrum, P.I.; Haslam, E.; Holyoake, S.; Kirkham, M.; Kuras, O.; Merrit, A.; Wragg, J. 4D electrical resistivity tomography monitoring of soil moisture dynamics in an operational railway embankment. Near Surf. Geophys. 2014, 12, 61–72. [Google Scholar]
- Atekwana, E.A.; Sauck, W.A.; Werkema, D.D., Jr. Investigations of geoelectrical signatures at a hydrocarbon contaminated site. J. Appl. Geophys. 2000, 44, 167–180. [Google Scholar] [CrossRef]
- Chambers, J.E.; Wilkinson, P.B.; Wealthall, G.P.; Loke, M.H.; Dearden, R.; Wilson, R.; Allen, D.; Ogilvy, R.D. Hydrogeophysical imaging of deposit heterogeneity and groundwater chemistry changes during DNAPL source zone bioremediation. J. Contam. Hydrol. 2010, 118, 43–61. [Google Scholar] [CrossRef] [PubMed]
- Kemna, A.; Kulessa, B.; Vereecken, H. Imaging and characterization of subsurface solute transport using electrical resistivity tomography (ERT) and equivalent transport models. J. Hydrol. 2002, 267, 125–146. [Google Scholar] [CrossRef]
- Robert, T.; Caterina, D.; Deceuster, J.; Kaufmann, O.; Nguyen, F. A salt tracer test monitored with surface ERT to detect preferential flow and transport paths in fractured/karstified limestones. Geophysics 2012, 77, B55–B67. [Google Scholar] [CrossRef]
- Schön, J.H. Physical Properties of Rocks, Fundamentals and Principles of Petrophysics. In Handbook of Geophysical Exploration, Seismic Exploration; Helbig, K., Treitel, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Revil, A.; Karaoulis, M.; Johnson, T.; Kemna, A. Review: Some low-frequency electrical methods for subsurface characterization and monitoring in hydrogeology. Hydrogeol. J. 2012, 20, 617–658. [Google Scholar] [CrossRef]
- Binley, A.; Kemna, A. DC resistivity and induced polarization methods. In Hydrogeophysics; Springer: Berlin, Germany, 2005; pp. 129–156. [Google Scholar]
- Hermans, T.; Wildemeersch, S.; Jamin, P.; Orban, P.; Brouyère, S.; Dassargues, A.; Nguyen, F. Quantitative temperature monitoring of a heat tracing experiment using cross-borehole ERT. Geothermics 2015, 53, 14–26. [Google Scholar] [CrossRef]
- Tikhonov, A.N.; Arsenin, V.A. Solution of Ill-Posed Problems; Winston & Sons: Washington, DC, USA, 1977. [Google Scholar]
- Sen, P.N.; Goode, P.A. Influence of temperature on electrical conductivity on shaly sands. Geophysics 1992, 46, 781–795. [Google Scholar] [CrossRef]
- Hayley, K.; Bentley, L.R.; Pidlisecky, A. Compensating for temperature variations in time-lapse electrical resistivity difference imaging. Geophysics 2010, 75, WA51–WA59. [Google Scholar] [CrossRef]
- Ma, R.; McBratney, A.; Whelan, B.; Minasny, B.; Short, M. Comparing temperature correction models for soil electrical conductivity measurement. Precis. Agric. 2011, 12, 55–66. [Google Scholar] [CrossRef]
- Sherrod, L.; Sauck, W.; Werkema, D.D., Jr. A low-cost, in-situ resistivity and temperature monitoring system. Ground Water Monit. Remediat. 2012, 32, 31–39. [Google Scholar] [CrossRef]
- Loke, M.H.; Dahlin, T.; Rucker, D.F. Smoothness-constrained time-lapse inversion of data from 3D resistivity survey. Near Surf. Geophys. 2014, 12, 5–24. [Google Scholar]
- Miller, C.; Routh, P.; Brosten, T.; McNamara, J. Application of time-lapse ERT imaging to watershed characterization. Geophysics 2008, 73, G7–G17. [Google Scholar] [CrossRef]
- Daily, W.; Ramirez, A.; LaBrecque, D.; Nitao, J. Electrical resistivity tomography of vadose water movement. Water Resour. Res. 1992, 28, 1429–1442. [Google Scholar] [CrossRef]
- LaBrecque, D.J.; Yang, X. Difference inversion of ERT data: A fast inversion method for 3-D in-situ monitoring. J. Environ. Eng. Geophys. 2001, 6, 83–90. [Google Scholar]
- Nguyen, F.; Hermans, T.; Robert, T. Minimum gradient support and geostatistics regularization approaches for inverting time-lapse data. In Proceedings of 2nd International Workshop on Geoelectrical Monitoring, Vienna, Austria, 4–6 December 2013.
- Karaoulis, M.; Tsourlos, P.; Kim, J.-H.; Revil, A. 4D time-lapse ERT inversion: Introducing combined time and space constraints. Near Surf. Geophys. 2014, 12, 25–34. [Google Scholar] [CrossRef]
- Karaoulis, M.C.; Kim, J.H.; Tsourlos, P.I. 4D active time constrained resistivity inversion. J. Appl. Geophys. 2011, 73, 25–34. [Google Scholar] [CrossRef]
- Revil, A.; Skold, M.; Karaoulis, M.; Schmutz, M.; Hubbard, S.S.; Mehlhorn, T.L.; Watson, D.B. Hydrogeophysical investigations of the former S-3 ponds contaminant plumes, Oak Ridge Integrated Field Research Challenge site, Tennessee. Geophysics 2013, 78, EN29–EN41. [Google Scholar] [CrossRef]
- Pidlisecky, A.; Haber, E.; Knight, R. RESINVM3D: A 3D resistivity inversion package. Geophysics 2007, 72, H1–H10. [Google Scholar] [CrossRef]
- Kemna, A. Tomographic Inversion of Complex Resistivity: Theory and Application. Ph.D. Thesis, University of Bochum, Bochum, Germany, 2000. [Google Scholar]
- Nimmer, R.E.; Osiensky, J.L.; Binley, A.M.; Williams, B.C. Three-dimensional effects causing artifacts in two-dimensional, cross-borehole, electrical imaging. J. Hydrol. 2008, 359, 59–70. [Google Scholar] [CrossRef]
- Vandenborght, J.; Kemna, A.; Hardelauf, H.; Vereecken, H. Potential of electrical resistivity tomography to infer aquifer transport characteristics from tracer studies: A synthetic case study. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- LaBrecque, D.J.; Miletto, M.; Daily, W.; Ramirez, A.; Owen, E. The effects of noise on Occam’s inversion of resistivity tomography data. Geophysics 1996, 61, 538–548. [Google Scholar] [CrossRef]
- Hermans, T.; Vandenbohede, A.; Lebbe, L.; Nguyen, F. A shallow geothermal experiment in a sandy aquifer monitored using electric resistivity tomography. Geophysics 2012, 77, B11–B21. [Google Scholar] [CrossRef]
- Irving, J.; Singha, K. Stochastic inversion of tracer test and electrical geophysical data to estimate hydraulic conductivities. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Kowalsky, M.B.; Finsterle, S.; Peterson, J.; Hubbard, S.; Rubin, Y.; Majer, E.; Ward, A.; Gee, G. Estimation of field-scale soil hydraulic and dielectric parameters through joint inversion of GPR and hydrological data. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Loke, M.H.; Acworth, I.; Dahlin, T. A comparison of smooth and blocky inversion methods in 2D electrical imaging surveys. Explor. Geophys. 2003, 34, 182–187. [Google Scholar] [CrossRef]
- Blaschek, R.; Hördt, A.; Kemna, A. A new sensitivity-controlled focusing regularization scheme for the inversion of induced polarization based on the minimum gradient support. Geophysics 2008, 73, F45–F54. [Google Scholar] [CrossRef]
- Doetsch, J.; Linde, N.; Pessognelli, M.; Green, A.G.; Günther, T. Constraining 3-D electrical resistance tomography with GPR reflection data for improved aquifer characterization. J. Appl. Geophys. 2012, 78, 68–76. [Google Scholar] [CrossRef]
- Zhou, J.; Revil, A.; Karaoulis, M.; Hale, D.; Doetsch, J.; Cuttler, S. Image-guided inversion of electrical resistivity data. Geophys. J. Int. 2014, 197, 292–309. [Google Scholar] [CrossRef]
- Caterina, D.; Hermans, T.; Nguyen, F. Case studies of prior information in electrical resistivity tomography: Comparison of different approaches. Near Surf. Geophys. 2014, 12, 451–465. [Google Scholar] [CrossRef]
- Kyriakidis, P.C.; Journel, A.G. Geostatistical space-time models: A review. Math. Geol. 1999, 31, 651–684. [Google Scholar] [CrossRef]
- Revil, A. Effective conductivity and permittivity of unsaturated porous materials in the frequency range 1 mHz–1 GHz. Water Resour. Res. 2013, 49, 306–327. [Google Scholar] [CrossRef] [PubMed]
- Revil, A.; Schwaeger, H.; Cathles, L.M.; Manhardt, P.D. Streaming potential in porous media: 2. Theory and application to geothermal systems. J. Geophys. Res. 1999, 104, 20033–20048. [Google Scholar] [CrossRef]
- Archie, G.E. The electrical resistivity log as an aid in determining some reservoir characteristics. Trans. AIME 1942, 146, 54–62. [Google Scholar] [CrossRef]
- Revil, A. On charge accumulations in heterogeneous porous materials under the influence of an electrical field. Geophysics 2013, 78, D271–D291. [Google Scholar] [CrossRef]
- Sorensen, J.A.; Glass, G.E. Ion and temperature dependence of electrical conductance for natural waters. Anal. Chem. 1987, 59, 1594–1597. [Google Scholar] [CrossRef]
- Jardani, A.; Revil, A.; Bolève, A.; Dupont, J.P.; Barrash, W.; Malama, B. Tomography of groundwater flow from self-potential (SP) data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Revil, A.; Mahardika, H. Coupled hydromechanical and electromagnetic disturbances in unsaturated clayey materials. Water Resour. Res. 2013, 49, 744–766. [Google Scholar] [CrossRef] [PubMed]
- Leinov, E.; Vinogradov, J.; Jackson, M.D. Salinity dependence of the thermoelectric coupling coefficient in brine-saturated sandstones. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Revil, A.; Karaoulis, M.; Srivastava, S.; Byrdina, S. Thermoelectric self-potential and resistivity data localize the burning front of underground coal fires. Geophysics 2013, 78, B259–B273. [Google Scholar] [CrossRef]
- Sill, W.R. Self-potential modeling from primary flows. Geophysics 1983, 48, 76–86. [Google Scholar] [CrossRef]
- Ikard, S.J.; Revil, A. Self-potential monitoring of a thermal pulse advecting through a preferential flow path. J. Hydrol. 2014, 2014. [Google Scholar] [CrossRef]
- Selker, J.S.; Thévenaz, L.; Huwald, H.; Mallet, A.; Luxemburg, W.; van de Giesen, N.; Stejskal, M.; Zeman, J.; Westhoff, M.; Parlange, M.B. Distributed fiber-optic temperature sensing for hydrologic systems. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Yilmaz, G.; Karlik, S.E. A distributed optical fiber sensor for temperature detection in power cables. Sens. Actuators A 2006, 125, 148–155. [Google Scholar] [CrossRef]
- Tyler, S.W.; Selker, J.S.; Hausner, M.B.; Hatch, C.E.; Torgersen, T.; Thodal, C.E.; Schladow, S.G. Environmental temperature sensing using Raman spectra DTS fiber-optic methods. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Arango-Galván, C.; Prol-Ledesma, R.M.; Flores-Márquez, E.L.; Canet, C.; Villanueva Estrada, R.E. Shallow submarine and subaerial, low-enthalpy hydrothermal manifestations on Punta Banda, Baja California, Mexico: Geophysical and geochemical characterization. Geothermics 2011, 40, 102–111. [Google Scholar]
- Bruno, P.P.G.; Paoletti, V.; Grimaldi, M.; Rapolla, A. Geophysical exploration for geothermal low enthalpy resources in Lipari Island, Italy. J. Volcanol. Geotherm. Res. 2000, 98, 173–188. [Google Scholar] [CrossRef]
- Garg, S.K.; Pritchett, J.W.; Wannamaker, P.E.; Combs, J. Characterization of geothermal reservoirs with electrical surveys: Beowave geothermal field. Geothermics 2007, 36, 487–517. [Google Scholar] [CrossRef]
- Pérez Flores, M.A.; Gomez Trevino, E. Dipole-dipole resistivity imaging of the Ahuachapan-Chipilapa geothermal field, El Salvador. Geothermics 1997, 26, 657–680. [Google Scholar]
- Revil, A.; Finizola, A.; Ricci, T.; Delcher, E.; Peltier, A.; Barde-Cabusson, S.; Avard, G.; Bailly, T.; Bennati, L.; Byrdina, S.; et al. Hydrogeology of Stromboli volcano, Aeolian Islands (Italy) from the interpretation of resistivity tomograms, self-potential, soil temperature and soil CO2 concentration measurements. Geophys. J. Int. 2011, 186, 1078–1094. [Google Scholar] [CrossRef]
- Revil, A.; Johnson, T.C.; Finizola, A. Three-dimensional resistivity tomography of Vulcan’s forge, Vulcano Island, southern Italy. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Benderitter, Y.; Tabbagh, J. Heat storage in a shallow confined aquifer: Geophysical tests to detect the resulting anomaly and its evolution with time. J. Hydrol. 1982, 56, 85–98. [Google Scholar] [CrossRef]
- Ramirez, A.; Daily, W.; LaBrecque, D.; Owen, E.; Chesnut, D. Monitoring an underground steam injection process using electrical resistance tomography. Water Resour. Res. 1993, 29, 73–87. [Google Scholar] [CrossRef]
- Ramirez, A.; Chesnut, D.A.; Daily, W.D. Using Electrical Resistance Tomography to Map Subsurface Temperatures. U.S. Patent US5346307 A, 3 June 1993. [Google Scholar]
- LaBrecque, D.J.; Ramirez, A.L.; Daily, W.D.; Binley, A.M.; Schima, S.A. ERT monitoring of environmental remediation processes. Meas. Sci. Technol. 1996, 7, 375–383. [Google Scholar] [CrossRef]
- Müller, K.; Vanderborght, J.; Englert, A.; Kemna, A.; Huisman, J.A.; Rings, J.; Vereecken, H. Imaging and characterization of solute transport during two tracer tests in a shallow aquifer using electrical resistivity tomography and multilevel groundwater samplers. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Firmbach, L.; Giordano, N.; Comina, C.; Mandrone, G.; Kolditz, O.; Vienken, T.; Dietrich, P. Experimental heat flow propagation within porous media using electrical resistivity tomography x(ERT). In Proceedings of the European Geothermal Congress 2013, Pisa, Italy, 3–7 June 2013.
- Supper, R.; Ottowitz, D.; Jochum, B.; Römer, A.; Pfeiler, S.; Kauer, S.; Keushnig, M.; Ita, A. Geoelctrical monitoring of frozen ground and permafrost in alpine areas: Field studies and considerations towards an improved measuring technology. Near Surf. Geophys. 2014, 12, 93–115. [Google Scholar]
- Auken, E.; Doetsch, J.; Fiandaca, G.; Christiansen, A.V.; Gazoty, A.; Cahill, A.G.; Jakobsen, R. Imaging subsurface migration of dissolved CO2 in a shallow aquifer using 3-D time-lapse electrical resistivity tomography. J. Appl. Geophys. 2013, 101, 31–41. [Google Scholar] [CrossRef]
- Hermans, T.; Daoudi, M.; Vandenbohede, A.; Robert, T.; Caterina, D.; Nguyen, F. Comparison of temperature estimates from heat transport model and electrical resistivity tomography during a shallow heat injection and storage experiment. Ber. Geol. Bundesanst. 2012, 93, 43–48. [Google Scholar]
- Robert, T.; Hermans, T.; Dumont, G.; Nguyen, F.; Rwabuhungu, D.E. Reliability of ERT-derived temperature: Insights from laboratory measurements. Near Surf. Geosci. 2013, 2013. [Google Scholar] [CrossRef]
- Caterina, D.; Beaujean, J.; Robert, T.; Nguyen, F. A comparison study of different image appraisal tools for electrical resistivity tomography. Near Surf. Geophys. 2013, 11, 639–657. [Google Scholar] [CrossRef]
- Perri, M.T.; Cassiani, G.; Gervasio, I.; Deiana, R.; Binley, A. A saline tracer test monitored via both surface and cross-borehole electrical resistivity tomography: Comparison of time-lapse results. J. Appl. Geophys. 2012, 79, 6–16. [Google Scholar] [CrossRef]
- Doetsch, J.A.; Coscia, I.; Greenhalgh, S.; Linde, N.; Green, A.; Günther, T. The borehole-fluid effect in electrical resistivity imaging. Geophysics 2010, 75, F107–F114. [Google Scholar] [CrossRef]
- Day-Lewis, F.D.; Singha, K.; Binley, A.M. Applying petrophysical models to radar travel time and electrical resistivity tomograms: Resolution-dependent limitations. J. Geophys. Res. Solid Earth 2005, 110. [Google Scholar] [CrossRef]
- Selker, J.; van de Giesen, N.; Westhoff, M.; Luxemburg, W.; Parlange, M.B. Fiber optics opens window on stream dynamics. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Lowry, C.S.; Walker, J.F.; Hunt, R.J.; Anderson, M.P. Identifying spatial variability of groundwater discharge in a wetland stream using a distributed temperature sensor. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Vogt, T.; Schneider, P.; Hahn-Woernle, L.; Cirpka, O.A. Estimation of seepage rates in a losing stream by means of fiber-optic high-resolution vertical temperature profiling. J. Hydrol. 2010, 380, 154–164. [Google Scholar] [CrossRef]
- Mamer, E.A.; Lowry, C.S. Locating and quantifying spatially distributed groundwater/surface water interactions using temperature signals with paired fiber-optic cables. Water Resour. Res. 2013, 49, 7670–7680. [Google Scholar] [CrossRef]
- Sebok, E.; Duque, C.; Kazmierczak, J.; Engesgaard, P.; Nilsson, B.; Karan, S.; Frandsen, M. High-resolution distributed temperature sensing to detect seasonal groundwater discharge into Lake Vaeng, Denmark. Water Resour. Res. 2013, 49, 5355–5368. [Google Scholar] [CrossRef]
- Lauer, F.; Frede, H.-G.; Breuer, L. Uncertainty assessment of quantifying spatially concentrated groundwater discharge to small streams by distributed temperature sensing. Water Resour. Res. 2013, 49, 400–407. [Google Scholar] [CrossRef]
- Krause, S.; Blume, T. Impact of seasonal variability and monitoring mode on the adequacy of fiber-optic distributed temperature sensing at aquifer-river interfaces. Water Resour. Res. 2013, 49, 2408–2423. [Google Scholar] [CrossRef]
- Mwakanyamale, K.; Day-Lewis, F.D.; Slater, L.D. Statistical mapping of zones of focused groundwater/surface-water exchange using fiber-optic distributed temperature sensing. Water Resour. Res. 2013, 49, 6979–6984. [Google Scholar] [CrossRef]
- Blume, T.; Krause, S.; Meinikmann, K.; Lewandowski, J. Upscaling lacustrine groundwater discharge rates by fiber-optic distributed temperature sensing. Water Resour. Res. 2013, 49, 7929–7944. [Google Scholar] [CrossRef]
- Ciocca, F.; Lunati, I.; van de Giesen, N.; Parlange, M.B. Heated optical fiber for distributed soil-moisture measurements: A lysimeter experiment. Vadose Zone J. 2012, 11. [Google Scholar] [CrossRef]
- Hurtig, E.; Groswig, S.; Jobmann, M.; Kuhn, K.; Marschall, P. Fibre-optic temperature measurements in shallow boreholes: Experimental application for fluid logging. Geothermics 1994, 23, 355–364. [Google Scholar] [CrossRef]
- Macfarlane, A.; Förster, A.; Merriam, D.; Schrötter, J.; Healey, J. Monitoring artificially stimulated fluid movement in the Cretaceous Dakota Aquifer, Western Kansas. Hydrogeol. J. 2002, 10, 662–673. [Google Scholar] [CrossRef]
- Yamano, M.; Goto, S. Long-term monitoring of the temperature profile in a deep borehole: Temperature variations associated with water injection experiments and natural groundwater discharge. Phys. Earth Planet. Inter. 2005, 152, 326–334. [Google Scholar] [CrossRef]
- Leaf, A.T.; Hart, D.J.; Bahr, J.M. Active thermal tracer tests for improved hydrostratigraphic characterization. Groundwater 2012, 50, 726–735. [Google Scholar] [CrossRef]
- Read, T.; Bour, O.; Bense, V.; le Borgne, T.; Goderniaux, P.; Klepikova, M.V.; Hochreutener, R.; Lavenant, N.; Boschero, V. Characterizing groundwater flow and heat transport in fractured rock using fiber-optic distributed temperature sensing. Geophys. Res. Lett. 2013, 40, 1–5. [Google Scholar] [CrossRef]
- Banks, E.W.; Shanafield, M.A.; Cook, P.G. Induced temperature gradients to examine groundwater flowpaths in open boreholes. Groundwater 2014, 2014. [Google Scholar] [CrossRef]
- Fujii, H.; Okubo, H.; Itoi, R. Thermal response tests using optical fiber thermometers. Geotherm. Resour. Counc. Trans. 2006, 30, 545–551. [Google Scholar]
- Fujii, H.; Okubo, H.; Nishi, K.; Itoi, R.; Ohyama, K.; Shibata, K. An improved thermal response test for U-tube ground heat exchanger based on optical fiber thermometers. Geothermics 2009, 38, 399–406. [Google Scholar] [CrossRef]
- Acuña, J.; Mogensen, P.; Palm, B. Distributed thermal response test on a U-pipe borehole heat exchanger. In Proceedings of the EFFSTOCK—The 11th International Conference on Energy Storage, Stockholm, Sweden, 14–17 June 2009.
- Reinsch, T.; Henninges, J.; Ásmundsson, R. Thermal, mechanical and chemical influences on the performance of optical fibres for distributed temperature sensing in a hot geothermal well. Environ. Earth Sci. 2013, 70, 3465–3480. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hermans, T.; Nguyen, F.; Robert, T.; Revil, A. Geophysical Methods for Monitoring Temperature Changes in Shallow Low Enthalpy Geothermal Systems. Energies 2014, 7, 5083-5118. https://doi.org/10.3390/en7085083
Hermans T, Nguyen F, Robert T, Revil A. Geophysical Methods for Monitoring Temperature Changes in Shallow Low Enthalpy Geothermal Systems. Energies. 2014; 7(8):5083-5118. https://doi.org/10.3390/en7085083
Chicago/Turabian StyleHermans, Thomas, Frédéric Nguyen, Tanguy Robert, and Andre Revil. 2014. "Geophysical Methods for Monitoring Temperature Changes in Shallow Low Enthalpy Geothermal Systems" Energies 7, no. 8: 5083-5118. https://doi.org/10.3390/en7085083
APA StyleHermans, T., Nguyen, F., Robert, T., & Revil, A. (2014). Geophysical Methods for Monitoring Temperature Changes in Shallow Low Enthalpy Geothermal Systems. Energies, 7(8), 5083-5118. https://doi.org/10.3390/en7085083