1. Introduction
No matter the claim and the quest for new answers to the needs of an energy-thirstier society, thermal conversion systems will play a key role in the energy supply chain. This awareness, along with the urgent need of CO2 reduction (currently the main driver of technology advance), has at least two direct consequences: the introduction in the energy cycle of CO2-neutral fuels (biomass-derived) and the design/development of more efficient conversion systems. The latter point can be anticipated to have a larger practical impact than the former, given the majority of energy sources will be represented by fossil fuels for many years to come.
Sometimes placed in the category of “alternative” fuels, methane (CH4) is indeed a hydrocarbon, sporting the peculiarity of the lowest C/H ratio, if compared to other fuels: by trivial reasoning, the less the carbon, the less the CO2. This feature has boosted a renewed attention to CH4, which represents the main constituent of natural gas. CH4 has been used with heat engines for a long time, even if with the status of a “niche” solution: as a fuel for internal combustion (i.c.) engines, it offers some advantages over gasoline, having wider flammable limits and better anti-knock characteristics, at the cost of a lower flame speed. A feasible opportunity to overcome the limits of CH4 is offered by H2: adding H2 to CH4 (or natural gas) can improve the flame speed/stability and lower the lean operating limit. The overall effect is to extend the stable operation map to extreme conditions (e.g., high EGR).
Crucial for the development and design of i.c. engines and gas turbine combustors is the knowledge of laminar combustion properties: they offer the basis for modelling and simulation of flame-turbulence interaction. Data on the combustion properties of pure gaseous fuels are widely available in the literature [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12], but hardly in a systematic form; moreover, data for multi-component fuels at high pressure are even scarcer: filling this gap is the scope of the
Device for Hydrogen-Air Reaction Mode Analysis (DHARMA) project, aiming at generating a comprehensive and coherent grid of data on the combustion properties of CH
4 and H
2, obtained in conditions as close as possible to those of actual engines.
The project relies on an optically accessible constant-volume bomb (static P ≤ 20 MPa), where test are carried out on spherical expanding flames; the operating conditions (P0, T0), the equivalence ratio, the relative composition of the mixture, the ignition energy can be varied in a meaningful range. A shadowgraph setup, based on a c.w. laser source and a CMOS camera, is used to follow the flame growth with high time and space resolution.
The present work was carried out in the above-described framework and deals specifically with the effect of the initial pressure and of the H2 amount on the combustion properties of CH4-H2-air mixtures.
The initial pressure varied between 3 and 18 bar; the H2 percentage varied from 0% to 30% (vol.): the equivalence ratio was 1.0. These conditions were selected to match the operating range of automotive internal combustion engines.
The experimental tests yielded the (unstretched) laminar burning velocity and the Markstein length in each condition. These flame characteristics constitute a necessary input for the development and validation of theoretical models of laminar flame propagation. In addition, the interaction between laminar burning velocity and stretch (expressed by the Markstein length) allows to highlight the relation between flame and turbulence within the wrinkled thin laminar flamelet regime of premixed turbulent flames. These theoretical models, in turn, represent the basis for the design and testing of i.c. engines and/or combustors.
Other than the laminar burning characteristics, the phenomenon of flame instability has been explicitly analyzed, offering further details on flame properties. Under certain conditions, instability may wrinkle and break the flame front into small combustion cells: the effective flame front area increases, and the combustion process accelerates. Flame cellularity can be considered as an intermediate regime between laminar and turbulent combustion. Since its relevance in real combustion systems cannot be overlooked, the dependence of cellularity on both pressure and H2 amount was suitably investigated.
2. Experimental Setup and Procedures
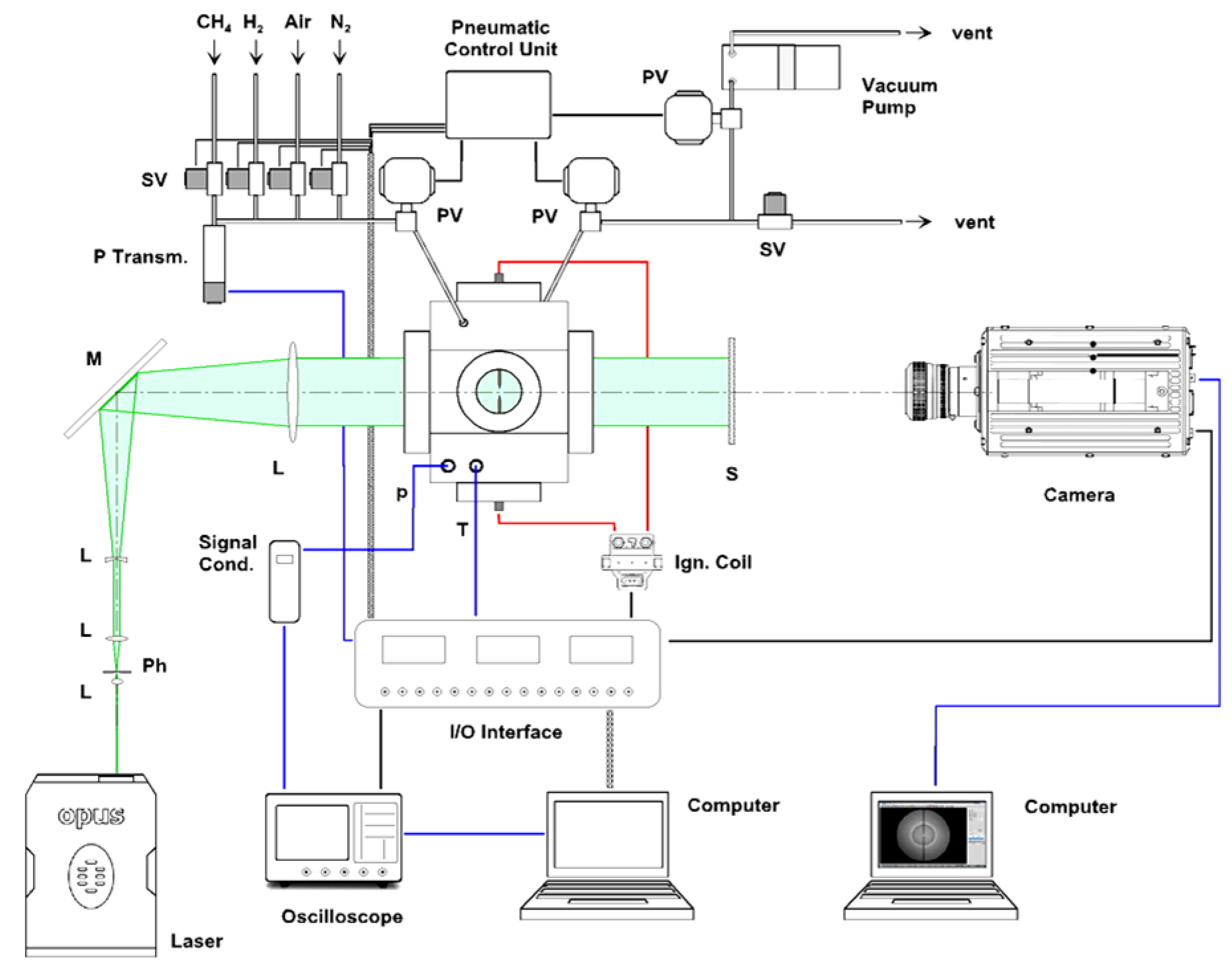
The general arrangement of the experimental layout is shown in
Figure 1: a detailed description is given in [
13]. The heart of the DHARMA laboratory is a constant-volume test reactor, made of stainless steel (AISI 316): the cylindrical chamber (i.d. = 70 mm,
h = 90 mm, aspect ratio = 1.29) is rated for a maximum pressure of ≤20 MPa (static).
A total of 6 optical accesses are available: the larger viewports (d = 65 mm) are located normal to the chamber axis, providing nearly full access to chamber bore; smaller diameter ports are positioned on the chamber side, along two orthogonal axes. Hi-grade quartz windows (85 mm diameter, 30 mm thick) are installed in the main ports, the smaller side ports can be fitted either with quartz windows (49 mm diameter, 20 mm thick) or with a variety of stainless steel adapters (i.e., transducers, electrodes, sampling ports, etc.).
Four additional service ports are available, e.g., for the intake of the combusting mixture and the vent of the exhaust gases.
The mixture is ignited with an automotive inductive ignition system (energy ≤ 60 mJ), which was characterized recording the time evolution of the voltage drop and the current flow between the electrodes: this allowed to evaluate the power and energy release. Being known the electrical behaviour of the coil, the energy of discharge can be set in the range 0÷60 mJ, adjusting the time of charge (dwell time). The spark discharge takes place in the center of the chamber between two pointed-tip tungsten electrodes (dia. = 1 mm, gap = 1 mm).
Figure 1.
Layout of the experimental apparatus.
Figure 1.
Layout of the experimental apparatus.
A high-frequency dynamic pressure transducer detects pressure history during the combustion events. A metal-shielded, type K thermocouple is used to monitor the temperature of the gases, save for the combustion phase.
The gas handling system was designed to prepare combustible mixtures of variable composition with high accuracy, spanning a range of initial pressures, which included values of relevance in spark-ignition engine operation.
High purity gases (CH
4: 99.9995%, H
2: 99.999%, dry air: 99.999%, N
2: 99.9995%) are used to prepare the mixtures, relying on the partial pressures method [
2]: the amount of each gas is metered by a solenoid valve, controlled by a high-resolution (100 MHz) counter/timer board installed in the main computer. The pressure is monitored by a high-accuracy pressure transmitter (0–30 bar, accuracy ±0.08% FS). The gas supply system allows one to prepare combustible mixtures up to 30 bar. After each test, the system is vented, purged with N
2 and pumped down to 10
−2 mbar. All the devices operate with a high degree of automation, to maximize safety and repeatability of the tests.
The entire lab conforms to current safety standards on the use of combustible gases, and is provided with interconnected gas leak sensors, cylinder cut-off devices and forced venting systems.
A parallel-beam direct shadowgraph layout [
14] was set up for the analysis of spherical expanding flames. A Diode-Pumped Solid-State c.w. laser (2W @532nm) is used as the light source. High-resolution, time-resolved image acquisition is accomplished by means of a CMOS camera (
Photron SA-5, 1024 × 1024 pixel, 1,000,000 fps, shutter time ≥368 ns), interfaced to an independent workstation.
4. Laminar Burning Properties
The following results refer to the combustion behaviour of CH
4 and of CH
4-H
2 mixtures, with a H
2 fraction of 20% and 30% in volume: these values optimize the trade-off between additional technical complexity and performance benefits, allowing for a direct utilization of CH
4-H
2 mixtures in current natural gas engines [
28,
29]. The initial temperature
T0 varied in the range 293÷305 K, while the initial pressure
P0 was set at 3, 6, 12 and 18 bar (abs.). The study was limited to stoichiometric air-fuel mixtures (equivalence ratio
= 1.0), since it was targeted to the development of automotive internal combustion engines, operating with closed-loop three-way catalyst.
Time-resolved shadowgraph images of spherical expanding flames were used to infer the laminar flame parameters. As stated earlier, laminar analysis can be meaningfully carried out in the constant-pressure phase only, before the chamber pressure shows a sensible increment. Moreover, as stated by Bradley
et al. [
6], the early stages of the flame kernel growth are affected by the spark energy release, and cannot be taken into account in the evaluation of laminar flame properties.
The resulting measurement time-window starts after the ignition disturbances are over, and ends when the pressure shows an appreciable rise. In the present tests, spark energy was set at 20 mJ (electrical). Since the ignition system is inductive, only a small fraction of this energy is released in the breakdown phase (<10 ns), which (due to the high power peaks) drives the early kernel growth and induces likely perturbations in the flame [
30,
31]. Given the small spark energy, the extent of the ignition disturbances can be expected to be accordingly limited.
Analysis of the flame radii in the early stages revealed no discernible evidence of ignition-induced effects: nonetheless, pending further investigation, a conservative criterion was applied, based on the morphology of the flame: flames with an aspect ratio (major axis/minor axis of the fitting ellipse) lower than 0.98 were discarded. Typical value for the minimum radius was about 4.5 mm.
As stated above, the maximum radius was obtained applying the constraint of constant pressure: typical value was ~9.5 mm, corresponding to ~27% of the chamber radius. This value meets the (
ru < 0.3
rchamber) criterion suggested by Burke
et al. [
32] to avoid the effects of confinement in a cylindrical chamber.
Figure 2 shows three sets of frames, each set coming from a single combustion event: they illustrate the flame development in the constant-pressure phase, at
P0 = 3 bar. The combustion behaviour is compared for CH
4 and H
2-CH
4 mixtures with a H
2 content of 20% and 30% (vol.). Recording speed was 7000 fps (143 µs between consecutive frames) with a shutter speed of 1 µs; optical magnification ratio was 3.27:1, resulting in a spatial resolution of 15.3 pixel/mm. Flames appear smooth and virtually free of wrinkles; the crack shown for the 30% mixture is the self-similar development of initial ignition disturbances. The effect of H
2 addition can be appreciated in the increased size of the flame ball at a given time.
Figure 2.
Flame propagation in the isobaric phase for stoichiometric CH4 and H2-enriched mixtures (20% and 30% vol.) at 3 bar and room temperature. Window dia. 65 mm.
Figure 2.
Flame propagation in the isobaric phase for stoichiometric CH4 and H2-enriched mixtures (20% and 30% vol.) at 3 bar and room temperature. Window dia. 65 mm.
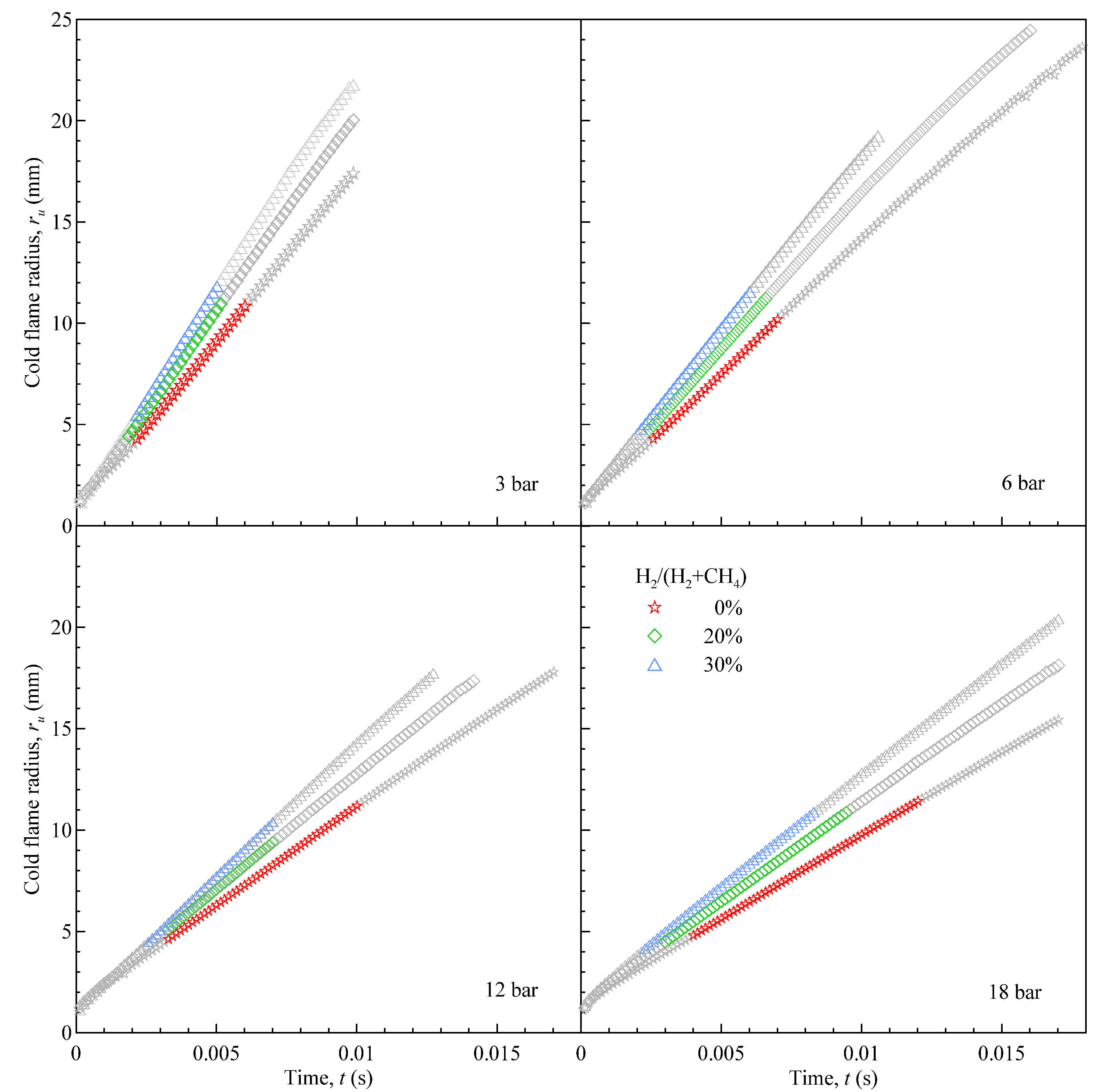
The output of shadowgraph image processing is shown in
Figure 3: the time-evolution of the flame radius is compared for CH4 and CH4-H2 mixtures, at different starting pressure: each set of data corresponds to a single, time-resolved combustion event, which has been selected as representative of the test point (
P0,
T0, % H
2,
). The useful range for data analysis is highlighted in colour for each case: grayed-out data were discarded in the extraction of laminar parameters.
As mentioned earlier, the analytical solution delivers
Vs0 and
Lb directly. The time evolution of
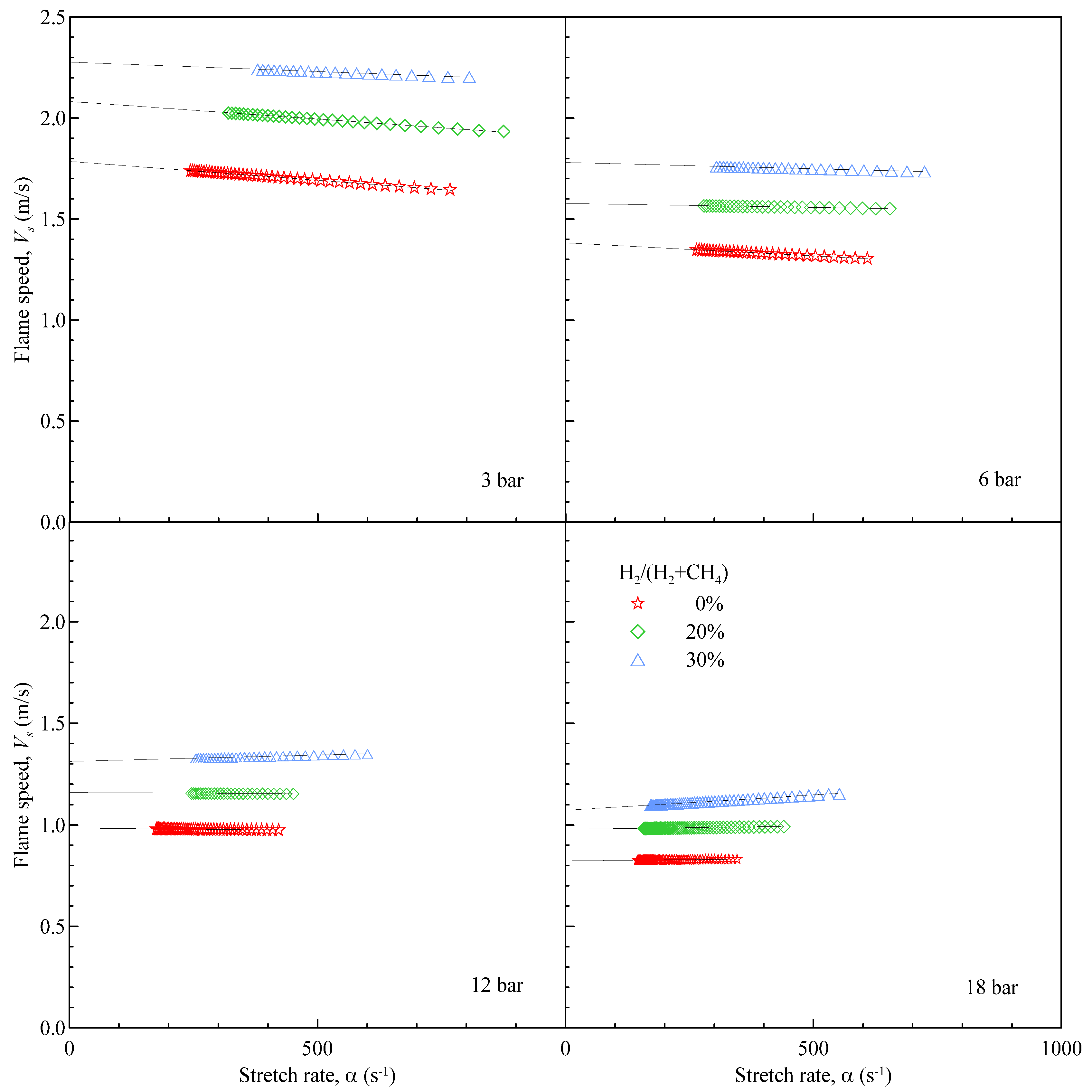
Vs can anyway be evaluated differentiating Equation (8). This allows one to trace the behavior of the stretched flame speed against α, as shown in
Figure 4 for the same test cases and conditions of
Figure 3.
Figure 4 clearly shows the effect of the starting pressure and of the Hydrogen amount on the flame behaviour: increasing the pressure has a detrimental effect on the flame speed; on the contrary, the addition of H
2, even in limited amounts, has always a positive effect on the flame speed.
Figure 3.
Time evolution of flame radius. Stoichiometric CH4 and H2-enriched mixtures (20% and 30% vol.) at room temperature. Starting pressure as indicated.
Figure 3.
Time evolution of flame radius. Stoichiometric CH4 and H2-enriched mixtures (20% and 30% vol.) at room temperature. Starting pressure as indicated.
The unstretched laminar burning velocity
ul0 was calculated with Equation (5). In a recent paper [
33], Varea
et al. proposed a new approach for the measurement of
ul0, which bypass the evaluation of the expansion factor. The authors highlighted the drawbacks of the approach generally used in the literature, which requires the evaluation of the ratio ρ
u/ρ
b: this can introduce errors if any of the hypotheses behind Equation (5) are not satisfied. In the case of CH
4, they concluded that the “old” method delivers reliable results. In the present work, the expansion factor was obtained from the properties of the reactant species and of equilibrated adiabatic products, evaluated with the GASEQ code [
34].
Figure 4.
Evolution of the flame speed
versus flame stretch. Same cases as
Figure 3.
Figure 4.
Evolution of the flame speed
versus flame stretch. Same cases as
Figure 3.
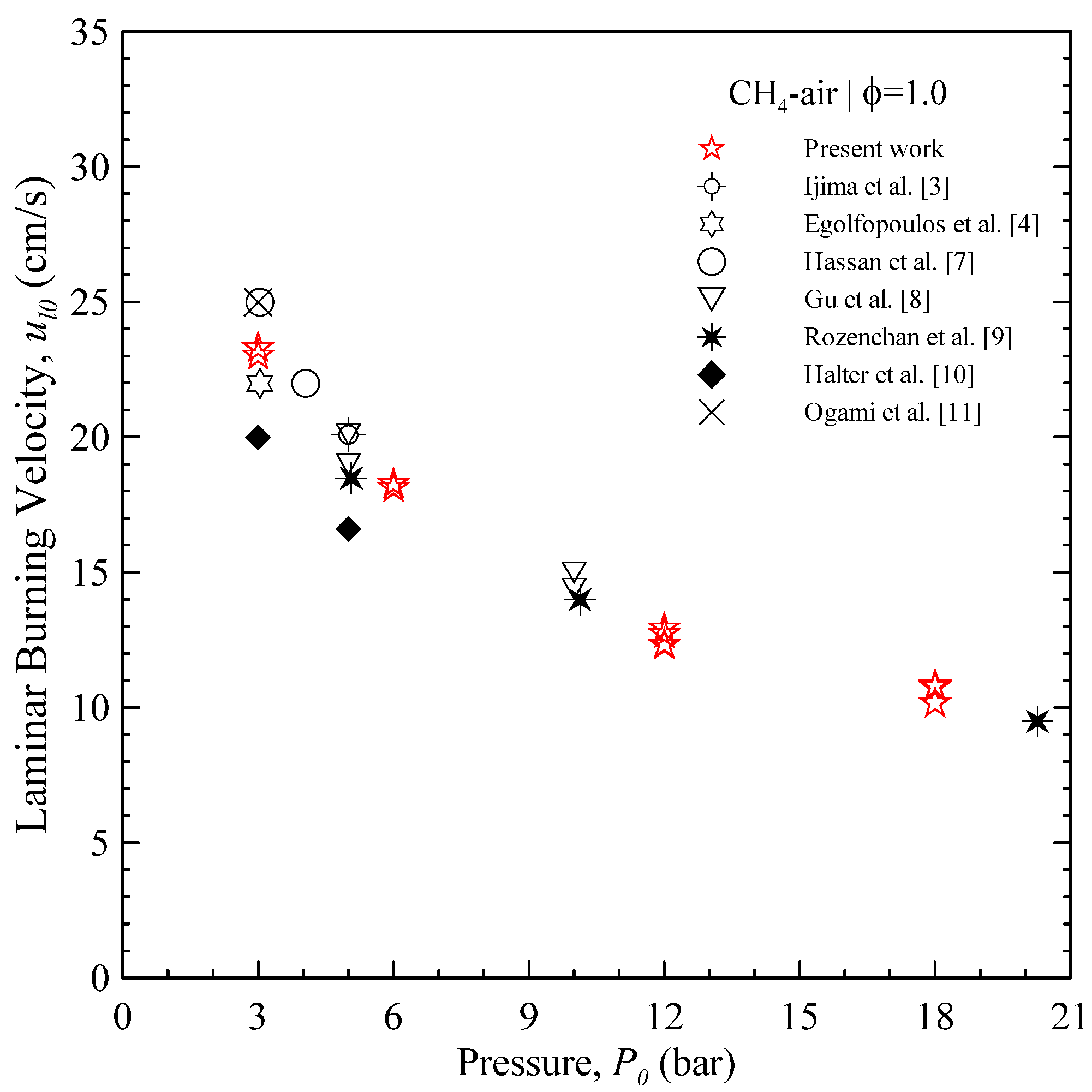
The
ul0 values for CH
4 are summarized in
Figure 5 as a function of initial pressure
P0. As the starting pressure is increased from 3 to 18 bars, a decrease of the laminar burning velocity can be observed;
ul0 at 18 bar is about 40% of 3 bar. The comparison is proposed with the results from other research groups [
3,
4,
7,
8,
9,
10,
11]. Data at high pressures are less readily available than atmospheric pressure: the present results for
ul0 show a fairly good agreement with most of published data, save for the values of Halter, which appear slightly lower.
The variation of the burning velocity with initial pressure and temperature can be expressed by the simple empirical correlation [
8,
10]:
where
ul0,r is the laminar burning velocity at the reference temperature
T0,r and pressure
P0,r. In the present study, only the pressure dependence was evidenced.
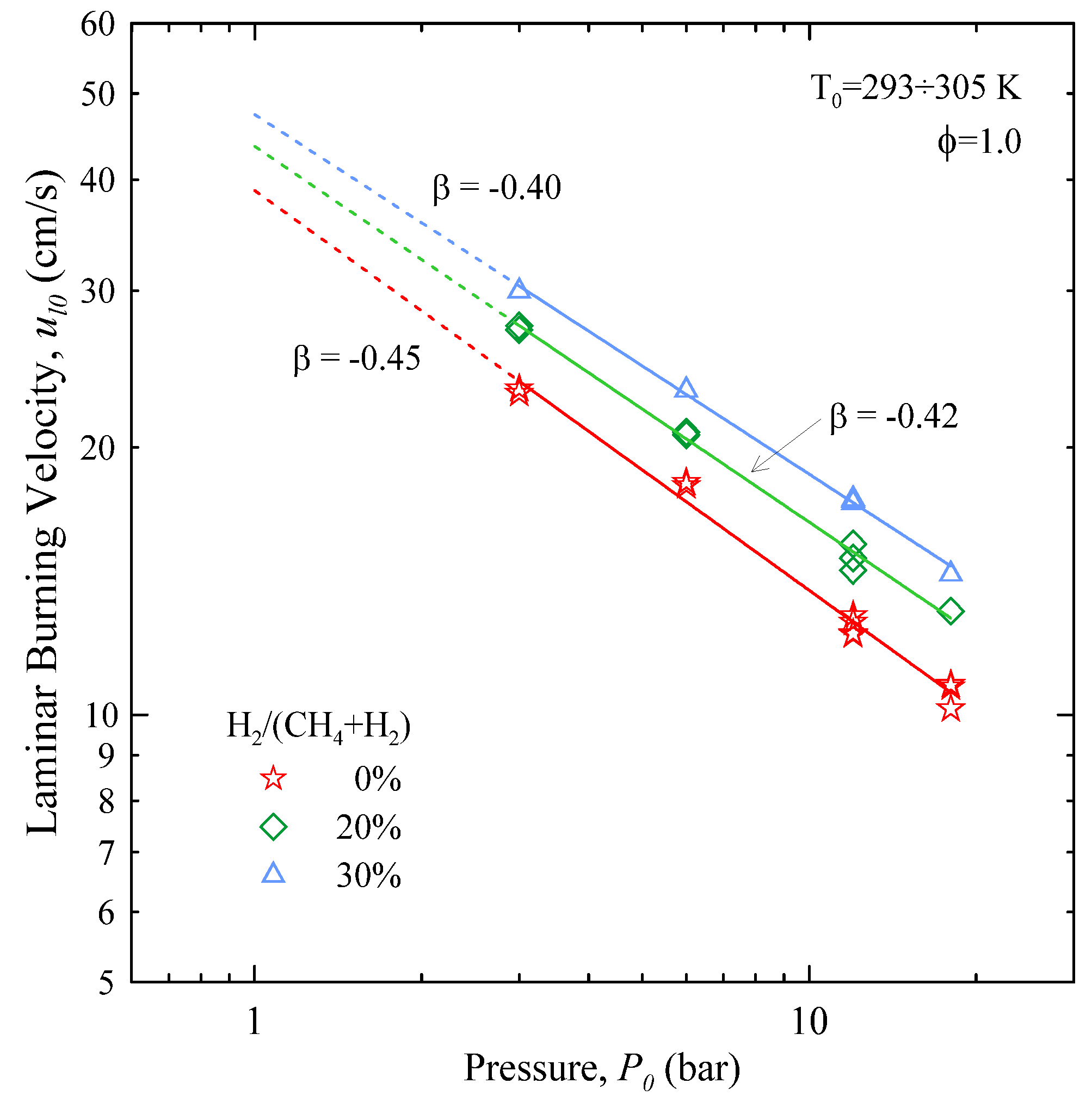
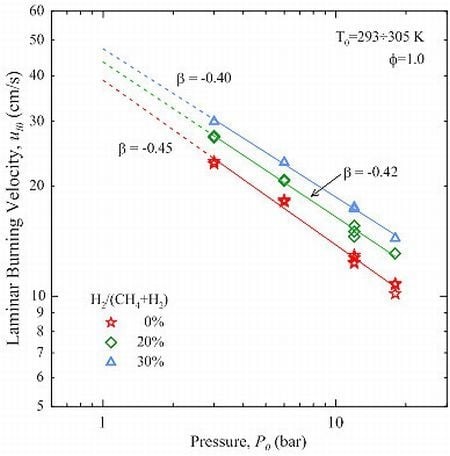
The parameter β was optimized in the range 3÷18 bar, using 3 bar as the reference pressure. As shown in
Figure 6, the results are well described by Equation (11): the coefficient of determination
R2 is >0.99. In the case of CH
4 the value of β is −0.45, which is bracketed between the findings of Gu
et al. [
8] and Halter
et al. [
10]. CH
4-H
2 mixtures show a minor reduction in the magnitude of β, which is proportional to the amount of H
2.
Figure 5.
Unstretched laminar burning velocity as a function of the starting pressure, for stoichiometric CH4 at room temperature.
Figure 5.
Unstretched laminar burning velocity as a function of the starting pressure, for stoichiometric CH4 at room temperature.
Figure 6.
Effect of initial pressure on the unstretched laminar burning velocity. Solid lines represent fits obtained by Equation (11): values of β as indicated.
Figure 6.
Effect of initial pressure on the unstretched laminar burning velocity. Solid lines represent fits obtained by Equation (11): values of β as indicated.
The effect of the addition of H2 to CH4 is twofold: the laminar burning velocity not only increases but becomes also less sensitive to the initial pressure.
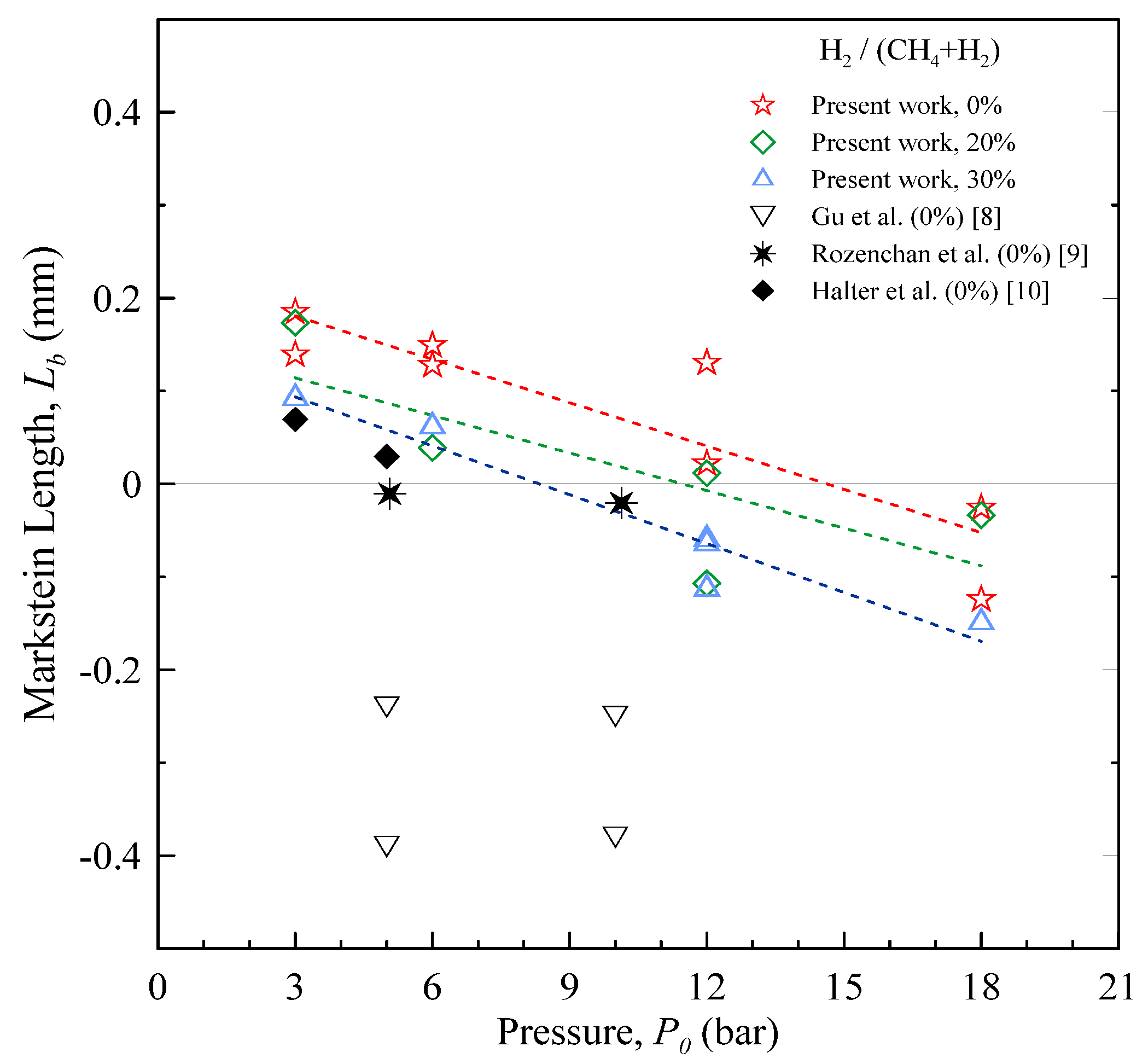
The Markstein length is shown in
Figure 7 as a function of the starting pressure. In the case of CH
4 at lower pressure,
Lb is positive, corresponding to a flame speed which increases as α decreases. As the pressure is increased, the Markstein length becomes smaller, and eventually negative: this result is in agreement with the findings of Gu
et al. [
8], who reported on CH
4 flames up to 10 bar. The effect is probably related to the decrease of flame thickness associated to the pressure increment: this reduces the effect of curvature in counteracting the hydrodynamic instabilities.
Figure 7.
Burned-gas Markstein length as a function of the starting pressure, for stoichiometric CH4 and H2-enriched mixtures at room temperature.
Figure 7.
Burned-gas Markstein length as a function of the starting pressure, for stoichiometric CH4 and H2-enriched mixtures at room temperature.
The addition of H
2 to CH
4 has the anticipated effect [
6] of lowering the Markstein length, since the mixture thermal equidiffusivity is altered.
Due to the combined effects of initial pressure and Hydrogen content, high-pressure CH4-H2 flames are characterized by the lowest values of Lb.
The obtained results confirm the selected procedure for data analysis as appropriate. Since −0.2 ≤
Lb ≤ 0.2 mm, and the minimum flame radius used in the image processing is ~4.5 mm, the ratio |
Lb/
ru min| results lower than ~0.045. According to Halter
et al. [
24], this legitimate the use of the
linear approach, as the relative error respect to the
nonlinear approach is negligible.
5. Flame Stability and Cellular Structures
The burned-gas Markstein length
Lb expresses how and how much the stretch rate affects the flame propagation. Aerodynamic stretch, induced by flame curvature, interacts with the propensity of the flame to develop instability (hydrodynamic and/or thermo diffusive). In this sense,
Lb can be considered an indicator of flame instability. Interestingly enough, the Markstein length is evaluated from the expanding flame in the constant-pressure regime, when the flame is smooth and there is little or no distortion (see e.g.,
Figure 2). In other words,
Lb has a predictive nature.
Evidence of flame instability, if any, appears afterwards, depending on the experimental setup. The flame travelling the chamber volume may go through various morphological alterations, characterized by the appearance and branching of large cracks and, eventually, fine cellular structures [
35,
36,
37,
38,
39,
40,
41].
Figure 8 shows three sets of frames at selected times after the spark: they were obtained in the case of pure and H
2-enriched CH
4 mixtures, ignited at
P0 = 6 bar. Recording conditions were as in
Figure 2.
Figure 8.
Evolution of flame instability for stoichiometric CH4 and H2-enriched mixtures (20% and 30% vol.). P0 = 6 bar, T0 = 298 K. Window dia. 65 mm.
Figure 8.
Evolution of flame instability for stoichiometric CH4 and H2-enriched mixtures (20% and 30% vol.). P0 = 6 bar, T0 = 298 K. Window dia. 65 mm.
It is worth stressing that these images refer to late stages of flame propagation, when the combustion process is no more isobaric.
At moderate values of the initial pressure (
P0 = 6 bar), the CH
4 flame keeps its laminar shape until it approaches the chamber walls. The addition of H
2 to the mixture, even in limited amount (20%), corresponds to the appearance of large cracks on the flame surface. This effect gets more striking as long as the flame travels the chamber, with the cracks being suddenly integrated by cellular structures [
36,
40].
As shown in
Figure 7, when the initial pressure is increased, the Markstein length decreases, suggesting that flame instability should increase. This is confirmed by
Figure 9, which reports three sets of frames obtained for mixtures ignited at
P0 = 12 bar: no matter the mixture composition, in all the cases the flame exhibits deviations from a smooth, laminar morphology. These phenomena take place earlier in the process (that is at smaller radii), if compared to
P0 = 6 bar. The typical sequence of large cracks followed by smaller, uniformly distributed “cells” is always present; if the amount of H
2 is increased, cellular structures show up at earlier times.
Figure 9.
Evolution of flame instability for stoichiometric CH4 and H2-enriched mixtures (20% and 30% vol.). P0 = 12 bar, T0 = 298 K. Window dia. 65 mm.
Figure 9.
Evolution of flame instability for stoichiometric CH4 and H2-enriched mixtures (20% and 30% vol.). P0 = 12 bar, T0 = 298 K. Window dia. 65 mm.
As suggested by Law
et al. [
39], two characteristic instants can be identified: the first is related to the branching of large cracks across the flame surface, the second to the sudden appearance of cells, almost uniformly over the same surface, with a characteristic size much smaller than the large cracks. Following the convention of Law
et al. [
39], we chose to adopt the second instant as representative of the flame loosing stability: this allows to define the critical radius
rcr for the onset of instability.
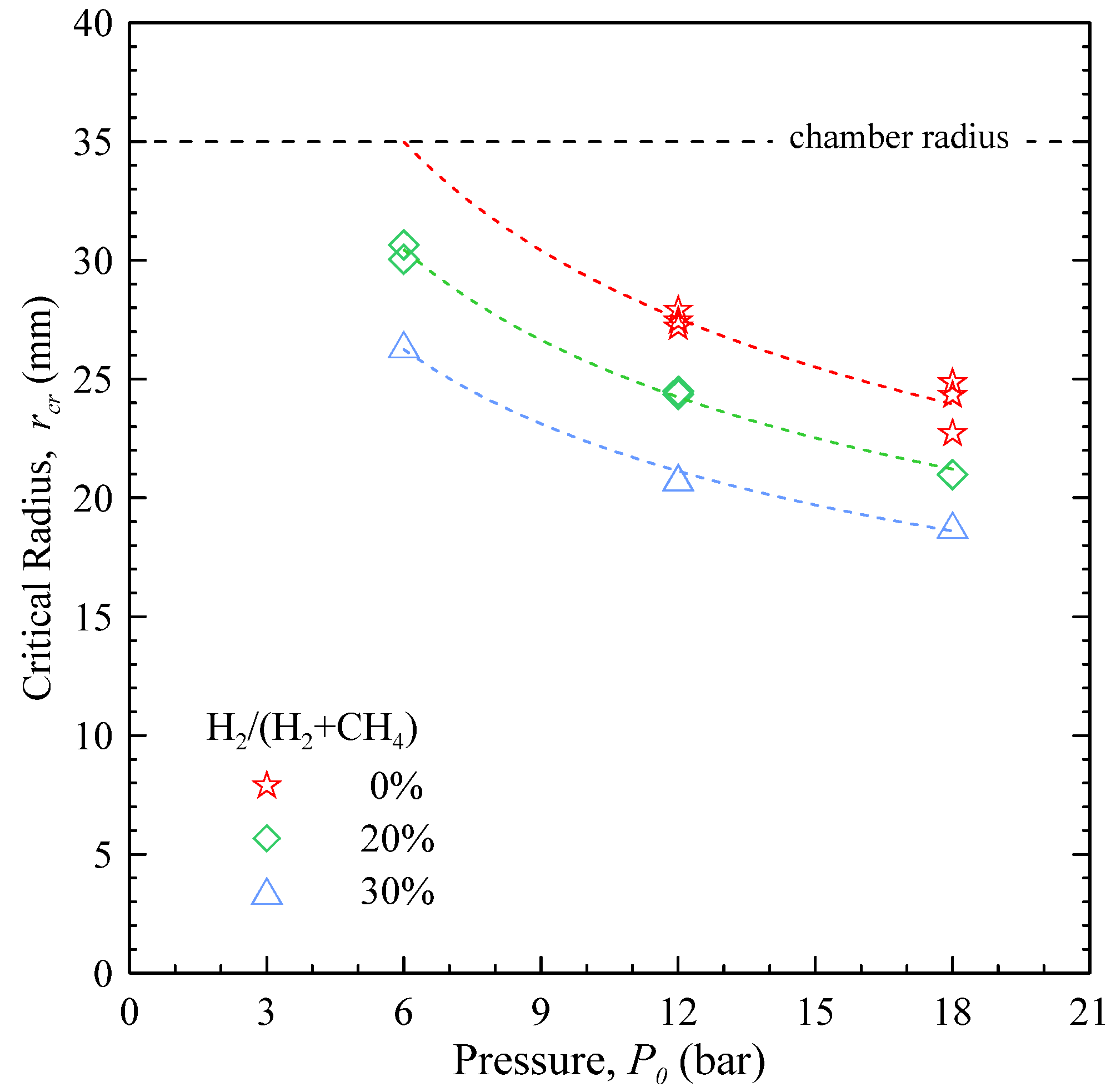
Figure 10 reports the values of
rcr as a function of the starting pressure, for different mixture compositions. All the flames at
P0 = 3 bar show a laminar behaviour, hence the lack of data points for this case.
At P0 = 6 bar, CH4 flames show the appearance of cellular structures when the flame approaches the chamber wall: these points are greyed-out, since they are likely influenced by additional phenomena, like flame-wall interaction.
These results show that increasing the pressure, the critical radius gets smaller: the resulting picture is of a flame that departs earlier from the laminar regime, and mostly develops under a wrinkled regime. Adding H2 to CH4 further reduces rcr (i.e., increases instability), even if the effect gets less marked as the pressure is increased: adding 30% of H2 to CH4 reduces rcr by 24% at 12 bar and by 21.5% at 18 bar.
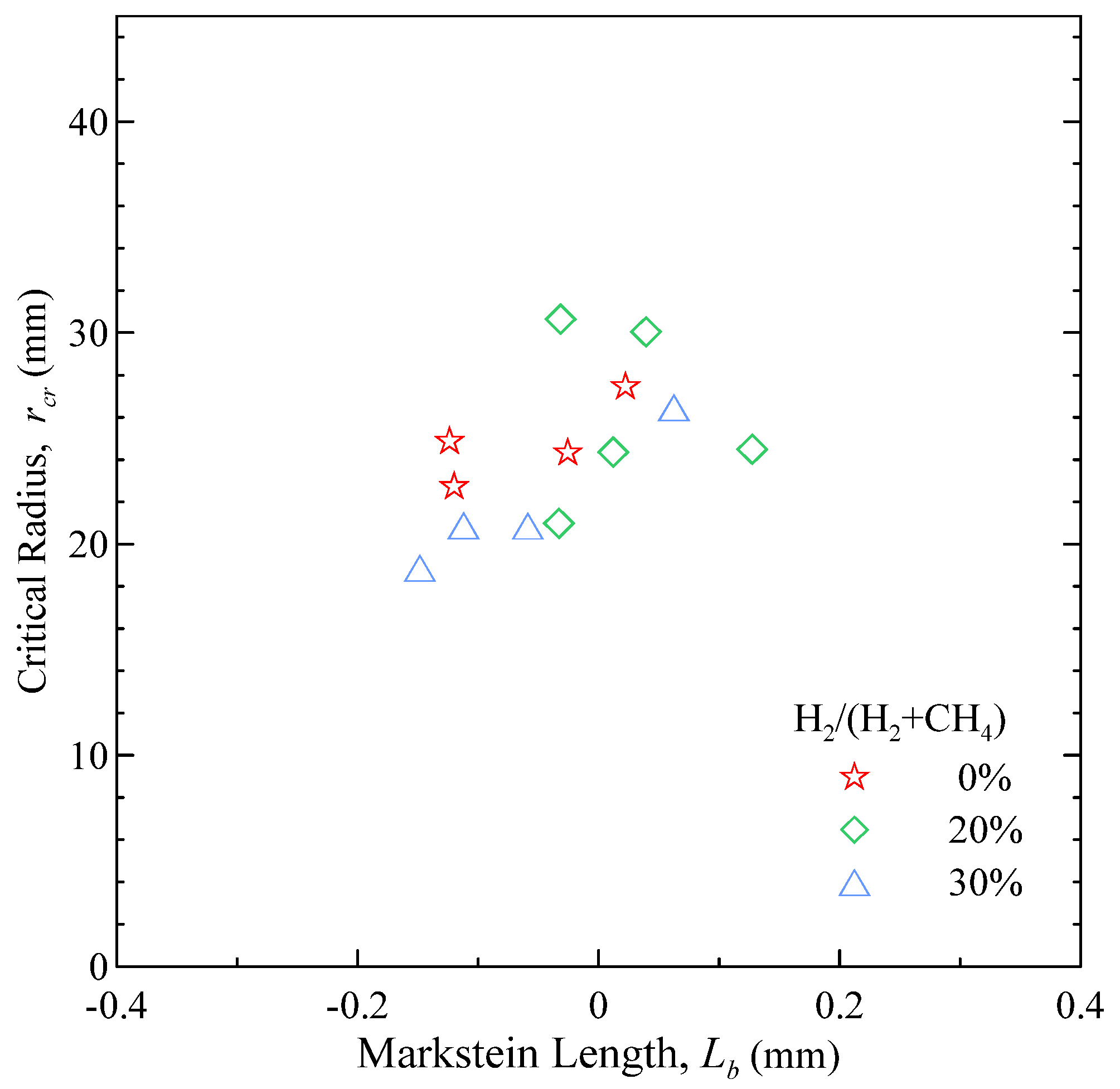
The morphological analysis appears to confirm the trends from the flame stretch analysis. As shown in
Figure 11, the critical radius
rcr exhibits a reasonable correlation with the Markstein length
Lb.
As far as the observed instabilities are concerned, it is well established that flame cellularity can be hydrodynamic and thermo-diffusional in nature (if body-force effects are absent).
Figure 10.
Critical radius for the onset of flame instability as a function of the starting pressure, for stoichiometric CH4 and H2-enriched mixtures at room temperature.
Figure 10.
Critical radius for the onset of flame instability as a function of the starting pressure, for stoichiometric CH4 and H2-enriched mixtures at room temperature.
Figure 11.
Critical radius for the onset of flame instability versus Markstein length.
Figure 11.
Critical radius for the onset of flame instability versus Markstein length.
Hydrodynamic instability is caused by the density difference across the flame. It is expressed by the thermal expansion ratio of the burned to the unburned mixtures, and is always present for all flames [
38].
Thermo-diffusional instability originates from the diffusive disparity of heat conduction from the flame and reactant diffusion towards the flame; it may not be present, if the flame is equidiffusive [
21]. The mixture parameter representing the effect of non-equidiffusion is the global Lewis number,
Le, defined as the ratio of the heat diffusivity of the mixture to the mass diffusivity of the limiting reactant to the abundant inert [
20,
21,
22]. Values of
Le > 1, =1 and <1 correspond to flames which are diffusionally stable, neutral of unstable, respectively.
In the case of a spherical expanding flame, cellular instability is initially suppressed by the strong curvature-induced stretch, associated with the corresponding small flame radii. As the flame expands, the stretch decreases, until a condition is reached in which cell development can no longer be suppressed and cells suddenly appear over the flame surface. This state depends on the combined effects of the hydrodynamic and diffusional–thermal instabilities.
The above-described transition can be expressed in terms of the critical Peclet number, obtained scaling the critical radius
rcr by the laminar flame thickness δ
l. An expression has been proposed of
Pecr as the sum of two terms, corresponding to hydrodynamic and diffusional–thermal instabilities [
40].
Being known
rcr and
Lb, the comparison can be drawn between the Markstein number (defined as
Lb/δ
l) and
Pecr: the results are shown in
Figure 12.
Actually, in the present conditions, expressing the comparison in terms of non-dimensional parameters does not add to a better understanding of the phenomena.
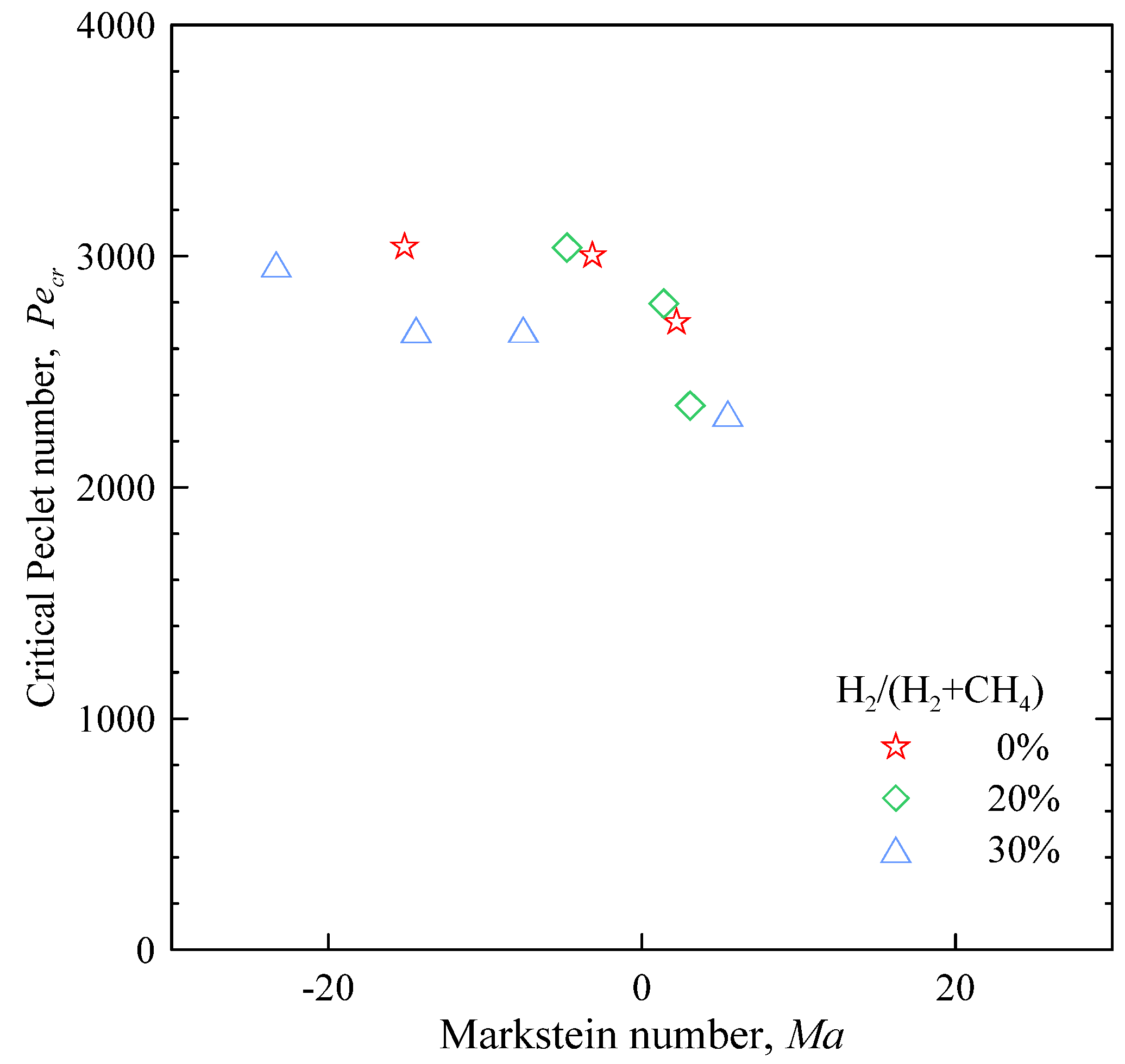
Figure 12.
Critical Peclet number versus Markstein number.
Figure 12.
Critical Peclet number versus Markstein number.
As shown in
Figure 12, the almost constant value of
Pecr suggests the flames are equidiffusive in nature [
40], yet negative values of
Ma stand for
Le < 1: such values correspond to flames where the deficient reactant is the more diffusive one, so that thermo-diffusive instability (of cellular nature) is promoted. Then one should expect
Pecr to increase with
Le, but data show a reversed trend.
The described behaviour prevents a straightforward identification of the role of the hydrodynamic and thermo-diffusive terms in the global Pecr. Pending a deeper theoretical analysis, a possible explanation of this apparent incongruity could reside in the different conditions in which Lb and rcr have been evaluated: while the former is a parameter obtained in the isobaric phase of flame development, the latter was measured later, when the global pressure in the chamber was increasing. The unpredictability of the results could be due to the scaling by δl, since this parameter is meaningfully defined in the isobaric phase.
6. Conclusions
The effect of the initial pressure and of the H2 content on the combustion of CH4-H2-air mixtures was investigated studying spherical expanding flames. Laminar burning parameters (unstretched burning velocity, burned-gas Markstein length) and flame instability characteristics (critical radius for the onset of cellularity) were evaluated for mixtures with different H2 percentage (0%, 20% and 30% vol.), equivalence ratio = 1.0, initial temperature T0 = 293÷305 K and initial pressure P0 = 3÷18 bar.
The obtained results allowed to assess quantitatively the effect of pressure and of H2 amount: the laminar burning velocity was found to decrease with the former and increase with the latter. The flame stability decreased when any of the two parameters was increased.
The laminar burning velocity and the Markstein length were found to be in good agreement with published data, wherever available. As a matter of fact, the present results extend the data published so far in literature, as far as high-pressure, stoichiometric H2-enriched mixtures are concerned.
In agreement with the observed behaviour of the Markstein length, the results on flame cellularity highlight the increasing relevance of the phenomenon at high pressures and/or for significant concentrations of hydrogen.
The main findings can be summarized as follows:
If the initial pressure is increased, the laminar burning velocity decreases and the Markstein length becomes negative. In the case of CH4, when P0 is raised from 3 to 18 bar, ul0 decreases by ~40%. In the same conditions, Lb shifts from about 0.20 to −0.07.
If H2 is added to CH4, the burning velocity increases. At P0 = 3 bar, ul0 increases by ~25% if the amount of H2 in the mixture is 30%. The Markstein length of H2-enhanced mixtures is shifted to smaller values, if compared to pure CH4, and becomes negative at P0 > 6 bar.
The behaviour of ul0 vs. P0 follows a power law, with exponent β = −0.45 for CH4. The magnitude of β decreases with the amount of H2.
The critical radius for the onset of cellularity was found to decrease when either the pressure or the H2 content in the mixture were increased. At P0 = 3 bar, regardless of the amount of H2, no sign of instability was observed; at P0 > 6 bar, the flame get increasingly unstable with the amount of H2. The critical radius shows a good correlation with the Markstein length.
The present findings offer a quantitative frame of reference for the burning properties of CH4-H2, highlighting the specific features of the combustion process in condition typical of i.c. engines.