1. Introduction
Photovoltaic (PV) systems can be characterized by their input voltages, currents, and number of inputs. A number of studies have been conducted to evaluate the efficiency and characteristics of the cell connection structure in multi-input PV systems [
1,
2,
3,
4,
5,
6]. Many studies have shown that multi-input systems have higher maximum power point tracking (MPPT) performance than single-input systems [
7,
8,
9].
There are two types of grid-connected PV system structures: (1) those that contain only a DC/AC converter and (2) those that contain both a DC/AC converter and a DC/DC converter. Systems containing only a DC/AC converter generally require a 600 V (three-phase) input and 350 V (single-phase) input for the grid-connection. Furthermore, PV systems cannot be operated under high temperature and low solar radiation conditions. These conditions cannot guarantee the 600 V (three-phase) PV input voltage or 350 V (single-phase) PV input voltage.
These drawbacks are eliminated when the PV system contains both a DC/DC converter and a DC/AC converter. In this structure, the DC/DC converter can be selectively designed as the boost converter, the buck converter, or the buck-boost converter, depending on the PV cell connection. The buck-boost converter is the best design for obtaining the maximum MPPT range; however, it is less efficient than a simple boost or buck converter [
10,
11]. For PV power systems of 10 kW or less, the boost converter is the best choice due to the high efficiency and the usability of the connection. Under the usual weather conditions, the PV cell connections of 10 kW has the voltage range below 600 V.
In a multi-input PV system with both a DC/DC converter and a DC/AC converter, there are two types of MPPT control methods. These methods depend on where the control system is implemented [
12]. In the first method, the boost converter controls the MPPT independently and the inverter implements DC-link voltage control for the grid-connection [
13]. In the second method, the boost converter controls the DC-link voltage and the inverter performs MPPT control [
14,
15]. Both of these methods offer similar performance, but the first method has better scalability. However, if the MPP input voltage of PV systems is higher than the DC-link voltage, the MPPT cannot be implemented for both of these methods. In other words, the MPPT range is limited by the reference voltage. In this case, if the high DC-link reference voltage is set to extend the MPPT range, it will cause a large output current ripple in the inverter. To solve this problem, the filter must be designed with higher inductance. Another solution to this problem is by making the input voltage of PV cells smaller than the value of the DC-link reference voltage; however, this solution limits the number of input PV cell combinations. Moreover, if the PV cells are connected to a low input voltage, this will increase the boost converter’s rated current. The switching device should be chosen on the basis of this information.
This paper presents an algorithm that varies the DC-link voltage based on the input voltage. The proposed algorithm is designed to have a wide MPPT estimation range while maintaining the DC-link voltage with minimal current ripple.
2. Configuration of a Two-String PV System
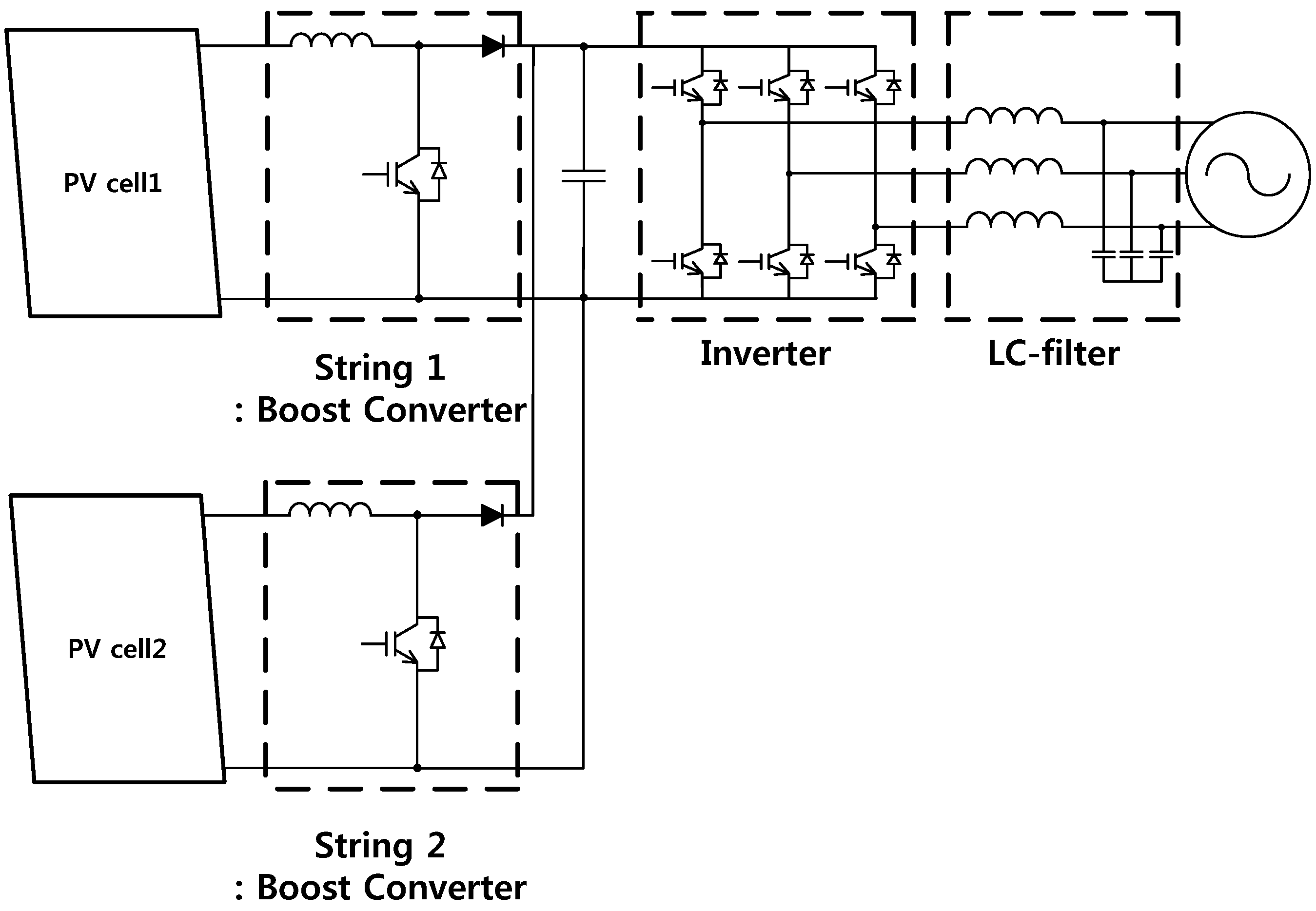
A PV system using two-string inputs consists of two boost converters, an inverter and an LC-filter and is depicted in
Figure 1. The boost converters share the output, which is connected to the DC-link capacitor. The DC-link capacitor transfers power to the grid. The total power is divided across the two inputs. In this paper, the total power is divided as 7 kW on string 1 and 3 kW on string 2.
The current ripples to the DC-link capacitor cause a DC-link voltage ripple. This voltage ripple causes a corresponding ripple in the output currents from the inverter. Therefore, the boost converters use the interleaved method to reduce the input current ripples [
16,
17]. The ON point of the switching device of string 1 is shifted from the ON point of the switching device of string 2 by half the switching period.
Figure 1.
The configuration of a two-string PV system.
Figure 1.
The configuration of a two-string PV system.
2.1. Boost Converter Control
The MPPT algorithm is implemented in the boost converters. Each boost converter’s operation is reflected in each MPPT algorithm. The MPPT algorithm for each string calculates the duty-cycle of the boost converter using its voltage and current. Therefore, each MPPT algorithm is implemented independently on the associated strings.
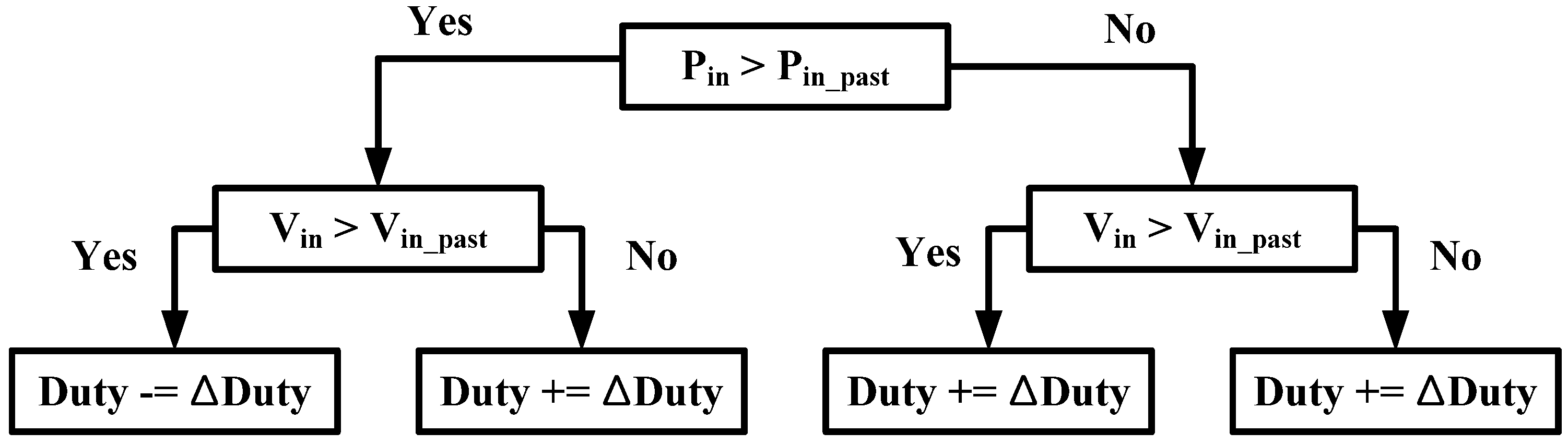
The MPPT algorithm is based on Perturb-and-Observe (P&O) algorithm. Many P&O algorithms have been studied [
18,
19,
20,
21], and most of them are simple. However, operation near the maximum power point (MPP) causes vibrations. The solution to this problem is to reduce the duty-cycle variation (Δduty) when operating near MPP [
22] or to use a PI controller [
23]. A drawback of the first approach is that the calculation for Δduty is sensitive to errors when the output power is low and the MPPT algorithm is initiated. If the sensing noise of the voltage and current is large, the calculation will not be accurate because Δpower is small relative to Δduty. The second approach requires accurate modeling of
Figure 1 and the steps of the controller’s gain setting.
In this paper, the first approach is used to prevent vibration at MPP, as shown in
Figure 2, and duty is increased or decreased according to the power and the voltage of the PV cells. An appropriate initial duty-cycle value is chosen to avoid the problem associated with low power. The power (P
in) from the strings is calculated as shown in Equation (1):
The input current (Iin) contains the switching ripple of the boost converter. Therefore, the filtering value of the input current (Iin) is used in the input power calculation.
Figure 2.
P&O algorithm for MPPT.
Figure 2.
P&O algorithm for MPPT.
The power delivery is required when the boost converter generates a higher output voltage than the DC-link voltage. There must be sufficient duty-cycle to enable this increase in power delivery and to avoid the problems associated with low power. The initial duty-cycle value is calculated as shown in Equation (2):
where
Vout is the DC-link voltage.
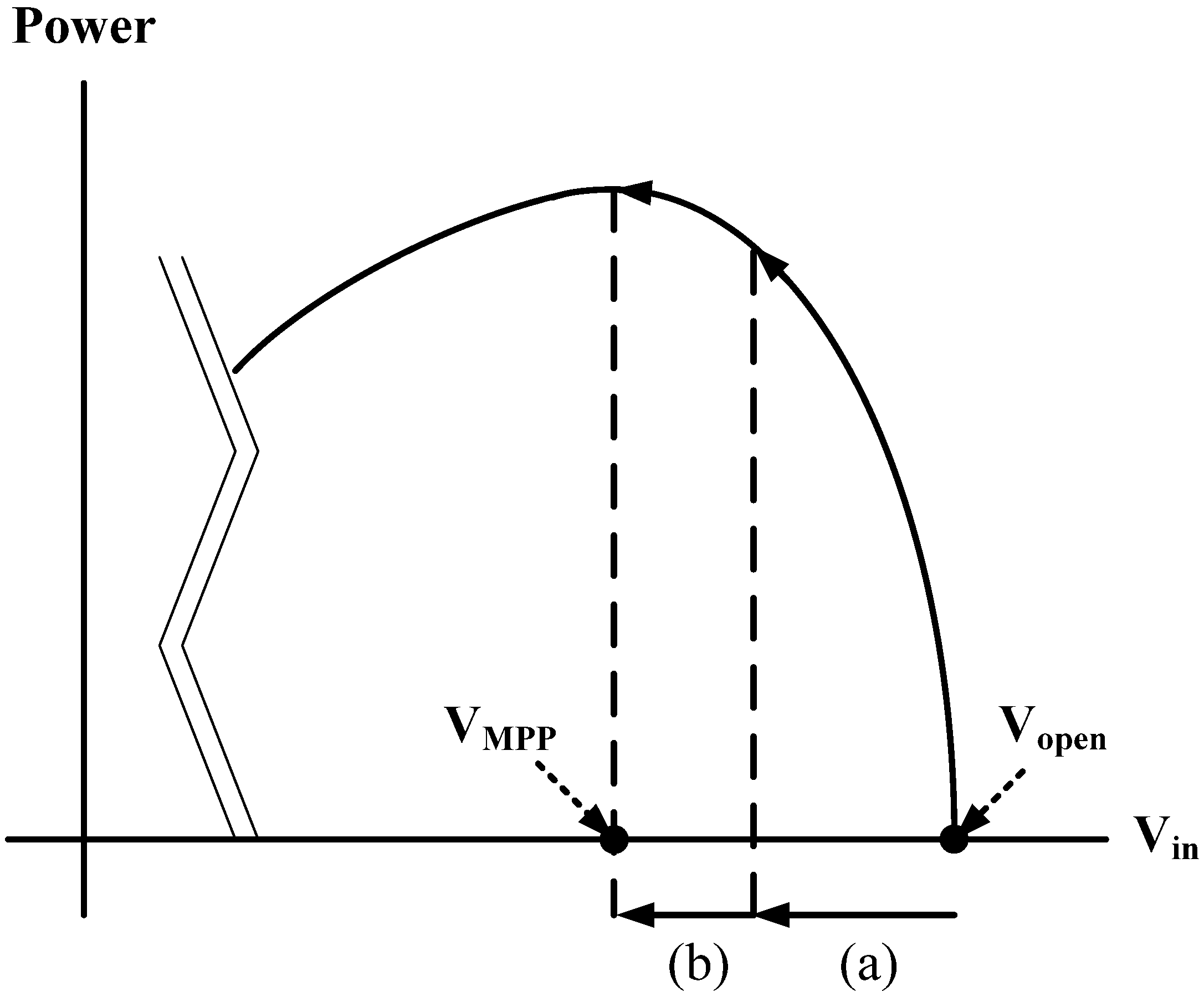
Figure 3 illustrates the operation of the MPPT algorithm at the initial duty-cycle (a) and MPP after the duty-cycle is reached (b).
Figure 3.
MPPT operation: the initial condition (a) and the later condition (b).
Figure 3.
MPPT operation: the initial condition (a) and the later condition (b).
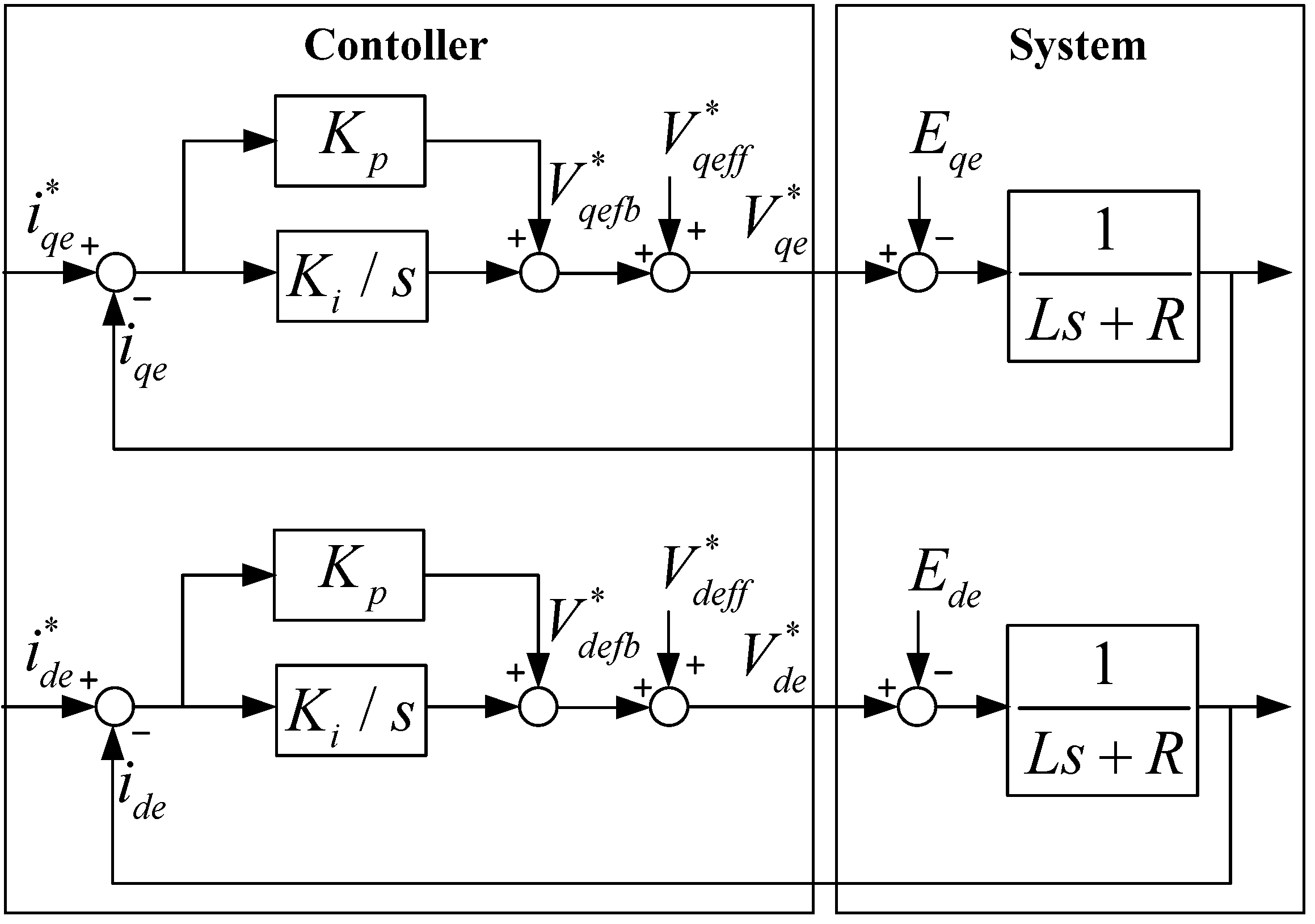
2.2. Inverter Control
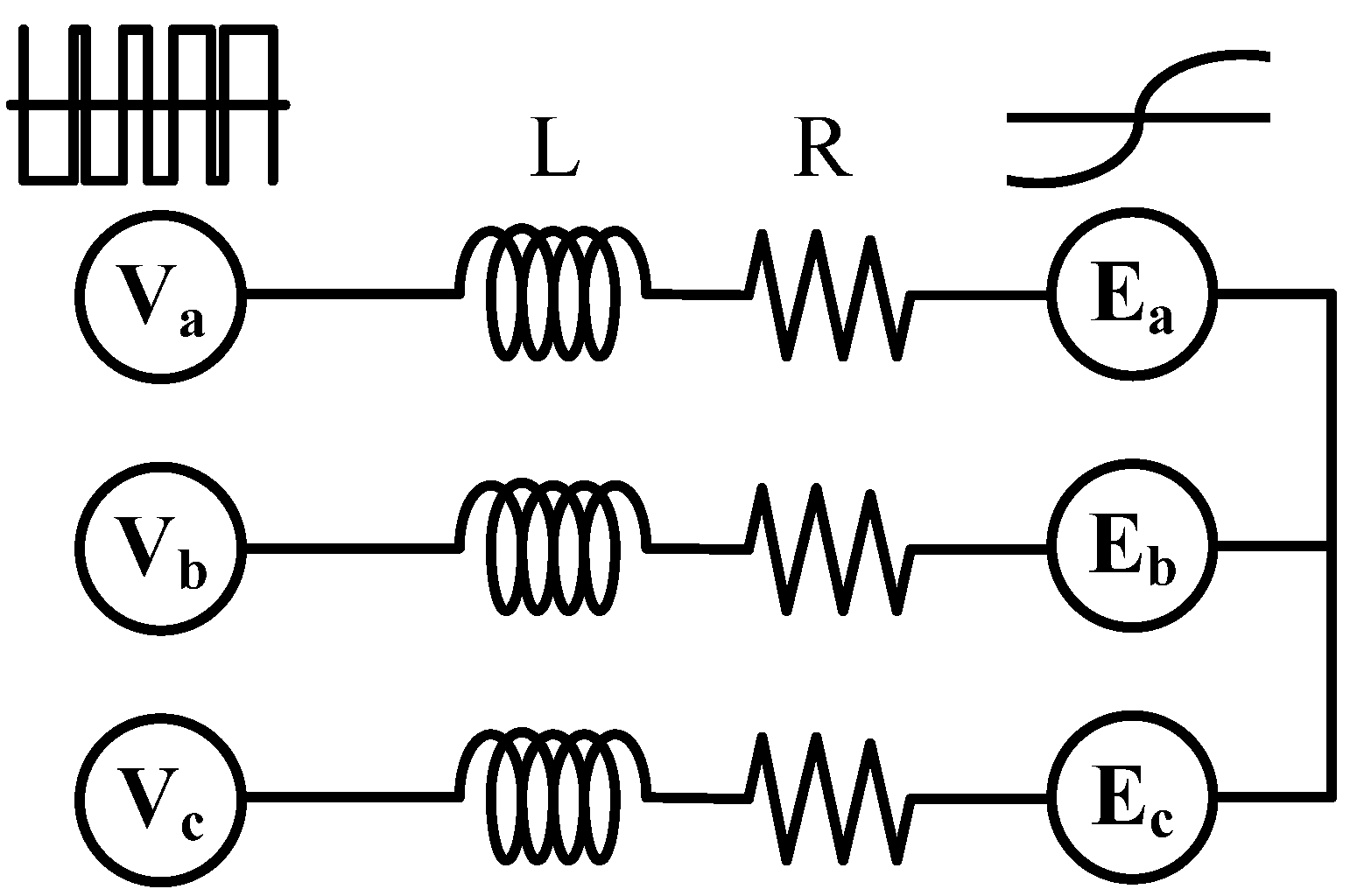
The inverter handles the grid connection control. The modeling for the DC-link voltage control is based on Sannino’s modeling method [
24]. An inverter with a grid is modeled for the current control as shown in
Figure 4.
Figure 4.
The model of the inverter with the grid.
Figure 4.
The model of the inverter with the grid.
Equation (3) shows the inverter output voltage values for
Va,
Vb, and
Vc:
Three-phase voltages (
Va,
Vb,
Vc) are transformed to voltages (
Vds,
Vqs) of stationary d-q axis by using Equation (4). The grid voltages (
Ea,
Eb,
Ec) and the grid currents (
Ia,
Ib,
Ic) are transformed to the stationary d-q axis.
Vds and
Vqs are expressed as shown in Equation (5):
The grid angle is used to change the value of the stationary d-q axis to the value of the rotating reference d-q axis. The calculated values to the rotating reference using the grid angle has only a DC-component and these are expressed as by Equation (6):
where
Eqe has a constant value that has the same magnitude of grid and
Ede is zero.
Equation (6) is transformed into an s-domain function by the Laplace transformation. The input signal of controller is grid currents and the output signal of controller is output voltages of the inverter. The transferred function which is the system function is expressed as in Equation (7):
To apply the PI-controller, Equation (7) and the feed-forward components (
Vdeff and
Vqeff) are considered as shown in
Figure 5. A proportional gain (
Kp) and a integration gain (
Ki) of the PI-controller should be selected by calculating the transfer function of
Figure 5 by assuming that
Vdeff is same as
Ede and
Vqeff is same as
Eqe. Then,
Eqe and
Ede are eliminated and the transfer function of
Figure 5 can be simplified as shown in Equation (8):
To simplify the transfer function,
Kp and
Ki gains are selected as shown in Equation (9).
The transfer function can then be represented as a first-order function with a bandwidth of
ωcc:
Figure 5.
The current controller block diagram of the inverter.
Figure 5.
The current controller block diagram of the inverter.
The controller applies compensation control for the 5th and 7th harmonics. It uses a PI-controller and the fundamental angle from Rolim’s PLL algorithm, which has outstanding performance owing to its use of disturbance injection [
25]. This algorithm detects the grid angle (
θg) by adding a low-pass filter to the basic PLL algorithm.
The 5th harmonic of the inverter’s output current is compensated by transferring the output current from the stationary reference frame to the rotating reference frame. Then the 5th harmonic component is represented as the DC value by five times fundamental angle. All the other components except the DC component are then eliminated using a low-pass filter:
Equation (11) shows the transformation equations which are used to translate the rotating reference frame in order to detect the 5th harmonic component. In Equation (11), the 5th harmonic compensation uses a negative angle because the 5th harmonic component is located in the negative region of the grid [
26]. The compensation for the 7th harmonic uses a positive angle and steps taken for 7th harmonic compensation are the same as those for the 5th harmonic compensation.
Figure 6 shows the inverter control block diagram which contains a DC-link voltage controller, a current controller which is the controller part of
Figure 5, and harmonic compensation controller.
Figure 6.
The total block diagram of the inverter.
Figure 6.
The total block diagram of the inverter.
3. Variable DC-Link Control Algorithm
Typically, a three-phase grid-connected inverter sets the DC-link voltage at 600 V to reduce the output current ripple. THD is affected by the grid side filter. The grid side filter design method is presented [
27,
28,
29,
30,
31]. References [
29] and [
30] show the current patterns according to the inverter switching method and present the grid current ripple corresponding to the grid angle (
θg). In the reference [
30], these values of grid current ripples with space vector pulse width modulation (SVPWM) are mathematically calculated as:
where
Ts is the switching period,
and:
From Equation (12), the high DC-link voltage can cause a THD increment. Furthermore, the results of the designed L-filter values according to the DC-link voltage are presented in [
31]. These results show that in the high DC-link voltage, a large value inductance is needed to maintain the current ripple equal to that of the low DC-link voltage. Equation (12) and the results from [
31] cover the inductance of the L-filter. In the LC-filter and LCL-filter design, the inductance calculation is based on the L-filter design method and the C-part or the CL-part is chosen for the additional ripple reduction.
If the inverter uses a higher DC-link voltage, a large filter will be needed for the same performance as the inverter with a DC-link voltage of 600 V. On the other hand, a higher DC-link voltage is necessary to achieve a wider MPPT range. The increase in THD for better performance is acceptable when the input voltage is greater than 600 V. However, it is unnecessary to increase THD when the input voltage is less than 600 V.
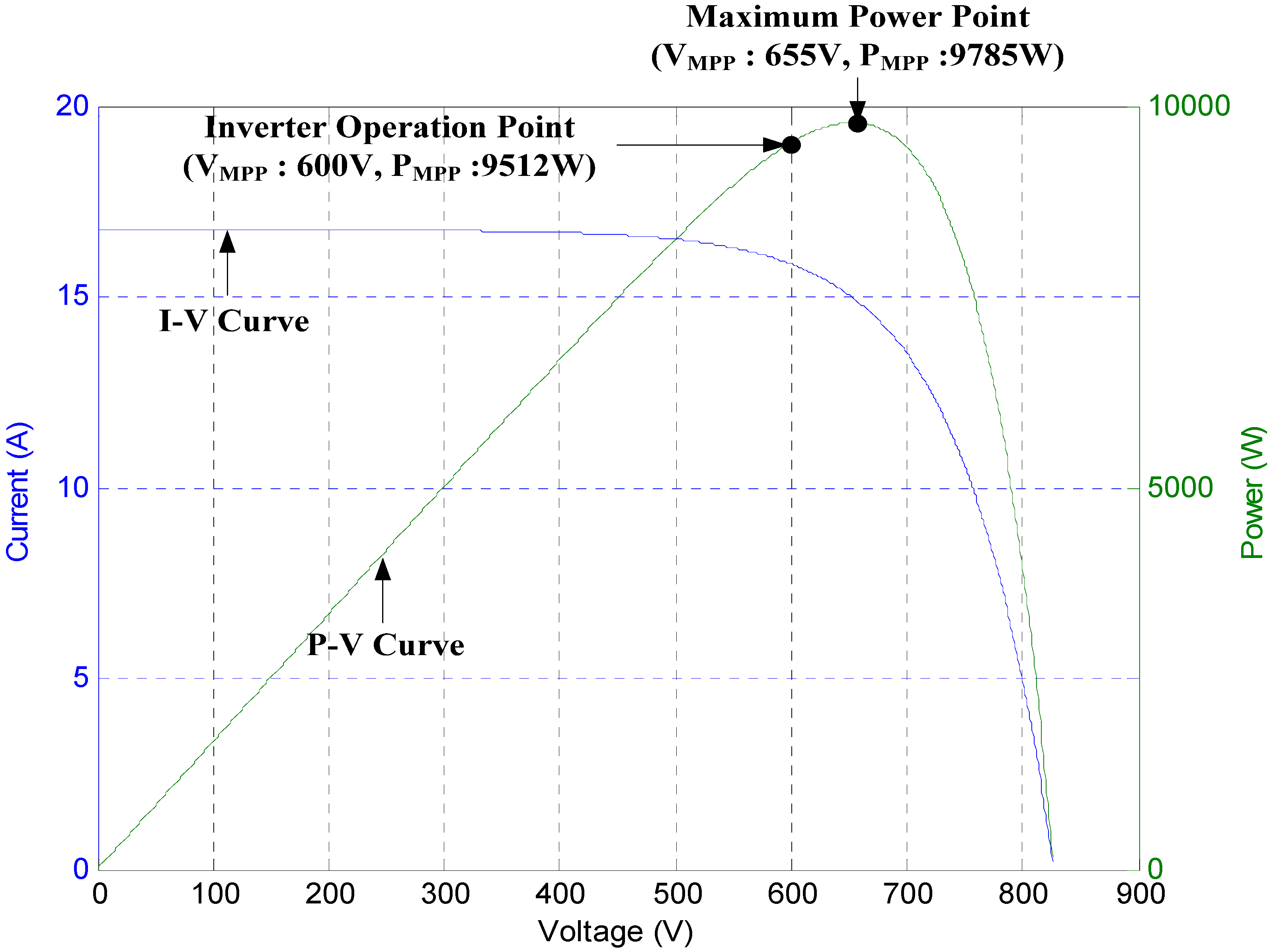
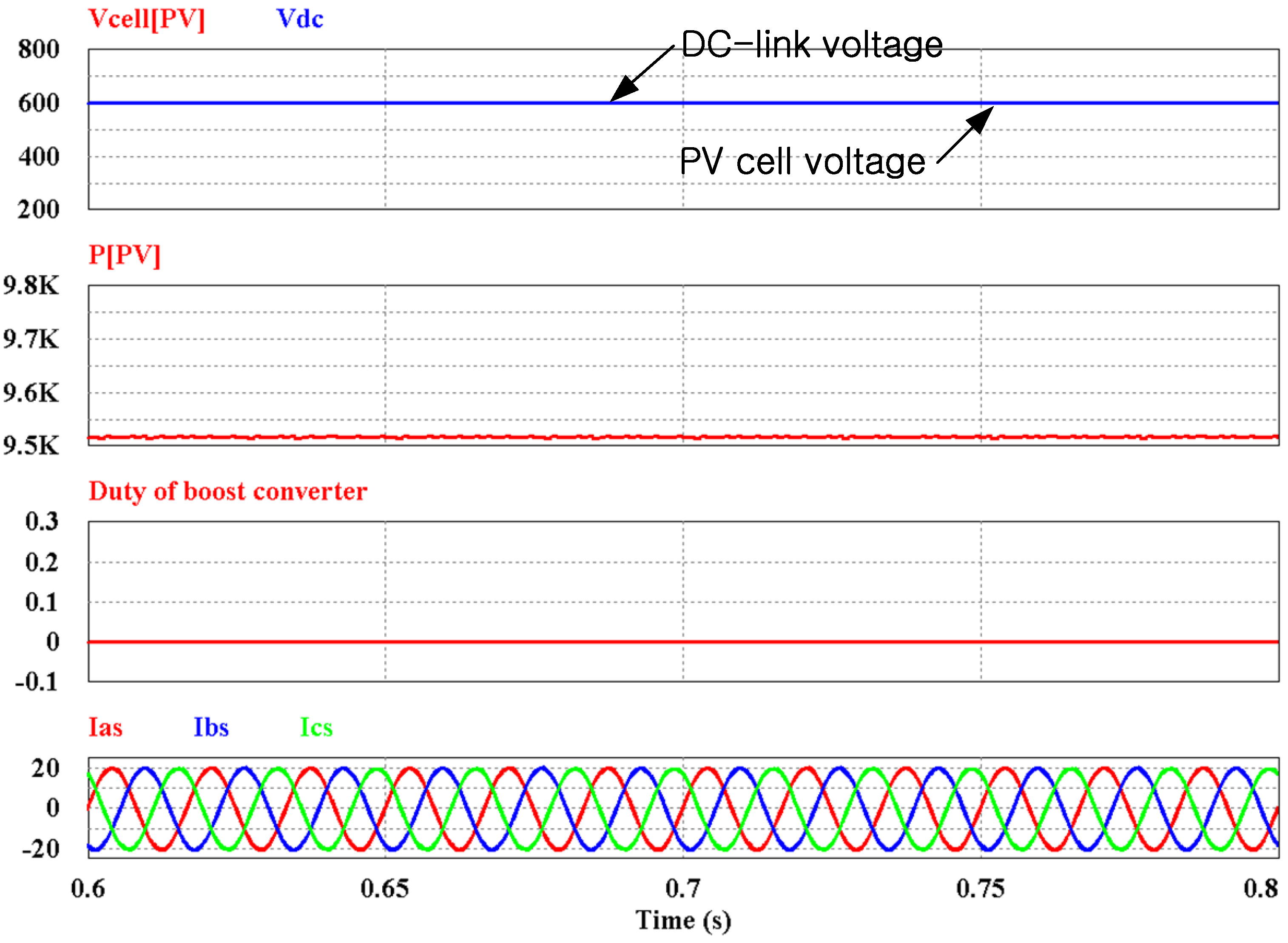
If the MPP voltage of PV cells is 655 V in the curve of
Figure 7 and the DC-link reference voltage is 600 V, the boost converter does not operate and the voltage of the PV cells is maintained at 600 V. This result is shown in
Figure 7 and
Figure 8. Although the PV cells maximum power is set to 9785 W, the power from the PV cells is 9512W because the inverter controls the DC-link voltage to be 600 V. Also the duty-cycle of the boost converter is zero. It means that the boost converter is not operating. The power loss is 233 W (
i.e., 9785–9552 W) due to the tracking limitation. As the MPP voltage is increased, the power loss is larger.
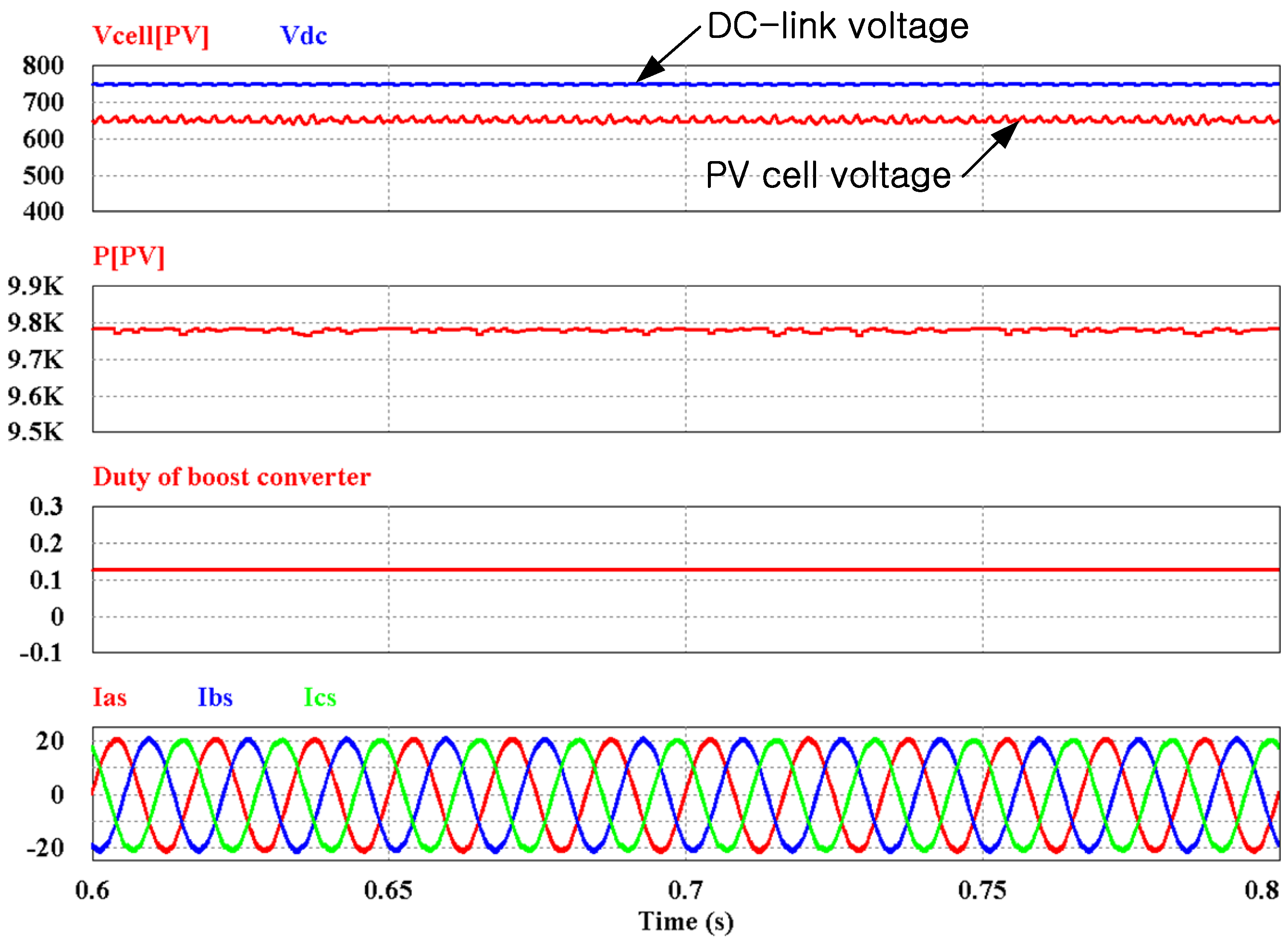
The maximum power is transferred by setting the DC-link reference voltage to be larger than the MPP voltage of PV cells.
Figure 9 shows these results. The DC-link voltage is 750 V, and the PV cells voltage is 655 V like the MPP voltage. The duty of boost converter is not zero because the MPPT algorithm is performed by the boost converter. In contrast with the result of
Figure 8, the power from the PV cells is increased to 9785 W which is the PV cells’ maximum power. Therefore, we propose a DC-link voltage control method that is based on the input voltage.
Equation (14) expresses the optimal method for changing the DC-link voltage over 600 V:
Figure 7.
The inverter operation point and the maximum power operation point in the PV cells characteristic curve.
Figure 7.
The inverter operation point and the maximum power operation point in the PV cells characteristic curve.
Figure 8.
Simulation results: MPP is 655 V and the DC-link reference voltage is 600 V.
Figure 8.
Simulation results: MPP is 655 V and the DC-link reference voltage is 600 V.
Figure 9.
Simulation results: MPP is 655 V and the DC-link reference voltage is 750 V.
Figure 9.
Simulation results: MPP is 655 V and the DC-link reference voltage is 750 V.
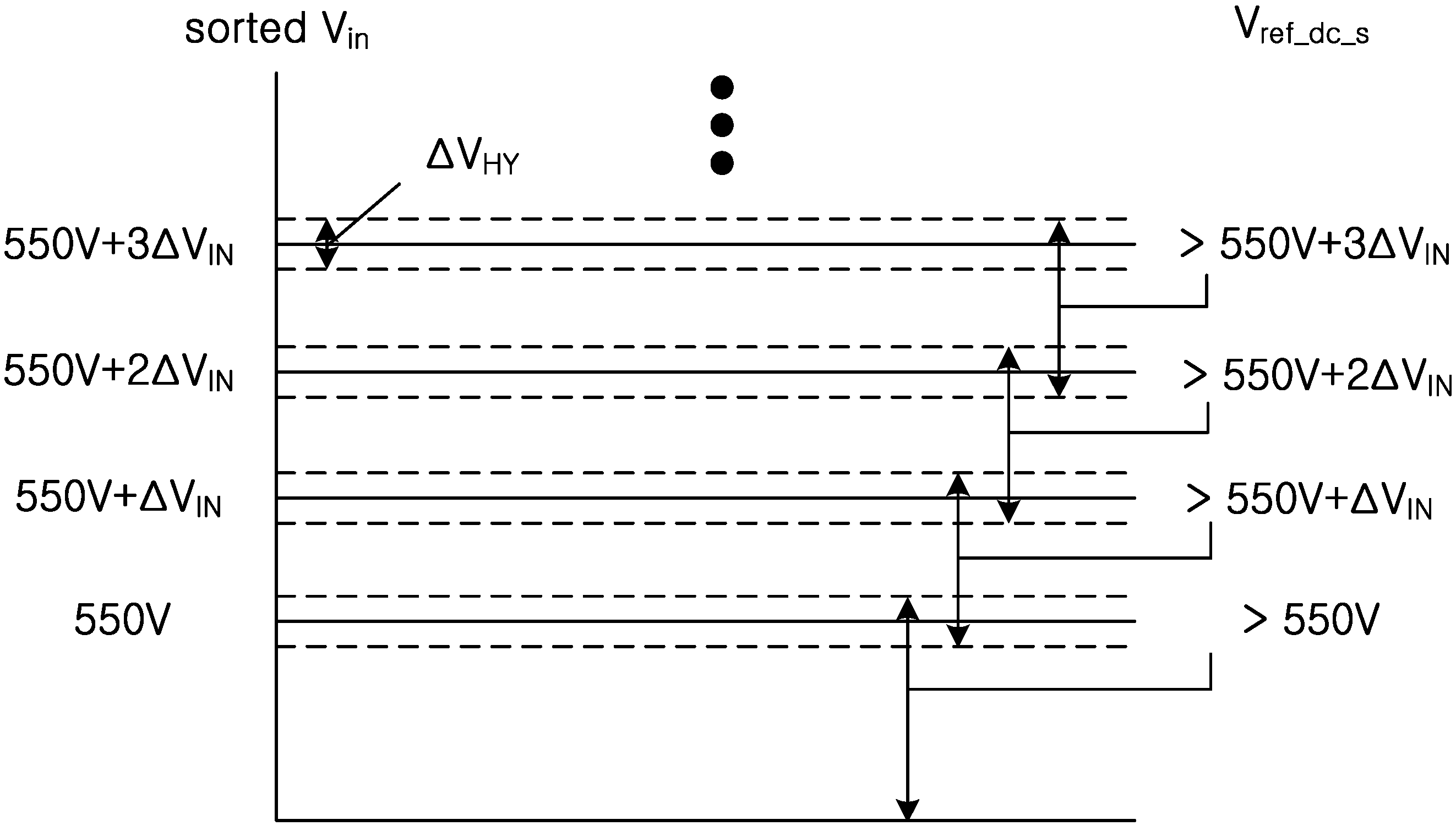
Figure 10 shows a basic concept of the proposed algorithm. The performance characteristics and THD of the output current are determined by the selection of Δ
VIN and Δ
VHY. THD will be unnecessarily increased if Δ
VIN is too large; therefore, a relatively small value has to be chosen for Δ
VIN by considering the sensing noise. This noise causes frequent changes in the DC-link voltage reference. Moreover, Δ
VIN should be larger than the variation of the DC-link voltage.
Figure 10.
Range setting of the variable DC-link algorithm.
Figure 10.
Range setting of the variable DC-link algorithm.
If the variation is larger than Δ
VIN, the DC-link reference is changed continuously. This also causes the stability problem. Δ
VHY must be chosen to prevent the change in the DC-link reference voltage at the boundary between input voltages and is not applied at the system initialization. The DC-link controller should not generate any overshoot because the overshoot halted the power delivery from the PV cells to the DC-link capacitor which leads to that the PV cells voltage increases to change the DC-link reference voltage. Therefore, the actual DC-link reference voltage (
Vref_dc_a) is designed to produce a ramp response after the DC-link voltage is selected (
Vref_dc_s) according to the sorted input voltage. The ramp response is calculated on the basis of the cut-off frequency of the DC-link voltage controller and should be slower than the response of the DC-link voltage controller. Finally, this algorithm is related to the MPPT operation of the boost converter. The boost converter should quickly increase and decrease the duty of the boost converter to maintain the current output power during the DC-link reference change. There are two cases of the DC-link reference change. One is when the DC-link reference is increased and another is when the DC-link reference is decreased. In the first case, the boost converter with the slow response speed cannot deliver the power of the PV cells due to the sudden DC-link voltage increase and the small duty it previously had. This means that the current of the PV cells is decreased and the input voltage of the PV cells is increased simultaneously and then the DC-link reference voltage is increased once more. Consequently, the DC-link voltage is increased until the input voltage of the PV cells becomes the same as the open voltage of the PV cells. In the second case, the boost converter cannot deliver the power due to the previous large duty. This previous large duty causes the large current and the PV (input) voltage to be decreased. Consequently, the DC-link reference voltage is decreased to the initial voltage of DC-link reference. The proposed algorithm has been simulated and demonstrated experimentally with the settings as shown in
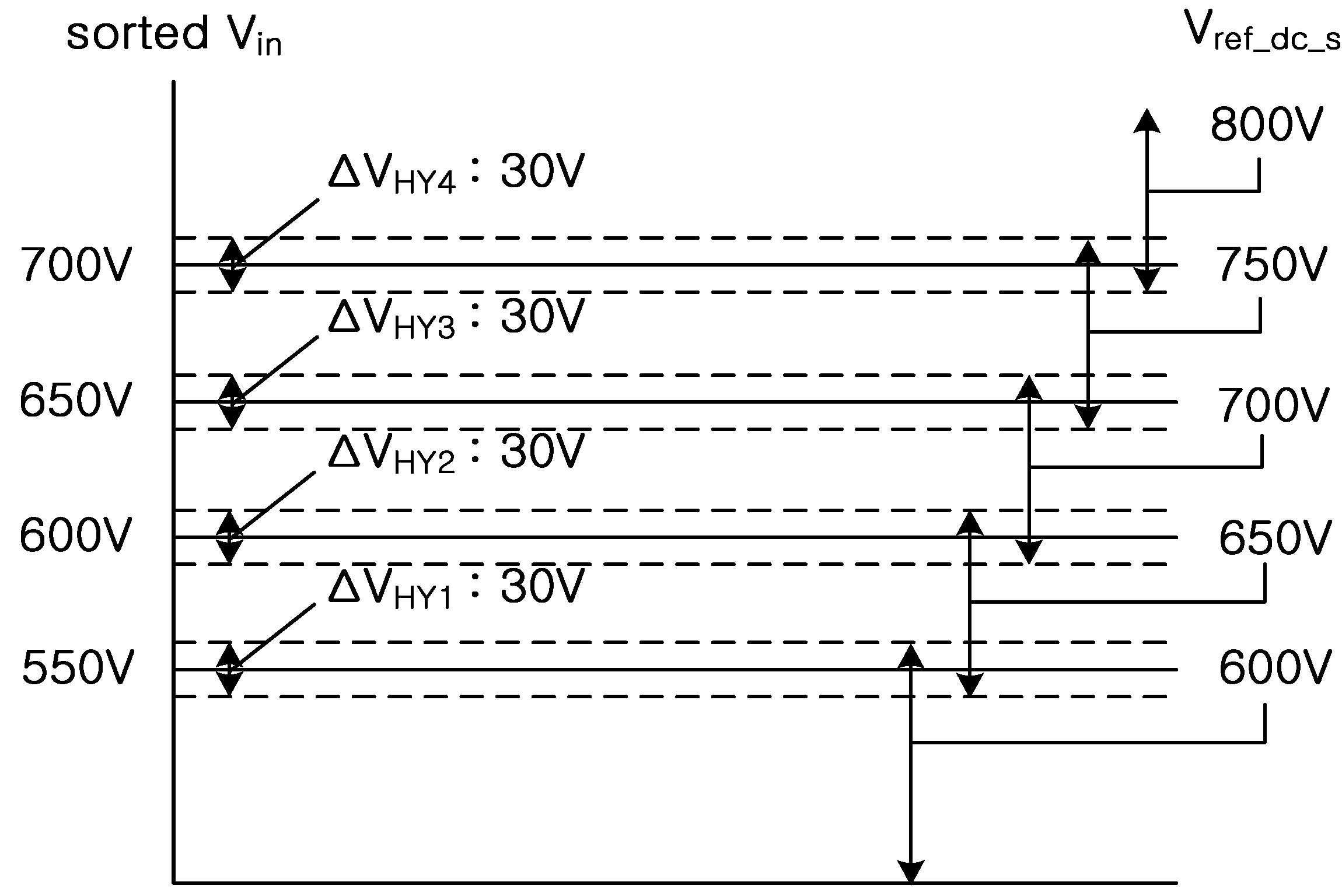
Figure 11.
Figure 11.
The used range in the simulations and the experiments.
Figure 11.
The used range in the simulations and the experiments.
The maximum voltage of the PV cells is assumed to be lower than 800 V. By considering the noise component of the experimental set, the value of ΔVIN has been chosen through experiments as 50 V to minimize the increment of THD; the value of ΔVHY is 30 V.
4. Simulation
The proposed algorithm has been simulated using PSIM. The simulation circuit is as shown in
Figure 1. The circuit parameters are chosen for a 10 kW system. The input inductances of the boost converters are 1.5 mH, the capacitance of DC-link capacitor is 1100 µF, and the inductance and capacitance of LC-filter parameters are 2 mH and 4.7 µF. The switching frequency for both the boost converter and the inverter is 20 kHz. The three-phase grid uses a 380 V line-to-line voltage. The
ωn value for the DC-link voltage controller is 300 rad/s, and 500 V/s is used as the ramp response of the DC-link reference voltage. The period of the MPPT algorithm calculation is 0.05 s and Δduty-cycle is 0.005. The temperature of the PV cells is increased or decreased in order to characterize the performance of the algorithm.
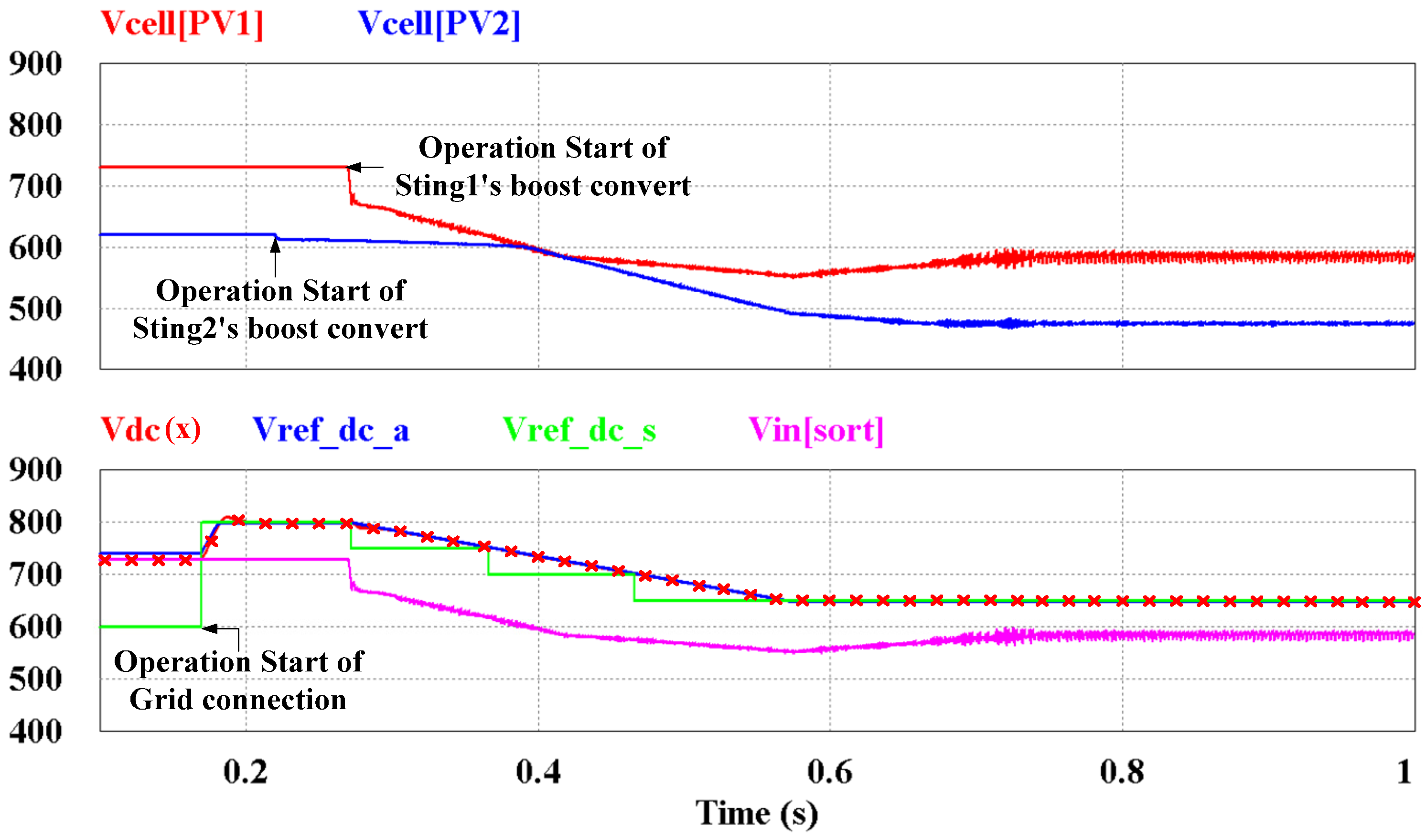
Figure 12 illustrates the performance of the proposed algorithm when the PV system is initiated. The temperature of PV1 is set as the lower value than that of PV2. The initial DC-link reference voltage is 600 V, but is then set to 800 V in accordance with
Figure 11 because the sorted voltage is 730 V (the input voltage of PV1 is 730 V). The input voltage decreases when the boost convert starts operating. The decrease in the input voltage changes the DC-link reference. The selected DC-link voltage and the actual DC-link reference voltage with the 500 V/s ramp response is changed according to
Figure 11.
Figure 12.
Simulation results for the PV cells voltages, the DC-link voltage,
Vref_dc_a,
Vref_dc_a, and
Vin,sort from
Figure 11 when the PV system is initiated.
Figure 12.
Simulation results for the PV cells voltages, the DC-link voltage,
Vref_dc_a,
Vref_dc_a, and
Vin,sort from
Figure 11 when the PV system is initiated.
During the operation, the DC-link voltage is maintained over the sorted input voltage. This approach yields the minimum THD. By choosing the slower ramp response than the response of the DC-link voltage controller, the DC-link voltage follows the DC-link reference voltage as shown in
Figure 13.
Figure 13.
Simulation results for the DC-link voltage and Vref_dc_a.
Figure 13.
Simulation results for the DC-link voltage and Vref_dc_a.
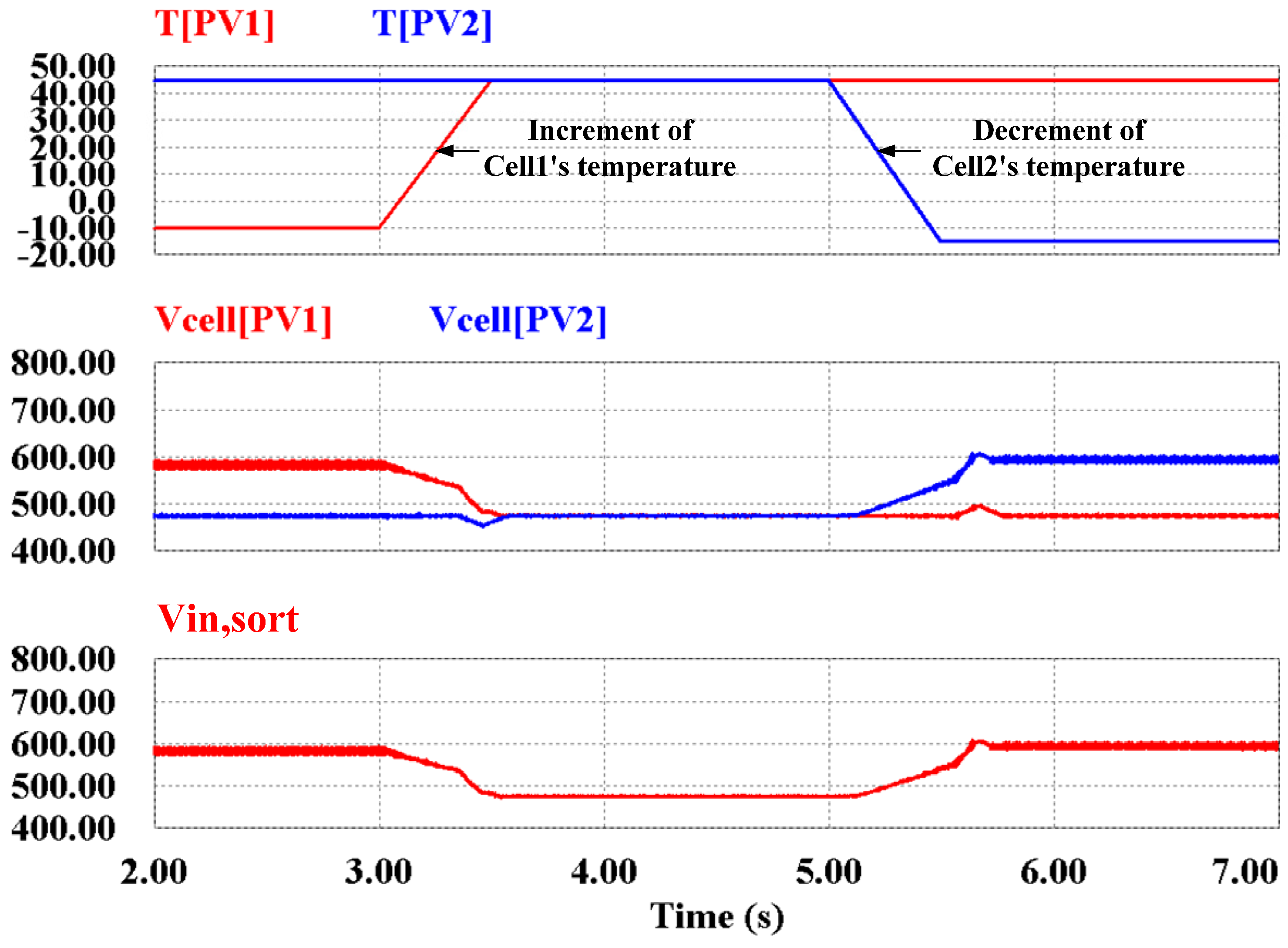
Figure 14 and
Figure 15 show the system’s performance when the temperature of PV1 is increased from −10 °C to 45 °C for 0.5 s and the temperature of PV2 is decreased from 45 °C to −15 °C for 0.5 s. The input voltage of PV1 decreases owing to the increase in the temperature, and the sorted voltage is chosen as the voltage of PV1. At this point, the MPPT algorithm of the string 1’s boost converter increases the duty-cycle to find MPP. In addition, the DC-link reference voltage decreases to 600 V when the sorted voltage decreases below the minimum of Δ
VHY3. Therefore the magnitude of the grid current is decreased because the PV’s temperature increase reduces its maximum power. Similarly, the input voltage of PV2 increases owing to the decrease in temperature, and the sorted voltage becomes the input voltage of PV2. Thus the DC-link reference voltage is selected according to the voltage of PV2. The DC-link reference voltage changes to 650 V when the sorted voltage increases above the maximum of Δ
VHY3. In addition, the duty-cycle of the MPPT algorithm for string 2’s boost converter is decreased to determine MPP and the grid current is increased.
Figure 14.
Simulation results for the temperatures of the PVs, two PV cells voltages, and the sorted voltage (Vin,sort) when the temperatures of the PV cells are changed.
Figure 14.
Simulation results for the temperatures of the PVs, two PV cells voltages, and the sorted voltage (Vin,sort) when the temperatures of the PV cells are changed.
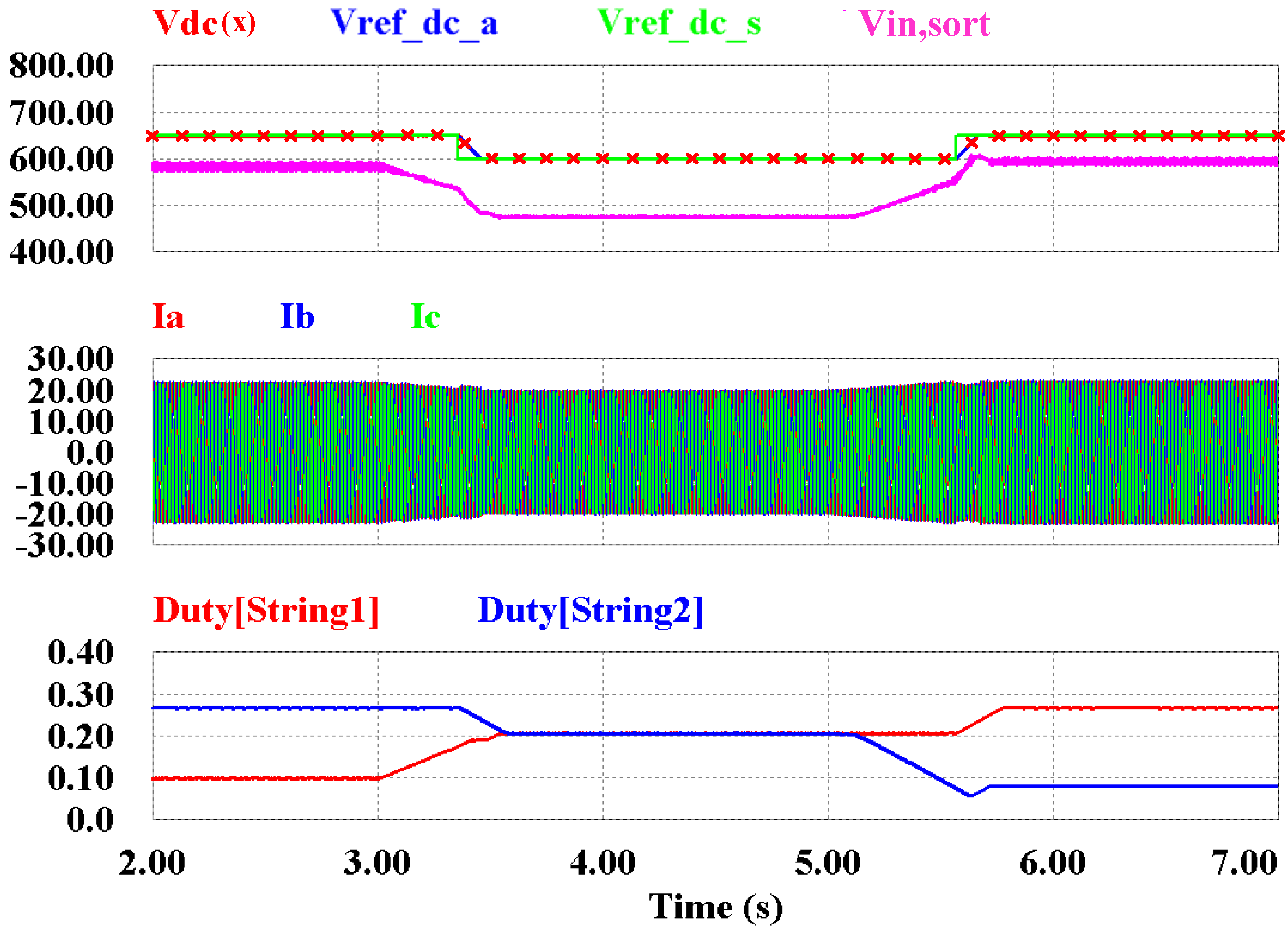
Figure 15.
Simulation results for the DC-link voltage, Vref_dc_a, Vref_dc_s, Vin,sort, grid currents and duty-cycles of the boost converters when the temperatures are changed.
Figure 15.
Simulation results for the DC-link voltage, Vref_dc_a, Vref_dc_s, Vin,sort, grid currents and duty-cycles of the boost converters when the temperatures are changed.
Figure 16a shows the results of the simulation using the DC-link reference voltage to 800 V at the same conditions and
Figure 16b is enlarged from
Figure 15.
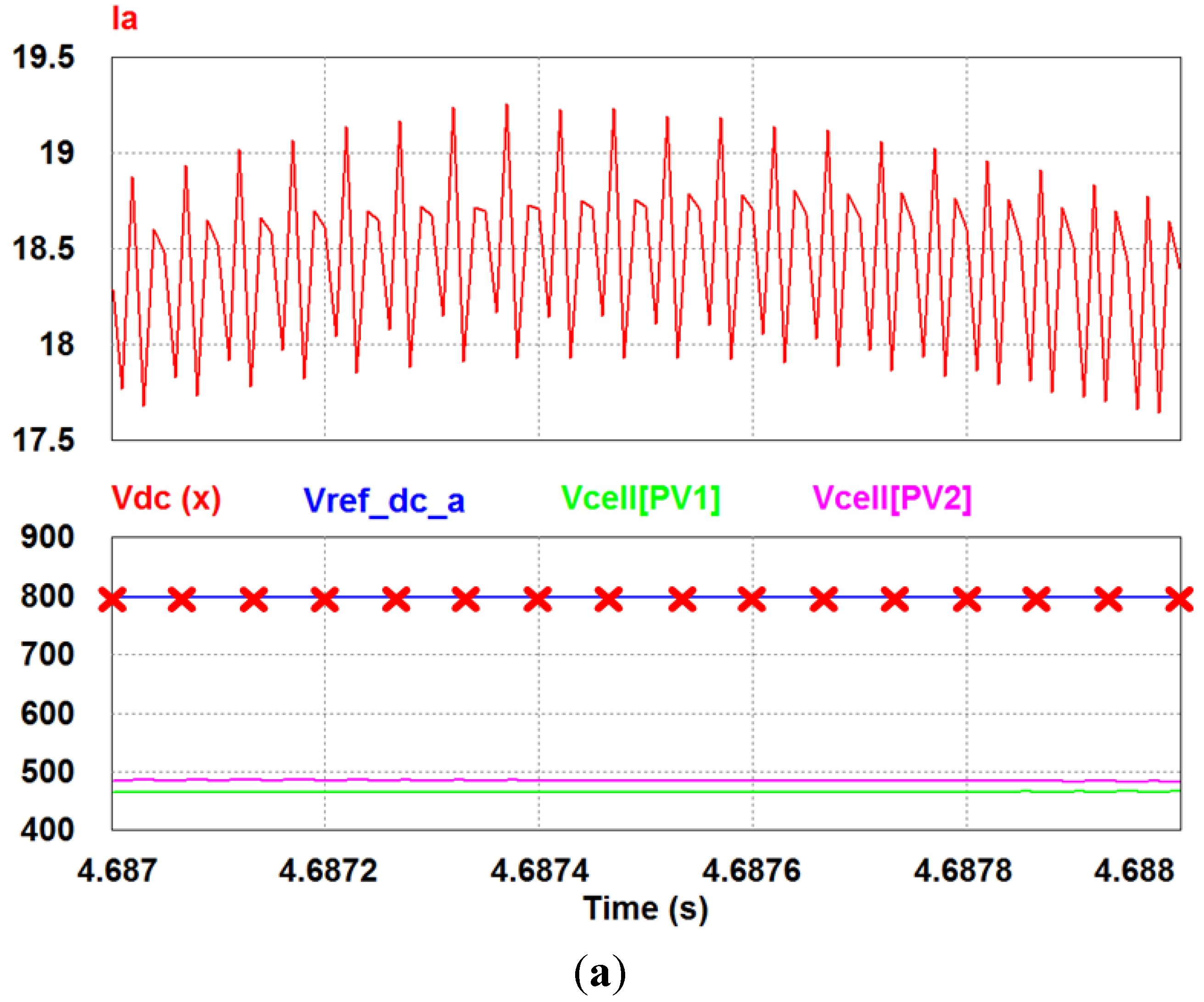
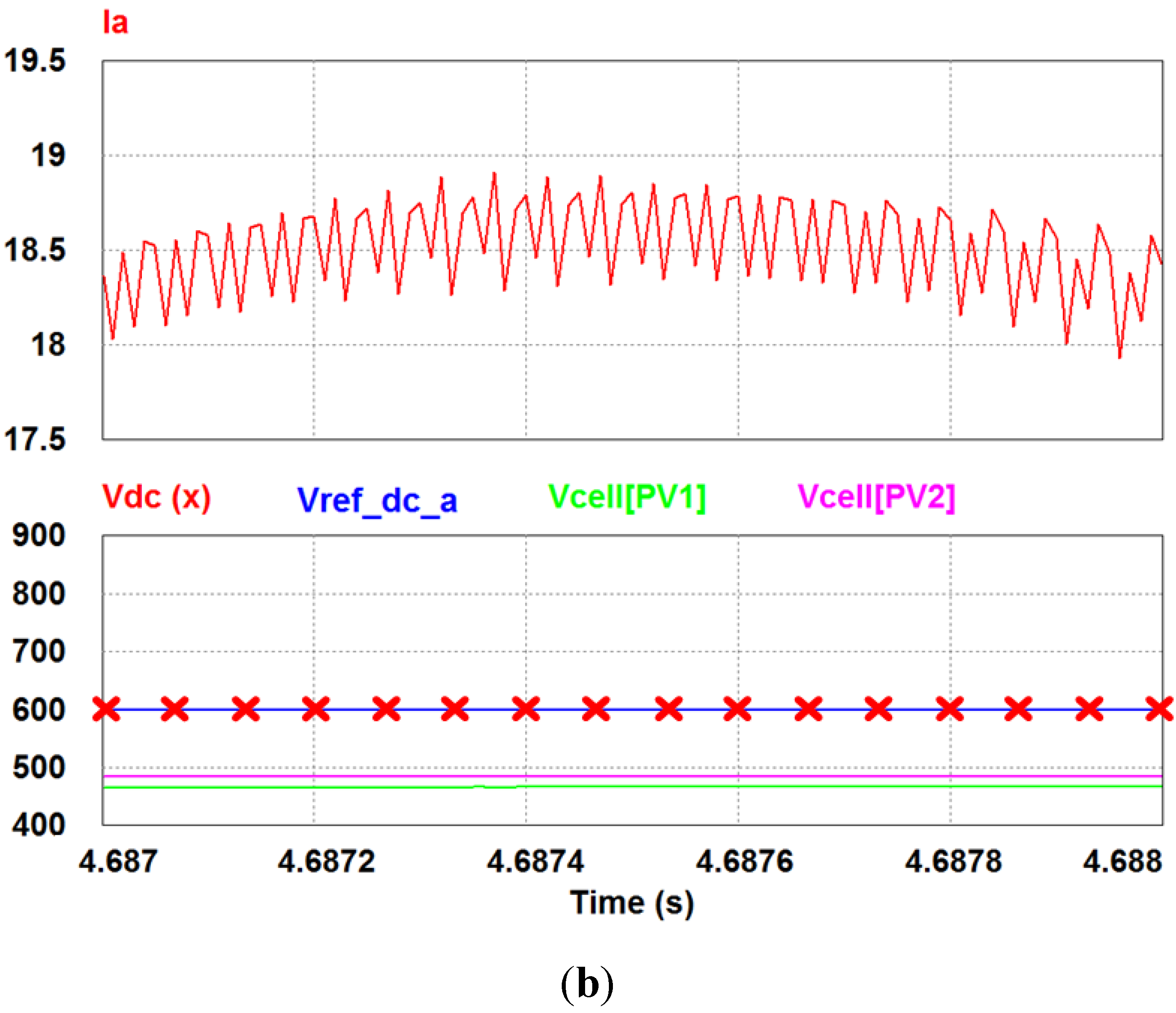
Figure 16.
Simulation results for the a-phase current, the DC-link voltage, Vref_dc_a and two PV cells voltages according to the DC-link reference voltage 800 V (a) and 600 V (b).
Figure 16.
Simulation results for the a-phase current, the DC-link voltage, Vref_dc_a and two PV cells voltages according to the DC-link reference voltage 800 V (a) and 600 V (b).
These shows that the a-phase current ripples are different according to the DC-link reference voltage. In
Figure 16a, the peak-to-peak value of the a-phase current ripple is 1 A when the DC-link reference voltage is set to 800 V. However, when the DC-link reference voltage is set to 600 V, the peak-to-peak value of the a-phase current ripple is 0.6 A in
Figure 16b. From the results, it is identified that changing the DC-link reference voltage according to the sorted voltage reduces THD increase.
4. Experimental Section
The algorithm has been tested using a 10 kW experimental setup. The experimental set consists of an inverter and two boost converters as shown
Figure 1; a photograph of the electronics is shown in
Figure 17.
Figure 17.
Experimental setup of the 10kW two-string PV system.
Figure 17.
Experimental setup of the 10kW two-string PV system.
The rated powers of the string 1 and string 2 boost converters are 7 kW and 3 kW. The rated power of the inverter is 10 kW. Most of the system parameters are the same as those used in the simulations: two input inductances of the boost converters are 1.5 mH, the capacitance of the DC-link capacitor is 1100 µF, and the inductance and capacitance of LC-filter parameters are 2 mH and 4.7 µF. The switching frequency for both the boost converter and the inverter is 20 kHz, and the three-phase grid uses a 380 V line-to-line voltage. However, ωn for the DC-link voltage controller is chosen to be 30 rad/s for system stability, and the ramp response of the DC-link reference voltage is 50 V/s. The calculation period for the MPPT algorithm is 0.5 s and Δduty-cycle is 0.005.
The inputs are connected to PV simulators. The temperature and solar radiation of the PV cells are increased or decreased to characterize the performance of the algorithm by using simulator software. A temperature change is applied to the simulator of string 1.
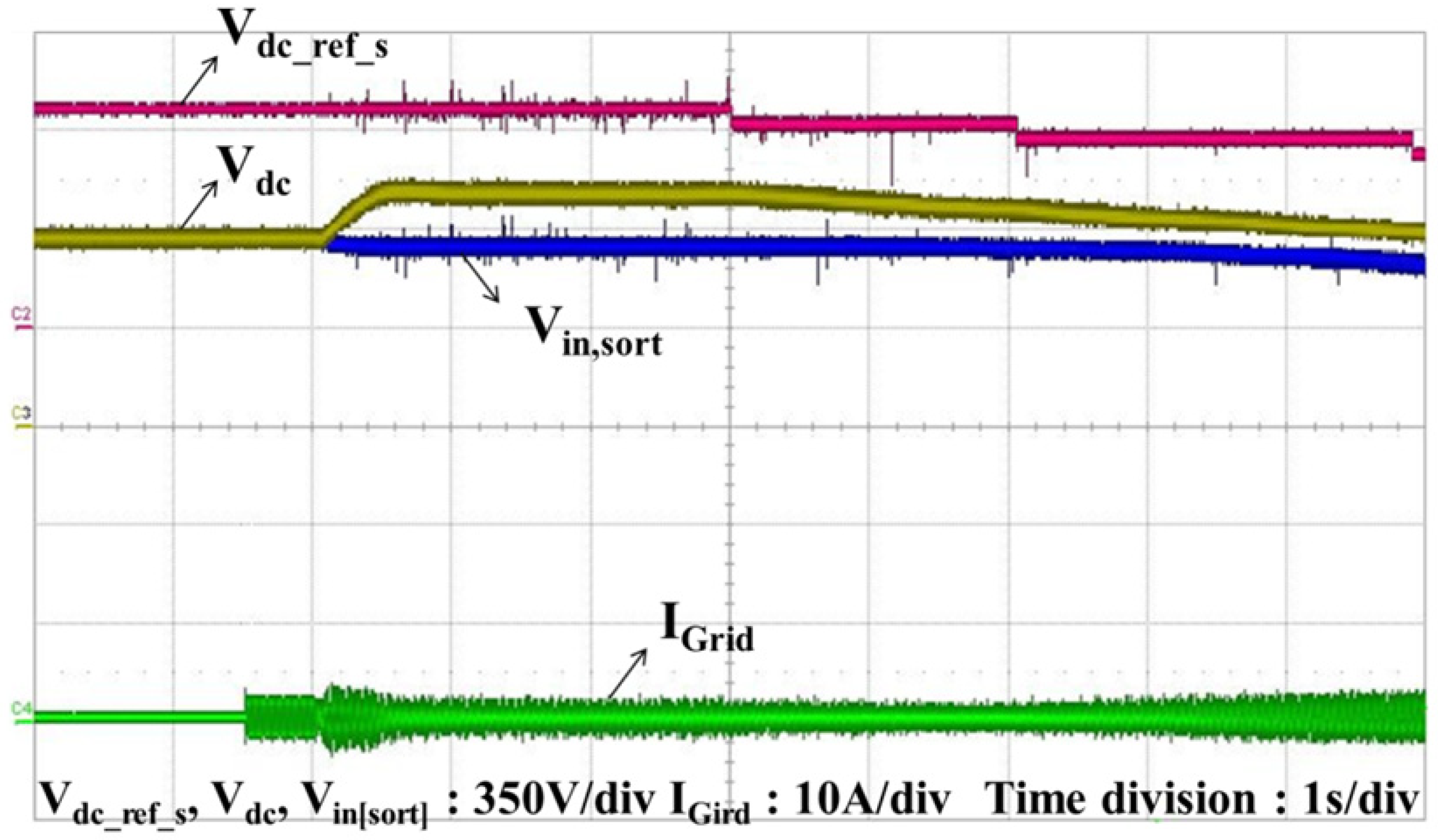
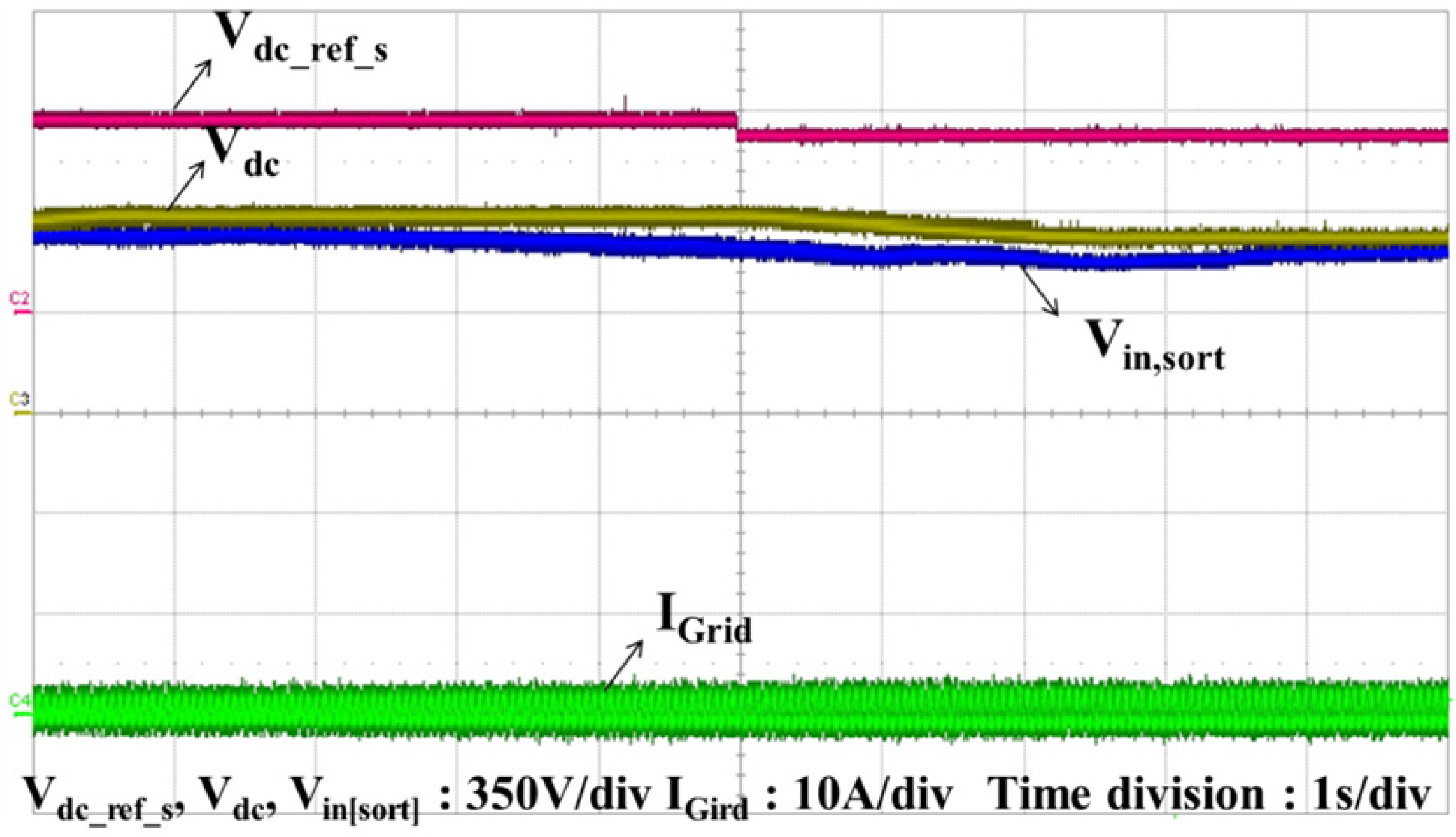
Figure 18 shows the experimental results when the PV system is initiated.
Figure 18.
Experimental results for the DC-link voltage,
Vin,sort and
Vref_dc_s from
Figure 11 when the PV system is initiated.
Figure 18.
Experimental results for the DC-link voltage,
Vin,sort and
Vref_dc_s from
Figure 11 when the PV system is initiated.
The DC-link reference voltage is chosen to be 800 V because the sorted voltage is higher than 700 V. The system operation is the same as that in simulations. The MPPT algorithm causes the sorted voltage to decrease and the grid current to increase; the DC-link reference voltage is decreased according to the sorted voltage.
Figure 19 and
Figure 20 show the change in the DC-link reference voltage that occurs owing to the sorted voltage. The temperature of PV1 is changed from 30 °C to 10 °C, as shown in
Figure 19, and the effects are shown in
Figure 21. The points of
Figure 21 present the operation point of the PV system. The DC-link voltage increases with the increase in the sorted voltage from 650 V to 700 V. The MPPT algorithm is appropriately carried out during Δtemperature.
Figure 20 plots the waveforms when the temperature of PV1 changes from 10 °C to 30 °C. In contrast with
Figure 19, the sorted voltage is decreased and the DC-link reference voltage is decreased, as well.
Figure 19.
Experimental results for the DC-link voltage,
Vin,sort and
Vref_dc_s from
Figure 11 when the temperatures of PV1 is decreased.
Figure 19.
Experimental results for the DC-link voltage,
Vin,sort and
Vref_dc_s from
Figure 11 when the temperatures of PV1 is decreased.
Figure 20.
Experimental results for the DC-link voltage,
Vin,sort and
Vref_dc_s from
Figure 11 when the temperatures of PV1 is increased.
Figure 20.
Experimental results for the DC-link voltage,
Vin,sort and
Vref_dc_s from
Figure 11 when the temperatures of PV1 is increased.
Figure 21.
PV-curves of a PV simulator according to the temperature: (a) 30 °C and (b) 10 °C.
Figure 21.
PV-curves of a PV simulator according to the temperature: (a) 30 °C and (b) 10 °C.
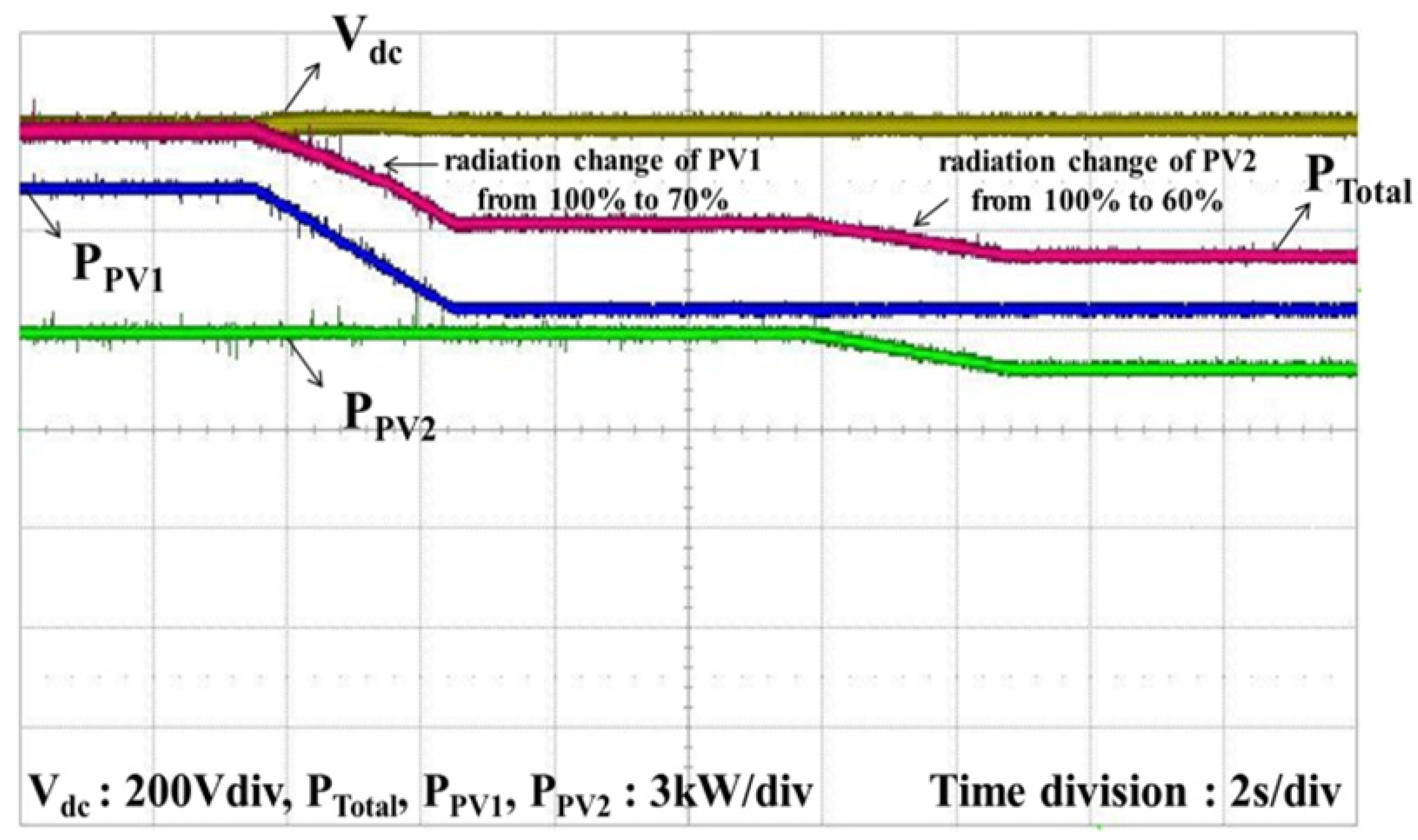
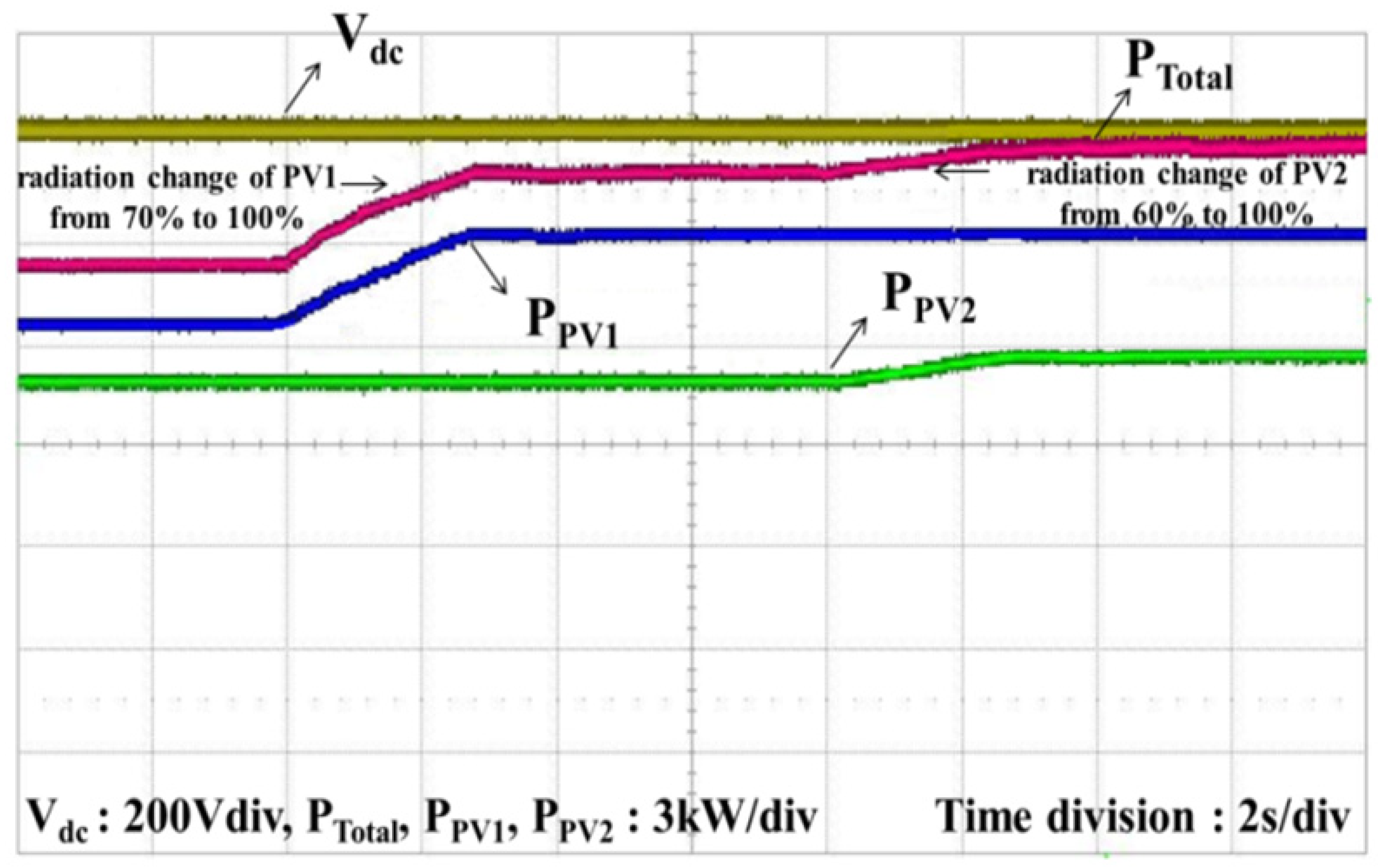
Figure 22 and
Figure 23 show the powers waveforms when the radiation is altered. In
Figure 22, the radiation of PV1 is changed from 100% to 70%, and the radiation of PV2 is changed from 100% to 60%. The radiation of PV1 is changed from 70% to 100% and the radiation of PV2 is changed from 60% to 100% in
Figure 23. The change in radiation does not cause the voltage of the PV cells to increase. Therefore, the DC-link voltage also remains unchanged. The total power changes, however, because the PV powers are increased or decreased. In this case, the maximum power point tracking is well conducted by the MPPT algorithm and is shown in
Figure 24.
Figure 22.
Experimental results for powers of inputs and output when the radiation of PVs is decreased.
Figure 22.
Experimental results for powers of inputs and output when the radiation of PVs is decreased.
Figure 23.
Experimental results for powers of inputs and output when the radiation of PV is increased.
Figure 23.
Experimental results for powers of inputs and output when the radiation of PV is increased.
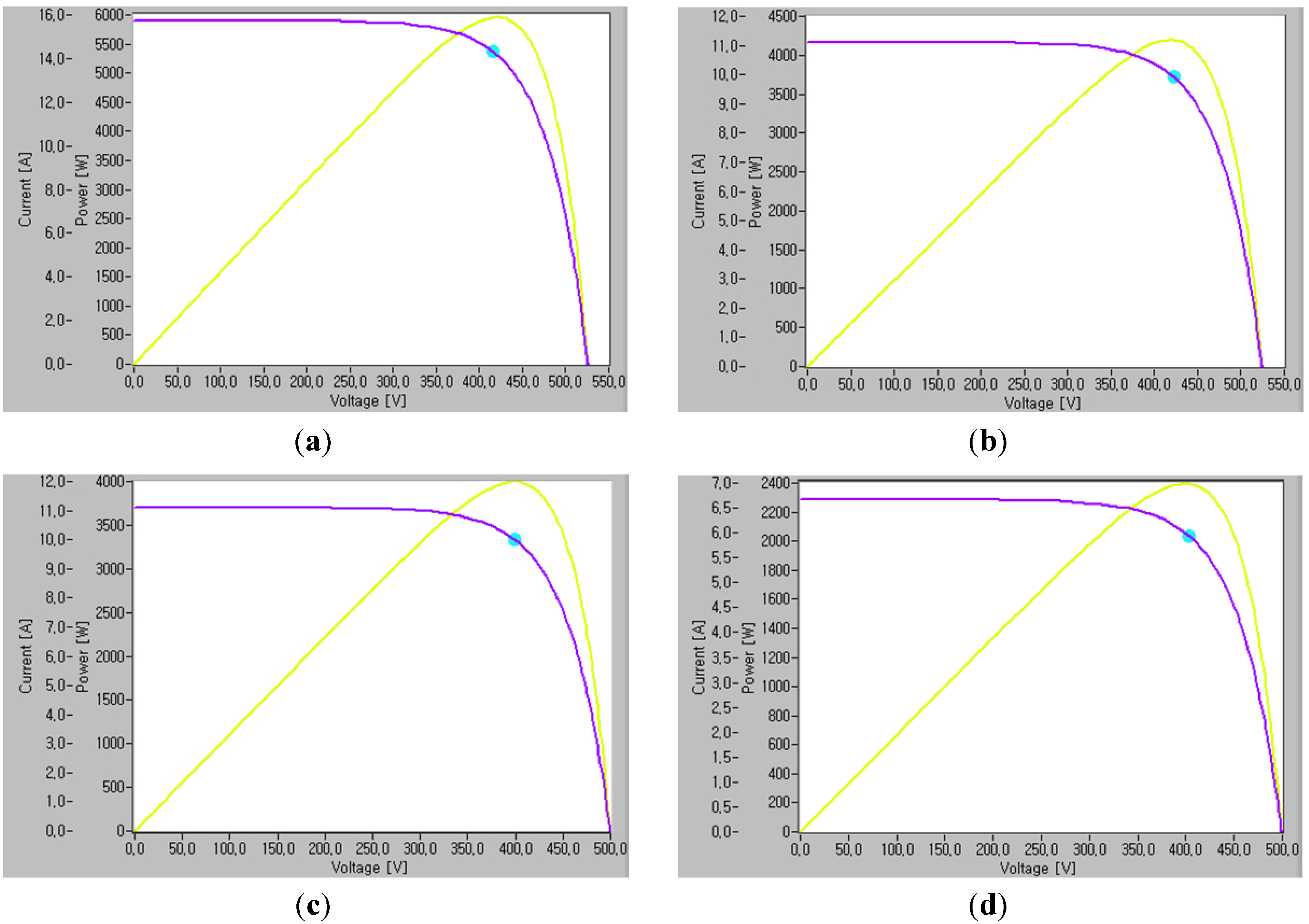
Figure 24.
PV-curves of PV1 and PV2 according to radiation. (a) PV-curve of PV1 at radiation of 100%; (b) PV-curve of PV1 at radiation of 70%; (c) PV-curve of PV2 at radiation of 100%; (d) PV-curve of PV2 at radiation of 60%.
Figure 24.
PV-curves of PV1 and PV2 according to radiation. (a) PV-curve of PV1 at radiation of 100%; (b) PV-curve of PV1 at radiation of 70%; (c) PV-curve of PV2 at radiation of 100%; (d) PV-curve of PV2 at radiation of 60%.