Decisions on Energy Demand Response Option Contracts in Smart Grids Based on Activity-Based Costing and Stochastic Programming

Abstract

Smart grids enable a two-way energy demand response capability through which a utility company offers its industrial customers various call options for energy load curtailment. If a customer has the capability to accurately determine whether to accept an offer or not, then in the case of accepting an offer, the customer can earn both an option premium to participate, and a strike price for load curtailments if requested. However, today most manufacturing companies lack the capability to make the correct contract decisions for given offers. This paper proposes a novel decision model based on activity-based costing (ABC) and stochastic programming, developed to accurately evaluate the impact of load curtailments and determine as to whether or not to accept an energy load curtailment offer. The proposed model specifically targets state-transition flexible and Quality-of-Service (QoS) flexible energy use activities to reduce the peak energy demand rate. An illustrative example with the proposed decision model under a call-option based energy demand response scenario is presented. As shown from the example results, the proposed decision model can be used with emerging smart grid opportunities to provide a competitive advantage to the manufacturing industry.

1. Introduction

Increasing energy demand and concerns about climate change have driven energy market participants to agree on establishing the so-called smart grid [1]. The main objective of the smart grid is to achieve and facilitate interoperable collaboration between energy producer and consumer, and generate benefits from collaboration. The benefits include more efficient distribution of energy resources, and engagement of energy use patterns in support of business objectives. The most important aspect of the smart grid initiative is the energy demand and response contract program that is a voluntary load curtailment contract between a utility company and industrial customers. The approaches for energy load curtailment fall into two categories: load-shedding (dropping load completely) and load-shifting (moving load from peak to off-peak periods). Note that this paper mainly focuses on the load-shedding approach.

This contract program allows industrial customers to obtain incentives in return for reducing their energy demand rate (kW) during specified times. In general, the program is modeled as an option contract with a specified curtailment amount in the rate of delivery (kW) associated with an option premium price and a strike price. In an energy option contract, a utility company and an industrial customer become a buyer and a seller, respectively. If a company has an extensive ability to understand their internal energy use processes well enough to shed or shift their energy demand according to the signed contract, then they can gain a competitive advantage from participating in the program. For a better understanding of the smart grid energy demand response program, a simple scenario is described below between an industrial customer and utility service provider (USP) where the utility service provider is the retailer who is selling electrical energy to the end customers (e.g., DTE Energy, Consumers Energy in Michigan, USA). The scenario is slightly modified from a load curtailment example in [2]:

(1)

USP’s call option offer: USP offers to an industrial customer a call option offer according to a predefined energy demand response program. The option has an option premium price of $20/kW per month and a strike price of $1/kW per hour for actual energy load curtailments. The option allows exercise during the life of the option that is in the months of June through September. The option is constrained to be exercised during peak hours (12 noon to 8 p.m.) of weekdays and up to 20 h per month.

(2)

Customer’s acceptance of the offer: The industrial customer agrees to provide 200 kW of load curtailment at any time during the contracted period. The total option premium given to the industrial customer is $16,000 (= 4 months × $20/kW × 200 kW).

(3)

USP’s exercise of the option: On a certain day during the contracted period, USP falls into a situation where the overall energy demand increases rapidly and so it needs to exercise the option. USP then commands the industrial customer to curtail 200 kW from 2 p.m. to 6 p.m.

(4)

Customer’s load curtailment: According to the contract, the industrial customer reduces 200 kW from its contracted baseline usage rate. The determination if the customer abides by the command is verified through reading of metering devices. If the load curtailment is not achieved, the customer is subject to penalty. If the reduction is made per contract, the customer is paid $800 (= 200 kW × 4 h × $1/kW per hour) that corresponds to the strike price.

From the aforementioned motivating scenario, again it is immediately evident that if the industrial customer accepts the offer (i.e., agreement with energy load curtailments) after having assessed the offer accurately, they will be paid both an option premium ($16,000) to participate and a strike price ($1/kW per hour) for any requested energy load curtailments. However, in the case that the customer did not assess the offer accurately, the acceptance of the offer should adversely affect the customer’s core business processes and so the customer may not realize the contract and accordingly, pay relevant penalties along with losing credibility for load-shedding.

In the end, the ability to make a right contract decision on energy demand response offers is the key enabler for industry customers who are interested in participating and benefiting from the smart grid. However, in reality, most industrial customers are limited in their capability to assess the energy demand response opportunities and risks in an optimal and rapid way. Especially, the limitation is evident in manufacturing industries because a manufacturing system is typically complex, large, and stratified so that it is very hard to understand the energy distribution across the system.

In order to determine if a specific energy demand and response offer is viable for a manufacturing company, the company should first build its energy accounting model which provides a high-resolution of energy distribution across the system and insight to the causes of energy usage. In a general term, energy accounting refers to a tool or system used to measure, analyze and report the energy consumption of different energy use activities on a regular basis. One way to build such an energy accounting model is to implement an energy monitoring system. However, this approach runs into accuracy problems if the target system is complex, large, and stratified as in manufacturing systems. For example, an automobile manufacturing process generally consists of three main processes: Body Shop, Paint Shop, and General Assembly. The body shop transforms the raw materials into the structure of the vehicle. Then the paint shop applies a protective and visual coating to the product. Finally general assembly assembles all sub-components into the vehicle such as the engine and seats [3,4]. Typically, energy monitoring in such complex automotive manufacturing processes is performed only at a main process level because the metering devices cost thousand dollars and the information gained at the sub-system level is not as useful as at the process levels—Body, Paint, General Assembly. Due to this lack of information, the modeling of energy usage based on an energy monitoring system in manufacturing facilities is usually done as a “black box” approach, leaving little visibility or understanding as to the causes of the energy usage by the system, or how to prioritize improvement efforts to curb their energy usage. The alternate method to build an energy accounting model is to use Activity-Based Costing (ABC) which offers a proven structure for evaluating the cost of processes and products in both the financial and industrial sectors. By applying ABC to the energy modeling in manufacturing sectors, it is possible to overcome limited metering devices to determine the energy distribution within the process and to predict energy loads in the future which is useful for effectively evaluating energy demand and response offers. The core idea of ABC is that cost objects (e.g., product or service) consume activities, which in turn consume resources (e.g., labor, materials, equipment) and the amount of consumption in these resources results in cost. The activities are discrete actions which must be performed to create the cost objects. A cost distribution created in ABC is used to trace resources to activities then to cost objects. Note that a traditional ABC method cannot be used for this purpose but this paper will use an advanced ABC method that is modified to include both economic and environmental factors [5,6]. Section 3 will discuss both traditional and advanced ABC methods in detail. This paper proposes a novel decision model based on activity-based costing (ABC) and stochastic programming, developed to evaluate the impact of load curtailments accurately and determine as to whether or not to accept a load curtailment offer. The proposed model targets state-transition flexible and QoS flexible activities to reduce the peak energy demand rate during the option exercising time period.

The paper is organized as follows: Section 2 surveys some efforts and studies related to energy, smart grid, ABC, chance-constrained stochastic programming and also discusses the benefits and challenges arising from participation in the energy demand response programs. Section 3 introduces ABC method and chance constraint stochastic model as background material. Section 4 proposes a new decision process based on ABC and chance-constrained stochastic programing. Section 5 concludes this paper. The notations used through this paper are summarized in Table 1.

Table 1. Summary of notations.

Notation	Description
$I$	Set of activity $i$ (e.g., $I$ = {operating robots, moving conveyors, air conditioning, building lighting, …}) where $I_{MC}$, $I_{STF}$, and $I_{QoSF}$ represent sets for mission-critical activities, state-transition flexible activities, and QoS flexible activities, respectively (See Section 3 for details)
$J$	Set of state $j$ where $J$ = {production, shutdown, startup, setback, maintenance}
$U$	Set of utility $u$ (e.g., $U$ = {electricity, natural gas, oil, compressed air, …})
$r_{i,j}\in ℝ$	Rate of energy demand (also called power, kW) of activity $i$ at state $j$
$Z_{i,j}\left(t\right)\in \left\{0,1\right\}$	Activity state time function; ${\sum }_j{Z}_{i,j}\left(t\right)=1$ at any given $i$ and time $t$ (See Section 4 for details)
$\tau \in ℝ$	Time period of energy demand response option exercising defined in an energy demand response option contract (e.g., 2 h starting from noon, which is represented by $t\in \left[t_s,t_s+\tau \right]$ where $t_s=12:00 p.m.$ and $\tau =2$)
$C\in ℝ$	Energy delivery rate (kW) during $t\in \left[t_s,t_s+\tau \right]$ defined in an energy demand response option contract
$P\in ℝ$	Peak rate of energy demand (kW) during $t\in \left[t_s,t_s+\tau \right]$ where $P_{MC}$, $P_{STF}$, and $P_{QoSF}$ represent the peak rate of energy demands (kW) for activities in $I_{MC}$, $I_{STF}$, $I_{QosF}$, respectively for a given time period
$L\in ℝ$	Energy load (kWh) during $t\in \left[t_s,t_s+\tau \right]$ where $L_{MC}$, $L_{STF}$, and $L_{QoSF}$ represent energy demands (kWh) for activities in $I_{MC}$, $I_{STF}$, $I_{QosF}$, respectively for a given time period
$x_u\in ℝ$	Energy supply rate (kW) of utility $u$ for activity $u\in U$
$y_i\in ℝ$	Energy demand rate (kW) of activity $i$ for activity $i\in I_{QoSF}$
${\alpha }_{i,u}\in ℝ$	Probability to fail meet a quality of service (QoS) required to activity $i\in I_{QoSF}$ that consumes utility $u$. Accordingly, (1-${\alpha }_{i,u}$) represents the probability to meet the required level of QoS

Table 1. Summary of notations.

Notation	Description
$I$	Set of activity $i$ (e.g., $I$ = {operating robots, moving conveyors, air conditioning, building lighting, …}) where $I_{MC}$, $I_{STF}$, and $I_{QoSF}$ represent sets for mission-critical activities, state-transition flexible activities, and QoS flexible activities, respectively (See Section 3 for details)
$J$	Set of state $j$ where $J$ = {production, shutdown, startup, setback, maintenance}
$U$	Set of utility $u$ (e.g., $U$ = {electricity, natural gas, oil, compressed air, …})
$r_{i,j}\in ℝ$	Rate of energy demand (also called power, kW) of activity $i$ at state $j$
$Z_{i,j}\left(t\right)\in \left\{0,1\right\}$	Activity state time function; ${\sum }_j{Z}_{i,j}\left(t\right)=1$ at any given $i$ and time $t$ (See Section 4 for details)
$\tau \in ℝ$	Time period of energy demand response option exercising defined in an energy demand response option contract (e.g., 2 h starting from noon, which is represented by $t\in \left[t_s,t_s+\tau \right]$ where $t_s=12:00 p.m.$ and $\tau =2$)
$C\in ℝ$	Energy delivery rate (kW) during $t\in \left[t_s,t_s+\tau \right]$ defined in an energy demand response option contract
$P\in ℝ$	Peak rate of energy demand (kW) during $t\in \left[t_s,t_s+\tau \right]$ where $P_{MC}$, $P_{STF}$, and $P_{QoSF}$ represent the peak rate of energy demands (kW) for activities in $I_{MC}$, $I_{STF}$, $I_{QosF}$, respectively for a given time period
$L\in ℝ$	Energy load (kWh) during $t\in \left[t_s,t_s+\tau \right]$ where $L_{MC}$, $L_{STF}$, and $L_{QoSF}$ represent energy demands (kWh) for activities in $I_{MC}$, $I_{STF}$, $I_{QosF}$, respectively for a given time period
$x_u\in ℝ$	Energy supply rate (kW) of utility $u$ for activity $u\in U$
$y_i\in ℝ$	Energy demand rate (kW) of activity $i$ for activity $i\in I_{QoSF}$
${\alpha }_{i,u}\in ℝ$	Probability to fail meet a quality of service (QoS) required to activity $i\in I_{QoSF}$ that consumes utility $u$. Accordingly, (1-${\alpha }_{i,u}$) represents the probability to meet the required level of QoS

2. Related Works

There have been many efforts implemented individually or jointly as countermeasures to steadily rising energy costs at present and to the prediction that the rising trend continues going into the future. As an example of individual effort, GM has built or retrofitted their facilities in such a way to use methane vented from local landfills to replace natural gas, thus reducing cost and the effect on the environment [7]. As an example of joint effort, energy market participants are beginning to agree upon establishing the smart grid to increase the efficiency of energy distribution [1]. There have been several studies related to smart grid. Yoo et al. [8] presented look-ahead energy management system for a grid-connected residential photovoltaic system with battery under critical peak pricing for electricity, enabling effective and proactive participation of consumers in the smart grid’s demand response. In their proposed system, the photovoltaic system is the primary energy source with the battery for storing (or retrieving) excessive (or stored) energy to pursue the lowest possible electricity bill. Soares et al. [9] presented a simulator for electric vehicles in the context of smart grids and distribution networks with an aim to support network operators’ planning and operations. However, few studies have been done to date on the impact of smart grid energy demand response program from the industrial energy consumer perspective, on which this paper intends to make a contribution.

It is true that the success of smart grid relies on efficient and seamless collaboration between utility companies and industrial consumers. To achieve the efficient and seamless collaboration, it is necessary to establish information standards for exchanging energy demand response signals. A group of experts have created the OASIS Energy Market Information Exchange Technical Committee (EMIX) and proposed a series of standards [2].

Although the participation in the energy demand response program can provide industrial customers with a chance for significant cost savings, it is still at an incipient stage to induce industrial customers to participate in the collaboration. In order to facilitate the participation, it is required to help industrial customers in assessing energy demand response options and addressing some key organizational and operational challenges before determining the participation. Ghatikar et al. [10] identified three challenges: (1) perception of risk to business and operations, (2) performance measurement strategies, and (3) lack of Information.

Industrial customers should themselves answer the question as to whether a specific energy demand and response offer is viable for their operations before determining to participate in the program. To answer this question correctly, they should first build their own energy accounting model which provides insight to the causes of energy usage. One way to build such an energy accounting model is to use Activity-Based Costing (ABC). Different from the traditional volume-based accounting approach, the ABC approach is useful, especially when the rapid assessment of energy load curtailment options is required. There were several studies to modify ABC with an intention to expand to include environmental factors. Jurek et al. [11] proposed an ABC-based energy consumption prediction model used to clarify the production energy load and non-production energy load rapidly, thereby being able to figure out the amount of possible load curtailment quickly. Another case involved utilization of ABC in the manufacturing industry to perform Life Cycle Assessments (LCA) on the manufacturing processes [12]. Also, successful studies to show how the flexibility of ABC contributes to process improvement were reported [13].

There have been many applications of optimization programming approaches to energy and environmental problems in the scientific literature. However, most of them had just focused on deterministic programming approaches. For example, Sirikitputtisak et al. [14] reported that they developed a large scale multi-period mixed integer linear programming optimization model for energy planning with consideration of multi-period constraints such as construction lead time, fluctuation of fuel price, CO₂ emission reduction targets, and so on.

To date, relatively few studies reported on the application of stochastic programming approaches to energy and environmental problems with consideration of uncertainty in energy demand and supply. When uncertainty is incorporated in an optimization process, two types of stochastic optimization models can be applicable: recourse type and chance constraint type [15,16]. When a circumstance allows an implicit acceptance of stochastic constrains, the chance constraint stochastic type is preferred. Luedtke et al. [17] studied the conversion of chance constraint type of stochastic programming model to a deterministic type of programming model. Oh et al. [18] studied the assessment of demand response options using stochastic programming where they proposed an optimal stochastic programming model in such a way that the economic values under the demand response scheme is maximized while the mission critical manufacturing processes are not sacrificed for that maximization.

This paper expands on previous research [11,18] and applies ABC-based energy accounting model and chance constraint stochastic programing model to build a new decision process through which industrial energy customers (focusing on manufacturing companies) evaluate the impact of energy demand response offer on their core business operations and determine whether or not to accept the offer.

3. Background Technologies

The objective of this section is to provide background knowledge on activity-based costing and chanced-constrained stochastic programing in the context of their specific application to energy demand response option assessment. This section is as part of a preliminary step to propose a new decision process to evaluate the impact of an energy demand and response offer accurately and determine as to whether or not to sign the contract and undertake the load curtailment.

3.1. Activity-Based Costing (ABC)

ABC was developed as an accounting method used to trace costs to a product or process of an organization. ABC is characterized by assigning costs to the activities performed by the organization, rather than assigning costs directly to the products. Due to this characteristic, the cost of the products can be calculated by determining how much each product uses each activity [19].

ABC is considered to be more accurate than classical volume-based costing methods that assign all indirect costs based on a certain rate such as direct labor rates or area rate, etc. Indeed, although ABC requires in-depth knowledge of the system under consideration, if it is properly used, it can show the high-resolution cost distribution across the system so that operation planning personnel can secure visibility into the causes of costs in the process and further allows for predictions of costs for future scenarios [20]. The concept of ABC can be also applied to energy management and provide an energy usage distribution for the process to identify and evaluate energy consumption and cost saving opportunities [21].

Figure 1 depicts the core idea of ABC that cost objects consume activities, which in turn consumes resources and the amount of consumption of these resources results in cost. A cost object is typically a product or service, while the activities are discrete actions which must be performed to create the cost objects. Resources are objects used by the activities which end up becoming costs such as labor, materials, equipment, and etc. Note that the diagram involves multiple dimensional cost units including energy (kWh), environmental factors (kgCO₂e) or other eco-indicators. The original purpose of using ABC was to distribute overhead costs more accurately and typically associated with monetary values. However, this method can easily be expanded to involve multiple dimensional cost units because it measures the amount of resources consumed by the products or services. For better understanding of this multi-dimensional cost unit feature, let us assume that one is interested in calculating the specific total costs consisting of energy costs and environmental impact. In the US, on the average, the electricity cost is $100 per MWh and the environmental impact is about 1000 kg CO₂ per MWh. If 5 MWh of electricity is required to produce a product, the total energy and environment costs of this product would be $500 and five metric tons CO₂. If the company needs to purchase CO₂ credits from a market in order to emit five metric tons CO₂ and if the CO₂ credit price in the market is $10 per CO₂ ton, then the monetary environment costs will be $50. Then, the total monetary costs will become $550.

Figure 1. Multi-dimensional ABC to trace resource and activity consumptions using each driver.

Figure 1. Multi-dimensional ABC to trace resource and activity consumptions using each driver.

From the manufacturing system perspective, ABC is a practical tool to help identify activities. For example, a well-automated manufacturing system performs common activities such as moving the product on conveyer belts, operating robots and controlling air movement for curing, etc. Note that these activities require equipment operations and the equipment requires energy as resources. Activities by ABC can be broken down into three categories: mission-critical, state-transition flexible, and QoS flexible activities. Mission critical business processed refers to any process of a system whose failure will result in the failure of business operations. So, mission critical business processes must be carried out in a given time period, otherwise there will be an occurrence of production loss. Those activities including moving the product on conveyer belts, operating robots and controlling air movement for curing are mission critical in the context of manufacturing system.

On the contrary, many activities taking place in a manufacturing system are flexible in terms of state transition or quality of service (QoS) requirements due to non-mission critical business needs. For example, there is a state-flexible activity such as the shift of building lighting system during daylight hours to the setback state that will save considerable amount of electricity usage. Meanwhile, the air conditioning activity is a QoS-flexible activity where the comfort cooling level can be lowered temporarily by raising the indoor temperature. Both building lighting and air conditioning activities are not kinds of aforementioned mission critical activities so that they do not cause a critical problem even though their states are changed or their QoS level is compromised in certain range for short periods of time. Figure 2 depicts the principle of ABC and the breakdown of activities into the three sets: mission critical activities, state-transition flexible activities and QoS flexible actives.

Figure 2. ABC costing model and three different sets of activities.

Figure 2. ABC costing model and three different sets of activities.

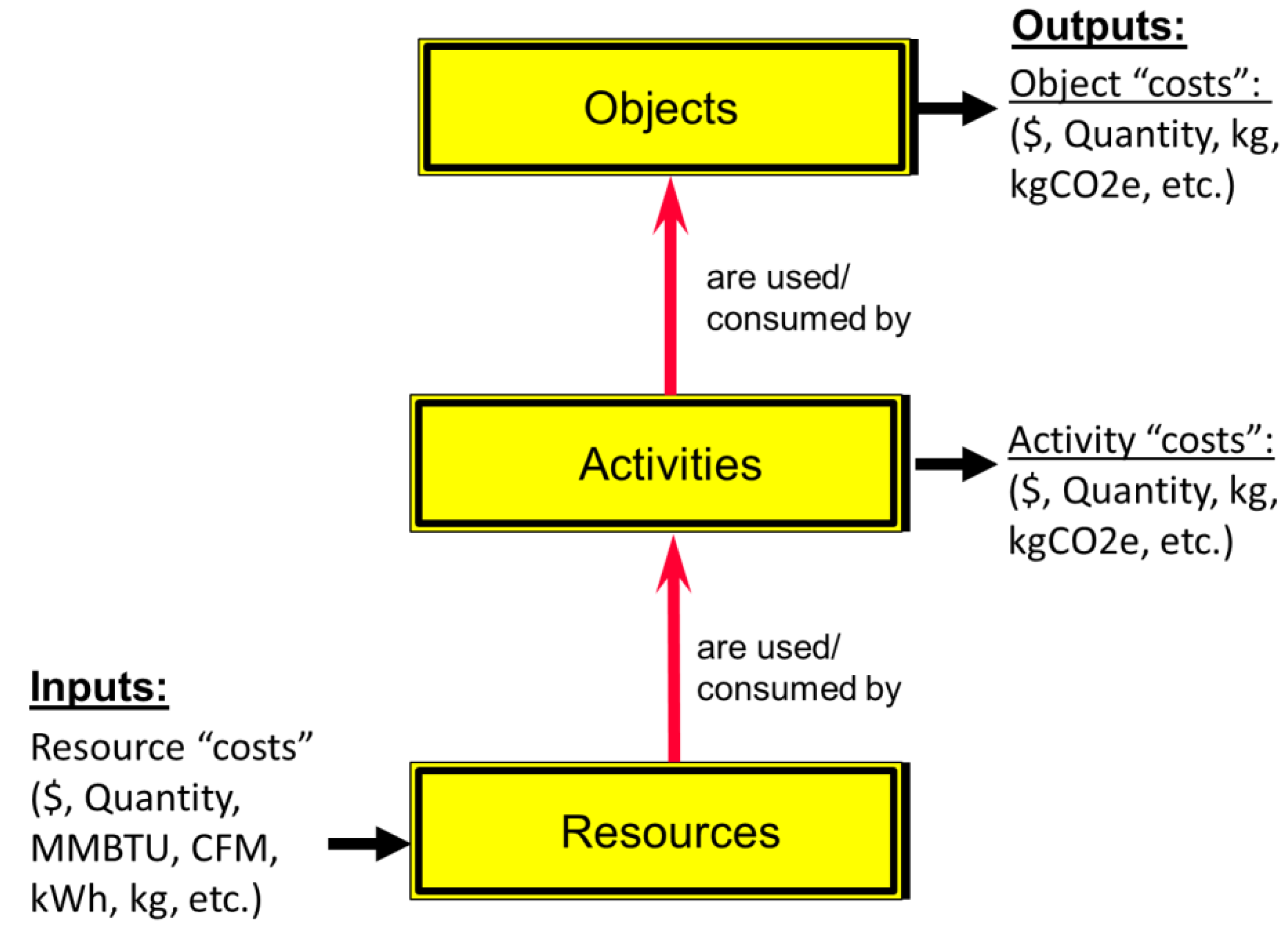
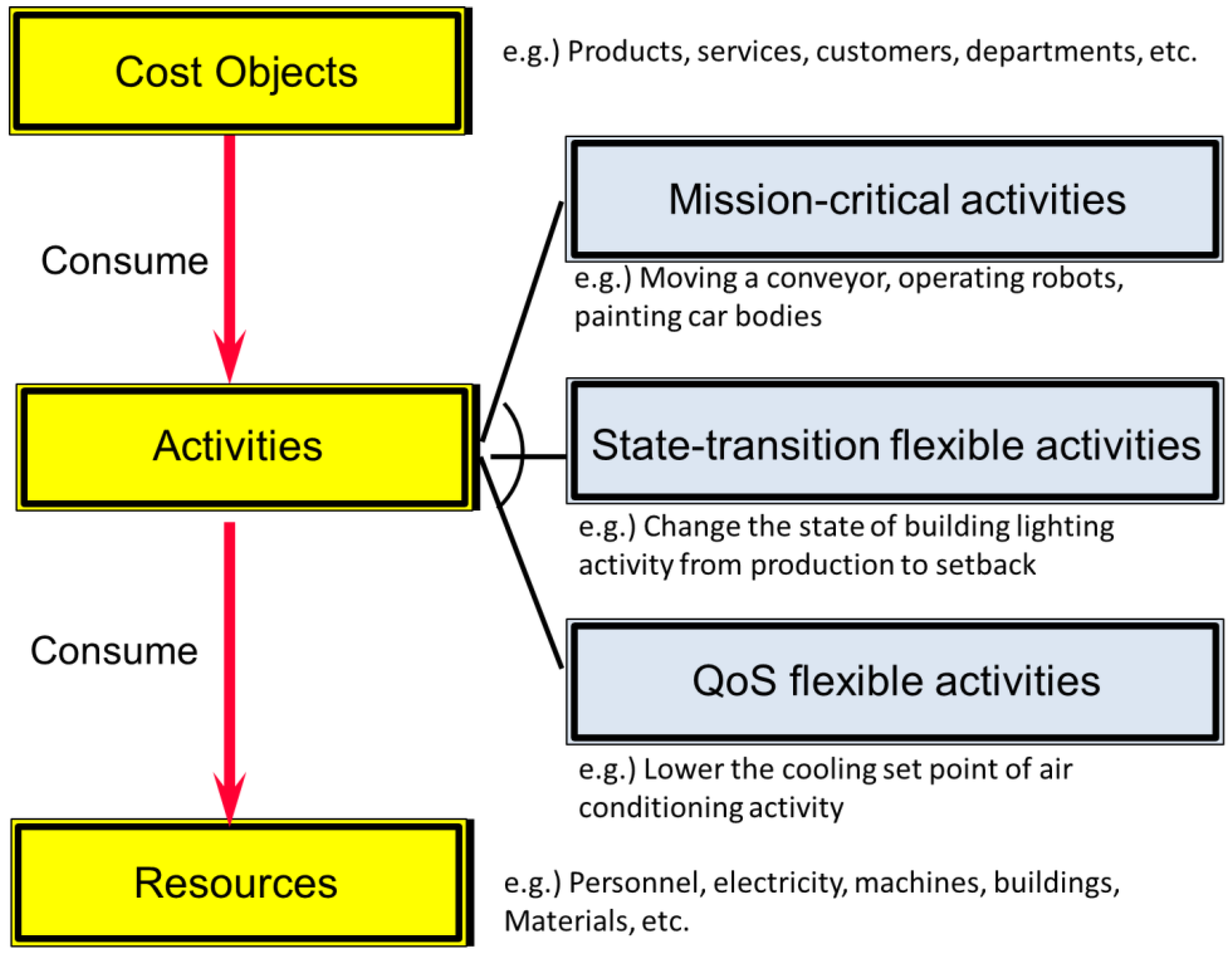
• Definition 1 (Mission critical activity) An activity is mission-critical if the activity’s failure results in the failure of business operations where $I_{MC}$ denotes a set of mission-critical activities.
• Definition 2 (State-transition flexible activity) An activity is state-transition flexible if the activity’s state can transition to any or some of the defined states as a result of energy load-shedding processes where $I_{STF}$ denotes a set of state-transition flexible activities.
• Definition 3 (QoS flexible activity) An activity is QoS flexible if the quality of service (QoS) level imposed on the activity can be adjusted in terms of the probability to meet the QoS where $I_{QoSF}$ denotes a set of QoS flexible activities.
• Proposition 1 (Flexibility of activities) Any activity $i$ is flexible if $i\in \left(I_{STF}{\cup }^{\text{}}{I}_{QoSF}\right)$.

In addition, any energy use activity in a manufacturing system has the following five distinct states: production, shutdown, startup, setback, maintenance where the activity can transition from one state to other state according to a production schedule in such a way that the activity is always put in only one state at any given time. The important observation is that all of these states use resources at different loads and there is an opportunity to change the states of activities to reduce energy consumption. Figure 3 shows these states in a Universal Modeling Language (UML) state diagram along with the transition options from each state.

Figure 3. Activity states in a manufacturing system.

Figure 3. Activity states in a manufacturing system.

The details of five distinct states are as follows:

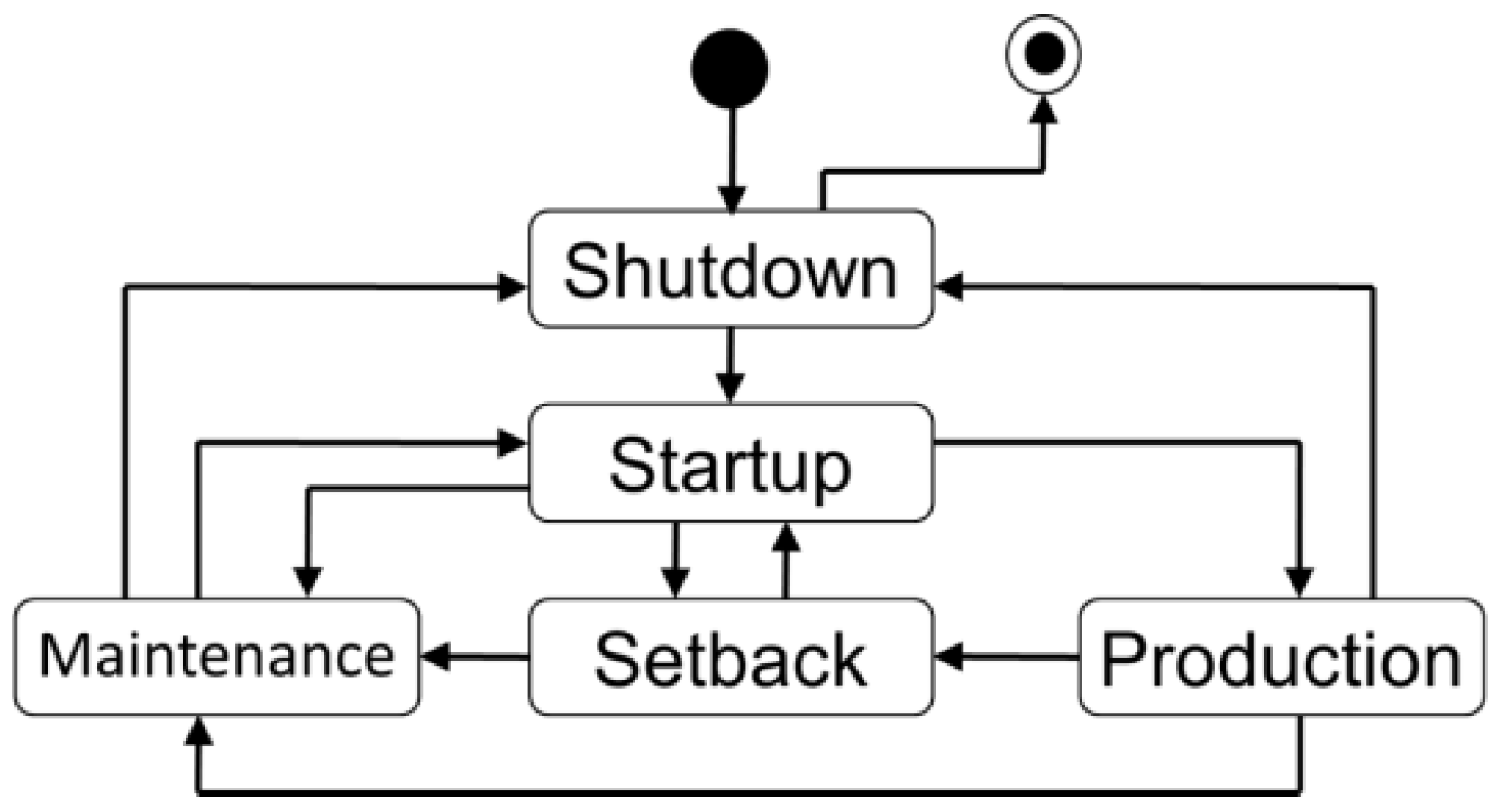
• Production state: It is a state in which products are being produced on the manufacturing system. This state requires a high level of energy due to most equipment in the facility running at high levels when in this state;
• Setback state: It is a state for lunch or between shifts which occur during a normal working days when the system can be put in a ready state to save energy. In this state, the equipment of the system is turned down to a lower level or off until production resumes again;
• Shutdown state: If there is an extended period in which the system does not need to run such as weekends or holidays, the system can be put in the shutdown state, in which the system is turned off and uses minimal energy;
• Startup state: To transfer from the shutdown state to the production state, the system requires a high level of energy and is put into a startup state. This state is a high consumer of energy because the system is operated to quickly increase system conditions to operating conditions. This is similar to the time when a vehicle accelerates, in which it requires more gas than when cruising or parked;
• Maintenance state: During the maintenance state, necessary repairs are performed with minimal energy requirement.

In general, a manufacturing system has its associated Bill of Equipment (BOE) which includes all pieces of information about equipment placed in the system including energy demand rate (kW) of equipment. Since most activities require equipment operations, the amount of energy consumed by each state of activities can be easily determined by averaging meter readings and estimated for future changes by investigating BOE. Let $r_{ij}$ denote the energy demand rate (kW) for each state $j$ of activity $i$. Since each activity changes its state in time depending on the production plan, it is useful to have a built-in function to keep track of the state of activity $i$ at time $t$. We denote $Z_{ij}\left(t\right)$ to be activity-state time function which is defined as below:

$$Z_{ij}\left(t\right)=\{\begin{array}{c}1, \mathrm{if} \mathrm{activity} i \mathrm{is} \mathrm{put} \mathrm{in} \mathrm{state} j \mathrm{at} \mathrm{time} t\\ \\ 0, \mathrm{otherwise}\end{array}$$

(1)

Note that ${\sum }_j{Z}_{i,j}\left(t\right)=1$ at any given$i$ and time $t$ because the activity is always put in only one state at any given time. Given the information of $r_{ij}$ and $Z_{ij}\left(t\right)$, one can calculate their peak rate of energy demand ($P$) and energy load ($L$) as follows:

$$P=ma{x}_t\left({\sum }_i{\sum }_j{r}_{ij}\times Z_{ij}\left(t\right)\right) \mathrm{for} t\in \left[t_s,t_s+\tau \right]$$

(2)

$$L={{\displaystyle \int }}_{t_s}^{t_s+\tau }{{\displaystyle \sum }}_i{{\displaystyle \sum }}_j{r}_{ij}\times Z_{ij}\left(t\right)dt$$

(3)

where, $\tau$ is the duration of exercising the option starting from $t_s$ (refer to Table 1 to find the notation description). Equations (2) and (3) are used to determine how much energy a company would save from the change of activity states later on. Since the operation specifications of activity $i\in I_{STF}$ are given in ranges allowing flexibility in the change of state, those flexible activities are targeted to investigate if the company is able to remain within operating specifications while still meeting the electricity reduction requirements. For example, a shift of some or the entire system to the setback state will save considerable amount of electricity usage. Cutting the amount of air or liquid moved for a short period of time will save some amount of electricity usage, as well. It is also meaningful to note that the ABC model also allows for a long-term future improvement by prioritizing target activities for improvement, as well as a short-term evaluation of energy demand and response offers.

3.2. Stochastic Programming

When uncertainty is incorporated in an optimization process, two types of stochastic optimization models can be applicable: recourse type and chance constraint type [15,16]. When a business condition allows an acceptance of flexibility in maintaining the level of quality of service (QoS) (e.g., comfort cooling level of air conditioning activity), the business condition can be represented as stochastic constraints where the constrains are not needed at all times but just enough to hold at least $\alpha$ of time, where $\alpha$ is referred to as the confidence level provided as an appropriate safety margin by the decision maker. If stochastic constraints are present, the chance constraint stochastic programming model type is preferred.

Luedtke et al. [17] studied the conversion of chance constraint type of stochastic programming model to a deterministic type of programming model. As a baseline model, let us assume that there are $m$—numbers of energy utilities indexed by $u$ (e.g., electricity, natural gas, compressed air, etc.) and $n$—numbers of energy use activities indexed by $i$ (e.g., manufacturing operation, air conditioning, etc). When $x$ denotes the vector of energy supply rate (kW) of utility$u\in U$, the goal of the problem is to obtain the optimal energy demand subject to energy balancing constraints. Then, the general structure of the Equation (total supply $\ge$ total demand) is formulated as follows:

$$\min c^{T}x; \mathrm{s}.\mathrm{t}.; Ax\ge \delta \left(\mathrm{demand}\right)$$

(4)

where $c\in R^m$ (energy utility unit cost), $A\in n\times m$ (energy demand and supply conservation equations), $\delta \in R^n$ (energy demand for each activity in the delivery rate). Let us consider the case where the demand, $\delta$ is a random variable that has K-bin discretized probability distribution. Then, the above optimal energy balancing Equation (4) can be rewritten as a chance-constraint stochastic optimization problem where $1-\alpha$ is a confidence rate with which the required demands are filled ($0\le \alpha \le 1$):

$$\min c^{T}x; \mathrm{s}.\mathrm{t}.; \mathrm{Pr}\left[Ax\ge \delta \right]\ge 1-\alpha , x\in R_{+}^m$$

(5)

where $\delta \in \left\{{\delta }^1 w.r.p. p^1, {\delta }^2 w.r.p. p^2, \dots , {\delta }^K w.r.p. p^K \right\}, {\delta }^k\ge 0, 0\le p^k\le 1, \forall k=1,2,\dots ,K$.

Equation (5) is a probabilistically constrained linear programming problem with random right-hand side and so can be reformulated as a mixed integer programming problem. To do so, a binary variable $z_i^k\in \left\{0,1\right\}$for each $k\in \left\{1,2,\dots ,K\right\}$ is introduced such that $z_i^k=0$ guarantees$Ax\ge \delta$ . Observe that $Ax\ge \delta$ must be true at least one $k\in \left\{1,2,\dots ,K\right\}$ because $\alpha <1$. Also, since ${\delta }^k>0$ for all $k$, this implies $Ax\ge 0$ in every feasible solution of (5). Then, letting $y=Ax$, the mixed integer programming formulation can be obtained as in Equation (6). Readers who want more information about the reformulation procedure can refer to Section 2 in [17].

$$\min c^{T}x; \mathrm{s}.\mathrm{t}.; y=Ax; y_i\ge {\delta }_i^k-{\delta }_i^k{z}_i^k k=1,\dots ,K; i=1,\dots , n;$$

(6)

where $z_i^k\in \left\{0,1\right\} k=1,2,\dots ,K$. ${\sum }_{k=1}^K{p}_i^k{z}_i^k\le {\alpha }_i$is equivalent to ${\sum }_{k=1}^K{p}_i^k\left(1-z_i^k\right)\ge (1-{\alpha }_i)$. Equation (6) is an energy resource allocation problem where decision variables can be disaggregated into energy supply side (utility denoted by $u\in U$) and energy demand side (activity denoted by$i\in I$). To meet the energy demand by energy use activities, Equation (6) enforces the flow conservation of energy utility $u$ across each energy use activity $i$. This concept of energy resource allocation and flow conservation can be captured as a transportation network as in Figure 4. Note that Equation (6) does not have any probabilistic constraints. So, the problem can be solved using standard solvers like Microsoft Excel Solver, CPLEX, or GLPK. For better understanding of Equation (6), an illustrative example will be provided in Section 5.

Figure 4. General energy demand and supply model with uncertainty in demand.

Figure 4. General energy demand and supply model with uncertainty in demand.

4. Decision Model for Determining Energy Demand Response Option Contract

This model expands on previous research [11,18] to specialize in accurately evaluating the impact of an energy demand and response offer and determine as to whether or not to sign the contract and undertake the load curtailment. This model is based on activity-based costing (ABC) and stochastic programming with a target on state-transition flexible and QoS flexible energy use activities to reduce the peak energy demand rate. This model is especially valuable when their energy demands are not deterministic values but stochastic variables following certain distributions. Even though the model would be applied to any industrial company, it is likely to be especially effective for a manufacturing company that has a complex, large and stratified system. Therefore, this Section will describe the decision model in the context of its specific application to a manufacturing system.

When an energy curtailment offer from a utility company arrives, in general, two baseline contracts are requested: (1) $C$: rate of energy delivery (kW); and (2) $\tau$: duration of exercising the option starting from $t_s$ (refer to Table 1 to find the notation description). With the arrived offer, the decision model proceeds as follows:

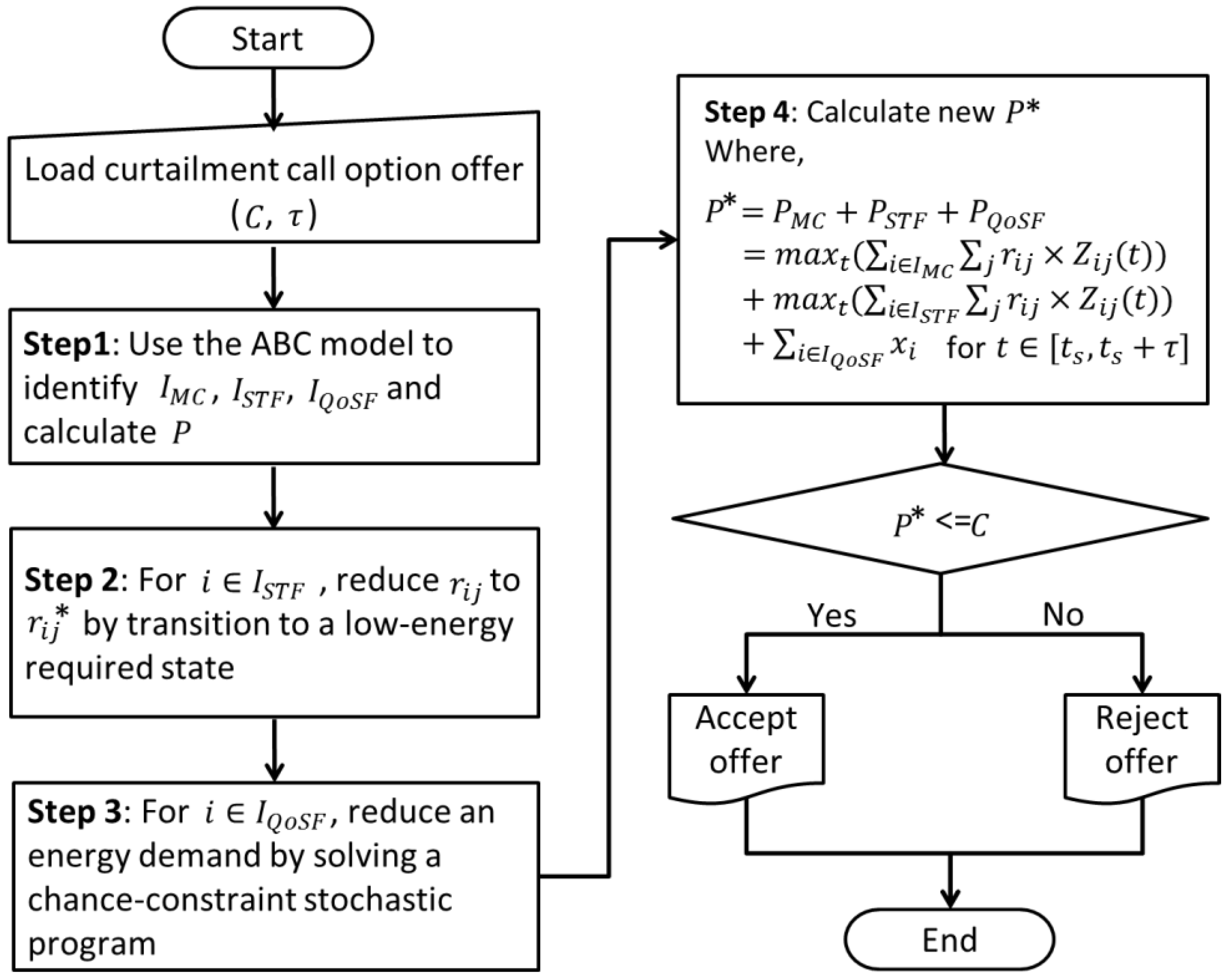
• Step 1: With a new load curtailment offer arrived, use the ABC model and identify $I_{MC}$,$I_{STF}$,$I_{QoSF}$ and calculate the current peak energy demand rate, $P$. This step requires an ABC-based energy accounting model for manufacturing operations. The basic idea in modeling is that each activity has five distinct states (i.e., production, shutdown, startup, setback, maintenance) and makes transitions from one state to other state according to a production schedule such that an activity is always put in only one state in any given time. The key point is that each state has a different energy load characteristic. And furthermore, the activities listed in the ABC-based energy accounting model are broken down into mission-critical ($I_{MC}$) and non-mission critical activities ($I_{STF}$,$I_{QoSF}$). Again, the operation specifications of non-mission critical activities are given in ranges allowing flexibility of the state transition or QoS adjustment, resulting in a lower energy demand.
• Step 2: Investigate the amount of possible reduction in the energy demand (kW) for each activity $i\in I_{STF}$ by transition to a low-energy required state (i.e., transition $j$ to $j^{*}$, such that $r_{i{j}^{*}}<r_{ij}$).
• Step 3: Investigate the amount of possible reduction in the energy demand (kW) for each activity $i\in I_{QoSF}$ by solving a chance-constraint stochastic problem through varying the QoS level (i.e., reduce $\left(1-{\alpha }_i\right)$ such that $y_i$ decreases).
• Step 4: Recalculate the peak energy demand level and denote the new peak energy demand level by $P^{*}$ and determine whether to accept or reject the offer based on $P^{*}$ and $C$.

Figure 5 depicts the proposed decision process and next Section will illustrate this process with a hypothetical simple manufacturing system considered as a target application.

Figure 5. Overview of energy demand response call option assessment decision process.

Figure 5. Overview of energy demand response call option assessment decision process.

5. Illustrative Example

The purpose of this section is to illustrate the decision process set forth in the previous section by applying it to a hypothetical example case where a simple manufacturing system is assumed to receive an energy demand response option and need to determine as to whether or not to accept the offer by figuring out their capability to reduce energy consumption as required by the offer. Throughout this illustration, the scenario for a manufacturing system and an energy curtailment option offer is assumed as follows:

• $I$= {Manual assembly, Operating robots, Moving conveyors, Operating repairing centers, Air conditioning, Building lighting, Operating chillers, Liquid moving, Air abatement};
• $J$ = {production, shutdown, startup, setback, maintenance};
• $U$= {electricity};
• $\tau$ = 2 h with the start time at 12:00 p.m., implying that the time period of energy demand response option exercising is $t\in \left[t_s,t_s+\tau \right],$ where $t_s$=12:00 p.m.;
• $C$ = 280 kW that is an energy delivery rate (kW) defined in the option contract.

The example activities presented herein $I$ are straightforward and easy to understand except the last three activities—“Operating chillers”, “Liquid moving” and “Air abatement”. First, the understanding of activities such as “Liquid moving” and “Air abatement” requires a specific knowledge on painting process although they are common processes in many manufacturing systems. A general paining process follows five steps: (1) pretreatment of product (2) application of ELPO (3) sealing application (4) paint booth (5) post-paint repairs (including cavity wax). The pretreatment stage cleanses contaminants from the product which may have been collected in the previous processes (e.g., welding process). This is performed over a series of water and cleaning solution rinses. These are usually performed in a combination of rinse and spray application methods to get optimal results. Also in this stage is where a phosphate coating is applied to the product to provide a layer of protective coating and assist in the application of the paint layers. After the pretreatment, the product is cleaned and prepped to move onto next stage. The Electro Coat Primer Operation (ELPO) applies a layer of charged primer solution to the product to increase the effectiveness of the paint application in the later stages. The product will remain in the charged solution for a specified period of time to build the appropriate layer thickness across the surface. The solution must be circulated to avoid settling of the particles. The solution is then baked onto the product and the product is processed to the next stage. After the ELPO application, the product moves to the sealing line where the seams of the product are sealed to protect against weather effects. Recently, a majority of these tasks are performed by robots, but there are some aspects which require human operators to perform. The sealants are then baked onto the product as it moves to the paint booth for the coating application. In the paint booth, primer, basecoat, and topcoat are applied depending on the product. To make the best result, the application of these layers is performed by robots to provide a consistent layer of paint to the product. This stage is very sensitive to temperature and humidity, so the environment is tightly controlled within the paint booth. Also, a large amount of air is circulating through the paint booth during operations to help capture overspray from the painting robots. Finally, the post paint stage is performed where the product is inspected for any defects and the cavity wax is applied, if required. If any defects are detected, the product is either fixed in a repair zone or reinserted into the line to go through the process again. These defects can be very costly to companies as they double the amount of activities which some of their products consume resulting in higher costs and time per vehicle. Each of these five processes requires common activities such as “Liquid moving” and “Air abatement”. However, due to the flexibility of paint process, the state of each activity can be transitioned for short time period unless the product quality or human safety requirement is compromised. Similarly, “Operating chillers” is a good enabler to control the environment conditions such as temperature and humidity, and maintain a constant machining tool temperature. Since this activity is more related to maintain the comfort cooling level, it can be considered to be a QoS-Flexible activity.

5.1. Identify $I_{MC}$,$I_{STF}$,$I_{QoSF}$ and Calculate the Current $P$

The first step of the proposed decision process is to identify I_MC, I_STF, I_QoSF and calculate the current peak energy demand rate (kW) as follows:

• $I_{MC }$ = {Manual assembly, Operating robots, Moving conveyors, Operating repairing centers};
• $I_{STF}$ = {Building lighting, Liquid moving, Air abatement};
• $I_{QoSF }$ = {Air conditioning, Operating chillers};
• The ordinary peak rate of energy demand (kW), $P$(=$P_{MC }$+$P_{STF}$+$P_{QoSF}$) during $t\in \left[t_s,t_s+\tau \right]$ is assumed to be higher than $C$ implying that the company needs to determine as to whether they can reduce their peak energy demand by ($P-C)$.

5.2. Reduction in the Rate of Energy Demand (kW) for State-Transition Flexible Activities

The second step is to investigate the amount of reduction in the rate of energy demand (kW) for each activity $i\in I_{STF}$ by transition to a low-energy required state (i.e., transition $j$ to $j^{*}$, such that $r_{i{j}^{*}}<r_{ij}$). Since there is only one state-transition flexible activity, that is the building lighting activity; the activity can simply reduce its energy demand rate from current 10 kW to 4 kW by transition from the production state to the setback state as in Table 2.

Table 2. Illustrative activities with different energy demand per state.

Activity ($i\in I_{STF}$)	State ($j\in J$)
	Startup	Production	Setback	Shutdown	Maintenance
Building lighting	10 kW	10 kW	4 kW	1 kW	4 kW
Liquid moving	55 kW	20 kW	10 kW	0 kW	0 kW
Air abatement	30 kW	10 kW	2 kW	0 kW	0 kW

Table 2. Illustrative activities with different energy demand per state.

Activity ($i\in I_{STF}$)	State ($j\in J$)
	Startup	Production	Setback	Shutdown	Maintenance
Building lighting	10 kW	10 kW	4 kW	1 kW	4 kW
Liquid moving	55 kW	20 kW	10 kW	0 kW	0 kW
Air abatement	30 kW	10 kW	2 kW	0 kW	0 kW

5.3. Reduction in the Rate of Energy Demand (kW) for QoS Flexible Activities

The third step is to investigate the amount of reduction in the rate of energy demand (kW) for each activity $i\in I_{QoSF}$ by solving a chance-constraint stochastic problem through varying the QoS level (i.e., reduce $\left(1-{\alpha }_i\right)$ such that $y_i$ decreases). Note that since $\left|U\right|=1$, we will omit writing index $u$ for simplicity. Furthermore, there is only one QoS flexible activity, that is, the air conditioning activity. Let us assume that we are aware of the demand’s K-bin discretized probability distribution as shown in Table 3. Note that the values of energy demand in the table are not real data but derived from an energy distribution over activities proportional to actual energy usage distribution.

Table 3. 5-bin discretized energy demand distribution for air conditioning activity.

Demand	$k=1$	$k=2$	$k=3$	$k=4$	$k=5$
${\delta }_5^k$	2 kW s.t.	3 kW s.t.	4 kW s.t.	5 kW s.t.	6 kW s.t.
	$\text{Pr}\left({\delta }_5\le {\delta }_5^1\right)$ = 0.65	$\text{Pr}\left({\delta }_5^1\le {\delta }_5\le {\delta }_5^2\right)$ = 0.1	$\text{Pr}\left({\delta }_5^2\le {\delta }_5\le {\delta }_5^3\right)$ = 0.1	$\text{Pr}\left({\delta }_5^3\le {\delta }_5\le {\delta }_5^4\right)$ = 0.1	$\text{Pr}\left({\delta }_5^4\le {\delta }_5\le {\delta }_5^5\right)$ = 0.05
${\delta }_7^k$	20kW s.t.	40kW s.t.	60kW s.t.	80kW s.t.	100kW s.t.
	$\text{Pr}\left({\delta }_5\le {\delta }_5^1\right)$ = 0.7	$\text{Pr}\left({\delta }_5^1\le {\delta }_5\le {\delta }_5^2\right)$ = 0.15	$\text{Pr}\left({\delta }_5^2\le {\delta }_5\le {\delta }_5^3\right)$ = 0.1	$\text{Pr}\left({\delta }_5^3\le {\delta }_5\le {\delta }_5^4\right)$ = 0.04	$\text{Pr}\left({\delta }_5^4\le {\delta }_5\le {\delta }_5^5\right)$ = 0.01

Table 3. 5-bin discretized energy demand distribution for air conditioning activity.

Demand	$k=1$	$k=2$	$k=3$	$k=4$	$k=5$
${\delta }_5^k$	2 kW s.t.	3 kW s.t.	4 kW s.t.	5 kW s.t.	6 kW s.t.
	$\text{Pr}\left({\delta }_5\le {\delta }_5^1\right)$ = 0.65	$\text{Pr}\left({\delta }_5^1\le {\delta }_5\le {\delta }_5^2\right)$ = 0.1	$\text{Pr}\left({\delta }_5^2\le {\delta }_5\le {\delta }_5^3\right)$ = 0.1	$\text{Pr}\left({\delta }_5^3\le {\delta }_5\le {\delta }_5^4\right)$ = 0.1	$\text{Pr}\left({\delta }_5^4\le {\delta }_5\le {\delta }_5^5\right)$ = 0.05
${\delta }_7^k$	20kW s.t.	40kW s.t.	60kW s.t.	80kW s.t.	100kW s.t.
	$\text{Pr}\left({\delta }_5\le {\delta }_5^1\right)$ = 0.7	$\text{Pr}\left({\delta }_5^1\le {\delta }_5\le {\delta }_5^2\right)$ = 0.15	$\text{Pr}\left({\delta }_5^2\le {\delta }_5\le {\delta }_5^3\right)$ = 0.1	$\text{Pr}\left({\delta }_5^3\le {\delta }_5\le {\delta }_5^4\right)$ = 0.04	$\text{Pr}\left({\delta }_5^4\le {\delta }_5\le {\delta }_5^5\right)$ = 0.01

5.3.1. Objective Function, Variables, and Parameters

Since this study assumes the utility unit cost ($c$) equal to 1 for simplicity, the objective function of the stochastic model becomes Equation (7) where variables and parameters of the stochastic model are summarized Table 4 and Table 5. Note that the values of energy demand in Table 5 are not real data but derived from an energy distribution over activities proportional to actual energy usage distribution:

$$\text{min }cx$$

(7)

Table 4. Definition of variables in the model.

Variables	Definition
$x\in R$	Total demand in electricity load
$y_5\in R$	Variables corresponding to the stochastic electricity demand for air conditioning
$z_5^k\in \left\{0,1\right\}$	1 if k-th demand (air conditioning) is satisfied in the K-bin discretized demand distribution, otherwise 0
$y_7\in R$	Variables corresponding to the stochastic electricity demand for air conditioning
$z_7^k\in \left\{0,1\right\}$	1 if k-th demand (operating chillers) is satisfied in the K-bin discretized demand distribution, otherwise 0

Table 4. Definition of variables in the model.

Variables	Definition
$x\in R$	Total demand in electricity load
$y_5\in R$	Variables corresponding to the stochastic electricity demand for air conditioning
$z_5^k\in \left\{0,1\right\}$	1 if k-th demand (air conditioning) is satisfied in the K-bin discretized demand distribution, otherwise 0
$y_7\in R$	Variables corresponding to the stochastic electricity demand for air conditioning
$z_7^k\in \left\{0,1\right\}$	1 if k-th demand (operating chillers) is satisfied in the K-bin discretized demand distribution, otherwise 0

Table 5. Definition of parameters in the model.

Variables	Definition
${\delta }_1\in R$	Electricity demand for manual assembly (6 kW)
${\delta }_2\in R$	Electricity demand for operating robots (8 kW)
${\delta }_3\in R$	Electricity demand for moving conveyors (163 kW)
${\delta }_4\in R$	Electricity demand for operating repairing centers (17 kW)
${\delta }_5\in R$	Stochastic electricity demand for air conditioning as specified in Table 3
${\delta }_6\in R$	Electricity demand for building lighting at Setback state (4 kW)
${\delta }_7\in R$	Stochastic electricity demand for operating chillers as specified in Table 3
${\delta }_8\in R$	Electricity demand for liquid moving at Setback state (10 kW)
${\delta }_9\in R$	Electricity demand for air abatement at Setback state (2 kW)
${\alpha }_5$	Probability to fail in meeting a quality of service (QoS) required for the air conditioning activity
${\alpha }_7$	Probability to fail in meeting a quality of service (QoS) required for the operating chillers activity

Table 5. Definition of parameters in the model.

Variables	Definition
${\delta }_1\in R$	Electricity demand for manual assembly (6 kW)
${\delta }_2\in R$	Electricity demand for operating robots (8 kW)
${\delta }_3\in R$	Electricity demand for moving conveyors (163 kW)
${\delta }_4\in R$	Electricity demand for operating repairing centers (17 kW)
${\delta }_5\in R$	Stochastic electricity demand for air conditioning as specified in Table 3
${\delta }_6\in R$	Electricity demand for building lighting at Setback state (4 kW)
${\delta }_7\in R$	Stochastic electricity demand for operating chillers as specified in Table 3
${\delta }_8\in R$	Electricity demand for liquid moving at Setback state (10 kW)
${\delta }_9\in R$	Electricity demand for air abatement at Setback state (2 kW)
${\alpha }_5$	Probability to fail in meeting a quality of service (QoS) required for the air conditioning activity
${\alpha }_7$	Probability to fail in meeting a quality of service (QoS) required for the operating chillers activity

5.3.2. Constraints

Equation (8) corresponds to the constraint of energy demand and supply conservation as described in Equation (4). Equations (9)–(13) jointly represent the constraints on the energy demand required by air conditioning activity in such a way to guarantee that $y_5\ge {\delta }_5^k$ must be true for at least one $k=1,2,\dots ,K$. Equation (14) is the knapsack inequality that enforces the QoS of air conditioning activity to meet $\left(1-{\alpha }_5\right)\%$. Similarly, Equations (15)–(19) jointly represent the constraints on the energy demand required for operating chillers in such a way to guarantee that $y_7\ge {\delta }_7^k$ must be true for at least one k = 1,2,…K. Equation (20) is the knapsack inequality that enforces the QoS of operating chillers to meet $\left(1-{\alpha }_7\right)\%$. Eventually, both Equations (14) and (20) imply the acceptance of the inability to meet the requirements for air conditioning and operating chillers at all times. Indeed, the manufacturing system under consideration continues to work properly even if the constraints to meet the energy demand for air conditioning and operating chillers are violated for a short time period. In such a circumstance, it makes sense that one would rather insist on decisions guaranteeing feasibility “as much as possible”:

$$6+8+163+17+y_5+4+y_7+10+2=x$$

(8)

$$y_5\ge 2-2z_5^1$$

(9)

$$y_5\ge 3-3z_5^2$$

(10)

$$y_5\ge 4-4z_5^3$$

(11)

$$y_5\ge 5-5z_5^4$$

(12)

$$y_5\ge 6-6z_5^5$$

(13)

$$0.65z_5^1+0.1z_5^2+0.1z_5^3+0.1z_5^4+0.05z_5^5\le {\alpha }_5\left(=0.35\right)$$

(14)

$$y_7\ge 20-20z_7^1$$

(15)

$$y_7\ge 40-40z_7^2$$

(16)

$$y_7\ge 60-60z_7^3$$

(17)

$$y_7\ge 80-80z_7^4$$

(18)

$$y_7\ge 100-100z_7^5$$

(19)

$$0.7z_7^1+0.15z_7^2+0.1z_7^3+0.04z_7^4+0.01z_7^5\le {\alpha }_7\left(=0.1\right)$$

(20)

where $x\ge 0;y_5,y_7\ge 0;z_5^k,z_7^k\in \left\{0,1\right\}k=1,2,\dots ,K.$

5.3.3. Results

Microsoft Excel Solver is used to solve the above deterministic linear problem consisting of Equations (7)–(20). Under 65% QoS for air conditioning activity (${\alpha }_5$= 0.35) and 90% QoS for operating chillers (${\alpha }_7$= 0.1), the optimal values of decision variables are: $\left[z_5^1, z_5^2, z_5^3, z_5^4, z_5^5\right]$ = [0, 1, 1, 1, 1]; $\left[z_7^1, z_7^2, z_7^3, z_7^4, z_7^5\right]$ = [0, 0, 0, 1, 1]; $\left[y_5, y_7\right]$ = [2, 60];$x$ = 272. The corresponding optimal value of the objective function that is, Equation (7) becomes 272 because we assume that c = 1. The illustrative example still has a relatively small size, however, this approach still holds effective even when it is expanded to include real life multiple stochastic variables and constraints where the computation complexity is so high that the manual solving is no longer tractable.

5.4. Calculate a New Peak Energy Demand ($P^{*}$) and Make a Decision on the Offer

The final step is to recalculate the peak energy demand level ( $P^{*}$) and determine whether to accept or reject the offer. In this study, each activity $i\in I_{MC}$ is set to receive energy at the demand rate (kW) corresponding to the production state. Meanwhile, each activity $i\in I_{STF}$ = {Building lighting, Liquid moving, Air abatement} is set to demand energy corresponding to its setback state. Furthermore, for activities in $I_{QoSF}$ = {Air conditioning, Operating chillers }, the air conditioning activity and the chiller operation activity lower its QoS level down to 65% and 90%, respectively. As a result, the overall peak energy demand rate $P^{*}$ becomes as follows:

$$P^{*}=P_{MC} + P_{STF} + P_{QoSF}=ma{x}_t\left({\sum }_{i\in I_{MC}}{\sum }_j{r}_{ij}\times Z_{ij}\left(t\right)\right) + ma{x}_t\left({\sum }_{i\in I_{STF}}{\sum }_j{r}_{ij}\times Z_{ij}\left(t\right)\right)+ {\sum }_{i\in I_{QoSF}}{y}_i= 272 \mathrm{kW}$$

since $P^{*}\le C$=(280 kW), the offer is finally accepted.

6. Conclusions

This paper proposes a new decision process to assess the impact pertaining to energy demand response program participation and determination as to whether or not to participate in the program. The participation in the program will offer an opportunity to reduce the cost of electricity or to gain incentives, but in the meantime requires facing a challenge to secure a high-resolution understanding of energy usage and its causes. The decision process presented here uses ABC-based energy accounting model and chance constraint stochastic programing model as assessment methodologies and focuses on state-transition flexible activities and QoS-flexible activities to reduce the peak energy demand rate. Also, the paper illustrates the proposed decision process in the context of its specific application to a simple hypothetical manufacturing system where mission-critical activities and other non-mission critical activities are mixed. The illustrative study result showed that the proposed decision model can be used with emerging smart grid opportunities to provide a competitive advantage to the manufacturing industry.

Although there are many ways to extend this work, one direction is to further investigate the possibility of the integration of the proposed decision process with transactional energy market information system (e.g., OpenADR or Open Auto-DR) so that energy demand response transactions can be implemented automatically. While all work presented here has been based on the “load-shedding” approach to demand response targeting at state-transition or QoS flexible activities, there may be additional opportunities in “load-shifting” for mission-critical activities through utilizing variable real-time energy demand profiles.