An Efficiency-Optimized Isolated Bidirectional DC-DC Converter with Extended Power Range for Energy Storage Systems in Microgrids
Abstract
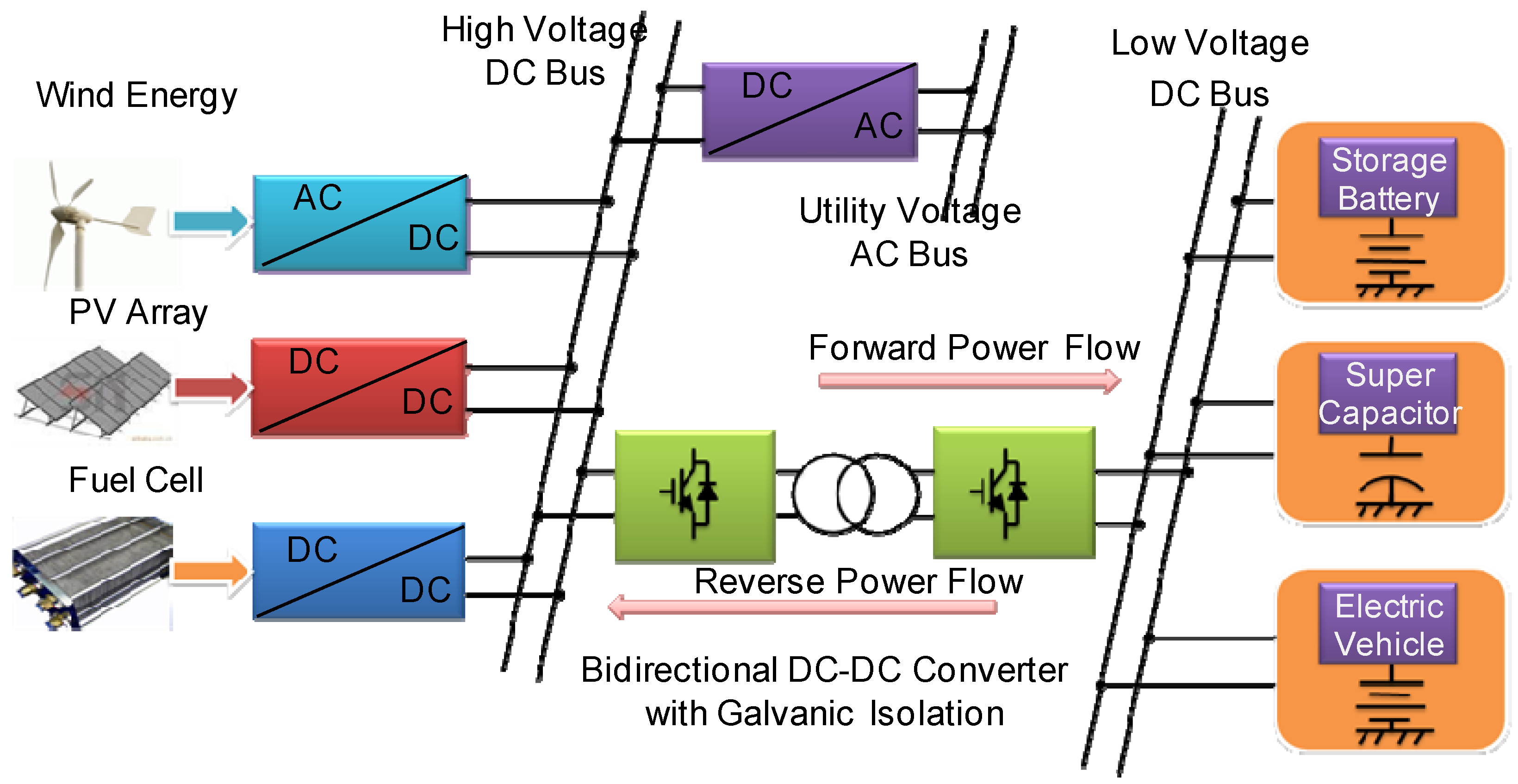
:1. Introduction
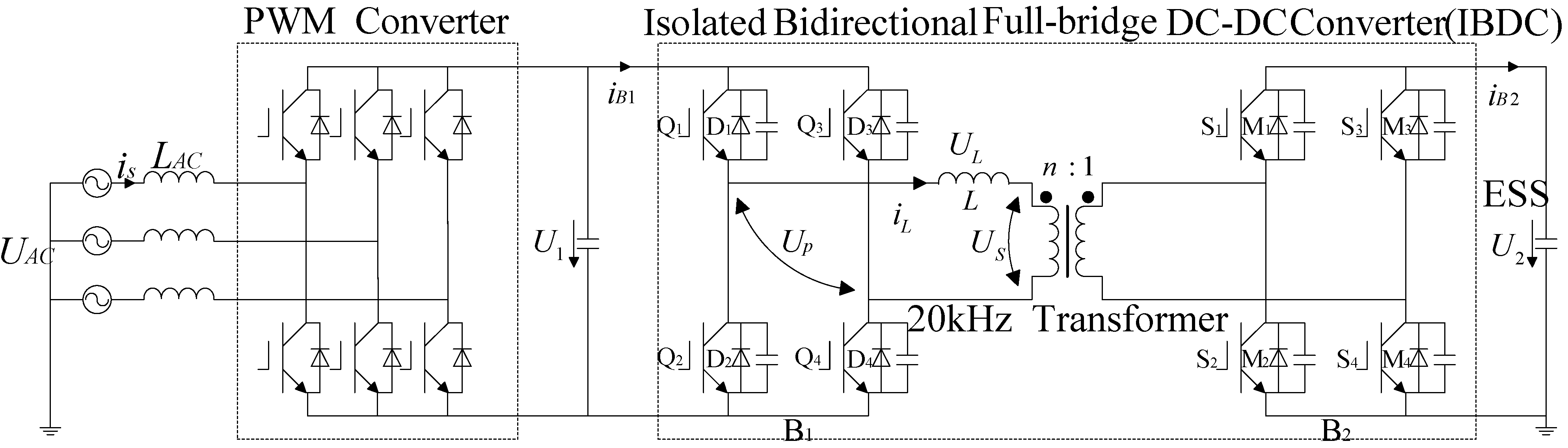
2. Phase Shift Operation in ESPS Control
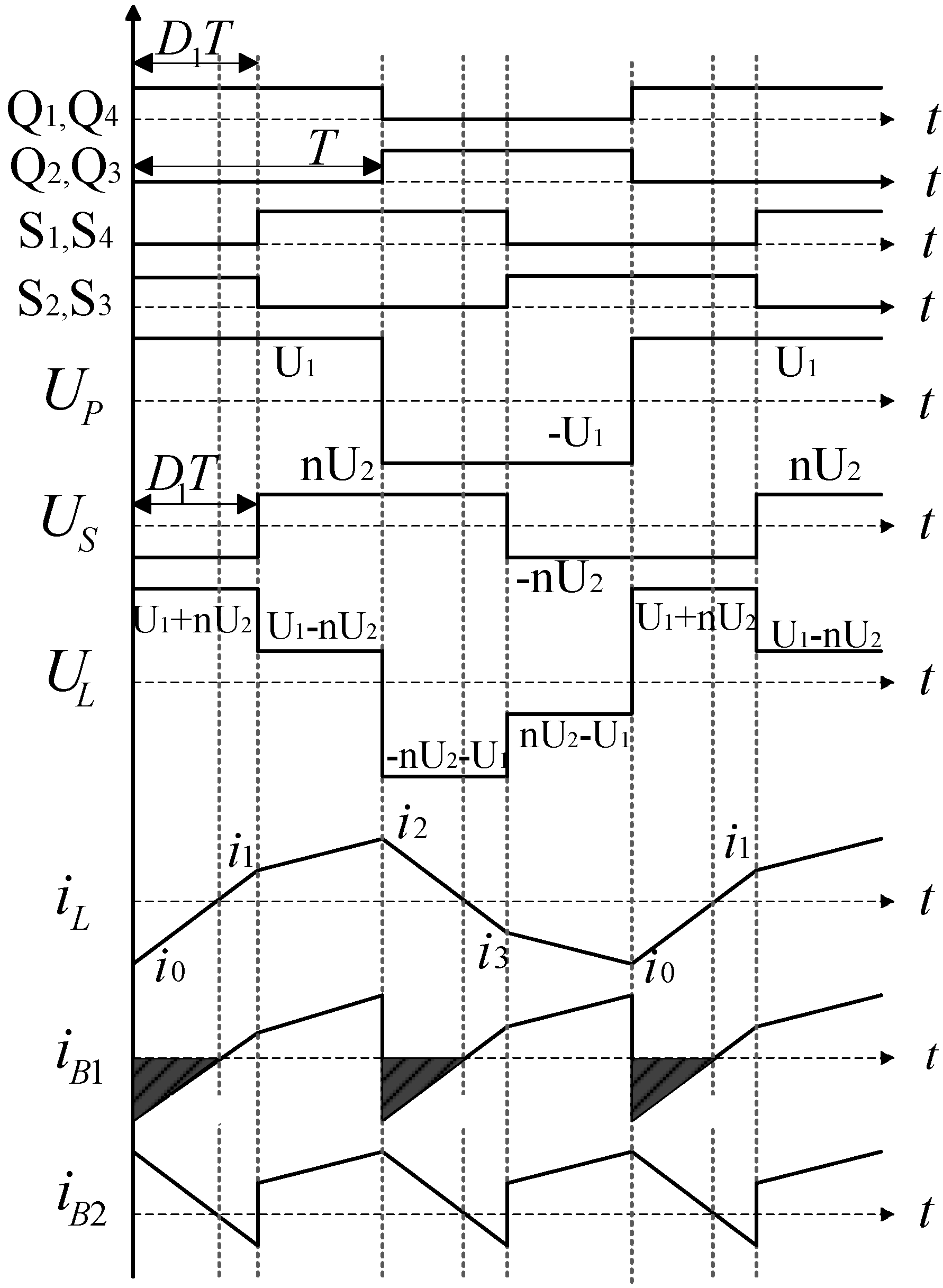
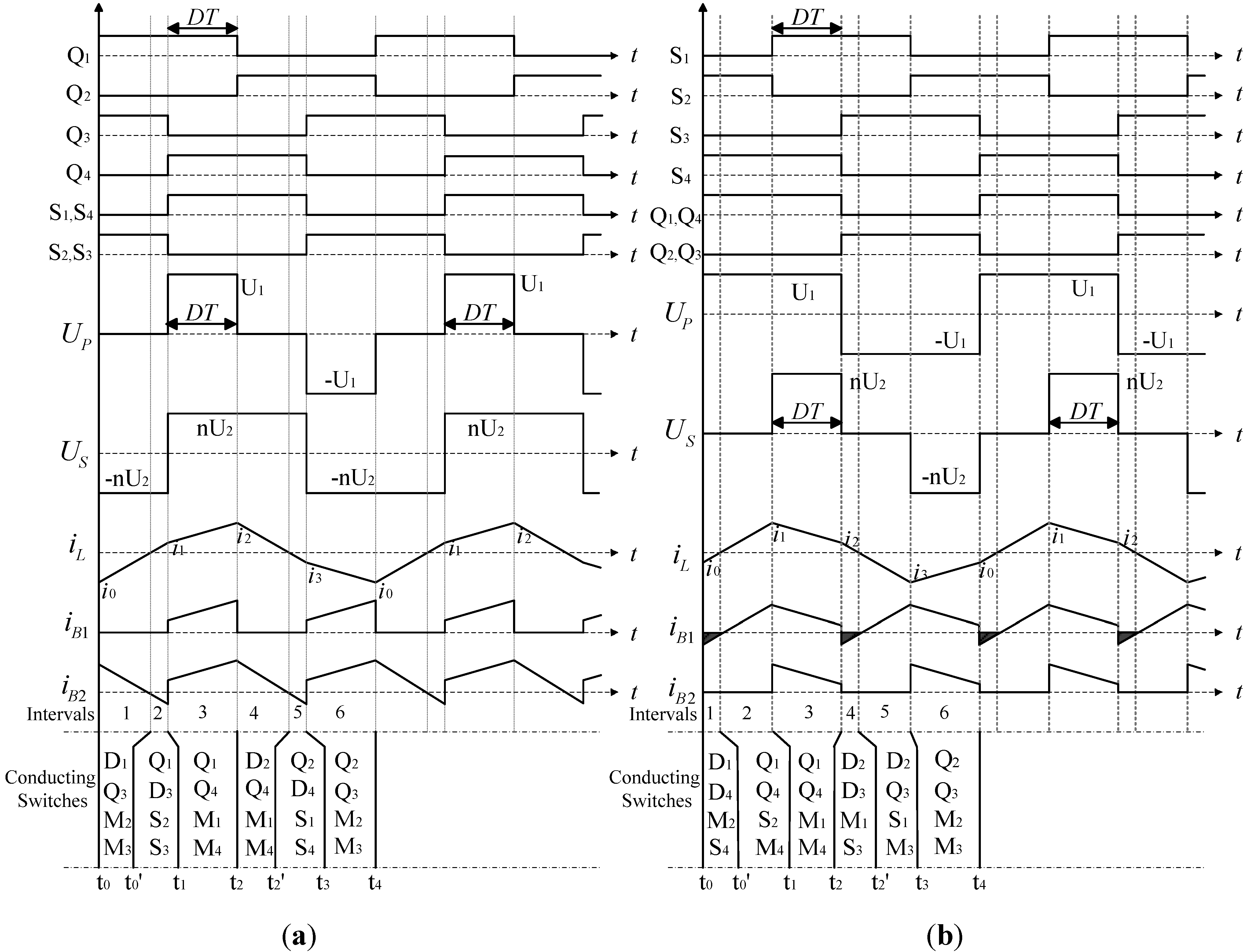
3. Mathematical Models of ESPS Control in Steady-State Conditions
| iL(t) | t = t0 | t = t1 | t = t2 |
|---|---|---|---|
| Buck | |||
| Boost |
| Condition | ||
|---|---|---|
| Buck | ||
| Boost |
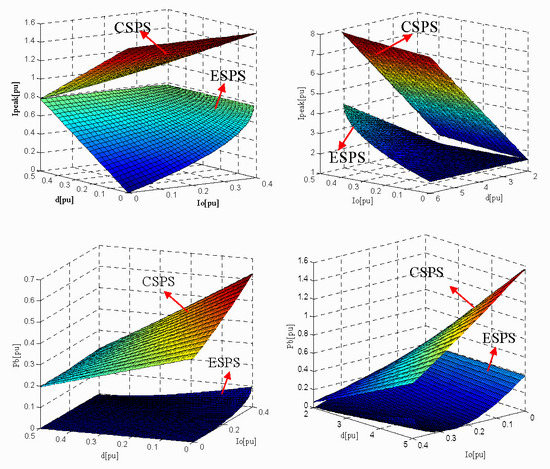
4. Analysis and Comparisons of ESPS and CSPS Control
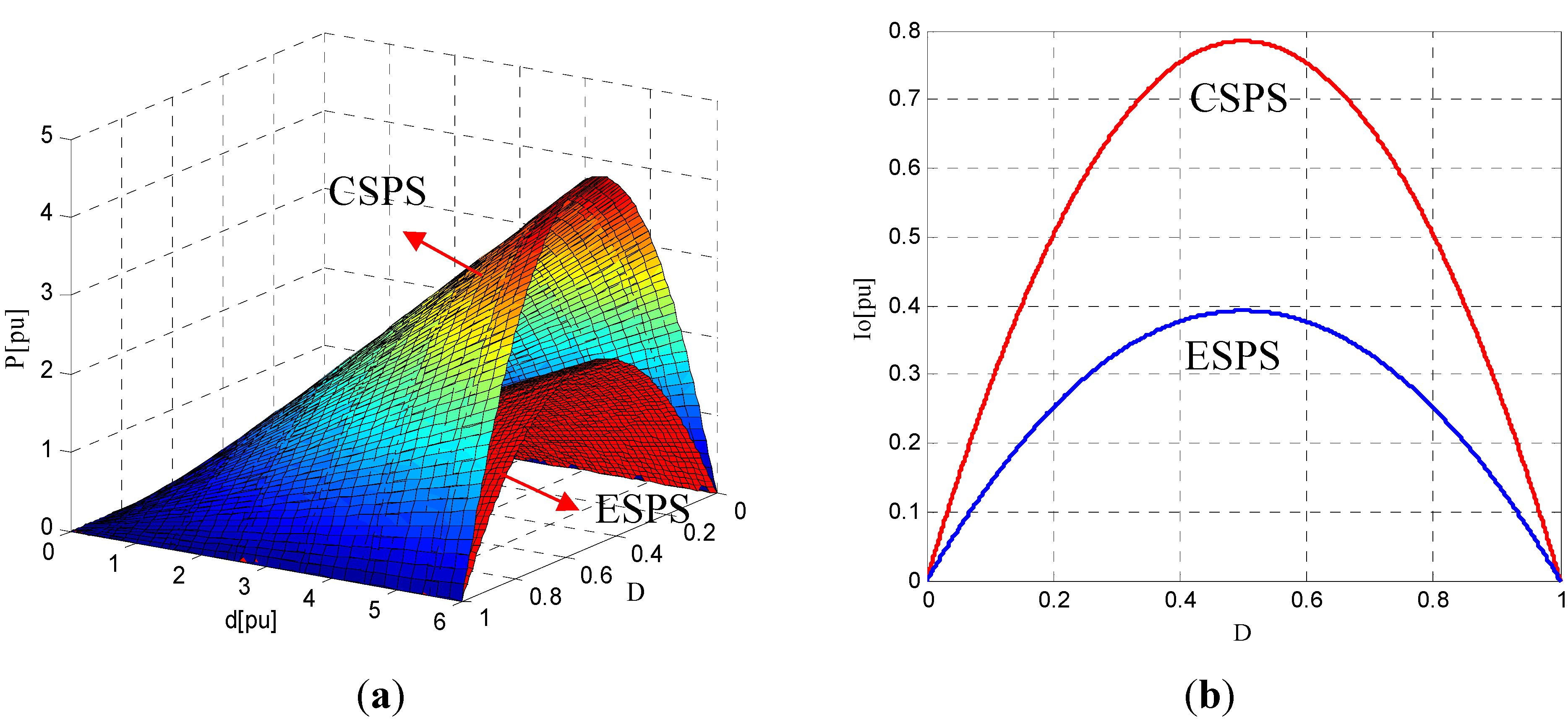
4.1. Comparative Analysis of Transmission Power
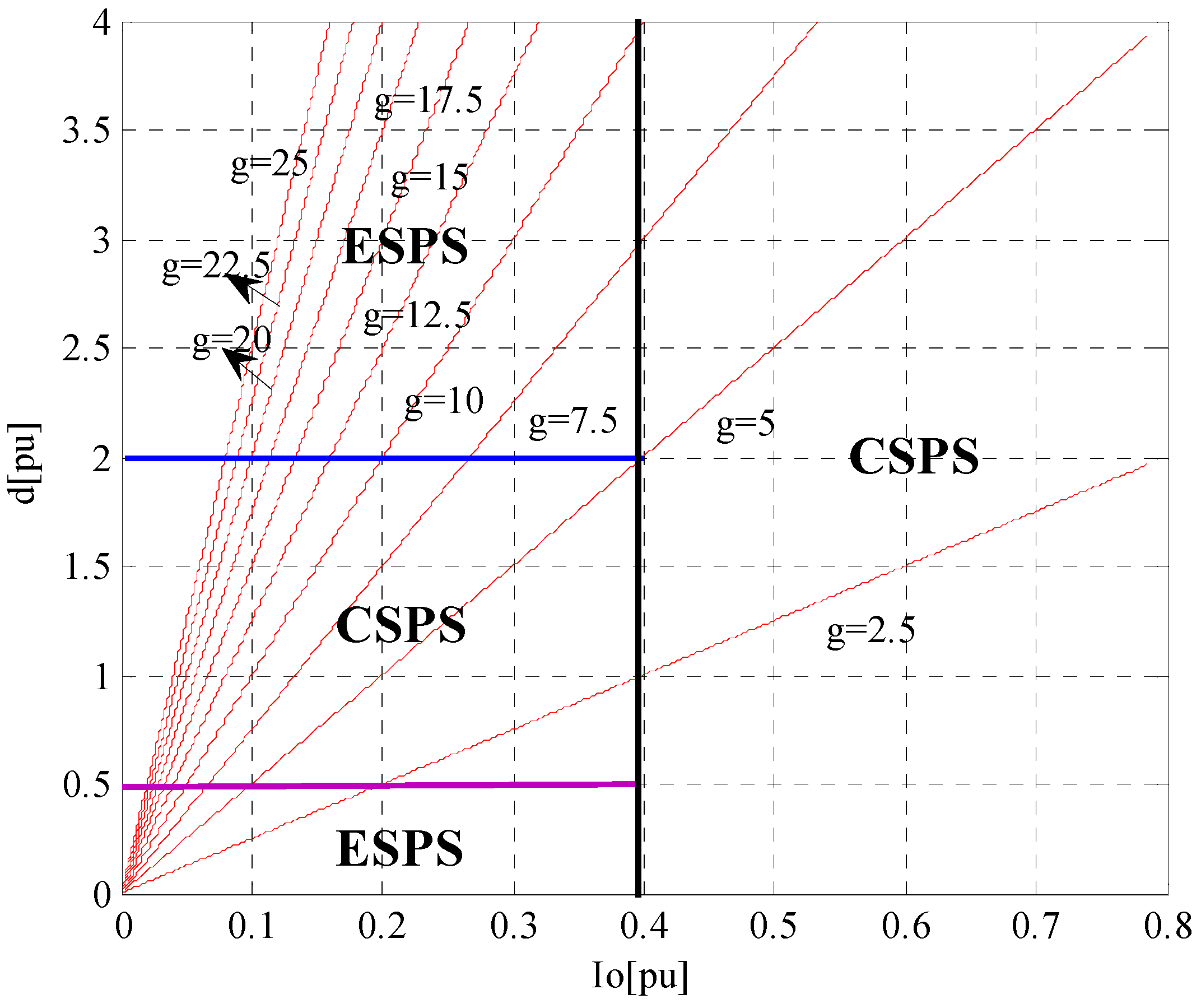
4.2. The Algorithm to Implement ESPS in Light and Medium Load with Wide Voltage Ratio Range
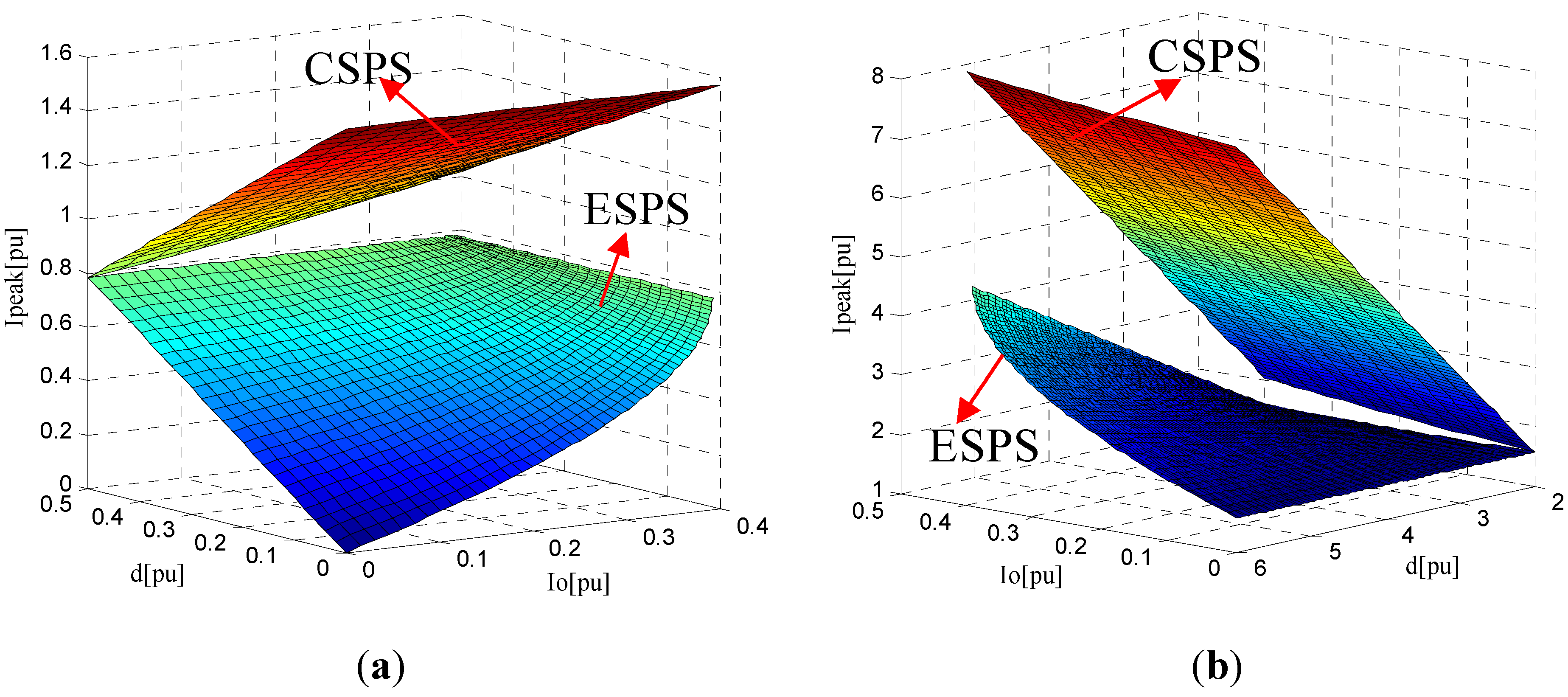
4.3. Comparative Analysis of Current Stress
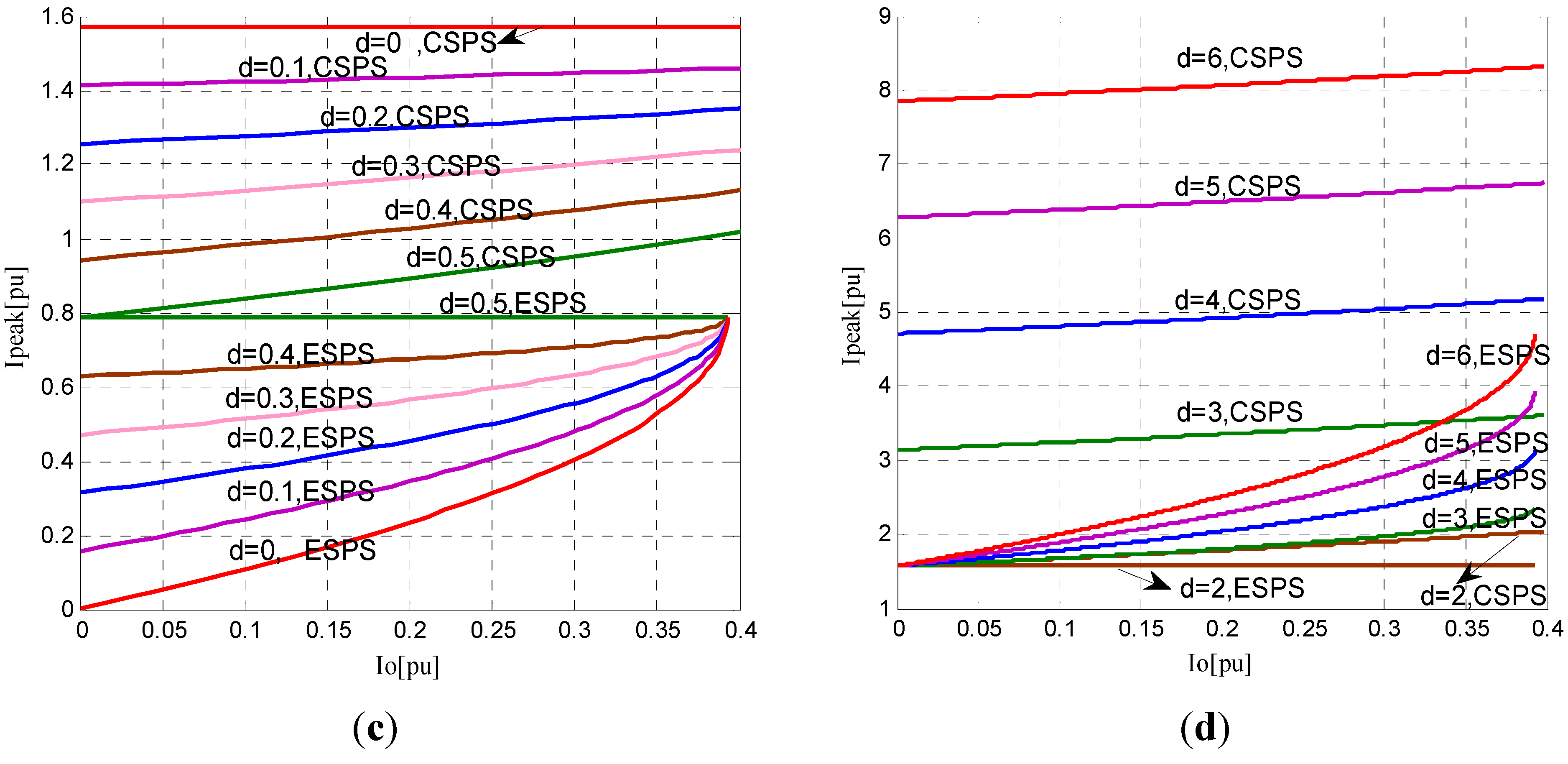
4.4. The Comparative Analysis of Backflow Power
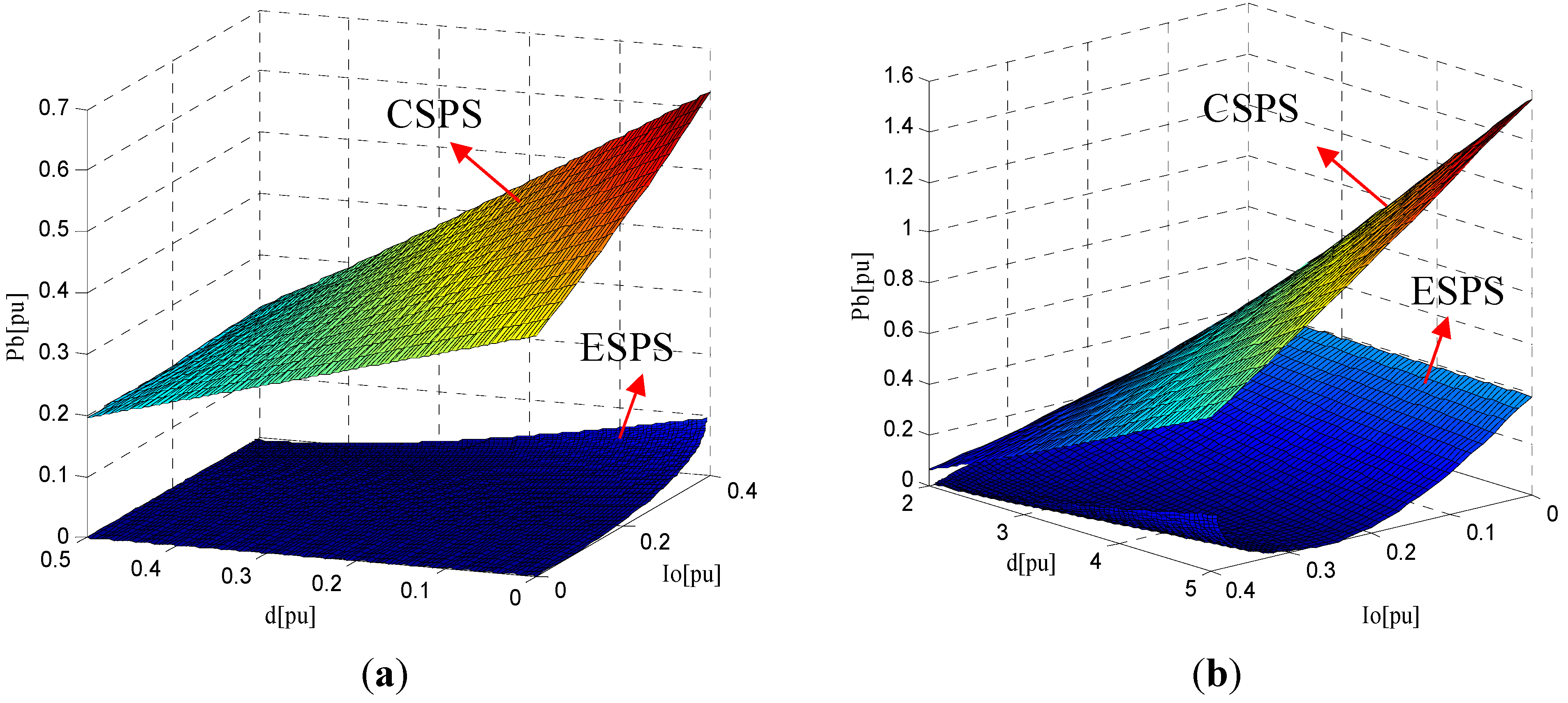
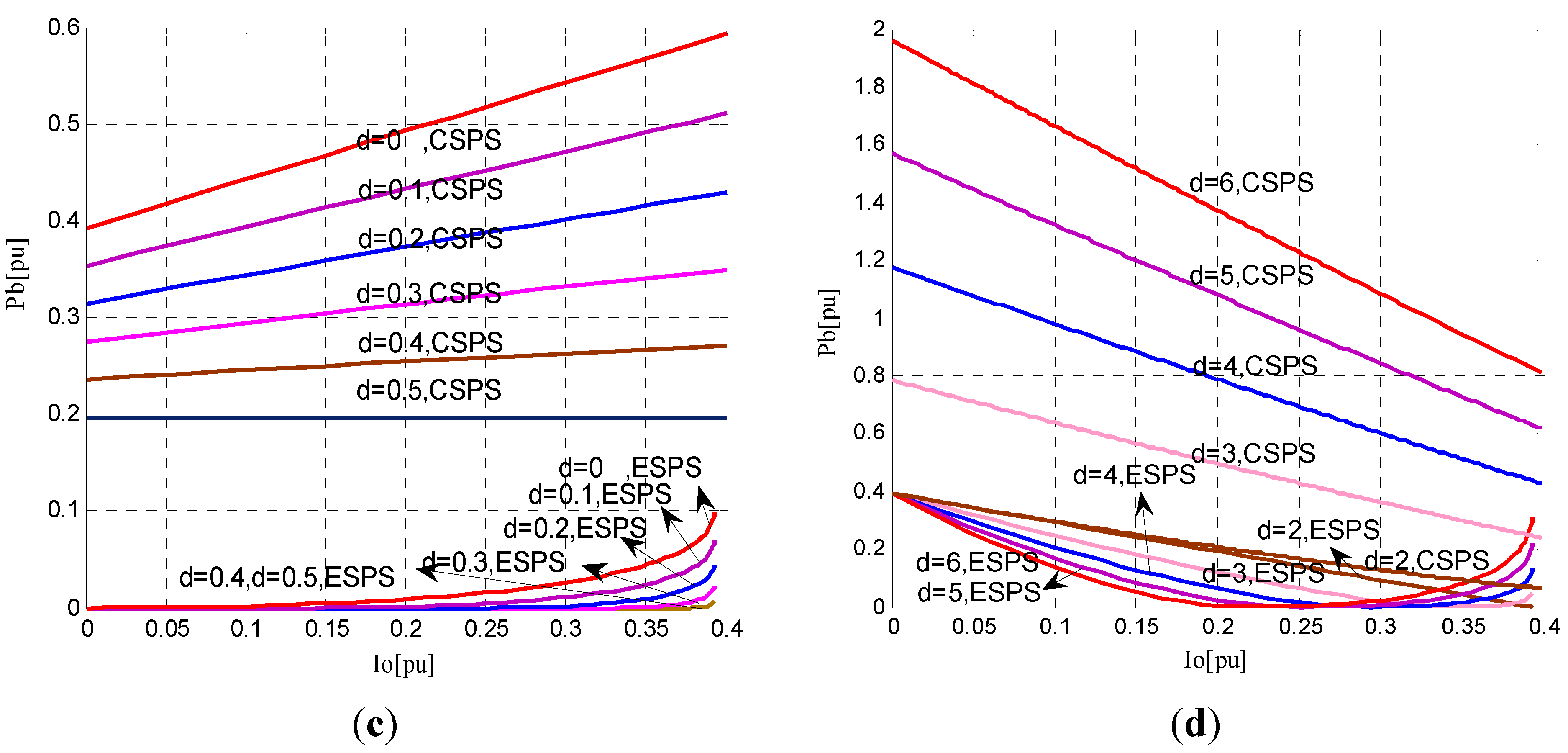
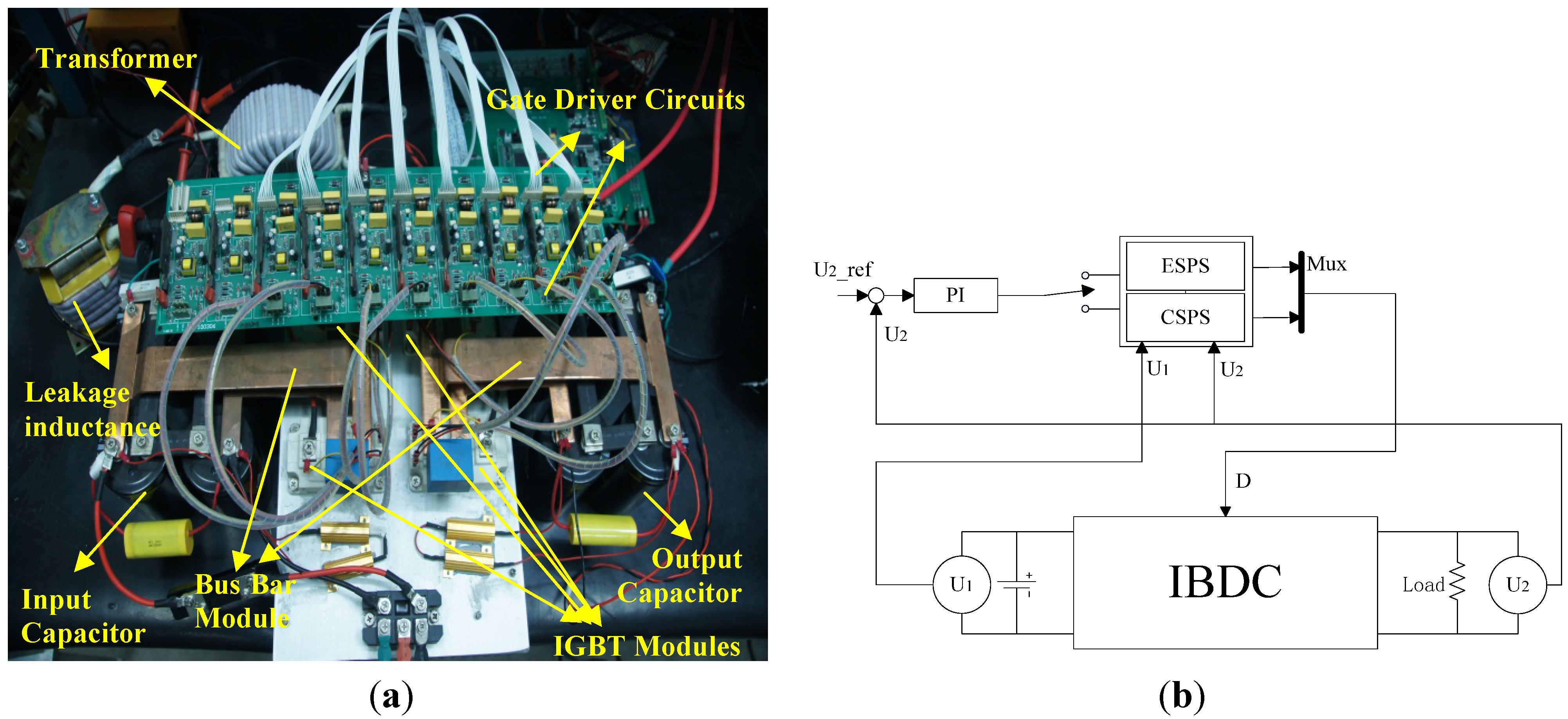
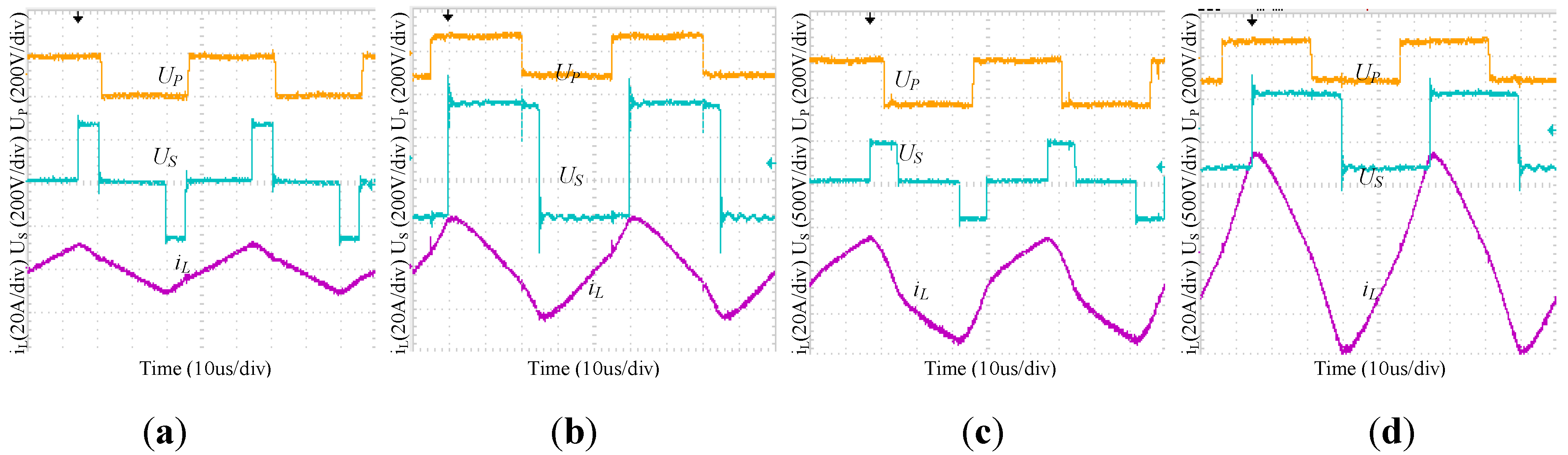
5. Experimental Results
| Output Power(PO) | 0–10 kW |
|---|---|
| Switching Frequency(f) | 20 kHz |
| Input DC Voltage(U1) | 100–500 V |
| Output DC Voltage(U2) | 0–500 V |
| Transformer Turns Ratio(n) | 1:1 |
| Series Inductance(L) | 120 μH |
| Output Load (R) | 25/200 Ω |
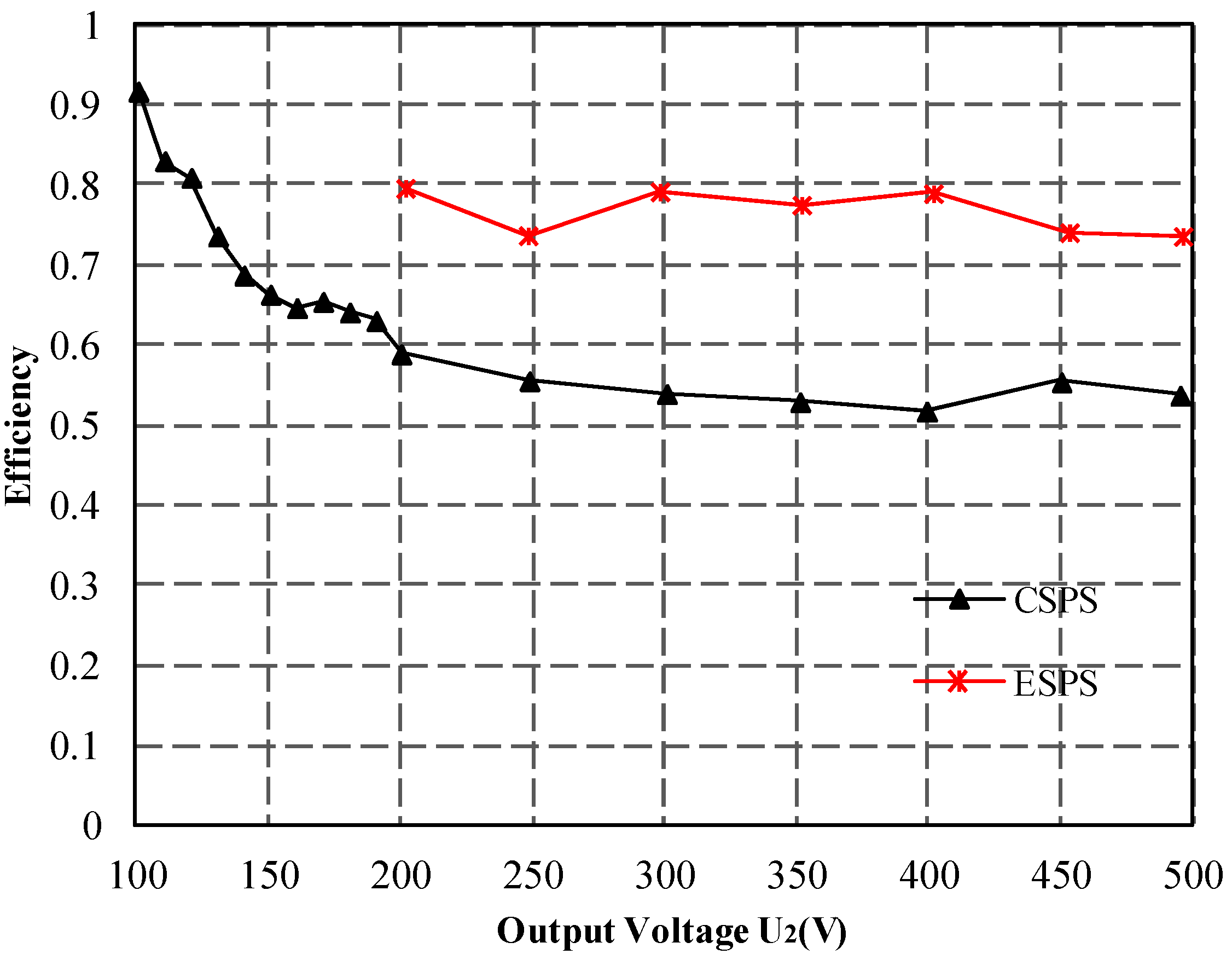
5.1. The Comparisons of ESPS and CSPS Control in Low Voltage Ratio Range
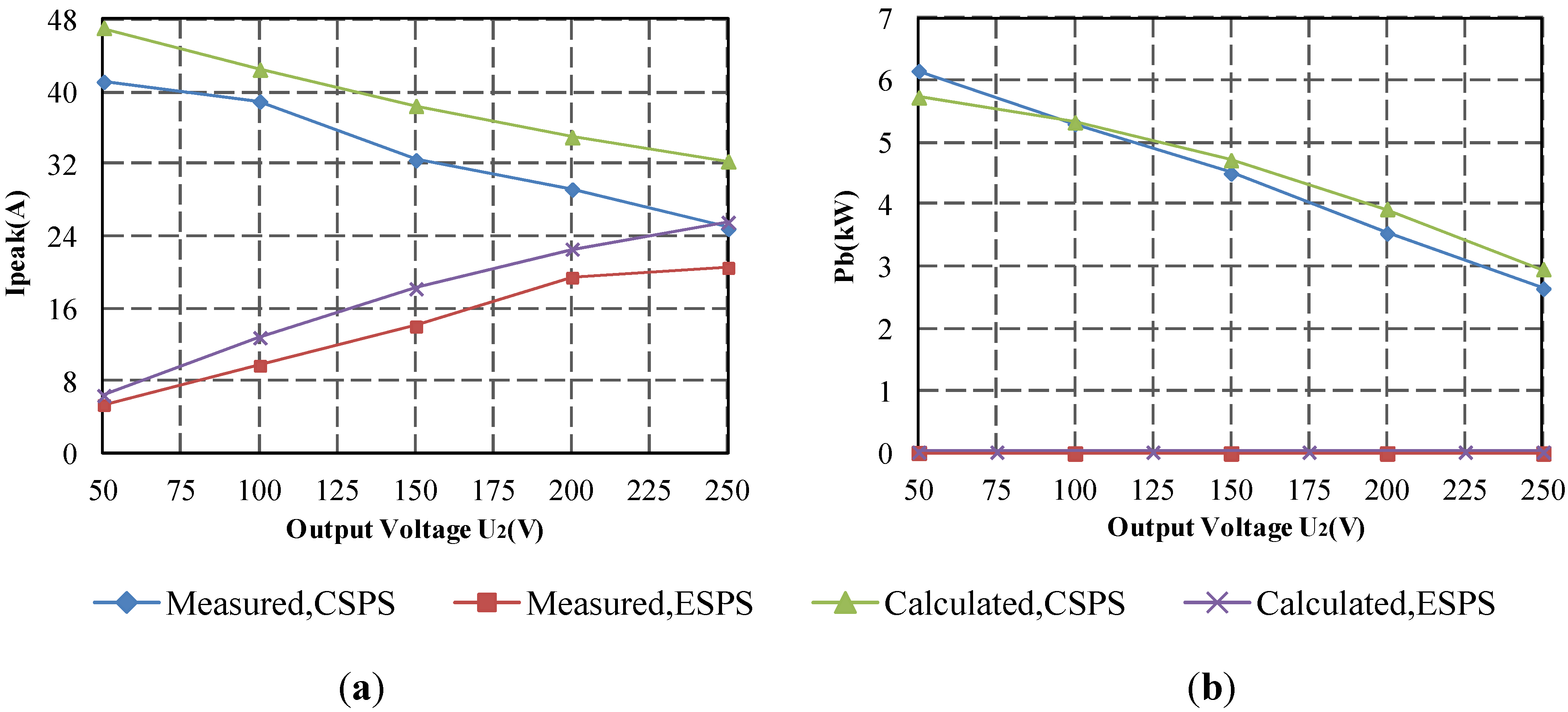
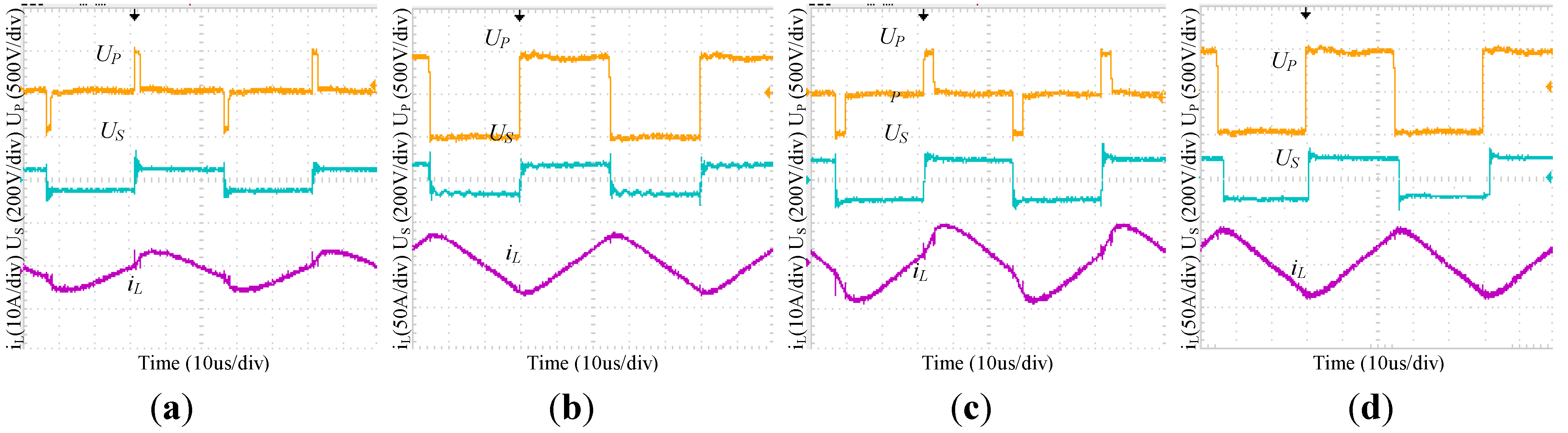
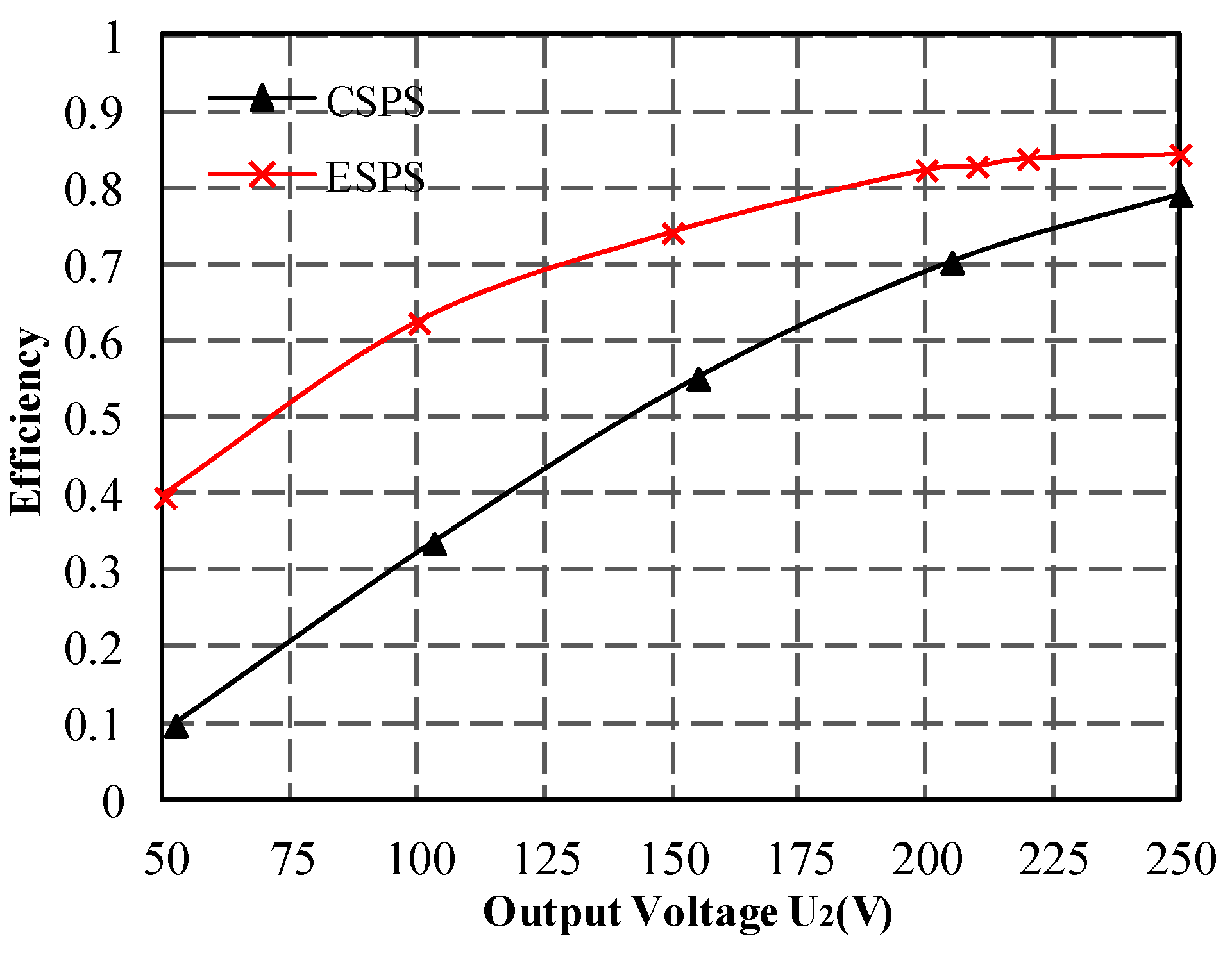
5.2. The Comparisons of ESPS and CSPS Control in High Voltage Ratio Range
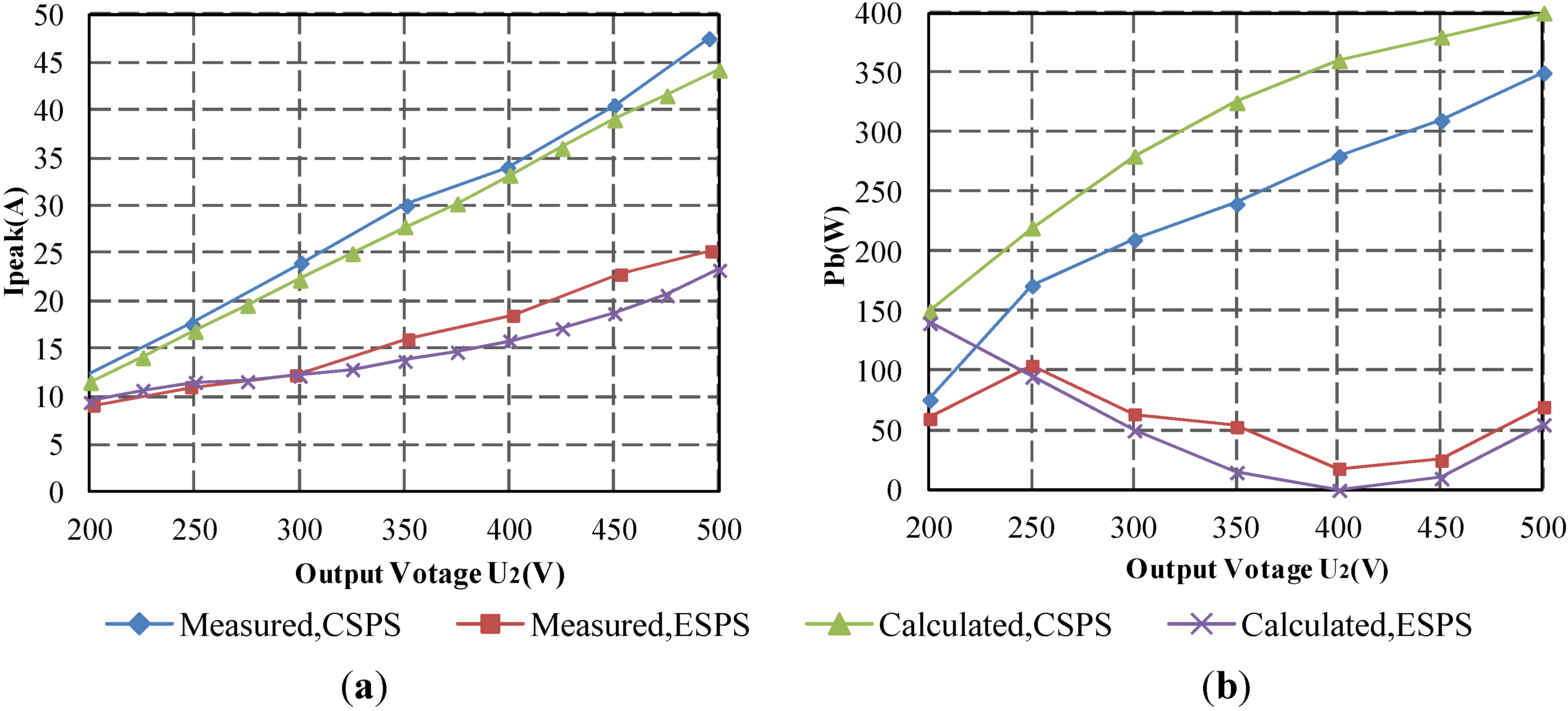
6. Conclusions
- ESPS control reduces both current stress and backflow power dramatically when d < 0.5 and d > 2 under light and medium load, thus saving costs and reducing system losses considerably.
- The overall system efficiency is significantly optimized in the defined operation region.
- ESPS control only needs to control one single variation, thus it is very simple in principle and easy to implement for microgrid applications.
- The hybrid modulation scheme based on ESPS and CSPS control is an advanced control strategy to ensure high system efficiency of IBDC with extended power range in microgrids while retaining implementation simplicity.
Acknowledgments
References
- Inoue, S.; Akagi, H. A bidirectional isolated DC-DC converter as a core circuit of the next-generation medium-voltage power conversion system. IEEE Trans. Power Electron. 2007, 22, 535–542. [Google Scholar]
- Inoue, S.; Akagi, H. A bidirectional DC-DC converter for an energy storage system with galvanic isolation. IEEE Trans. Power Electron. 2007, 22, 2299–2306. [Google Scholar]
- Wang, X.J.; Tian, W.Q.; He, H.J.; Huang, M.; Jiang, J.C.; Han, H.Y. The application of electric vehicles as mobile distributed energy storage units in smart grid. In Proceedings of Asia-Pacific Power Energy Engineering Conference, Wuhan, China, 25–28 March 2011.
- Li, W.; Joos, G.; Abbey, C.A. A parallel bidirectional DC/DC converter topology for energy storage systems in wind applications. In Proceedings of IEEE Industry Applications Society Annual Meeting (IAS), New Orleans, LA, USA, 23–27 September 2007; pp. 179–185.
- De Doncker, R.W.; Divan, D.M.; Kheraluwala, M.H. A three-phase soft-switched high power-density Dc/Dc converter for high-power applications. IEEE Trans. Ind. Appl. 1991, 27, 63–73. [Google Scholar]
- Kim, J.; Song, H.S.; Nam, K. Asymmetric duty control of a dual-half-bridge DC/DC converter for single-phase distributed generators. IEEE Trans. Power Electron. 2011, 26, 973–982. [Google Scholar]
- Xie, Y.; Sun, J.; Freudenberg, J.S. Power flow characterization of a bidirectional galvanically isolated high-power DC/DC converter over a wide operating range. IEEE Trans. Power Electron. 2010, 25, 54–66. [Google Scholar]
- Naayagi, R.T.; Forsyth, A.J.; Shuttleworth, R. High-Power bidirectional DC-DC converter for aerospace applications. IEEE Trans. Power Electron. 2012, 27, 4366–4379. [Google Scholar]
- Chen, W.; Rong, P.; Lu, Z.Y. Snubberless bidirectional DC-DC converter with new CLLC resonant tank featuring minimized switching loss. IEEE Trans. Ind. Electron. 2010, 57, 3075–3086. [Google Scholar]
- Zhao, B.; Song, Q.; Liu, W.H. Power characterization of isolated bidirectional dual-active-bridge DC-DC converter with dual-phase-shift control. IEEE Trans. Power Electron. 2012, 27, 4172–4176. [Google Scholar]
- Wu, K.Y.; De. Silva, C.W.; Dunford, W.G. Stability analysis of isolated bidirectional dual active full-bridge DC-DC Converter with triple phase-shift control. IEEE Trans. Power Electron. 2012, 27, 2007–2017. [Google Scholar]
- Wai, R.J.; Duan, R.Y. High-efficiency bidirectional converter for power sources with great voltage diversity. IEEE Trans. Power Electron. 2007, 22, 1986–1996. [Google Scholar]
- Kheraluwala, M.H.; Gascoigne, R.W.; Divan, D.M.; Baumann, E.D. Performance characterization of a high-power dual active bridge Dc-to-Dc converter. IEEE Trans. Ind. Appl. 1992, 28, 1294–1301. [Google Scholar]
- Zhou, H.; Khambadkone, A.M. Hybrid modulation for dual active bridge bi-directional converter with extended power range for ultracapacitor application. IEEE Trans. Ind. Appl. 2009, 45, 1434–1442. [Google Scholar]
- Bai, H.; Mi, C. Eliminate reactive power and increase system efficiency of isolated bidirectional dual-active-bridge DC-DC converter using novel dual-phase-shift control. IEEE Trans. Power Electron. 2008, 23, 2905–2914. [Google Scholar]
- Oggier, G.G.; Garcia, G.O.; Oliva, A.R. Switching control strategy to minimize dual active bridge converter losses. IEEE Trans. Power Electron. 2009, 24, 1826–1838. [Google Scholar]
- Zhang, J.; Lai, J.S.; Kim, R.Y.; Yu, W. High-power density design of a soft-switching high-power bidirectional Dc-Dc converter. IEEE Trans. Power Electron. 2007, 22, 1145–1153. [Google Scholar]
- Segaran, D.; Holmes, D.G.; McGrath, B.P. Comparative analysis of single and three-phase dual active bridge bidirectional DC-DC converters. In Proceedings of Australian Universities Power Engineering Conference, Sydney, Australia, 14–17 December 2008; pp. 1–6.
- Bai, H.; Nie, Z.; Mi, C. Experimental comparision of traditional phase-shift, dual-phase-shift, and model-based control of isolated bidirectional dc-dc converters. IEEE Trans. Power Electron. 2010, 25, 1444–1449. [Google Scholar]
- Krismer, F.; Kolar, J.W. Closed form solution for minimum conduction loss modulation of IBDC converters. IEEE Trans. Power Electron. 2012, 27, 174–188. [Google Scholar]
- Oggier, G.G.; Garcia, G.O.; Oliva, A.R. Modulation strategy to operate the dual active bridge DC-DC converter under soft switching in the whole operating range. IEEE Trans. Power Electron. 2011, 26, 1228–1236. [Google Scholar]
- Guo, X.T.; Jiang, J.C.; Niu, L.Y.; Li, J.X.; Qu, Y.Q. A 10kW DC-DC system based on a bidirectional high-frequency isolated dual active bridge DC-DC topology. In Proceedings of IEEE Power Engineering and Automation Conference, Wuhan, China, 8–9 September 2011; pp. 50–54.
- Jain, A.K.; Ayyanar, R. PWM control of dual active bridge; Comprehensive analysis and experimental verification. IEEE Trans. Power Electron. 2011, 26, 1215–1227. [Google Scholar]
- Krismer, F.; Kolar, J.W. Efficiency-optimized high current dual active bridge converter for automotive applications. IEEE Trans. Ind. Electron. 2012, 59, 2745–2760. [Google Scholar]
- Kim, M.; Rosekeit, M.; Sul, S.K.; De Doncker, R.W.A.A. A dual-phase-shift control strategy for dual-active-bridge DC-DC converter in wide voltage range. In Proceedings of 8th International Conference Power Electronics—ECCE Asia, 30 May–3 June 2011; pp. 364–371.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Shi, X.; Jiang, J.; Guo, X. An Efficiency-Optimized Isolated Bidirectional DC-DC Converter with Extended Power Range for Energy Storage Systems in Microgrids. Energies 2013, 6, 27-44. https://doi.org/10.3390/en6010027
Shi X, Jiang J, Guo X. An Efficiency-Optimized Isolated Bidirectional DC-DC Converter with Extended Power Range for Energy Storage Systems in Microgrids. Energies. 2013; 6(1):27-44. https://doi.org/10.3390/en6010027
Chicago/Turabian StyleShi, Xiaolong, Jiuchun Jiang, and Xintao Guo. 2013. "An Efficiency-Optimized Isolated Bidirectional DC-DC Converter with Extended Power Range for Energy Storage Systems in Microgrids" Energies 6, no. 1: 27-44. https://doi.org/10.3390/en6010027