Analytical Modeling of Partially Shaded Photovoltaic Systems
Abstract
:1. Introduction
- Being a basic tool for researchers to predict the output characteristics of the photovoltaic systems in both normal and partial shading conditions.
- Having a reliable and robust model is the first requirement for designers who want to analyze the performance and efficiency of different configurations of PV systems before installation.
- It is the first step to study and define the effectiveness of Maximum Power point tracking methods applied in different configuration of a PV system under variable environmental conditions.
- It is an aid for users who want to build actual PV systems without going into the intricate details such as semiconductor physics.
2. Modeling of Photovoltaic System Parameters
2.1. PV Cell Model
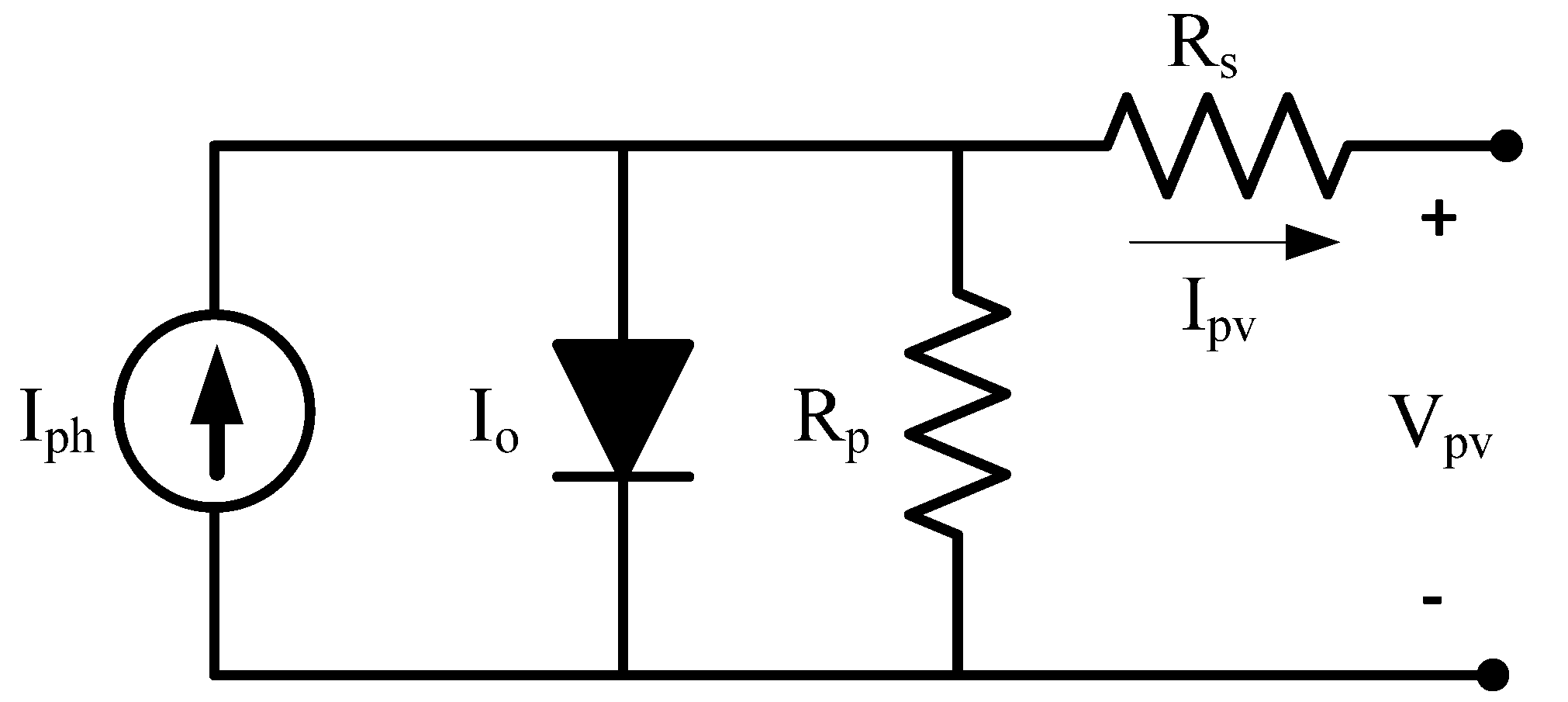
2.2. PV Module Model
| Electrical Characteristic | BP SX 150s |
|---|---|
| Open circuit voltage | 43.5 V |
| Short circuit current | 4.75 A |
| Maximum power voltage | 34.5 V |
| Maximum power current | 4.35 A |
| Maximum power | 150 W |
| Temperature coefficient of ISC | (0.065 ± 0.015)%/°C |
| Temperature coefficient of VOC | −(160 ± 20) mV/°C |
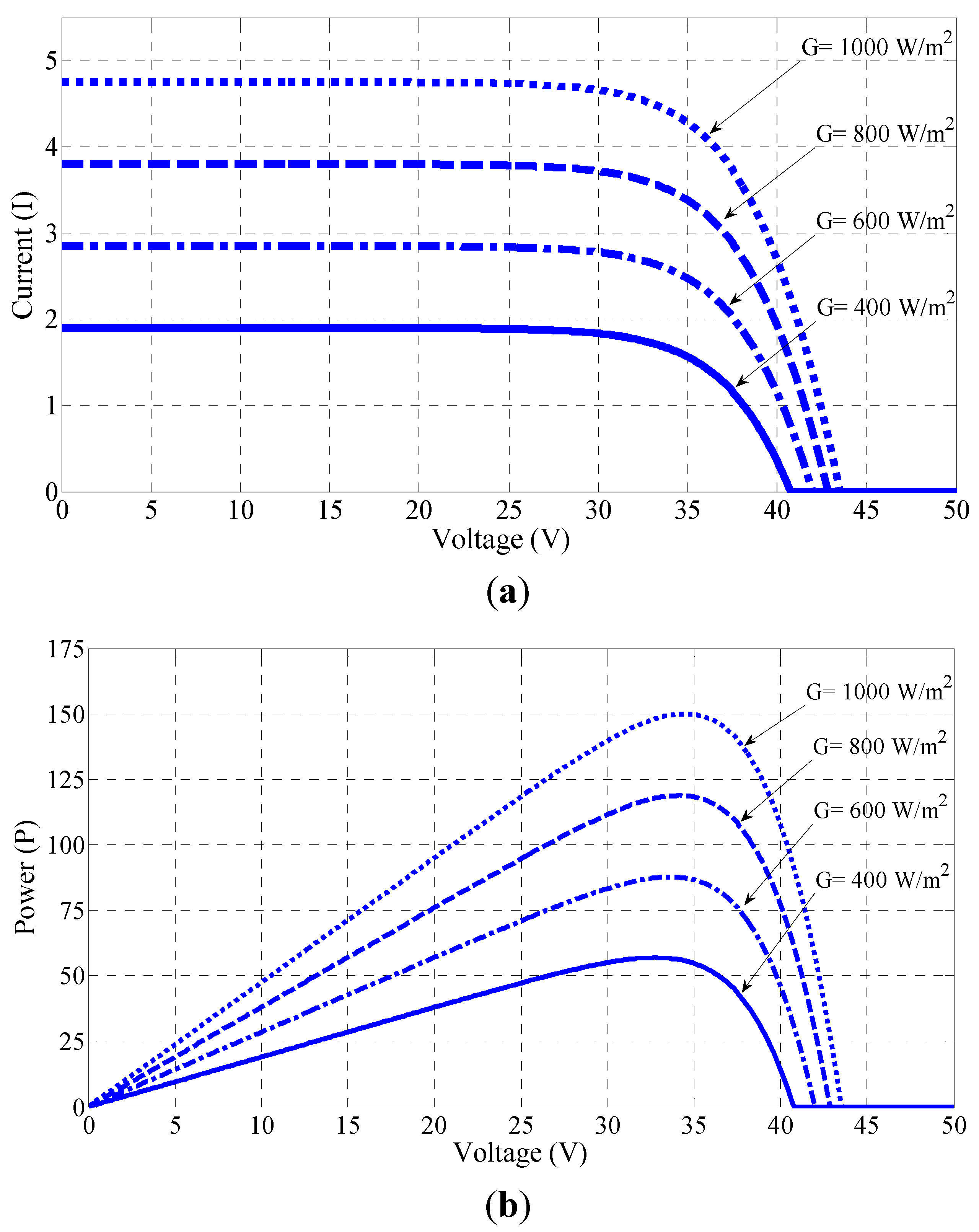
3. Characteristics of the PV System under Partial Shading
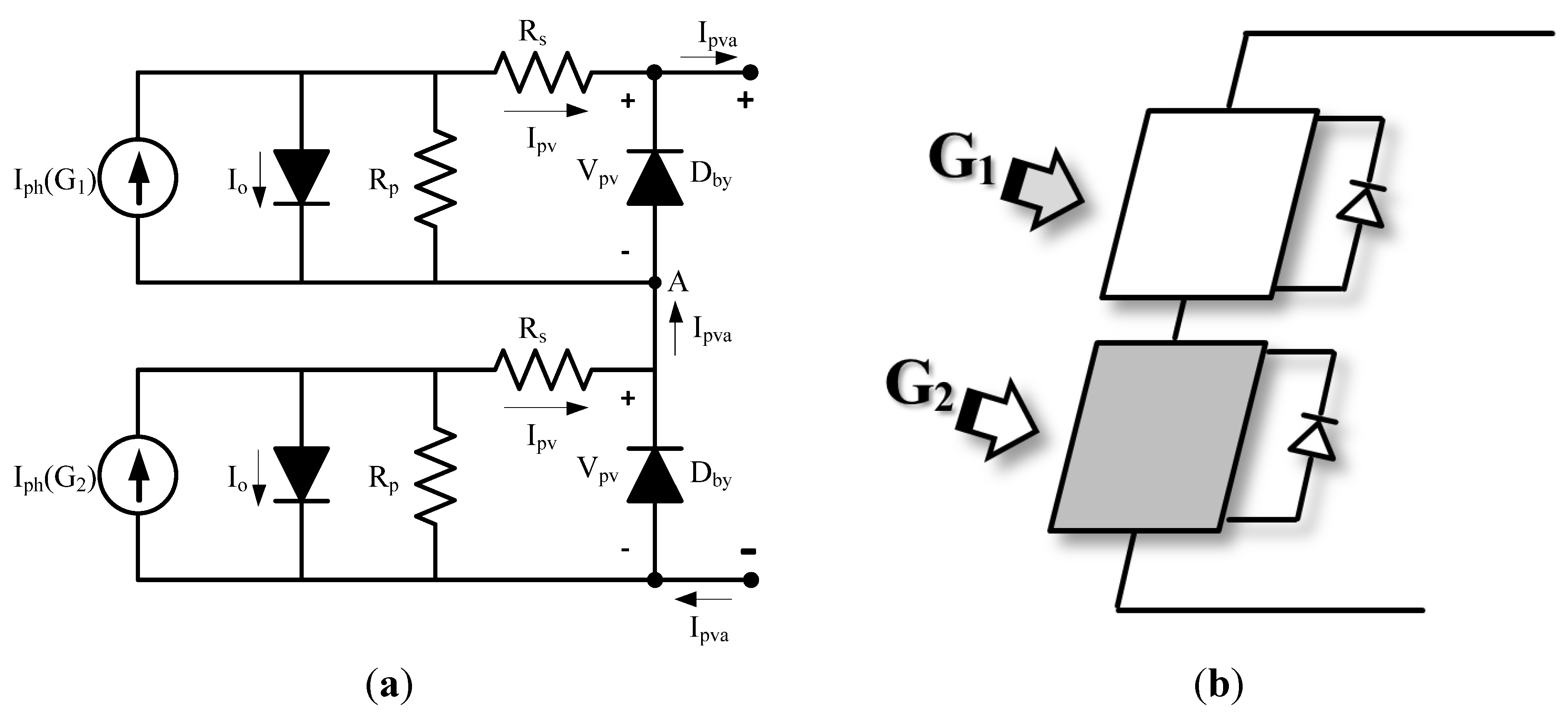
3.1. Effect of Bypass and Blocking Diodes on PV Characteristics
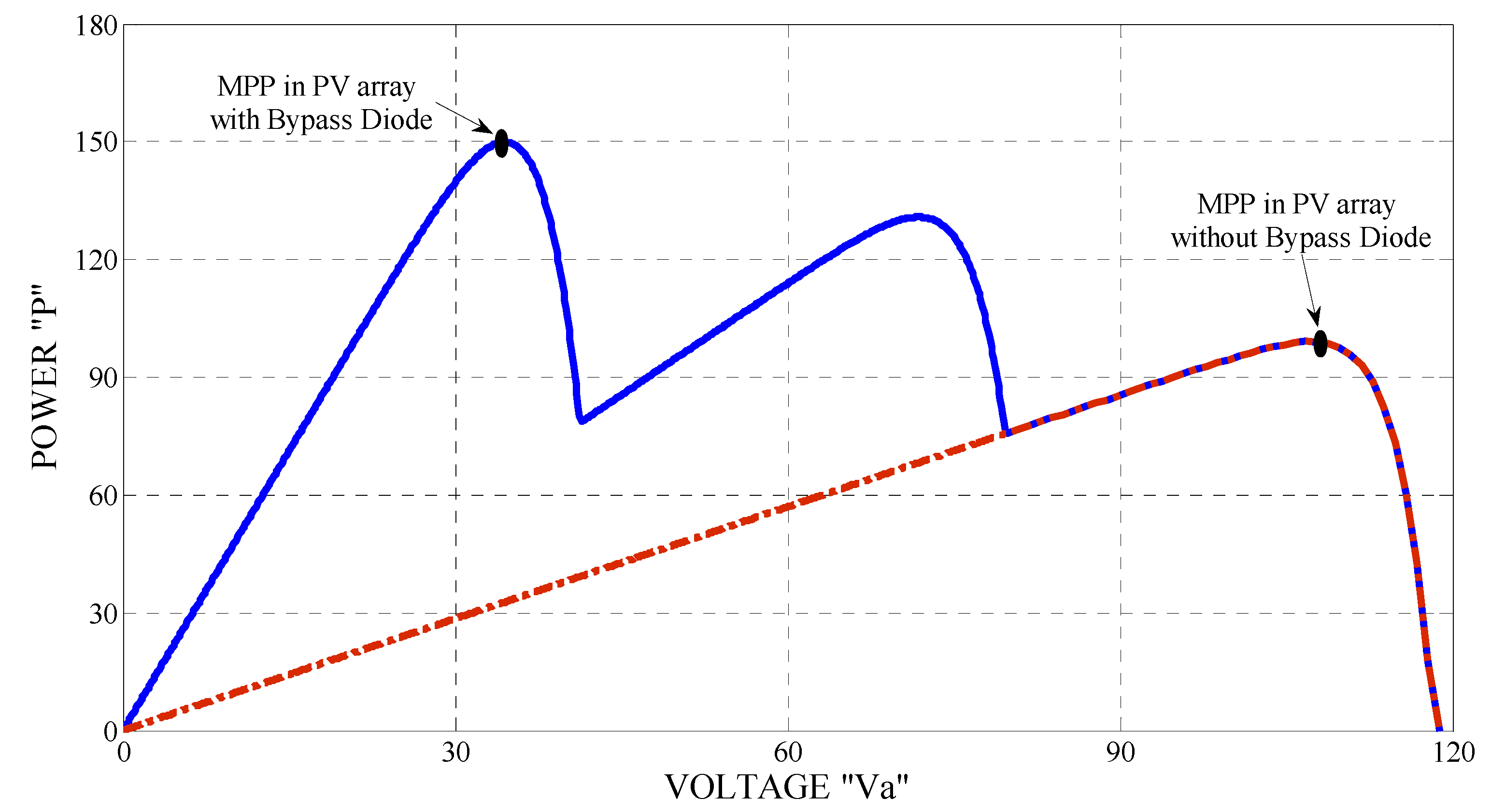
3.2. Partially Shaded Module
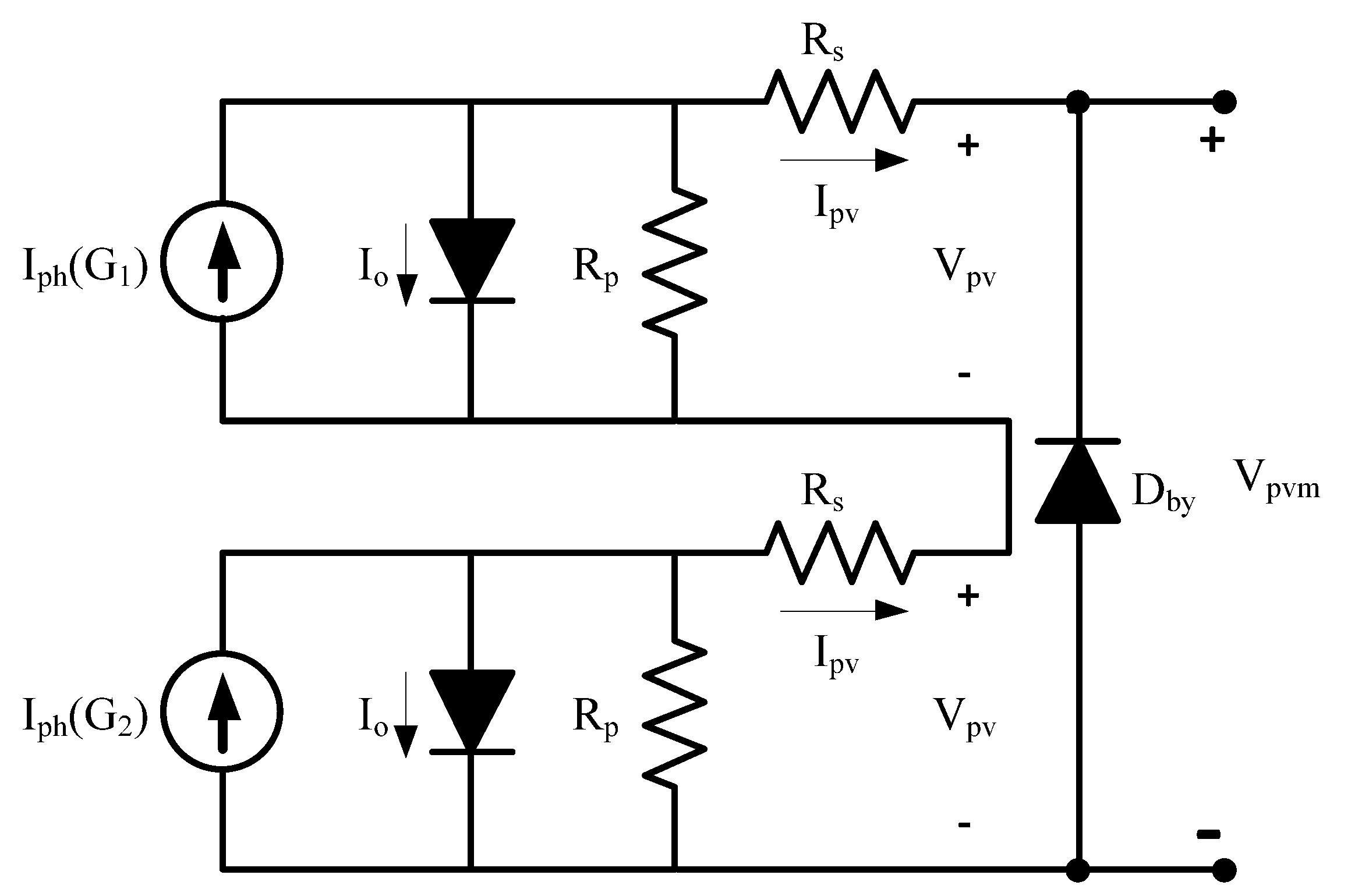
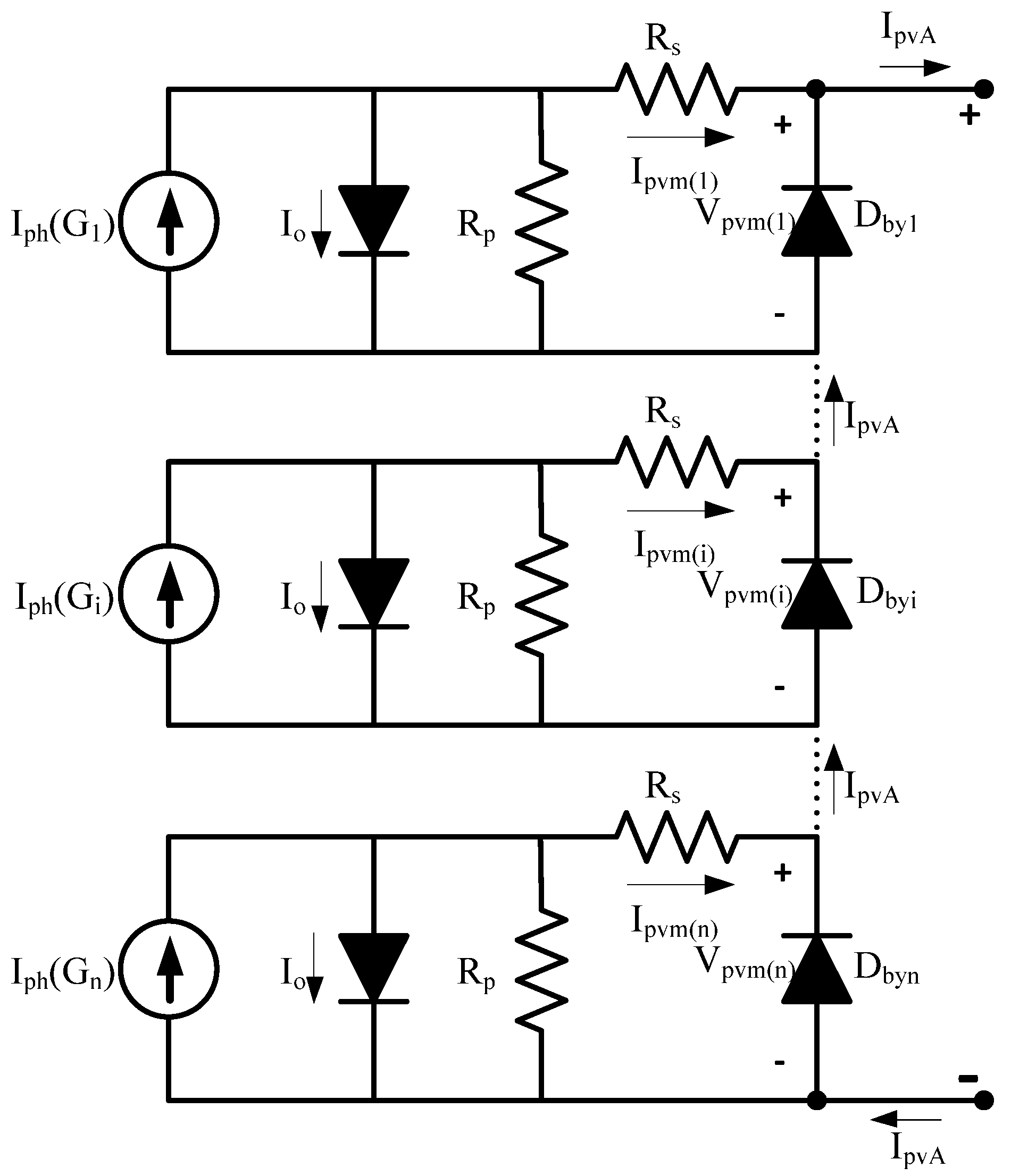
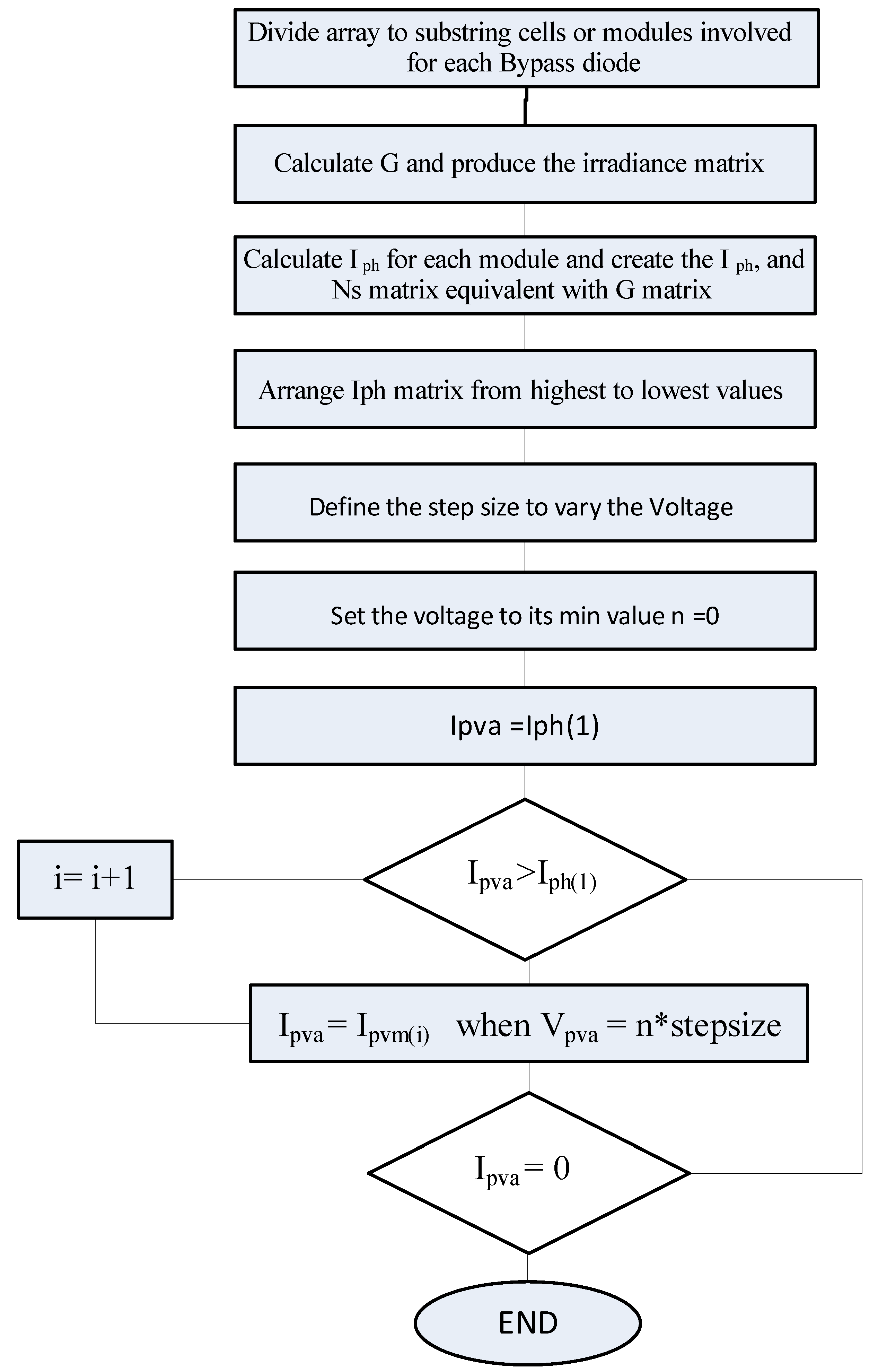
3.3. Partially Shaded Array
- Calculate the solar irradiance received by each individual PV module and determine the irradiance matrix. This point must be mentioned that in accordance with assuming a single bypass diode for each PV module, if the partial shading occurs in the PV module, the lowest irradiance level will be considered.
- Compute the Iph and Ns of each module using Equation (11) and define the Iph, Ns matrix respective to their solar irradiances.
- Rearrange Iph matrix from the highest toward the lowest value.
- Calculate the output current of array (Ipva) using Equation (13) in which the Ipvm(i) is the output current of ith module.
- Calculate the output PV voltage (Vpva) using Equation (13) in which the Vpvm(i) is the output voltage of ith module:
4. Numerical Examples
4.1. Partially Shaded Module Series with Fully Illuminated Module
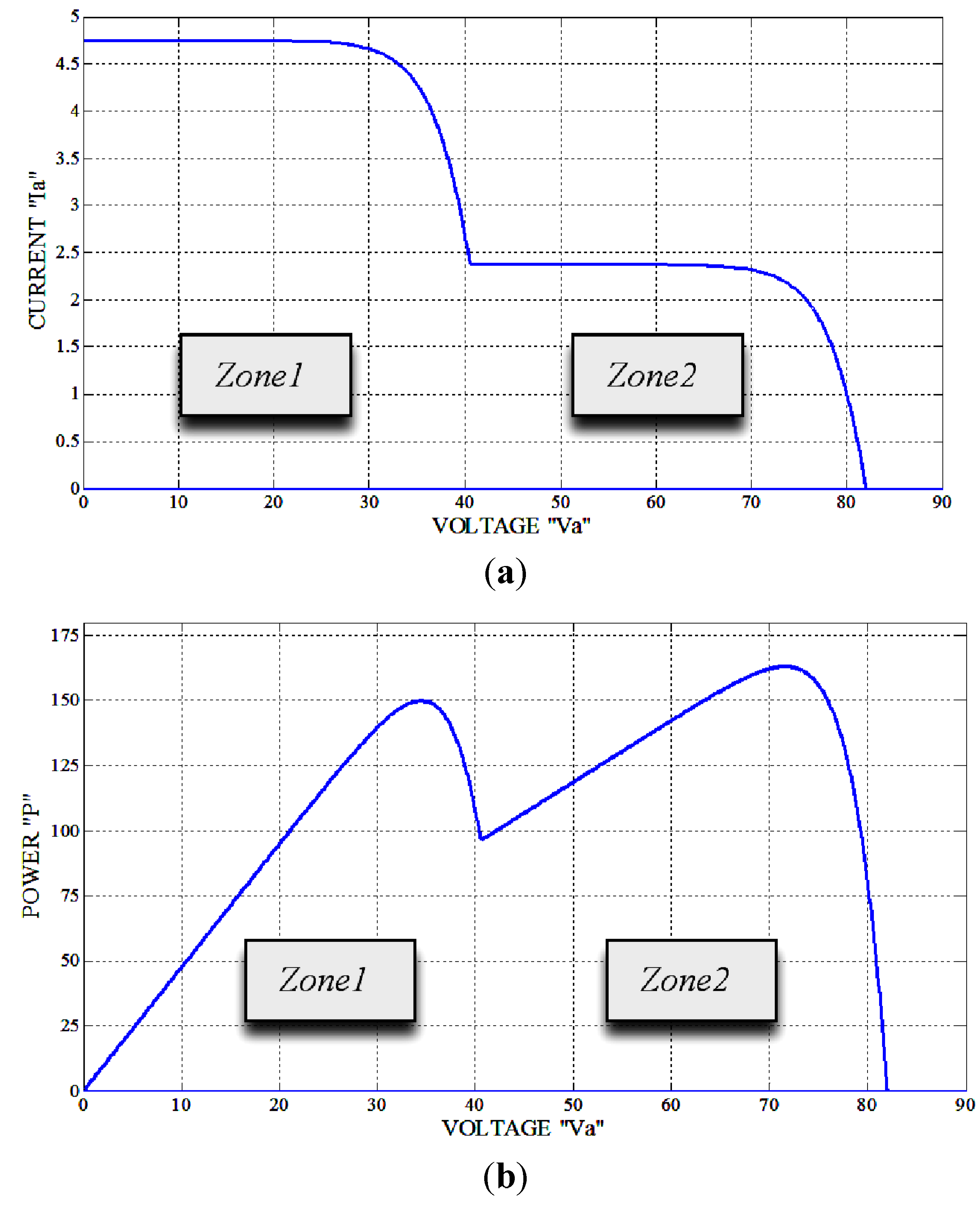
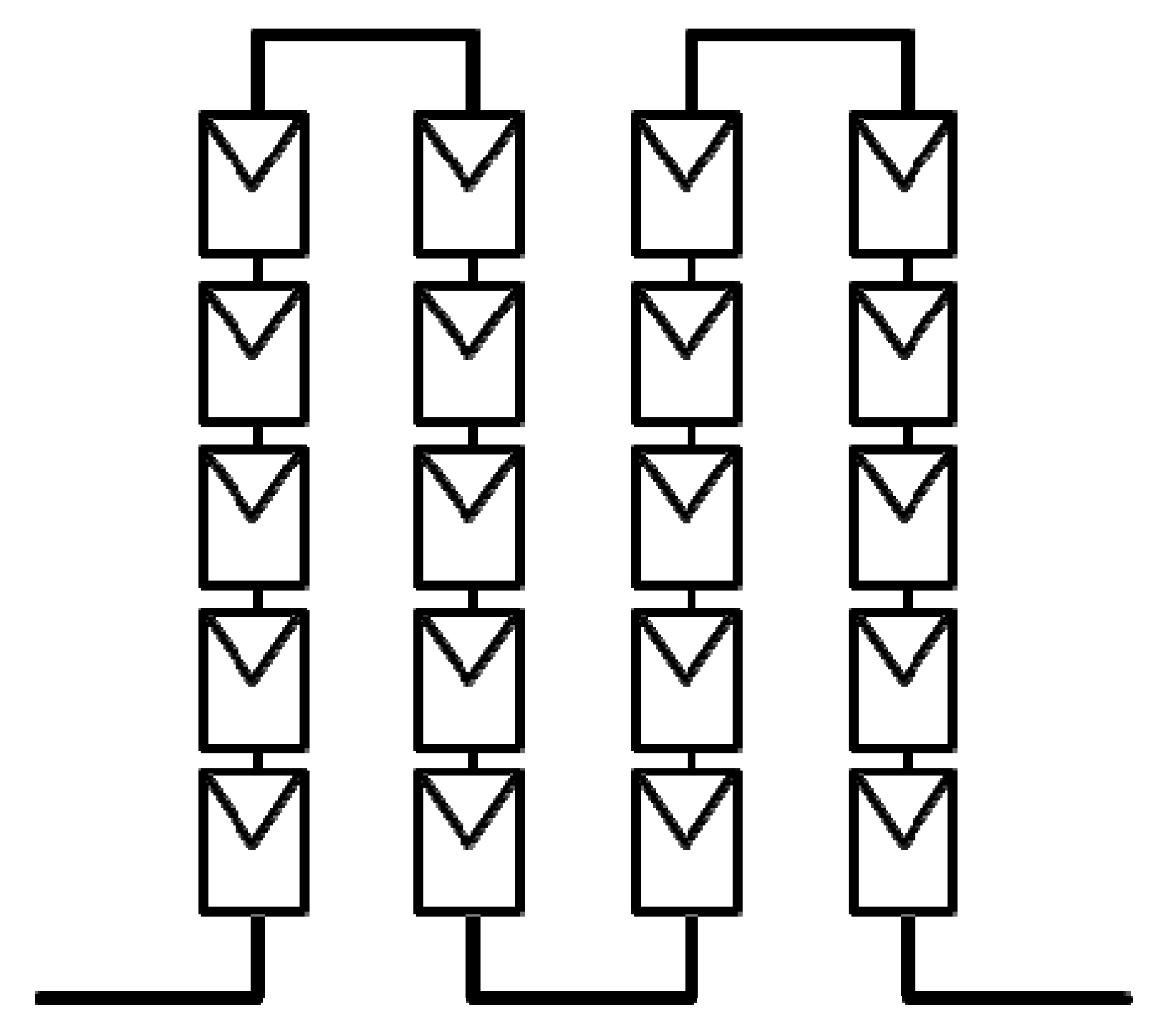
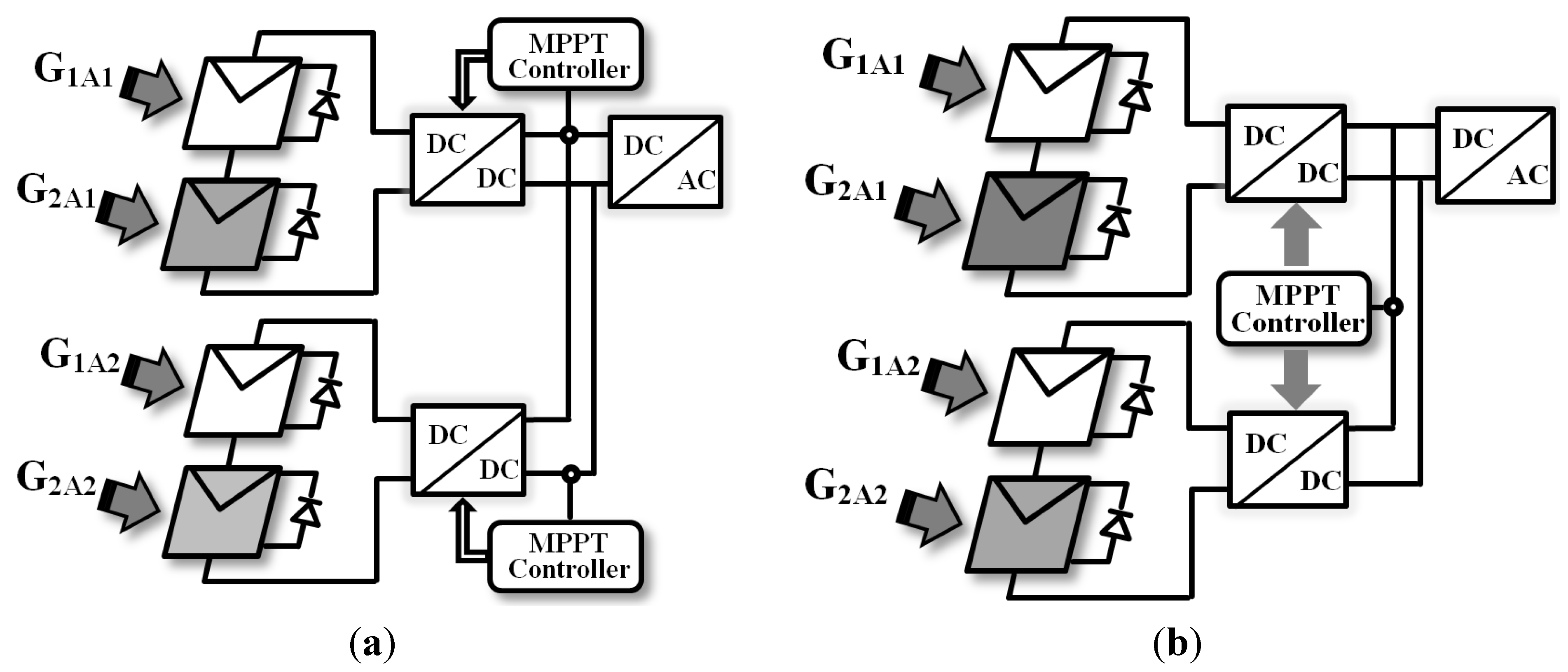
4.2. Multidimensional PV System
- The lower number of sensors and transducers which significantly reduces the overall system cost.
- The lower space required for the control unit, even in a large scale PV system.
- High flexibility of this configuration helps the designers to develop the system without increasing the control units. Only some amendments in programming are required.
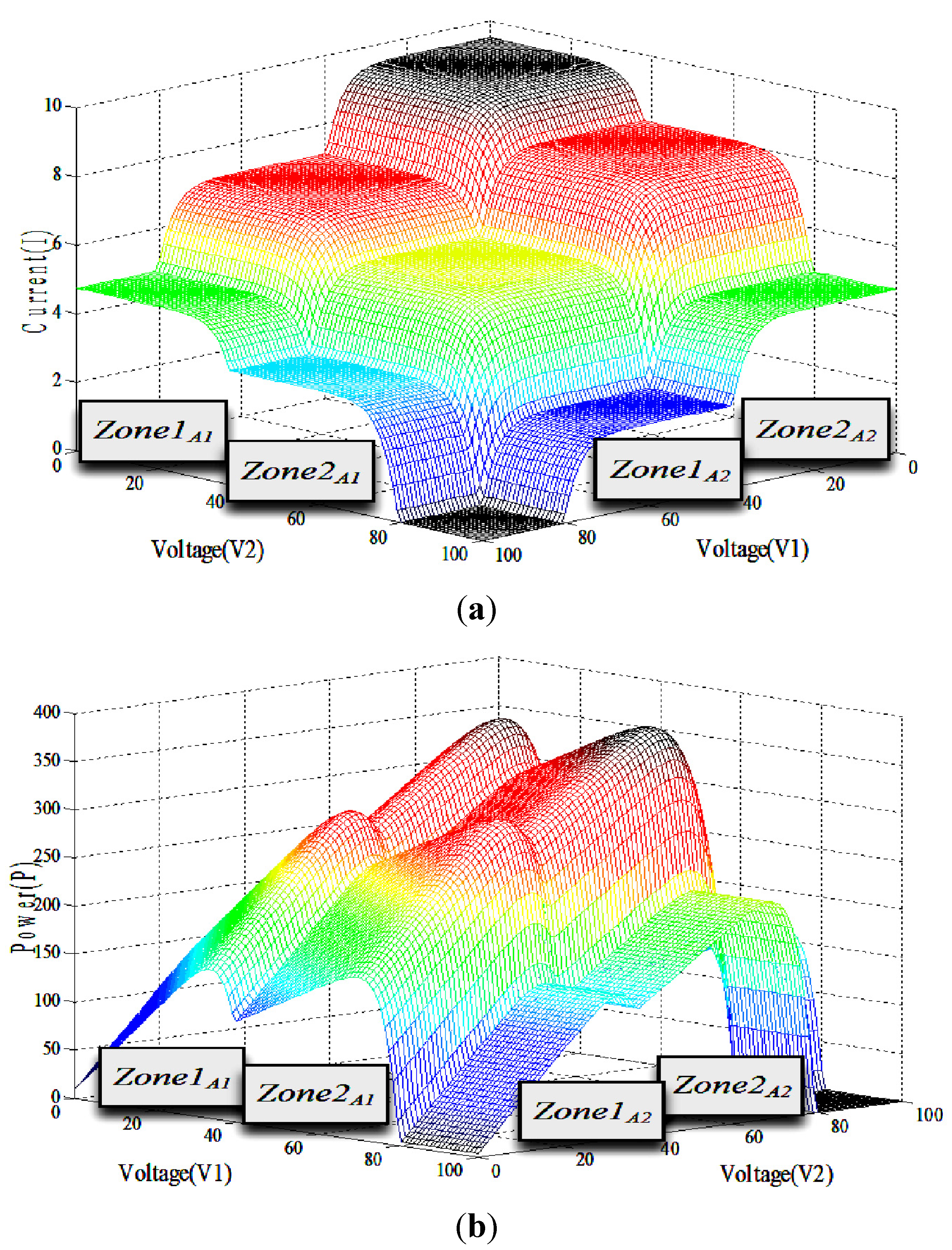
- Region 1 = Contribution of PV arrays in Zone2A2 + Zone1A1
- Region 2 = Contribution of PV arrays in Zone2A2 + Zone2A1
- Region 3 = Contribution of PV arrays in Zone1A2 + Zone1A1
- Region 4 = Contribution of PV arrays in Zone2A2 + Zone2A1

5. Conclusions
Nomenclature:
| Iph | Solar-Generated current |
| A | Diode ideality factor |
| Ki | Short-circuit temperature/current coefficient |
| Q | Electron charge constant |
| G | Operating irradiance level (W/m2) |
| K | Boltzmann constant |
| Gr | Nominal irradiance level (W/m2) |
| Ns | Number of series connected cells |
| Tk | Operating temperature (K) |
| Irs | Solar generated current |
| Tr | Reference cell temperature(K) |
| Isc | Short circuit current |
| Vpv | PV output voltage |
| Io1 | Diode saturation current |
| Vpvm | PV module output voltage |
| Ipv | PV output current |
| Vpva | PV array output voltage |
| Ipvm | PV module output current |
| Rs | Series connected resistance |
| Ipva | PV array output current |
| Io | Diode current |
| Rp | Parallel connected resistance |
Acknowledgments
References
- Bastidas, J.D.; Ramos-Paja, C.A.; Franco, E.; Spagnuolo, G.; Petrone, G. Modeling of photovoltaic fields in mismatching conditions by means of inflection voltages. In Proceedings of Engineering Applications (WEA) 2012 Workshop, Bogota, Colombia, 2–4 May 2012; pp. 1–6.
- Mekhilef, S.; Saidur, R.; Safari, A. A review on solar energy use in industries. Renew. Sustain. Energy Rev. 2011, 15, 1777–1790. [Google Scholar] [CrossRef]
- Elhassan, Z.A.M.; Zain, M.F.M.; Sopian, K.; Abass, A. Building integrated photovoltaics (BIPV) module in urban housing in Khartoum: Concept and design. Int. J. Phys. Sci. 2012, 7, 487–494. [Google Scholar]
- Esram, T.; Chapman, P.L. Comparison of photovoltaic array maximum power point tracking techniques. IEEE Trans. Energy Convers. 2007, 22, 439–449. [Google Scholar] [CrossRef]
- Hohm, D.; Ropp, M. Comparative study of maximum power point tracking algorithms. Prog. Photovolt. Res. Appl. 2003, 11, 47–62. [Google Scholar] [CrossRef]
- Jewell, W.T.; Unruh, T.D. Limits on cloud-induced fluctuation in photovoltaic generation. IEEE Trans. Energy Convers. 1990, 5, 8–14. [Google Scholar] [CrossRef]
- El Ouariachi, M.; Mrabti, T.; Tidhaf, B.; Kassmi, Ka.; Kassmi, K. Regulation of the electric power provided by the panels of the photovoltaic systems. Int. J. Phys. Sci. 2009, 4, 294–309. [Google Scholar]
- Safari, A.; Mekhilef, S. Simulation and hardware implementation of incremental conductance MPPT With direct control method using Cuk Converter. IEEE Trans. Ind. Electron. 2011, 58, 1154–1161. [Google Scholar] [CrossRef]
- Salas, V.; Olias, E.; Barrado, A.; Lazaro, A. Review of the maximum power point tracking algorithms for stand-alone photovoltaic systems. Sol. Energy Mater. Sol. Cells 2006, 90, 1555–1578. [Google Scholar] [CrossRef]
- Petrone, G.; Ramos-Paja, C.A.; Spagnuolo, G.; Vitelli, M. Granular control of photovoltaic arrays by means of a multi-output Maximum Power Point Tracking algorithm. Prog. Photovolt. Res. Appl. 2012. [Google Scholar] [CrossRef]
- Ahmed, M.; Yahya, I.Y.; Kader, A. Behavior and performance of a photovoltaic generator in real time. Int. J. Phys. Sci. 2011, 6, 4361–4367. [Google Scholar]
- Durgadevi, A.; Arulselvi, S.; Natarajan, S.P. Photovoltaic modeling and its characteristics. In Proceedings of International Conference on Emerging Trends in Electrical and Computer Technology (ICETECT), 23–24 March 2011; pp. 469–475.
- Nordin, A.H.M.; Omar, A.M. Modeling and simulation of Photovoltaic (PV) array and maximum power point tracker (MPPT) for grid-connected PV system. In Proceedings of the 3rd International Symposium & Exhibition in Sustainable Energy & Environment (ISESEE), Shah Alam, Malaysia, 1–3 June 2011; pp. 114–119.
- Wasynczuk, O. Modeling and dynamic performance of a line-commutated photovoltaic inverter system. IEEE Trans. Energy Convers. 1989, 4, 337–343. [Google Scholar] [CrossRef]
- Yusof, Y.; Sayuti, S.H.; Abdul Latif, M.; Wanik, M.Z.C. Modeling and simulation of maximum power point tracker for photovoltaic system. In Proceedings of Power and Energy Conference, Kuala Lumpur, Malaysia, 29–30 November 2004; pp. 88–93.
- Mahmodian, M.S.; Rahmani, R.; Taslimi, E.; Mekhilef, S. Step by step analyzing, modeling and simulation of single and double array PV system in different environmental variability. In Proceedings of International Conference on Future Environment and Energy, Singapore, 26–28 February 2012; pp. 37–42.
- Villalva, M.G.; Gazoli, J.R. Comprehensive approach to modeling and simulation of photovoltaic arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Guangyu, L.; Sing Kiong, N. A general modeling method that simulates photovoltaic arrays for environmental and electrical variability. In Proceedings of IEEE International Conference on Information and Automation (ICIA), Harbin, China, 20–23 June 2010; pp. 195–200.
- Yuncong, J.; Qahouq, J.A.A.; Orabi, M. Matlab/Pspice hybrid simulation modeling of solar PV cell/module. In Proceedings of the Twenty-Sixth Annual IEEE on Applied Power Electronics Conference and Exposition (APEC), 6–11 March 2011; pp. 1244–1250.
- Kajihara, A.; Harakawa, A.T. Model of photovoltaic cell circuits under partial shading. In Proceedings of IEEE International Conference on Industrial Technology (ICIT), Hong Kong, China, 14–17 December 2005; pp. 866–870.
- Petrone, G.; Ramos-Paja, C.A. Modeling of photovoltaic fields in mismatched conditions for energy yield evaluations. Electr. Power Syst. Res. 2011, 1, 1003–1013. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Amjad, M.; Mekhilef, S. An improved particle swarm optimization (PSO)-based MPPT for PV with reduced steady-state oscillation. IEEE Trans. Power Electron. 2012, 27, 3627–3638. [Google Scholar] [CrossRef]
- Keyrouz, F.; Georges, S. Efficient multidimensional maximum power point tracking using bayesian fusion. In Proceedings of the 2nd International Conference on Electric Power and Energy Conversion Systems (EPECS), Sharjah, United Arab Emirates, 15–17 November 2011; pp. 1–5.
- Patel, H.; Agarwal, V. Maximum power point tracking scheme for PV systems operating under partially shaded conditions. IEEE Trans. Ind. Electron. 2008, 55, 1689–1698. [Google Scholar] [CrossRef]
- Wang, Y.J.; Hsu, P.C. Analytical modelling of partial shading and different orientation of photovoltaic modules. Renew. Power Gener. IET 2010, 4, 272–282. [Google Scholar] [CrossRef]
- Pandiarajan, N.; Muthu, R. Mathematical modeling of photovoltaic module with simulink. In Proceedings of the 1st International Conference on Electrical Energy Systems (ICEES), Newport Beach, CA, USA, 3–5 January 2011; pp. 258–263.
- Maki, A.; Valkealahti, S. Power losses in long string and parallel-connected short strings of series-connected silicon-based photovoltaic modules due to partial shading conditions. IEEE Trans. Energy Convers. 2012, 27, 173–183. [Google Scholar] [CrossRef]
- Paraskevadaki, E.V.; Papathanassiou, S.A. Evaluation of MPP voltage and power of mc-Si PV modules in partial shading conditions. IEEE Trans. Energy Convers. 2011, 26, 923–932. [Google Scholar] [CrossRef]
- Silvestre, S.; Boronat, A.; Chouder, A. Study of bypass diodes configuration on PV modules. Appl. Energy 2009, 86, 1632–1640. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Seyedmahmoudian, M.; Mekhilef, S.; Rahmani, R.; Yusof, R.; Renani, E.T. Analytical Modeling of Partially Shaded Photovoltaic Systems. Energies 2013, 6, 128-144. https://doi.org/10.3390/en6010128
Seyedmahmoudian M, Mekhilef S, Rahmani R, Yusof R, Renani ET. Analytical Modeling of Partially Shaded Photovoltaic Systems. Energies. 2013; 6(1):128-144. https://doi.org/10.3390/en6010128
Chicago/Turabian StyleSeyedmahmoudian, Mohammadmehdi, Saad Mekhilef, Rasoul Rahmani, Rubiyah Yusof, and Ehsan Taslimi Renani. 2013. "Analytical Modeling of Partially Shaded Photovoltaic Systems" Energies 6, no. 1: 128-144. https://doi.org/10.3390/en6010128






