Sensitivity of the Drift-Diffusion Approach in Estimating the Power Conversion Efficiency of Bulk Heterojunction Polymer Solar Cells
Abstract
:1. Introduction
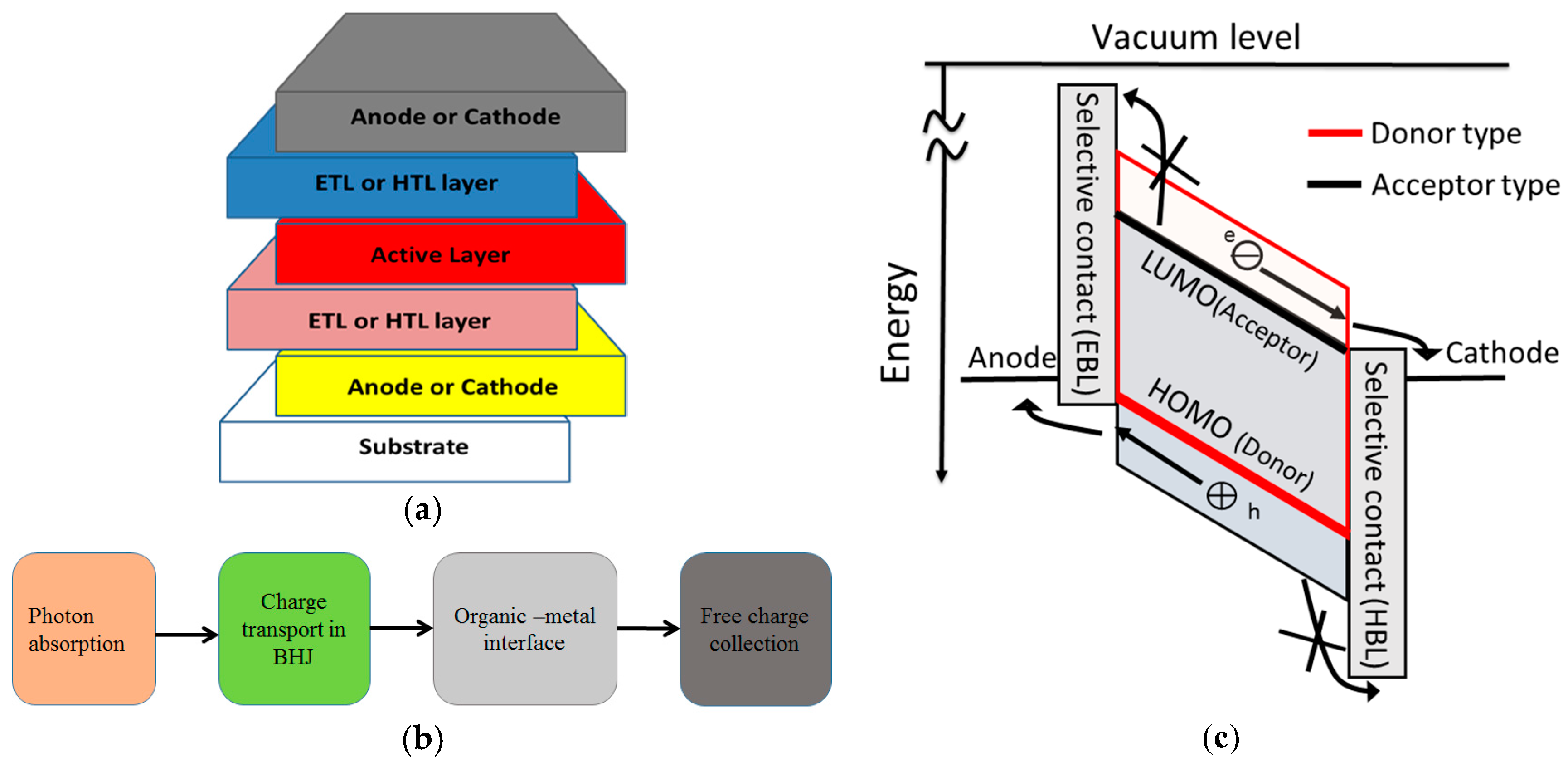
2. Theoretical Background and Modeling Approach
3. Ultimate PCE within Drift-Diffusion Framework
4. Results and Discussion
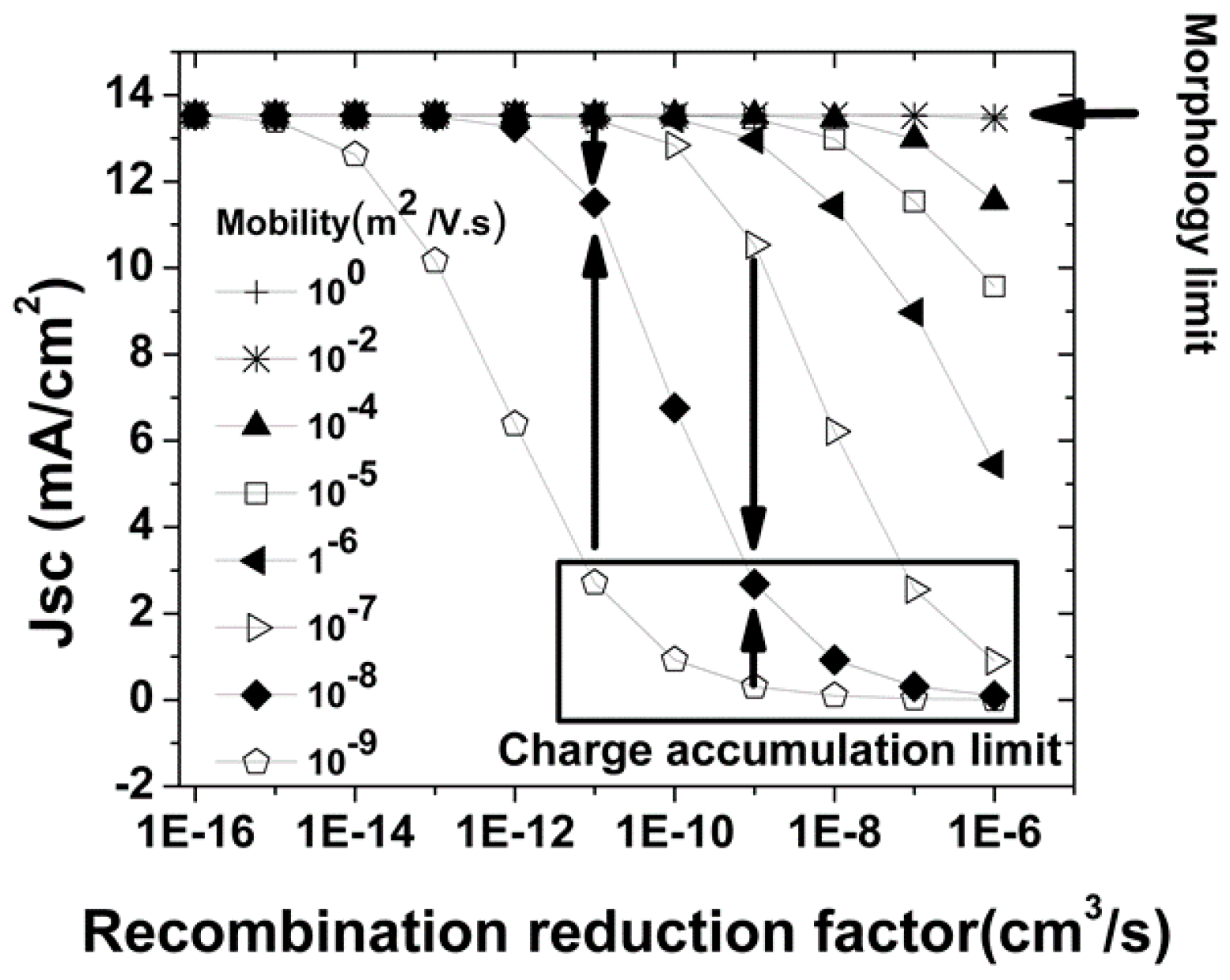
4.1. Loss Mechanism and Mobility Effect
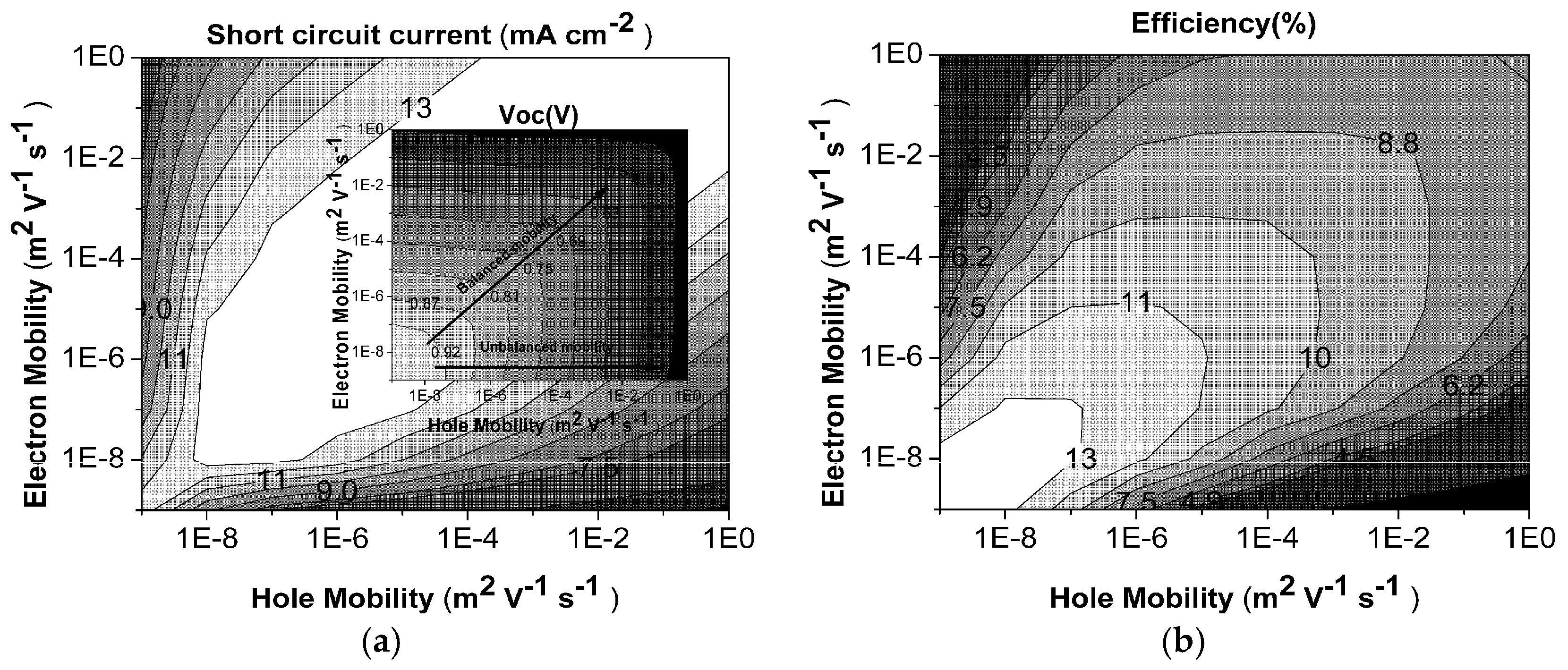
4.1.1. Ultimate PCE Map for the Carrier Density-Dependent (Bimolecular-Type) Loss Mechanism
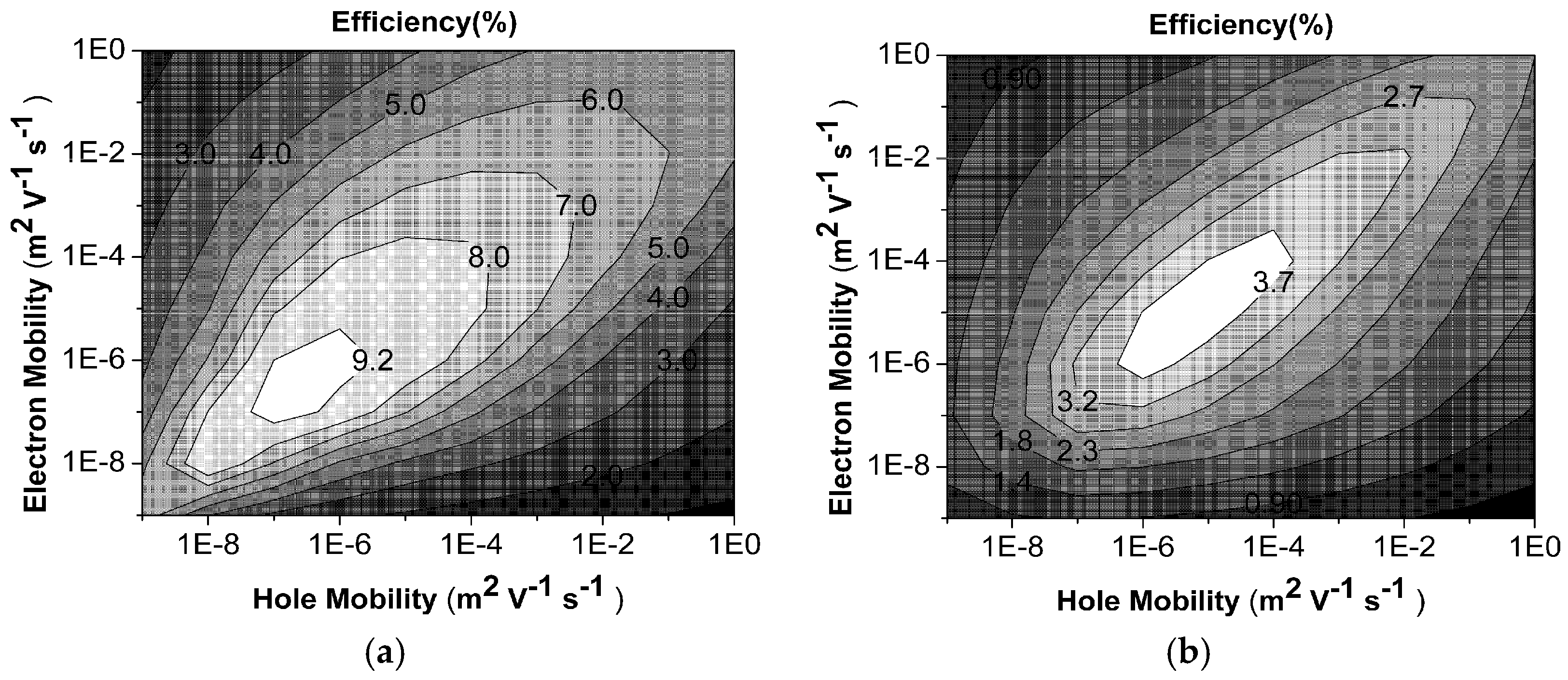
4.1.2. Ultimate PCE Map for Mobility-Dependent (Lagevin Type) Losses
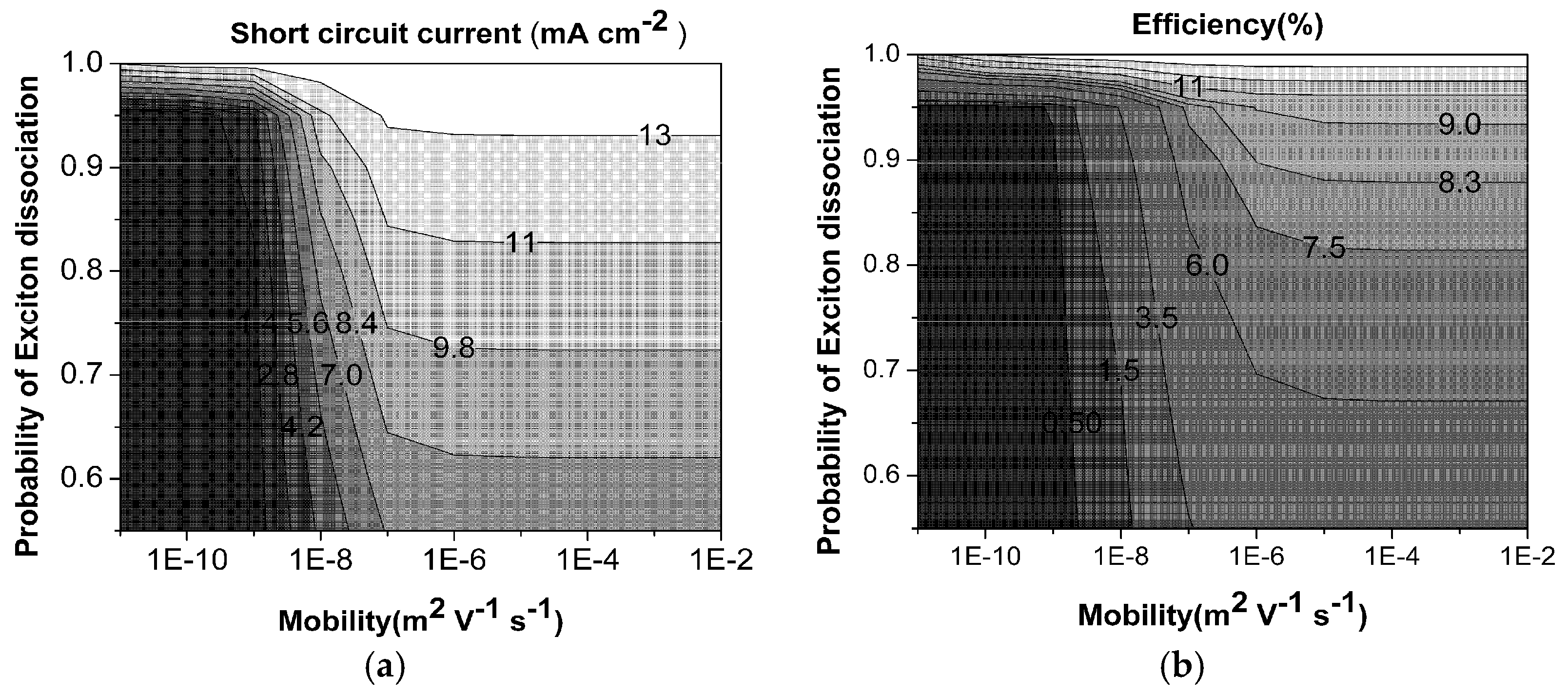
4.2. Role of Exciton State
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shockley, W.; Queisser, H.J. Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 1961, 32, 510–519. [Google Scholar] [CrossRef]
- Green, M.A. Limits on the open-circuit voltage and efficiency of silicon solar cells imposed by intrinsic auger processes. IEEE Trans. Electron. Devices 1984, 31, 671–678. [Google Scholar] [CrossRef]
- Kirchartz, T.; Taretto, K.; Rau, U. Efficiency limits of organic bulk heterojunction solar cells. J. Phys. Chem. C 2009, 113, 17958–17966. [Google Scholar] [CrossRef]
- Green, M.A.; Emery, K.; Hishikawa, Y.; Warta, W.; Dunlop, E.D. Solar cell efficiency tables (Version 48). Prog. Photovolt. Res. Appl. 2016, 24, 905–913. [Google Scholar] [CrossRef]
- Scharber, M.C.; Sariciftci, N.S. Efficiency of bulk-heterojunction organic solar cells. Prog. Polym. Sci. 2013, 38, 1929–1940. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Qian, D.; Zhang, S.; Li, S.; Inganäs, O.; Gao, F.; Hou, J. Fullerene-free polymer solar cells with over 11% efficiency and excellent thermal stability. Adv. Mater. 2016, 28, 4734–4739. [Google Scholar] [CrossRef] [PubMed]
- Green, M.A.; Emery, K.; Hishikawa, Y.; Warta, W.; Dunlop, E.D. Solar cell efficiency tables (Version 47). Prog. Photovolt. Res. Appl. 2016, 24, 3–11. [Google Scholar] [CrossRef]
- He, Z.; Xiao, B.; Liu, F.; Wu, H.; Yang, Y.; Xiao, S.; Wang, C.; Russell, T.P.; Cao, Y. Single-junction polymer solar cells with high efficiency and photovoltage. Nat. Photonics 2015, 9, 174–179. [Google Scholar] [CrossRef]
- Lu, L.; Zheng, T.; Wu, Q.; Schneider, A.M.; Zhao, D.; Yu, L. Recent advances in bulk heterojunction polymer solar cells. Chem. Rev. 2015, 115, 12666–12731. [Google Scholar] [CrossRef] [PubMed]
- Fallahpour, A.H.; Ulisse, G.; Auf der Maur, M.; Di Carlo, A.; Brunetti, F. 3-D simulation and optimization of organic solar cell with periodic back contact grating electrode. IEEE J. Photovolt. 2015, 5, 591–596. [Google Scholar] [CrossRef]
- Nayak, P.K.; Garcia-Belmonte, G.; Kahn, A.; Bisquert, J.; Cahen, D. Photovoltaic efficiency limits and material disorder. Energy Environ. Sci. 2012, 5, 6022–6039. [Google Scholar] [CrossRef]
- Fallahpour, A.H.; Gagliardi, A.; Santoni, F.; Gentilini, D.; Zampetti, A.; Auf der Maur, M.; Di Carlo, A. Modeling and simulation of energetically disordered organic solar cells. J. Appl. Phys. 2014, 116, 184502. [Google Scholar] [CrossRef]
- Zampetti, A.; Fallahpour, A.H.; Dianetti, M.; Salamandra, L.; Santoni, F.; Gagliardi, A.; Auf der Maur, M.; Brunetti, F.; Reale, A.; Brown, T.M.; et al. Influence of the interface material layers and semiconductor energetic disorder on the open circuit voltage in polymer solar cells. J. Polym. Sci. Part B Polym. Phys. 2015, 53, 690–699. [Google Scholar] [CrossRef]
- Scott, J.C.; Malliaras, G.G. Charge injection and recombination at the metal–organic interface. Chem. Phys. Lett. 1999, 299, 115–119. [Google Scholar] [CrossRef]
- Neher, D.; Kniepert, J.; Elimelech, A.; Koster, L.J.A. A new figure of merit for organic solar cells with transport-limited photocurrents. Sci. Rep. 2016, 6, 24861. [Google Scholar] [CrossRef] [PubMed]
- Bartelt, J.A.; Lam, D.; Burke, T.M.; Sweetnam, S.M.; McGehee, M.D. Charge-carrier mobility requirements for bulk heterojunction solar cells with high fill factor and external quantum efficiency >90%. Adv. Energy Mater. 2015, 5, 1500577. [Google Scholar] [CrossRef]
- Coehoorn, R.; Pasveer, W.F.; Bobbert, P.A.; Michels, M.A.J. Charge-carrier concentration dependence of the hopping mobility in organic materials with gaussian disorder. Phys. Rev. B 2005, 72, 155206. [Google Scholar] [CrossRef]
- Tessler, N.; Preezant, Y.; Rappaport, N.; Roichman, Y. Charge transport in disordered organic materials and its relevance to thin-film devices: A tutorial review. Adv. Mater. 2009, 21, 2741–2761. [Google Scholar] [CrossRef]
- Pasveer, W.F.; Cottaar, J.; Tanase, C.; Coehoorn, R.; Bobbert, P.A.; Blom, P.W.M.; de Leeuw, D.M.; Michels, M.A.J. Unified description of charge-carrier mobilities in disordered semiconducting polymers. Phys. Rev. Lett. 2005, 94, 206601. [Google Scholar] [CrossRef] [PubMed]
- Proctor, C.M.; Kuik, M.; Nguyen, T.-Q. Charge carrier recombination in organic solar cells. Prog. Polym. Sci. 2013, 38, 1941–1960. [Google Scholar] [CrossRef]
- Bergqvist, J.; Tress, W.; Forchheimer, D.; Melianas, A.; Tang, Z.; Haviland, D.; Inganäs, O. New method for lateral mapping of bimolecular recombination in thin-film organic solar cells. Prog. Photovolt. Res. Appl. 2016, 24, 1096–1108. [Google Scholar] [CrossRef]
- Paulke, A.; Stranks, S.D.; Kniepert, J.; Kurpiers, J.; Wolff, C.M.; Schön, N.; Snaith, H.J.; Brenner, T.J.K.; Neher, D. Charge carrier recombination dynamics in perovskite and polymer solar cells. Appl. Phys. Lett. 2016, 108, 113505. [Google Scholar] [CrossRef]
- Pivrikas, A.; Juška, G.; Mozer, A.J.; Scharber, M.; Arlauskas, K.; Sariciftci, N.S.; Stubb, H.; Österbacka, R. Bimolecular recombination coefficient as a sensitive testing parameter for low-mobility solar-cell materials. Phys. Rev. Lett. 2005, 94, 176806. [Google Scholar] [CrossRef] [PubMed]
- Shuttle, C.G.; O’Regan, B.; Ballantyne, A.M.; Nelson, J.; Bradley, D.D.C.; Durrant, J.R. Bimolecular recombination losses in polythiophene: Fullerene solar cells. Phys. Rev. B 2008, 78, 113201. [Google Scholar] [CrossRef]
- Koster, L.J.A. Charge carrier mobility in disordered organic blends for photovoltaics. Phys. Rev. B 2010, 81, 205318. [Google Scholar] [CrossRef]
- Shieh, J.-T.; Liu, C.-H.; Meng, H.-F.; Tseng, S.-R.; Chao, Y.-C.; Horng, S.-F. The effect of carrier mobility in organic solar cells. J. Appl. Phys. 2010, 107, 084503. [Google Scholar] [CrossRef]
- Tress, W.; Leo, K.; Riede, M. Optimum mobility, contact properties, and open-circuit voltage of organic solar cells: A drift-diffusion simulation study. Phys. Rev. B 2012, 85, 155201. [Google Scholar] [CrossRef]
- Fallahpour, A.H.; Gentilini, D.; Gagliardi, A.; Auf der Maur, M.; Lugli, P.; Di Carlo, A. Systematic study of the PCE and device operation of organic tandem solar cells. IEEE J. Photovolt. 2016, 6, 202–210. [Google Scholar] [CrossRef]
- Wagenpfahl, A.; Deibel, C.; Dyakonov, V. Organic solar cell efficiencies under the aspect of reduced surface recombination velocities. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 1759–1763. [Google Scholar] [CrossRef]
- Kirchartz, T.; Pieters, B.E.; Taretto, K.; Rau, U. Mobility dependent efficiencies of organic bulk heterojunction solar cells: Surface recombination and charge transfer state distribution. Phys. Rev. B 2009, 80, 035334. [Google Scholar] [CrossRef]
- Mandoc, M.M.; Koster, L.J.A.; Blom, P.W.M. Optimum charge carrier mobility in organic solar cells. Appl. Phys. Lett. 2007, 90, 133504. [Google Scholar] [CrossRef]
- Deibel, C.; Wagenpfahl, A.; Dyakonov, V. Influence of charge carrier mobility on the performance of organic solar cells. Phys. Status Solidi Rapid Res. Lett. 2008, 2, 175–177. [Google Scholar] [CrossRef]
- Albes, T.; Lugli, P.; Gagliardi, A. Investigation of the blend morphology in bulk-heterojunction organic solar cells. IEEE Trans. Nanotechnol. 2016, 15, 281–288. [Google Scholar] [CrossRef]
- Tress, W.; Pfuetzner, S.; Leo, K.; Riede, M. Open circuit voltage and IV curve shape of ZnPc:C60 solar cells with varied mixing ratio and hole transport layer. J. Photonics Energy 2011, 1, 011114. [Google Scholar] [CrossRef]
- Pivrikas, A.; Sariciftci, N.S.; Juška, G.; Österbacka, R. A review of charge transport and recombination in polymer/fullerene organic solar cells. Prog. Photovolt. Res. Appl. 2007, 15, 677–696. [Google Scholar] [CrossRef]
- Tzabari, L.; Tessler, N. Shockley–read–hall recombination in P3Ht:PCBM solar cells as observed under ultralow light intensities. J. Appl. Phys. 2011, 109, 064501. [Google Scholar] [CrossRef]
- Nelson, J. Diffusion-limited recombination in polymer-fullerene blends and its influence on photocurrent collection. Phys. Rev. B 2003, 67, 155209. [Google Scholar] [CrossRef]
- Koster, L.J.A.; Smits, E.C.P.; Mihailetchi, V.D.; Blom, P.W.M. Device model for the operation of polymer/fullerene bulk heterojunction solar cells. Phys. Rev. B 2005, 72, 085205. [Google Scholar] [CrossRef]
- Fallahpour, A.H.; Gagliardi, A.; Gentilini, D.; Zampetti, A.; Santoni, F.; Auf der Maur, M.; Di Carlo, A. Optoelectronic simulation and thickness optimization of energetically disordered organic solar cells. J. Comput. Electron. 2014, 13, 933–942. [Google Scholar] [CrossRef]
- Koster, L.J.A.; Mihailetchi, V.D.; Blom, P.W.M. Bimolecular recombination in polymer/fullerene bulk heterojunction solar cells. Appl. Phys. Lett. 2006, 88, 052104. [Google Scholar] [CrossRef]
- Christ, N.S.; Kettlitz, S.W.; Valouch, S.; Zufle, S.; Gartner, C.; Punke, M.; Lemmer, U. Nanosecond response of organic solar cells and photodetectors. J. Appl. Phys. 2009, 105, 104513. [Google Scholar] [CrossRef]
- Motta, C.; El-Mellouhi, F.; Sanvito, S. Charge carrier mobility in hybrid halide perovskites. Sci. Rep. 2015, 5, 12746. [Google Scholar] [CrossRef] [PubMed]
- Heiber, M.C.; Baumbach, C.; Dyakonov, V.; Deibel, C. Encounter-limited charge-carrier recombination in phase-separated organic semiconductor blends. Phys. Rev. Lett. 2015, 114, 136602. [Google Scholar] [CrossRef] [PubMed]
- Groves, C.; Greenham, N.C. Bimolecular recombination in polymer electronic devices. Phys. Rev. B 2008, 78, 155205. [Google Scholar] [CrossRef]
- Deibel, C. Charge carrier dissociation and recombination in polymer solar cells. Phys. Status Solidi 2009, 206, 2731–2736. [Google Scholar] [CrossRef]
- Pivrikas, A.; Neugebauer, H.; Sariciftci, N.S. Charge carrier lifetime and recombination in bulk heterojunction solar cells. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 1746–1758. [Google Scholar] [CrossRef]
- Petersen, A.; Kirchartz, T.; Wagner, T.A. Charge extraction and photocurrent in organic bulk heterojunction solar cells. Phys. Rev. B 2012, 85, 045208. [Google Scholar] [CrossRef]
- Wetzelaer, G.-J.A.H.; Van der Kaap, N.J.; Koster, L.J.A.; Blom, P.W.M. Quantifying bimolecular recombination in organic solar cells in steady state. Adv. Energy Mater. 2013, 3, 1130–1134. [Google Scholar] [CrossRef]
- Murthy, D.H.K.; Melianas, A.; Tang, Z.; Juška, G.; Arlauskas, K.; Zhang, F.; Siebbeles, L.D.A.; Inganäs, O.; Savenije, T.J. Origin of reduced bimolecular recombination in blends of conjugated polymers and fullerenes. Adv. Funct. Mater. 2013, 23, 4262–4268. [Google Scholar] [CrossRef]
- Wehrenfennig, C.; Eperon, G.E.; Johnston, M.B.; Snaith, H.J.; Herz, L.M. High charge carrier mobilities and lifetimes in organolead trihalide perovskites. Adv. Mater. 2014, 26, 1584–1589. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.-X.; Tseng, S.-R.; Meng, H.-F.; Lee, K.-C.; Liu, C.-H.; Horng, S.-F. Dark carrier recombination in organic solar cell. Appl. Phys. Lett. 2008, 93, 163303. [Google Scholar] [CrossRef]
- Kuzmich, A.; Padula, D.; Ma, H.; Troisi, A. Trends in the electronic and geometric structure of non-fullerene based acceptors for organic solar cells. Energy Environ. Sci. 2017, 10, 395–401. [Google Scholar] [CrossRef]
- Ma, H.; Troisi, A. Modulating the exciton dissociation rate by up to more than two orders of magnitude by controlling the alignment of lumo + 1 in organic photovoltaics. J. Phys. Chem. C 2014, 118, 27272–27280. [Google Scholar] [CrossRef]
- Arkhipov, V.I.; Heremans, P.; Bassler, H. Why is exciton dissociation so efficient at the interface between a conjugated polymer and an electron acceptor? Appl. Phys. Lett. 2003, 82, 4605–4607. [Google Scholar] [CrossRef]
- Deibel, C.; Strobel, T.; Dyakonov, V. Role of the charge transfer state in organic donor–acceptor solar cells. Adv. Mater. 2010, 22, 4097–4111. [Google Scholar] [CrossRef] [PubMed]




| Parameters | Ultimate PCE | Bimolecular Losses | Langevin Losses | Exciton State | Unit |
|---|---|---|---|---|---|
| Bandgap | 0.7–2 | 1.2 | 1.2 | 1.2 | eV |
| LUMO | −3.8 | −3.8 | −3.8 | −3.8 | eV |
| HOMO | −4.5–−5.8 | −5 | −5 | −5 | eV |
| Effective density | 1021 | 1021 | 1021 | 1021 | cm−3 |
| Permittivity | 3.5 | 3.5 | 3.5 | 3.5 | - |
| Exciton separation rate | N/A | N/A | N/A | 0.55 to 1 | - |
| Exciton decay rate | N/A | N/A | N/A | 0.45 to 0 | - |
| Recombination velocity | 108 (~∞) | 108 | 108 | 108 | m·s−1 |
| Electron mobility | 100 (~∞) | 10−10–100 | 10−10–100 | 10−10–100 | m2/V·s |
| Hole mobility | 100 (~∞) | 10−10–100 | 10−10–100 | 10−10–100 | m2/V·s |
| Recombination factor | N/A | 10−16–10−6 | 10−16–10−6 | 10−16–10−6 | cm3·s−1 |
| Active layer thickness | 60–320 | 200 | 200 | 200 | Nm |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fallahpour, A.H.; Di Carlo, A.; Lugli, P. Sensitivity of the Drift-Diffusion Approach in Estimating the Power Conversion Efficiency of Bulk Heterojunction Polymer Solar Cells. Energies 2017, 10, 285. https://doi.org/10.3390/en10030285
Fallahpour AH, Di Carlo A, Lugli P. Sensitivity of the Drift-Diffusion Approach in Estimating the Power Conversion Efficiency of Bulk Heterojunction Polymer Solar Cells. Energies. 2017; 10(3):285. https://doi.org/10.3390/en10030285
Chicago/Turabian StyleFallahpour, Amir Hossein, Aldo Di Carlo, and Paolo Lugli. 2017. "Sensitivity of the Drift-Diffusion Approach in Estimating the Power Conversion Efficiency of Bulk Heterojunction Polymer Solar Cells" Energies 10, no. 3: 285. https://doi.org/10.3390/en10030285
APA StyleFallahpour, A. H., Di Carlo, A., & Lugli, P. (2017). Sensitivity of the Drift-Diffusion Approach in Estimating the Power Conversion Efficiency of Bulk Heterojunction Polymer Solar Cells. Energies, 10(3), 285. https://doi.org/10.3390/en10030285







