1. Introduction
Adapting the common terminology in energy meteorology to differentiate between the power and energy of the solar radiation, the word ‘irradiance’ is used in this work to denote the instantaneous solar power per square meter in W/m², whereas the word ‘irradiation’ refers to the integral of the irradiance over time, thus denoting the energy of the solar radiation in Ws/m² or kWh/m² [
1].
In photovoltaic (PV) system simulations, the global horizontal irradiance and the ambient temperature are the two most important inputs in order to determine the PV system’s energy output. The global horizontal irradiance is split up in its direct and diffuse components. These components are then separately translated to a tilted plane if the PV system in question has a module orientation that differs from the horizontal plane. In simple terms the global irradiance incident on a tilted module is then calculated as the sum of the direct and the diffuse irradiance on the tilted plane.
The model for estimating the diffuse fraction of the global horizontal irradiance is hence the first element in a chain of models that is necessary to simulate the electrical output of a PV system. As such, it has strong influence on the final output of the simulation, which is demonstrated by the following comparative simulations for two locations: Lindenberg, Germany and Gobabeb, Namibia. The analysed PV system is a standard 8 kWp (kilo Watt peak) grid connected system, the simulation is conducted in one-minute resolution with measurement data from the Baseline Surface Radiation Network (BSRN) [
2].
During the four exemplary days in June in Lindenberg, Germany, chosen for
Figure 1, the model used for this comparison (reduced version of Reindl et al. [
3]) underestimates the diffuse irradiance by 18%. In the next step of the simulation, the global irradiance on the tilted plane is calculated. In this case the modules are facing south and are elevated by 30° from the horizontal. The model applied for this step is from Hay and Davies [
4]. When using the modelled horizontal diffuse irradiance, the resulting global irradiance on the modules is still 9% lower than using the measured horizontal diffuse irradiance.
The rest of the PV system model chain is then simulated with the help of the simulation core of PV software provider Valentin Software (Berlin, Germany) [
5].
Table 1 lists the results of the comparison.
During these four days, the total PV energy yield would be 65.6 kWh when using the measured horizontal diffuse irradiance values. With the diffuse irradiance modelled by Reindl et al. [
3], the total PV energy yield is only 60.2 kWh—an underestimation of 8.3%. The comparison was also conducted for the whole year 2003 in Lindenberg, where the annual deviation of the modelled diffuse irradiance is −7.2%, leading to a deviation of the annual PV energy output of −2.7%.
The second half of
Table 1 lists the results of the same comparison that was conducted for the location of Gobabeb in Namibia, for the year 2014. Here, the deviation of the annual diffuse irradiation is as high as 42% which leads to an overestimation of the global irradiation of the module surface of 8.3% and to an overestimation of the annual PV energy yield of 7.6%.
These examples highlight the importance of a more accurate estimation of the horizontal diffuse irradiance. An inaccurately calculated diffuse irradiance can lead to significant over- or underestimations in the annual energy yield of a PV system. This is especially relevant in the price sensitive market of PVs, where only few percent more or less of PV energy output can render a project possible or uneconomical [
6].
3. Presentation of a New Model for the Diffuse Fraction of Solar Irradiance
In order to reduce the uncertainty of PV system simulations, a new model for calculating the diffuse fraction of global horizontal irradiance is presented in this section. The model consists of three parts that are calculated independently and then combined depending on statistic features of the clearness index. Each part is presented and afterwards the combination of the three parts into a single resulting diffuse fraction is explained.
3.1. Part One. Diffuse Fraction as Function of Clearness Index
Like existing models with one parameter, this part of the new model makes use of the relation between the clearness index
and the diffuse fraction. Instead of parameterized functions, a matrix of probabilities is utilized. For the generation of the matrix, the one-minute time series of global and diffuse horizontal irradiance are converted into value pairs of the clearness index
and the diffuse fraction
, following the equations in
Section 2.2. Each value pair is then stored into a matrix with
ranging from 0 to 1.5 and
ranging from 0 to 1, both with a step size of 0.01. The frequency of occurrence of a specific
value for a given
value is then converted into a probability value, so that for every value of
a function of cumulated probabilities can be calculated.
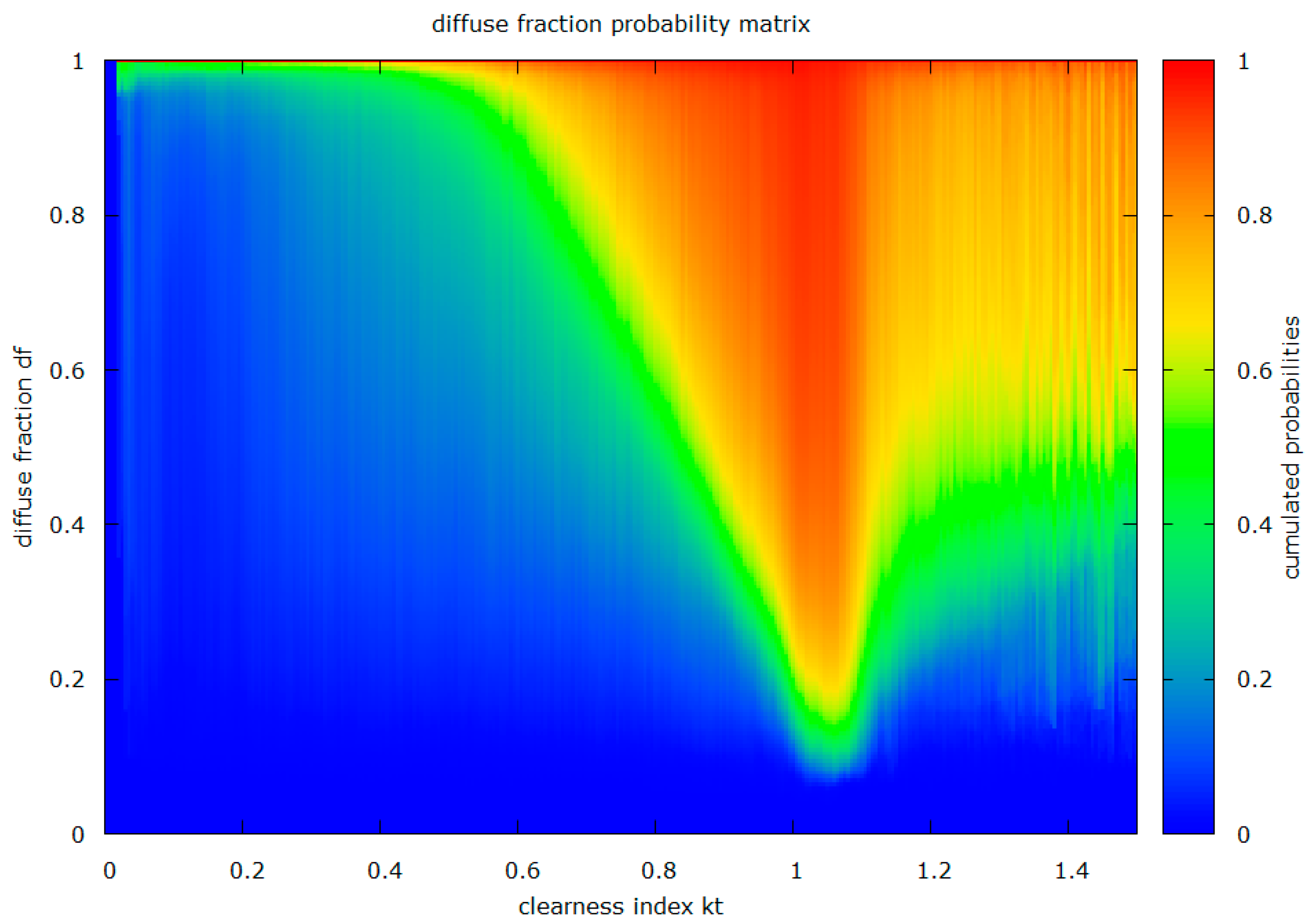
Figure 4 shows an example of such a probability matrix. In the matrix shown here, measurement values from Alice Springs, Australia (2009), Billings, USA (2005), Boulder, USA (2010), Brasilia, Brazil (2011), Cabauw, The Netherlands (2011), Cener, Spain (2010), De Aar, South Africa (2003), Fukuoka, Japan (2013), Gobabeb, Namibia (2013), Lauder, New Zealand (2007), Lerwick, UK (2002), Lindenberg, Germany (2002), Payerne, Switzerland (2010), Regina, Canada (2011), Tateno, Japan (2003) and Xianghe, China (2006) were incorporated.
In order to determine a value for
for a given
, the procedure is as follows. Since this is the first part of the new model, the diffuse fraction of this part is referred to as
:
- (1)
Select column of probability matrix that corresponds to the value;
- (2)
Generate a Markov number
(randomized number between 0 and 1) [
28];
- (3)
Select the row where is smaller than the cumulated probabilities for the first time;
- (4)
The selected row corresponds to value.
The usage of real measurement values, incorporated into a matrix of probabilities, holds the advantage of preserving the natural relationship of the diffuse fraction and the clearness index and additionally resulting in a more realistic variability of the modelled value series.
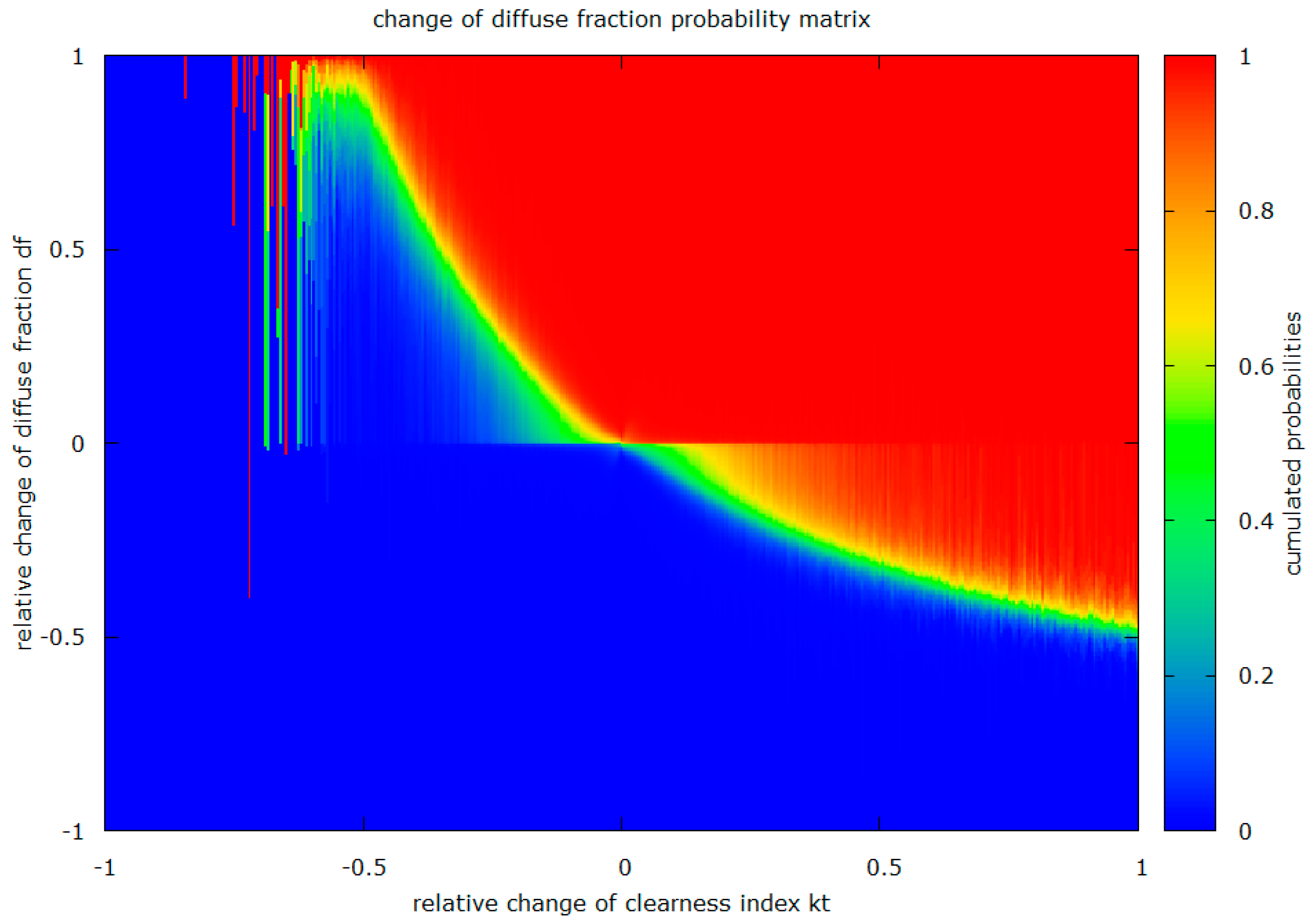
3.2. Part Two. Change of df as Function of Change of kt
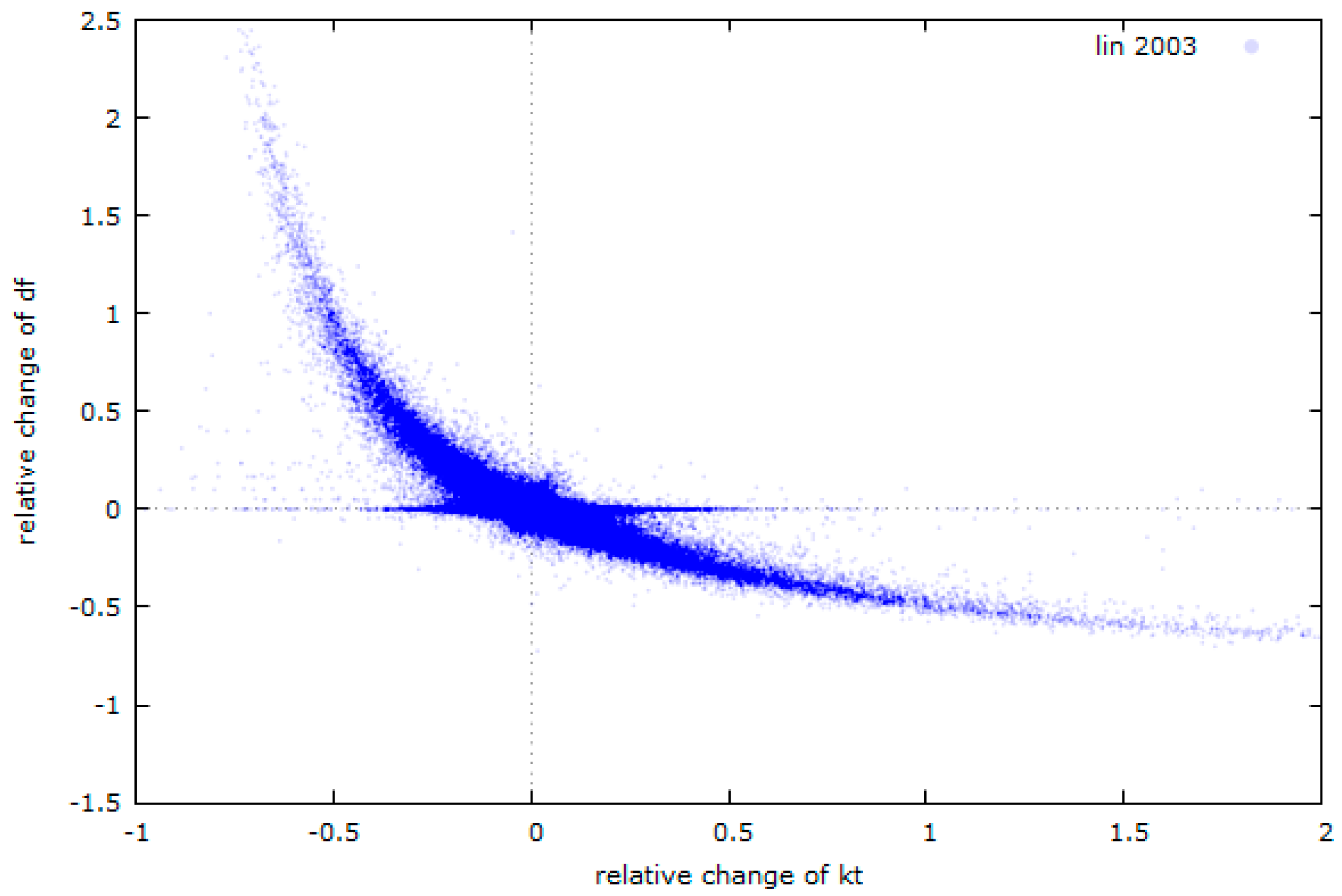
By analyzing the extensive BSRN measurement database, a strong correlation has been found between the relative changes of the clearness index (from one minute to the next) to changes of the diffuse fraction. In
Figure 5 this correlation is shown for Lindenberg, Germany, for the year 2003.
It was observed that for positive relative changes of (when the current is higher than the one minute before), the diffuse fraction will most likely show a negative relative change. If the relative change of is negative, the change of the diffuse fraction will be positive.
There are situations, however, where is changing from one minute to the next without an observable change of (compare the horizontal value accumulation at ). These situations are typical for days with rapid irradiance enhancements due to moving broken clouds.
In correspondence to part 1, the relationship between the relative change of
and the relative change of
kt (
) is also expressed in a matrix of probabilities, displayed in
Figure 6. This matrix is only used in the
range of −0.5 to 1, since the amount of measurement values outside of this range is too small, which results in unwanted noise. The procedure to retrieve a value for the diffuse fraction in this part,
, is as follows:
- (1)
Calculate the relative change of
as:
- (2)
For
greater than −0.5 and smaller than 1
- (3)
For
smaller than −0.5,
is not taken from the matrix, but extrapolated as:
- (4)
For
greater than 1,
is extrapolated as:
- (5)
The diffuse fraction for part 2,
, can now be calculated as:
3.3. Part Three. Geometric Calculation for Days with Clear Sky
3.3.1. Calculation of the Daily Course of
In the case of clear sky,
is mainly dependent on the air mass relative to its daily minimum. For that reason, in this part of the model a geometric approach has been chosen capable of reproducing the characteristic daily course of the diffuse fraction for clear sky days. The diffuse fraction of this part is calculated as:
The air mass can be modelled as a function of the elevation of the sun. The minimal air mass
is calculated for each day by using the maximum elevation angle
:
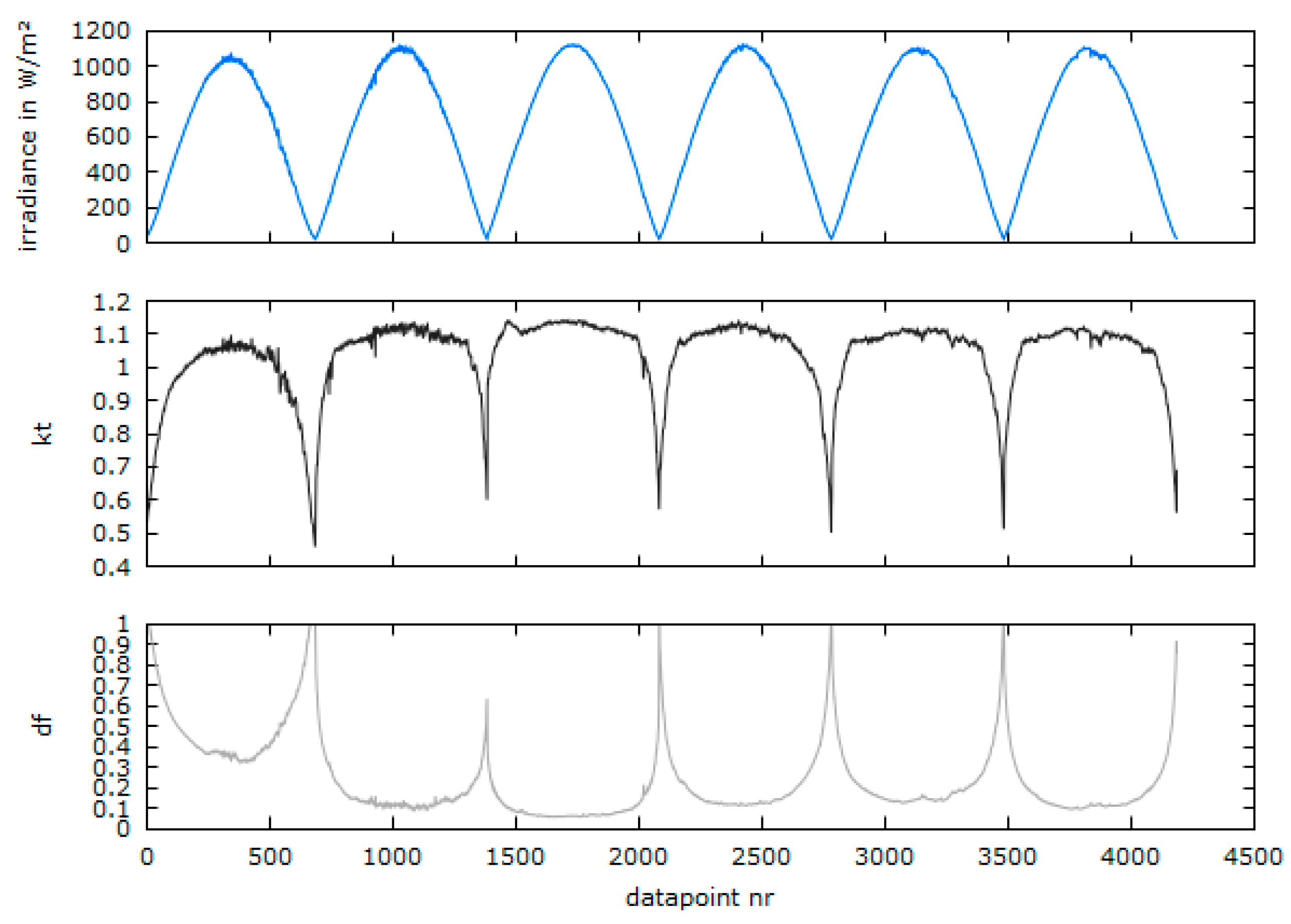
Figure 7 displays the measured (blue) and modelled (green dashed) course of the diffuse fraction over an exemplary day in Tateno, Japan (13 February 2006). While the clearness index
(black) is relatively stable around 1, the diffuse fraction is around 0.5 shortly after sunrise and before sunset and is falling down to a minimal diffuse fraction
at noon, to 0.136 in this example.
However, the main challenge in modelling the diffuse fraction over the course of a clear sky day is to find a good approximation for the minimal diffuse fraction of the day, since this factor is subject to strong variations in every possible respect: from location to location, from season to season and even from day to day.
3.3.2. Daily Variation of
In order to illustrate the daily variation of
, seven consecutive days in Tamanrasset, Algeria, are shown in
Figure 8. Even for this non-cloudy site
may vary significantly from day to day: The minimal value of the diffuse fraction (grey, bottom plot) of each day is varying between 0.328 on the first day (21 March 2006) and 0.062 on the third day (23 March 2006).
3.3.3. Seasonal Variation of
In addition to daily variations,
also shows seasonal variation on some locations.
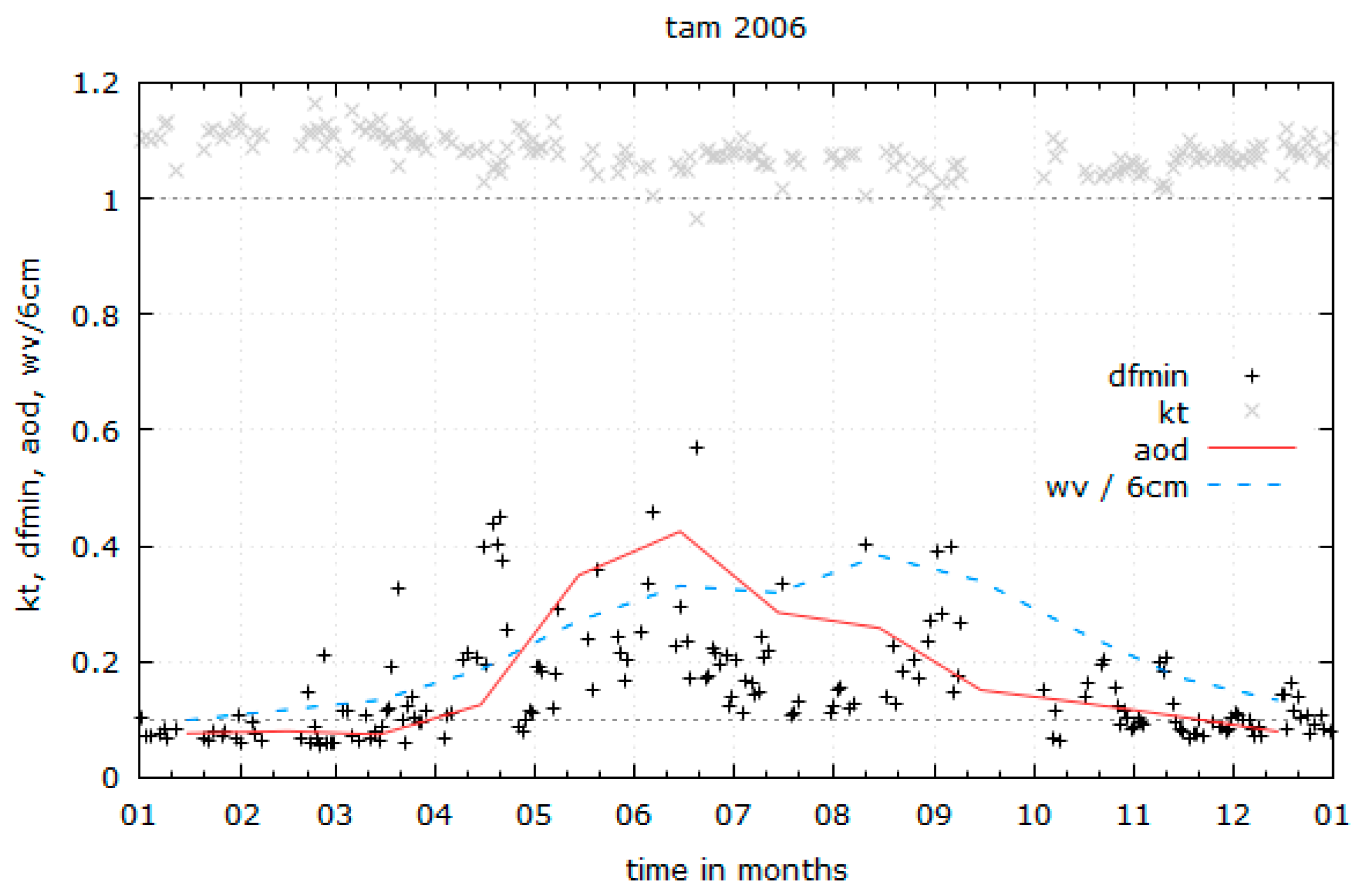
Figure 9 displays the minimal diffuse fractions of all clear days in Tamanrasset, Algeria, in 2006 (black plus symbols) over the course of a year. While in wintertime
ranges mostly between 0.05 and 0.15, it almost never falls below 0.1 in summertime and features values between 0.15 and 0.5. When looking at the daily mean
values (grey crosses), no significant correlation can be observed which implies that other factors must have influence on the minimal daily diffuse fraction. The monthly means of aerosol optical depth (red) and the water vapor (blue dashed) taken from the NASA Terra/MODIS satellite [
29,
30] however feature a seasonal behavior similar to
.
3.3.4. Summary of Factors Influencing
This leads to the conclusion that
is dependent on a series of factors. A list of factors that proved influential on
is given below:
- (1)
The clearness index
. The values of
are averaged in a range of 120 min around noon:
- (2)
The variability of the clearness index,
. For the same period of time, the changes of
are registered:
- (3)
The maximum elevation of the sun during the day, and the minimum air mass during the day, , compare to top of this section.
- (4)
The aerosol optical depth (AOD) and the water vapour (wv) of the respective month. These values are taken from the NASA Terra/MODIS satellite [
29,
30] and averaged on a month per month basis between 2001 and 2015.
Figure 10 gives an impression of the worldwide seasonal characteristics of AOD and wv.
- (5)
The up and down time of in the morning and in the evening. As a measure of the steepness of the curve, the time span is determined between sunrise and when first reaches the threshold of 1 in the morning. A second time span between the moment when is at last above 1 in the evening and sunset is measured as well. The two values are averaged and are a good indicator for in places with high day-to-day variation of : The longer the up/down time, the higher will be.
3.3.5. Resulting Equations for
The factors that influence
mentioned in the above section are combined in a series of posynomials, depending on the location and availability of data. The coefficients and exponents of the following posynomials were fitted with the help of the Levenberg-Marquardt algorithm implementation of the software gnuplot 5.0 [
31].
The datasets used for the posynomial fits are taken from the same locations as in
Table 2, but for different years of measurement:
asp 2009, bil 2005, bou 2010, brb 2011, cab 2011, cam 2002, clh 2014, cnr 2010, coc 2007, daa 2003, dar 2010, fua 2013, gob 2013, iza 2010, lau 2007, ler 2002, lin 2002, pal 2010, pay 2010, reg 2011, sap 2013, sbo 2011, sms 2006, sov 2002, tam 2003, tat 2003, tor 2005, xia 2006. For Case 1 only the subset
bou 2010, iza 2010, sbo 2011, sov 2002, tam 2003 and
xia 2006 was used.
Case 1: AOD and water vapor data available, location features strong seasonal changes of AOD (indicator for seasonal aerosol concentrations e.g., due to sandstorms in desert regions, see
Table 3 the values for factors
a,
b and
c).
Case 2: AOD and water vapor data available, no strong seasonal changes of AOD (see
Table 4 the values for factors
a,
b and
c).
Case 3: AOD and water vapor data are not available (see
Table 5 the values for factors
a,
b and
c):
Case 4: AOD, water vapor and up/down time data are not available (see
Table 6 the values for factors
a,
b and
c).
3.4. Combination of the Three Parts
The three parts of the algorithm generate the values
,
and
. Depending on the current weather situation, expressed by characteristics and statistical features of
, they are combined to one single, resulting
:
The mean absolute deviation of
at a given time of day
that is used as condition above is calculated as follows:
with
. For illustration of the weighing conditions mentioned in
Table 7,
Figure 11 displays all-sky camera images from the Institute of Meteorology and Climatology of the Leibniz University Hannover [
32,
33]. Picture A shows a moment where no clouds are visible. It is classified as “
Clear Sky” since
and
. Picture B shows a moment where
and
, hence being classified as “
Standard”. In picture C some light clouds are visible around the sun. This moment is classified as “
Transition” as
and
. The “
Transition” condition can be interpreted as clear sky with only few light clouds.
The generated matrices and other model data can be obtained from the authors upon request.
4. Results
In this section, the results of the validation of the new algorithm are presented. As mentioned in
Section 2.1, the validation is conducted for 28 locations with one year of one-minute values each, basing the validation on more than seven million data points worldwide.
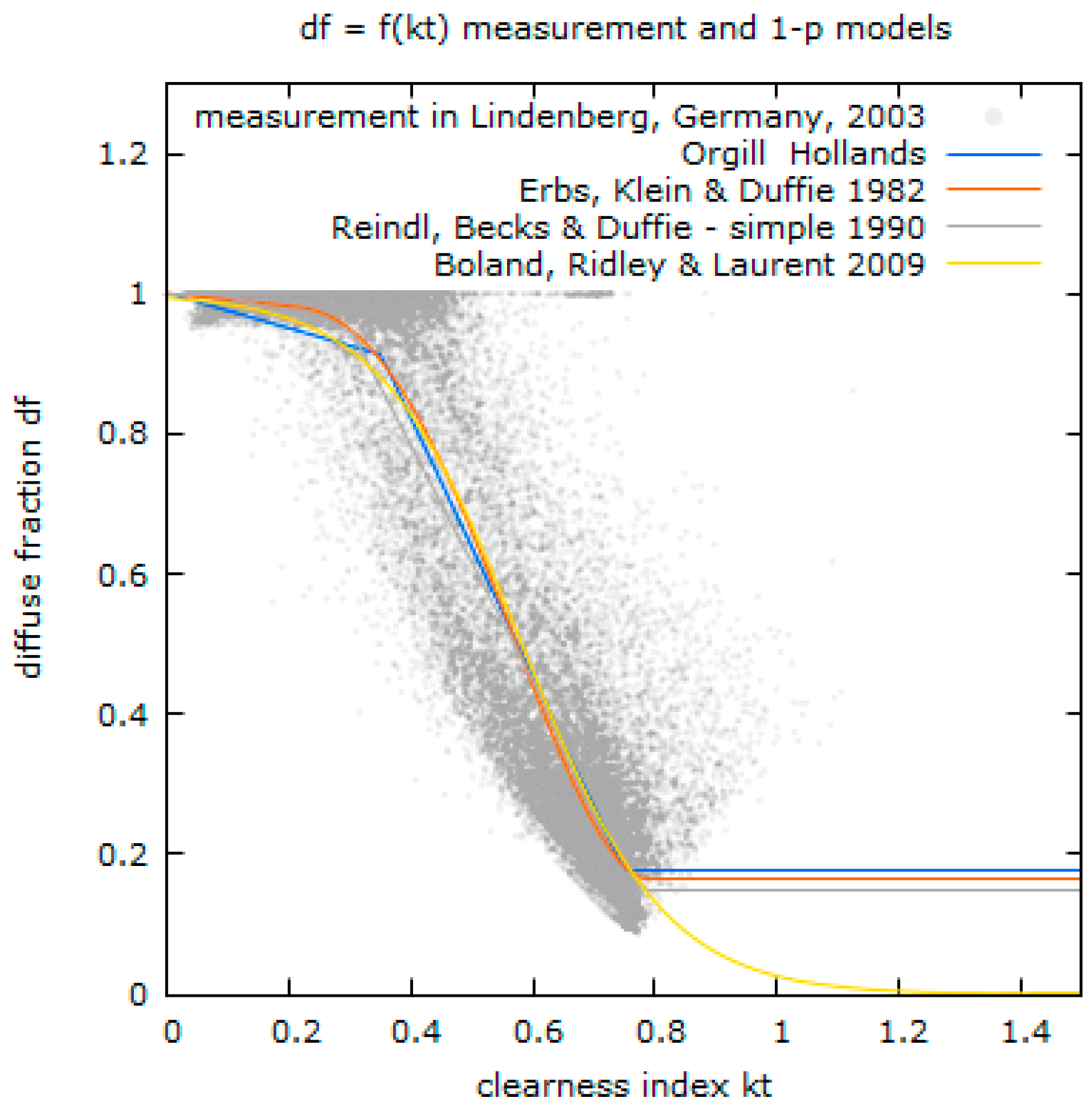
The overall results are then compared to the results of three existing models for the diffuse fraction: the model of Orgill and Hollands [
18] (OH), a one-parameter model, the reduced version of the two-parameter model of Reindl et al. [
3] (RR), and the model by Perez and Ineichen [
23] (PZ), all introduced in
Section 2.3. The first two models were also identified as two of the three best performing models among the eight investigated approaches by Dervishi [
27]. The model by Perez and Ineichen [
23] is still popular in the community and widely made use of. The model by Skartveit [
12] was not used for the model comparison since no indications were found that show a significant advantage of this model over Orgill and Hollands [
18], Reindl et al. [
3] or Perez and Ineichen [
23].
Figure 12 displays two weeks in Alice Springs, Australia, 2005. The measured global horizontal irradiance is plotted on top (green); the resulting clearness index
is plotted for reference underneath (black). In the three following plots, the measured diffuse fraction (black) is displayed, together with the diffuse fraction that was modelled with the new approach (blue), with the model from Orgill and Hollands [
18] (grey) , the model from Reindl et al. [
3] (orange) and the model from Perez and Ineichen [
23].
While the new model is able to reproduce the diffuse fraction in good accordance to the measurement values most of time, the inherent problem of models with static one- or two-parameter relationships between the clearness index and the diffuse fraction becomes apparent. Especially on clear sky days the existing models fail to reproduce the characteristic behavior of the diffuse fraction.
In order to evaluate the performance of the new model in statistical terms, the root mean squared errors (
RMSEs) are calculated for the new model as well as for the three reference models.
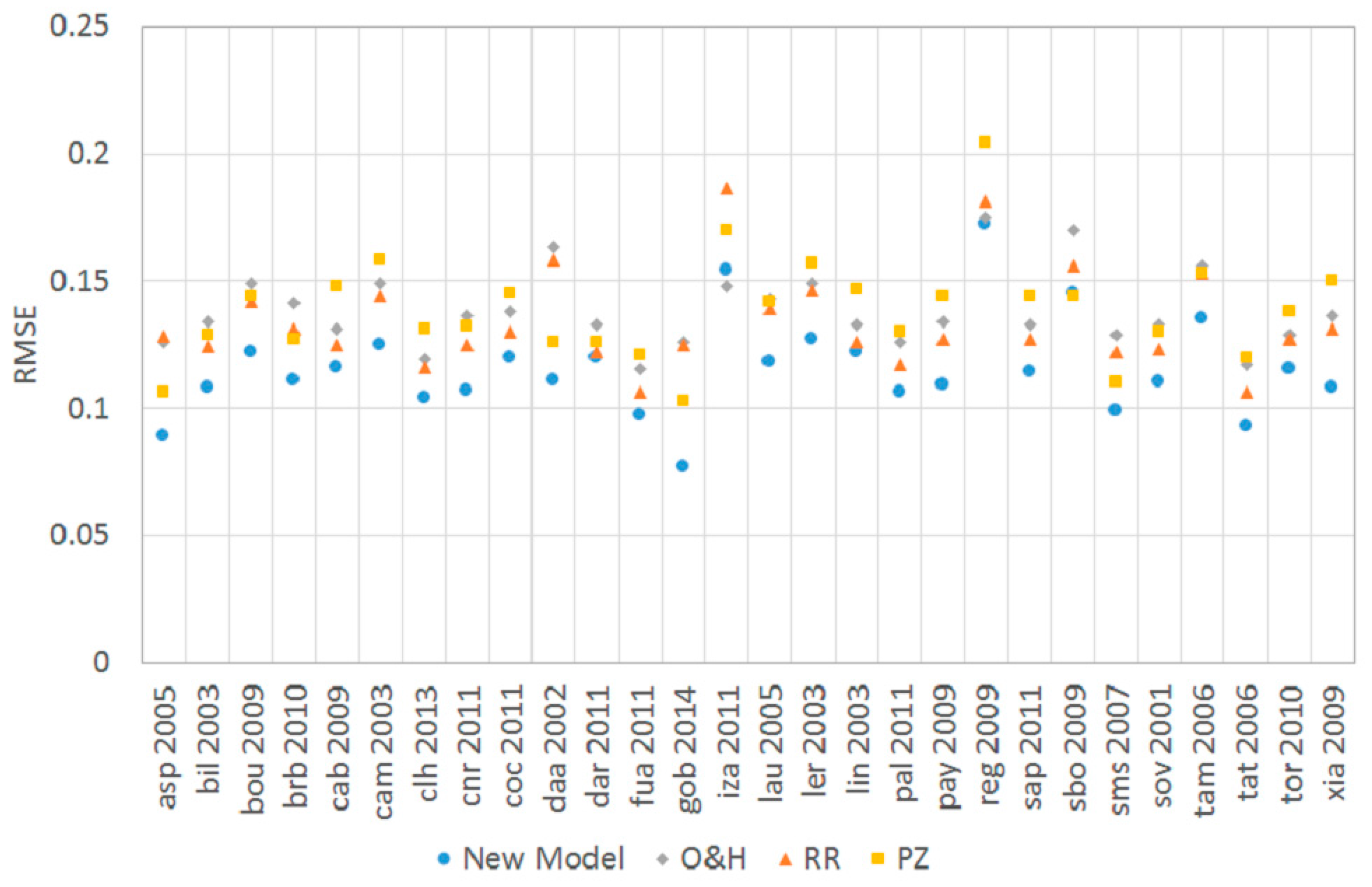
Figure 13 shows the
RMSE for the four models over all test data sets. The
RMSE produced by the new model is smaller than those produced by the models of Orgill and Hollands [
18], Reindl et al. [
3] and Perez and Ineichen [
23], in parts significantly, except for one case in Izaña, Spain, 2011 (
iza 2011). The overall
RMSE, averaged over all test data sets, can be reduced from 0.138 (OH), 0.134 (RR) and 0.139 (PZ) to 0.116 for the new model, which equals an amelioration of 16%–20%.
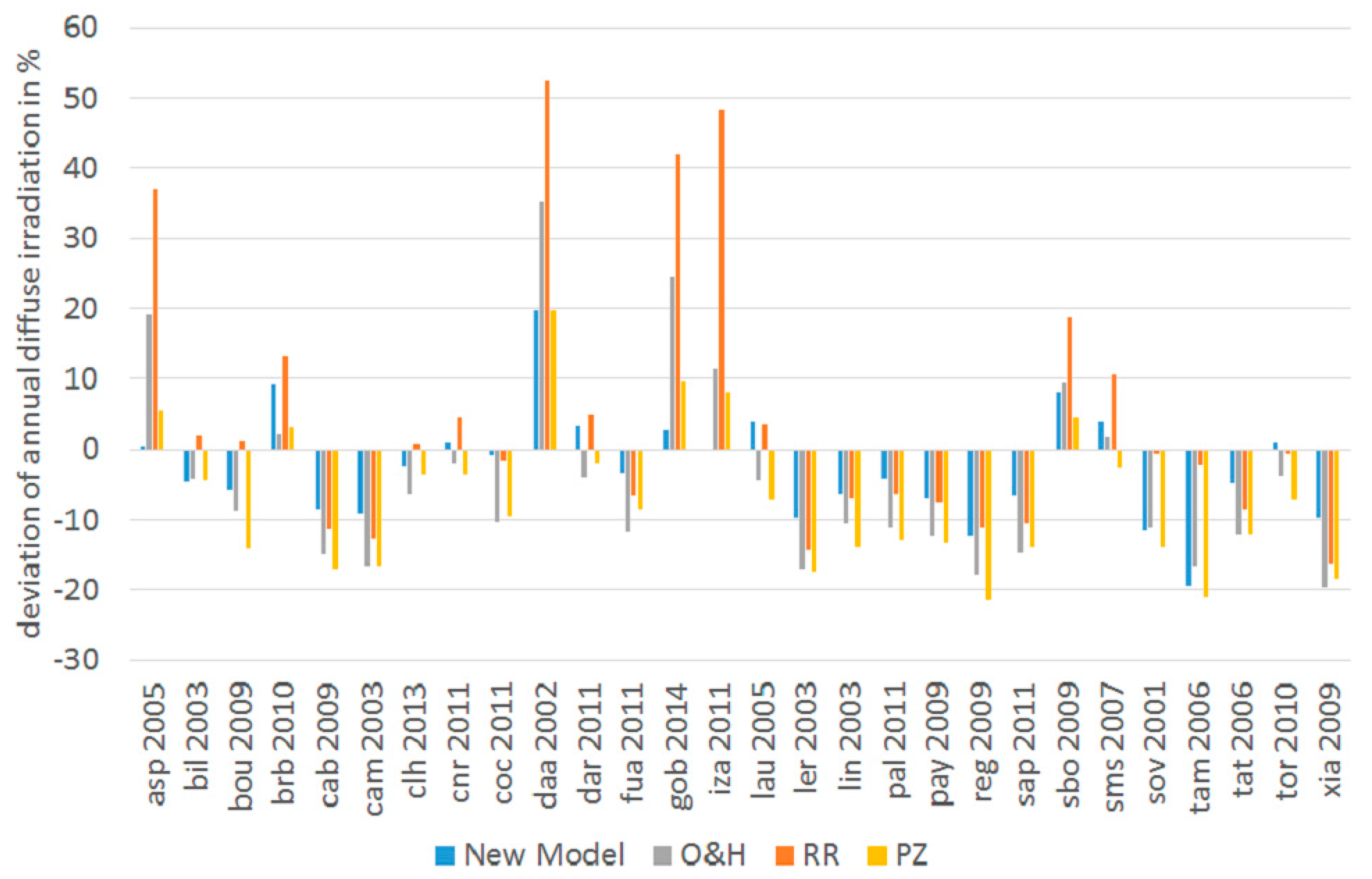
A further validation is conducted by comparing the annual diffuse irradiation values that are estimated by the models with the measured value.
Figure 14 lists the relative deviations of the modelled from the measured annual diffuse irradiation. In most of the cases, the deviation resulting from the new model is significantly smaller than the deviation resulting from the models of OH, RR or PZ. There are few cases where the model leads to higher deviations than the existing ones, e.g., for Billings, USA (
bil 2003), Solar Village, Saudi Arabia (
sov 2001) or Tamanrasset, Algeria (
tam 2006). Extreme deviations of more than 20%, however, as apparent in some of the test cases for the two existing models, do not occur when using the new model. The average of the absolute (i.e. unsigned) relative deviations for all test cases can be reduced by nearly 50% from 11.9% for OH, 12.7% for RR and 10.9% for PZ to only 6.4% for the new model.
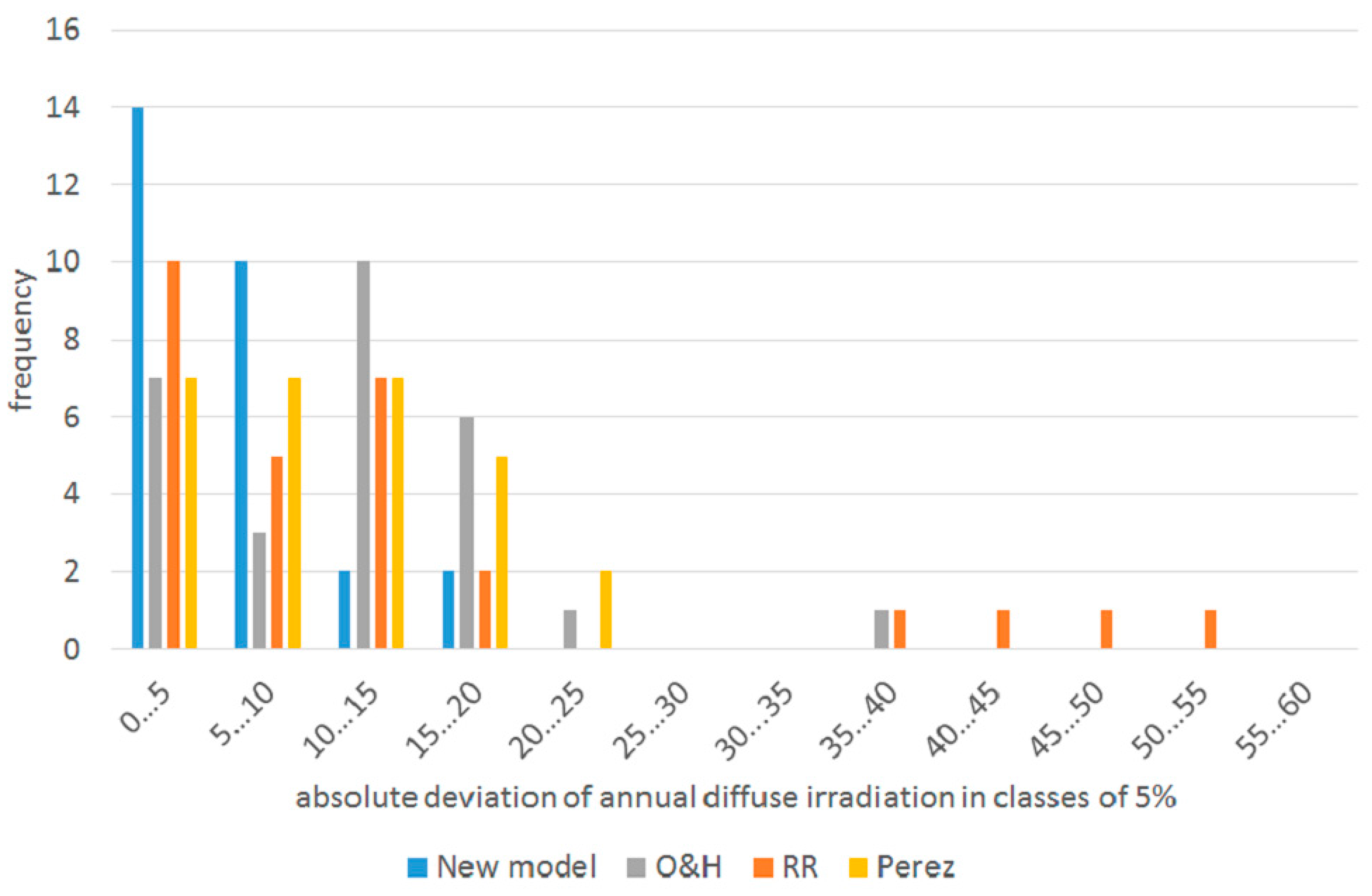
The histogram of the mean absolute deviations of the annual diffuse irradiation displayed in
Figure 15 illustrates the frequency of the deviations each model produces. While the model of Reindl et al. [
3] (RR) has its peak in the class of 0 to 5%, it still has several outliers of 35%–55%. The model of Orgill and Hollands [
18] (OH) features only one extreme outlier at 35%–40%, but has most of its results lying in the class of 10 to 15%. The model by Perez and Ineichen [
23] shows no outliers of more than 25% but has its results evenly distributed between 0 and 15%. The new model does not produce any outliers and has its peak in the class of 0%–5%, covering 50% of the test cases alone.
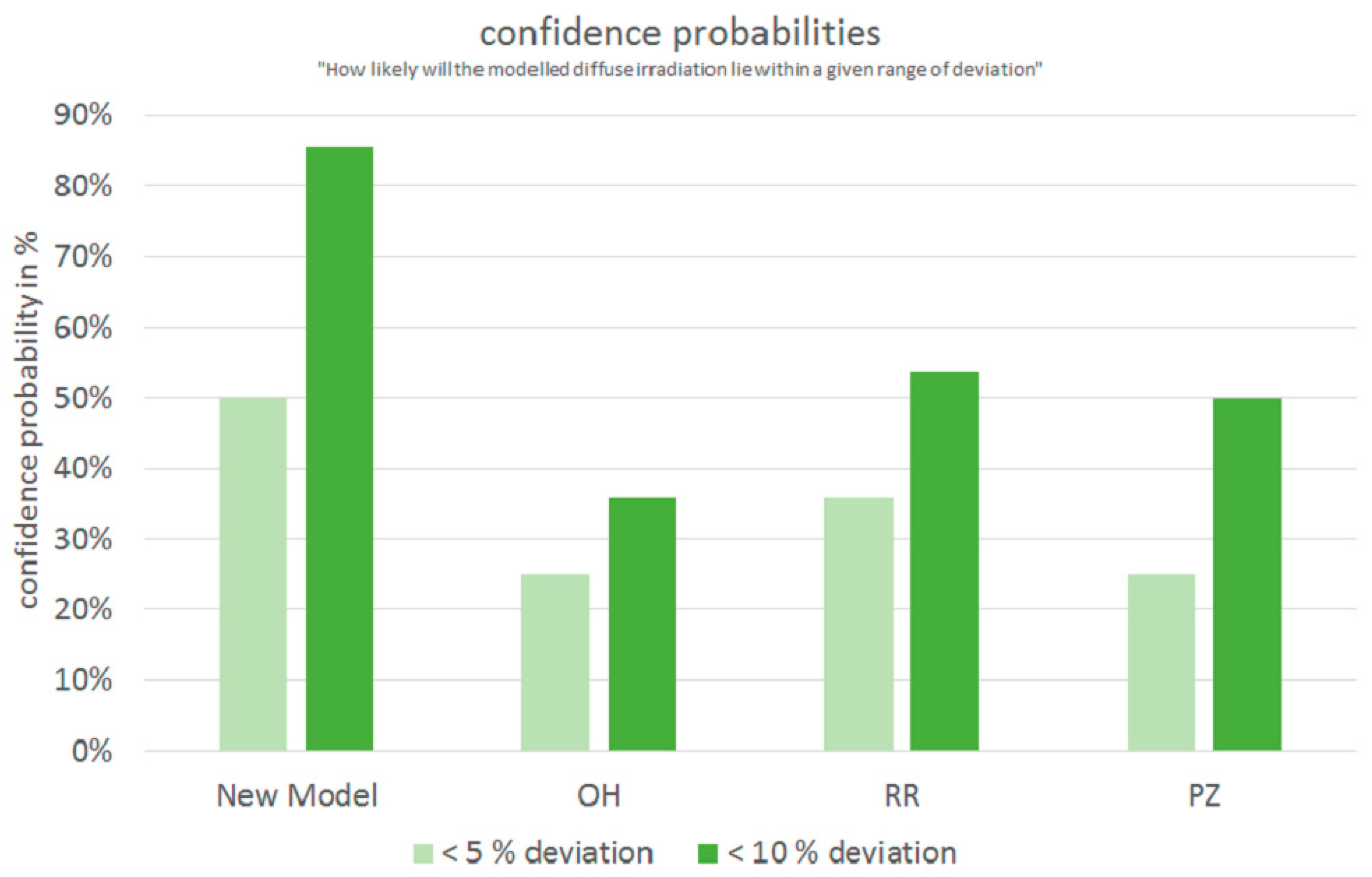
This histogram can be converted into confidence probabilities, depicted in
Figure 16. The new model results in mean absolute deviations of less than 5% in 50% of the cases. In more than 80% of the cases, the deviation is less than 10%. Compared to the other three models this is a significant improvement, where the probability of producing less than 5% deviation is only 25% (OH), 36% (RR) and 25% (PZ) and the probability of producing less than 10% deviation is 36% (OH), 54% (RR) and 50% (PZ).
5. Conclusions
The newly developed model for the diffuse fraction of solar irradiance on PV systems provides significantly better agreement with measurements than the other models published so far. This is achieved by the following features: the first part utilizes the dependency of the diffuse fraction on the clearness index , in analogy to existing one-parameter models. In the new model, the correlation is expressed as probability matrices rather than single functions, leading to realistic, more natural diffuse fraction characteristics. Also taking advantage of probability matrices, the second part uses the relation of the relative changes of over the relative changes of . The third part takes into account the diffuse fraction characteristics of days with clear sky only using a geometrical approach. The crucial factor for the third part is the minimum daily diffuse fraction for which a posynomial model has been introduced.
The presented new model was analyzed and compared to two other models for 28 locations worldwide with one year of one-minute measurement data each. It was shown that the new model has a high quality of modeling the diffuse irradiance. The mean RMSE over all test cases was reduced by 16%–20%, whereas the mean absolute deviation of the annual diffuse irradiation was found to be nearly 50% smaller compared to the reference models. In more than 80% of the test cases, the deviation of the annual diffuse irradiation is smaller than 10%, with an overall maximum deviation of 20%.
With the new model, the diffuse irradiance can be calculated with much lower uncertainty, hence significantly reducing the uncertainty of PV energy yield simulations. Possible future work for the improvement of the model will include further investigations on the minimal daily diffuse fraction that has a very decisive influence on the model quality for clear sky days. Such days may be identified by cloud cameras that will allow for a much better estimation of the cloud fraction compared to satellite images [
33].