Nonparametric Estimation of a Conditional Quantile Function in a Fixed Effects Panel Data Model
Abstract
:1. Introduction
2. Methodology
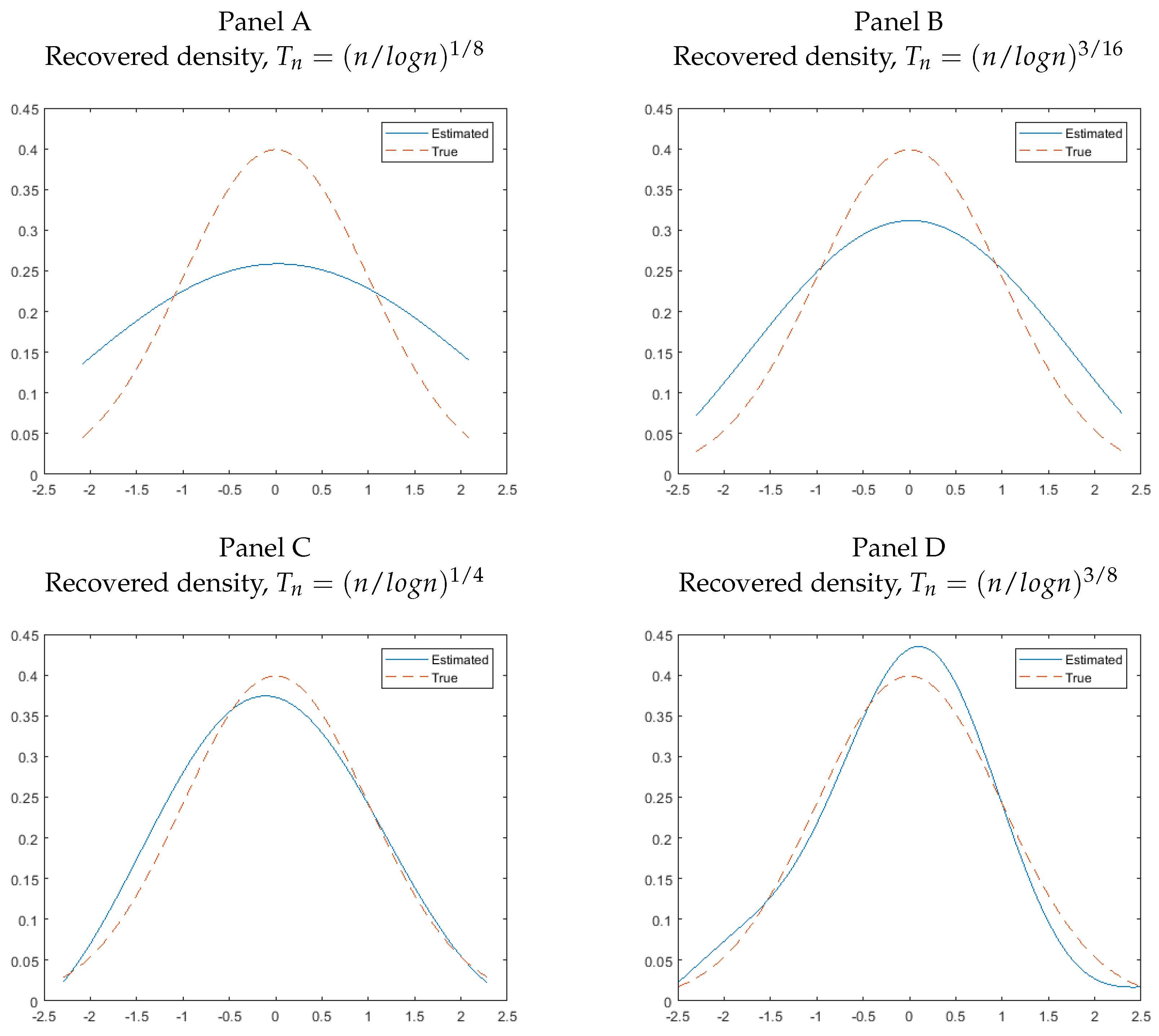
3. Monte Carlo Simulation
4. Extension: Conditional Heteroskedastistic Error Case
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abrevaya, Jason, and Christian M. Dahl. 2008. The effects of birth inputs on birthweight. Journal of Business & Economic Statistics 26: 379–97. [Google Scholar]
- Al Rahahleh, Naseem, Iman Adeinat, and M. Ishaq Bhatti. 2016. On ethnicity of idiosyncratic risk and stock returns puzzle. Humanomics 32: 48–68. [Google Scholar] [CrossRef]
- Al Rahahleh, Naseem, and M. Ishaq Bhatti. 2017. Co-movement measure of information transmission on international equity markets. Physica A: Statistical Mechanics and its Applications 470: 119–31. [Google Scholar] [CrossRef]
- Al Rahahleh, Naseem, M. Ishaq Bhatti, and Iman Adeinat. 2017. Tail dependence and information flow: Evidence from international equity markets. Physica A: Statistical Mechanics and its Applications 474: 319–29. [Google Scholar] [CrossRef]
- Al Shubiri, Faris Nasif, and Syed Ashsan Jamil. 2018. The impact of idiosyncratic risk of banking sector on oil, stock market, and fiscal indicators of Sultanate of Oman. International Journal of Engineering Business Management, 10. [Google Scholar] [CrossRef]
- Bartram, Söhnke M., Gregory W. Brown, and René M. Stulz. 2018. Why Has Idiosyncratic Risk Been Historically Low in Recent Years? National Bureau of Economic Research Working Paper NO. 24270. Cambridge, MA, USA: National Bureau of Economic Research, January. [Google Scholar]
- Bassett, Gilbert, Jr., and Roger Koenker. 1982. An empirical quantile function for linear models with iid errors. Journal of the American Statistical Association 77: 407–15. [Google Scholar] [CrossRef]
- Belloni, Alexandre, Victor Chernozhukov, and Ivan Fernández-Val. 2016. Conditional quantile processes based on series and many regressors. arXiv, arXiv:1105.6154. [Google Scholar]
- Chen, Songnian, and Shakeeb Khan. 2008. Semiparametric estimation of nonstationary censored panel data models with time varying factor loads. Econometric Theory 24: 1149–73. [Google Scholar] [CrossRef]
- Chernozhukov, Victor, Iván Fernández-Val, and Alfred Galichon. 2010. Quantile and probability curves without crossing. Econometrica 78: 1093–25. [Google Scholar]
- Evdokimov, Kirill. 2010. Indentification and Estimation of a Nonparametric Panel Data Model with Unobserved Heterogeneity. Working Paper. Princeton, NJ, USA: Princeton University. [Google Scholar]
- Fang, Zheng, Qi Li, and Karen Yan. 2018. A Simple Nonparametric Method for Estimation and Inference of Conditional Quantile Functions. Working Paper. Available online: https://ssrn.com/abstract=3223015 (accessed on 3 August 2018).
- Firpo, Sergio, Nicole M. Fortin, and Thomas Lemieux. 2009. Unconditional quantile regressions. Econometrica 77: 953–73. [Google Scholar]
- Firpo, Sergio P., Nicole M. Fortin, and Thomas Lemieux. 2018. Decomposing wage distributions using recentered influence function regressions. Econometrics 6: 28. [Google Scholar] [CrossRef]
- Hall, Peter, Qi Li, and Jeffrey S. Racine. 2007. Nonparametric estimation of regression functions in the presence of irrelevant regressors. The Review of Economics and Statistics 89: 784–89. [Google Scholar] [CrossRef]
- Harding, Matthew, and Carlos Lamarche. 2014. Estimating and testing a quantile regression model with interactive effects. Journal of Econometrics 178: 101–13. [Google Scholar] [CrossRef]
- He, Xuming. 1997. Quantile curves without crossing. The American Statistician 51: 186–92. [Google Scholar]
- Henderson, Daniel J., Raymond J. Carroll, and Qi Li. 2008. Nonparametric estimation and testing of fixed effects panel data models. Journal of Econometrics 144: 257–75. [Google Scholar] [CrossRef] [PubMed]
- Horowitz, Joel L., and Marianthi Markatou. 1996. Semiparametric estimation of regression models for panel data. The Review of Economic Studies 63: 145–68. [Google Scholar] [CrossRef]
- Hu, Yingyao, and Geert Ridder. 2010. On deconvolution as a first stage nonparametric estimator. Econometric Reviews 29: 365–96. [Google Scholar] [CrossRef]
- Kato, Kengo, Antonio F. Galvao, and Gabriel V. Montes-Rojas. 2012. Asymptotics for panel quantile regression models with individual effects. Journal of Econometrics 170: 76–91. [Google Scholar] [CrossRef]
- Koenker, Roger. 2004. Quantile regression for longitudinal data. Journal of Multivariate Analysis 91: 74–89. [Google Scholar] [CrossRef]
- Li, Qi, Juan Lin, and Jeffrey S. Racine. 2013. Optimal bandwidth selection for nonparametric conditional distribution and quantile functions. Journal of Business & Economic Statistics 31: 57–65. [Google Scholar]
- Li, Qi, and Jeffrey Scott Racine. 2007. Nonparametric Econometrics: Theory and Practice. Princeton: Princeton University Press. [Google Scholar]
- Lin, Wei, Zongwu Cai, Zheng Li, and Li Su. 2015. Optimal smoothing in nonparametric conditional quantile derivative function estimation. Journal of Econometrics 188: 502–13. [Google Scholar] [CrossRef]
- Nguyen, Cuong, and M. Ishaq Bhatti. 2015. Investor sentiment and idiosyncratic volatility puzzle: Evidence from the chinese stock market. Journal of Stock and Forex Trading 4: 2. [Google Scholar]
- Pagan, Adrian, and Aman Ullah. 1999. Nonparametric Econometrics. Cambridge: Cambridge University Press. [Google Scholar]
- Qu, Zhongjun, and Jungmo Yoon. 2015. Nonparametric estimation and inference on conditional quantile processes. Journal of Econometrics 185: 1–19. [Google Scholar] [CrossRef] [Green Version]
| 1. | For ease of exposition, we assume is univariate, the extension to multivariate case can be carried over straightforwardly. |
| 2. | This can be achieved by using de-mean data for the dependent variable, i.e., replacing by in Equation (1). For notational simplicity, we still use to denote the dependent variable although it is actually the de-mean version of it. |
| 3. | Recently, Fang et al. (2018) proposes a new nonparametric method for estimating a conditional quantile function with cross-sectional data. We refer readers to Fang et al. (2018) for a detailed discussion. |
| 4. | For ease of exposition, we drop the subscript in and use to denote the -th quantile of in general, since is an sequence. |
| 5. | The consistency can be straightforwardly shown using similar arguments as in Fang et al. (2018) and Horowitz and Markatou (1996). |
| 6. | There is no rule-of-thumb to choose the optimal bandwidth in the deconvolution method. In practice, researchers can try different bandwidths as a robust check to see how results vary across the different bandwidths. |
| 7. | Fang et al. (2018) also considers the same form of heteroskedastic error as described here. |
| 8. | This implies the conditional density of given is symmetric, since, given that , the symmetry of is equivalent to the symmetry of . |
| Sample Size | Estimators | ||||||
|---|---|---|---|---|---|---|---|
| 0.0149 | 0.0037 | 0.0022 | 0.0006 | 0.0204 | 0.0185 | 0.0163 | |
| 0.0092 | 0.0012 | 0.0007 | 0.0002 | 0.0107 | 0.0102 | 0.0096 | |
| 0.0048 | 0.00051 | 0.00028 | 0.000082 | 0.0052 | 0.0050 | 0.0048 | |
| Sample Size | Estimators | ||||||
|---|---|---|---|---|---|---|---|
| 0.0139 | 0.0423 | 0.0235 | 0.0065 | 0.0642 | 0.0433 | 0.0235 | |
| 0.0094 | 0.0210 | 0.0128 | 0.0036 | 0.0304 | 0.0222 | 0.0130 | |
| 0.0048 | 0.0091 | 0.0063 | 0.0019 | 0.0104 | 0.0112 | 0.0067 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, K.X.; Li, Q. Nonparametric Estimation of a Conditional Quantile Function in a Fixed Effects Panel Data Model. J. Risk Financial Manag. 2018, 11, 44. https://doi.org/10.3390/jrfm11030044
Yan KX, Li Q. Nonparametric Estimation of a Conditional Quantile Function in a Fixed Effects Panel Data Model. Journal of Risk and Financial Management. 2018; 11(3):44. https://doi.org/10.3390/jrfm11030044
Chicago/Turabian StyleYan, Karen X., and Qi Li. 2018. "Nonparametric Estimation of a Conditional Quantile Function in a Fixed Effects Panel Data Model" Journal of Risk and Financial Management 11, no. 3: 44. https://doi.org/10.3390/jrfm11030044




