Estimation of River Pollution Index in a Tidal Stream Using Kriging Analysis
Abstract
:1. Introduction
2. Theory and Methods
2.1. Kriging Analysis
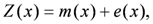
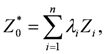
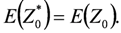
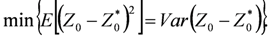
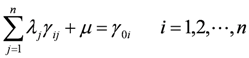

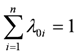
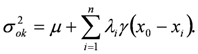
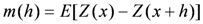
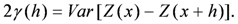
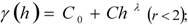
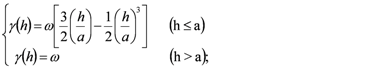
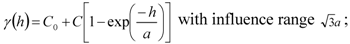
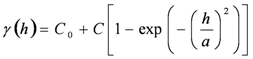



2.2. River Pollution Index
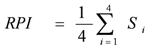
| Items | Ranks | |||
|---|---|---|---|---|
| Unpolluted | Negligibly polluted | Moderately polluted | Severely polluted | |
| DO (mg/L) | Above 6.5 | 4.6–6.5 | 2.0–4.5 | Under 2.0 |
| BOD5 (mg/L) | Under 3.0 | 3.0–4.9 | 5.0–15 | Above 15 |
| SS (mg/L) | Under 20 | 20–49 | 50–100 | Above 100 |
| NH3-N (mg/L) | Under 0.5 | 0.5–0.99 | 1.0–3.0 | Above 3.0 |
| Index Scores (Si) | 1 | 3 | 6 | 10 |
| RPI | Under 2 | 2.0–3.0 | 3.1–6.0 | Above 6.0 |
3. Study Site Descriptions

4. Results and Discussion
4.1. One-Dimensional Design along the Tanshui River

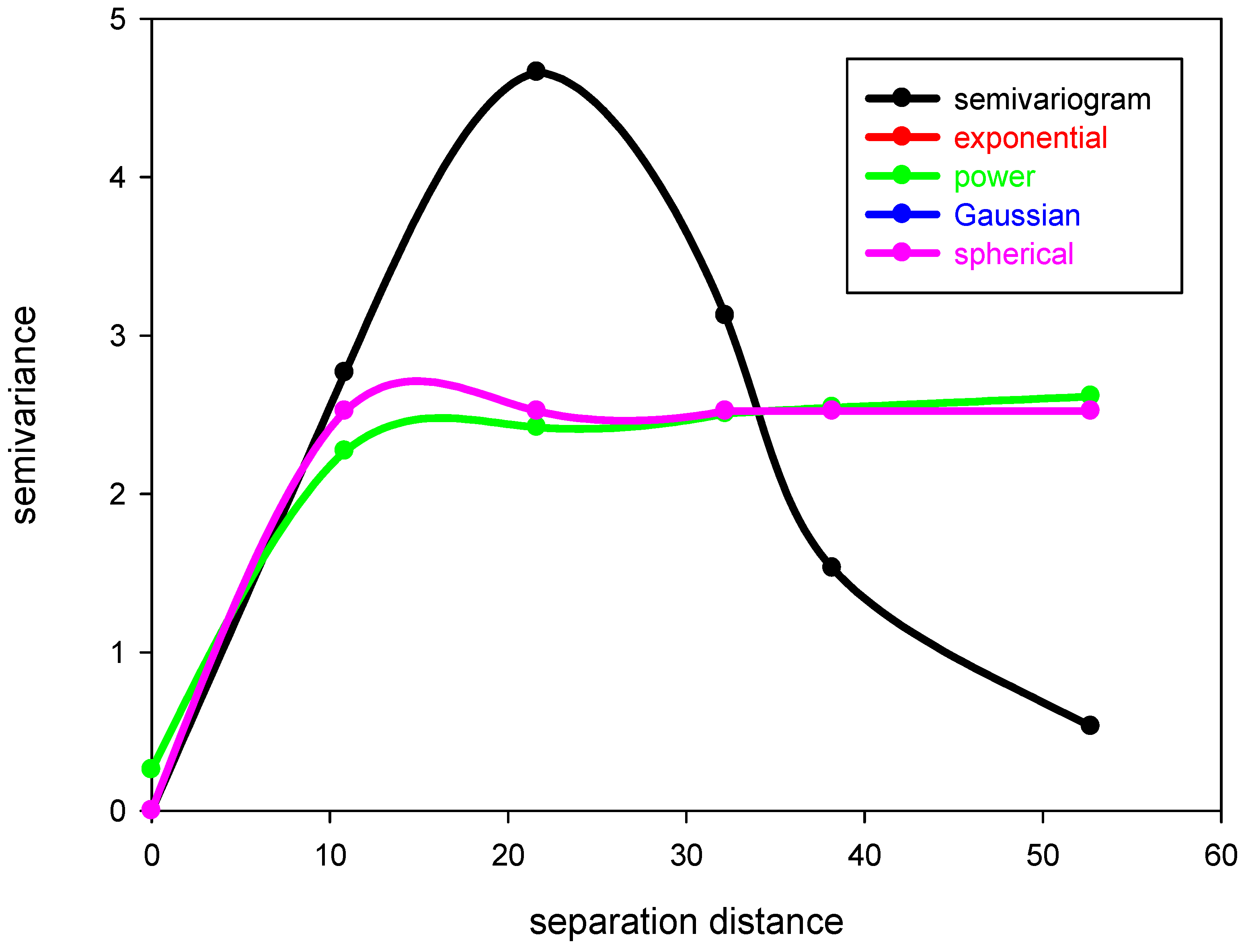
4.2. Spatial Variability Analysis
| Water quality | DO (mg/L) | BOD5 (mg/L) | NH3-N (mg/L) | SS (mg/L) | RPI | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Station | mean ± std | Min. | Max. | mean ± std | Min. | Max. | mean ± std | Min. | Max. | mean ± std | Min. | Max. | mean ± std | Min. | Max. |
| Shain Bridge | 4.45 ± 0.84 | 2.8 | 6.1 | 2.21 ± 0.33 | 1.7 | 2.6 | 0.02 ± 0.01 | 0.01 | 0.04 | 13.76 ± 3.91 | 10.1 | 23.1 | 1.98 ± 0.43 | 1.50 | 2.75 |
| Shinhai Bridge | 1.22 ± 0.77 | 0.1 | 2.8 | 8.45 ± 2.77 | 4.3 | 12.7 | 5.72 ± 0.94 | 4.37 | 7.40 | 32.08 ± 6.55 | 23.2 | 44.2 | 7.04 ± 0.54 | 5.50 | 7.25 |
| Zonan Bridge | 3.39 ± 0.43 | 2.7 | 4.0 | 1.89 ± 0.58 | 1.3 | 2.8 | 0.53 ± 0.37 | 0.13 | 1.25 | 17.39 ± 5.00 | 7.0 | 24.5 | 2.71 ± 0.42 | 2.25 | 3.50 |
| Chung Cheng Bridge | 4.07 ± 0.75 | 2.9 | 5.1 | 2.48 ± 0.61 | 1.5 | 3.7 | 1.58 ± 0.44 | 0.82 | 2.41 | 23.88 ± 10.32 | 13.9 | 54.0 | 3.67 ± 0.59 | 2.75 | 4.50 |
| Jansho Bridge | 3.99 ± 0.46 | 3.1 | 4.8 | 1.20 ± 0.15 | 1.0 | 1.4 | 0.01 ± 0.01 | 0.01 | 0.03 | 13.95 ± 9.48 | 3.4 | 28.9 | 2.38 ± 0.26 | 2.00 | 2.75 |
| Nanhu Bridge | 3.32 ± 0.57 | 2.4 | 4.2 | 3.11 ± 0.81 | 1.8 | 4.5 | 0.70 ± 0.22 | 0.37 | 0.96 | 38.94 ± 26.07 | 15.8 | 95.8 | 3.52 ± 0.81 | 2.25 | 4.50 |
| Banlin Bridge | 1.76 ± 0.22 | 1.4 | 2.1 | 2.98 ± 0.59 | 2.2 | 4.1 | 1.98 ± 0.14 | 1.64 | 2.16 | 13.45 ± 2.88 | 10.5 | 18.9 | 4.50 ± 0.46 | 3.50 | 5.00 |
| Taipei Bridge | 1.78 ± 0.38 | 1.4 | 2.6 | 2.98 ± 0.96 | 1.6 | 4.4 | 3.73 ± 0.71 | 2.55 | 5.33 | 30.51 ± 14.75 | 14.2 | 61.5 | 5.88 ± 1.12 | 3.50 | 7.25 |
| Guandu Bridge | 2.27 ± 0.34 | 1.5 | 2.7 | 1.96 ± 1.49 | 0.01 | 6.1 | 1.66 ± 0.44 | 0.53 | 2.21 | 20.81 ± 6.09 | 12.5 | 33.2 | 3.96 ± 0.67 | 2.75 | 5.25 |
| Parameter | Power | Exponential | Gaussian | Spherical |
|---|---|---|---|---|
| C0 | −0.005 | −135.409 | 0.001 | −0.006 |
| c | 2.318 | 136.996 | 2.312 | 2.320 |
| a | 0.417 | 0.002 | 1.000 | 0.480 |
| Least Error Sum of Squares (RSS) | 3.968 | 4.558 | 3.968 | 3.968 |
| Coefficient of Determination (R2) | 0.5289 | 0.4589 | 0.5289 | 0.5289 |
| Time 29 September 2010 | C0 | C | a | RSS | R2 |
|---|---|---|---|---|---|
| 5 a.m. | −0.005 | 2.528 | 0.420 | 9.949 | 0.3476 |
| 6 a.m. | −0.003 | 2.300 | 0.528 | 6.114 | 0.4181 |
| 7 a.m. | −0.006 | 2.773 | 0.424 | 16.512 | 0.2787 |
| 8 a.m. | −0.005 | 2.318 | 0.417 | 3.968 | 0.5289 |
| 9 a.m. | −0.007 | 3.549 | 0.437 | 11.234 | 0.4818 |
| 10 a.m. | −0.002 | 2.215 | 0.617 | 6.567 | 0.3829 |
| 11 a.m. | −0.004 | 3.355 | 0.631 | 18.835 | 0.3317 |
| noon | −0.002 | 2.003 | 0.607 | 5.725 | 0.3678 |
| 1 p.m. | −0.015 | 3.201 | 5.662 | 6.497 | 0.5555 |
| 2 p.m. | −0.002 | 2.073 | 0.623 | 11.562 | 0.2174 |
| 3 p.m. | −0.002 | 1.906 | 0.692 | 4.571 | 0.3727 |
| 4 p.m. | −0.002 | 1.609 | 0.605 | 4.969 | 0.3020 |
| 5 p.m. | −0.002 | 2.221 | 0.609 | 9.146 | 0.3095 |
4.3. Estimation of RPI
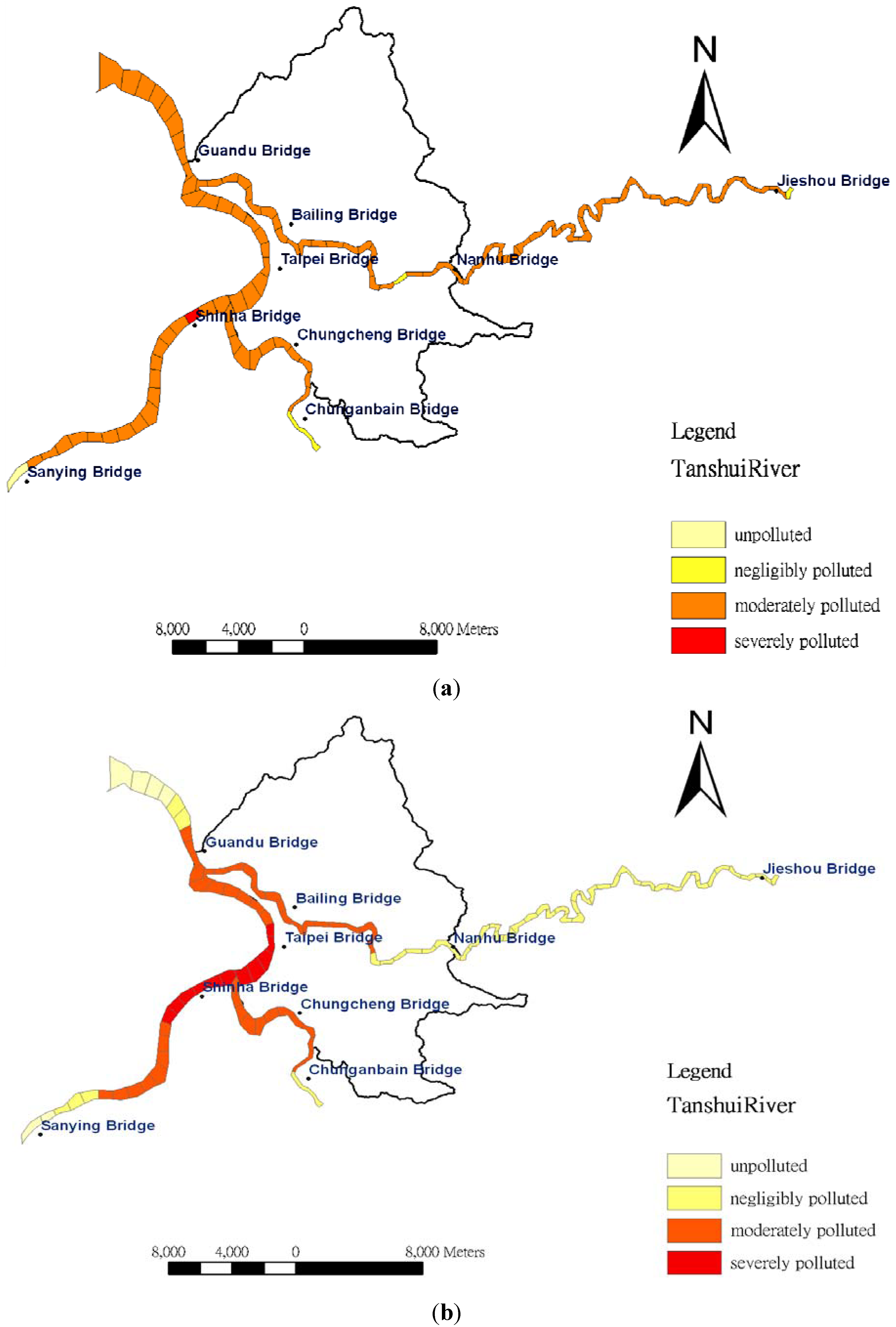
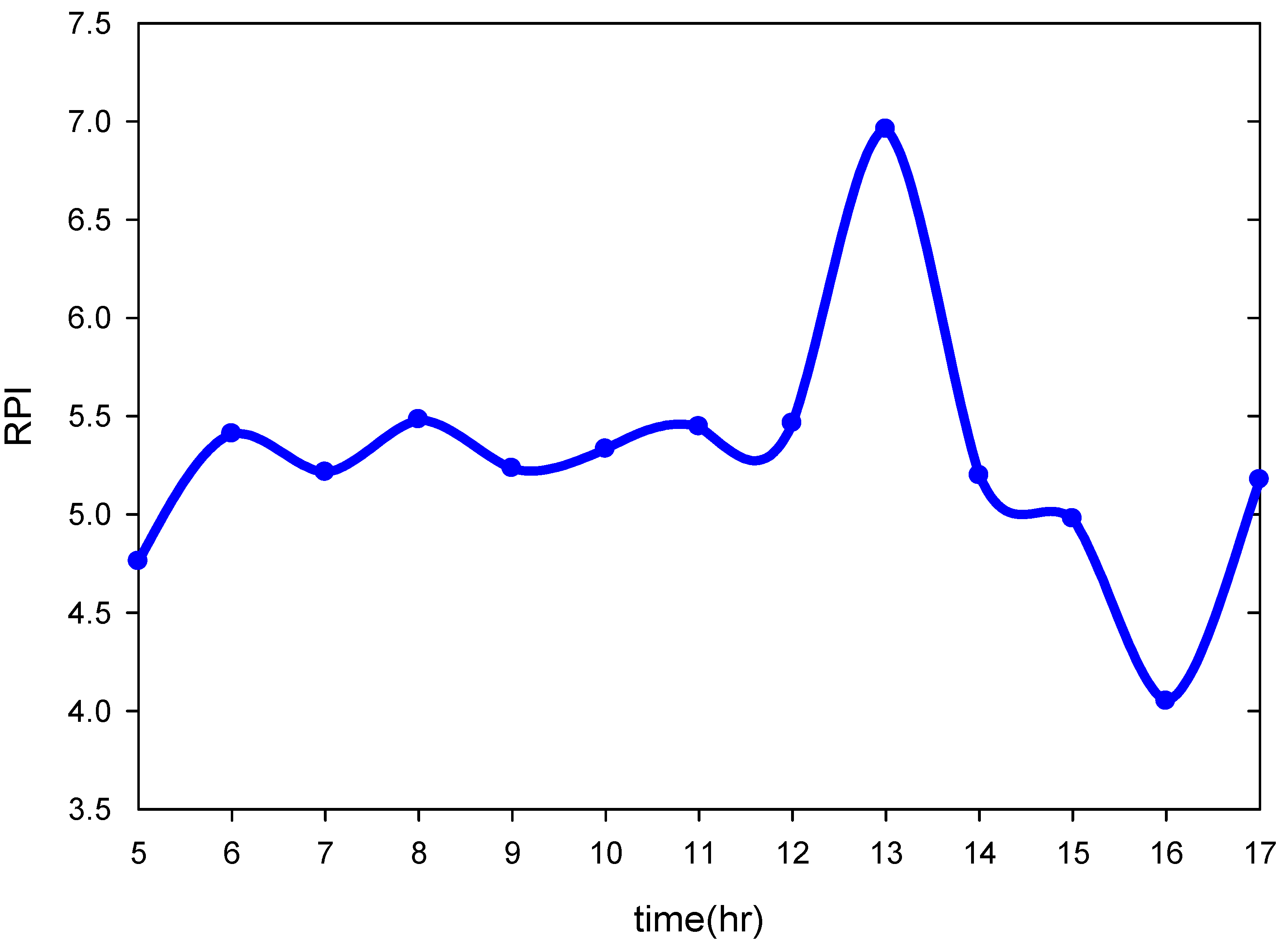
5. Conclusions
Acknowledgments
Conflict of Interest
References
- Kjerfve, B.; Magill, K.E. Geographic and hydrodynamic characteristics of shallow coastal lagoons. Mar. Geol. 1989, 88, 187–199. [Google Scholar] [CrossRef]
- Dronkers, J.; Leussen, W.V. Physical Processes in Estuaries; Springer-Verlag: Berlin, Germany, 1988. [Google Scholar]
- Dyer, K.R. Estuaries—A Physical Introduction; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Chen, C.-H.; Lung, W.-S.; Li, S.-W.; Lin, C.-C. Technical challenges with BOD/DO modeling of rivers in Taiwan. J. Environ. Res. 2012, 6, 3–8. [Google Scholar]
- Ekdal, A.; Gürel, M.; Guzel, C.; Erturk, A.; Tanik, A.; Gonenc, I.E. Application of WASP and SWAT models for a Mediterranean coastal lagoon with limited seawater exchange. J. Coast. Res. 2011, 64, 1023–1027. [Google Scholar]
- Chen, W.-B.; Liu, W.-C.; Hsu, M.-H. Water quality modeling in a tidal estuarine system using a three-dimensional model. Environ. Eng. Sci. 2011, 28, 443–459. [Google Scholar]
- Chen, Y.-C.; Wei, C.; Yeh, H.-C. Rainfall network design using kriging and entropy. Hydrol. Process. 2008, 22, 340–346. [Google Scholar] [CrossRef]
- Lo, S.-L.; Kuo, J.-T.; Wang, S.-M. Water quality network design of Keelung river, northern Taiwan. Water Sci. Technol. 1996, 34, 49–57. [Google Scholar]
- Mohammad, K.; Kerachian, R.; Akhbari, M.; Hafez, B. Design of river water quality monitoring networks: A case study. Environ. Model. Assess. 2009, 14, 705–714. [Google Scholar]
- Yang, X.; Jin, W. GIS-based spatial regression and prediction of water quality in river networks: A case study in IOWA. J. Environ. Manage 2010, 91, 1943–1951. [Google Scholar] [CrossRef]
- Polus, E.; Flipo, N.; de Fouquet, C.; Poulin, M. Geostatistics for assessing the efficiency of a distributed physically-based water quality model: Application to nitrate in the Seine River. Hydrol. Process. 2011, 25, 217–233. [Google Scholar]
- Liu, W.-C.; Yu, H.-L.; Chung, C.-E. Assessment of water quality in a subtropical alpine lake using multivariate statistical techniques and geostatistical mapping: A case study. Int. J. Environ. Res. Public Health 2011, 8, 1126–1140. [Google Scholar] [CrossRef]
- Militino, A.F.; Ugarte, M.D.; Ibáñez, B. Longitudinal analysis of spatially correlated data. Stoch. Env. Res. Risk A. 2008, 22, S49–S57. [Google Scholar] [CrossRef]
- Garreta, V.; Monestiez, P.; Ver Hoef, J.M. Spatial modeling and prediction on river networks: Up model, down model or hybrid? Environmetics 2010, 21, 439–456. [Google Scholar]
- Velasco-Forero, C.A.; Sempere-Torres, D.; Cassiraga, E.F.; Gómez-Hernández, J.J. A non-parametric automatic blending methodology to estimate rainfall fields from rain gauge and radar data. Adv. Water Resour. 2009, 32, 986–1002. [Google Scholar]
- Lin, Y.P.; Wang, C.L.; Chang, C.R.; Yu, H.H. Estimation of nested spatial patterns and seasonal variation in the longitudinal distribution of Sicyopterus japonicus in the Datuan Stream, Taiwan by using geostatistical methods. Environ. Monit. Assess. 2011, 178, 1–18. [Google Scholar]
- Darrouzet-Nardi, A.; Erbland, J.; Bowman, W.D.; Savarino, J.; Williams, M.W. Landscape-level nitrogen import and export in an ecosystem with complex terrain, Colorado Front Range. Biogeochemistry 2012, 109, 271–285. [Google Scholar] [CrossRef]
- Räty, M.; Kangas, A. Comparison of k-MSN and kriging in local prediction. Forest Ecol. Manag. 2012, 263, 47–56. [Google Scholar]
- Matheron, G. Principles of geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar]
- Matheron, G. Theory of R egionalized Variables and Its Applications; Ecole National Superieure des Mines: Paris, France, 1971. [Google Scholar]
- Journel, A.G.; Huijbregts, C.J. Mining Geostatistics; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Liou, S.-M.; Lo, S.-L.; Wang, S.-H. A generalized water quality index for Taiwan. Environ. Monit. Assess. 2004, 96, 35–52. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chen, Y.-C.; Yeh, H.-C.; Wei, C. Estimation of River Pollution Index in a Tidal Stream Using Kriging Analysis. Int. J. Environ. Res. Public Health 2012, 9, 3085-3100. https://doi.org/10.3390/ijerph9093085
Chen Y-C, Yeh H-C, Wei C. Estimation of River Pollution Index in a Tidal Stream Using Kriging Analysis. International Journal of Environmental Research and Public Health. 2012; 9(9):3085-3100. https://doi.org/10.3390/ijerph9093085
Chicago/Turabian StyleChen, Yen-Chang, Hui-Chung Yeh, and Chiang Wei. 2012. "Estimation of River Pollution Index in a Tidal Stream Using Kriging Analysis" International Journal of Environmental Research and Public Health 9, no. 9: 3085-3100. https://doi.org/10.3390/ijerph9093085





