Using the Gravity Model to Estimate the Spatial Spread of Vector-Borne Diseases
Abstract
:1. Introduction
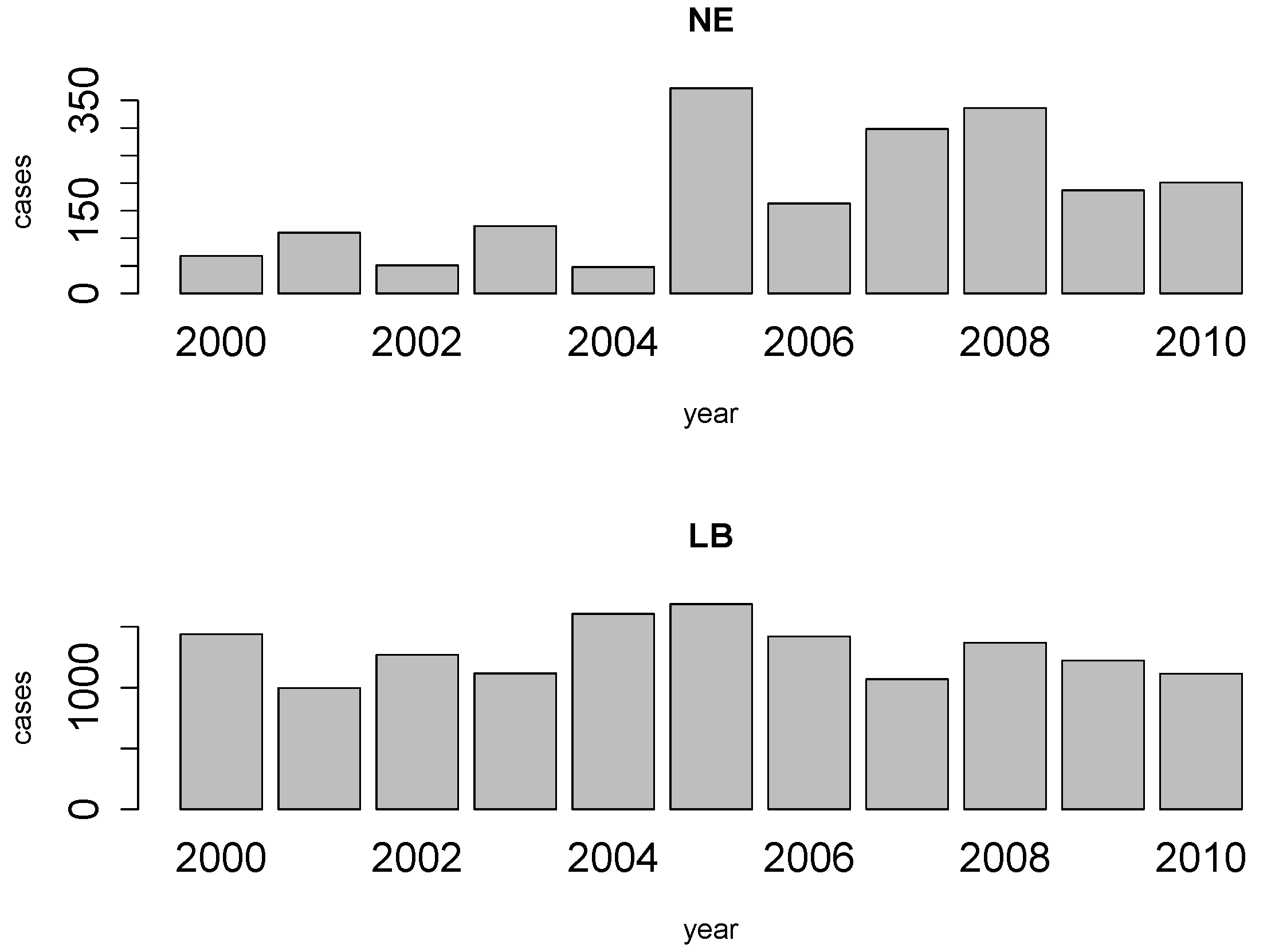
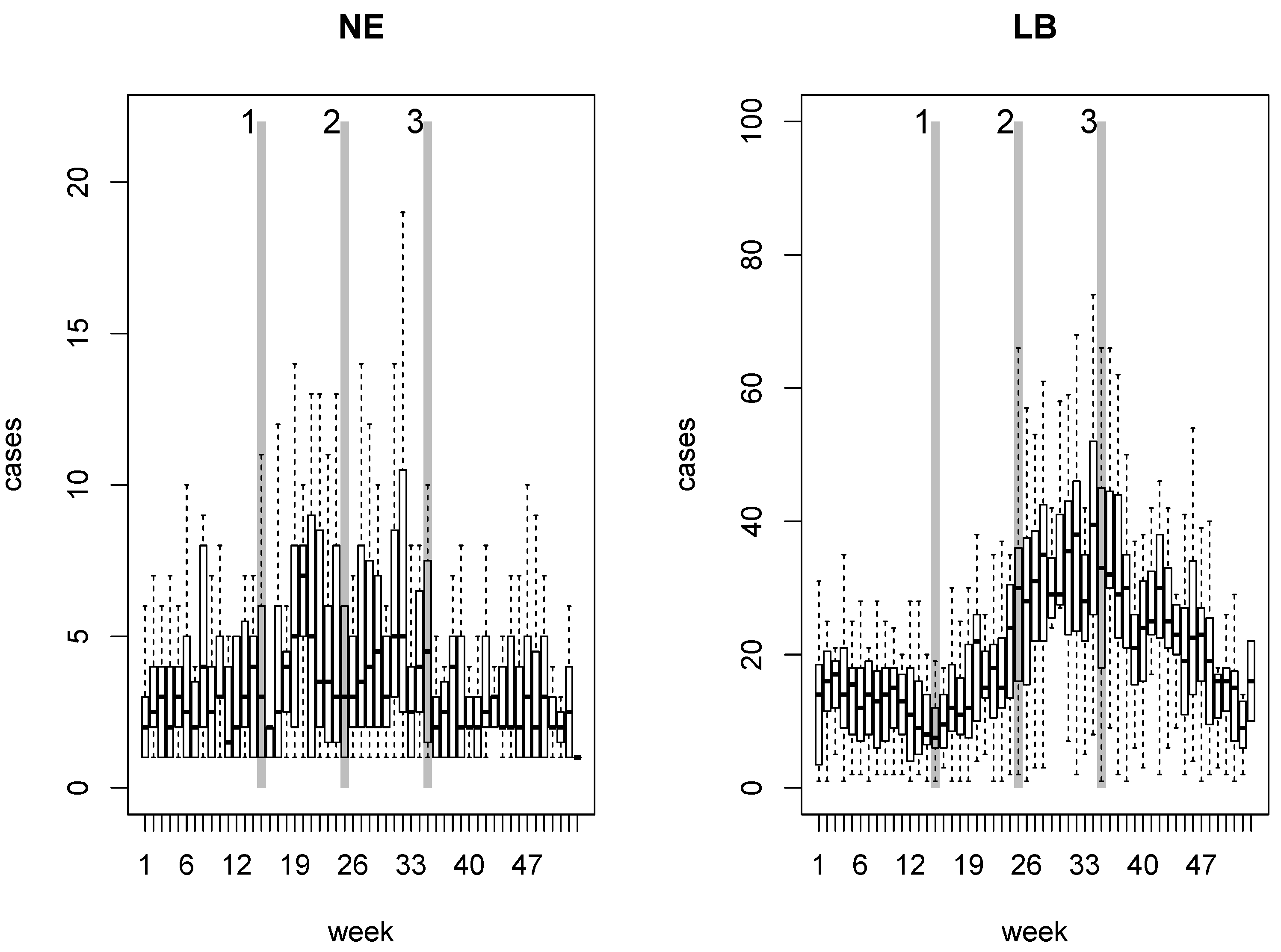
2. NE and LB in Belgium
3. Methods
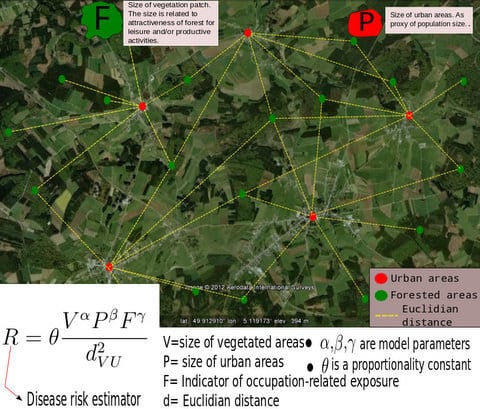
3.1. The Gravity Model
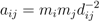
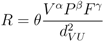
- The surface covered by vegetative systems is also an important determinant of the magnitude of disease risk and incidence [30]. Besides the ecological effects related to the size and degree of fragmentation of ecosystems, these attributes of vegetated areas affect the kind and intensity of interaction humans have with them. For instance, the size of vegetated areas is an important determinant of the attraction value of green areas [31].
- Accounting for human activities and their relation to disease risk is a complex matter [32] and no single model element is able to represent this complexity. Nonetheless, it is known that certain occupational groups are highly exposed to tick-bites and/or rodent-borne pathogens. Case-control studies report that foresters, hunters, farmers, amongst other professions, present specially high disease risk as consequence of intensive interaction with the habitat of vector organisms [33,34,35,36]. The connection between occupation and disease risk supports the consideration of the variable F in the model as proxy of the exposure to NE and LB pathogens linked to professional activities, as it represents the share of activities like forester, hunter or ranger in the economic structure of the municip
3.2. Disease Risk Estimator
 is the EBE for municipality i, θi was calculated as the ratio between the number of cases to person-years at risk (n) in municipality i.
is the EBE for municipality i, θi was calculated as the ratio between the number of cases to person-years at risk (n) in municipality i.  and âi are the prior mean and variance of relative risk, respectively, calculated over municipalities adjacent to i.
and âi are the prior mean and variance of relative risk, respectively, calculated over municipalities adjacent to i. 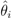 were computed for NE and LB for all municipalities. The estimation of model parameters was done on a sample of 10% of the municipalities. The sample municipalities were chosen such that the whole range of variability of EBE values was represented. The adequacy of the model was tested then against the totality of municipalities.
were computed for NE and LB for all municipalities. The estimation of model parameters was done on a sample of 10% of the municipalities. The sample municipalities were chosen such that the whole range of variability of EBE values was represented. The adequacy of the model was tested then against the totality of municipalities. 3.3. Area and Location of Vegetative Systems
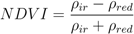

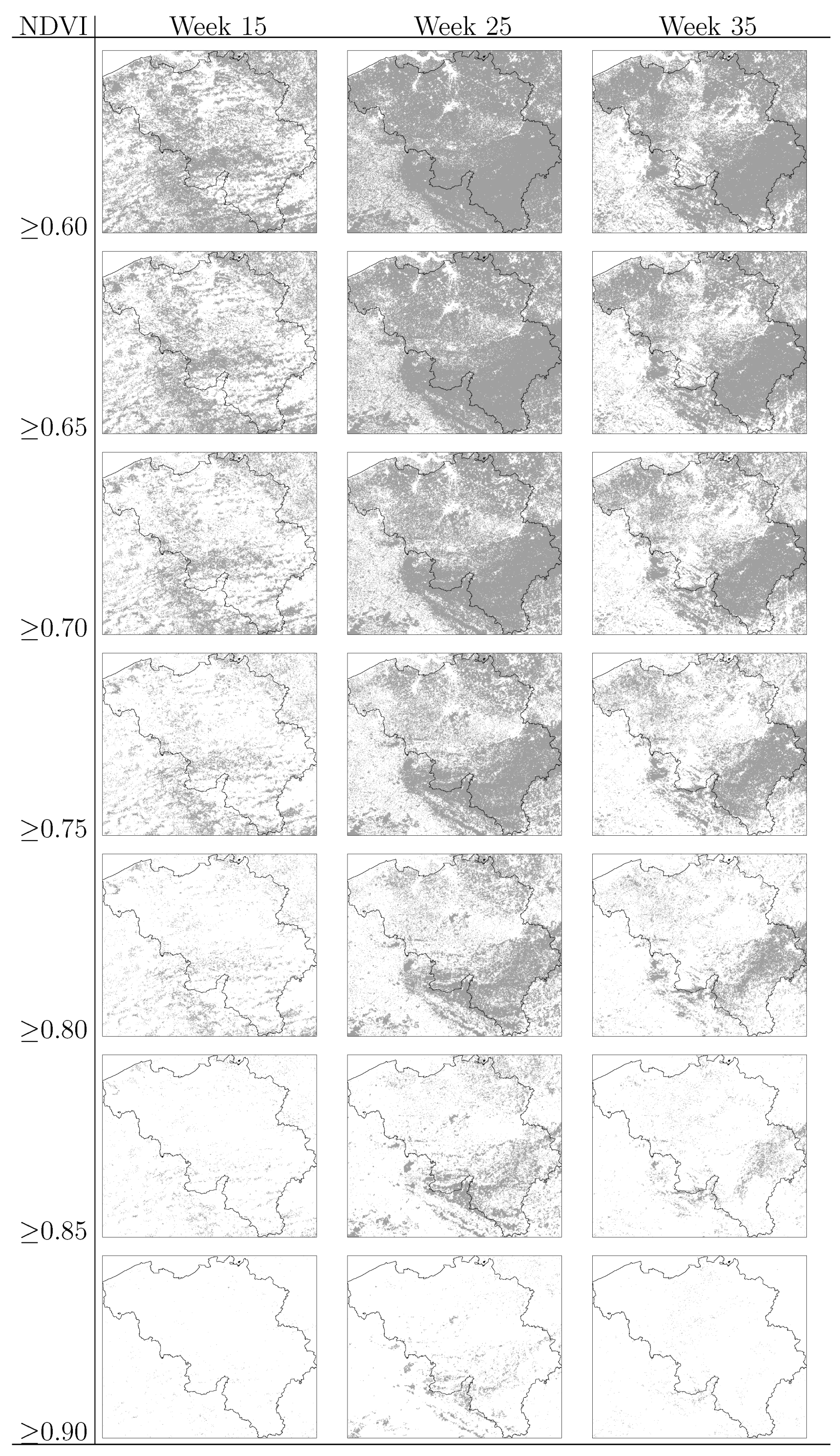
3.4. Human Population

4. Results
4.1. Disease Risk
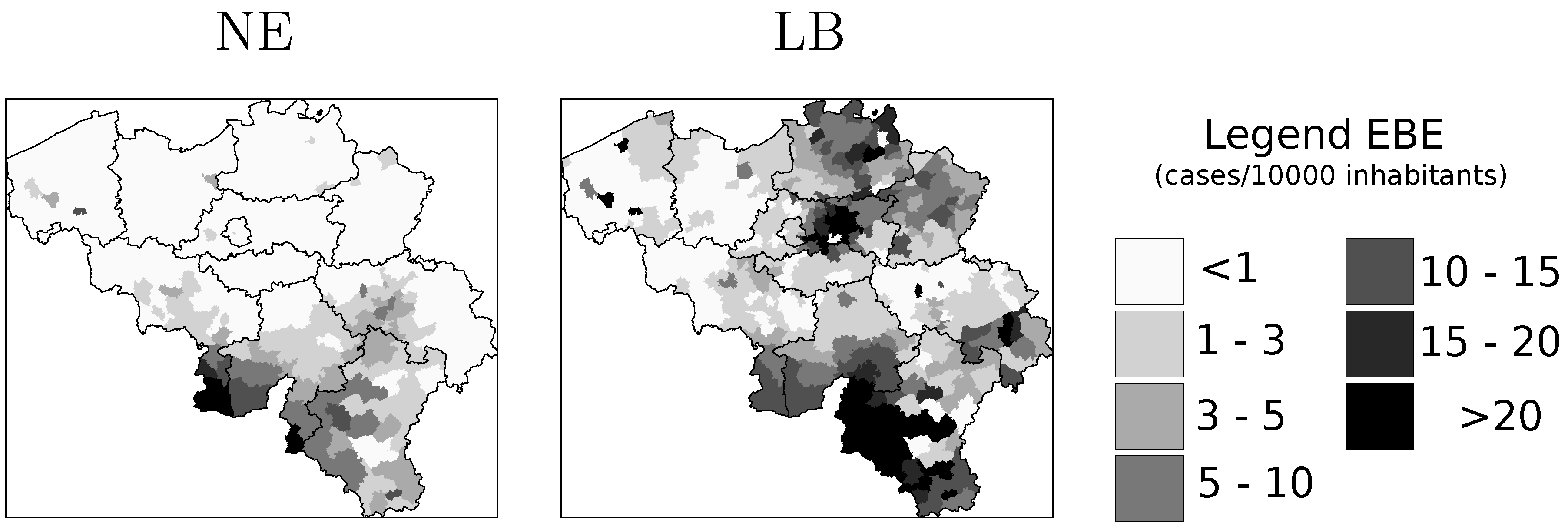
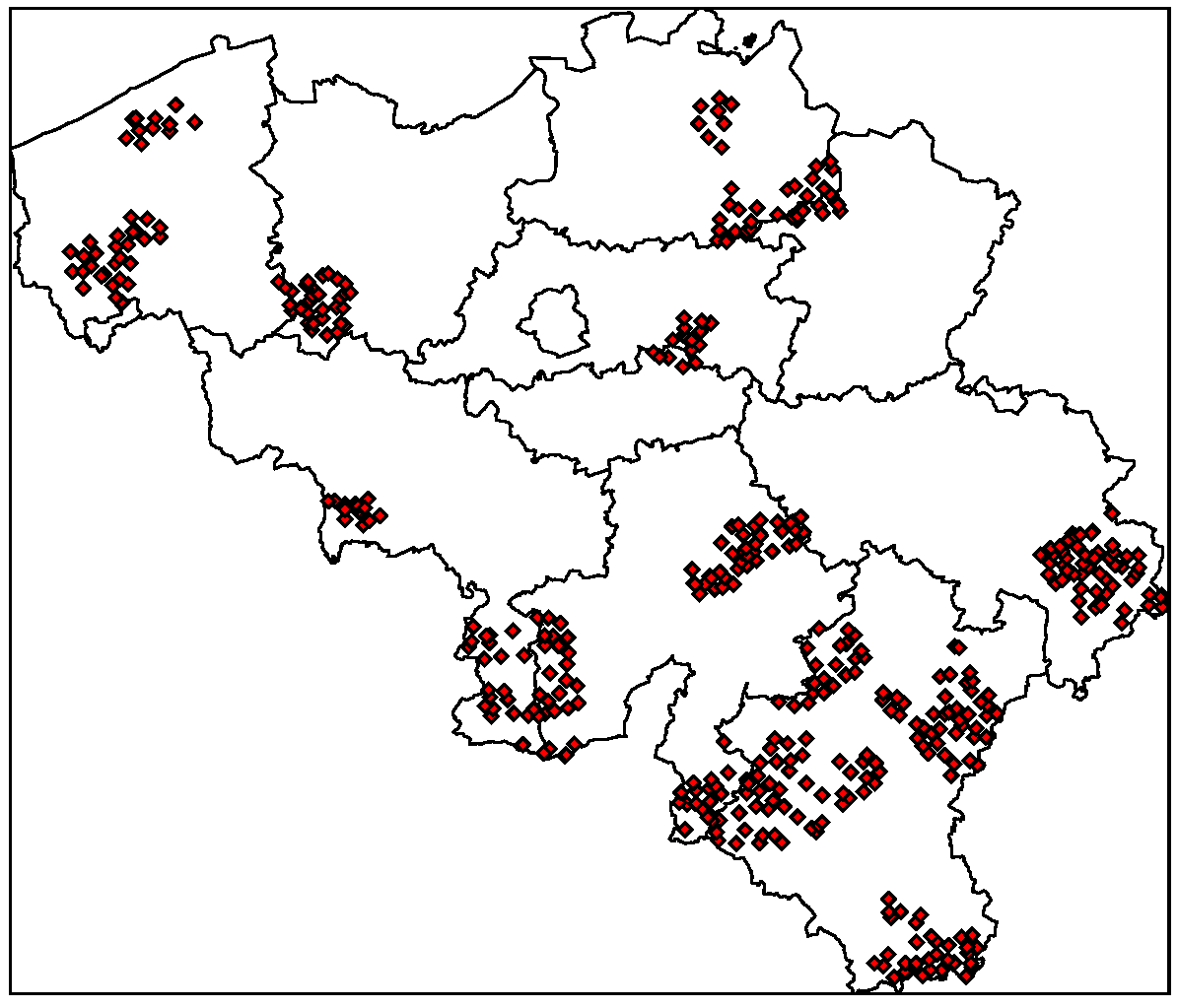
4.2. Model Selection

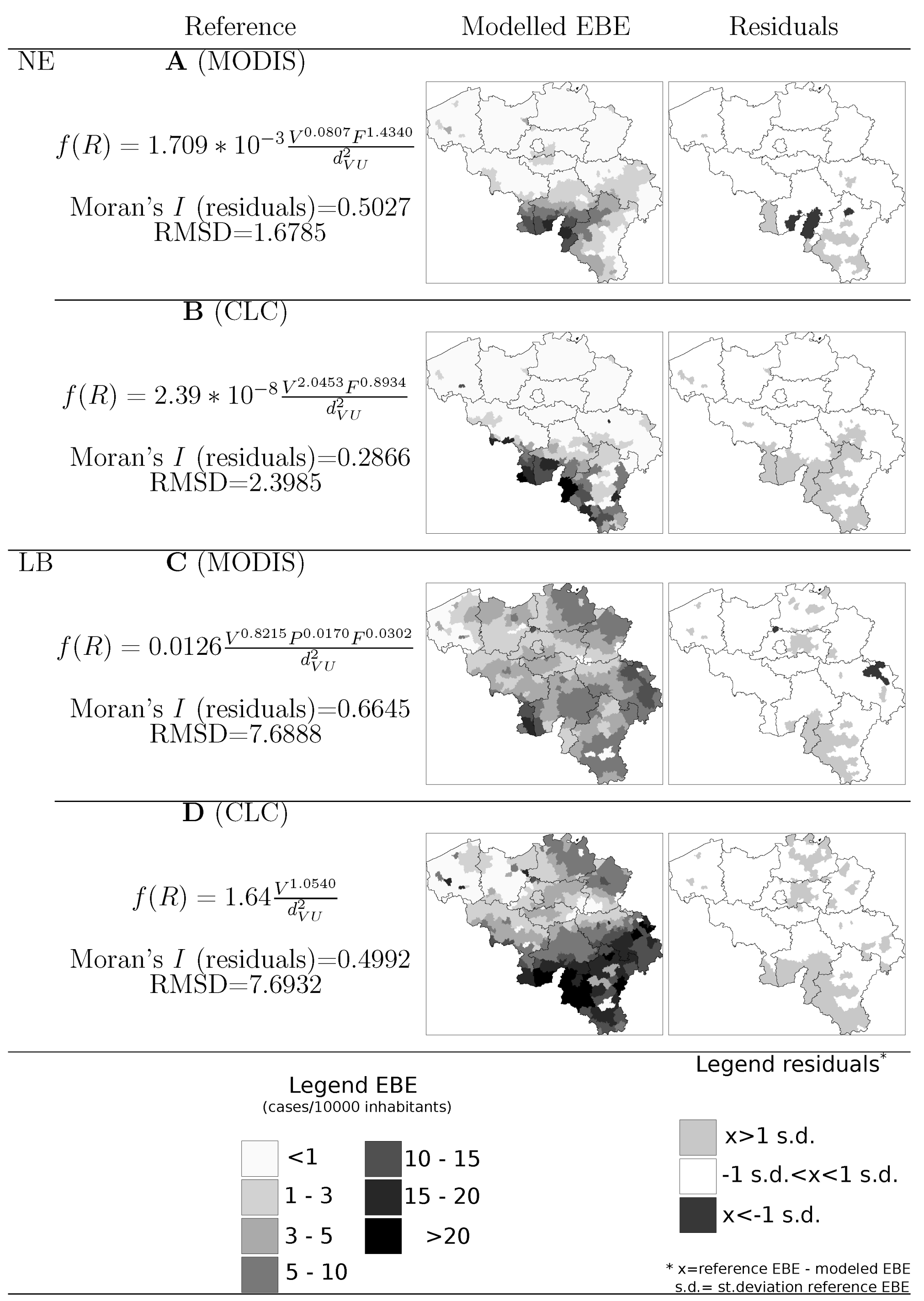
5. Discussion
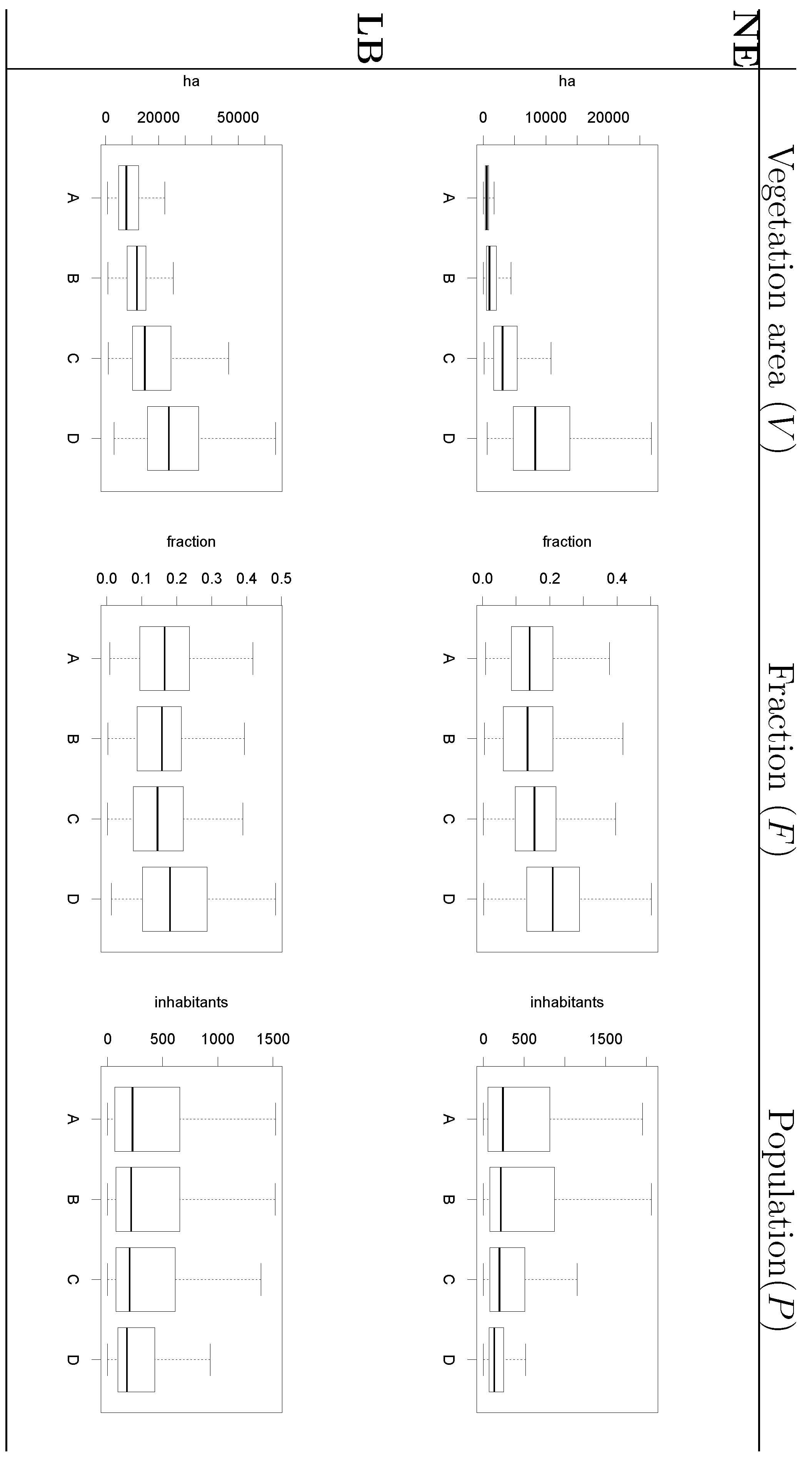

6. Conclusions
- Information on location, size and composition of vegetated areas is of great importance in modelling the spatial spread of NE, LB and other VBD. Our results show the suitability of both static (land cover maps) and dynamic (space-borne datasets) data sources to derive that information and incorporate it as input of the models.
- Accounting for habitat conditions is of paramount importance when attempting to model VBD. Nevertheless, the models should be enriched by including variables that may come from domains different than ecology or biophysics but that inform on human exposure to pathogens. In the particular case of NE and LB, previous studies highlighted the elevated risk associated to certain occupational groups. Our results showed that data on the number of active companies per branch of the economy at municipal level can provide a significant covariate of risk grade.
- Spatial interaction models have been applied in a large variety of domains where distance and attracting attributes of entities are relevant. The results obtained in this study support the idea of adopting GM or other forms of spatial interaction analysis to model the spread of NE and LB risk and encourage the investigation of the applicability of spatial interaction models in the study of other VBD.
Acknowledgments
References
- Bailey, T.; Gatrell, A. Interactive Spatial Data Analysis; Longman: Essex, England, 1996. [Google Scholar]
- Mailles, A.; Sin, M.; Ducoffre, G.; Heyman, P.; Koch, J.; Zeller, H. Larger Than Usual Increase in Cases of Hantavirus Infections in Belgium, France and Germany. Available online: www.eurosurveillance.org/ViewArticle.aspx?ArticleId=2754 (accessed on 20 July 2012).
- Rizzoli, A.; Hauffe, H.; Carpi, G.; Vourc’h, G.; Neteler, M.; Rosa, R. Lyme Borreliosis in Europe. Available online: http://www.eurosurveillance.org/ViewArticle.aspx?ArticleId=19906 (accessed on 9 August 2012).
- Lindgren, E.; Andersson, Y.; Suk, J.; Sudre, B.; Semenza, J. Monitoring EU emerging infectious disease risk due to climate change. Science 2012, 336, 418–419. [Google Scholar]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar]
- Belgian Federal Government. Structuur van de Bevolking. Available online: statbel.fgov.be/nl/statistieken/cijfers/bevolking/index.jsp (accessed on 20 July 2012).
- Clement, J.; Maes, P.; van Ypersele de Strihou, C.; van der Groen, G.; Barrios, J.M.; Verstraeten, W.W.; van Ranst, M. Beechnuts and outbreaks of nephropathia epidemica (NE): Of mast, mice and men. Nephrol. Dial. Transplant. 2010, 25, 1740–1746. [Google Scholar]
- Clement, J.; Maes, P.; van Ypersele de Strihou, C.; van der Groen, G.; Barrios, J.M.; Verstraeten, W.W.; van Ranst, M. Relating increasing hantavirus incidences to the changing climate: The mast connection. Int. J. Health Geogr. 2009, 8, 1–11. [Google Scholar]
- Ducoffre, G. Surveillance des Maladies Infectieuses par un Réseau de Laboratoires de Microbiologie 2009. Tendances Epidémiologiques 1983–2008. Available online: www.iph.fgov.be/epidemio/epifr/plabfr/plabanfr/index09.htm (accessed on 20 July 2012).
- Nijkamp, P. Reflections on gravity and entropy models. Reg. Sci. Urban Econ. 1975, 5, 203–225. [Google Scholar] [CrossRef]
- Roy, J.; Thill, J.C. Spatial interaction modelling. Pap. Reg. Sci. 2003, 83, 339–361. [Google Scholar]
- Potapov, A.; Muirhead, J.R.; Lele, S.R.; Lewis, M.A. Stochastic gravity models for modeling lake invasions. Ecol. Modell. 2011, 222, 964–972. [Google Scholar]
- Ferrari, M.; Björnstad, O.; Partain, J.; Antonovics, J. A gravity model for the spread of a pollinator-borne plant pathogen. Am. Nat. 2006, 168, 294–303. [Google Scholar]
- Guagliardo, M. Spatial accessibility of primary care: Concepts, methods and challenges. Int. J. Health Geogr. 2004, 3, 1–13. [Google Scholar]
- Signorino, G.; Pasetto, R.; Gatto, E.; Mucciardi, M.; La Rocca, M.; Mudu, P. Gravity models to classify commuting vs. resident workers. An applications to the analysis of residential risk in a contaminated area. Int. J. Health Geogr 2011, 10, 1–10. [Google Scholar]
- Xia, Y.; Björnstad, O.; Grenfell, B. Measles metapopulation dynamics: A gravity model for epidemiological coupling and dynamics. Am. Nat. 2004, 164, 267–281. [Google Scholar]
- Li, X.; Tian, H.; Lai, D.; Zhang, Z. Validation of the gravity model in predicting the global spread of influenza. Int. J. Environ. Res. Public Health 2011, 8, 3134–3143. [Google Scholar]
- Viboud, C.; Björnstad, O.; Smith, D.; Simonsen, L.; Miller, M.; Grenfell, B. Synchrony, waves, and spatial hierarchies in the spread of influenza. Science 2006, 312, 447–451. [Google Scholar]
- Tuite, A.; Tien, J.; Eisenberg, M.; Earn, D.; Ma, J.; Fisman, D. Cholera epidemic in Haiti, 2010: Using a transmission model to explain spatial spread of disease and identify optimal control interventions. Ann. Int. Med. 2011, 154, 593–601. [Google Scholar]
- Dreassi, E.; Biggeri, A. Incorporating gravity model principles into disease mapping. Biom. J. 2003, 45, 207–217. [Google Scholar]
- Carter, R.; Mendis, K.; Roberts, D. Spatial targeting of interventions against malaria. Bull. World Health Org. 2000, 78, 1401–1411. [Google Scholar]
- Crowcroft, N.; Infuso, A.; Ilef, D.; Le Guenno, B.; Desenclos, J.C.; van Loock, F.; Clement, J. Risk factors for human hantavirus infection: Franco-Belgian collaborative case-control study during 1995-6 epidemic. Br. Med. J. 1999, 318, 1737–1738. [Google Scholar]
- Glass, G.; Schwartz, B.; Morgan, J.; Johnson, D.; Noy, P.; Israel, E. Environmental risk factors for Lyme disease identified with geographic information systems. Am. J. Public Health 1995, 85, 944–948. [Google Scholar]
- Ostfeld, R.; Glass, G.; Keesing, F. Spatial epidemiology: An emerging (or re-emerging) discipline. Trends Ecol. Evol. 2005, 20, 328–336. [Google Scholar]
- Sin, M.; Stark, K.; van Treeck, U.; Dieckmann, H.; Uphoff, H.; Hautmann, W.; Bornhofen, B.; Jensen, E.; Pfaff, G.; Koch, J. Risk factors for hantavirus infection in Germany, 2005. Emerg. Infect. Dis. 2007, 13, 1364–1366. [Google Scholar]
- Smith, G.;Wileyto, E.; Hopkins, R.; Cherry, B.; Maher, J. Risk factors for Lyme disease in Chester county, Pennsylvania. Public Health Rep. 2001, 116, 146–156. [Google Scholar]
- Van Loock, F.; Thomas, I.; Clement, J.; Ghoos, S.; Colson, P. A case-control study after a hantavirus infection outbreak in the south of Belgium: Who is at risk? Clin. Infect. Dis. 1999, 28, 834–839. [Google Scholar]
- Zeman, P. Objective assessment of risk maps of tick-borne encephalitis and Lyme borreliosis based on spatial patterns of located cases. Int. J. Epidemiol. 1997, 26, 1121–1130. [Google Scholar]
- Roovers, P.; Hermy, M.; Gulinck, H. Visitor profile, perceptions and expectations in forests from a gradient of increasing urbanisation in central Belgium. Lands. Urban Plan. 2002, 59, 129–145. [Google Scholar]
- Barrios, J.M.; Verstraeten, W.W.; Maes, P.; Aerts, J.M.; Farifteh, J.; Coppin, P. Relating land cover and spatial distribution of nephropathia epidemica and Lyme borreliosis in Belgium. Int. J. Environ. Health Res. 2012. [Google Scholar] [CrossRef]
- de Vries, S.; Goossen, M. Modelling recreational visits to forests and nature areas. Urban Fory & Urban Green 2002, 1, 5–14. [Google Scholar]
- Randolph, S. Human Activities Predominate in Determining Changing Incidence of Tick-borne Encephalitis in Europe. Available online: www.eurosurveillance.org/ViewArticle.aspx?ArticleId= 19606 (accessed on 20 July 2012).
- Lindgren, E.; Jaenson, T.G.T. Lyme Borreliosis in Europe. Influences of Climate and Climate Change, Epidemiology, Ecology and Adaptation Measures; Technical report; World Health Organization: Geneva, Switzerland, 2006. [Google Scholar]
- Tomao, P.; Ciceroni, L.; D’Ovidio, M.C.; de Rosa, M.; Vonesch, N.; Iavicoli, S.; Signorini, S.; Ciarrocchi, S.; Ciufolini, M.G.; Fiorentini, C.; et al. Prevalence and incidence of antibodies to Borrelia burgdorferi and to tick-borne encephalitis virus in agricultural and forestry workers from Tuscany, Italy. Eur. J. Clin. Microbiol. Infect. Dis. 2005, 24, 457–463. [Google Scholar]
- van Charante, A.M.; Groen, J.; Mulder, P.; Rijpkema, S.; Osterhaus, A. Occupational risks of zoonotic infections in Dutch forestry workers and muskrat catchers. Eur. J. Epidemiol. 1998, 14, 109–116. [Google Scholar]
- Vapalahti, K.; Paunio, M.; Brummer-Korvenkontio, M.; Vaheri, A.; Vapalahti, O. Puumala virus infection in Finland: Increased occupational risk for farmers. Am. J. Epidemiol. 1999, 149, 1142–1151. [Google Scholar]
- Marshall, R.J. Mapping disease and mortality rates using empirical Bayes estimators. J. R. Stat. Soc. Series C, Appl. Stat. 1991, 40, 283–294. [Google Scholar]
- European Commission–Eurostat. Population. Available online: epp.eurostat.ec.europa.eu/portal/page/portal/population/data/database (accessed on 20 July 2012).
- European Environment Agency. CORINE Land Cover 2000. Available online: www.eea.europa.eu/themes/landuse/clc-download (accessed on 20 July 2012).
- USGS-Land Processes Distributed Active Archive Center. Surface reflectance 8-Day L3 Global 250 m. Available online: lpdaac.usgs.gov/products/modis products table/surface reflectance/8 day l3 global 250m/mod09q1 (accessed on 26 May 2011).
- Bossard, M.; Feranec, J.; Otahel, J. CORINE Land Cover Technical Guide-Addendum 2000; Technical report 40; European Environment Agency: Copenhagen, Denmark, 2000. [Google Scholar]
- Clercq, E.M.D.; Wulf, R.D.; Herzele, A.V. Relating spatial pattern of forest cover to accessibility. Lands. Urban Plan. 2007, 80, 14–22. [Google Scholar]
- Algemene Directie Statiestiek en Economische Informatie. Be.STAT Home. Available online: statbel.fgov.be/nl/statistieken/webinterface/beSTAT home/index.jsp (accessed on 14 January 2012).
- Symonds, M.; Moussalli, A. A brief guide to model selection, multimodel inference and model averaging in behavioural ecology using Akaike´s information criterion. Behav. Ecol. Sociobiol. 2011, 65, 13–21. [Google Scholar]
- Anselin, L. The Moran Scatterplot as an ESDA Tool to Assess Local Instability in Spatial Association. In Spatial Analytical Perspectives on GIS: GISDATA 4; Fischer, M., Scholten, H.J., Unwin, D., Eds.; Taylor & Francis: London, UK,, 1996; pp. 111–125. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Barrios, J.M.; Verstraeten, W.W.; Maes, P.; Aerts, J.-M.; Farifteh, J.; Coppin, P. Using the Gravity Model to Estimate the Spatial Spread of Vector-Borne Diseases. Int. J. Environ. Res. Public Health 2012, 9, 4346-4364. https://doi.org/10.3390/ijerph9124346
Barrios JM, Verstraeten WW, Maes P, Aerts J-M, Farifteh J, Coppin P. Using the Gravity Model to Estimate the Spatial Spread of Vector-Borne Diseases. International Journal of Environmental Research and Public Health. 2012; 9(12):4346-4364. https://doi.org/10.3390/ijerph9124346
Chicago/Turabian StyleBarrios, José Miguel, Willem W. Verstraeten, Piet Maes, Jean-Marie Aerts, Jamshid Farifteh, and Pol Coppin. 2012. "Using the Gravity Model to Estimate the Spatial Spread of Vector-Borne Diseases" International Journal of Environmental Research and Public Health 9, no. 12: 4346-4364. https://doi.org/10.3390/ijerph9124346