1. Background
Profiling geographic variations in health care need is important for equitable and effective targeting of resources that reflects inequalities in morbidity [
1]. Coronary heart disease (CHD) is an important part of the overall disease burden faced by government health agencies and demonstrates considerable geographic inequality. Assessing prevalence variations between populations and areas for chronic diseases such as CHD is a central aspect of defining health care need. However, prevalence is not necessarily as well recorded as other health outcomes (e.g., mortality, hospitalisations). For example, in some countries such as the US, area prevalence estimates can only be made on the basis of health survey data. Focussed studies, such as the British Regional Heart Study (BRHS) considered by Morris
et al. [
2] may also provide evidence of geographic prevalence variations, but generally provide only limited geographic coverage; thus the BRHS included only 24 British towns. In recent years, prevalence of major conditions (including CHD) treated in primary care in England has been administratively recorded under a system known as the Quality Outcomes Framework (QOF), but not at a disaggregated spatial scale (e.g., for small areas with populations under 10 thousand). However, small area contrasts are important in defining variations in health need within local health authorities.
While treated prevalence totals are only available for local health agencies (known as Primary Care Trusts or PCTs, with 152 such PCTs in England), deaths and hospital admissions for coronary heart disease are available for smaller areas known as wards, of which there are over 8000. As argued above, estimating CHD prevalence at small area level is important, and this paper develops a shared random effect (or common factor) method to pool information regarding spatial morbidity contrasts over multiple indicators (deaths, hospitalizations, prevalence). This provides a summary index for representing small area CHD morbidity which is applied to estimate small area CHD prevalence totals and hence relative prevalence risks (comparing actual to expected prevalence). Geographic variations in latent constructs relevant to population health are typically spatially correlated, and this is recognised in the derivation of the common morbidity factor [
3]. The shared random effect approach also incorporates differences between areas in deprivation levels and other forms of population risk (e.g., ethnic structure). That is, the common factor is partly predicted on the basis of known ecological risk factors or ”multiple causes”, so providing a spatial adaptation of a multiple indicator-multiple cause approach [
4].
An illustration is provided by data for London. London may be disaggregated into 625 small areas known as wards, and into 31 Primary Care Trust areas. Some observed data on CHD are at ward level, namely hospital admissions and mortality totals. However, some data (namely CHD prevalence totals) are only observed for considerably larger PCTs. We wish to obtain a summary index of CHD morbidity (as a shared random effect) using all the observations, and use this index to estimate the disaggregated prevalence totals for the 625 wards.
A fully Bayesian approach is used in specifying the model and in the London case study application. This involves ascribing prior densities to model parameters and updating those densities via the likelihood for the observed data. Iterative Monte Carlo Markov Chain (MCMC) techniques [
5] are used for estimation, as implemented in the WINBUGS program [
6].
2. Modelling Latent Morbidity at the Lower Spatial Scale
Let j = 1, .., NL denote the set of lower level small areas within a particular region, and let i = 1, .., NH denote the set of aggregated higher level areas (e.g., local health authorities) within which the small areas are nested. The available data contain P observed indicators yj = (yj1, .., yjP) at the small area scale (such as small area death totals), and counts Zi = (Zi1, .., ZiQ) (e.g., disease prevalence totals) observed only at the aggregated area scale. However, one aim of the modelling process is to develop estimates zj = (zj1, .., zjQ) of these indicators at a small area scale.
It is assumed that correlations between the observed indicators can be represented by underlying common latent factors f = (f1, .., fR), where R is of typically of much smaller dimension than the total number P + Q of observed indicators. For simplicity, a univariate common factor f = (f1, ...fNL) is considered (i.e. R = 1). In the parlance of factor analysis techniques, the set of observed indicators are proxies for, or ”measures of”, the underlying latent factor.
The first set of small area measurement equations describe the relationship between the observations
yjp (
j = 1, ..,
NL,
p = 1, …,
P) and the latent factor. In population health applications, the indicators are typically discrete counts (e.g., deaths, hospital admissions), assumed either Poisson or binomial, so that a general linear mixed model is appropriate for the measurement equations. In the application here, mortality or admission is infrequent in relation to population at risk, and Poisson sampling is relevant. Expected mortality or admission counts
Ojp are obtained by applying a standard age-sex schedule (for the entire region, providing an internal standard, or for the nation, providing an external standard) to small area populations at risk. Then one has
where
ρjp is the relative risk of outcome
p in small area
j. In the present application, expectations
Ojp are scaled to equal the total of expected counts over all small areas, namely
, so that the region wide average relative risk
ρp for indicator
p is 1 if an internal standard is used.
As is conventional for Poisson responses, a log link is employed [
7]. So one has measurement models for small area indicators
p = 1, ..,
P,where the unique errors
may be necessary for explaining any residual overdispersion. In substantive terms, the
ujp also control for structural influences unrelated to population morbidity per se (e.g., effectiveness of health care services, hospital configuration). Intercepts are not included in
(2), so providing a form of location constraint on the latent variable
f [
8]. The coefficients
λp are typically known as loadings, the specification of which is considered below.
Variations in population morbidity, whether observed or latent, typically display spatial correlation between adjacent areas-unmeasured aspects of population structure relevant to health risk typically straddle administrative boundaries [
9]. However, rather than a priori assume exclusively spatial dependence, the model here determines an appropriate mix between spatial and non-spatial (”exchangeable”) dependence in the latent morbidity construct.
There may also be observed variables (
i.e., known rather than latent risk factors) that are relevant to defining the common morbidity factor. For example, many indices of health need are composites of variables such as unemployment rates, poverty rates, car ownership,
etc. Here a spatial adaptation of the multiple indicators-multiple causes (MIMIC) approach is used, with
L measured causes
xj = (
xj1, ..,
xjL)
′ (such as small area socio-economic or population risk variables) of the latent morbidity index. These influence the latent morbidity index
fj via regression terms
where the regression excludes an intercept, with residuals denoted
Additionally if the xjl are standardised, the absolute size of the β coefficients measures the relative importance of different population risk factors or socio-economic variables in defining the morbidity index.
To allow a mix between spatial and non-spatial dependence in the latent index, define a spatial correlation parameter
k ∈ (0, 1), and assume symmetric spatial interactions
wjh. Also let
f[j] = (
f1, …
fj−1,
fj+1, …,
fNL) denote the collection of morbidity effects for all areas but area
j. Under the scheme of Leroux
et al. [
10], though adapted here to include regression effects, as in
(3.1) (3.2), the expected value of the latent effect in area
j and its variance are
where
is a variance parameter. A value of
k close to 1 indicates high spatial dependence in latent morbidity, while values near zero imply lack of spatial correlation.
The
wjh may incorporate factors such as distances between areas
j and
h. However, in many applications the
wjh simply represent adjacency, namely
wjh =
whj = 1 if areas
h and
j are adjacent, zero otherwise. In this case it is relevant to define the neighbourhood
∂j of small area
j, which contains the
mj areas adjacent to area
j, and one then has
. The expectations are then
To uniquely determine the scale of the
f scores, constraints are needed on the loadings
λp, or on the variance
in
(4.2). The first kind involves standardized factors, with
, as in the spatial factor model of Wang and Wall [
11], with all loadings then unknowns. An alternative constraint involves appropriately fixed loadings, such as setting one of the loadings
λp to a particular fixed value, usually 1. The variance
is then an unknown parameter.
3. Methods: Estimating Prevalence at Small Area Level based on the Morbidity Index
We wish not just to obtain a latent morbidity index, but to use this index to estimate unknown indicator totals (zj1, …, zjQ) (e.g., prevalence totals) for small areas j = 1, …, NL. Estimation of the missing lower area scale data takes account (a) of values of the small area morbidity index f = (f1, …, fNL), and (b) of the known prevalence totals (Zi1, …, ZiQ) for the i = 1, …, NH higher level areas. The small areas are nested within the higher level areas, with Hj ∈ {1, …,NH} denoting the higher level area to which small areas j belong, and the region is defined equivalently by all the higher level areas or all the lower level areas.
Also assumed known are age-sex structures for the small area populations, and from these can be obtained expected totals Ejq of the small area counts zjq. This involves using an external schedule of prevalence rates rqsk for the qth outcome by age k and sex s, and applying this schedule to small area population estimates Pjsk, so that
.
To ensure the estimates of (
zj1,…,
zjQ) take account of the observed prevalence counts
Ziq of the higher level areas they are located in, the Poisson means
Δiq in the likelihood
Ziq ∼
Po(
Δiq) for the higher level observed totals
Ziq are defined by totals of small area means
δjq located within each higher area. Thus let
denote the total mean prevalence counts for large areas
i obtained from the small area model for the
z-indicators.
The small area model (
i.e., the model for the
δjq) can be set up to ensure that the posterior means of the
Δiq equal (to a close approximation) the known higher level totals
Ziq. One way to achieve thus is via a collection of
NH fixed effects
γq,Hj in the model for the
δjq, equivalent to using dummy variables in the small area model for each higher scale area, and providing a Poisson equivalence to the multinomial [
12]. Thus the
zjq for
Hj =
i are multinomial within
Ziq. We also wish the values of the latent morbidity index
fj to influence the multinomial allocation of
Ziq to small areas in a manner analogous to that in
Equation (2). So the small area model is
where
λP+q are additional loadings on the latent spatial morbidity index. Whether they are set to known values or taken as unknowns depends on the identification constraint adopted for the scale of the
fj.
Other priors for (γ1, …,γNH), for example, as random rather than fixed effects, in practice have a very similar consequence. that the means of the Δiq equal (to a close approximation) the known higher level total Ziq. For example, one might use random effect spatial priors, comparable to (4)–(5) but at the higher area level.
In some circumstances, there may be doubts about how far the
Ziq are accurate measures of morbidity, and a constraint to reproduce them may not be advantageous. For example, the prevalence counts obtained under the QOF system in England may under-record prevalence in deprived areas, since the quality of primary care is lower in such areas [
13], this may result in less effective case-finding [
14]. To allow unconstrained estimation of small area prevalence counts, one may use an intercept in the model for
δjq that is not specific to the higher area, namely
This model ensures
, but does not guarantee that
, as the constrained model does.
To recap, the model is a form of spatial structural equation model (SEM) that seeks to estimate small area health outcomes z for which only large area observations Z are available. The model works in practice by using observed small area health indicators y (e.g., mortality from a particular disease) which are likely to be correlated with the missing small area outcomes z (e.g., prevalence of the same disease). The information in the correlated multiple indicators y is summarised in a latent variable f that depends on observed area risk factors x, but is also spatially correlated, reflecting spatial clustering in unobserved area risk factors. The decomposition of large area totals Z to small areas is based on the latent variable f, and the decomposition can be constrained so that total small area prevalences zj sum to the known Zi for large area i within which areas j are located. It seems reasonable to use socioeconomic variables x as causes of variability in f, but another strategy would be to use small area socioeconomic variables as additional indicators of the latent variable.
4. CHD Morbidity in London: Data
The motivating case study illustrating the above methodology involves derivation of a univariate index of CHD morbidity (
i.e. R = 1) for London small areas using
P = 4 observed small area health indicators, and a single health indicator (
Q = 1) observed only at an aggregated area scale. The two area scales are wards and Primary Care Trusts (PCTs): there are
NL = 625 wards and
NH = 31 PCTs in London. The first two small area indicators (
yj1, yj2) are male and female CHD deaths over 2004–2006, while (
yj3, yj4) are male and female hospitalisations for CHD over three financial years 2003–2004 to 2005–2006. Expected deaths and hospitalisations
Ojp in
(2) are based on London wide death and hospitalisation rates specific to gender and five year age bands.
CHD prevalence totals
Zi (for 2004–2005 and 2005–2006 combined) are observed only for PCTs, but one goal of the model is to estimate missing small area CHD prevalence totals
zj. Expected CHD prevalence totals
Ejq =
Ej at ward level in
(7.2) are obtained with an external schedule of CHD prevalence rates by age and sex, and applying this schedule to small area population estimates (here 2005 intercensal estimates of ward populations developed by the UK Office of National Statistics). The external schedule used is based on the 2003 Health Survey for England [
15], with the expectations
Ej scaled so that the London wide standard prevalence ratio is 1 (
i.e., the total of observed prevalence counts
Zi across all London PCTs equals the total of expected prevalence counts
Ej over all London wards).
In the multiple cause sub-model (3), there are
L = 3 socio-economic indicators of population CHD risk. These are
x1 = average weekly household income in 2001–2002 [
16],
x2 = proportion of population of south Asian ethnicity, 2001 Census [
17,
18], and
x3 = estimated ward level smoking prevalences [
19]. These predictors are converted to standardised form so that their relative importance can be assessed.
5. CHD Morbidity in London: Models
Two models are compared. One assumes intercepts in the small area prevalence model that vary by PCT, as in
(7.2). The other is unconstrained, as in
(8). Identifiability is achieved by setting
λP+1 =
λ5 = 1, so that
is an unknown, the inverse variance
is accordingly assigned a Gamma(1,1) prior. To ensure the model produces a positive index of CHD morbidity, the remaining
λp parameters also follow Gamma(1,1) priors [
20]. Fixed effect parameters, namely
β parameters in (3) and
γ parameters in
(7.2) and
(8) are assigned diffuse
N(0, 100) priors, while a uniform prior
k ∼
U(0, 1) is assumed for the spatial correlation coefficient in (4)–(5).
Comparisons of model fit use the deviance information criterion (
DIC) [
21], obtained as the average deviance plus a complexity measure. The focus is on goodness of fit for the y-indicators (deaths and hospital admissions). Model 1 will automatically fit the higher level (PCT) prevalence data better as it has separate intercepts for each PCT. Model checking is based on the posterior predictive density,
p(
yrep|
y)
, under a mixed predictive approach [
22], where sampled replicates
yrep are based on model means that include replicate samples from random effects (
f and
u effects). Then a mixed-predictive test for area
j and outcome
p has the form
with extreme tail values indicating poorly fitted cases. One may compare the proportion of cases under-fitted (
pjp,mix < 0:05) or over-fitted (
pjp,mix > 0:95) with the expected proportions in these two tails (namely 0.05 in each).
Inferences are based on the second halves of two chain runs of 10000 iterations with convergence before iteration 5000 assessed using Gelman-Rubin scale reduction factors [
23].
Table 1 presents model fit and checking criteria. It can be seen that model 1 (ward totals constrained to reproduce the QOF totals at PCT level) has a lower DIC, and satisfactory predictive performance.
Table 2 summarises parameter estimates under the two models.
The estimated
k coefficients in
Table 2 indicate a high spatial correlation in the latent CHD morbidity index under both models. The estimated
βl parameters from the multiple cause regression (3) show income differences between wards to be the most important known influence on the index, though concentrations of south Asian ethnic groups are also important. As expected, higher income levels are negatively associated with morbidity (so the 95% interval for the coefficient
β1 is confined to negative values). The importance of area socioeconomic status to CHD outcomes is confirmed by other studies [
24,
25].
The income effect is weaker in the constrained model. This is likely to reflect discrepancies in some deprived parts of London between officially recorded prevalence (used as a constraint in model 1), and what would be expected on the basis of socioeconomic structure. Examples are the apparently low prevalence in some deprived areas in inner South East London. The consequence is that the effect of income is deflated, providing an example of measurement error affecting regression estimates.
Table 3 compares prevalence (in the higher level PCT areas) based on the official QOF totals, with average income levels in such areas (weekly income in hundreds of pounds). Outliers in the negative relation between prevalence and income (there is a-0.50 correlation between PCT ranks for prevalence risk and for income, even though using official CHD prevalence data) include the deprived inner SE London area of Southwark. The latter area has the sixth lowest income, but also low measured prevalence. So while the DIC criterion prefers model 1, the geographic prevalence pattern implied by the unconstrained model 2 might be preferred on the basis of epidemiological arguments.
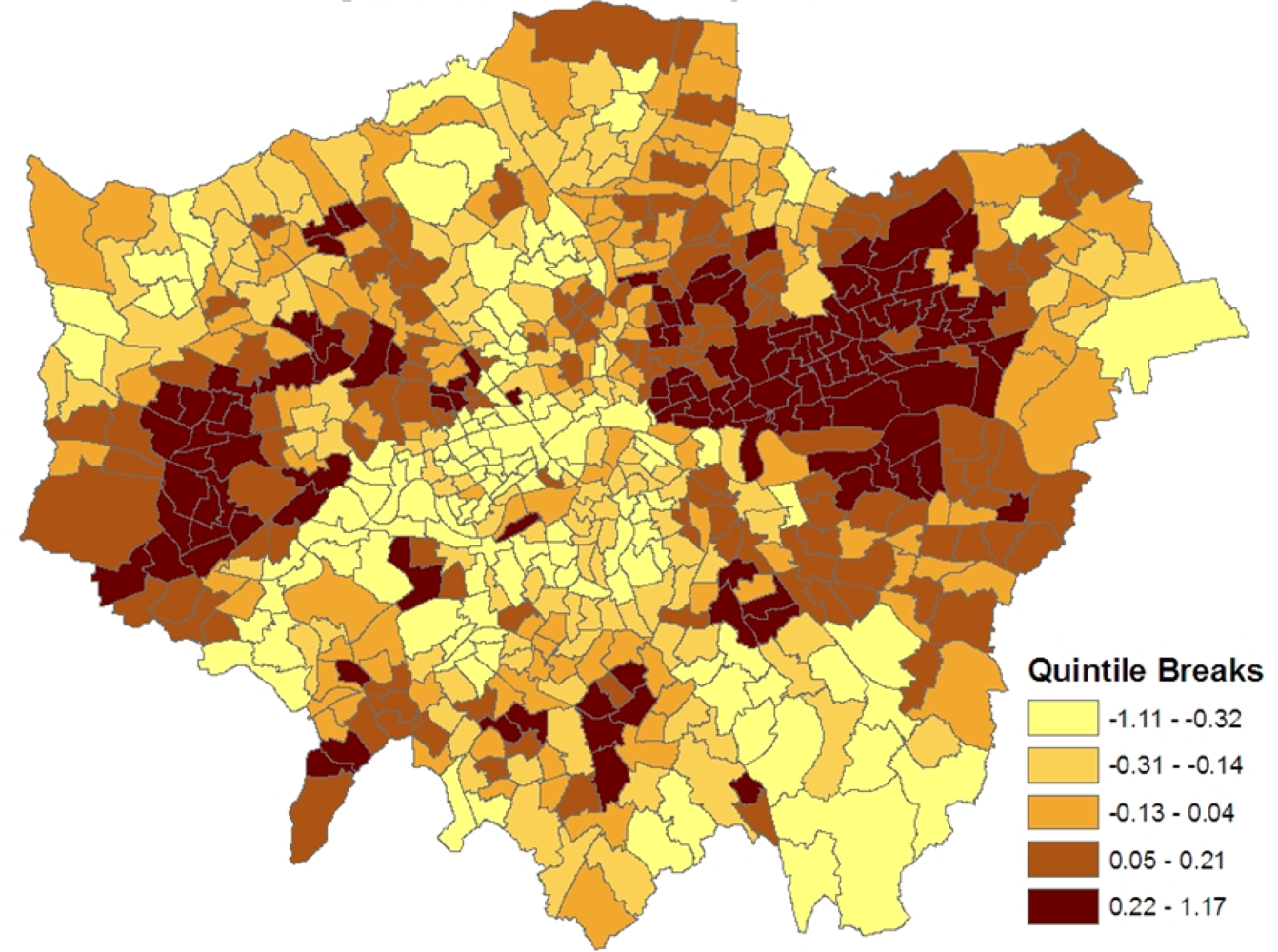
Figure 1 shows the spatial patterning of the CHD morbidity scores in model 1, higher values are in inner east (though not central) London and in certain parts of west London.
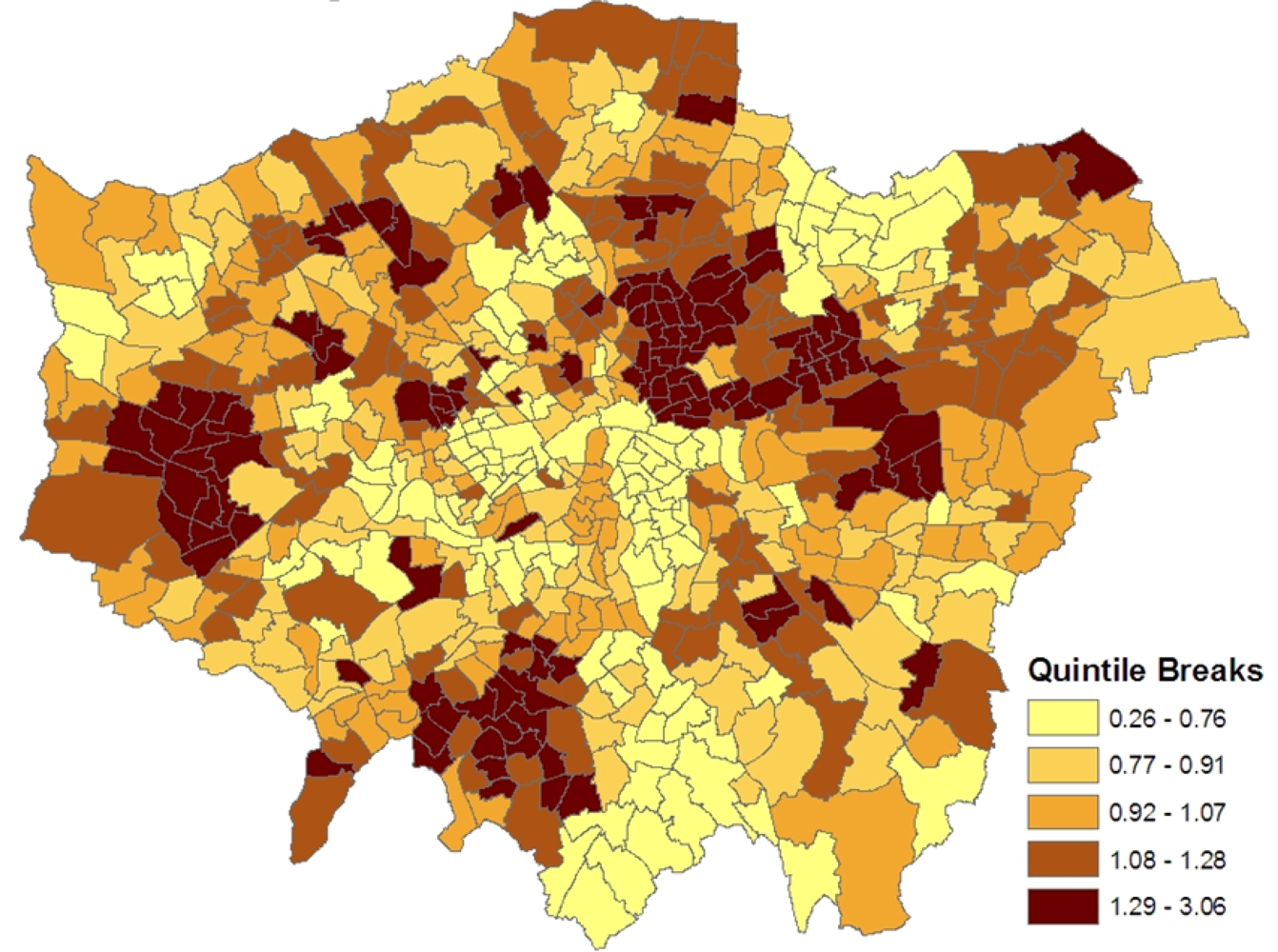
Figure 2 maps the estimated ward level prevalences in terms of relative risks under the constrained model 1, namely the posterior means of
ξj =
zj/
Ej. For policy purposes, the probability that a small area has significantly higher relative risk and thus possibly needs special resources is important. Therefore the marginal variance
ω2 =
var(
ξj) is monitored during the MCMC run, and the standardized relative risks (SRRs)
are also monitored. High posterior means for these SRRs (e.g., SRRs above 1 or 2, namely 1 or 2 standard deviations above average) indicate significantly elevated prevalence, while low values (under −1, or under −2) indicate significantly low prevalence.
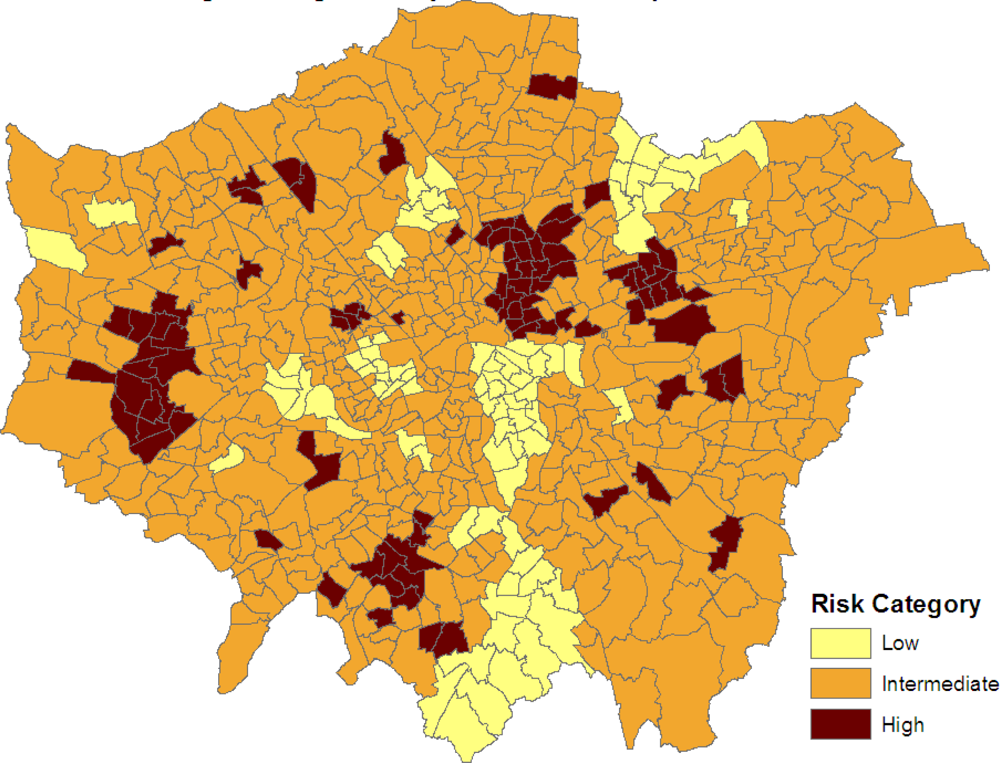
Figure 3 maps the three categories:
SRRj > 1, −1
< SRRj < 1 and
SRRj < −1. Clusters of elevated risk are now clearly apparent.
6. Discussion
Estimates of prevalence at small area level are often necessary, as prevalence is less likely to be routinely reported for such areas, whereas outcomes such as mortality and hospitalization often are. Prevalence totals may, however, be reported for relatively aggregated large areas, either from health surveys, or (in the case of the UK) systems of chronic disease monitoring in primary care. The present paper has employed a common spatial factor model to disaggregate large area CHD prevalence totals to small areas. Various forms of common spatial factor model have been proposed for spatial health outcomes epidemiology. For example, Hogan & Tchernis [
26] develop a small area measurement model for a socioeconomic deprivation score, while Liu
et al. [
27] develop a spatial structural equation model linking health outcomes to spatially correlated latent indices.
The present paper includes three main extensions on such work: first, it allows for known risk factors to influence the composite index via a multiple cause sub-model, second, it allows the data to determine the extent of spatial correlation rather than presuming a priori that latent factors are necessarily spatially dependent, and third, it applies the model to estimate missing health outcomes at a lower area scale (CHD prevalence for wards in the London case study), when observations on such outcomes are only available at a higher scale (PCTs in the London study). The essence of the method is to use all available lower scale information (both from levels of related health outcomes y and from measures of socioeconomic structure x) to provide a reasonable imputation of the missing outcomes z at the lower scale.
The case study has considered deaths and hospital admissions for CHD as the lower scale observed data (the y-variables), and a single higher scale outcome (CHD prevalence), with x-variables (causes) being income, ethnicity and smoking. It has also had a primarily urban focus, being confined to London. Under a broader geographic focus (including rural small areas), it might be relevant to consider adding an urban-rural indicator to the x-variables.
As demonstrated in
Figure 3, one application of the modelling scheme is to highlight small areas with significantly elevated prevalence. This is important for prioritizing resourcing and intervention, and is based on a method that seeks to make use of all relevant information (comorbid outcomes, area social structure, and the spatial configuration of small areas). By contrast, many other health needs measures used to distribute resources are based simply on socioeconomic variables (e.g., the Jarman score) [
28], or on regressions of single health indicators (e.g., hospitalizations) on socioeconomic variables [
29], when multiple indicators may in fact be relevant. Existing methods also neglect spatial clustering in unobserved risk factors.
The methodology set out here has potential application to small area prevalence estimation for other chronic diseases, though the appropriate mix of y and x-variables would be different. For example, the Quality Outcomes Framework system in the UK monitors prevalence of several chronic diseases. In particular, PCT (higher scale) level counts of the prevalence of serious mental illness (SMI) are available, but one may seek ward level measures of SMI prevalence. The available y-indicators in this situation might be small area hospital admissions for conditions such as schizophrenia and bipolar disorder, while x-variables would include indicators of risk for psychiatric morbidity, such as small area income or deprivation, urban-rural status, social capital and so on.
Another potential application area is to use health survey information on disease prevalence, often obtained only for higher scale regional units. For example, the public release version of recent Health Surveys for England only contains prevalence rate estimates for chronic conditions included in the survey (e.g., obesity, diabetes) for 10 Strategic Health Authorities. However, one may wish to use this information in making estimates of such conditions for lower scale geographies such as the 354 local authorities in England. Using survey based regional estimates Zi of prevalence, one can estimate lower scale totals zj, using information on both socioeconomic structure (xj) and related outcomes (yj) at the lower spatial scale. The procedures outlined in the paper could in fact be used to disaggregate survey based estimates Zik which include relevant demographic stratifiers k (e.g. age, sex, ethnicity). Relevant spatial SEM coefficients (β and λ parameters) may well differ between demographic category. For example, one might seek to disaggregate survey-based regional estimates of diabetes by ethnicity to a lower spatial scale.