A Rainfall- and Temperature-Driven Abundance Model for Aedes albopictus Populations
Abstract
:1. Introduction
2. Material and Methods
2.1. Study Area

2.2. Entomological Data
| Campaign | Trapping season | Ovitrap network | Result | ||||
|---|---|---|---|---|---|---|---|
| Location | Year | Beginning | End | Nb traps | Surface of the trapping area (ha) * | Sampling frequency | Annual max. of the mean number of collected eggs per ovitrap per capture session |
| Nice 1 | 2008 | 25 Mar | 8 Dec | 30 | 328.7 | biweekly | 170 |
| Nice 1 | 2009 | 16 Apr | 9 Dec | 50 | 517.7 | biweekly | 233 |
| Nice 1 | 2010 | 15 Apr | 2 Dec | 50 | 517.7 | biweekly | 462 |
| Nice 1 | 2011 | 21 Apr | 14 Dec | 50 | 517.7 | biweekly | 311 |
| Cagnes-sur-Mer | 2010 | 21 Jun | 15 Nov | 15 | 30.5 | weekly | 177 |
| Cagnes-sur-Mer | 2011 | 28 Mar | 28 Nov | 18 | 41.6 | weekly | 169 |
| La Gaude | 2010 | 16 Jul | 8 Oct | 22 | 17.9 | biweekly | 566 |
| Biot | 2010 | 16 Jul | 8 Oct | 25 | 40.3 | biweekly | 830 |
| Villeneuve-Loubet | 2011 | 6 May | 30 Nov | 15 | 3.8 | biweekly | 1,108 |
| Nice 2 | 2011 | 11 May | 18 Nov | 15 | 2.7 | biweekly | 654 |
2.3. Environmental Data
2.4. Model Description
2.4.1. Aedes albopictus Life Cycle
2.4.2. Modelling Aedes albopictus Population Dynamics
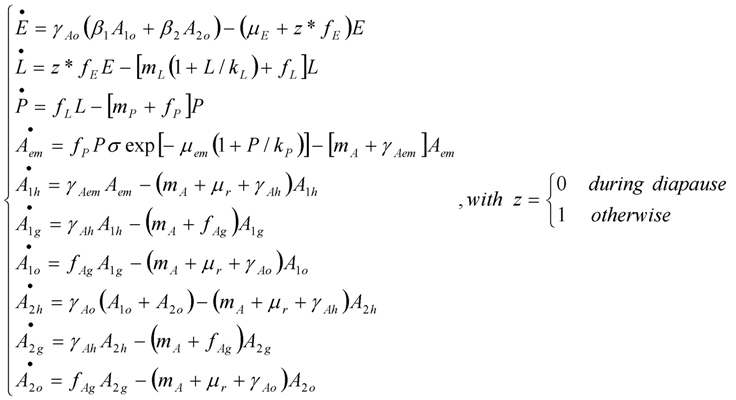
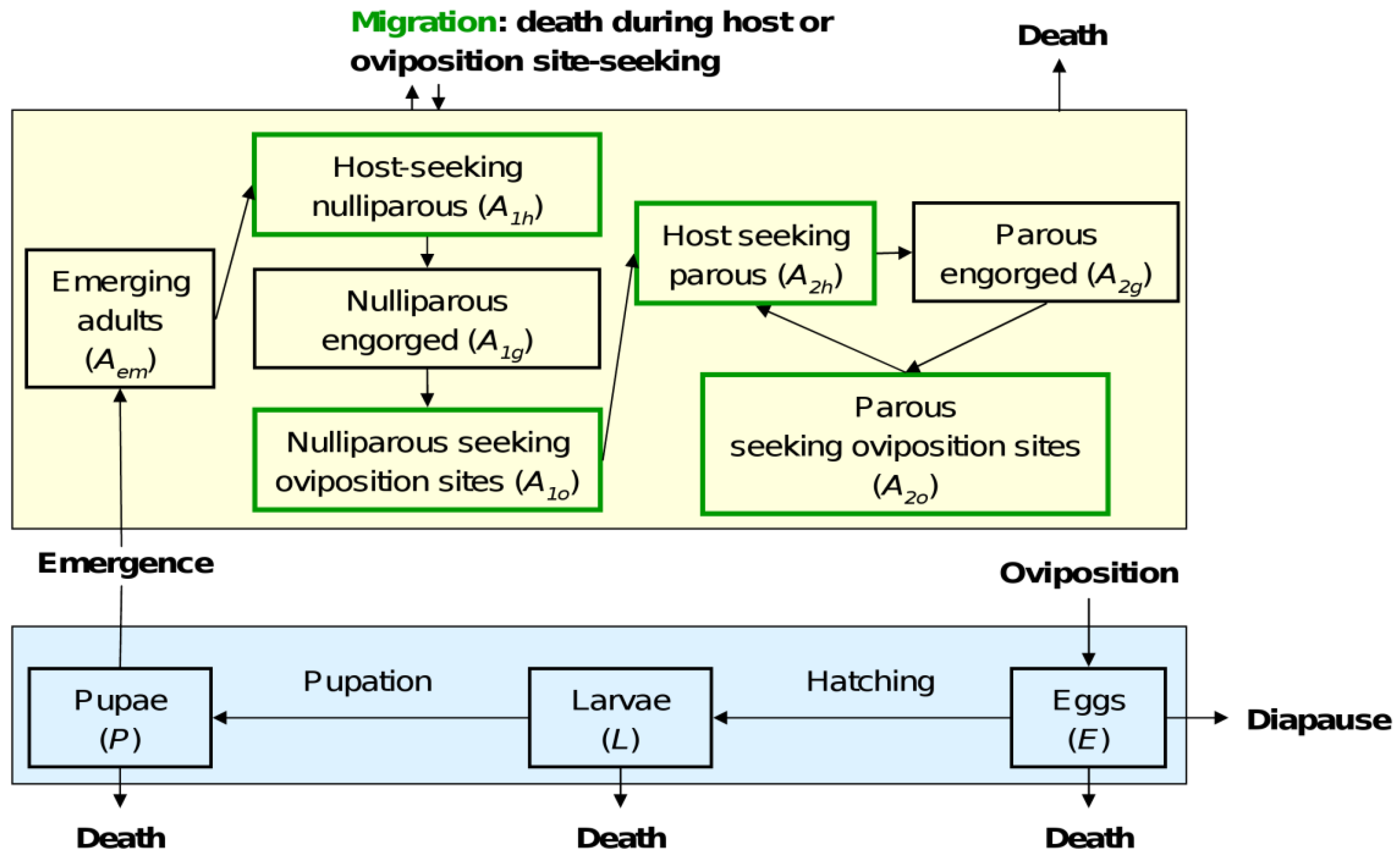
2.4.3. Parameters and Functions of the Model
| Parameter | Definition | Value | Reference |
|---|---|---|---|
| β1 | Number of eggs laid by ovipositing nulliparous females (per female) | 95 | [25] |
| β2 | Number of eggs laid by ovipositing parous females (per female) | 75 | [25] |
| κL | Standard environment carrying capacity for larvae (larvae ha−1) | 250,000 | To our best knowledge |
| κP | Standard environment carrying capacity for pupae (pupae ha−1) | 250,000 | To our best knowledge |
| σ | Sex-ratio at the emergence | 0.5 | [24] |
| μE | Egg mortality rate (day−1) | 0.05 | (Lacour, unpublished) |
| μL | Minimum larva mortality rate (day−1) | 0.08 | (Lacour, unpublished) |
| μP | Minimum pupa mortality rate (day−1) | 0.03 | (Lacour, unpublished) |
| μem | Mortality rate during adult emergence (day−1) | 0.1 | (Lacour, unpublished) |
| μA | Minimum adult mortality rate (day−1) | 0.02 | [25] |
| μr | Adult mortality rate related to seeking behavior (day−1) | 0.08 | To our best knowledge |
| TE | Minimal temperature needed for egg development (°C) | 10.4 | [24] |
| TDDE | Total number of degree-day necessary for egg development (°C) | 110 | (Lacour, unpublished) |
| γAem | Development rate of emerging adults (day−1) | 0.4 | To our best knowledge |
| γAh | Transition rate from host-seeking to engorged adults (day−1) | 0.2 | To our best knowledge |
| γAo | Transition rate from oviposition site-seeking to host-seeking adults (day−1) | 0.2 | To our best knowledge |
| TAg | Minimal temperature needed for egg maturation (°C) | 10 | [24] |
| TDDAg | Total number of degree-days necessary for egg maturation (°C) | 77 | [24] |
| tstart | Start of the favorable season | 10 Mar | [32] |
| tend | End of the favorable season | 30 Sept | [32] |
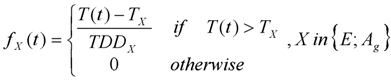
| Function | Definition | Expression |
|---|---|---|
| fE | Transition function from egg to larva | Equation (2) |
| fL | Transition function from larva to pupa | fL(t) = −0.0007. T²(t) + 0.0392. T(t) − 0.3911 |
| fP | Transition function from pupa to emerging adult | fP(t) = 0.0008. T²(t) − 0.0051. T(t) + 0.0319 |
| fAg | Transition function from engorged adult to oviposition site—seeking adult | Equation (2) |
| mL | Larva mortality (day−1) | mL(t) = exp(−T(t)/2) + μL |
| mP | Pupa mortality rate (day−1) | mP(t) = exp(−T(t)/2) + μP |
| mA | Adult mortality rate (day−1) | mA(t) = max(μA; 0.04417 + 0.00217. T(t)) |
| kL | Environment carrying capacity of larvae (ha−1) | Equation (3) |
| kP | Environment carrying capacity of pupae (ha−1) | Equation (3) |
2.4.4. Model Outputs
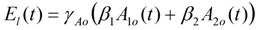
2.4.5. Initial Conditions and Simulations
2.5. Validation
2.6. Sensitivity Analysis
3. Results and Discussion
3.1. Aedes albopictus Population Dynamics in Urban Areas of South Eastern France
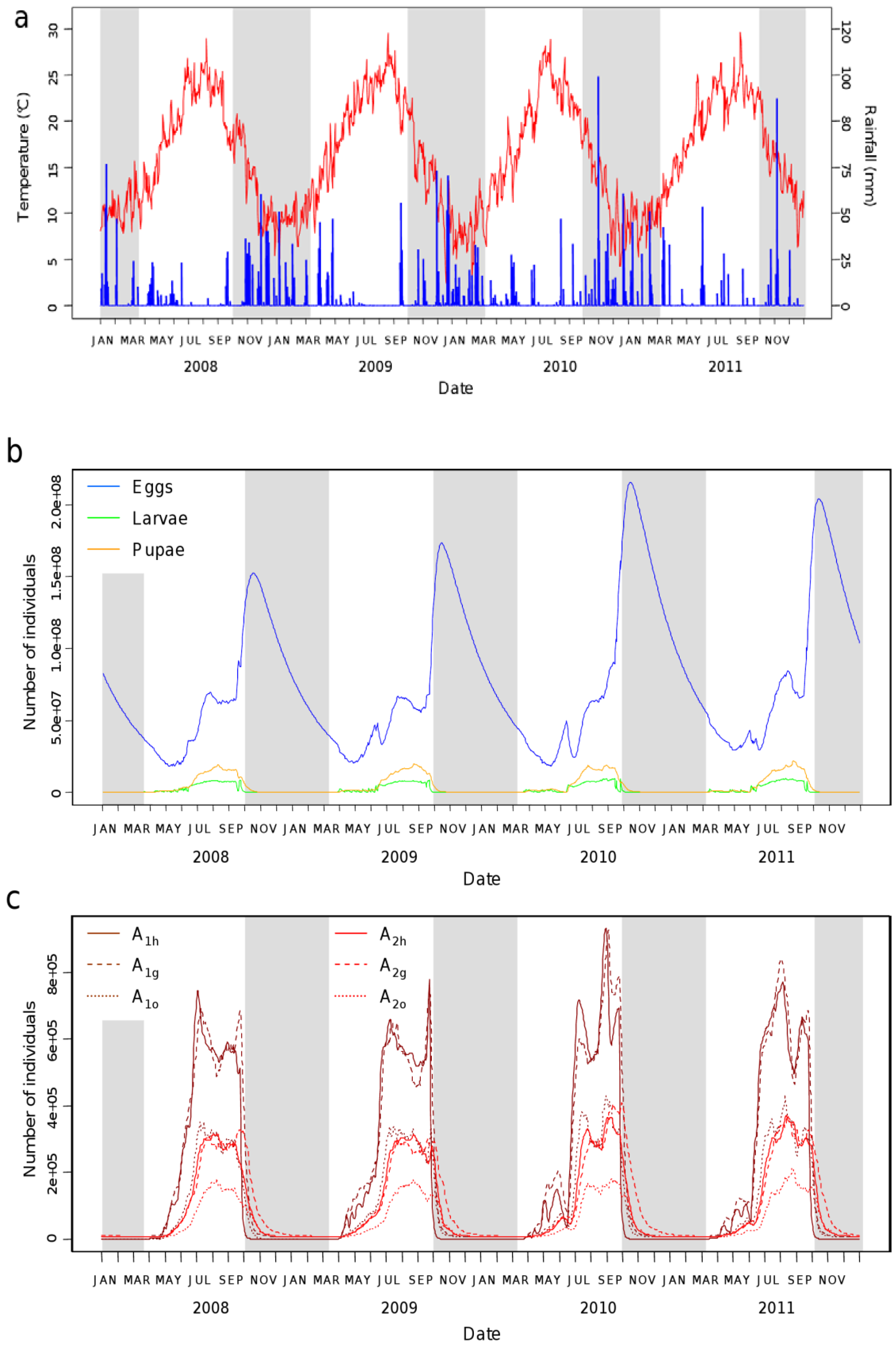
3.2. Model Validation

3.3. Key Model Parameters

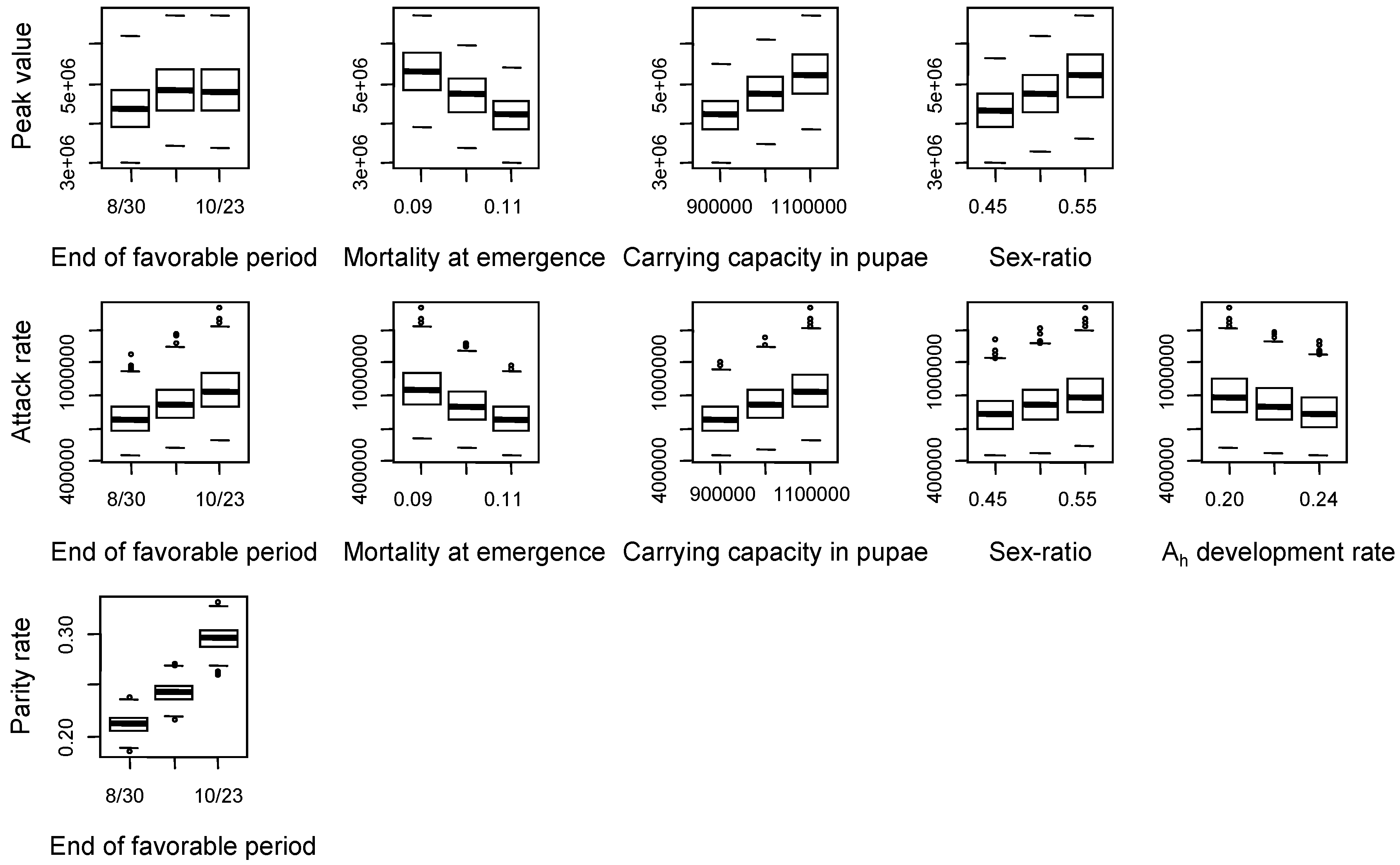
3.4. Discussion

4. Conclusions
Acknowledgments
Conflict of Interest
References
- Mitchell, C.J. The role of Aedes albopictus as an arbovirus vector. Parassitologia 1995, 37, 109–113. [Google Scholar]
- Gratz, N.G. Critical review of the vector status of Aedes albopictus. Med. Vet. Entomol. 2004, 18, 215–227. [Google Scholar] [CrossRef]
- European Network for Arthropod Vector Surveillance for Human Public Health (ECDC VBORNET). Available online: http://www.vbornet.eu/index.php?p=11 (accessed on 11 March 2013).
- Delaunay, P.; Mathieu, B.; Marty, P.; Fauran, P.; Schaffner, F. Chronology of the development of Aedes albopictus in the Alpes-Maritimes Department of France, from 2002 to 2005. Med. Trop. 2007, 67, 310–311. [Google Scholar]
- ECDC Guidelines for the Surveillance of Invasive Mosquitoes in Europe. Available online: http://ecdc.europa.eu/en/publications/Publications/TER-Mosquito-surveillance-guidelines.pdf (accessed on 12 March 2013).
- Medlock, J.M.; Hansford, K.M.; Schaffner, F.; Versteirt, V.; Hendrickx, G.; Zeller, H.; van Bortel, W. A review of the invasive mosquitoes in Europe: Ecology, public health risks, and control options. Vector Borne Zoonotic. Dis. 2012, 12, 435–447. [Google Scholar] [CrossRef] [Green Version]
- Rezza, G.; Nicoletti, L.; Angelini, R.; Romi, R.; Finarelli, A.C.; Panning, M.; Cordioli, P.; Fortuna, C.; Boros, S.; Magurano, F.; et al. Infection with chikungunya virus in Italy: An outbreak in a temperate region. Lancet 2007, 370, 1840–1846. [Google Scholar] [CrossRef]
- La Ruche, G.; Souares, Y.; Armengaud, A.; Peloux-Petiot, F.; Delaunay, P.; Despres, P.; Lenglet, A.; Jourdain, F.; Leparc-Goffart, I.; Charlet, F.; et al. First two autochthonous dengue virus infections in metropolitan France, September 2010. Euro Surveill. 2010, 15. Available online: http://www.eurosurveillance.org/ViewArticle.aspx?ArticleId=19676 (accessed on 11 March 2013). [Google Scholar]
- Grandadam, M.; Caro, V.; Plumet, S.; Thiberge, J.M.; Souares, Y.; Failloux, A.B.; Tolou, H.J.; Budelot, M.; Cosserat, D.; Leparc-Goffart, I.; et al. Chikungunya virus, southeastern France. Emerg. Infect. Dis. 2011, 17, 910–913. [Google Scholar] [CrossRef]
- Neteler, M.; Roiz, D.; Rocchini, D.; Castellani, C.; Rizzoli, A. Terra and Aqua satellites track tiger mosquito invasion: Modelling the potential distribution of Aedes albopictus in north-eastern Italy. Int. J. Health Geogr. 2011, 10. [Google Scholar] [CrossRef] [Green Version]
- Development of Aedes albopictus Risk Maps; European Centre for Disease Prevention and Control: Stockholm, Sweden, 2009; p. 52.
- Otero, M.; Solari, H.G.; Schweigmann, N. A stochastic population dynamics model for Aedes aegypti: Formulation and application to a city with temperate climate. Bull. Math. Biol. 2006, 68, 1945–1974. [Google Scholar] [CrossRef]
- Focks, D.A.; Haile, D.G.; Daniels, E.; Mount, G.A. Dynamic life table model for Aedes aegypti (Diptera: Culicidae): Simulation results and validation. J. Med. Entomol. 1993, 30, 1018–1028. [Google Scholar]
- Dumont, Y.; Chiroleu, F. Vector control for the Chikungunya disease. Math. Biosci. Eng. 2010, 7, 313–345. [Google Scholar] [CrossRef]
- Moulay, D.; Aziz-Alaoui, M.A.; Cadivel, M. The chikungunya disease: Modeling, vector and transmission global dynamics. Math. Biosci. 2011, 229, 50–63. [Google Scholar] [CrossRef]
- Poletti, P.; Messeri, G.; Ajelli, M.; Vallorani, R.; Rizzo, C.; Merler, S. Transmission potential of chikungunya virus and control measures: The case of Italy. PLoS One 2011, 6, e18860. [Google Scholar] [CrossRef]
- Cailly, P.; Tran, A.; Balenghien, T.; L’Ambert, G.; Toty, C.; Ezanno, P. A climate-driven abundance model to assess mosquito control strategies. Ecol. Model. 2012, 227, 7–17. [Google Scholar] [CrossRef]
- Carrieri, M.; Albieri, A.; Angelini, P.; Baldacchini, F.; Venturelli, C.; Zeo, S.M.; Bellini, R. Surveillance of the chikungunya vector Aedes albopictus (Skuse) in Emilia-Romagna (northern Italy): Organizational and technical aspects of a large scale monitoring system. J. Vector Ecol. 2011, 36, 108–116. [Google Scholar] [CrossRef]
- Carrieri, M.; Masetti, A.; Albieri, A.; Maccagnani, B.; Bellini, R. Larvicidal activity and influence of Bacillus thuringiensis var. israelensis on Aedes albopictus oviposition in ovitraps during a two-week check interval protocol. J. Am. Mosq. Control. Assoc. 2009, 25, 149–155. [Google Scholar]
- Roiz, D.; Rosa, R.; Arnoldi, D.; Rizzoli, A. Effects of temperature and rainfall on the activity and dynamics of host-seeking Aedes albopictus females in northern Italy. Vector Borne Zoonotic. Dis. 2010, 10, 811–816. [Google Scholar]
- Abramides, G.C.; Roiz, D.; Guitart, R.; Quintana, S.; Guerrero, I.; Gimenez, N. Effectiveness of a multiple intervention strategy for the control of the tiger mosquito (Aedes albopictus) in Spain. Trans. R Soc. Trop. Med. Hyg. 2011, 105, 281–288. [Google Scholar] [CrossRef] [Green Version]
- Matsuo, K.; Yoshida, Y.; Kunou, I. The scanning electron microscopy of mosquitoes (Diptera: Culicidae). I. The egg surfaces of five species of Aedes and Armigeres. subalbatus. J. Kyoto Pref. Univ. Med. 1972, 81, 358–363. [Google Scholar]
- Encinas Grandes, A. Taxonomía y Biología de los Mosquitos del área Salmantina (Diptera, Culicidae); University de Salamanca: Salamanca, Spain, 1982. [Google Scholar]
- Delatte, H.; Gimonneau, G.; Triboire, A.; Fontenille, D. Influence of temperature on immature development, survival, longevity, fecundity, and gonotrophic cycles of Aedes albopictus, vector of chikungunya and dengue in the Indian Ocean. J. Med. Entomol. 2009, 46, 33–41. [Google Scholar] [CrossRef]
- Lacour, G.; Carron, A.; Jeannin, C.; Delaunay, P.; Benoît, R.; Perrin, Y.; Lagneau, C. Aedes albopictus (Skuse, 1894) (Diptera: Culicidae) in France: Gonotrophic Cycle, Fecundity and Longevity. In Proceedings of the International Conference “Emerging Vector-borne Diseases in a Changing European Environment”, Montpellier, France, 10–12 May 2010.
- EID-Med. In Surveillance du Moustique Aedes albopictus en France Métropolitaine: Bilan 2011; Entente Interdépartementale Pour la Démoustication du Littoral Méditerranéen: Montpellier, France, 2011; p. 39.
- Hawley, W.A. The biology of Aedes albopictus. J. Am. Mosq. Control. Assoc. Suppl. 1988, 1, 1–39. [Google Scholar]
- Clements, A.N. The Biology of Mosquitoes: Development; Nutrition and Reproduction; CABI Publishing: Eastbourne, UK, 2000. [Google Scholar]
- Lord, C.C. Density dependence in larval Aedes albopictus (Diptera: Culicidae). J. Med. Entomol. 1998, 35, 825–829. [Google Scholar]
- Jetten, T.H.; Takken, W. Anophelism Without Malaria in Europe: A Review of the Ecology and Distribution of the Genus Anopheles in Europe; Wageningen Agricultural University Press: Wageningen, The Netherlands, 1994; p. 69. [Google Scholar]
- Marini, F.; Caputo, B.; Pombi, M.; Tarsitani, G.; della Torre, A. Study of Aedes albopictus dispersal in Rome, Italy, using sticky traps in mark-release-recapture experiments. Med. Vet. Entomol. 2010, 24, 361–368. [Google Scholar] [CrossRef]
- Lacour, G.; Marquereau, L.; Dujardin, J.P.; Benoît, R.; Chanaud, L.; Viano, M.; Boussès, P.; Lagneau, C.; Hance, T. Winter is Coming: Diapause Phenology, Wing Shape and Size Seasonality of a Temperate Population of Aedes albopictus (Diptera: Culicidae). In Proceedings of the 18th European Society of Vector Ecology Conference, Montpellier, France, 8–11 October 2012.
- Tsuda, Y.; Takagi, M.; Wada, Y. Preliminary laboratory study on population growth of Aedes albopictus. Trop. Med. 1991, 33, 41–46. [Google Scholar]
- Soti, V.; Tran, A.; Degenne, P.; Chevalier, V.; Lo Seen, D.; Thiongane, Y.; Diallo, M.; Guegan, J.F.; Fontenille, D. Combining hydrology and mosquito population models to identify the drivers of rift valley Fever emergence in semi-arid regions of west Africa. PLoS Negl. Trop. Dis. 2012, 6, e1795. [Google Scholar] [CrossRef] [Green Version]
- Shaman, J.; Spiegelman, M.; Cane, M.; Stieglitz, M. A hydrologically driven model of swamp water mosquito population dynamics. Ecol. Model. 2006, 194, 395–404. [Google Scholar] [CrossRef]
- Chan, K.L.; Ho, B.C.; Chan, Y.C. Aedes aegypti (L.) and Aedes albopictus (Skuse) in Singapore City. 2. Larval habitats. Bull. World Health Organ. 1971, 44, 629–633. [Google Scholar]
- Ho, B.C.; Chan, K.L.; Chan, Y.C. Aedes aegypti (L.) and Aedes albopictus (Skuse) in Singapore City. 3. Population fluctuations. Bull. World Health Organ. 1971, 44, 635–641. [Google Scholar]
- Lourenco-de-Oliveira, R.; Castro, M.G.; Braks, M.A.; Lounibos, L.P. The invasion of urban forest by dengue vectors in Rio de Janeiro. J. Vector Ecol. 2004, 29, 94–100. [Google Scholar]
- Scilab. Available online: http://www.scilab.org/ (accessed on 11 March 2013).
- Saltelli, A.; Chan, K.; Scott, E.M. Sensitivity Analysis; John Wiley and Sons: New York, NY, USA, 2000. [Google Scholar]
- Romi, R.; Severini, F.; Toma, L. Cold acclimation and overwintering of female Aedes albopictus in Roma. J. Am. Mosq. Control. Assoc. 2006, 22, 149–151. [Google Scholar] [CrossRef]
- Toma, L.; Severini, F.; Di Luca, M.; Bella, A.; Romi, R. Seasonal patterns of oviposition and egg hatching rate of Aedes albopictus in Rome. J. Am. Mosq. Control. Assoc. 2003, 19, 19–22. [Google Scholar]
- Giatropoulos, A.; Emmanouel, N.; Koliopoulos, G.; Michaelakis, A. A study on distribution and seasonal abundance of Aedes albopictus (Diptera: Culicidae) population in Athens, Greece. J. Med. Entomol. 2012, 49, 262–269. [Google Scholar] [CrossRef]
- Aranda, C.; Eritja, R.; Roiz, D. First record and establishment of the mosquito Aedes albopictus in Spain. Med. Vet. Entomol. 2006, 20, 150–152. [Google Scholar] [CrossRef]
- Adhami, J.; Reiter, P. Introduction and establishment of Aedes (Stegomyia) albopictus skuse (Diptera: Culicidae) in Albania. J. Am. Mosq. Control. Assoc. 1998, 14, 340–343. [Google Scholar]
- Urbanelli, S.; Bellini, R.; Carrieri, M.; Sallicandro, P.; Celli, G. Population structure of Aedes albopictus (Skuse): The mosquito which is colonizing Mediterranean countries. Heredity (Edinb.) 2000, 84((Pt. 3)), 331–337. [Google Scholar]
- Alto, B.W.; Juliano, S.A. Precipitation and temperature effects on populations of Aedes albopictus (Diptera: Culicidae): Implications for range expansion. J. Med. Entomol. 2001, 38, 646–656. [Google Scholar] [CrossRef]
- Hawley, W.A.; Pumpuni, C.B.; Brady, R.H.; Craig, G.B., Jr. Overwintering survival of Aedes albopictus (Diptera: Culicidae) eggs in Indiana. J. Med. Entomol. 1989, 26, 122–129. [Google Scholar]
- Urbanski, J.M.; Aruda, A.; Armbruster, P. A transcriptional element of the diapause program in the Asian tiger mosquito, Aedes albopictus, identified by suppressive subtractive hybridization. J. Insect Physiol. 2010, 56, 1147–1154. [Google Scholar] [CrossRef]
- Toma, T.; Miyagi, I. Seasonal changes in the hatchability of Aedes albopictus (Diptera: Culicidae) eggs in Okinawajima, Ryukyu Archipelago, Japan. Jpn J. Sanit. Zool. 1990, 41, 195–204. [Google Scholar]
- Hanson, S.M. Field overwinter survivorship of Aedes albopictus eggs in Japan. J. Am. Mosq. Control. Assoc. 1995, 11, 354–357. [Google Scholar]
- Hanson, S.M.; Craig, G.B., Jr. Aedes albopictus (Diptera: Culicidae) eggs: Field survivorship during northern Indiana winters. J. Med. Entomol. 1995, 32, 599–604. [Google Scholar]
- Anon, A. A system of world-wide surveillance for vectors. Wkly. Epidemiol. Rec. World Health Organ. 1972, 47, 73–84. [Google Scholar]
- Breteau, H. Yellow fever in French West Africa; an aspect of mass-preventive medicine. Bull. World Health Organ. 1954, 11, 453–481. [Google Scholar]
- Carrieri, M.; Angelini, P.; Venturelli, C.; Maccagnani, B.; Bellini, R. Aedes albopictus (Diptera: Culicidae) population size survey in the 2007 Chikungunya outbreak area in Italy. I. Characterization of breeding sites and evaluation of sampling methodologies. J. Med. Entomol. 2011, 48, 1214–1225. [Google Scholar] [CrossRef]
- Barker, R.J.; Cohen, C.F.; Mayer, A. Photoflashes: A potential new tool for control of insect populations. Science 1964, 145, 1195–1197. [Google Scholar]
- Beach, R.F.; Craig, G.B. Photoinhibition of diapause in field populations of Aedes atropalpus. Environ. Entomol. 1979, 8, 392–396. [Google Scholar]
- Labbe, P.; Berticat, C.; Berthomieu, A.; Unal, S.; Bernard, C.; Weill, M.; Lenormand, T. Forty years of erratic insecticide resistance evolution in the mosquito Culex pipiens. PLoS Genet. 2007, 3, e205. [Google Scholar] [CrossRef]
- Marcombe, S.; Darriet, F.; Tolosa, M.; Agnew, P.; Duchon, S.; Etienne, M.; Yp Tcha, M.M.; Chandre, F.; Corbel, V.; Yebakima, A. Pyrethroid resistance reduces the efficacy of space sprays for dengue control on the island of Martinique (Caribbean). PLoS Negl. Trop. Dis. 2011, 5, e1202. [Google Scholar] [CrossRef]
- Poncon, N.; Tran, A.; Toty, C.; Luty, A.J.; Fontenille, D. A quantitative risk assessment approach for mosquito-borne diseases: Malaria re-emergence in southern France. Malar. J. 2008, 7, 147. [Google Scholar] [CrossRef]
- Chen, S.C.; Hsieh, M.H. Modeling the transmission dynamics of dengue fever: Implications of temperature effects. Sci. Total Environ. 2012, 431, 385–391. [Google Scholar] [CrossRef]
- Linard, C.; Poncon, N.; Fontenille, D.; Lambin, E.F. A multi-agent simulation to assess the risk of malaria re-emergence in southern France. Ecol. Model. 2009, 220, 160–174. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Tran, A.; L'Ambert, G.; Lacour, G.; Benoît, R.; Demarchi, M.; Cros, M.; Cailly, P.; Aubry-Kientz, M.; Balenghien, T.; Ezanno, P. A Rainfall- and Temperature-Driven Abundance Model for Aedes albopictus Populations. Int. J. Environ. Res. Public Health 2013, 10, 1698-1719. https://doi.org/10.3390/ijerph10051698
Tran A, L'Ambert G, Lacour G, Benoît R, Demarchi M, Cros M, Cailly P, Aubry-Kientz M, Balenghien T, Ezanno P. A Rainfall- and Temperature-Driven Abundance Model for Aedes albopictus Populations. International Journal of Environmental Research and Public Health. 2013; 10(5):1698-1719. https://doi.org/10.3390/ijerph10051698
Chicago/Turabian StyleTran, Annelise, Grégory L'Ambert, Guillaume Lacour, Romain Benoît, Marie Demarchi, Myriam Cros, Priscilla Cailly, Mélaine Aubry-Kientz, Thomas Balenghien, and Pauline Ezanno. 2013. "A Rainfall- and Temperature-Driven Abundance Model for Aedes albopictus Populations" International Journal of Environmental Research and Public Health 10, no. 5: 1698-1719. https://doi.org/10.3390/ijerph10051698





