A Geometric Modelling Approach to Determining the Best Sensing Coverage for 3-Dimensional Acoustic Target Tracking in Wireless Sensor Networks
Abstract
:1. Introduction
2. Related Work
3. Basics of 3-Dimensional Acoustic Target Tracking
3.1. 3-Dimensional Acoustic Target Localization Model
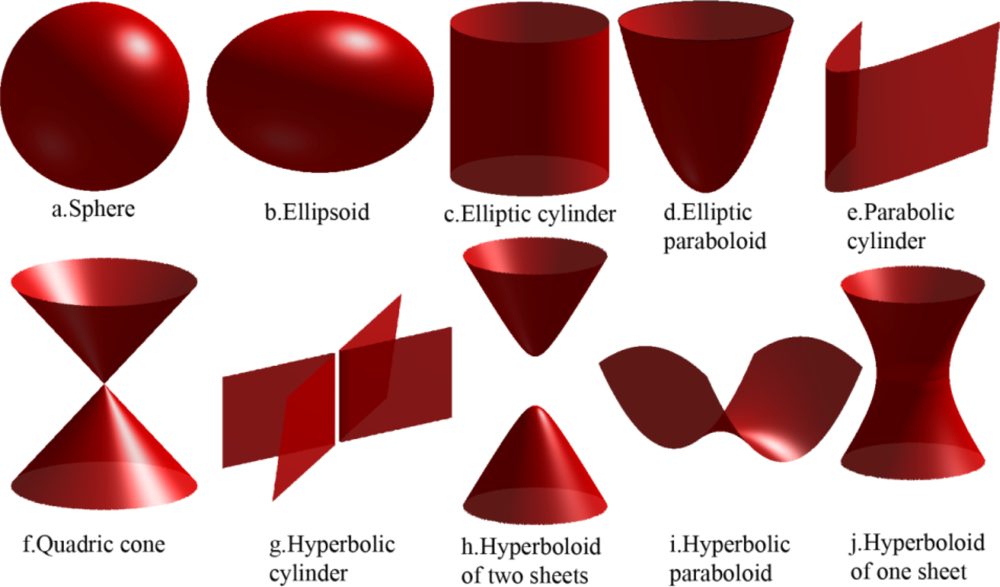
3.2. Geometric Representation of 3-Dimensional Acoustic Target Localization
3.3. Dual Geometric Representation of Acoustic Target Localization
4. Combined Algebraic and Geometric Solution to 3-Dimensional Acoustic Target Localization
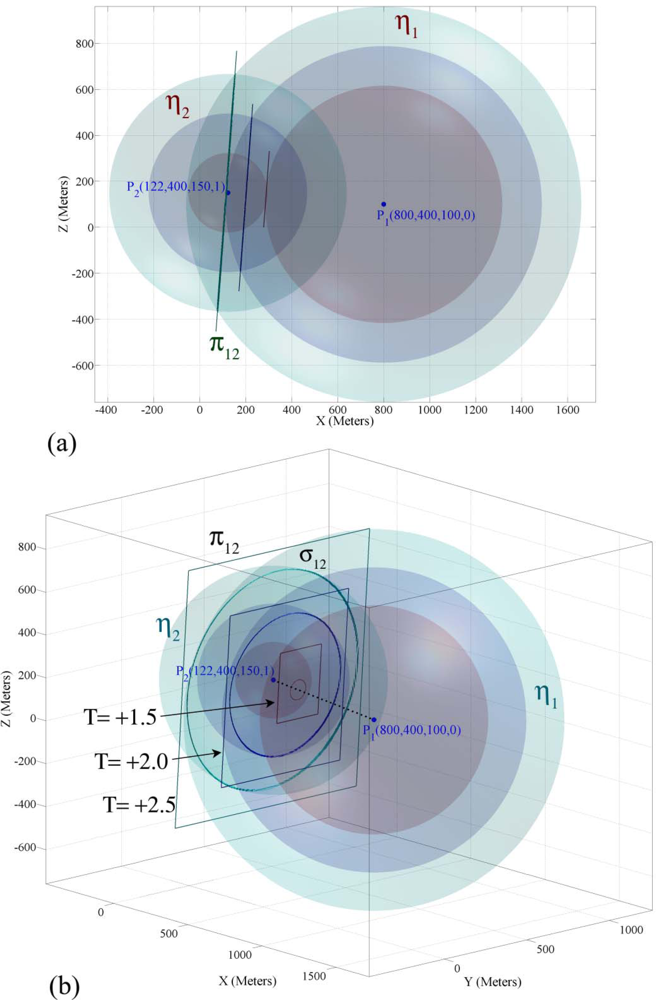
4.1. Geometric Properties of Two Sensor Node’s Information
4.2. Demonstrating Geometric Properties of Two Sensor Node’s Information
4.3. An Algebraic Representation of 3-Dimensional Acoustic Target Localization
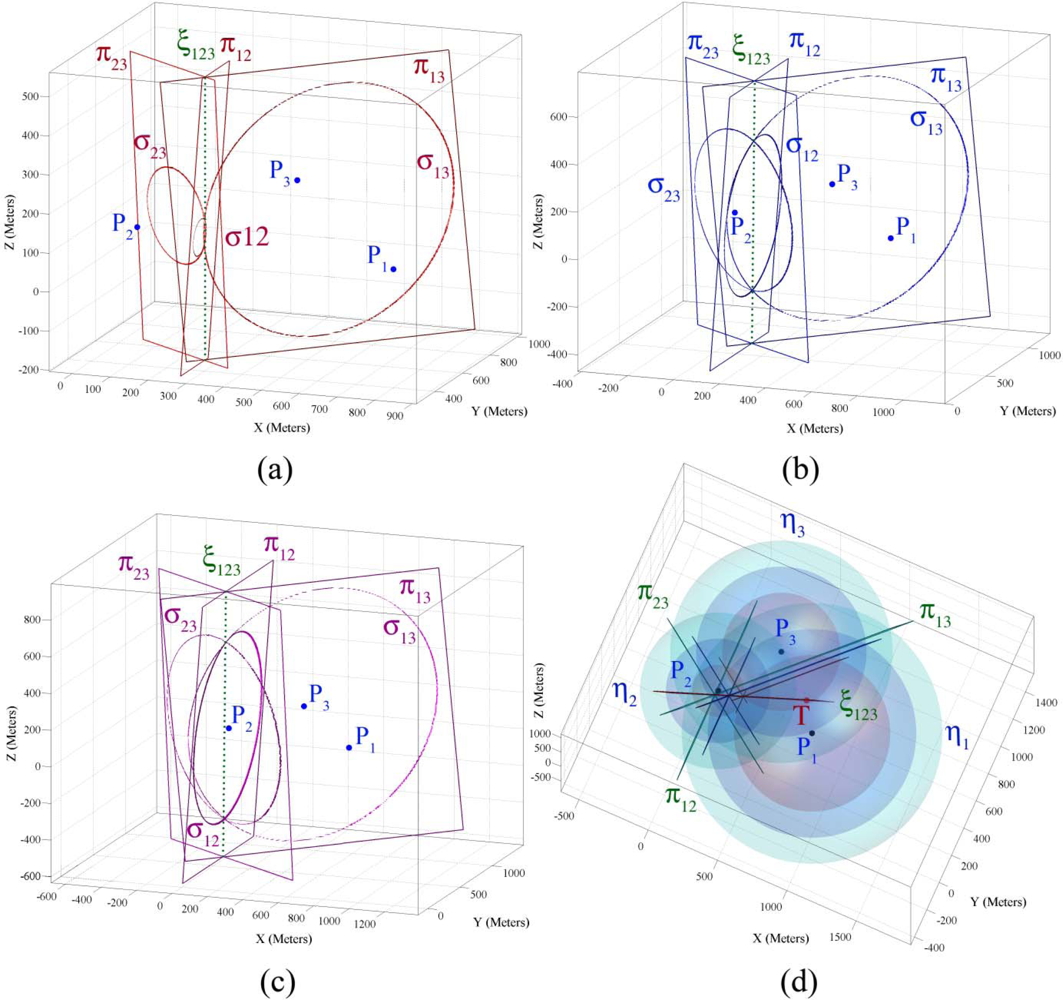
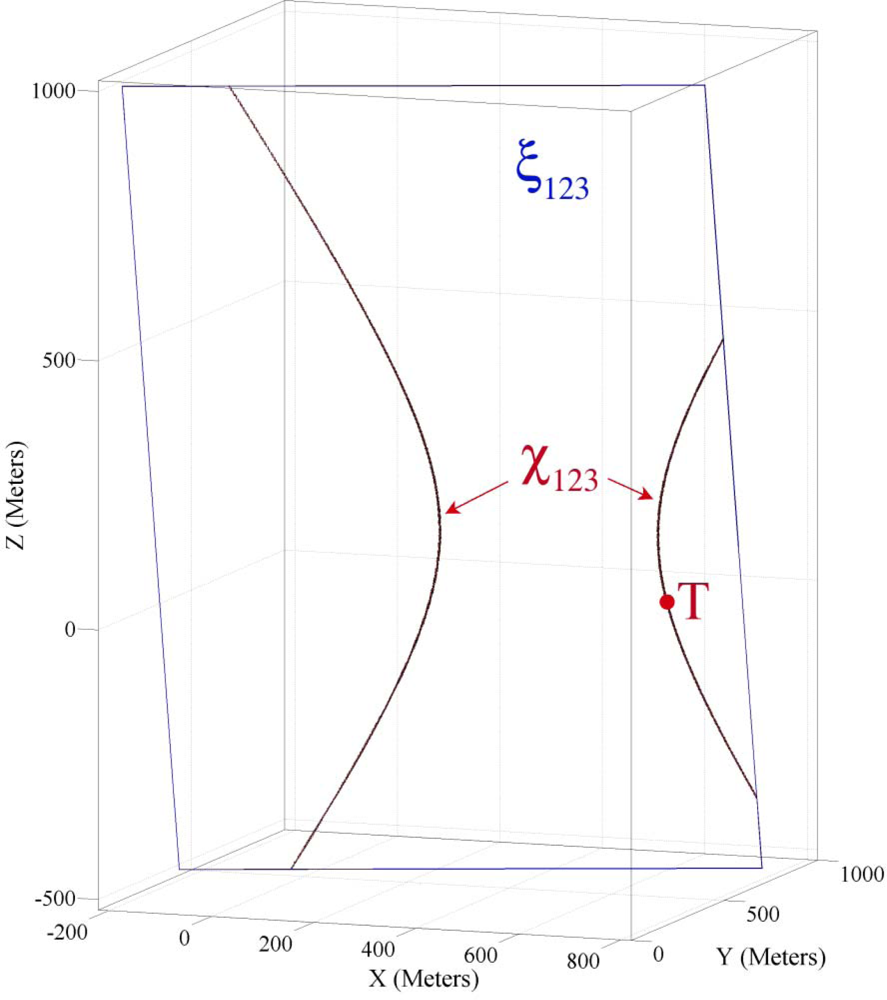
4.4. Geometric Properties of Three Sensor Node’s Information
4.5. Demonstrating Geometric Properties of Three Sensor Node’s Information
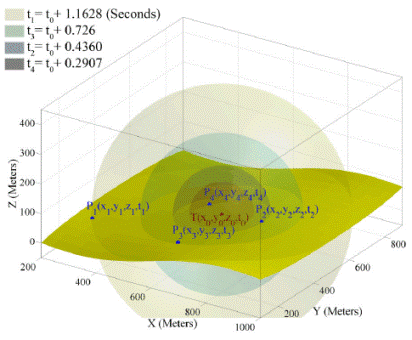
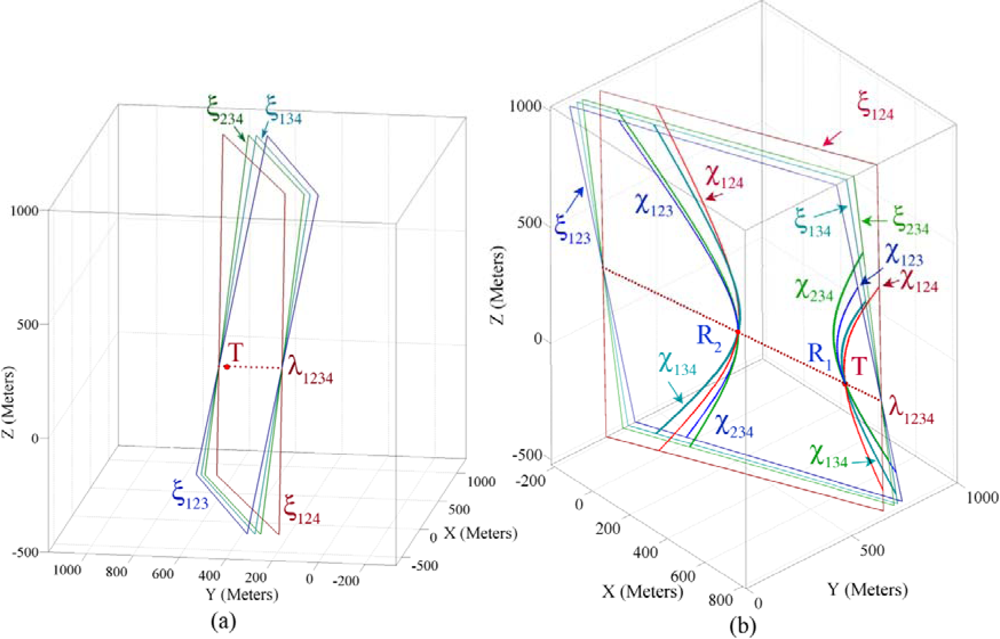
4.6. Geometric Properties of Four Sensor Nodes’ Information
4.7. Demonstrating the Geometric Properties of Four Sensor Node’s Information
4.8. Elimination of the False Positive Answer of 3-Dimensional Acoustic Target Localization
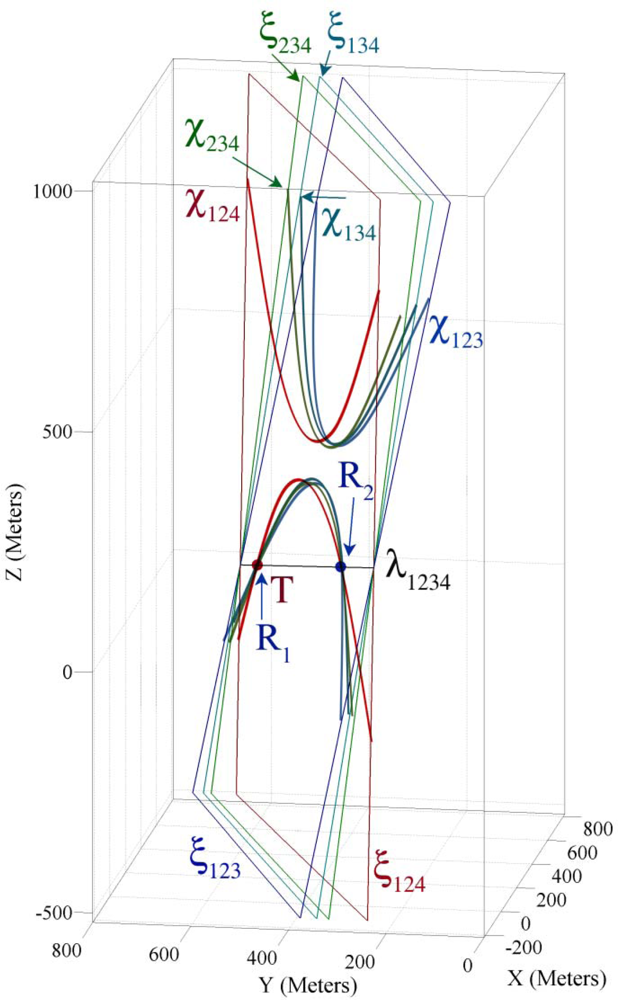
- Case I: If the time of one of the answers say R1 is before the times of the sound sensing by all four sensor nodes and the time of the other answer, R2 is after the time of the sound sensing of at least one of the four sensing nodes, answer R1 is related to past time and answer R2 is related to future time and is the infeasible answer. An example of case I was shown in Figure 7b.
- Case II: If the times of both computed answers R1 and R2 is before the reported times of sound sensing by all sensor nodes, both answers are related to the past and time test cannot help the FCAL method to detect the feasible spatio-temporal information of a target object. Figure 8 shows this case which demonstrates the pitfall of four degree sensing coverage and the FCAL method. In this case we can randomly select one of the answers or we cans or refuse to report any answer. Another approach is to report both answers and assign a 50% confidence degree to each answer. In simulation of this method in Part 5.3, if a redundant set of simultaneous equations with sensing information of different set of sensor nodes is constructed, the application of majority voter increases the probability of selecting the feasible answer. This is because it is probable that other set of simultaneous equations do not fall in case II.
- Case III: If the axis line is tangent to sound broadcasting hypercone of target object intersects with it on a single point, both answers R1 and R2 are the same and both of them are the feasible spatio-temporal information of a target object. The time test method is successful in cases I and III but it cannot detect the correct answer in case II.
5. A Proposed Four Sensing Coverage Based Method
5.1. Four Coverage Axis Line Method for 3-Dimensional Acoustic Target Localization
5.2. Discussion on FCAL Method
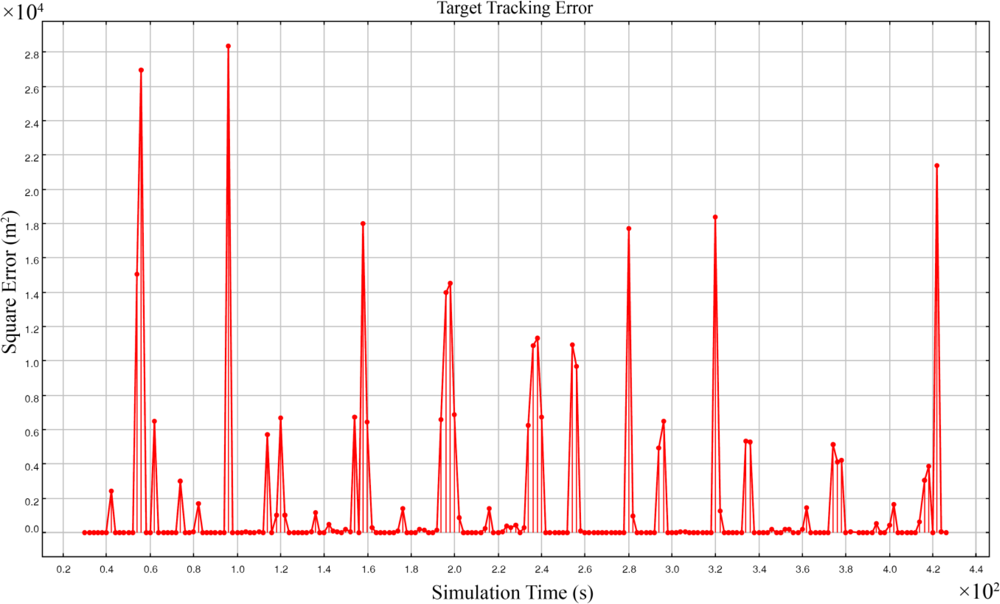
5.3. Simulation Model
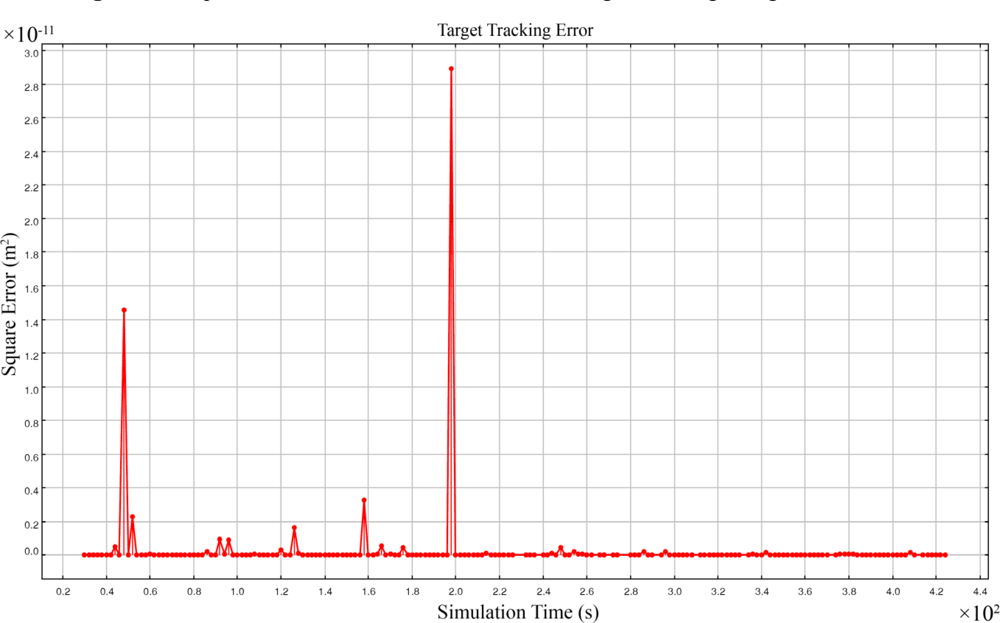
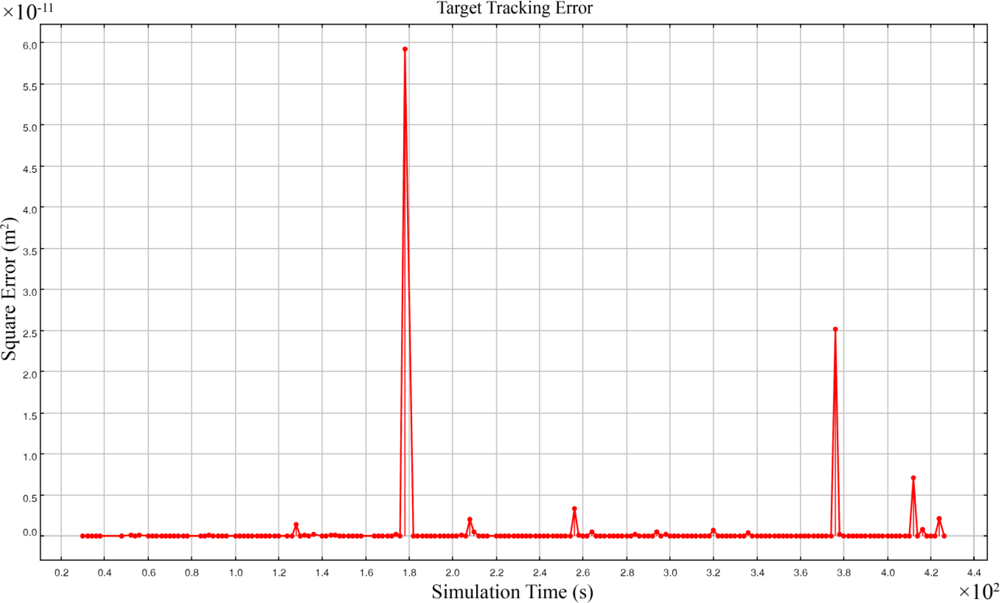
5.4. Simulation Results
5.5. Elimination Condition for False Positive Answer
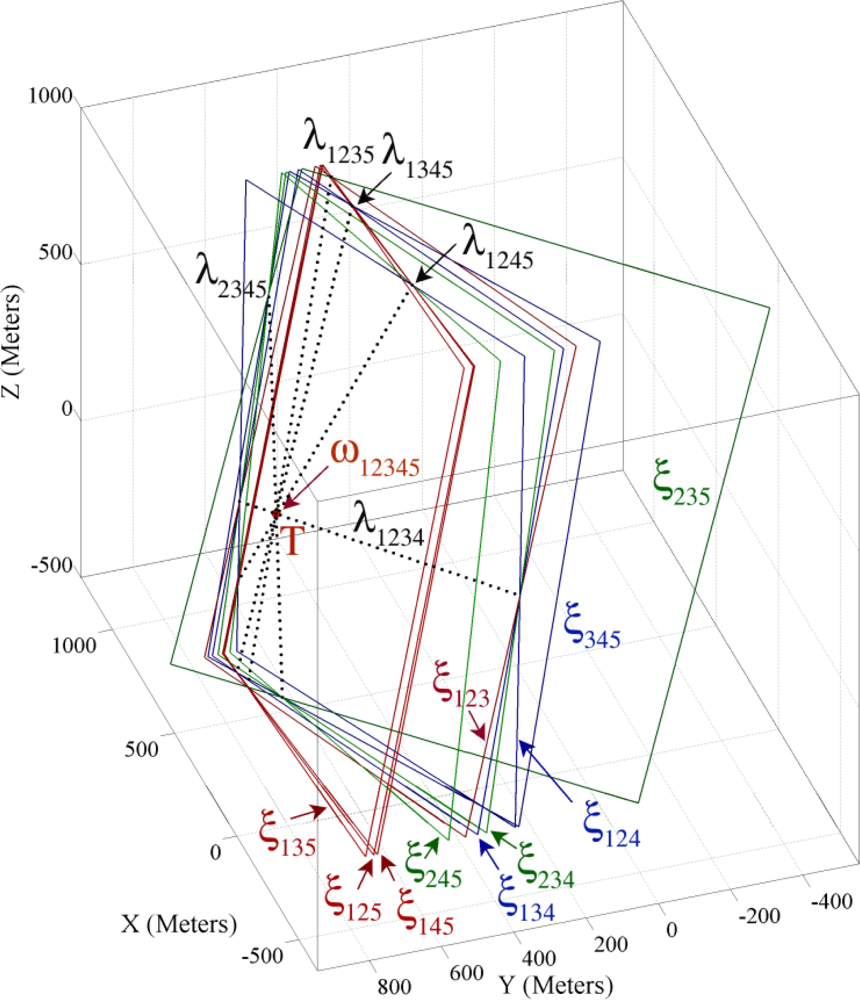
6. Five Sensing Coverage Proposed Methods
6.1. Five Coverage Extent Point Method
6.2. Five Coverage Extended Axis Line Method
6.3. Five Coverage Redundant Axis Lines Method
6.4. Application of Proposed Methods in Bayesian Filters
7. Conclusions and Future Work
7.1. Conclusions
7.2. Future work
Acknowledgments
References and Notes
- Chen, Z. Bayesian Filtering: From Kalman Filters to Particle Filters, and Beyond; Adaptive System Lab, McMaster University: Hamilton, Ontario, Canada, 2003. Available at: http://www.dsi.unifi.it/users/chisci/idfric/Nonlinear_filtering_Chen.pdf (accessed August 20, 2009).
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A Tutorial on Particle Filters for Online Nonlinear/Non-Gaussian Bayesian Tracking. IEEE Trans. Signal Proc 2002, 50, 174–188. [Google Scholar]
- Karl, H.; Willig, A. Protocols and Architectures for Wireless Sensor Networks; John Wiley & Sons Ltd: West Sussex, UK, 2005; pp. 231–249. [Google Scholar]
- Tseng, Y.C.; Huang, C.F.; Kuo, S.P. Positioning and Location Tracking in Wireless Sensor Networks. In Handbook of Sensor Networks: Compact Wireless and Wired Sensing Systems; Ilyas, M., Mahgoub, I., Eds.; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Wang, Q.; Chen, W.P.; Zheng, R.; Lee, K.; Sha, L. Acoustic Target Tracking Using Tiny Wireless Sensor Devices. Proceedings of 2nd International Workshop on Information Processing in Sensor Networks (IPSN'03), Palo Alto, CA, USA, April 22–23, 2003; pp. 642–657.
- Gupta, R.; Das, S.R. Tracking Moving Targets in a Smart Sensor Network. Proceedings of the 58th IEEE Vehicular Technology Conference (VTC '03), Orlando, FL, USA, October 2003; pp. 3035–3039.
- Brooks, R.R.; Ramanathan, P.; Sayeed, A.M. Distributed Target Classification and Tracking in Sensor Networks. Proc. IEEE 2003, 91, 1163–1171. [Google Scholar]
- Lin, C.Y.; Tseng, Y.C. Structures for In-Network Moving Object Tracking in Wireless Sensor Networks. Proceedings of the First International Conference on Broadband Networks (BROADNETS’04), San Jose, CA, USA, October 25–29, 2004; pp. 718–727.
- Ekman, M.; Davstad, K.; Sjoberg, L. Ground Target Tracking using Acoustic Sensors. Proceedings of the Information, Decision and Control, 2007 (IDC '07), Adelaide, Australia, February 12–14, 2007; pp. 182–187.
- Taylor, C.; Rahimi, A.; Bachrach, J.; Shrobe, H. Simultaneous Localization, Calibration, and Tracking in an ad Hoc Sensor Network. Proceedings of the 5th International Conference on Information Processing in Sensor Networks (IPSN’06), Nashville, TN, USA, April 19–21, 2006; pp. 27–33.
- Hue, C.; Le Cadre, J.-P.; Perez, P. Tracking Multiple Objects with Particle Filtering. IEEE Trans. Aerosp. Electron. Syst 2002, 38, 791–812. [Google Scholar]
- Intanagonwiwat, C.; Estrin, D.; Govindan, R.; Heidemann, J. Impact of Network Density on Data Aggregation in Wireless Sensor Networks. Proceedings of the 22nd International Conference on Distributed Computing Systems, Vienna, Austria, July 2–5, 2002; pp. 457–458.
- He, T.; Vicaire, P.A.; Yan, T.; Luo, L.; Gu, L.; Zhou, G.; Stoleru, R.; Cao, Q.; Stankovic, J.A.; Abdelzaher, T. Achieving Real-Time Target Tracking using Wireless Sensor Networks. Proceedings of the 12th IEEE Real-Time and Embedded Technology and Applications Symposium (RTAS'06), San Jose, CA, USA, April 4–7, 2006.
- Chen, L.; Cetin, M.; Willsky, A.S. Distributed Data Association for Multi-Target Tracking in Sensor Networks. Proceedings of the 8th Int. Conference on Information Fusion, Philadelphia, PA, USA, July 2005.
- Chen, W.; Hou, J.C.; Sha, L. Dynamic Clustering for Acoustic Target Tracking in Wireless Sensor Networks. Proceedings of the 11th IEEE International Conference on Network Protocols, Atlanta, GA, USA, November 4–7, 2003; pp. 284–294.
- Sheng, X.; Hu, Y.H. Maximum Likelihood Wireless Sensor Network Source Localization using Acoustic Signal Energy Measurements. IEEE Trans. Signal Process 2005, 52, 44–53. [Google Scholar]
- Barsanti, R.J.; Tummala, M. Combined Acoustic Target Tracking and Sensor Localization. Proceedings of the IEEE SoutheastCon 2002, Columbia, SC, USA, April 5–7, 2002; pp. 437–440.
- Girod, L.; Bychkovskiy, V.; Elson, J.; Estrin, D. Locating Tiny Sensors in Time and Space: A Case Study. Proceedings of the IEEE International Conference on Computer Design: VLSI in Computers and Processors (ICCD '02), Freiburg, Germany, September 16–18, 2002; pp. 214–219.
- Dan, L.; Wong, K.D.; Yu, H.H.; Sayeed, A.M. Detection, Classification, and Tracking of Targets. IEEE Signal Process. Mag 2002, 19, 17–29. [Google Scholar]
- Chuang, S.C. Survey on Target Tracking in Wireless Sensor Networks; Dept. of Computer. Science National Tsing Hua University: Kowloon, Taiwan, 2005. [Google Scholar]
- Pashazadeh, S.; Sharifi, M. Determining the Best Sensing Coverage for 2-Dimensional Acoustic Target Tracking. Sensors 2009, 9, 3405–3436. [Google Scholar]
- Thornhill, C.K. Real or Imaginary Space-Time? Reality or Relativity? Hadronic J. Suppl 1996, 11, 209–224. [Google Scholar]
- Robbin, T. Shadows of Reality: The Fourth Dimension in Relativity, Cubism, and Modern Thought; Yale University Press: London, UK, 2006; pp. 61–81. [Google Scholar]
- Roman, S. Graduate Texts in Mathematics, Advanced Linear Algebra, 3rd ed; Springer: New York, NY, USA, 2008. [Google Scholar]
- Casey, J. A Treatise on Spherical Trigonometry, and Its Application to Geodesy and Astronomy, with Numerous Examples; Hodges, Figgis, & Co.: Dublin, Ireland, 1889; pp. 2–3. [Google Scholar]
- Fuller, G. Analytic Geometry; Addison-Wesley Publishing Company, Inc.: Reading, MA, USA, 1954; pp. 56–57. [Google Scholar]
- Gutenmacher, V.; Vasilyev, N.B. Lines and Curves: A Practical Geometry Handbook; Birkhauser Boston, Inc.: New York, NY, USA, 2004. [Google Scholar]
- Gibson, C.G. Elementary Euclidean Geometry: An Introduction; Cambridge University Press: Cambridge, UK, 2003; pp. 161–162. [Google Scholar]
- Keyton, N. Sections of n-Dimensional Spherical Cones. Math. Mag 1969, 42, 80–83. [Google Scholar]
- Pressley, A. Elementary Differential Geometry; Springer-Verlag: London, UK, 2001; pp. 84–89. [Google Scholar]
- Galarza, A.I.R.; Seade, J. Introduction to Classical Geometries; Birkhäuser: Basel, Switzerland, 2007; pp. 28–33. [Google Scholar]
- Lipschutz, S. Schaum's Outline of Theory and Problems of Linear Algebra, 2nd ed; McGraw-Hill: New York, NY, USA, 1991; pp. 152–153. [Google Scholar]
- Strang, G. The Fundamental Theorem of Linear Algebra. Amer. Math. Month 1993, 100, 848–855. [Google Scholar]
- Hefferon, J. Linear Algebra; Colchester, VT, USA, 2001; pp. 128–129, (accessed August 20, 2009).. Book URL: simbol.math.unizg.hr/LA/joshua/book.pdf.
- Gruenberg, K.W.; Weir, A.J. Linear Geometry, 2nd ed; Springer-Verlag: New York, NY, USA, 1977; pp. 49–51. [Google Scholar]
- Gellert, W.; Gottwald, S.; Hellwich, M.; Kästner, H.; Künstner, H. VNR Concise Encyclopedia of Mathematics, 2nd ed; Van Nostrand Reinhold: New York, NY, USA, 1989. [Google Scholar]
- Woods, F.S. Higher Geometry: An Introduction to Advanced Methods in Analytic Geometry; Dover: New York, NY, USA, 1961. [Google Scholar]
- Vaisman, I. Analytical Geometry; World Scientific Publishing Co Pte Ltd: River Edge, NJ, Singapore, 1997. [Google Scholar]
- Schay, G. Introduction to Linear Algebra, 1st ed; Jones & Bartlett Publishers: Sudbury, MA, USA, 1996. [Google Scholar]
- Hogben, L. Handbook of Linear Algebra; Chapman & Hall/CRC: Boca Raton, FL, USA, 2007; pp. 9–10. [Google Scholar]
- Harville, D.A. Matrix Algebra: Exercises and Solutions; Springer: New York, NY, USA, 2001. [Google Scholar]
- Baldwin, P.; Kohli, S.; Lee, E.A.; Liu, X.; Zhao, Y. Visualsense: Visual Modeling for Wireless and Sensor Network Systems. Proceedings of Technical Memorandum UCB/ERL M04/08, University of California, Berkeley, CA, USA, April 23, 2004.
- Baldwin, P.; kohli, S.; Lee, E.A.; Liu, X.; Zhao, Y. Modeling of Sensor Nets in Ptolemy II. Proceedings of the Information Processing in Sensor Networks (IPSN), Berkeley, CA, USA, April 26–27, 2004; pp. 359–368.
- Brooks, C.; Lee, E.A.; Liu, X.; Neuendorffer, S.; Zhao, Y.; Zheng, H. Heterogeneous Concurrent Modeling and Design in Java (Volume 1: Introduction to Ptolemy II). Proceedings of Technical Memorandum UCB/ERL M04/27, University of California, Berkeley, CA, USA, July 29, 2004. Chap. 1,2..
- Ganeriwal, S.; Kumar, R.; Adlakha, S.; Srivastava, M. Network-Wide Time Synchronization in Sensor Networks; NESL Technical Report, NESL 01-01-2003; UCLA: Los Angeles, CA, USA, May 2003. [Google Scholar]
- Ganeriwal, S.; Kumar, R.; Srivastava, M.B. Timing-Sync Protocol for Sensor Networks. Proceedings of the 1st ACM International Conference on Embedded Networking Sensor Systems (SenSys), Los Angeles, CA, USA, November 2003; pp. 138–149.
- Lorczak, P.R.; Caglayan, A.K.; Eckhardt, D.E. A Theoretical Investigation of Generalized Voters for Redundant Systems. Proceedings of the 19th Int. Symp. on Fault-Tolerant Computing (FTCS-19), Chicago, IL, USA, 1989; pp. 444–451.
- Corman, T.H.; Leiserson, C.E; Rivest, R.L.; Stein, C. Introduction to Algorithms, 2nd ed; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Lyu, M.R. Software Fault Tolerance; John Wiley & Sons: New York, NY, USA, 1995; Chap. 2. [Google Scholar]
- Pashazadeh, S.; Sharifi, M. Simulative Study of Error Propagation in Target Tracking Based on Time Synchronization Error in Wireless Sensor Networks. Proceedings of the Innovations in Information Technology (IIT 2008), Al Ain, UAE, December 16–18, 2008; pp. 563–567.


© 2009 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Pashazadeh, S.; Sharifi, M. A Geometric Modelling Approach to Determining the Best Sensing Coverage for 3-Dimensional Acoustic Target Tracking in Wireless Sensor Networks. Sensors 2009, 9, 6764-6794. https://doi.org/10.3390/s90906764
Pashazadeh S, Sharifi M. A Geometric Modelling Approach to Determining the Best Sensing Coverage for 3-Dimensional Acoustic Target Tracking in Wireless Sensor Networks. Sensors. 2009; 9(9):6764-6794. https://doi.org/10.3390/s90906764
Chicago/Turabian StylePashazadeh, Saeid, and Mohsen Sharifi. 2009. "A Geometric Modelling Approach to Determining the Best Sensing Coverage for 3-Dimensional Acoustic Target Tracking in Wireless Sensor Networks" Sensors 9, no. 9: 6764-6794. https://doi.org/10.3390/s90906764