Improvement of the Accuracy of InSAR Image Co-Registration Based On Tie Points – A Review
Abstract
:1. Introduction
2. Synthetic Aperture Radar Interferometric Processing
2.1. Acquisition of SAR Images
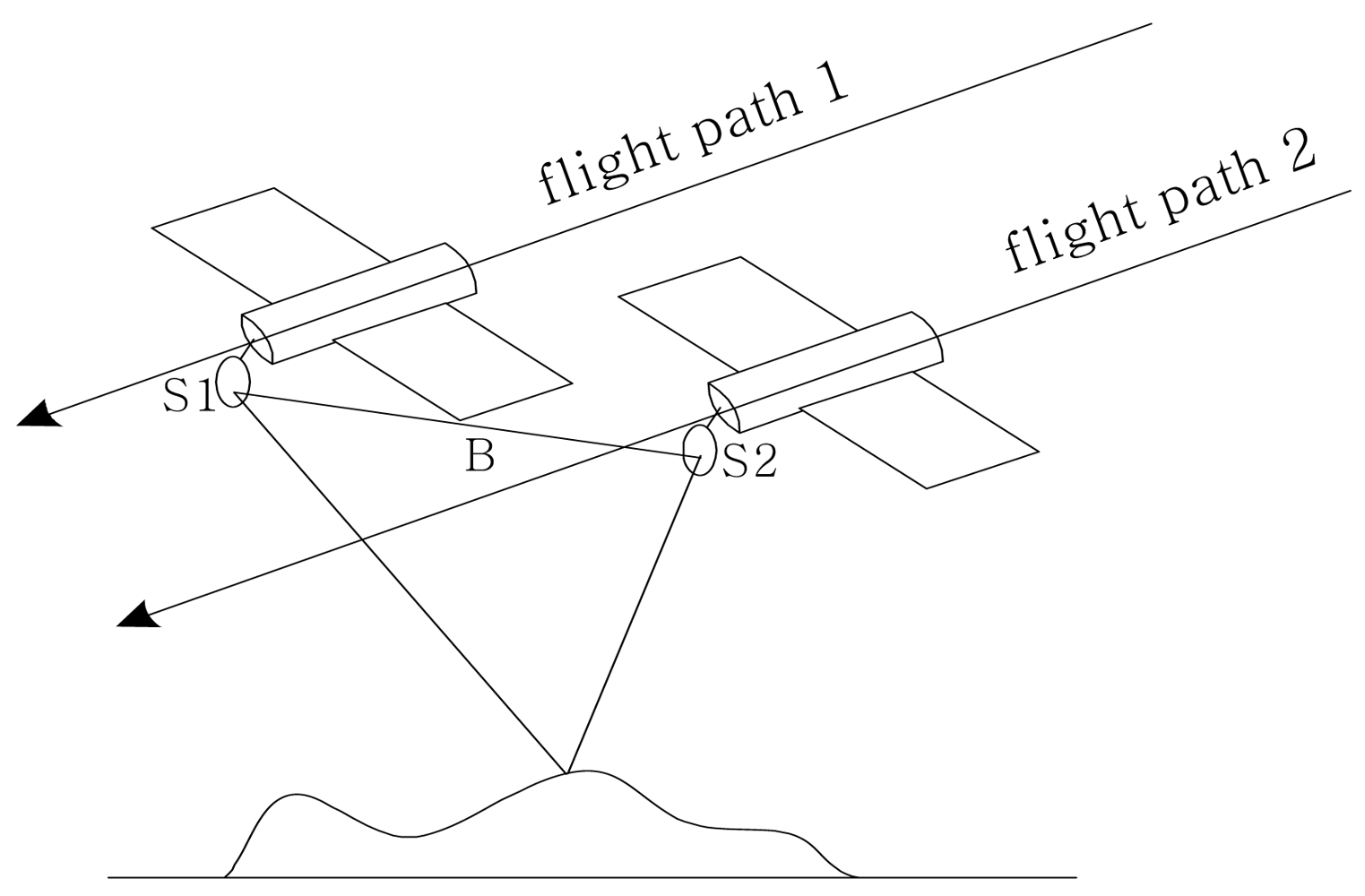
2.1.1. Acquiring SAR Images by Repeat-pass
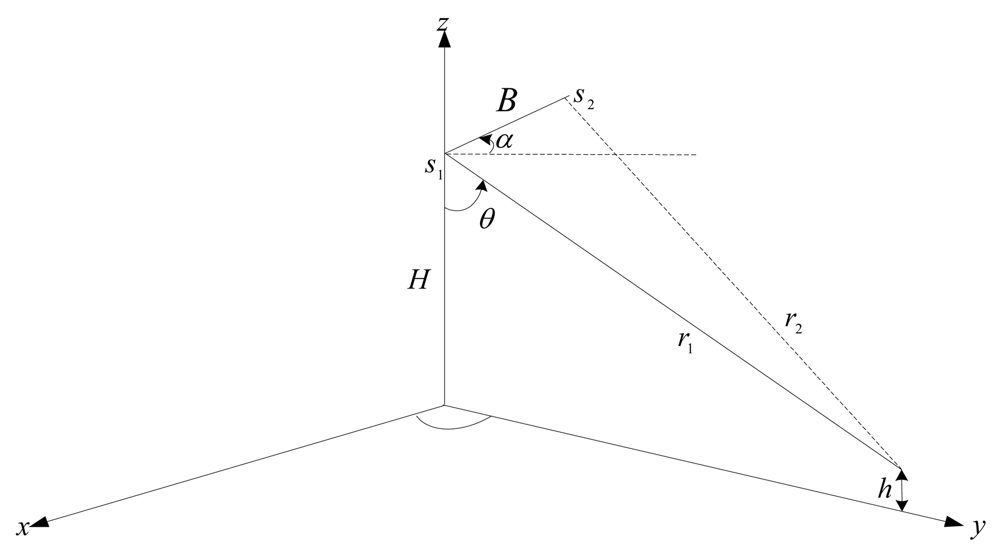
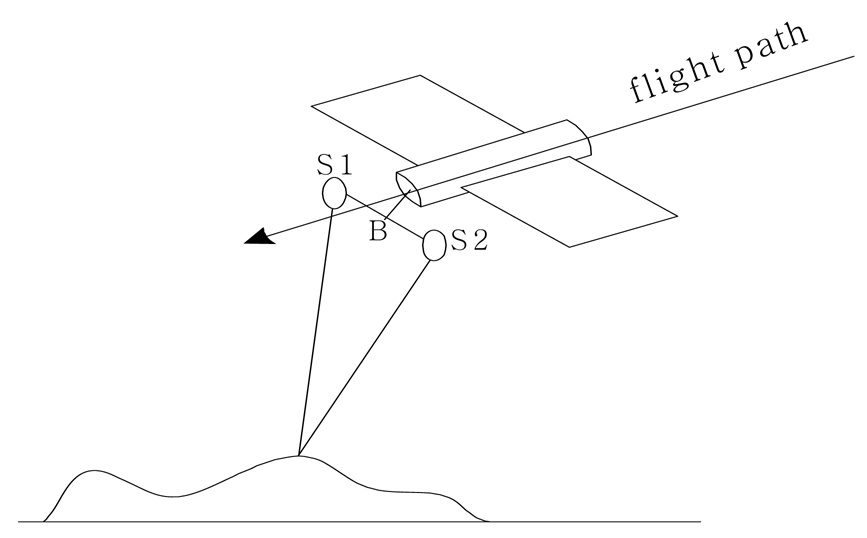
2.1.2. Acquiring SAR Images by Across-track
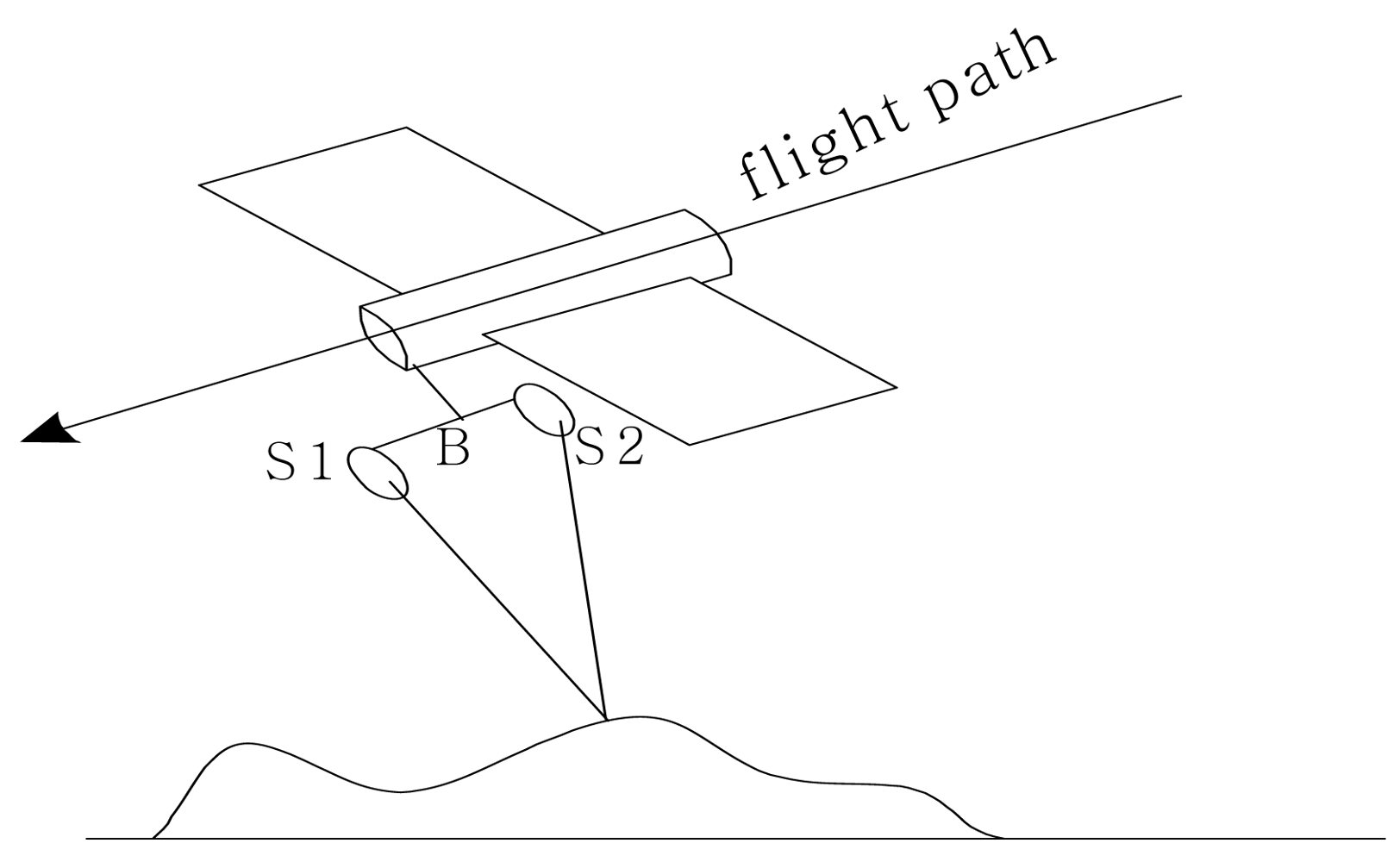
2.1.3. Acquiring SAR Images by Along-track
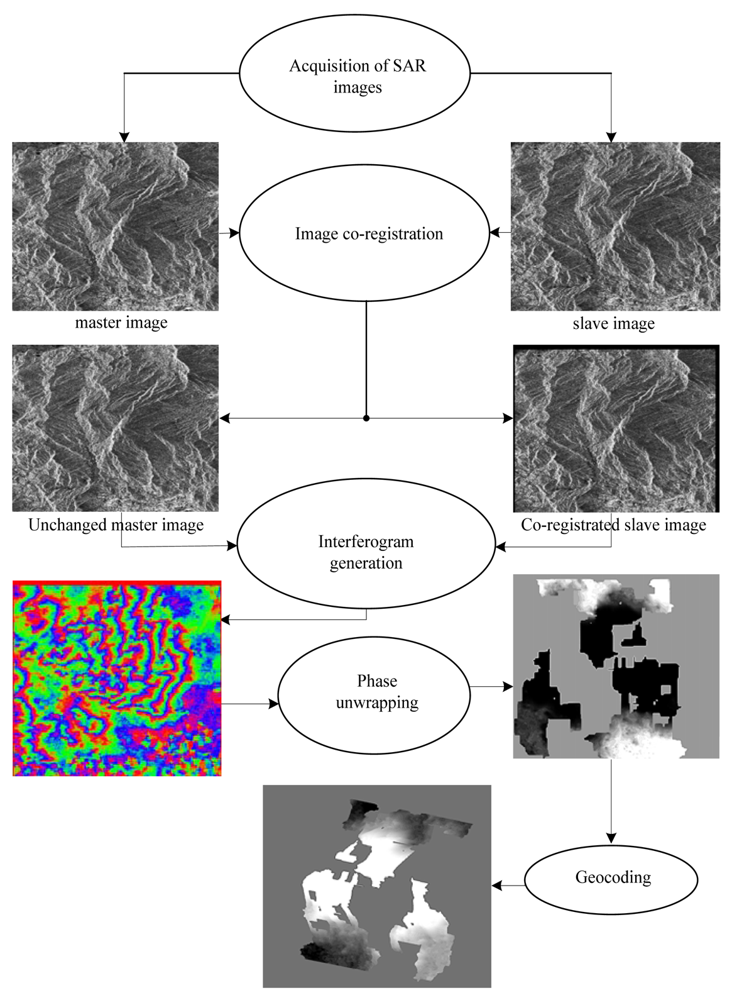
2.2. Interferometric Processing of SAR Images
- Acquisition of SAR images;
- Co-registration of two SAR images;
- Generation of interferogram;
- Phase unwrapping of the wrapped interferometric phase;
- Geocoding of DEM.
- DEM is the final product of InSAR image processing.
3. Procedures of InSAR Image Co-registration
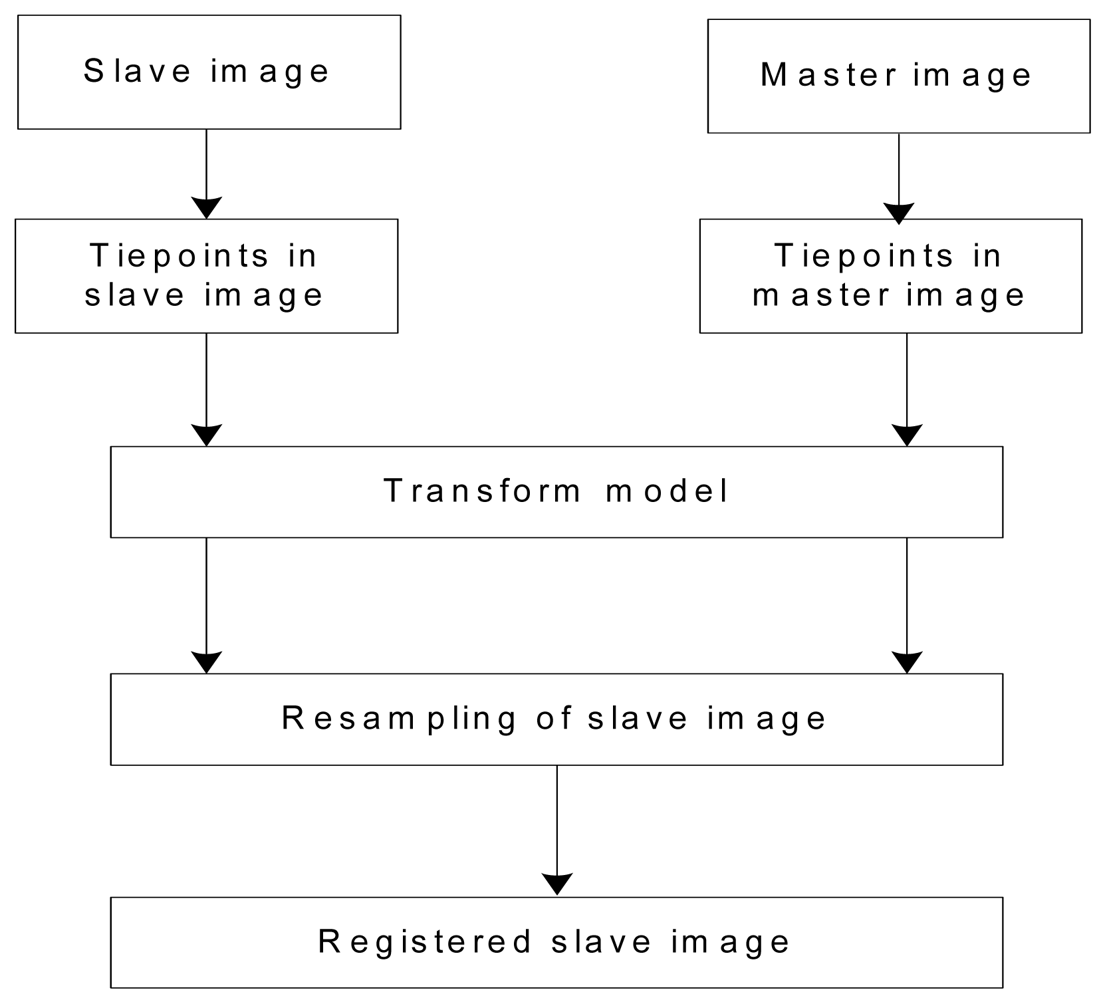
3.1. Co-registration of InSAR Image
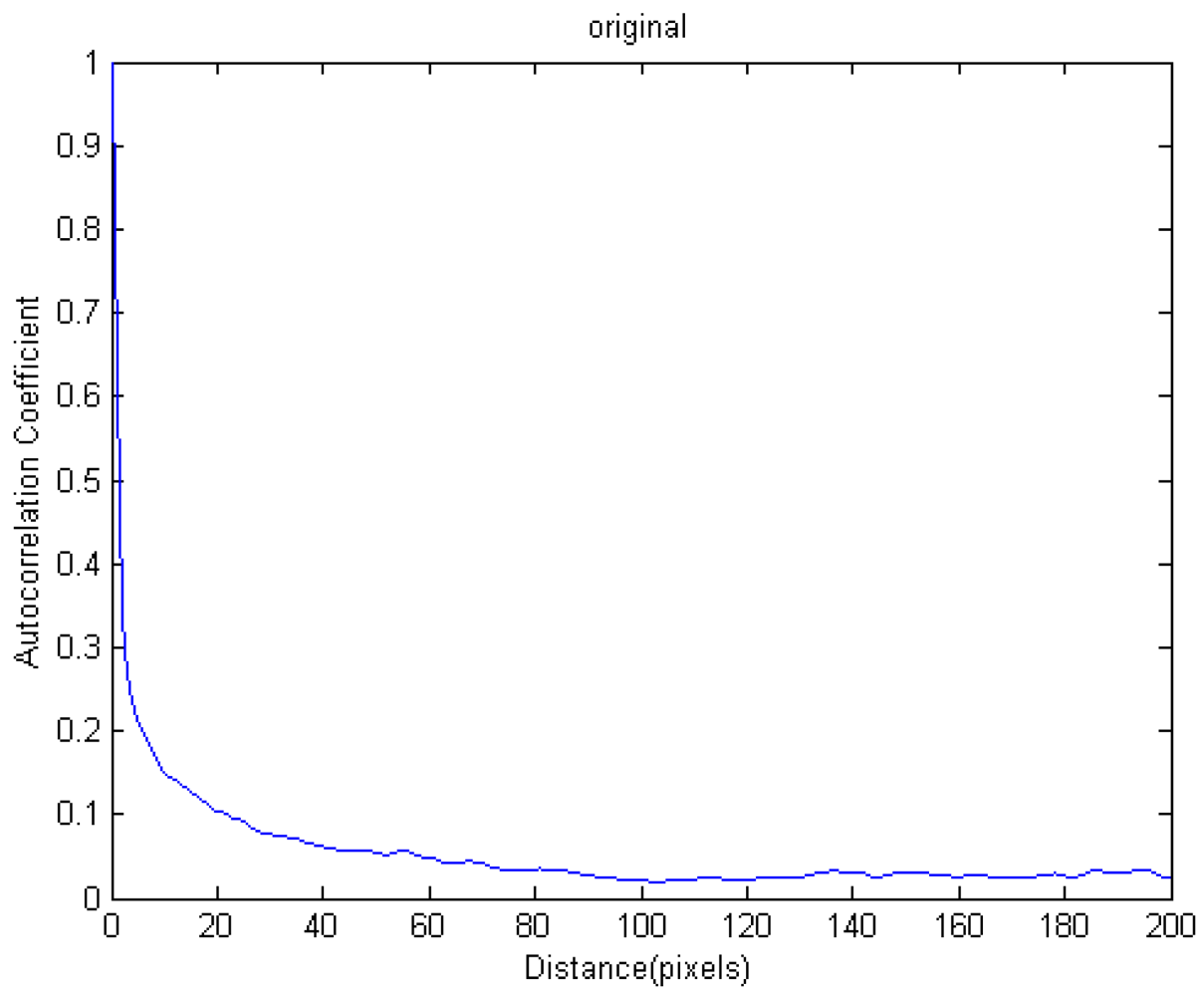
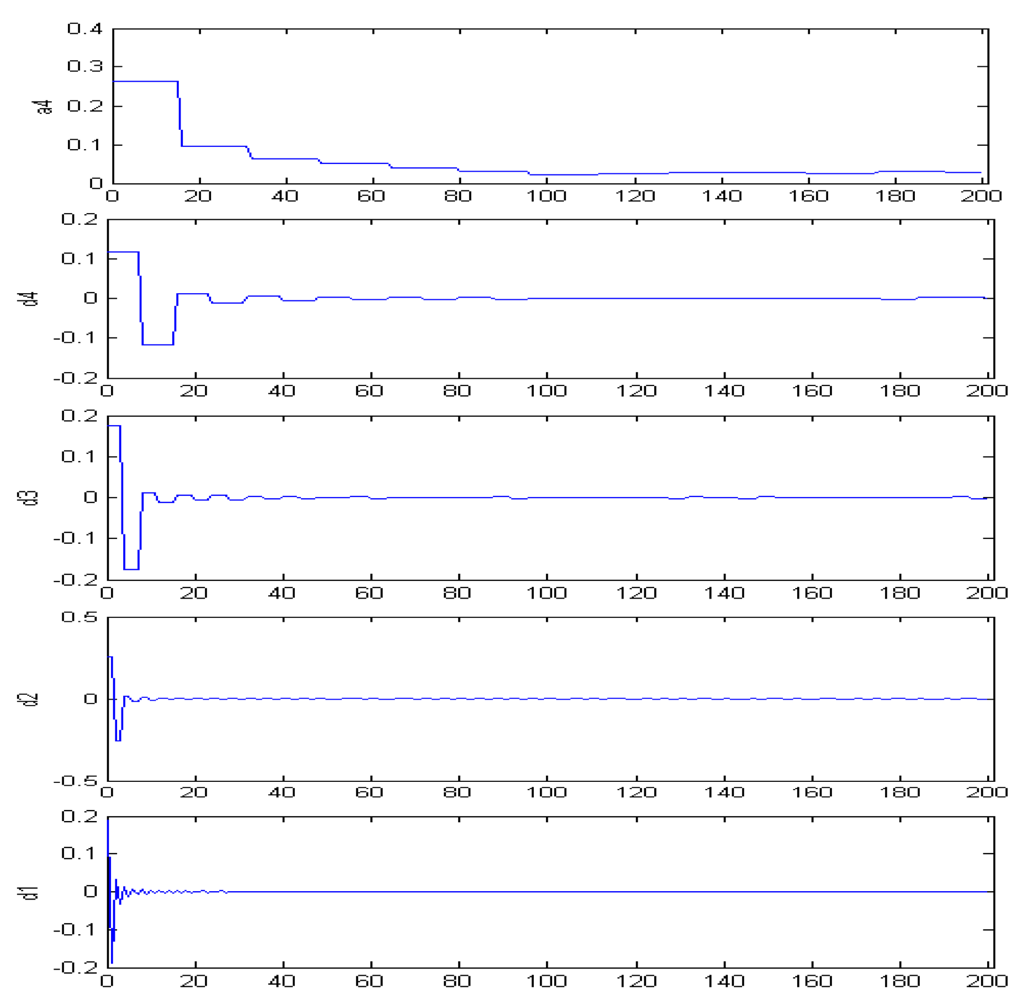
3.2. Determination of Interval of Tie Points for Co-registration
3.3. Extraction of Feature Points for Tie Point Matching
3.4. Strategy for Tie Point Matching
3.5. Determination of Window Size for Tie Point Matching
3.6. Selection of Transformation Models
3.7. Measurement for Quality of an Interferogram
4. Summary
Acknowledgments
References
- Zebker, H.A.; Rosen, P.A.; Goldstein, R.M.; Gabriel, A.; Werner, C.L. On the derivation of coseismic displacement fields using differential radar interferometry: The Landers earthquake. J. Geophys. Res. 1994, 99, 19617–19634. [Google Scholar]
- Hanssen, R.F. Radar Interferometry Data Interpretation and Error Analysis; Kluwer Acadamic Publishers Press: Dordrecht, Netherlands, 2000; p. 308. [Google Scholar]
- Rosen, P.A.; Hensley, S.; Zebker, H.A.; Webb, F.H.; Fielding, E.J. Surface deformation and coherence measurements of Kilauea Volcano, Hawaii, from SIR-C radar interferometry. J. Geophys. Res. 1996, 101, 23109–23125. [Google Scholar]
- Tobita, M.; Fujiwara, S.; Ozawa, S.; Rosen, P.A. Deformation of the 1995 North Sakhalin earthquake detected by JERS-1/SAR interferometry. Earth Planet. Space 1998, 50, 313–335. [Google Scholar]
- Liu, G.X. Mapping of earth deformations with satellite SAR interferometry: a study of its accuracy and reliability performances. Ph.D Dissertation, The Hong Kong Polytechnic University, Hong Kong, P.R. China, 2003. [Google Scholar]
- Askne, J.; Hagberg, J.O. Potential of interferometric SAR for classification of land surfaces. Proceedings of the International Geoscience and Remote Sensing Symposium, Tokyo, Japan, August 18-21, 1993; 3, pp. 985–987.
- Varkekamp, C.; Hoekman, D.H. Segmentation of high-resolution InSAR data of a tropic forest using Fourier parameterized deformable models. Int. J. Remote Sens. 2001, 22, 2339–2350. [Google Scholar]
- Wegmuller, U.; Werner, C. Retrieval of vegetation parameters with SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1997, 35, 18–24. [Google Scholar]
- Weydahl, D.J. Analysis of ERS SAR coherence images acquired over vegetated areas and urban features. Int. J. Remote Sen. 2001, 22, 2811–2830. [Google Scholar]
- Mattar, K.E.; Vachon, P.W.; Geudtner, D.; Gray, A.L.; Cumming, I.G.; Brubman, M. Validation of Alpine glacier velocity measurements using ERS tandem-mission SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 974–984. [Google Scholar]
- Joughin, I.R.; Kwok, R.; Fahnestock, A. Interferometric estimation of three-dimensional ice-flow using ascending and descending passes. IEEE Trans. Geosci. Remote Sens. 1998, 36, 25–37. [Google Scholar]
- Wangensteen, B.; Weydahl, D.J.; Hagen, J.O. Mapping glacier velocities at Spitsbergen using ERS tandem SAR data. Proceedings of International Geoscience and Remote Sensing Symposium, Hamburg, Germany, June 28 – July 2, 1998; 4, pp. 1954–1956.
- Ludwig, R.; Lampart, G.; Mauser, W. The determination of hydrological model parameters from airborne interferometric SAR-data. Int. J. Remote Sens. 1998, 2609–2611. [Google Scholar]
- Madsen, S.N.; Zebker, H.A.; Martin, J. Topographic mapping using radar interferometry: processing techniques. IEEE Trans. Geosci. Remote Sens. 1993, 31, 246–256. [Google Scholar]
- Shi, J.C.; Dozier, J.; Rott, H. Snow mapping in Alpine regions with synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 1994, 32, 152–158. [Google Scholar]
- Gens, R. Quality assessment of SAR interferometric data. Ph.D. Dissertation, Hanover University, Hanover, Germany, 1998. [Google Scholar]
- Hilland, J.E.; Stuhr, F.V.; Anthony, F.; Imel, D.; Shen, Y.; Jordan, R.; Caro, E.R. Future NASA spaceborne SAR missions. IEEE AES Syst. Mag. 1998, 11, 9–16. [Google Scholar]
- Burgett, S. Target location in WGS-84 coordinates using synthetic aperture radar images. Proceedings of the Institute of Navigation's 49th Annual Meeting; 1993; pp. 57–65. [Google Scholar]
- Guarino, R.; Ibsen, P. Integrated GPS/INS/SAR/GMTI radar precision targeting flight test results. Proceedings of the Institute of Navigation's 51th Annual Meeting; 1995; pp. 373–379. [Google Scholar]
- Li, J.; Zelnio, E. Target detection with Synthetic Aperture Radar. IEEE Trans. Aeros. Electron. Syst. 1996, 32, 613–627. [Google Scholar]
- Fotnaro, G. Trajectory deviations in airborne SAR: analysis and compensation. IEEE Trans. Aeros. Electron. Syst. 1996, 35, 997–1009. [Google Scholar]
- Zyl, J.J.V. The shuttle radar topography mission (SRTM): a breakthrough in remote sensing of topography. Acta Astron. 2001, 48, 559–565. [Google Scholar]
- Miliaresis, G.C.; Paraschou, C.V.E. Vertical accuracy of the SRTM DTED level 1 of Crete. Int. J. Appl. Earth Observ. Geoinf. 2005, 7, 49–59. [Google Scholar]
- Hofton, M.A.; Dubayah, R.; Blair, J.B.; Rabine, D. Validation of SRTM Elevations over vegetated and non-vegetated terrain using medium footprint Lidar. Photogramm. Eng. Remote Sens. 2006, 72, 279–285. [Google Scholar]
- Walker, W.S.; Kellndorfer, J.M.; Pierce, L.E. Quality assessment of SRTM C-and X-band interferometric data: implications for the retrieval of vegetation canopy height. Remote Sens. Environ. 2007, 106, 428–448. [Google Scholar]
- Renno, C.D.; Nobre, A.D.; Cuartas, L.A.; Soares, J.V.; Hodnett, M.G.; Tomasella, J.; Waterloo, M.J. HAND, a new terrain descriptor using SRTM-DEM: mapping terra-firme rainforest environments in Amazonia. Remote Sens. Environ. 2008, 112, 3469–3481. [Google Scholar]
- Berthier, E.; Arnaud, Y.; Vincent, C.; Remy, F. Biases of SRTM in high-mountain areas: implications for the monitoring of glacier volume changes. Geophys. Res. Lett. 2006, 33, L08502. [Google Scholar]
- Kaab, A. Remote sensing of permafrost-related problems and hazards. Permafr. Periglac. Proc. 2008, 19, 107–136. [Google Scholar]
- Rodriguez, E.; Morris, C.S.; Belz, J.E. A global assessment of the SRTM performance. Photogramm. Eng. Remote Sens. 2006, 72, 249–260. [Google Scholar]
- Braun, A.; Fotopoulos, G. Assessment of SRTM, ICESat, and survey control monument elevations in Canada. Photogramm. Eng. Remote Sens. 2007, 73, 1333–1342. [Google Scholar]
- Hubbard, B.E.; Sheridan, M.F.; Carrasco-Nunez, G.; Diaz-Castellon, R.; Rodriguez, S.R. Comparative lahar hazard mapping at volcan Citlaltepetl, Mexico using SRTM, ASTER and DTED-1 digital topographic data. J. Volcanol. Geothermal. Res. 2007, 160, 99–124. [Google Scholar]
- Schumann, G.; Matgen, P.; Cutler, M.E.J.; Black, A.; Hoffmann, L.; Pfister, L. Comparison of remotely sensed water stages from LiDAR, topographic contours and SRTM. ISPRS J. Photogramm. Remote Sens. 2008, 63, 283–296. [Google Scholar]
- Carabajal, C.C.; Harding, D.J. SRTM C-band and ICESat laser altimetry elevation comparisons as a function of tree cover and relief. Photogramm. Eng. Remote Sens. 2006, 72, 287–298. [Google Scholar]
- Guth, P.L. Geomorphometry from SRTM: Comparison to NED. Photogramm. Eng. Remote Sens. 2006, 72, 269–277. [Google Scholar]
- Van, Niel T.G.; McVicar, T.R.; Li, L.T.; Gallant, J.C.; Yang, Q.K. The impact of misregistration on SRTM and DEM image differences. Remote Sens. Environ. 2008, 112, 2430–2442. [Google Scholar]
- Kiel, B.; Alsdorf, D.; LeFavour, G. Capability of SRTM C- and X-band DEM data to measure water elevations in Ohio and the Amazon. Photogramm. Eng. Remote Sens. 2006, 72, 313–320. [Google Scholar]
- Gorokhovich, Y.; Voustianiouk, A. Accuracy assessment of the processed SRTM-based elevation data by CGIAR using field data from USA and Thailand and its relation to the terrain characteristics. Remote Sens. Environ. 2006, 104, 409–415. [Google Scholar]
- Goncalves, J.A.; Korgado, A.M. Use of the SRTM DEM as a geo-referencing tool by elevation matching. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, XXXVII, 879–883. [Google Scholar]
- Galiatsatos, N.; Donoghue, D.N.M.; Philip, G. High resolution elevation data derived from stereoscopic CORONA imagery with minimal ground control: an approach using Ikonos and SRTM data. Photogramm. Eng. Remote Sens. 2007, 74, 1093–1106. [Google Scholar]
- Huggel, C.; Schneider, D.; Miranda, P.J.; Grannados, H.D.; Kaab, A. Evaluation of ASTER and SRTM DEM data for lahar modeling: a case study on lahars from Popocatepetl volcano, Mexico. J. Volcanol. Geothermal. Res. 2008, 170, 99–110. [Google Scholar]
- Menze, B.H.; Ur, J.A.; Sherrat, A.G. Detection of ancient settlement mounds: archaeological survey based on the SRTM terrain model. Photogramm. Eng. Remote Sens. 2006, 72, 321–327. [Google Scholar]
- Luedeling, E.; Siebert, S.; Buerkert, A. Filling the voids in the SRTM elevation model – a TIN-based delta surface approach. ISPRS J. Photogramm. Remote Sens. 2007, 62, 283–294. [Google Scholar]
- Schetselaar, E.M.; Tiainen, M.; Woldai, T. Integrated geological interpretation of remotely sensed data to support geological mapping in Mozambique. Geol. Surv. Finland 2008, 48, 35–63. [Google Scholar]
- Zou, W.; Li, Z.; Ding, X. Effects of the intervals of tiepoints used in co-registration on the accuracy of digital elevation models (DEM) generated by InSAR. Photogramm. Rec. 2006, 21, 232–254. [Google Scholar]
- Zou, W.; Li, Z.; Ding, X. Determination of optimum window size for SAR image co-registration with decomposition of auto-correlation. Photogramm. Rec. 2007, 22, 237–255. [Google Scholar]
- Masoud, A.; Raghavan, V.; Masumoto, S.; Shiono, K. Repeat-pass JERS-1 INSAR for DEM Generation in Safaga Area, Red Sea Coast of Egypt. Geoinformatics 2002, 13, 84–85. [Google Scholar]
- Zhou, C.; Ge, L.; E, D.; Chang, H. A case study of using external DEM in InSAR DEM generation. Geo-Spat. Inf. Sci. 2005, 8, 14–18. [Google Scholar]
- Bamler, R.; Eineder, M.; Kampes, B.; Runge, H.; Adam, N. SRTM and beyond: current situation and new developments in spaceborne InSAR. Proceedings of the ISPRS Workshop on High Resolution Mapping from Space, Istanbul, Turkey, October 6-8, 2003; University Hannover Germany, International Society for Photogrammetry and Remote Sensing.
- Schulz-stellenfleth, J.; Horstmann, J.; Lehner, S.; Rosenthal, W. Sea surface imaging with an across-track interferometric synthetic aperture radar: The SINEWAVE experiment. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2017–2028. [Google Scholar]
- Lehner, S.; Gunther, H.; Horstmann, J.; Bao, M.; Schulz-Stellenfleth, J. Joint along-across track interferometry of ocean waves. Geoscience and Remote Sensing Symposium; 2001; 1, pp. 581–583. [Google Scholar]
- Gray, A.L.; Van der Kooij, M.W.A.; Mattar, K.E.; Farris-Manning, P.J. Progress in the development of the CCRS along-track interferometer. Geoscience and Remote Sensing Symposium; 1994; 4, pp. 2285–2287. [Google Scholar]
- Eberhard, G.; Hartmut, R. Tight formation flying for an along-track SAR interferometer. Acta Astron. 2004, 55, 473–485. [Google Scholar]
- Weydahl, D.J. Change detection in SAR images. In IEEE IGRSS; Espoo, Finland, June 3-6 1991; pp. 1421–1424. [Google Scholar]
- Lin, Q. New Approaches in Interferometric SAR Data Processing. IEEE Trans. Geosci. Remote Sens. 1992, 30, 560–567. [Google Scholar]
- Zebker, H.A.; Werner, C.L.; Rosen, P.A.; Hensley, S. Accuracy of topographic maps derived from ERS-1 interferometric radar. IEEE Trans. Geosci. Remote Sens. 1994, 32, 823–836. [Google Scholar]
- Guarnieri, A.M.; Prati, C. SAR Interferometry: A “Quick and Dirty” Coherence Estimatior for DATA Browsing. IEEE Trans. Geosci. Remote Sens. 1997, 35, 660–669. [Google Scholar]
- Bamler, R.; Just, D. phase statistics and decorrelation in SAR interferograms. IEEE International Geoscience and Remote Sensing Symposium, Tokoy, Japan, Aug 18-21, 1993; pp. 980–984.
- Lim, I.; Yeo, T.S.; Ng, C.S.; Lu, Y.H.; Zhang, B.C. Phase noise filter for interferometric SAR. IEEE Int. Geosci. Remote Sens. 1997, 1, 445–447. [Google Scholar]
- Ainsworth, T.L.; Lee, J.S. A joint adaptive interferometric phase unwrapping and filtering algorithm. IEEE IGRSS. 1998, 1, 71–73. [Google Scholar]
- Bamler, R.; Adam, N.; Davidson, G.W.; Just, D. Noise-induced slope distortion in 2-D phase unwrapping by linear estimators with application to SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1998, 36, 913–921. [Google Scholar]
- Bao, M.; Kwoh, L. K.; Singh, K. An improved least-squares method for INSAR phase unwrapping. IEEE IGRSS. 1998, 1, 62–64. [Google Scholar]
- Wivell, C.E.; Steinwand, D.R.; Kelly, G.G.; Meyer, D.J. Evaluation of terrain models for the geocoding and terrain correction of synthetic aperture radar (SAR) image. IEEE Trans. Geosci. Remote Sens. 1992, 30, 1137–1143. [Google Scholar]
- Liao, M.; Lin, H.; Zhang, Z.X. Automatic registration of InSAR data based on Least-square matching and multi-step strategy. Photogramm. Eng. Remote Sens. 2004, 70, 1139–1144. [Google Scholar]
- Abdelfattah, R.; Nicolas, J.-M. Sub-pixelic Image Registration for SAR Interferometry Coherence Optimization. Proceedings of the XXth ISPRS Congress, Istanbul, Turkey, July 12-23, 2004; XXXV, p. 3.
- Wan, F.G. Digital Processing of Remotely Sensed Images; Huazhong Polytechnical University, 1990. [Google Scholar]
- Yang, Q. Y.; Wang, C. Registration of INSAR complex images and interferogram enhancement. J. Remote Sens. 1999, 3, 122–131. (In Chinese) [Google Scholar]
- Liu, G.X.; Ding, X.L.; Li, Z.L.; Chen, Y.Q.; Zhang, G.B. Co-registration of satellite SAR complex images. Acta Geod. Cartogr. Sinica. 2001, 30, 60–66. (in Chinese). [Google Scholar]
- Zou, W.; Li, Z.; Ding, X.; Chen, Y.; Liu, G. Effects of the interval of tiepoints on the reliability of SAR image co-registration. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Xi'an, China, Aug 20-23, 2002; XXXIV, pp. 639–644.
- Urban, M. Harris Interest Operator. http://cmp.felk.cvut.cz/cmp/courses/dzo/resources/lecture_harris_urban.pdf, 2003. (accessed 2 January 2008).
- Moigne, J.L.; Campbell, W.J.; Cromp, R.F. An Automated Parallel Image Registration Technique Based on the Correlation of Wavelet Features. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1849–1864. [Google Scholar]
- Zou, W.B. Improving the Accuracy of Image Co-registration in InSAR. Ph.D. Dissertation, Hong Kong Polytechnic University, 2005. [Google Scholar]
- Franceschetti, G.; Lanari, R. Synthetic Aperture Radar Processing; CRC Press: New York, NY, USA, 1999. [Google Scholar]
- Shi, X.; Zhang, Y.; Jiang, J. InSAR image registration using modified correlation coefficient algorithm. ISAPE '06 7th International Symposium on Antennas, Propagation & EM Theory; 2006; pp. 1–4. [Google Scholar]
- Li, Z.; Fan, X.T. Registration between remote sensing images based on multi-window cross-correlation. J. Image Graph. A 2001, 6, 129–132. (in Chinese). [Google Scholar]
- Li, Z. L. Orthoimage Generation and Measurement from Single Images. In Geographical data acquisition; Chen, Y.Q., Lee, Y.CH., Eds.; Springer: Wien, NewYork, 2001; pp. 173–183. [Google Scholar]
- Wolf, P.R.; Dewitt, B.A. Elements of Photogrammetry with Applications in GIS, 3rd Ed. ed; McGraw-Hill Science Engineering: New York, NY, USA, 2000. [Google Scholar]
- Zou, B.; Hao, L.; Bao, X. An accurate co-registration method of spaceborne repeat-pass InSAR based on matrix transformation. IEEE IGRSS 2005, 7, 4560–4563. [Google Scholar]
- Eldhuset, K.; Aanvik, F.; Aksnes, K. First results from ERS tandem InSAR processing on Svalbard. http://www.geo.unizh.ch/rsl/fringe96/papers/eldhuset-et-al/, 1996. (accessed 8 January 2008).
- Li, Z.; Zou, W.B.; Ding, X.L.; Chen, Y.Q.; Liu, G.X. A quantitative measure for the quality of InSAR interferogram based on phase differences. Photogramm. Eng. Remote Sens. 2004, 70, 1131–1137. [Google Scholar]
- Li, Z.W.; Ding, X.L.; Huang, C.; Zheng, D.W.; Zou, W.B. Filtering method for SAR interferograms with strong noise. Int. J. Remote Sens. 2006, 27, 2991–3000. [Google Scholar]





© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zou, W.; Li, Y.; Li, Z.; Ding, X. Improvement of the Accuracy of InSAR Image Co-Registration Based On Tie Points – A Review. Sensors 2009, 9, 1259-1281. https://doi.org/10.3390/s90201259
Zou W, Li Y, Li Z, Ding X. Improvement of the Accuracy of InSAR Image Co-Registration Based On Tie Points – A Review. Sensors. 2009; 9(2):1259-1281. https://doi.org/10.3390/s90201259
Chicago/Turabian StyleZou, Weibao, Yan Li, Zhilin Li, and Xiaoli Ding. 2009. "Improvement of the Accuracy of InSAR Image Co-Registration Based On Tie Points – A Review" Sensors 9, no. 2: 1259-1281. https://doi.org/10.3390/s90201259
APA StyleZou, W., Li, Y., Li, Z., & Ding, X. (2009). Improvement of the Accuracy of InSAR Image Co-Registration Based On Tie Points – A Review. Sensors, 9(2), 1259-1281. https://doi.org/10.3390/s90201259




