1. Introduction
The concept of particle swarms originated from the simulation of the social behavior commonly observed in animal kingdom and evolved into a very simple but efficient technique for global numerical optimization in recent past. The Particle Swarm Optimization (PSO) [
1,
2], as it is called now, does not require any gradient information of the function to be optimized, uses only primitive mathematical operators and is conceptually very simple. PSO emulates the swarming behavior of insects, animals herding, birds flocking and fish schooling, where these swarms forage for food in a collaborative manner. PSO also draws inspiration from the boids method of Craig Reynolds and Socio-Cognition [
2].
Since its inception, the research on PSO has centered on the improvement of the particle dynamics and the algorithm. Shi and Eberhart incorporated the
inertia factor [
3] in the basic PSO dynamics for faster convergence of the algorithm. Clerc and Kennedy [
4] considered in their work an alternative form of PSO dynamics using a parameter called
constriction factor, and gave a detailed theoretical analysis to determine the value of the parameter. Eberhart and Shi compared the effect of inertia factor and constriction factor on PSO performance [
5]. Angeline [
6] introduced a form of selection operation in the PSO algorithm, so that the characteristics of good particles are transferred to the less effective members of the swarm to improve their behavior. Suganthan [
7] employed a neighborhood operator in the basic particle swarm optimization scheme to study the swarm behavior. Extension of the PSO algorithm to deal with dynamic environment and efficient explorations are undertaken in [
8,
9]. Ratnaweera
et al., while proposing a new model of self-organizing hierarchical PSO [
10], ignored the term involving inertia factor from the velocity adaptation rule. Another contribution of this paper is the inclusion of time-varying inertia weight and time-varying acceleration coefficients for better performance of the algorithm.
In [
11], a new crossover operator is defined to swap information between two individuals in order to determine their next position on the search landscape. Miranda
et al. in [
12] proposed a mutation operator on the parameters of the PSO dynamics and the position of the neighborhood best particle, so as to enhance the diversity of the particles, thereby increasing the chances of escaping local minima. In [
13], the inertia weight is mutated and the particles are relocated when they are too close to each other. A further increase in the diversity of the population has been attained in [
14,
15] through introduction of a new collision-avoiding mechanism among the particles. Xie
et al. [
16] added negative entropy to the PSO to discourage premature convergence. In [
2], a cooperative PSO (CPSO) is implemented to significantly improve the performance of the classical PSO. Hendtlass
et al. [
17] combined Ant Colony Optimization with PSO to determine the neighborhood best of a particle from a list of best positions found so far by all the particles.
Most of existing works on PSO refer to single objective optimization problems. Coello
et al. first proposed a formulation of multi-objective optimization problem using PSO [
18], and later extended it to include a constraint-handling mechanism and a mutation operator [
19] to improve the power of exploration of the optimization algorithm. Agrawal, Panigrahi and Tiwari [
20] in a recent paper proposed a fuzzy clustering-based PSO algorithm to solve the highly constrained environmental/economic dispatch problem involving conflicting objectives.
There exists an extensive literature on improving the performance of the PSO algorithm. This has been undertaken by two alternative approaches. First, the researchers are keen to improve swarm behavior by selecting the appropriate form of the swarm dynamics. Alternatively, considering a given form of particle dynamics, researchers experimentally, or theoretically, attempted to find the optimal settings of the range of parameters to improve PSO behavior. In this paper, we adopt the first policy to determine a suitable dynamics, and then attempted to empirically determine the optimal parameter settings.
The classical PSO dynamics adapts the velocity of individual particles by considering the inertia of the particle and the position of local and global attractors. The positions of the attractors are also adapted over the iterations of the algorithm. The motion of the particles thus continues until most of the particles converge in the close vicinity of the global optima. In this paper, we consider different versions of the swarm dynamics to study the relative performance of the PSO algorithm both from the point of view of accuracy and convergence time.
The formal basis of our study originates from the well-known Lyapunov's theorem of classical control theory. The Lyapunov's theorem is widely used in nonlinear system analysis to determine the necessary conditions for stability of a dynamical system. In this paper, we indirectly used Lyapunov's stability theorem to determine a dynamics that necessarily converges to an optima of the Lyapunov-like search landscape. The principles of guiding particle dynamics towards the global and local optima, here too, is ensured by adding local and global attractor terms to the modified PSO dynamics. The rationale of selecting a dynamics that converges at one of the optima on a multimodal surface, and the principle of forcing the dynamics to move towards local and global optima together makes it attractive for use in continuous nonlinear optimization.
There are, however, search landscapes that do not possess the necessary characteristics of a Lyapunov surface. This calls for an alternative dynamics, which maintains the motivation of this research but can avoid the restriction on the objective function to necessarily be Lyapunov-like. A look at the dynamics constructed for Lyapunov-like benchmark functions essentially reveals an inclusion of a negative position term in the velocity adaptation rule. This prompted us to realize different variants of the classical PSO dynamics, such as (a) replacement of the inertial term by a negative partial derivative of the Lyapunov-like search landscape, (b) inclusion of a negative particle position in the velocity adaptation rule, (c) replacement of the inertial term by the negative positional term in the dynamics. Computer simulations undertaken on a set of eight benchmark functions reveals that the modifications in the PSO dynamics results in a significant improvement in the PSO algorithm with respect to both convergence speed and accuracy. Note that the extensions developed in this article are primarily meant for fast and accurate optimization of continuous and differentiable functions, as all of them involve first derivatives of the objective function to be used.
The rest of the paper is organized as follows. Section 2 provides a set of formal definitions on Lyapunov stability of nonlinear dynamics. It explains the basis of selection of a dynamics for a given Lyapunov-like objective function. The rationale of speed-up of the proposed swarm algorithm using the selected dynamics is given in this section. Experimental results over several numerical benchmarks are presented in Section 3. Finally the paper is concluded in Section 4.
2. Proposed Extensions of the Classical PSO Dynamics
In this section, we briefly outline one typical PSO dynamics, and the PSO algorithm. We next present the possible modifications that we need to undertake in the dynamics to study their relative performance with the classical PSO algorithm.
The global-best (g-best) PSO dynamics for the
jth particle is given in vector form through
Equations 1 and
2:
where:
Vj(t) = [vj1(t) vj2(t)…………… vjD(t)] is a D-dimensional velocity vector at time t,
Xj(t) = [xj1(t) xj2(t)…………… xjD(t)] is a D-dimensional position vector at time t,
is a D-dimensional personal (local) best position vector of particle j, so far achieved until iteration t,
is a D-dimensional global best position vector found so far by the entire swarm at iteration t.
Empirically, ω is a random no. in [0,1], αl(t) and αg(t) are random coefficients in [0, 2] and [0, 4] respectively. Inertia factor ω is selected randomly only once in the PSO algorithm, whereas αl(t) and αg(t) are selected randomly in each iteration of the PSO algorithm.
The basic PSO algorithm is presented here for convenience of the readers. The notion of time t is dropped from the algorithm for simplicity.
PSO-Algorithm
Begin
Initialize population;
While terminating conditions not reached do
Begin
For j = 1 to N do // N = Number of particles//
Begin
Evaluate fitness f(·)of particle j;
If For j = 1 to N do
Begin
Adapt
Adapt Xj = Xj + Vj;
End for;
End while;
End.
A look at the PSO algorithm reveals that it attempts to determine the optima on a search landscape by allowing several particles (agents) to explore on the surface with an ultimate aim to terminate at the global optima. The terminating condition usually includes an upper limit on the iterations or a lower limit to the unsigned successive difference in the best particle position, or whichever occurs earlier.
In the next sub-section, we would look for a dynamics that has a tendency to move towards optima, which need not essentially be the global optima. This can be attained by identifying a suitable dynamics that ensures asymptotic stability in the vicinity of an optimum over the search landscape. This, of course, needs additional restriction on the surface to satisfy the necessary conditions to be Lyapunov-like [
24]. If a suitable dynamics ensuring the convergence to an optimum is identified, we can control the motion of the particles towards the global/local optima by adding global and local attractors in the dynamics as used in the PSO dynamics.
2.1. Identifying a Stable Dynamics for a Lyapunov-like Surface
This section begins with a few definitions, available in the standard literature in Nonlinear Control Theory in [
21-
24], to explain the methodology of determining a stable dynamics for a Lyapunov-like surface. In what follows we shall use the following special notations: ‖X‖ to define the Euclidean norm of a vector.
S(ε) to denote an ε-neighborhood surrounding a point defined by the position-vector Xe. S(ε) is basically a set containing all the points in the vector space for which ‖X − Xe‖ ≤ ε.
Definition 2.1
A point X = X
e is called an
equilibrium state, if the dynamics of the system which is given by
becomes zero at X = X
e for any
t. The equilibrium state is also called equilibrium (stable) point in
D-dimensional hyperspace, when the state X
e has
D-components.
Definition 2.2
A scalar function V(X) is said to be positive definite with respect to the point Xe in the region ‖X − Xe‖ ≤ K, if V(X) > 0 at all points of the region except at Xe where it is zero.
Note that V(X) will be called negative definite if −V(X) is positive definite. A scalar function V(X) is said to be indefinite in the region ‖X − Xe‖ ≤ K, if it assumes both positive and negative values within this region.
Definition 2.3
A scalar function V(X) is said to be positive semi-definite with respect to the point Xe in the region ‖X − Xe‖ ≤ K, if its value is positive at all points of the region except at finite number of points including origin where it is zero.
Note that similar as definition 2.2, the scalar function V(X) is said to be negative semi-definite if –V(X) is positive semi-definite.
Definition 2.4
A scalar function
V(X) is called a
Lyapunov surface with respect to the origin, if it satisfies the three conditions listed below:
Definition 2.5
A dynamics
dX
/dt =
f(X(
t)) is
asymptotically stable at the equilibrium point X
e, if
it is stable in the sense of Lyapunov, i.e., for any neighborhood S(ε) surrounding Xe there is a region S(δ), δ < ε, such that trajectories of the dynamics starting within S(δ) do not leave S(ε) as time t → ∞ and
the trajectory starting within S(δ) converges to the origin as time t approaches infinity
The sufficient condition for stability of a dynamics can be obtained from the Lyapunov's theorem, presented below.
Lyapunov's Stability Theorem [21]
Given a scalar function
V(X) and some real number ε > 0, such that for all X in the region S(ε) the following conditions hold:
Then the equilibrium state X
e of the system
dX
/dt =
f(X(
t)) is
asymptotically stable if dV/dt is negative definite, and
asymptotically stable in the large if dV/dt is negative definite, and in addition, V(X) → ∞ as ‖X − Xe‖ → ∞
Example 1
Let
be a Lyapunov energy function for the given dynamics
and
with the equilibrium point X
e = [0,0]. Then:
i.e., negative definite.
Here, V(X) satisfies the first two criterions indicated in the theorem, and the partial derivatives ∂V/∂x1 and ∂V/∂x2 are also continuous functions of x1 and x2. Consequently, the asymptotic stability of the dynamics is ensured as dV/dt is found to be negative definite for all points except at x = 0. Further, as ‖X‖ → ∞, V(X) also approaches infinity. Therefore, the asymptotic stability of the dynamics in the large is also ascertained.
The condition for asymptotic stability, as indicated in Theorem1, can be applied to the particle swarm optimization to ensure stability of the dynamics, thereby reducing the convergence time of the algorithm.
When all the three underlying conditions of a Lyapunov function, indicated in Definition 2.4 are supported by the objective function, we would be interested to determine the dynamics that satisfies the necessary conditions for asymptotic stability of the dynamics. It follows from Lyapunov's Theorem that the asymptotic stability of an equilibrium state guided by the dynamics
dxi/dt is ascertained if:
The inequality (3) essentially holds when:
It is indeed important to note that the condition (4) holds for the
i-th dimension of a particle roaming over the Lyapunov-like surface for 1 ≤
i≤
D.
Example 2
In this example, we would like to determine a stable dynamics for a Lyapunov-like objective function. Consider for instance the Griewank function in D-dimension:
In order to have asymptotic stability of the dynamics, we set:
It is also apparent to note that the given function
f(X) satisfies the three necessary conditions of a Lyapunov function. Now, if we replace the term involving inertia factor by the obtained value of
dxi/dt in the PSO dynamics, then the PSO is expected to converge very quickly as the necessary condition for asymptotic stability has been satisfied while deriving the dynamics:
Table 1 provides a list of eight typical benchmark functions along with the derived expressions for
dxi/dt that ensures the asymptotic stability of the derived dynamics over the Lyapunov-like objective function.
We now define Lyapunov-based PSO dynamics (LyPSO) by adding the local and global attractor terms of classical PSO to the derived expression for asymptotically stable Lyapunov dynamics, given in
Equations (5) and
(6):
Note that ∇⃗
f = [∂
f/∂
x1,…, ∂
f/∂
xD] denotes the gradient of the scalar function
f to be optimized. The first term in the right hand side of
Equation (5) ensures motion of the particle towards minima, while the second and third term controls the motion towards local and global optima respectively. It is apparent from
Table 1 that
dxi/dt obtained for different Lyapunov-like surfaces include a factor of (−
xi). The condition for
dxi/dt = −
ωxi is tabulated for all the eight benchmark functions in
Table 2. Consequently, instead of computing
dxi/dt by the approach stated earlier, we can simply add a term –
ωxi to the
ith component of the updated velocity in the classical PSO. The resulting dynamics then looks like
Equations (7) and
(8):
The dynamics given by
Equations (7) and
(8) is referred to as Position-based PSO (PPSO).
For the sake of completeness of our study, we consider a third category of the dynamics, where the inertial term is dropped from the PSO dynamics, indicated in
Equations (9) and
(10). The modified dynamics, called Steepest-PSO (SPSO) for its fast convergence (vide Section 3), is formally given below:
In the next section, we would justify the reason for accuracy and speed-up of PPSO and SPSO over classical PSO.
2.2. The Rationale of Speed-up of the PPSO and SPSO Dynamics over Classical PSO
To compare the relative performance in speed-up and convergence of the proposed algorithms, we study the stability behavior of the proposed PPSO and SPSO dynamics, in absence of the local and the global attractors. This is performed by solving the first order difference equations. The condition for asymptotic stability and the location of the stable point can be ascertained from the solution of the dynamics. Theorems 1 to 2 provide interesting results, indicating asymptotic stability of the SPSO and PPSO dynamics to the origin irrespective of the search landscape, whereas Theorem 3 indicates asymptotic stability of the classical PSO to a stable point, which need not essentially be the origin. The rate at which the particle position approaches the origin further indicates that the speed of convergence of the SPSO algorithm far exceeds that of PPSO, while the speed of PPSO algorithms beats classical PSO.
Theorem 1
The dynamics of the jth particle in the ith dimension given byhas a stable point at the origin, when ω ≤ 1.
Proof
Let
E be an extended difference operator, such that
Now extending the concept of derivatives to the discrete time domain,
Equation (11) now can be written as
Replacing
xj,i (
t+1) by E(
xj,i (
t)) in (12) we obtain:
Consequently, the solution of the dynamics (11) is given by
where A is a constant. The expression (13) indicates that for
ω < 1,
xj,i (
t)→0 when
t→∞.Therefore, the dynamics is asymptotically stable at the origin for
ω < 1. When
ω = 1,
xj,i (
t) = 0 at all time
t. Hence, the theorem follows.
Theorem 2
The dynamics of the jth particle in the ith dimension given by Is asymptotically stable with a stable point at the origin, when ω < 1.
Proof
Replacing
xj,i (
t + 1) by
E(
xj,i(
t)) and
xj,i (
t − 1) by
E−1(
xj,i(
t)) in
Equation (15), we obtain
So, the solution of the dynamics (16) is given by:
where A and B are constants. It is apparent from expression (16) that
xj,i(
t) asymptotically converges to the origin for
ω < 1. Therefore, the dynamics is asymptotically stable with a stable point at the origin for
ω < 1. When
ω = 1,
xi(
t) = 0 for all
t. This proves the Theorem.
Theorem 3
The dynamics of jth particle in the ith dimension given by:is asymptotically stable and it converges to a stable point, which need not essentially be zero.
Proof
Let
E be an extended difference operator, such that
Enxj,i(
t) =
xj,i(
t +
n), and
E−nxj,i(
t) =
xj,i(
t −
n) for any positive integer
n. Consequently,
Equation (18) is transformed to:
So, the solution of the dynamics (17) is given by:
whereAand Bare constants. It is apparent from expression (21) that xj,i(t) asymptotically converges to Aas time tapproaches infinity. SinceAis not zero unconditionally, therefore the statement of the theorem follows.
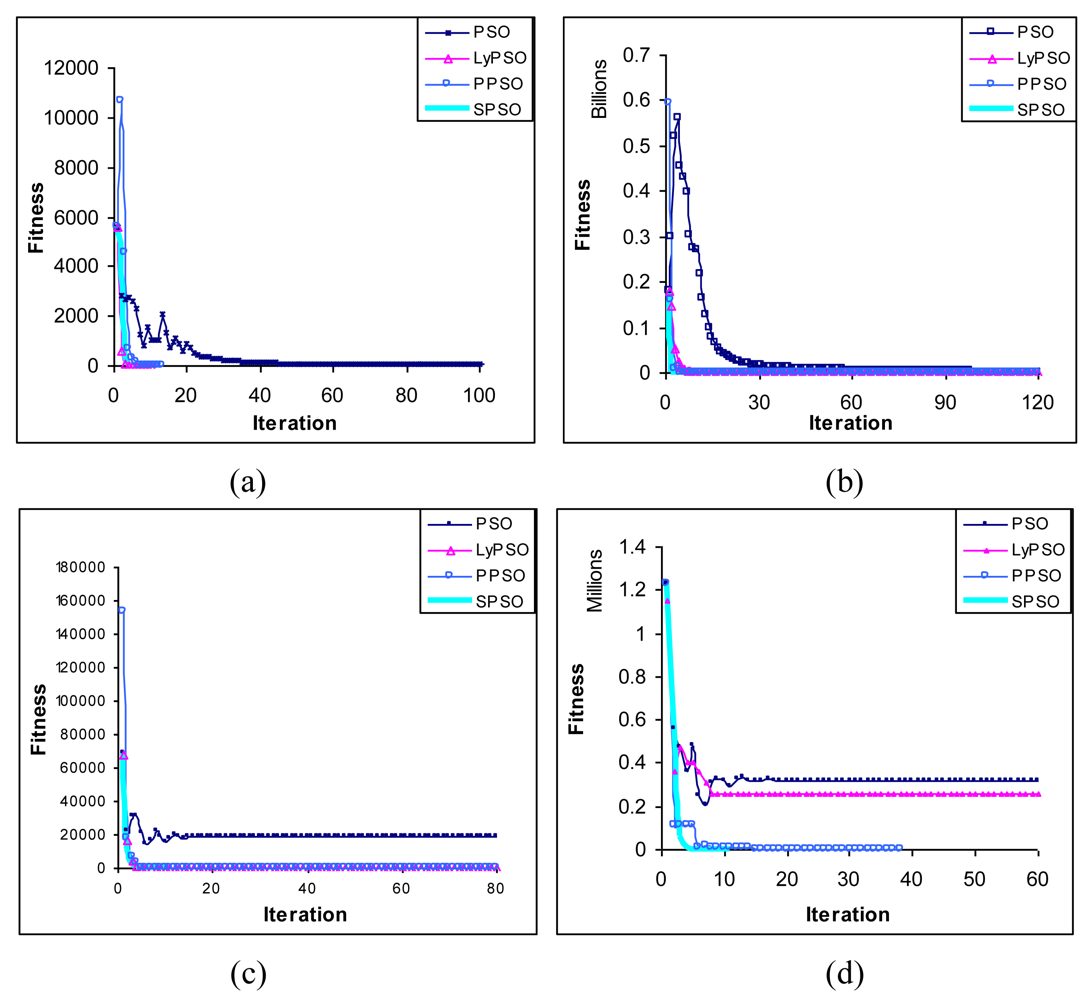
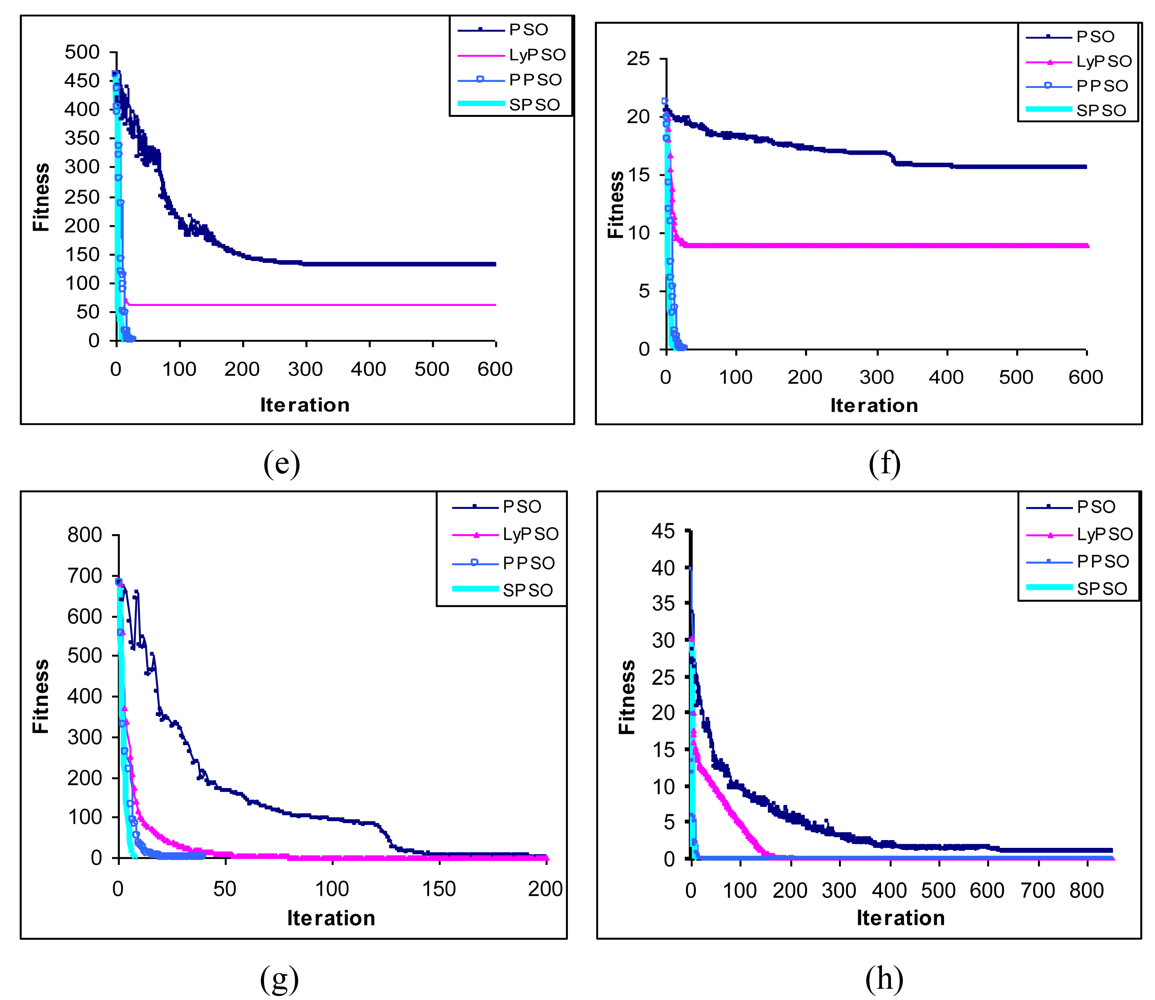
Table 3 provides the results of computation of dxi/dt for SPSO, PPSO and classical PSO. The computations in the table are performed from
Equations 13,
16 and
19 respectively.
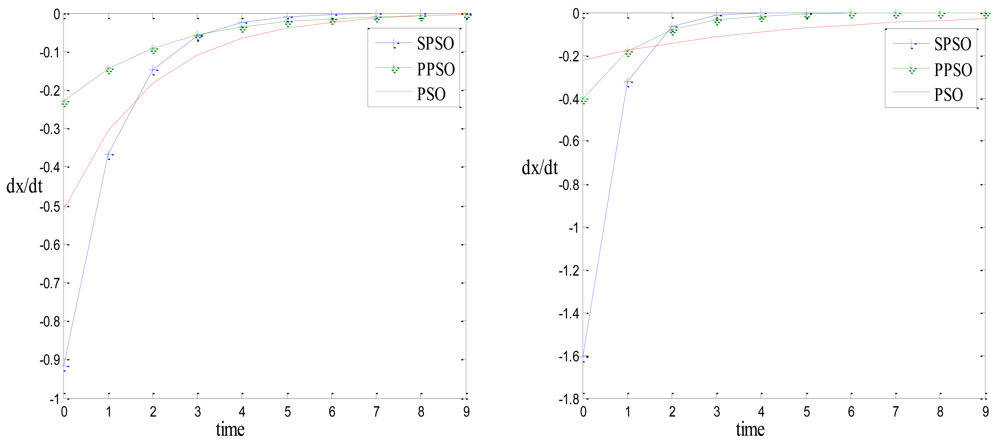
Figure 1 shows the variation of dxi/dtwith respect to time forω=0.6 andω=0.8. It is apparent from the graphs that in the absence of local and global attractors, the dynamics of SPSO converges faster than that of PPSO, which further converges faster than the classical PSO.
4. Conclusions
Classical g-best PSO has a proven impact in optimization of multi-modal nonlinear objective functions. However, for many nonlinear continuous multi-modal functions, where partial derivatives with respect to objective function variables exist, classical g-best PSO is not very efficient as it does not utilize gradient information of the search landscape. The paper bridges the gap between gradient-free and gradient-based optimization algorithm. It does not truly utilize gradient information of the search space, but it requires the background information that the gradient of the surface exists. When the prerequisite knowledge about the search space is known, we extend the classical g-best PSO algorithm by the principles outlined in the paper.
Three alternative approaches to improve the speed of convergence of the PSO dynamics over continuous fitness landscapes is discussed in the paper. The first approach attempted to replace the inertial term in the dynamics by a factor that ensures asymptotic stability of the PSO dynamics. Construction of such dynamics presumes the characteristics of the surface being Lyapunov-like. This, however, is not a very restrictive assumption as many multi-modal surfaces support the conditions for Lyapunov function. On the contrary, the Lyapunov-based extension, even without local and global attractors, has a natural tendency to move towards optima on the surface. The convergence of the algorithm to local and global optima, however, is controlled by the presence of attractors in the PSO dynamics.
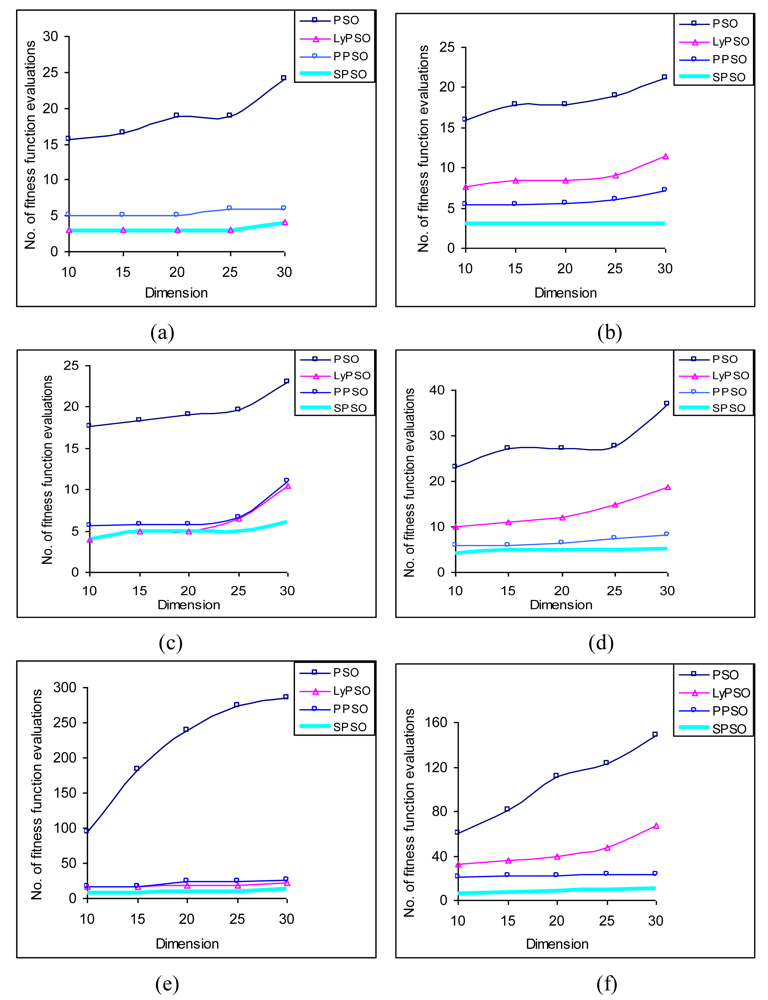
The second alternative approach to make the PSO smarter was derived from the Lyapunov-based formulation, just by noting that the Lyapunov-based dynamics includes a factor of negatively weighted position of the particle. Incorporation of this new term to the existing velocity adaptation rule classical PSO gives birth to the second alternative form of the extended PSO dynamics. The resulting dynamics has been found to have asymptotic stability for a selective range of ω < 1, i.e., same as in classical PSO. The third extension lies in replacement of the inertial term by the negative position of the particle itself. A random factor is attached to this term to maintain explorative power of the PSO dynamics to avoid its premature convergence. Computer simulations undertaken ensure that the third alternative form of extended PSO dynamics results in significant improvement in convergence time and accuracy compared to the results obtained by the first and second attempt. However, all three approaches outperform the classical PSO dynamics from the point of view of the convergence time and accuracy.
Future research efforts will focus on the extensions of Lyapunov-based dynamics of gbest PSO for handling non-continuous multi-modal functions. The particle dynamics will be combined with an estimate of the gradient of the function, instead of using any analytical expression of the partial derivatives of the objective function. Also the Lyapunov-based particle dynamics will be examined in context to non-linearly constrained optimization problems, where only a portion of the search space will be used to generate feasible optimal solutions.