Thin Magnetically Soft Wires for Magnetic Microsensors
Abstract
:1. Introduction
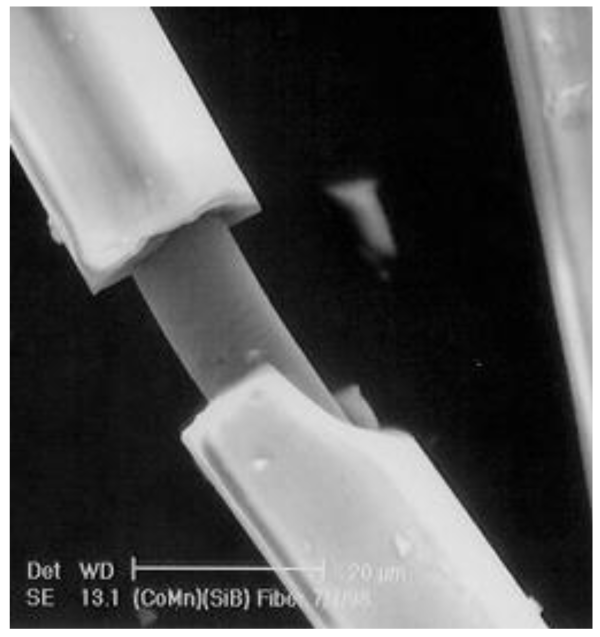
2. Results and Discussion
2.1. Effect of composition. Properties relevant for applications
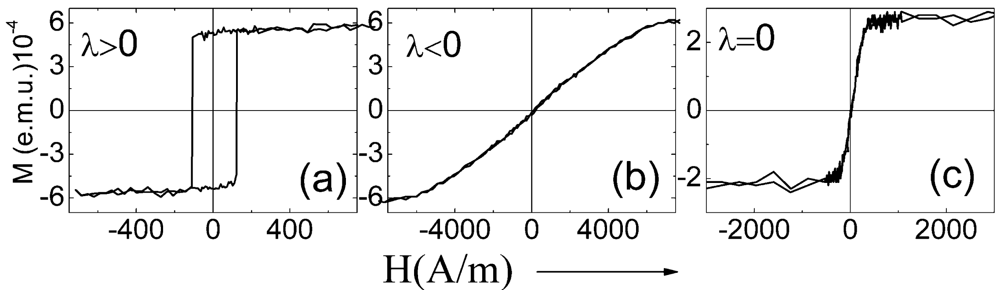
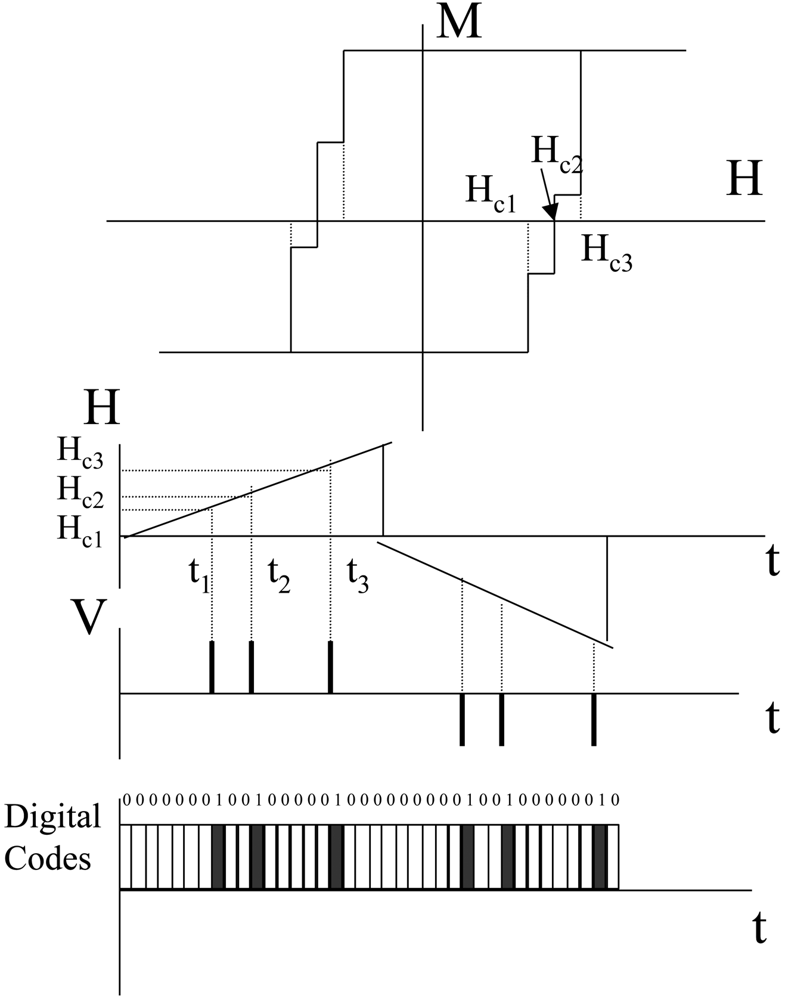
2.2. Magnetic bistability
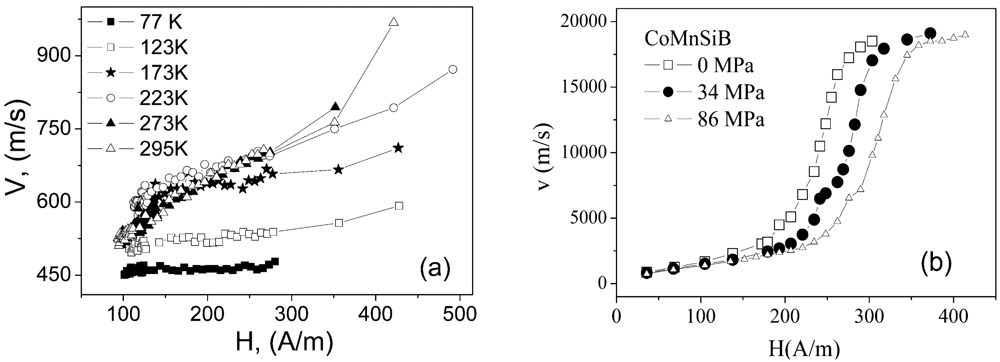
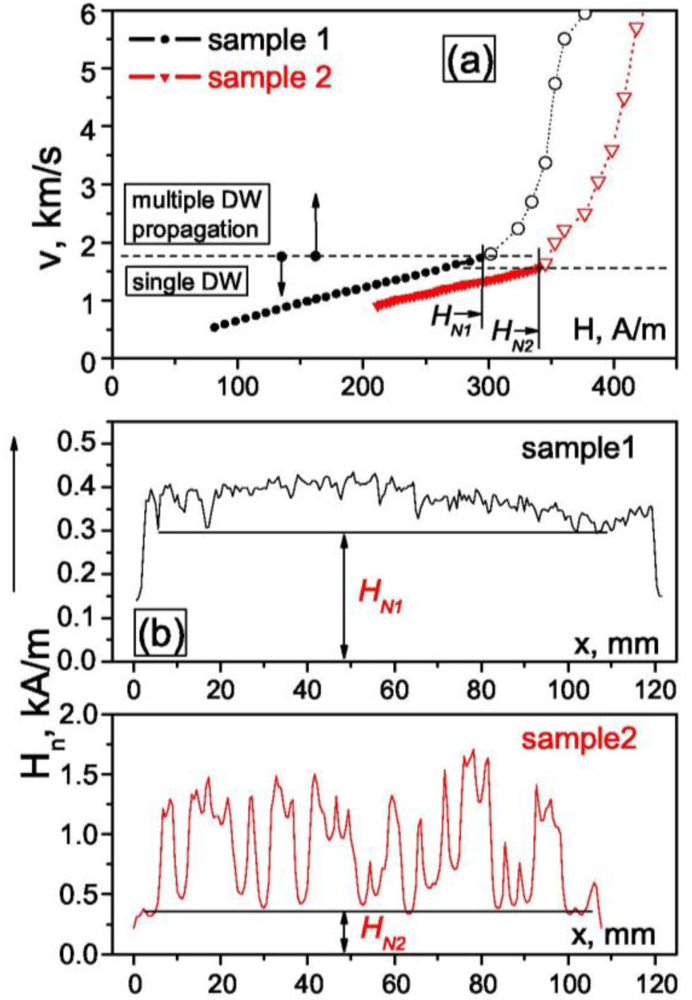
2.3. Fast domain wall propagation
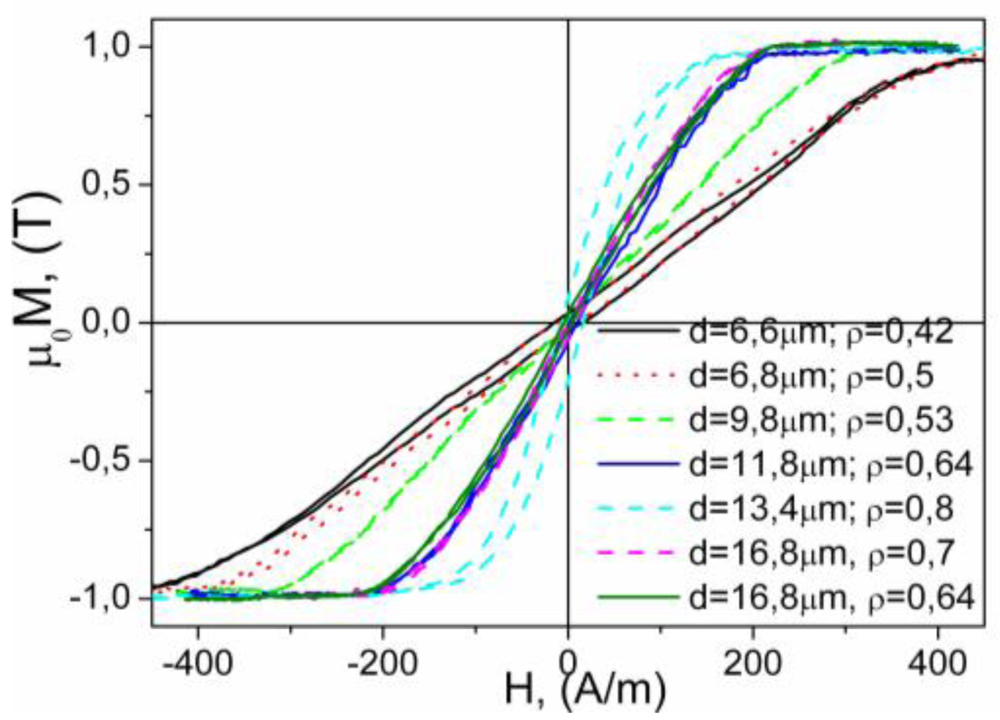
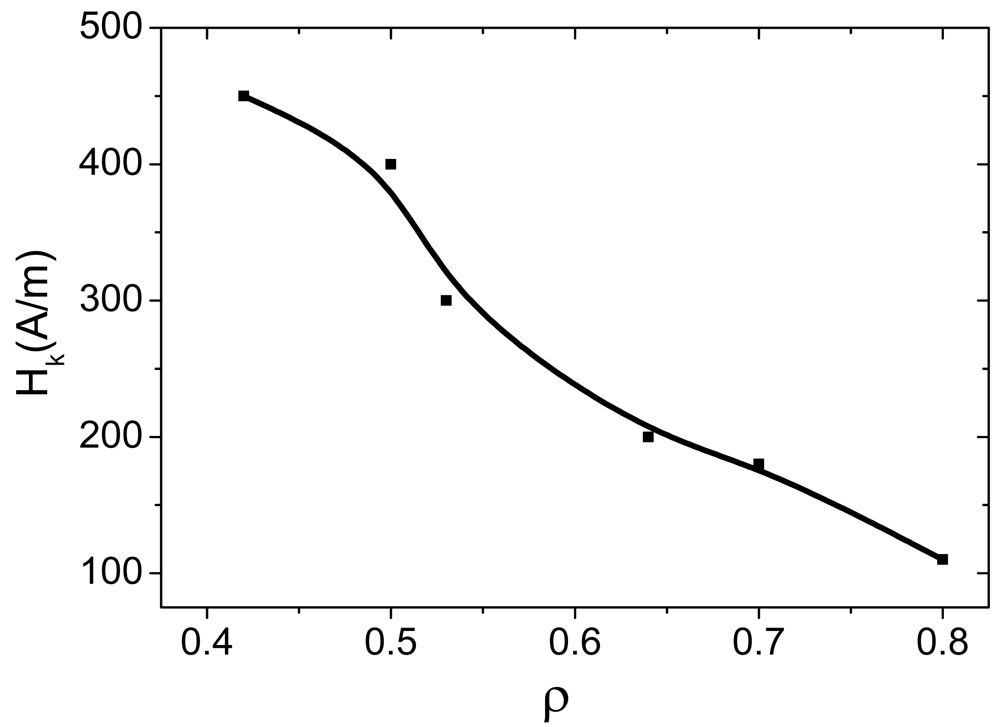
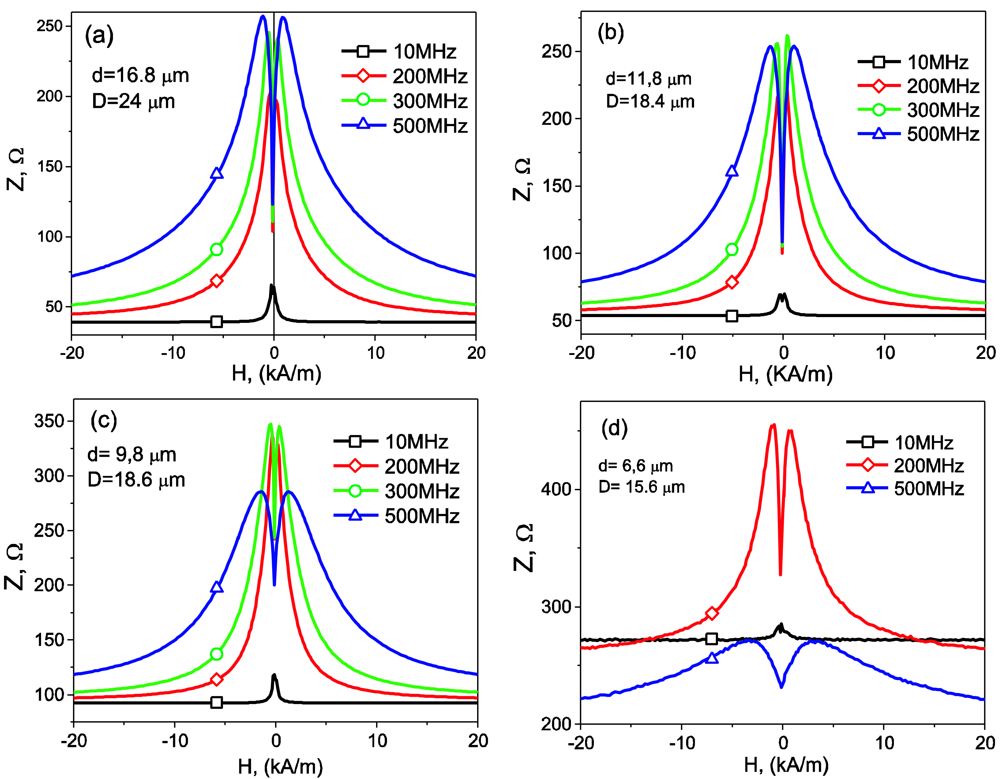
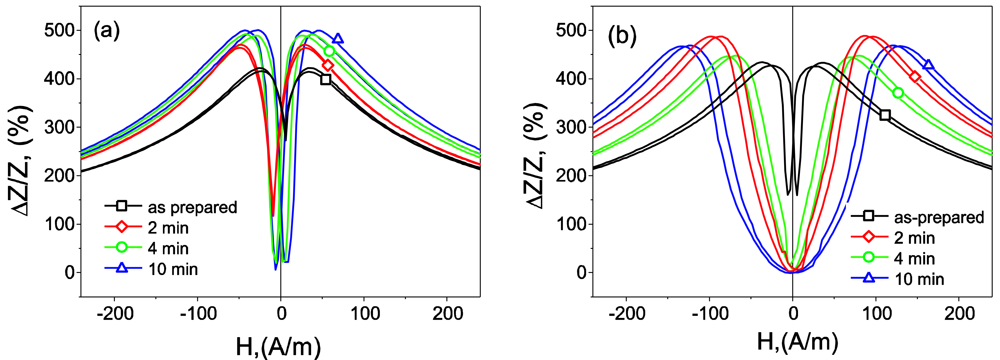
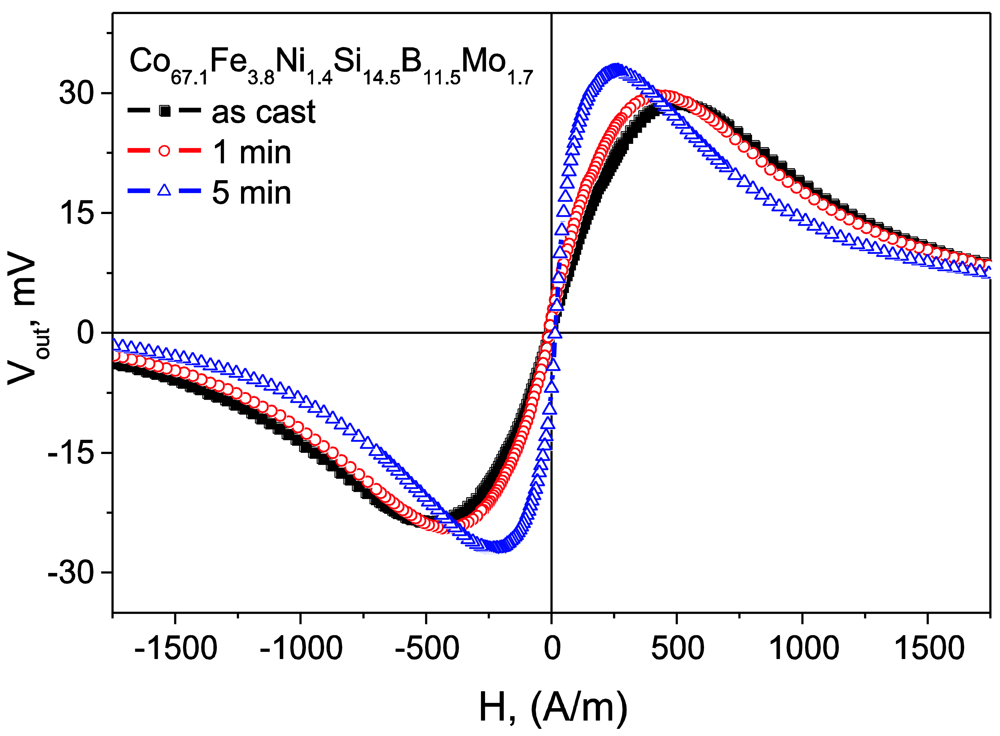
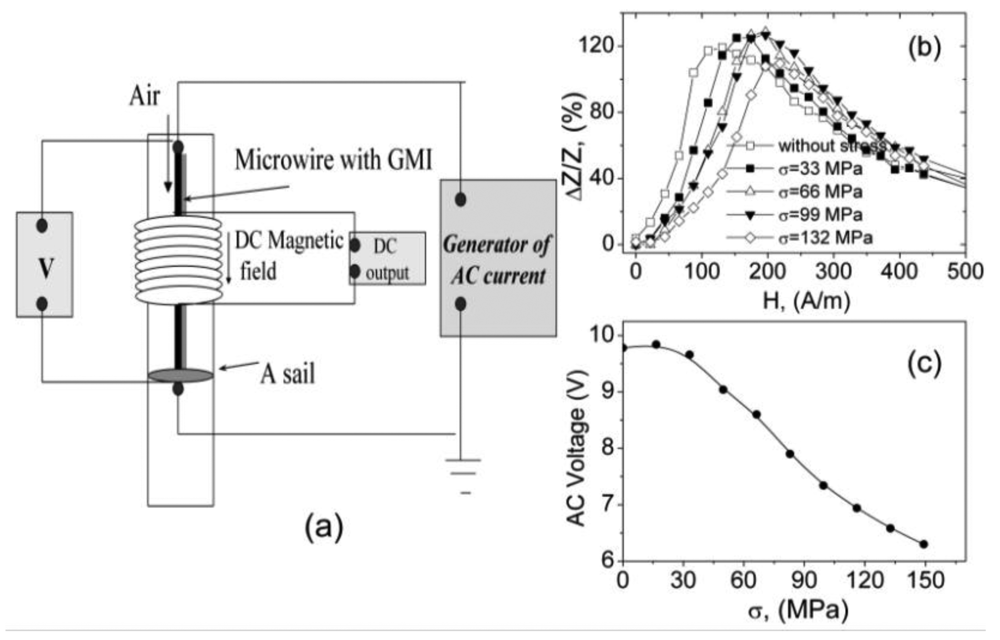
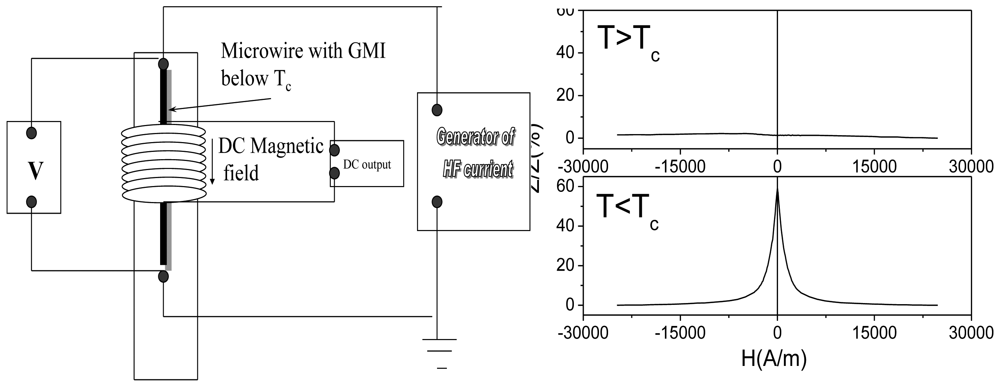
2.4. Giant magneto-impedance effect and enhanced magnetic softness. Tailoring of magnetic properties and GMI
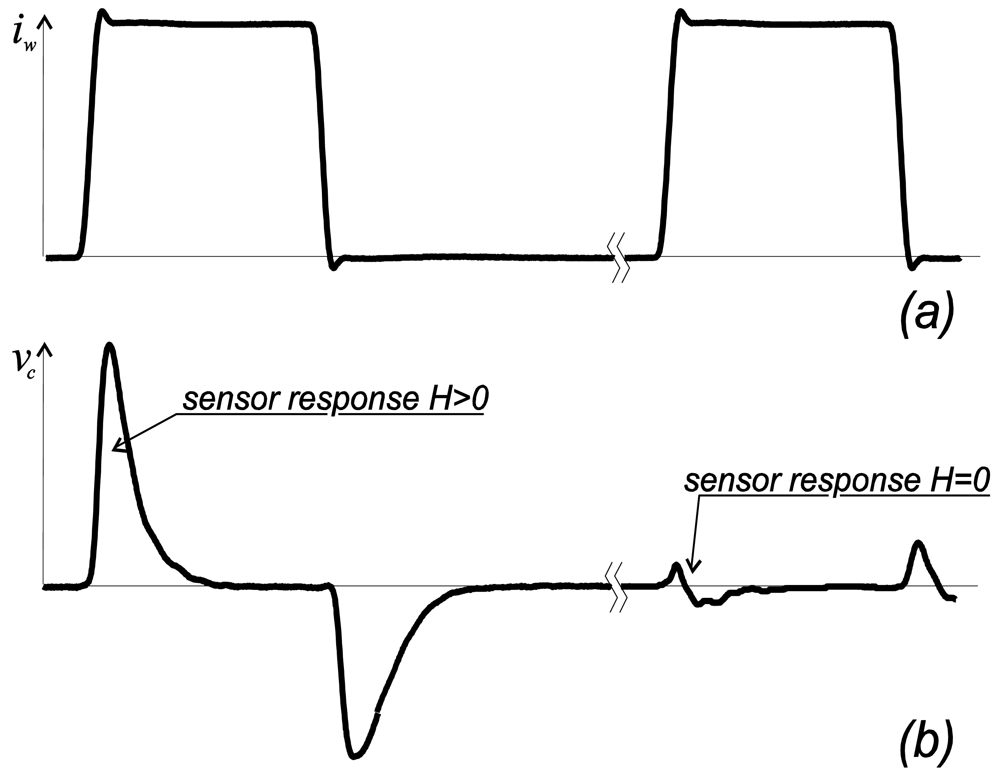
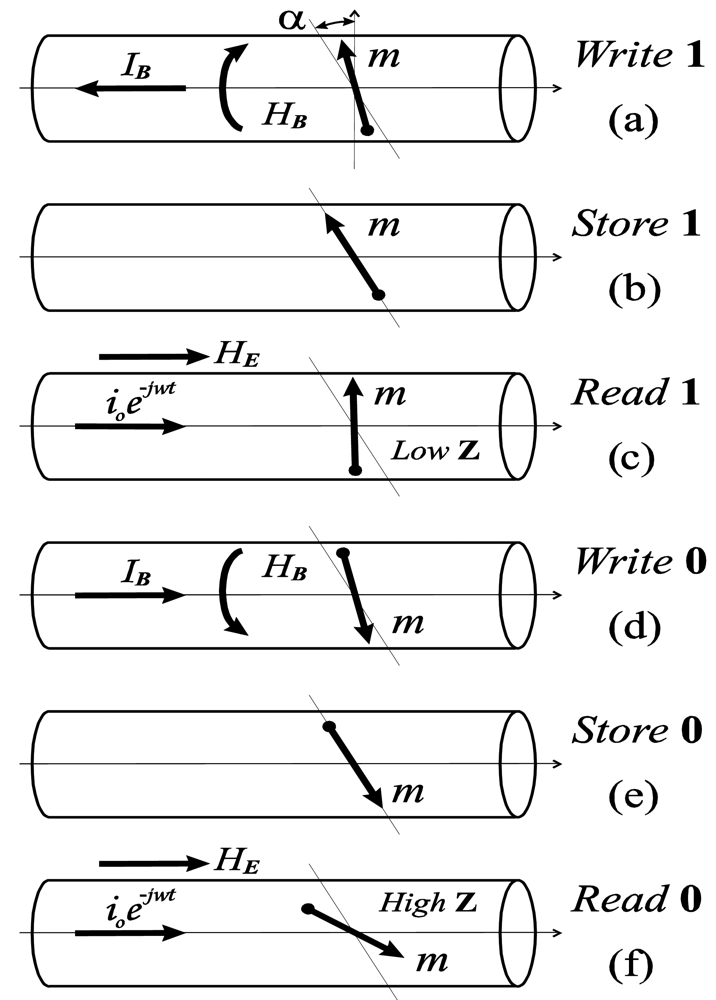
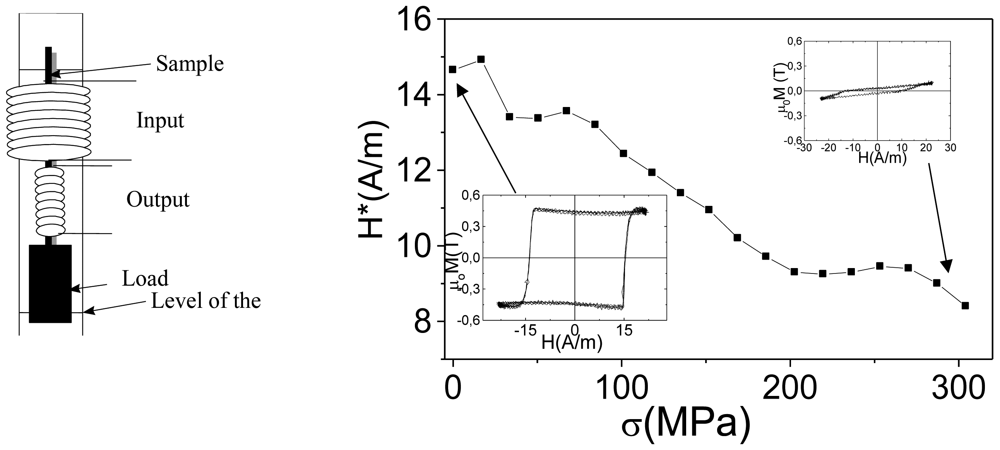
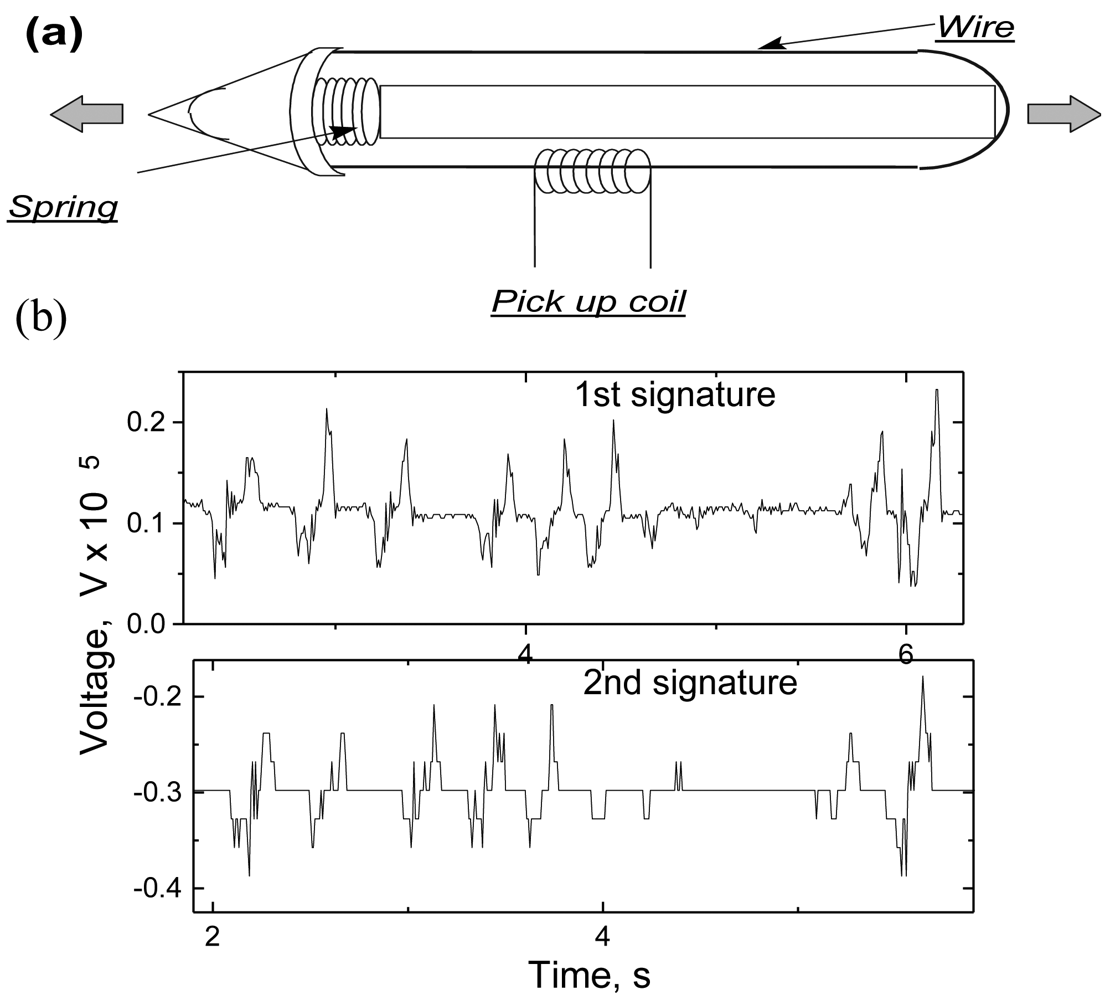
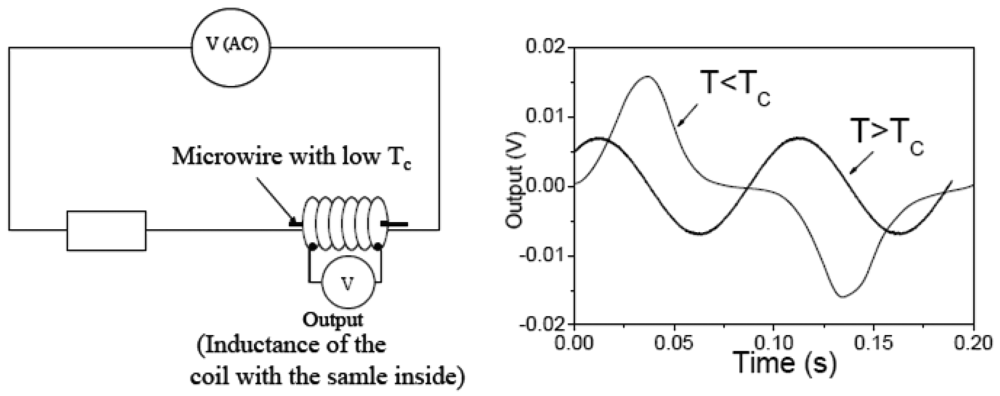
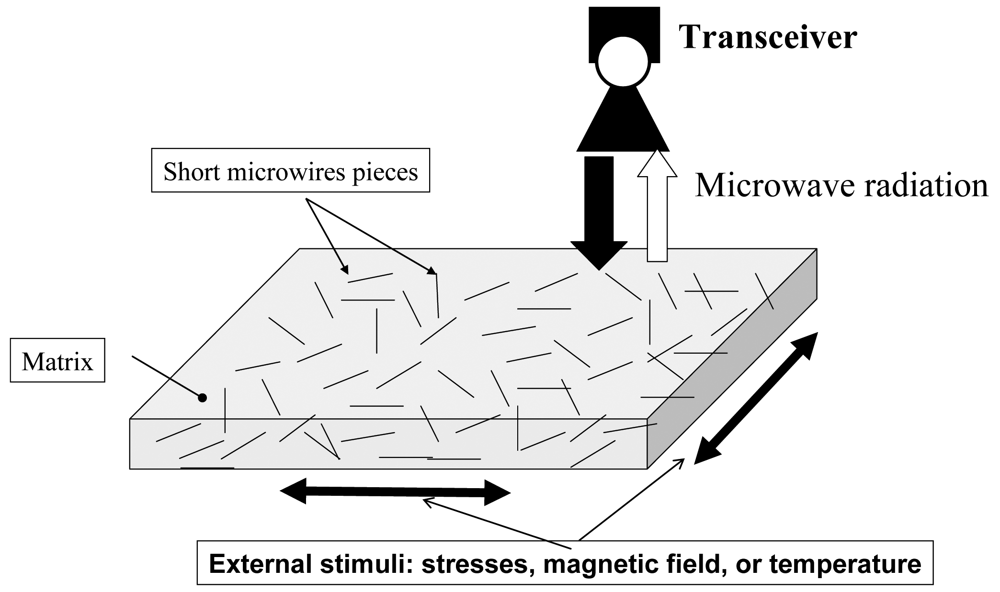
2.5. Applications of thin magnetically soft wires. Sensor prototypes
3. Conclusions
Acknowledgments
References
- Jiles, D.C. Recent advances and future directions in magnetic materials. Acta. Mater. 2003, 51, 5907–5939. [Google Scholar]
- Zhukov, A.; González, J.; Vázquez, M.; Larin, V.; Torcunov, A. Nanocrystalline and amorphous magnetic microwires. In Encyclopedia of Nanoscience and Nanotechnology; American Scientific Publishers: Valencia, CA, USA, 2004; Volume 6, pp. 365–387. [Google Scholar]
- Zhukov, A.; Ipatov, M.; Zhukova, V.; García, C.; Gonzalez, J.; Blanco, J.M. Development of ultra-thin glass-coated amorphous microwires for HF magnetic sensor applications. Phys. Stat. Sol. A 2008, 205, 1367–1372. [Google Scholar]
- Garcia Prieto, M.J.; Pina, E.; Zhukov, A.P.; Larin, V.; Marin, P.; Vázquez, M.; Hernando, A. Glass-coated Co-rich amorphous microwires with enhanced permeability. Sens. Actuat. A 2000, 81, 227–231. [Google Scholar]
- Varga, R.; Zhukov, A.; Zhukova, V.; Blanco, J.M.; Gonzalez, J. Supersonic domain wall in magnetic microwires. Phys. Rev. B 2007, 76, 132406:1–132406:2. [Google Scholar]
- Chiriac, H.; Ovari, T.A. Amorphous glass-covered magnetic wires: Preparation, properties, applications. Progr. Mater. Sci. 1996, 40, 333–407. [Google Scholar]
- Miroshnichenko, I.S.; Salli, I.V. A device for the crystallization of alloys at a high cooling rate. Ind. Lab. 1959, 25, 1463–1466. (in English). [Google Scholar]
- Duwez, P.; Williams, R.J.; Klement, K. Continuous series of metastable solid solutions in Ag-Cu alloys. J. Appl. Phys. 1966, 31, 1136–1142. [Google Scholar]
- Duwez, P. Metastable phases obtained by rapid quenching from the liquid state. In Progress in Solid State Chemistry; Reiss, H., Ed.; Pergamon: New York, NY, USA, 1966; Volume 3, pp. 377–406. [Google Scholar]
- Jones, H. Splat cooling and metastable phases. Rep. Prog. Phys. 1973, 36, 1425–1497. [Google Scholar]
- Luborsky, F.E. Amorphous metallic alloys. In Amorphous Metallic Alloys; Luborsky, F., Ed.; Butterworth and Co (Publishers): London, UK, 1983. [Google Scholar]
- Mohri, K.; Takeuchi, S. Stress-magnetic effects in iron-rich amorphous-alloys and shock-stress sensors with no power. IEEE Trans. Magn. 1981, 17, 3379–3381. [Google Scholar]
- Yoshizawa, Y.; Oguma, S.; Yamauchi, K. New Fe-based soft magnetic alloys composed of ultrafine grain structure. J. Appl. Phys. 1988, 64, 6044–6046. [Google Scholar]
- Herzer, G. Grain size dependence of coercivity and permeability in nanocrystalline ferromagnets. IEEE Trans. Magn. 1990, 26, 1397–1402. [Google Scholar]
- Hernando, A.; Vázquez, M. Engineering properties of rapidly solidified alloys. In Rapidly Solidified Alloys; Liebermann, H.H., Ed.; CRC: Boca Raton, FL, USA, 1993; pp. 553–590. [Google Scholar]
- Herzer, G. Nanocrystalline soft magnetic materials. Phys. Scrip. 1993, T49, 307–314. [Google Scholar]
- Arcas, J.; Gómez-Polo, C.; Zhukov, A.; Vázquez, M.; Larin, V.; Hernando, A. Structural, mechanical and magnetic properties in heat-treated Fe73.5Si22.5-xBxNb3Cul (6 ≤ × ≤ 12) alloy ribbons. Nanostruct. Mater. 1996, 7, 823–834. [Google Scholar]
- Miguel, C.; Zhukov, A.P.; González, J. Stress and/or field induced magnetic anisotropy in the amorphous Fe73.5Cu1Nb3Si15.5B7 alloy: influence on the coercivity, saturation magnetostriction and magneto-impedance response. Phys. Stat. Sol. A 2002, 194, 291–303. [Google Scholar]
- Humphrey, F.B.; Mohri, K.; Yamasaki, J.; Kawamura, H.; Malmhäll, R.; Ogasawara, I. Re-entrant magnetic flux reversal in amorphous wires. In Magnetic Properties of Amorphous Metals; Hernando, A., Madurga, V., Sánchez-Trujillo, M.C., Vázquez, M., Eds.; Elsevier Science: Amsterdam, the Netherlands, 1987; pp. 110–116. [Google Scholar]
- Mohri, K.; Humphrey, F.B.; Kawashima, K.; Kimura, K.; Muzutani, M. Large barkhausen and matteucci effects in FeCoSiB, FeCrSiB, and FeNiSiB amorphous wires. IEEE Trans. Magn. 1990, 26, 1789–1791. [Google Scholar]
- Honkura, Y. The development of MI sensor and its applications to mobile phone. In Advanced Magnetic Materials for Technolological Applications; Zhukov, A., Gonzalez, J., Eds.; Transworld Research Network: Kerala, India, 2008; pp. 71–94. [Google Scholar]
- Vázquez, M.; Knobel, M.; Sánchez, M.L.; Valenzuela, R.; Zhukov, A.P. Giant magneto-impedance effect in soft magnetic wires for sensor applications. Sens. Actuat. A 1997, 59, 20–29. [Google Scholar]
- Panina, L.V.; Mohri, K. Magneto-impedance effect in amorphous Wires. Appl. Phys. Lett. 1994, 65, 118911–118991. [Google Scholar]
- Beach, R.S.; Berkowicz, A.E. Giant magnetic field dependence of amorphous FeCoSiB wire. Appl. Phys. Lett. 1994, 64, 3652–3654. [Google Scholar]
- Makhnovskiy, D.P.; Panina, L.V.; Mapps, D.J. Field-dependent surface impedance tensor in amorphous wires with two types of magnetic anisotropy: Helical and circumferential. Phys. Rev. B 2001, 63, 144424:1–144424:17. [Google Scholar]
- Cobeño, A.F.; Blanco, J.M.; Zhukov, A.; Dominguez, L.; Gonzalez, J.; Torcunov, A.; Aragoneses, P. Matteucci effect in glass coated microwires. IEEE Trans. Magn. 1999, 35, 3382–3384. [Google Scholar]
- Blanco, J.M.; Zhukov, A.; Gonzalez, J. Effect of tensile and torsion on GMI effect in amorphous wire. J. Magn. Magn. Mat. 1999, 196–197, 377–379. [Google Scholar]
- Zhukov, A. Design of the magnetic properties of Fe-rich, glass-coated microwires for technical applications. Adv. Func. Mat. 2006, 16, 675–680. [Google Scholar]
- Prida, V.M.; Hernando, B.; Sanchez, M.L.; Li, Y.F.; Tejedor, M.; Vazquez, M. Torsional impedance effect in Fe-rich amorphous wires. J. Magn. Magn. Mater. 2003, 258–259, 158–160. [Google Scholar]
- Allwood, D.A.; Xiong, G.; Faulkner, C.C.; Atkinson, D.; Petit, D.; Cowburn, R.P. Magnetic domain-wall logic. Science 2005, 309, 1688–1692. [Google Scholar]
- Parkin, S.S.P. Shiftable magnetic shift register and method of using the same. US patent 6,834,005, 2004. [Google Scholar]
- Zhukov, A. Domain wall propagation in a Fe-rich glass-coated amorphous microwire. Appl. Phys. Lett. 2001, 78, 3106–3108. [Google Scholar]
- Zhukov, A.P.; Vázquez, M.; Velázquez, J.; Chiriac, H.; Larin, V. The remagnetization process in thin and ultra-thin Fe-rich amorphous wires. J. Magn. Magn. Mater. 1995, 151, 132–138. [Google Scholar]
- Zhukov, A.; Zhukova, V. Magnetic Properties and Applications of Ferromagnetic Microwires with Amorphous and Nanocrystalline Structure; Nova Science Publishers: Hauppauge, NY, USA, 2009; pp. 1–162. [Google Scholar]
- Makhnovskiy, D.; Zhukov, A.; Zhukova, V.; Gonzalez, J. Tunable and self-sensing microwave composite materials incorporating ferromagnetic microwires. Advs. Sci. Technol. 2008, 54, 201–210. [Google Scholar]
- Makhnovskiy, D.P.; Panina, L.V.; Sandacci, S.I. Tuneable microwave composites based on ferromagnetic microwires. In Progress in Ferromagnetism Research; Murray, V.N., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2005; pp. 257–295. [Google Scholar]
- Zhukova, V.; Zhukov, A.; Larin, V.; Torcunov, A.; Gonzalez, J.; de Arellano Lopez, A.R.; Quispe-Cancapa, J.J.; Pinto-Gómez, A.R. Magnetic and mechanical properties of magnetic glass-coated microwires with different glass coating. Mater. Sci. Forum 2005, 480–481, 293–297. [Google Scholar]
- Zhukov, A.; González, J.; Blanco, J.M.; Vázquez, M.; Larin, V. Microwires coated by glass: a new family of soft and hard magnetic materials. J. Mat. Res. 2000, 15, 2107–2113. [Google Scholar]
- Nakatani, Y.; Thiaville, A.; Miltat, J. Faster magnetic walls in rough wires. Nature Mater 2003, 2, 521–523. [Google Scholar]
- Ono, T.; Miyajima, H.; Shigeto, K.; Mibu, K.; Hosoito, N.; Shinjo, T. Propagation of a magnetic domain wall in a submicrometer magnetic wire. Science 1999, 284, 468–470. [Google Scholar]
- Cowburn, R.P.; Allwood, D.A.; Xiong, G.; Cooke, M.D. Domain wall injection and propagation in planar Permalloy nanowires. J. Appl. Phys. 2002, 91, 6949–6951. [Google Scholar]
- Kunz, A.; Reiff, S.C. Enhancing domain wall speed in nanowires with transverse magnetic fields. J. Appl. Phys. 2008, 103, 07D903:1–07D903:3. [Google Scholar]
- Zhukova, V.; Blanco, J.M.; Ipatov, M.; Gonzalez, J.; Zhukov, A. Domain-wall propagation in thin Fe-rich glass-coated amorphous wires. Phys. Stat. Sol. A 2009, 206, 679–682. [Google Scholar]
- Sixtus, K.J.; Tonks, L. Propagation of large barkhausen discontinuities. Phys. Rev. 1932, 42, 419–435. [Google Scholar]
- Kostyk, Y.; Varga, R.; Vazquez, M.; Vojtanik, P. Domain wall propagation in adiabatic regime. Phys. B 2008, 403, 386–389. [Google Scholar]
- Ipatov, M.; Usov, N.A.; Zhukov, A.; González, J. Local nucleation fields of Fe-rich microwires and their dependence on applied stresses. Phys. B 2008, 403, 379–381. [Google Scholar]
- Ipatov, M.; Zhukova, V.; Zvezdin, A.K.; Zhukov, A. Mechanisms of the ultrafast magnetization switching in bistable amorphous microwires. J. Appl. Phys. 2009, in press. [Google Scholar]
- Sandacci, S.I.; Makhnovskiy, D.P.; Panina, L.V.; Mohri, K.; Honkura, Y. Off-diagonal impedance in amorphous wires and its application to linear magnetic sensors. IEEE Trans. Magn. 2004, 40, 3505–3511. [Google Scholar]
- Wiegand, J.R. Bistable magnetic device. US Patent 3,820,090, 1974. [Google Scholar]
- Mohri, K.; Takeuchi, B.; Fujimoto, T. Sensitive magnetic sensors using amorphous wiegand-type ribbons. IEEE Trans. Magn. 1981, 17, 3370–3372. [Google Scholar]
- Mohri, K.; Takeuchi, S. Sensitive bistable magnetic sensors using twisted amorhous magnetostricive ribbons due to matteucci effect. J. Appl. Phys. 1982, 53, 8386–8388. [Google Scholar]
- Ho, W.; Yamasaki, J.J. Multi-thread re-entrant marker with simultaneous switching. US patent 5,519,379, 1996. [Google Scholar]
- Humphrey, F.B. Article surveillance magnetic marker having a hysteresis loop with large Barkhausen discontinuities. US patent 4,660,025, 1987. [Google Scholar]
- Jahnes, C.; Gambino, R.J.; Paunovic, M.; Schroff, A.G.; von Guftel, R.J. Identification tags using amorphous wire. US patent 5,729,201, 1998. [Google Scholar]
- Zhukov, A. Glass-coated magnetic microwires for technical applications. J. Magn. Magn. Mater. 2002, 242–245, 216–223. [Google Scholar]
- Zhukov, A.; Gonzalez, J.; Blanco, J.M.; Aragoneses, P.; Domínguez, L. Magnetoelastic sensor of level of the liquid based on magnetoelastic properties of Co-rich microwires. Sens. Actuat. A-Phys. 2000, 81, 129–133. [Google Scholar]
- Zhukov, A.; Garcia-Beneytez, J.M.; Vázquez, M. Magnetoelastic sensor for signature identification based on mechanomagnetic effect in amorphous wires. J. Phys. IV 1998, 8, Pr2-763–Pr2-766. [Google Scholar]
- Honkura, Y. Development of amorphous wire type MI sensors for automobile use. J. Magn. Magn. Mater. 2002, 249, 375–381. [Google Scholar]
- Mohri, K.; Uchiyama, T.; Shen, L.P.; Cai, C.M.; Panina, L.V. Sensitive micro magnetic sensor family utilizing magneto-impedance (MI) and stress-impedance (SI) effects for intelligent measurements and control. Sens. Actuat. A 2001, 91, 85–90. [Google Scholar]
- Cobeño, A.F.; Zhukov, A.; Blanco, J.M.; Larin, V.; Gonzalez, J. Magnetoelastic sensor based on GMI of amorphous microwire. Sens. Actuat. A 2001, 91, 95–98. [Google Scholar]

© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhukova, V.; Ipatov, M.; Zhukov, A. Thin Magnetically Soft Wires for Magnetic Microsensors. Sensors 2009, 9, 9216-9240. https://doi.org/10.3390/s91109216
Zhukova V, Ipatov M, Zhukov A. Thin Magnetically Soft Wires for Magnetic Microsensors. Sensors. 2009; 9(11):9216-9240. https://doi.org/10.3390/s91109216
Chicago/Turabian StyleZhukova, Valentina, Mihail Ipatov, and Arcady Zhukov. 2009. "Thin Magnetically Soft Wires for Magnetic Microsensors" Sensors 9, no. 11: 9216-9240. https://doi.org/10.3390/s91109216
APA StyleZhukova, V., Ipatov, M., & Zhukov, A. (2009). Thin Magnetically Soft Wires for Magnetic Microsensors. Sensors, 9(11), 9216-9240. https://doi.org/10.3390/s91109216






