Vehicle Lateral State Estimation Based on Measured Tyre Forces
Abstract
:1. Introduction
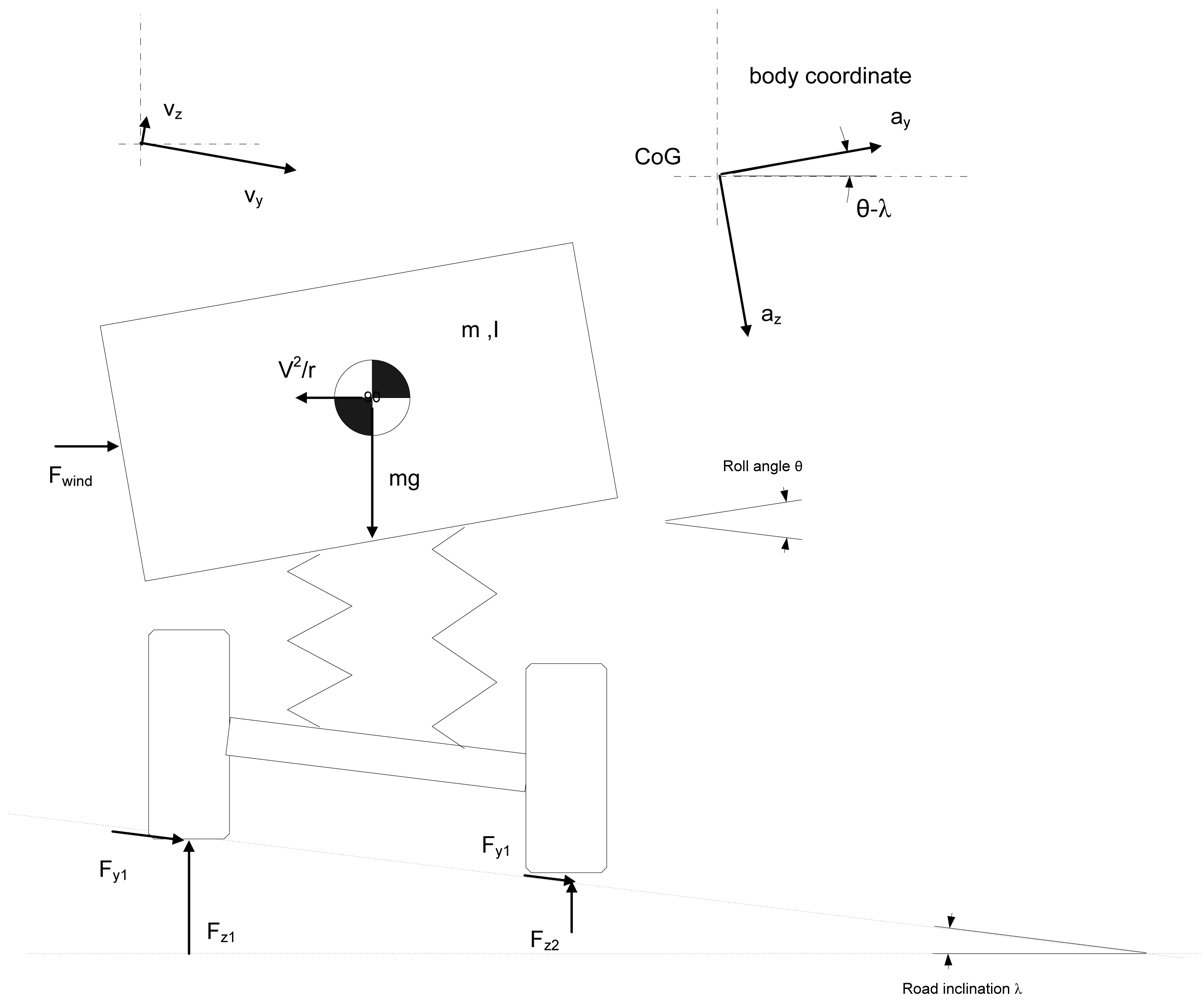
- roll angle θ and road inclination λ introduce offset for lateral acceleration ay sensor due to gravity component (5,7° roll angle results 0.1g error for lateral acceleration)
- Influence of side wind is not properly captured from the measured acceleration, but has to be carried by the tyres (and influence for vy is missing)
- vy is not even parallel to compensated lateral acceleration
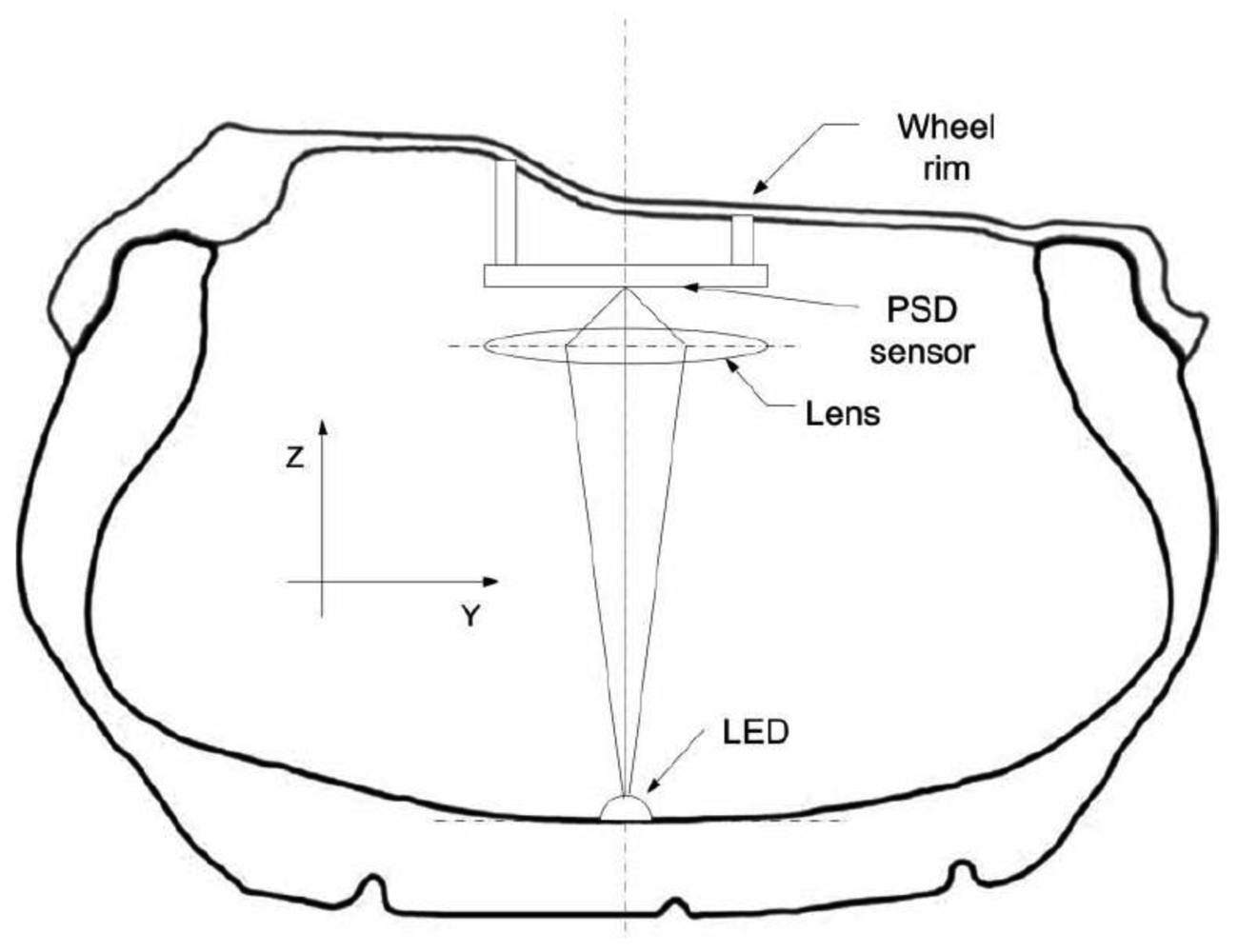
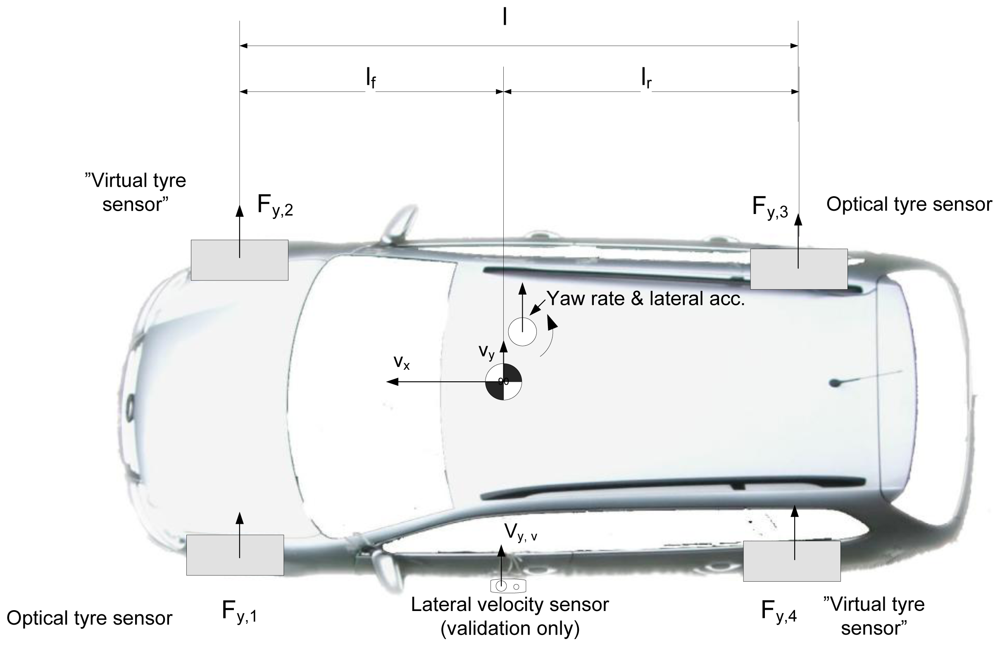
2. Optical Tyre Sensor (OTS) Concept
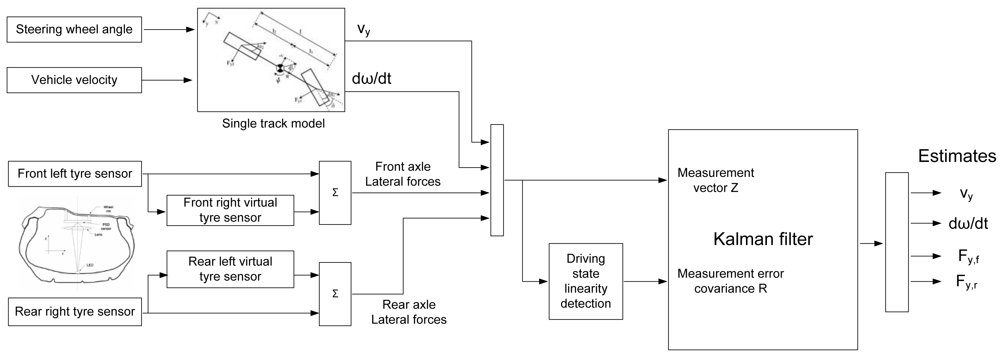
3. Vehicle State Estimator
3.1. Kalman filter
3.2. Virtual tyre sensors
3.2.1. Inverse magic formula
3.2.2. Normalised lateral force
3.3. Vehicle model for the estimator
3.4. Single track model for the linear operation region
3.5. Covariance matrixes for Kalman filter
3.5.1. Process noise covariance matrix
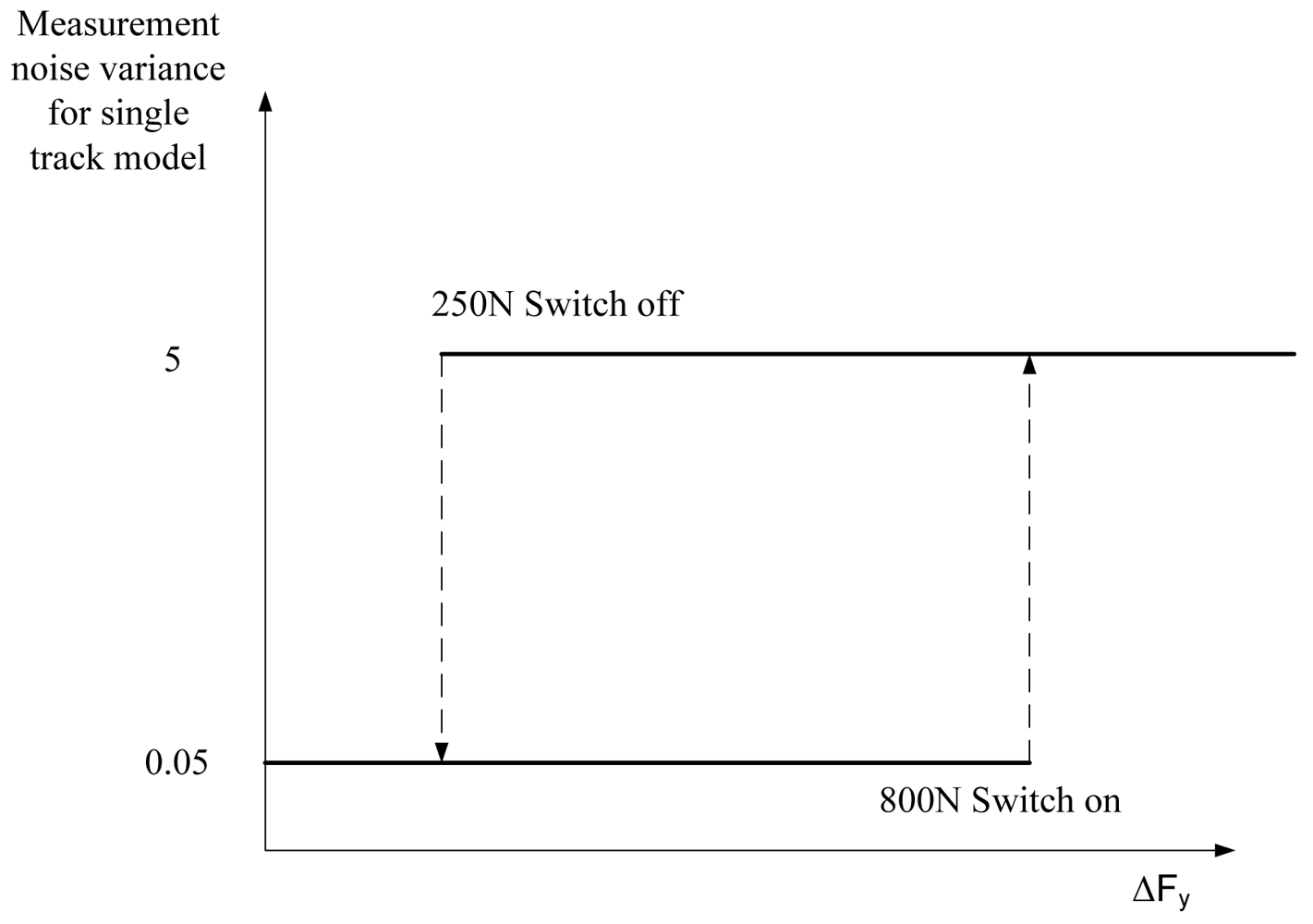
3.5.2. Measurement noise covariance matrix
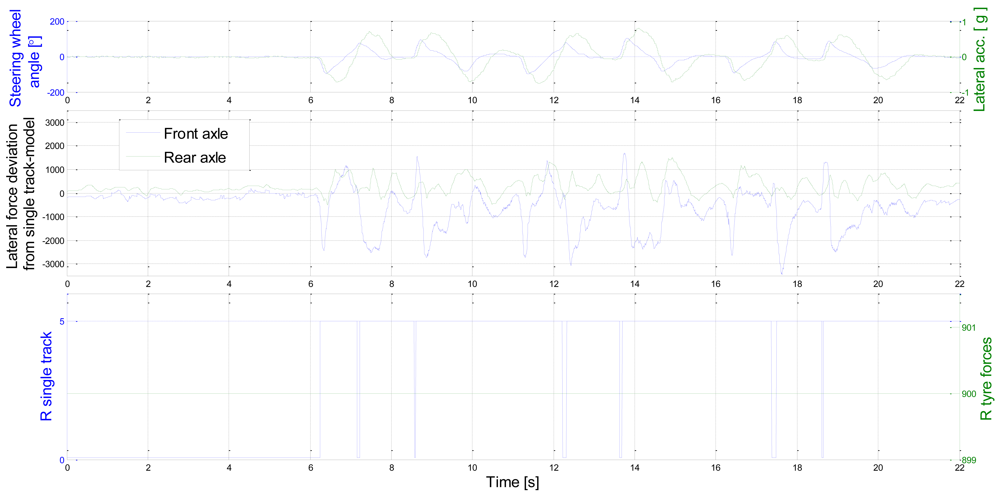
3.5.3. Evaluation of linearity of vehicle operating state
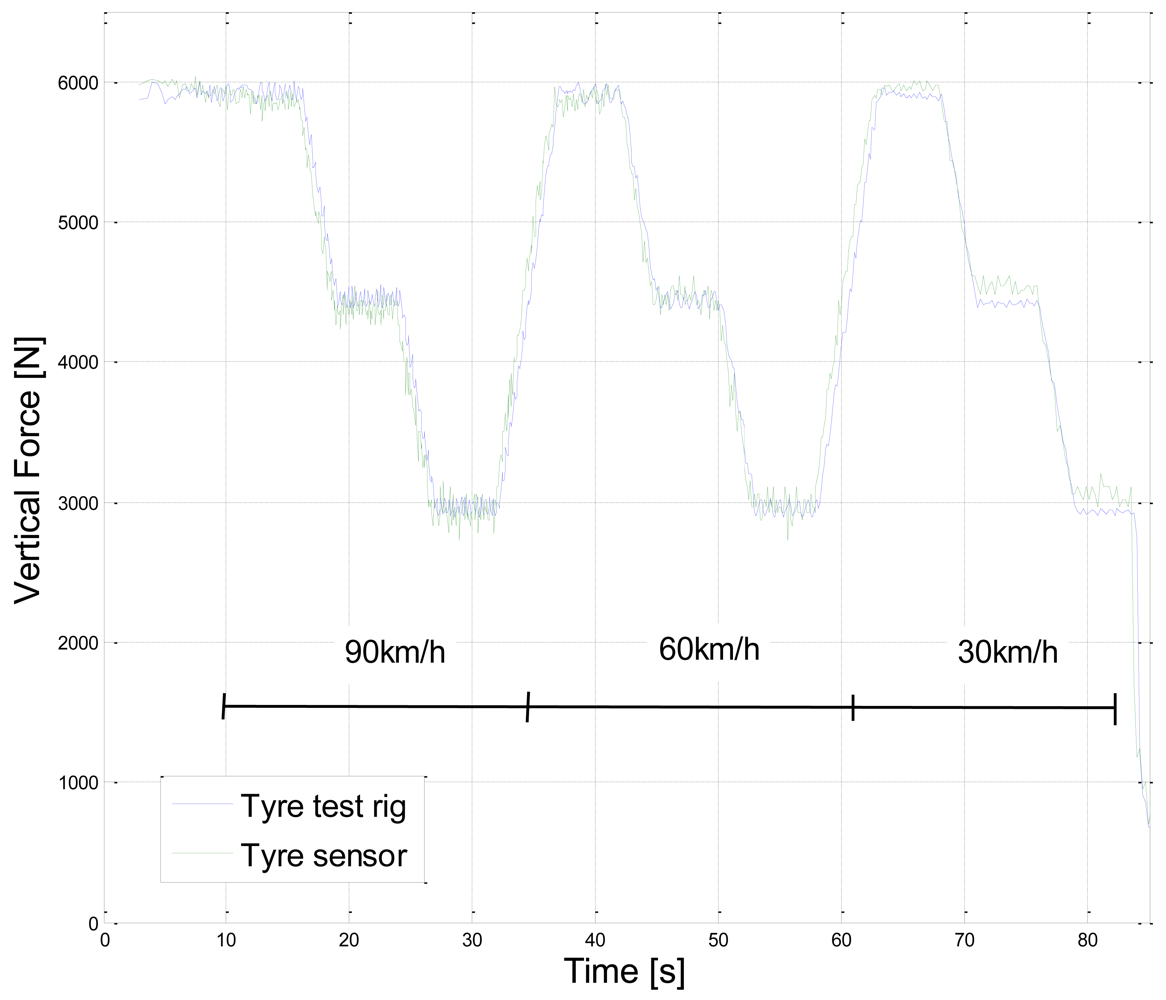
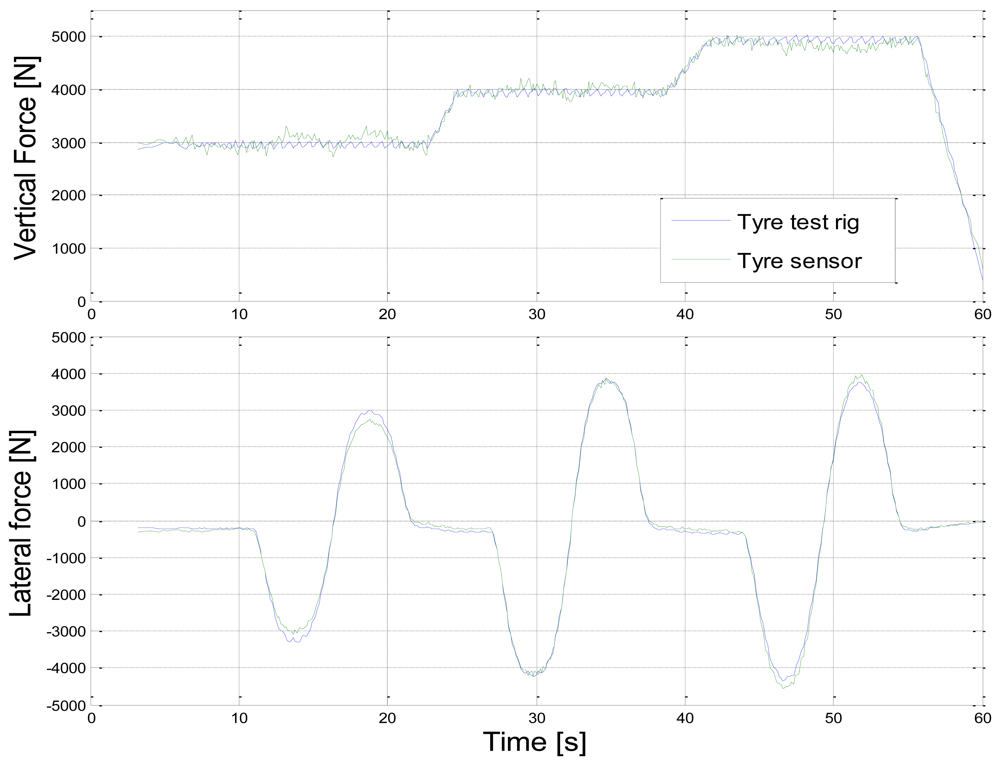
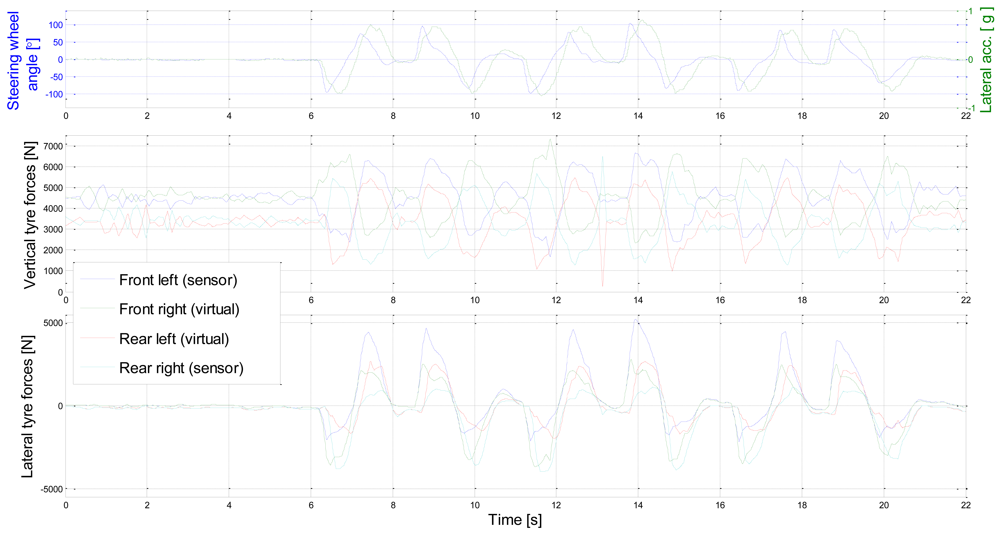
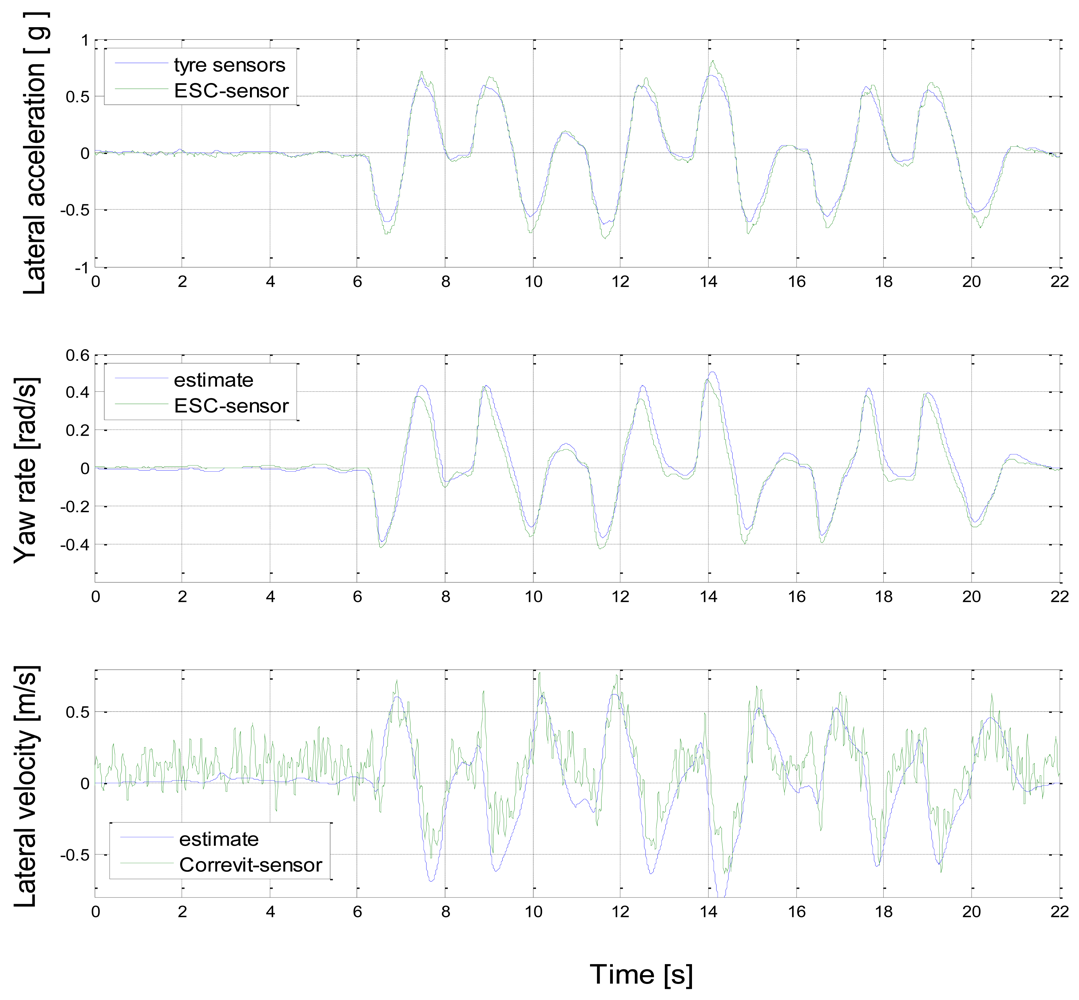
4. Results
5. Discussion
5.1. Can a tyre force sensor replace any of the existing vehicle sensors?
5.2. Required vehicle parameters by the estimator
5.3. Further research
References
- van Zanten, A.T.; Erhardt, R.; Pfaff, G.; Kost, F.; Hartmann, U.; Ehret, T. Control aspects of the Bosch-VDC. Proceedings of AVEC96, Aachen, Germany, September, 1996.
- Fukada, Y. Slip-angle estimation for vehicle stability control. Veh. Syst. Dyn. 1999, 32, 375–388. [Google Scholar]
- Best, M.C.; Gordon, T.J. Combined state and parameter estimation of vehicle handling dynamics. Proceeding of AVEC 2000 5th International Symposium on Advanced Vehicle Control, Ann Arbor, MI, USA, August 22–24, 2000.
- Abe, M.; Kato, A.; Suzuki, K.; Kano, Y. Estimation of vehicle side-slip angle for DYC by using On-Board-Tire-Model. Proceedings of 4th International Symposium on Advanced Vehicle Control, Nagoya, Japan, September 14–18, 1998; pp. 437–442.
- Klier, W.; Reim, A.; Stapel, D. Robust Estimation of Vehicle Sideslip Angle — An Approach w/o Vehicle and Tire Models. SAE World Congress & Exhibition, Detroit, MI, USA, April, 2008.
- Cheli, F.; Sabbioni, E.; Pesce, M.; Melzi, S. A methodology for vehicle sideslip angle identification: comparison with experimental data. Veh. Syst. Dyn. 2007, 45, 549–563. [Google Scholar]
- Pasterkamp, W.R. The Tyre as Sensor to Estimate Friction; Delft University: Delft, The Netherlands, 1997; p. 148. [Google Scholar]
- Gobbi, M.; Botero, J.C.; Mastinu, G. Improving the active safety of road vehicles by sensing forces and moments at the wheels. Veh. Syst. Dyn. 2008, 46, 957–968. [Google Scholar]
- Becherer, T. The Sidewall Torsion Sensor System, 2. Darmstädter Reifenkolloquium; VDI-Verlag: Düsseldorf, Germany, 1998; pp. 130–137. [Google Scholar]
- Tuononen, A.J. Optical position detection to measure tyre carcass deflections. Veh. Syst. Dyn. 2008, 46, 471–481. [Google Scholar]
- Morinaga, H. The possibility of intelligent tire (technology of contact area information sensing). Proceedings of 31st Fisita World Automotive Congress, Yokohama, Japan, October, 2006.
- Breuer, B.; Eichhorn, U. Measurement of tyre/road-friction ahead of the car and inside the tyre. Proceedings of AVEC'92, Yokohama, Japan; 1992. [Google Scholar]
- van Leeuwen, B.; Pepe, F. SKF Load Sensing HBU, ATA Advanced chassis Control Systems; Orbassano, Italy, 2008. [Google Scholar]
- Krantz, W.; Neubeck, J.; Wiedemann, J. Estimation of Side Slip Angle Using Measured Tire Forces; SAE: Warrendale, PA, USA, March 2002; pp. 59–64. [Google Scholar]
- Kamada, T.; Fukudome, H.; Fujita, T.; Murase, M. Study on ABS control by measuring forces between road surface and tires. Proceedings of the International Symposium on Advanced Vehicle Control, Arnhem, The Netherlands, August, 2004; pp. 239–244.
- Holtschulze, J. Analyse der Reifenverformungen für eine Identifikation des Reibwerts und weiterer Betriebsgröβen zur Unterstützung von Fahrdynamikregelsystemen. PhD thesis, RWTH Aachen University, Aachen, Germany, April 2006. [Google Scholar]
- Tuononen, A.J. On-board estimation of dynamic tyre forces from optically measured tyre carcass deflections. Int. J. Heavy Veh. Syst. 2009, 16, 362–378. [Google Scholar]
- Tuononen, A.J.; Hartikainen, L. Optical position detection sensor to measure tyre carcass deflections in aquaplaning. Int. J. Veh. Syst. Model. Test. 2008, 3, 189–197. [Google Scholar]
- Tuononen, A.J.; Matilainen, M.J. Real-time estimation of aquaplaning with an optical tyre sensor. J. Automobile Eng. 2009, 223, 1263–1272. [Google Scholar]
- Kalman, R.E. A new approach to linear filtering and prediction problems. Trans. ASME J. Basic Eng. 1960, 82, 35–45. [Google Scholar]
- Welch, G.; Bishop, G. An introduction to the Kalman filter; Technical Report TR 95-041; Department of Computer Science, University of North Carolina: Chapel Hill, NC, USA, 2006. [Google Scholar]
- Pacejka, H.B. Tyre and Vehicle Dynamics; Elsevier: Burlington, UK, 2005. [Google Scholar]
- Gillespie, T.D. Fundamentals of Vehicle Dynamics; SAE: Warrendale, PA, USA, 1992. [Google Scholar]
- Pauwelussen, J. Plane Vehicle Behaviour, lecture material; HAN-University: Arnhem, The Netherlands, 2003. [Google Scholar]
| Parameter | Definition | Source | Value |
|---|---|---|---|
| m | Vehicle mass | available from vertical tyre forces | 1,603 kg |
| l | axle length | vehicle parameter | 2,575 m |
| lf | Centre of gravity distance from front axle | available from vertical tyre forces in steady state condition | 1.05m |
| lr | Centre of gravity distance from rear axle | available from vertical tyre forces in steady state condition | 1.525m |
| Iz | Vehicle yaw moment of inertia | roughly m·lr·lr [24] or adapted | 3,156 kg m2 |
| Q | Process noise covariance | constant | diag([0.01 0.01 1e4 1e4]) |
| R | Measurement noise covariance | derived in section 3.5 | variable |
| Cf & Cr | Cornering stiffness of the linear model (or characteristic velocity | ESC-system (nominal behaviour of a vehicle) | 76,614 N/rad & 82,087N/rad |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Tuononen, A.J. Vehicle Lateral State Estimation Based on Measured Tyre Forces. Sensors 2009, 9, 8761-8775. https://doi.org/10.3390/s91108761
Tuononen AJ. Vehicle Lateral State Estimation Based on Measured Tyre Forces. Sensors. 2009; 9(11):8761-8775. https://doi.org/10.3390/s91108761
Chicago/Turabian StyleTuononen, Ari J. 2009. "Vehicle Lateral State Estimation Based on Measured Tyre Forces" Sensors 9, no. 11: 8761-8775. https://doi.org/10.3390/s91108761




