State-of-The-Art and Applications of 3D Imaging Sensors in Industry, Cultural Heritage, Medicine, and Criminal Investigation
Abstract
:1. Introduction
2. Overview of 3D imaging techniques
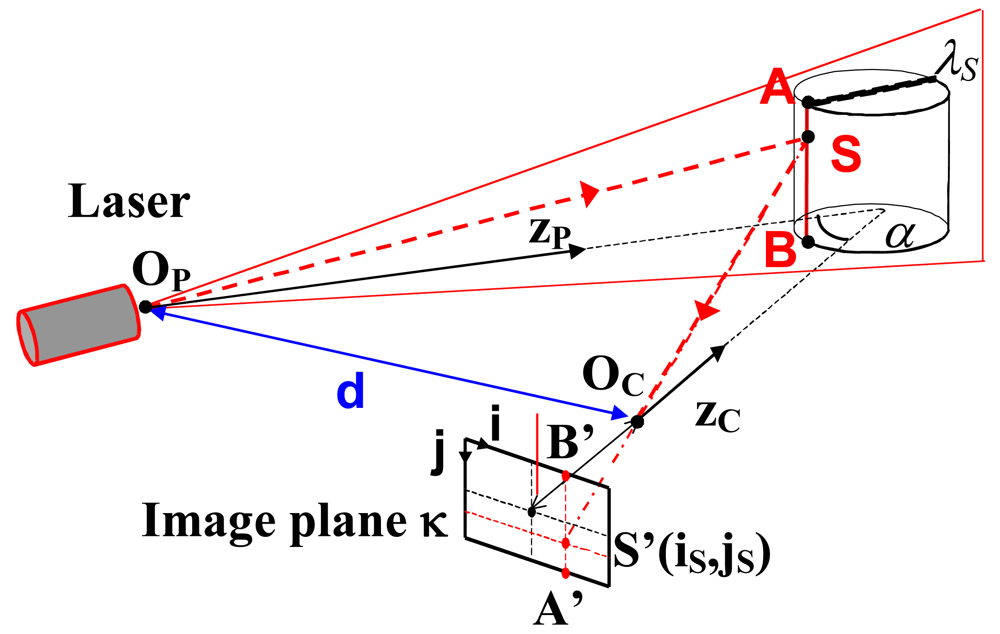
2.1 Laser triangulators
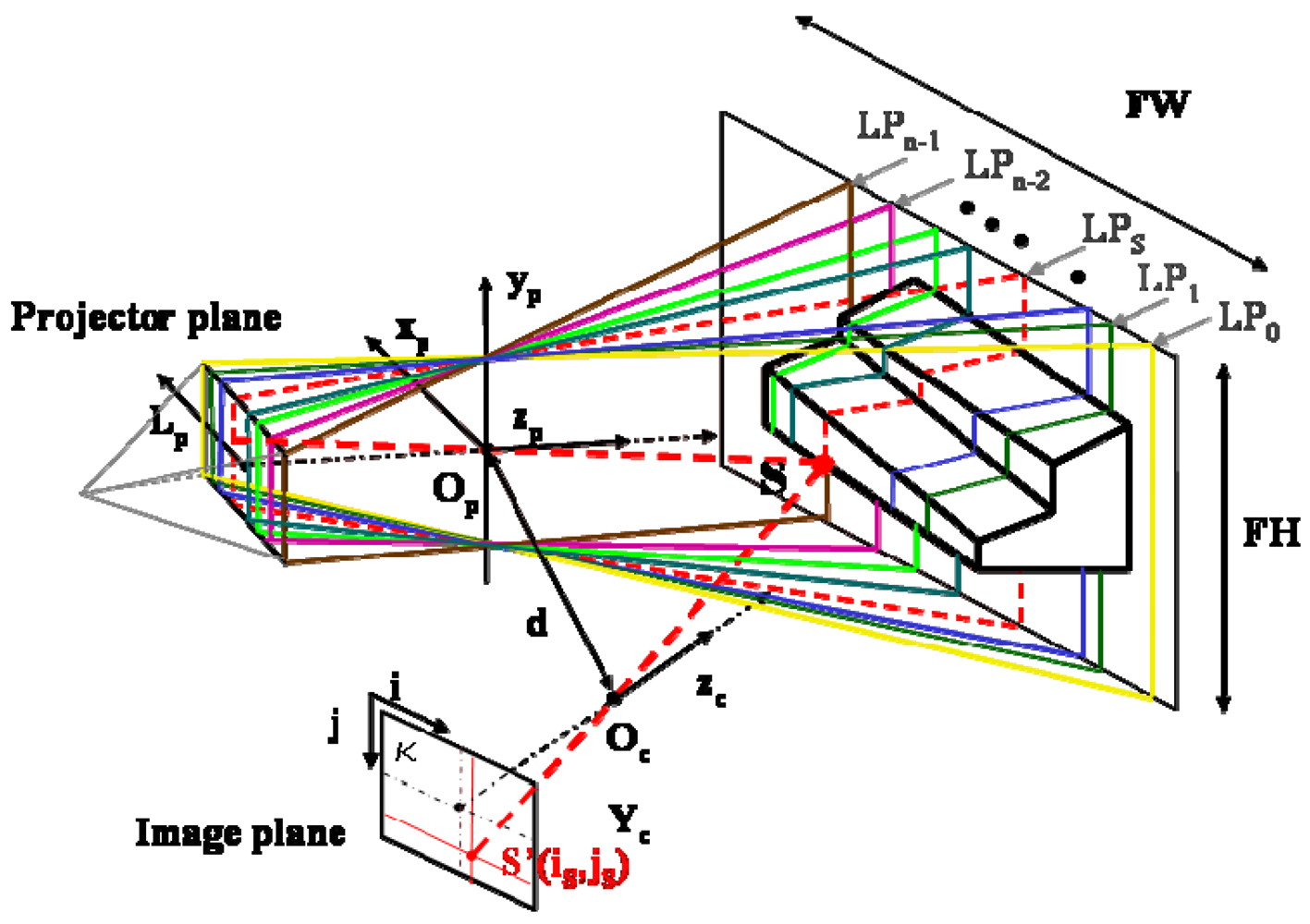
2.2 Structured light
2.3 Stereo vision
2.4 Photogrammetry
2.5 Time of Flight
2.6 Interferometry
2.7 Moiré fringe range contours
2.8 Shape from focusing
2.9 Shape from shadows
2.10 Shape from texture
2.11 Shape from shading
2.12 Strengths and weaknesses of 3D imaging techniques
2.13 The software for the elaboration of 3D data
- Registration of multiple images;
- Integration of registered images into a fused single point cloud and determination of the tessel mesh that models the surface;
- Acquisition of reflection data, for surface visualization.
3. Experience in the application of 3D imaging sensors
3.1 Industrial applications
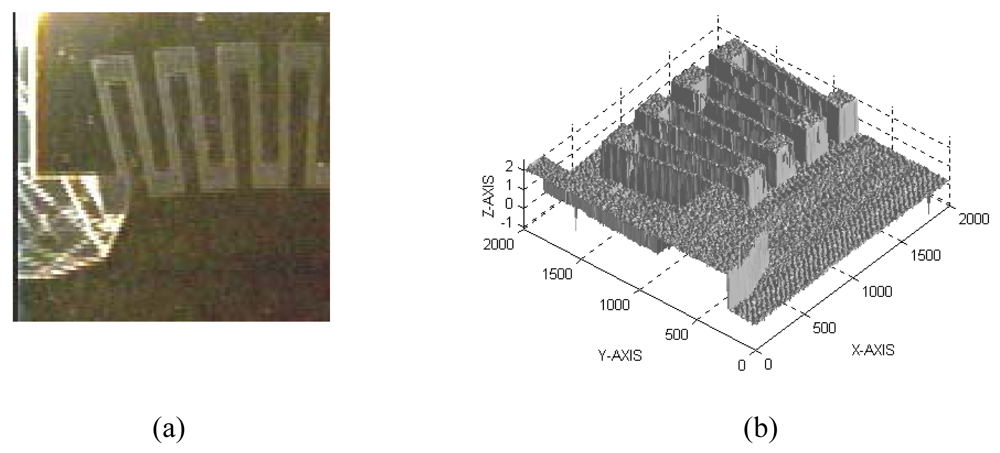
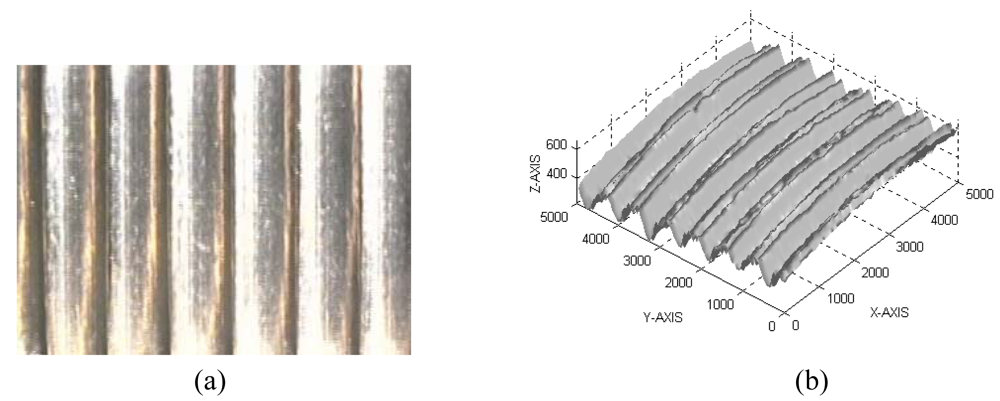
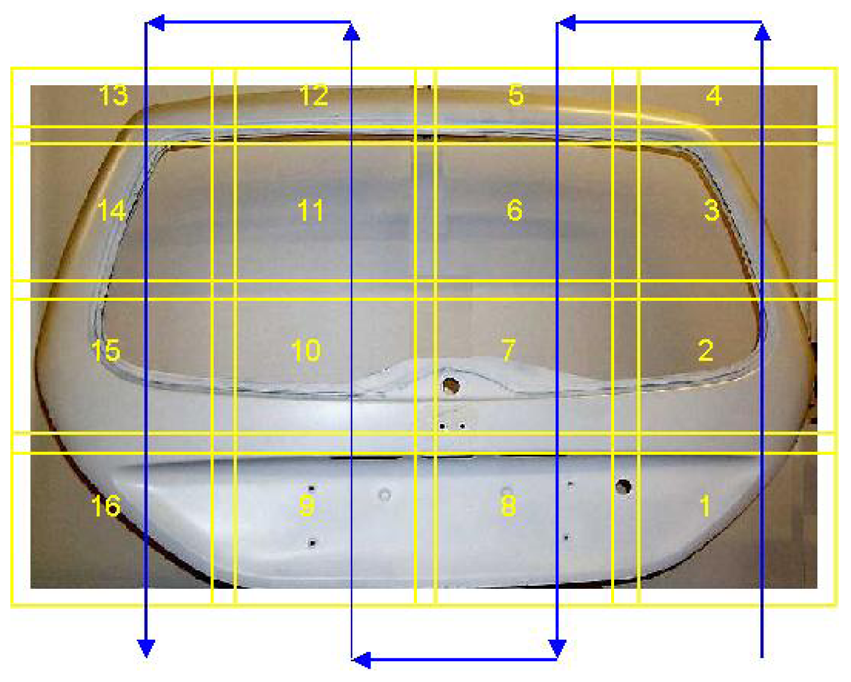
3.1.1 Surface quality control
3.1.2 Dimensional measurement and quality control
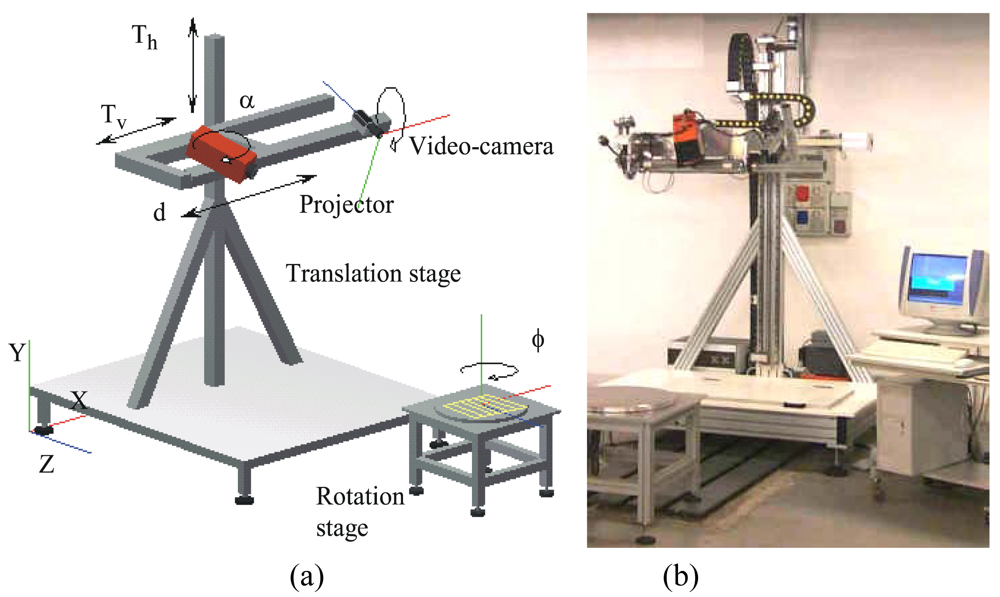
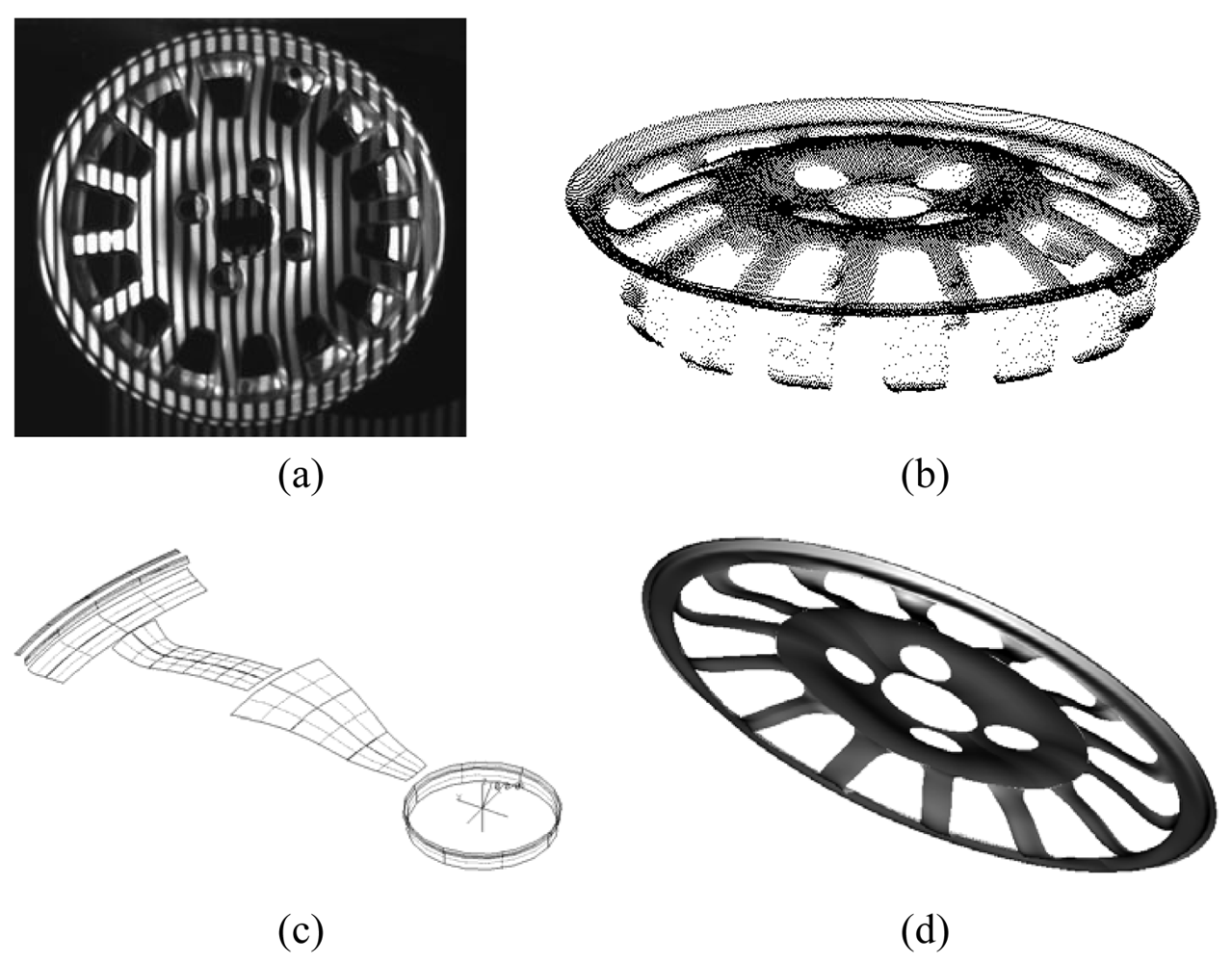
3.1.3 Reverse engineering of free-form shapes
3.2 Cultural heritage applications
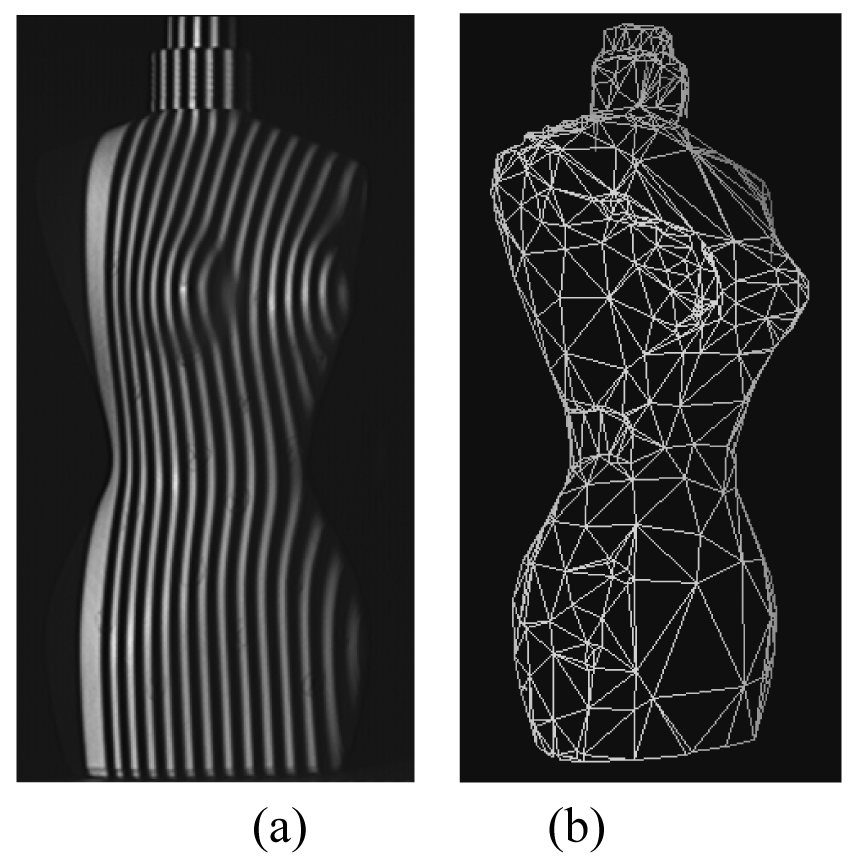
3.3 Medical applications
3.4 Crime scene documentation
4. Conclusions
References and Notes
- Blais, F. A review of 20 years of range sensors development. J. Electronic Imaging 2004, 13, 231–240. [Google Scholar]
- Jarvis, R.A. A perspective on range finding techniques for computer vision. IEEE Trans. Pattern Anal. Mach. Intell. 1983, 5, 122–139. [Google Scholar]
- Besl, P.J. Active, optical range imaging sensors. Mach. Vision Appl. 1988, 1, 127–152. [Google Scholar]
- Tiziani, H.J. Optical metrology of engineering surfaces-scope and trends. In Optical Measurement Techniques and Applications; Rastogi, P.K., Ed.; Artech House: Boston, MA, 1997; pp. 15–50. [Google Scholar]
- Chen, F.; Brown, G.M.; Song, M. Overview of three-dimensional shape measurement using optical methods. Opt. Eng. 2000, 39, 10–22. [Google Scholar]
- Beraldin, J.A.; Blais, F.; Cournoyer, L.; Godin, G.; Rioux, M. Active 3D sensing; NRC Publication Number, Technical Report 44159; Ottawa, 2001. [Google Scholar]
- Nitzan, D.; Brain, A.E.; Duda, R.O. The measurement and use of registered reflectance and range data in scene analysis. Proceedings of the IEEE, New York, February 1977; 65, pp. 206–220.
- Li, Y.; Gu, P. Free-form surface inspection techniques state of the art review. Comput. Aided D. 2004, 36, 1395–1417. [Google Scholar]
- Chen, L.C. Surface digitization techniques for reverse engineering. 2002. http://www.cc.ntut.edu/coop/atc/aoi/html2/tecedu.html.
- Cheng, W.L.; Menq, C.H. Integrated laser/CMM system for the dimensional Inspection of objects made on soft material. Int. J. Adv. Manuf. Tech. 1995, 10, 36–45. [Google Scholar]
- Saitoh, K.; Machida, T.; Kiyokawa, K.; Takemura, H. A 2D-3D integrated interface for mobile robot control using omnidirectional images and 3D geometric models. Proc. IEEE/ACM International Symposium on Mixed and Augmented Reality, Santa Barbara, USA, October 2006; pp. 173–176.
- Abellán, A.; Vilaplana, J.M.; Martinez, J. Application of a long-range Terrestrial Laser Scanner to a detailed rockfall study at Vall de Núria (Eastern Pyrenees, Spain). Eng. Geol. 2006, 88, 136–148. [Google Scholar]
- Godin, G.; Beraldin, J.A.; Taylor, J.; Cournoyer, L.; Rioux, M.; El-Hakim, S.; Baribeau, R.; Blais, F.; Boulanger, P.; Domey, J.; Picard, M. Active optical 3D imaging for heritage applications. IEEE Comput. Graph. Appl. 2002, 22, 24–35. [Google Scholar]
- Xu, Z.Q.; Ye, S.H.; Fan, G.Z. Color 3D reverse engineering. J. Mater. Process. Tech. 2002, 129, 495–499. [Google Scholar]
- Blais, F.; Beraldin, J.A. Recent Developments in 3D Multi-Model Laser Imaging Applied to Cultural Category. Mach. Vis. Appl. 2006, 17, 395–409. [Google Scholar]
- D'Apuzzo, N.; Mitchell, H. Medical applications. In Advances in Photogrammetry, Remote Sensing and Spatial Information Sciences: 2008 ISPRS Congress Book; Li, Chen, Baltsavias, Eds.; Taylor & Francis Group: London, UK, 2008; pp. 425–438. [Google Scholar]
- Blais, F.; Rioux, M.; Beraldin, J.A. Practical considerations for the design of a high precision 3D laser scanner system. Proc. SPIE 1988, 959, 225–246. [Google Scholar]
- Rioux, M. Laser rangefinder based on synchronized scanners. Appl. Opt. 1984, 23, 3837–3844. [Google Scholar]
- Rioux, M.; Blais, F. Compact three-dimensional camera for robotics applications. J. Opt. Soc. Am. 1986, 3, 1518–1521. [Google Scholar]
- McIvor, A.M. Calibration of a laser stripe profiler. Proc. Second Int. Conf. 3-D Digital Imaging and Modeling (3DIM '99), Ottawa, Canada; 1999; pp. 92–98. [Google Scholar]
- Blais, F.; Rioux, M.; Domey, J. Optical Range Image Acquisition for the Navigation of a Mobile Robot. Proc. 1991 IEEE Int. Conf. Robotics Automation, Sacramento, CA, April 1991; 3, pp. 2574–2580.
- Trucco, E.; Fisher, R.B.; Fitzgibbon, A.W.; Naidu, D.K. Calibration, data consistency and model acquisition with laser stripes. Int. J. Comput. Integrated Manuf. 1998, 11, 293–310. [Google Scholar]
- Lang, S.; Dorba, L.; Blais, F.; Lecavalier, M. Characterization and testing of the BIRIS range sensor. IMTC/93 Conference Record, Ottawa, May 18-20, 1993; pp. 459–464.
- www.sick.com.
- Sansoni, G.; Patrioli, A.; Docchio, F. OPL-3D: a novel, portable optical digitiser for fast acquisition of free-form surfaces. Rev. Scient. Instr. 2003, 74, 2593–2603. [Google Scholar]
- Le Moigne, J.; Waxman, A.M. Projected light patterns for short range navigation of autonomous robots. Proc. Int. Conf. on Pattern Recognition, August 1984; 1, pp. 203–206.
- Le Moigne, J.; Waxman, A.M. Multi-resolution grid patterns for building range maps. Proc. Vision Conf. 1985, 8, 22–39. [Google Scholar]
- Morita, H.; Yajima, K.; Sakata, S. Reconstruction of surfaces of 3-D objects by M-array pattern projection method. Proc. Int. Conf. on Computer Vision, Annapolis, March 1988; pp. 468–473.
- Maruyama, M.; Abe, S. Range sensing by projecting multiple slits with random cuts. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 647–651. [Google Scholar]
- Boyer, K.L.; Kak, A.C. Color-encoded structured light for rapid active ranging. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 9, 14–28. [Google Scholar]
- Tang, S.; Hung, Y.Y. Fast profilometry for the automatic measurement of 3-D object shape. Appl. Opt. 1990, 29, 3012–3018. [Google Scholar]
- Srinivasan, V.; Liu, H.C.; Halioua, M. Automated phase-measuring profilometry of 3-D diffuse objects. Appl. Opt. 1984, 23, 3105–3108. [Google Scholar]
- Sansoni, G.; Redaelli, E. A 3D vision system based on one-shot projection and phase demodulation for fast profilometry. Meas. Sci. Technol. 2005, 16, 1109–1118. [Google Scholar]
- Sansoni, G.; Trebeschi, M.; Docchio, F. Fast 3D profilometer based upon the projection of a single fringe pattern and absolute calibration. Meas. Sci. Technol. 2006, 17, 1757–1766. [Google Scholar]
- Kwon, H.; Park, J.; Kak, A. A new approach for active stereo camera calibration. IEEE International Conference on Robotics and Automation, Rome, Italy, April 10-14, 2007; pp. 3180–3185.
- DeSouza, G.; Kak, A. Vision for Mobile Robot Navigation: A Survey. IEEE T. Pattern. Anal. 2002, 24, 237–267. [Google Scholar]
- Nitzan, D. Three-Dimensional Vision Structure for Robot Applications. IEEE T. Pattern. Anal. 1988, 10, 291–308. [Google Scholar]
- Pavlidis, G.; Koutsoudis, A.; Arnaoutoglou, F.; Tsioukas, V.; Chamzas, C. Methods for 3D digitization of Cultural Heritage. J. Cult. Herit. 2007, 8, 93–98. [Google Scholar]
- Baumberg, A.; Lyons, A.; Taylor, R. 3DS.O.M.-A commercial software solution to 3D scanning, Vision, Video, and Graphics (2003), The Euro- Association 2003. Eurographics Partner Event, Video, and Graphics; 2003. [Google Scholar]
- Remondino, F; El-Hakim, S. Image-based 3D modelling: A review. Photogramm. Rec. 2006, 21, 269–291. [Google Scholar]
- Remondino, F.; El-Hakim, S. Critical overview of image-based 3D modeling. Workshop 3D laser Scanning and Photogrammetry for Building Information Modeling, Trondheim, Norway, September 2008; pp. 340–351.
- Remondino, F. From point cloud to surface: the modeling and visualization problem. Workshop on Visualization and Animation of Reality based 3D Models, Tarasp-Vulpera, Switzerland, February 24-28, 2003.
- Remondino, F.; El-Hakim, S.; Gruen, A.; Zhang, L. Turning Images into 3-D Models. IEEE Signal Proc. Mag. 2008, 25, 55–65. [Google Scholar]
- Hartley, R.I.; Mundy, J.L. The relationship between photogrammetry and computer vision. In Integrating Photogrammetry Techniques with Scene Analysis and Machine Vision, SPIE 1944, Orlando, FL, USA, April 11-16, 1993; Barret, E.B, McKeown, M., Eds.; 19, pp. 92–105.
- El-Hakim, S.F.; Beraldin, J.A.; Blais, F. A comparative Evaluation of the Performance of passive and Active 3-D Vision Systems. SPIE Proc. Conf. Digital Photogrammetry, St. Petersburg, Russia, June 25-30, 1995; 2646, pp. 14–25.
- Remondino, F.; Guarnieri, A.; Vettore, A. 3D modeling of close-range objects: photogrammetry or laser scanning? Proc. SPIE Videometrics VIII, Istanbul, Turkey, July 12-23, 2004; 5665, pp. 216–225.
- Ronnholm, P.; Honkavaara, E.; Litkey, P.; Hyyppa, H.; Hyyppa, J. Integration of laser scanning and photogrammetry. IAPRS 2007, XXXVI part 3/W52, 355–362. [Google Scholar]
- Van Gool, L.; Zeng, G.; Van den Borre, F.; Muller, P. Photogrammetric Image Analysis; Stilla, U., Mayer, H., Eds.; Institute of Photogrammetry and Cartography: Munich, Germany, September 19–21 2007; Volume 36, pp. 209–220. [Google Scholar]
- Cornelis, N.; Leibe, B.; Cornelis, K.; Van Gool, L. 3D Urban Scene Modeling Integrating Recognition and Reconstruction. Int. J. Comput. Vis. 2008, 78, 121–141. [Google Scholar]
- Leibe, B.; Schindler, K.; Cornelis, N.; Van Gool, L. Coupled Object Detection and Tracking from Static Cameras and Moving Vehicles. IEEE Trans. Patt. Anal. Mach. Intell. 2008, 30, 1683–1698. [Google Scholar]
- Nielsen, T.; Bormann, F.; Wolbeck, S.; Spiecker, H.; Burrows, M.D.; Andersen, P. Time-of-light analysis of light pulses with a temporal resolution of 100ps. Rev. Sci. Instrum. 1996, 67, 1721–1724. [Google Scholar]
- Beraldin, J.A.; Blais, F.; Cournoyer, L.; Rodella, R.; Bernier, F.; Harrison, N. Digital 3D imaging system for rapid response on remote sites. Proc. Second Int. Conf. on 3-D Digital Imaging and Modeling (3DIM '99), Ottawa, Canada, October 1999; pp. 34–43.
- Berner, J. The holography Book; Avon Books: New York, 1980. [Google Scholar]
- Moore, D.T.; Traux, B.E. Phase-locked Moiré fringe analysis for automated contouring of diffuse surfaces. Appl. Opt. 1979, 18, 91–96. [Google Scholar]
- Nayar, S.; Watanabe, M.; Noguchi, M. Real-time focus range sensor. Proc. IEEE Int. Conf. Computer Vision, Cambridge, Ma, June 20-23, 1995; pp. 995–1001.
- Heekenjann, P.B.; Schmidt, H. New UV optic for submicron laser processing with a frequency quadrupled Nd:YAG laser. SPIE, Laser Materials Processing and Machining, Frankfurt, Germany, June 20-21, 1994; 2246, pp. 6–15.
- Bouguet, J.Y.; Perona, P. 3D photography on your desk. Proc. Sixth Int. Conf. Computer Vision, Bombay, India, January 4-7, 1998; pp. 43–48.
- Stevens, K.A. Representing and analyzing surface orientation. In Artificial Intelligence: an MIT Perspective; Winston, P.H., Brown, R.H., Eds.; Publisher: The MIT Press: Cambridge, March 20 1979; Volume 2, pp. 104–125. [Google Scholar]
- Horn, B.; Brooks, M.J. Shape from Shading; MIT Press: Cambridge, MA, 1989. [Google Scholar]
- Dorsch, R.G.; Häusler, G.; Herrmann, J.M. Laser triangulation: fundamental uncertainty in distance measurement. Appl. Opt. 1994, 33, 1306–1314. [Google Scholar]
- Besl, P.J; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Patt. Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar]
- Chen, Y.; Medioni, G. Object modeling by registration of multiple range images. IEEE Int. Conf. Robotics and Automation, Sacramento, California, April 1991; pp. 2724–2729.
- Chen, Y.; Medioni, G. Object modeling by registration of multiple range images. Image Vision Comput. 1992, 14, 145–155. [Google Scholar]
- Curless, B.; Levoy, M. A volumetric method for building complex models from range images. SIGGRAPH'96, New Orleans, LA, USA, August 4-9, 1996; pp. 303–312.
- Hoppe, H.; DeRose, T.; Duchamp, T.; McDonald, J.; Stuelzle, W. Surface reconstruction from unorganized points. SIGGRAPH'92, Chicago, July 26-31, 1992; pp. 71–78.
- Soucy, M.; Laurendeau, D. A general surface approach to the integration of a set of range views. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 348–353. [Google Scholar]
- Turk, G.; Levoy, M. Zippered polygon meshes from range images. SIGGRAPH'94, Orlando, Florida, July 24-29, 1994; pp. 311–318.
- Hilton, A.; Stoddart, A; Illingworth, J.; Windeatt, T. Marching triangles: Range image fusion for complex object modeling. IEEE Int. Conf. Image Processing, Lausanne, Switzerland, September 1996; pp. 381–384.
- Bernardini, F.; Mittleman, J.; Rushmeier, H.; Silva, C.; Taubin, G. The ball-pivoting algorithm for surface reconstruction. IEEE T. Vis. Comput. Gr. 1999, 5, 349–359. [Google Scholar]
- Bajaj, C.; Bernardini, F.; Xu, G. Automatic reconstruction of surfaces and scalar fields from 3D scans. SIGGRAPH'95, Los Angeles, CA, USA, August 6-11, 1995; pp. 109–118.
- Sato, Y.; Wheeler, M.; Ikeuchi, K. Object shape and reflectance modeling from observation. SIGGRAPH'97, Los Angeles, August 3-8, 1997; pp. 379–387.
- Pulli, K.; Cohen, M.; Duchamp, T.; Hoppe, H.; Shapiro, L.; Stuetzle, W. View-based rendering: Visualizing real objects from scanned range and color data. 8th Eurographics Workshop on Rendering, Saint-Etienne, France, June 1997; pp. 23–34.
- Park, J.; DeSouza, G.N. Machine Learning and Robot Perception; Patnaik, S, Jain, L.C., Tzafestas, G., Bannore, V, Eds.; Springer-Verlag: New York, 2005; pp. 203–264. [Google Scholar]
- Bernardini, F.; Rusheimer, H. The 3D Model Acquisition Pipeline. Comp. Graph. F. 2002, 21, 149–172. [Google Scholar]
- Salvi, J.; Matabosch, C.; Fofi, D.; Forest, J. A Review of recent range image registration methods with accuracy evaluation. Image Vision Comput. 2007, 25, 578–596. [Google Scholar]
- Wang, S.H.; Tay, C.J.; Quan, C.; Shang, H.M.; Zhou, Z.F. Laser integrated measurement of surface roughness and micro-displacement. Meas. Sci. Technol. 2000, 11, 454–458. [Google Scholar]
- Shiou, F.J.; Cheng, W.Y. Development of an innovative multi-detector triangulation probe. IEEE Int. Conf. Mechatronics, Ontario, Canada, July 24-28, 2005; pp. 318–322.
- Sansoni, G.; Redaelli, E. A 3D vision system based on one-shot projection and phase demodulation for fast profilometry. Meas. Sci. Technol. 2005, 16, 1109–1118. [Google Scholar]
- Sansoni, G.; Trebeschi, M.; Docchio, F. Fast 3D profilometer based upon the projection of a single fringe pattern and absolute calibration. Meas. Sci. Technol. 2006, 17, 1757–1766. [Google Scholar]
- Dorsch, R.G.; Häusler, G.; Herrmann, J.M. Laser triangulation: fundamental uncertainty in distance measurement. Appl. Opt. 1994, 33, 1306–1314. [Google Scholar]
- Tomassini, P.; Rovati, L.; Sansoni, G.; Docchio, F. Novel optical sensor for the measurement of surface texture. Rev. Scient. Instr. 2001, 72, 2207–2213. [Google Scholar]
- Sansoni, G.; Patrioli, A. Non contact 3D sensing of free-form complex surfaces. SPIE-Videometrics and Optical methods for 3D shape Measurement, San Jose, CA, January 20-26, 2001; 4309, pp. 232–239.
- Krattenthaler, W.; Mayer, K.J.; Duwe, H.P. 3D-Surface measurement with coded light approach. Proc. Öesterr. Arbeitsgem. MustererKennung 1993, 12, 103–114. [Google Scholar]
- Bidanda, B.; Hosni, Y.A. Reverse engineering and its relevance to industrial engineering: a critical review. Computers Ind. Eng. 1994, 26, 343–348. [Google Scholar]
- L. Chen, L.; Lin, C.; Grier, C. A vision-aided reverse engineering approach to reconstructing free-form surfaces. Robot. Comp. Integr. Manuf. 1997, 13, 323–336. [Google Scholar]
- Motovalli, S.; Suharitdamron, V.; Alrashdan, A. Design model generation for reverse engineering using multi-sensors. IIE Trans. 1998, 30, 357–366. [Google Scholar]
- Cauchick, M.; King, T.; Davis, J. CMM verification: a survey. Measurement 1996, 17, 1–16. [Google Scholar]
- Carbone, V.; Carocci, M.; Savio, E.; Sansoni, G.; De Chiffre, L. Combination of a vision system and a Coordinate Measuring Machine for the Reverse Engineering of Freeform Surfaces. Int. J. Adv. Manuf. Tech. 2001, 17, 263–271. [Google Scholar]
- Li, L.; Schemenauer, N.; Peng, X.; Zeng, Y.; Gu, P. A reverse engineering system for rapid manufacturing of complex objects. Robot. Comp. Integr. Manuf. 2002, 18, 53–67. [Google Scholar]
- Chow, J.; Xu, T.; Lee, S.M.; Kengskool, K. Development of an Integrated Laser-Based Reverse Engineering and Machining System. Int. J. Adv. Manuf. Tech. 2000, 19, 186–191. [Google Scholar]
- Clark, J. Implementing Non-Contact Digitization Techniques within the Mechanical Design Process. Sensor Rev. 2000, 20, 195–201. [Google Scholar]
- Lee, K.H.; Park, H. Automated Inspection of Free-Form Shape Parts by Laser Scanning. Robot. Comp. Integr. Manuf. 2000, 16, 201–210. [Google Scholar]
- Sansoni, G.; Docchio, F. Three-dimensional optical measurements and reverse engineering for automotive applications. Robot. Comp. Integr. Manuf. 2004, 20, 359–367. [Google Scholar]
- Hemsley, J. Digital Application for Cultural and Heritage Institutions; Ashgate Publishing Group: Aldershot, UK, 2005. [Google Scholar]
- Guidi, G.; Beraldin, J.-A.; Atzeni, C. High accuracy 3D modeling of Cultural Heritage: the digitizing of Donatello's “Maddalena”. IEEE Trans. Image Proc. 2004, 13, 370–380. [Google Scholar]
- Bernardini, F.; Martin, I.; Mittleman, J.; Rusheimer, H.; Taubin, G. Building a digital model of Michelangelo's Florentine Pietà. IEEE Comput. Graph. 2002, 22, 59–67. [Google Scholar]
- Levoy, M; et al. The digital Michelangelo project: 3D scanning of large statues. Proc. SIG-GRAPH 00, Computer Graph. Proc., Annu. Conf. Ser., New Orleans, Louisiana, USA; 2000; pp. 131–144. [Google Scholar]
- Lambers, K.; Eisenbeiss, H.; Sauerbier, M.; Kupferschmidt, D.; Gaisecker, T.; Sotoodeh, S.; Hanusch, T. Combining photogrammetry and laser scanning for the recording and modeling of the Late Intermediate Period site of Pinchango Alto, Palpa, Peru. J. Archaeol. Sci. 2007, 34, 1702–1712. [Google Scholar]
- Balzani, M.; Callieri, M.; Fabbri, M.; Fasano, A.; Montani, C.; Pingi, P.; Santopuoli, N.; Scopigno, R.; Uccelli, F.; Varone, A. Digital representation and multimodal presentation of archeological graffiti ad Pompei. 5th Int. Symp. Virtual Reality Archeology and Cultural Heritage, Eurograhics Symp. Proc., Brussels: Belgium, December 6-10, 2004; Chrysanthou, Y., Cain, K., Silberman, N., Niccolucci, F., Eds.; pp. 93–103.
- Boulanger, P.; Taylor, J.; El-Hakim, S.F.; Rioux, M. How to virtualize reality: an application to re-creation of world heritage site. Proc. Conf. Virtual Systems and Multimedia, Gifu, Japan, November 18-20, 1998; pp. 18–20.
- Kampel, M.; Sablatnig, R. Rule based system for archaeological pottery classification. Patt. Recogn. Lett. 2007, 28, 740–747. [Google Scholar]
- Anderson, S.; Levoy, M. Unwrapping and Visualizing Cuneiform Tablets. IEEE Comput. Graph. 2002, 22, 82–88. [Google Scholar]
- Sansoni, G.; Docchio, F. 3-D optical Measurements in the Field of Cultural heritage: The Case of the Vittoria Alata of Brescia. IEEE Trans. Instr. Meas. 2005, 54, 359–368. [Google Scholar]
- Sansoni, G.; Docchio, F.; Trebeschi, M.; Filippi, S.; Motyl, B. Virtual and rapid prototyping by means of 3D optical acquisition and CAD modeling: application to cultural heritage and to the automotive domain. In Virtual Modelling and Rapid Manufacturing - Advanced Research in Virtual and Rapid Prototyping; Bártolo, P.J., et al., Eds.; Taylor & Francis Group: London, UK, 2005; pp. 251–257. [Google Scholar]
- Sansoni, G.; Cavagnini, G.; Modonesi, N.; Piccoli, A.; Marchesini, S. Generazione ed elaborazione di misure mediante sensori non a contatto per l'analisi e l'interpretazione di reperti archeologici. Proc. XXV Congresso Nazionale Associazione GMEE; 2008; pp. 289–290. [Google Scholar]
- Jones, P.R.M.; Rioux, M. Three-dimensional surface anthropometry: applications to human body. Opt. Laser. Eng. 1997, 28, 89–117. [Google Scholar]
- Simmons, K.P. Body measurement techniques: a comparison of three-dimensional body scanning and physical anthropometric methods. Ph.D. Thesis, North Carolina State University, Raleigh, NC, 2001. [Google Scholar]
- Tukuisis, P.; Meunier, P.; Jubenville, C.E. Human body surface area: measurement and prediction using three dimensional body scans. Eur. J. Appl. Physiol. Occup. Physiol. 2001, 85, 264–271. [Google Scholar]
- Cheah, C.M.; Chua, C.K.; Tan, K.H.; Teo, C.K. Integration of laser surface digitizing with CAD/CAM techniques for developing facial prostheses. Part 1: Design and fabrication of prosthesis replicas. Int. J. Prosthodont. 2003, 16, 435–441. [Google Scholar]
- Remondino, F. 3-D reconstruction of static human body shape from image sequence. Comput. Vis. Image Understand. 2004, 93, 65–85. [Google Scholar]
- D'Apuzzo, N. Surface Measurement and Tracking of Human Body Parts from Multi Station Video Sequences. Ph.D. Thesis, Institute of Geodesy and Photogrammetry, ETH, Zurich, Switzerland, 2003. [Google Scholar]
- Thali, M.J.; Braun, M.; Dirnhofer, R. Optical 3D surface digitizing in forensic medicine: 3D documentation of skin and bone injuries. Forensic Sci. Int. 2003, 137, 203–208. [Google Scholar]
- Bruschweiler, W.; Braun, M.; Dirnhofer, R. Analysis of patterned injuries and injury-causing instruments with forensic 3D/CAD supported photogrammetry (FPHG): an instruction manual for the documentation process. Forensic Sci. Int. 2003, 132, 130–138. [Google Scholar]
- Banno, A.; Masuda, T.; Ikeuchi, K. Three dimensional visualization and comparison of impressions on fired bullets. Forensic Sci. Int. 2004, 140, 233–240. [Google Scholar]
- Goos, MI.; Alberink, I.B.; Ruifrok, A.C.C. 2D/3D image (facial) comparison using camera matching. Nether. Forens. Inst. 2006, 163, 10–17. [Google Scholar]
- Park, HK.; Chung, J.W.; Kho, H.S. Use of hand-held laser scanning in the assessment of craniometry. Forens. Sci. Int. 2006, 160, 200–206. [Google Scholar]
- Cavagnini, G.; Scalvenzi, M.; Trebeschi, M.; Sansoni, G. Reverse engineering from 3D optical acquisition: application to Crime Scene Investigation. In Virtual and Rapid Manufacturing - Advanced Research in Virtual and Rapid Prototyping; Bártolo, P.J., Ed.; Taylor & Francis Group: London, UK, 2007; pp. 195–201. [Google Scholar]
- Sansoni, G.; Docchio, F.; Trebeschi, M.; Scalvenzi, M.; Cavagnini, G. Application of three-dimensional optical acquisition to the documentation and the analysis of crime scenes and legal medicine inspection. Proc. 2nd IEEE Int. Workshop on Advances in Sensors and Interfaces, Bari, Italy, June 26-27, 2007; pp. 1–10.
- Little, C.; Small, D.; Carlson, J. 3D Imaging and Modeling for Crime Scene Documentation. Proc. ICIP99, Kobe, Japan; 1999; pp. 27–34. [Google Scholar]
- Altschuler, B.; Monson, K. Initial progress in the recording of crime scene simulations using 3D laser structured light imagery techniques for law enforcement and forensic applications. Proc. SPIE, San Diego, CA, USA, July 1998; 3240, pp. 230–241.
- Cavagnini, G.L.; Sansoni, G.; Trebeschi, M. Using 3D range cameras for crime scene documentation and legal medicine. Proc. SPIE, 3D Imaging Metrology; 2009; 3272. in press. [Google Scholar]











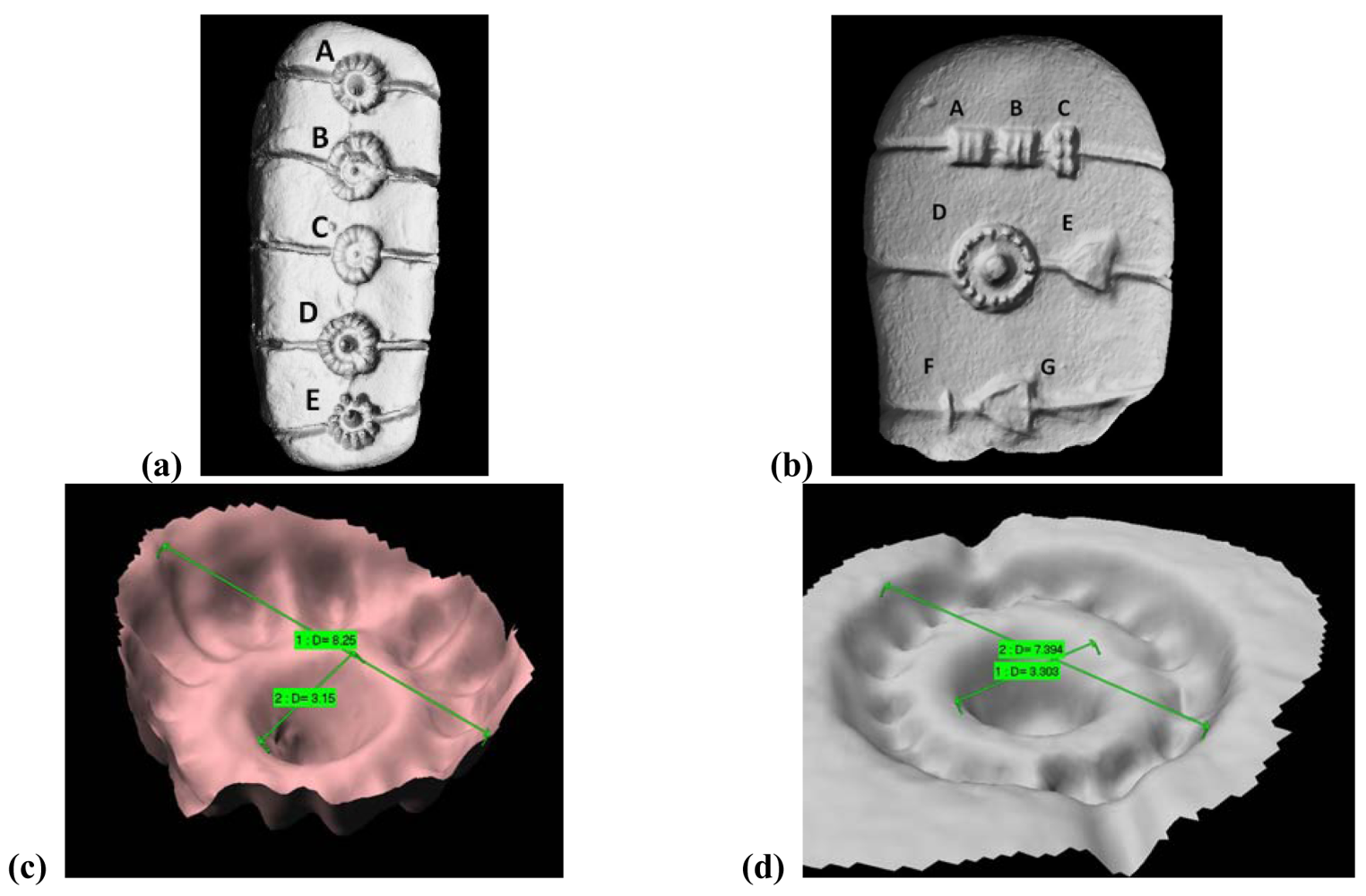
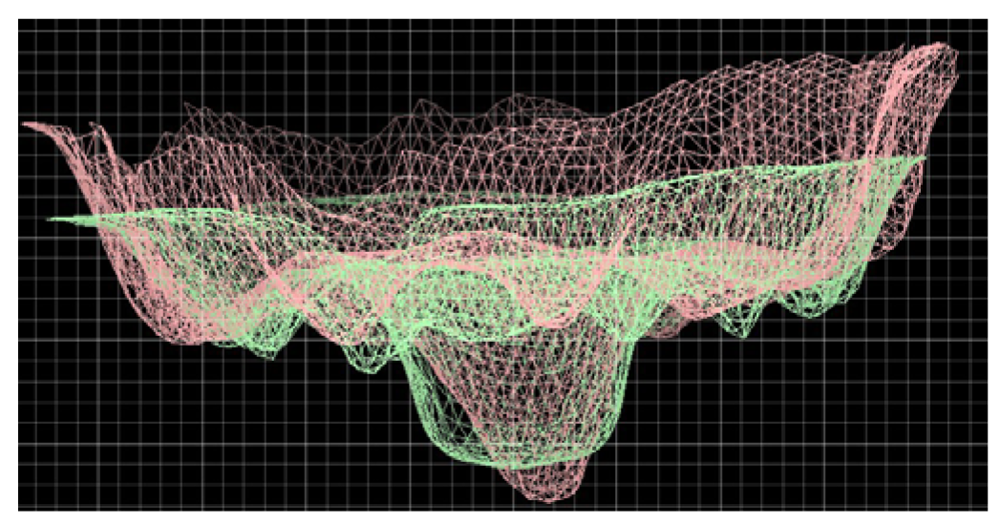
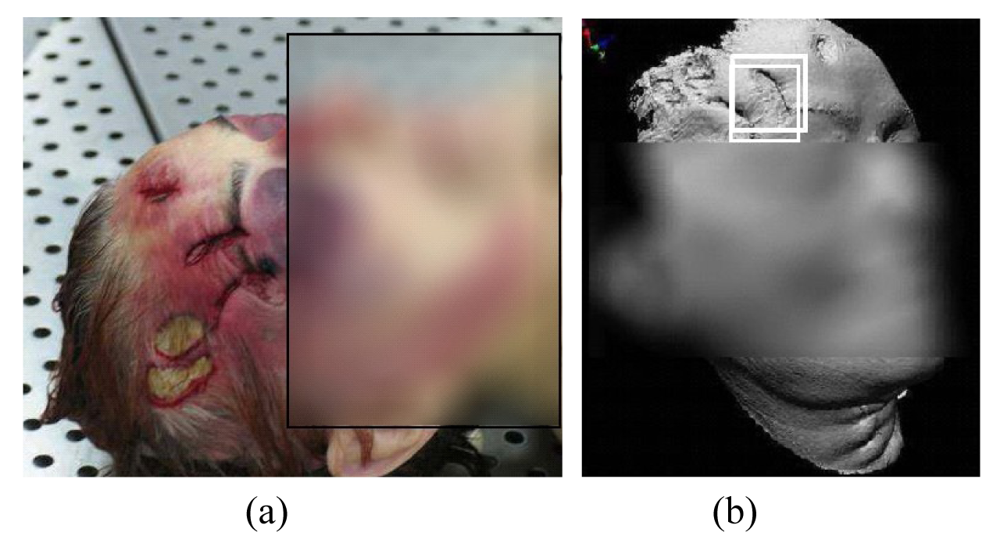




| Triangulation | Time delay | Monocular Images | Passive | Active | Direct | Indirect | Range | Surface Orientation | |
|---|---|---|---|---|---|---|---|---|---|
| Laser triangulators | X | X | X | X | |||||
| Structured light | X | X | X | X | |||||
| Stereo vision | X | X | X | X | |||||
| Photogrammetry | X | X | X | X | |||||
| Time of Flight | X | X | X | X | |||||
| Interferometry | X | X | X | X | |||||
| Moiré fringe range contours | X | X | X | X | |||||
| Shape from focusing | X | X | X | X | X | ||||
| Shape from shadows | X | X | X | X | |||||
| Texture gradients | X | X | X | X | |||||
| Shape from shading | X | X | X | X | |||||
| Shape from photometry | X | X | X | X |
| TECHNOLOGY | STRENGTH | WEAKNESS |
| Laser triangulators | Relative simplicity Performance generally independent of ambient light High data acquisition rate | Safety constraint associated with the use of laser source Limited range and measurement volume Missing data in correspondence with occlusions and shadows Cost |
| Structured Light | High data acquisition rate Intermediate measurement volume Performance generally dependent of ambient light | Safety constraints, if laser based Computationally middle-complex Missing data in correspondence with occlusions and shadows Cost |
| Stereo Vision | Simple and inexpensive High accuracy on well-defined targets | Computation demanding Sparse data covering Limited to well defined scenes Low data acquisition rate |
| Photogrammetry | Simple and inexpensive High accuracy on well-defined targets | Computation demanding Sparse data covering Limited to well defined scenes Low data acquisition rate |
| Time-of-Flight | Medium to large measurement range Good data acquisition rate Performance generally independent of ambient light | Cost Accuracy is inferior to triangulation at close ranges |
| Interferometry | Sub-micron accuracy in micro-ranges | Measurement capability limited to quasi-flat surfaces Cost Limited applicability in industrial environment |
| Moiré fringe range contours | Simple and low cost Short ranges | Limited to the measurement of smooth surfaces |
| Shape from focusing | Simple and inexpensive Available sensors for surface inspection and microprofilometry | Limited fields of view Non-uniform spatial resolution Performance affected by ambient light (if passive) |
| Shape from shadows | Low cost Limited demand for computing power | Low accuracy |
| Texture gradients | Simple and low cost | Low accuracy |
| Shape from shading | Simple and low cost | Low accuracy |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sansoni, G.; Trebeschi, M.; Docchio, F. State-of-The-Art and Applications of 3D Imaging Sensors in Industry, Cultural Heritage, Medicine, and Criminal Investigation. Sensors 2009, 9, 568-601. https://doi.org/10.3390/s90100568
Sansoni G, Trebeschi M, Docchio F. State-of-The-Art and Applications of 3D Imaging Sensors in Industry, Cultural Heritage, Medicine, and Criminal Investigation. Sensors. 2009; 9(1):568-601. https://doi.org/10.3390/s90100568
Chicago/Turabian StyleSansoni, Giovanna, Marco Trebeschi, and Franco Docchio. 2009. "State-of-The-Art and Applications of 3D Imaging Sensors in Industry, Cultural Heritage, Medicine, and Criminal Investigation" Sensors 9, no. 1: 568-601. https://doi.org/10.3390/s90100568
APA StyleSansoni, G., Trebeschi, M., & Docchio, F. (2009). State-of-The-Art and Applications of 3D Imaging Sensors in Industry, Cultural Heritage, Medicine, and Criminal Investigation. Sensors, 9(1), 568-601. https://doi.org/10.3390/s90100568




