On the Soil Roughness Parameterization Problem in Soil Moisture Retrieval of Bare Surfaces from Synthetic Aperture Radar
Abstract
:1. Introduction
2. Soil moisture retrieval
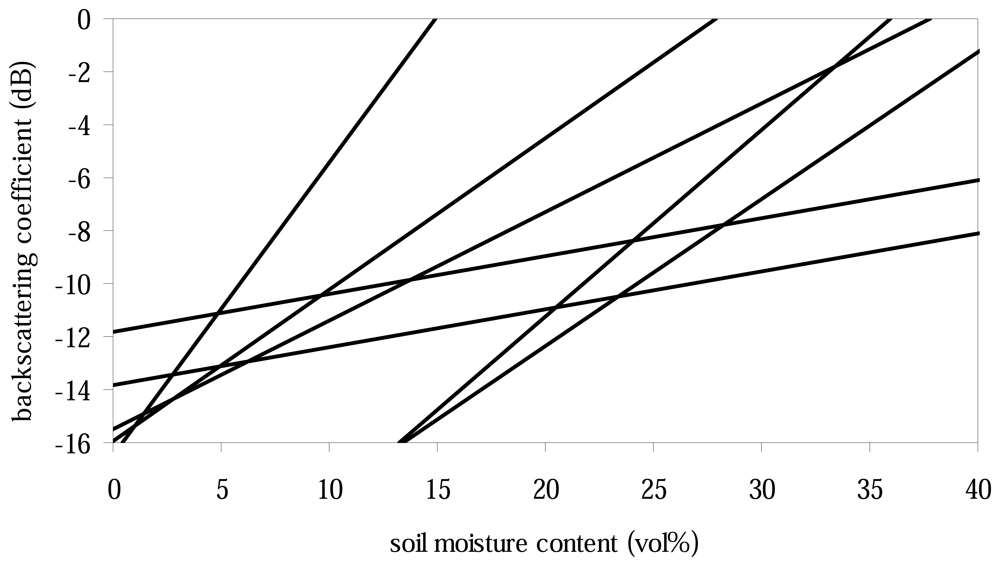
2.1. Empirical models
2.2. Semi-empirical models
2.3. Physically-based models
3. Soil roughness characterization
3.1. RMS height
3.2. Correlation length
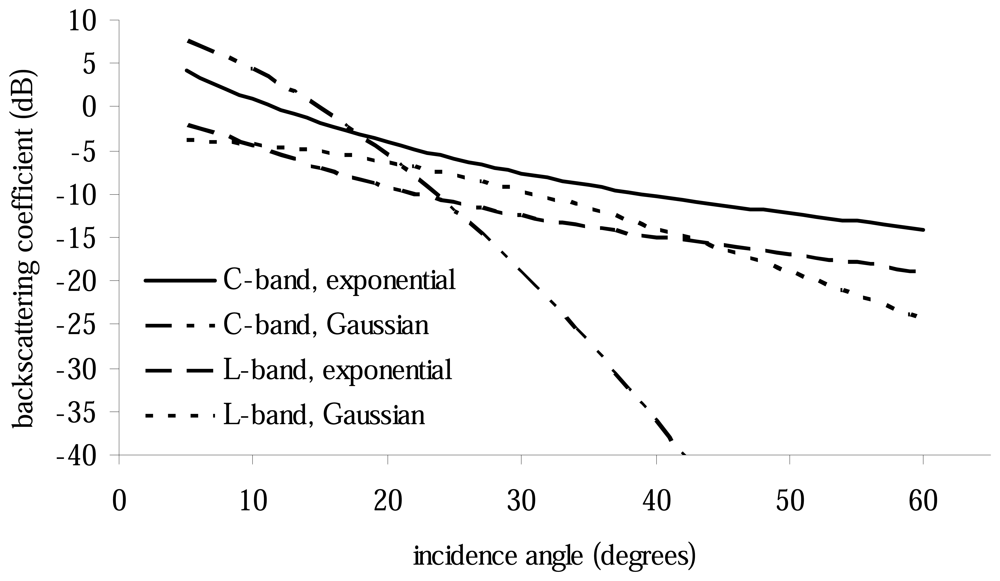
3.3. Autocorrelation function
4. Impact of in situ roughness characterization on soil moisture retrieval
4.1. Techniques
4.2. Preprocessing
4.3. Measurement accuracy
4.3.1. Horizontal resolution
4.3.2. Vertical resolution
4.3.3. Digitization error
4.4. Profile length
4.5. Number of measurements
4.6. Spatial variability of soil roughness
4.7. Temporal changes of soil roughness
5. Alternative approaches to the roughness problem
5.1. Multi-scale processes
5.2. Calibration of parameters
5.3. Two-dimensional surface roughness characterization
5.4. Multi-image approach
5.5. Using polarimetric data
5.6. Using prior knowledge on roughness state
6. Conclusions
Acknowledgments
References
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied hydrology; McGraw-Hill Inc.: New York, 1988. [Google Scholar]
- Ulaby, F.T.; Batlivala, P.P.; Dobson, M.C. Microwave backscatter dependence on surface roughness, soil moisture and soil texture: Part I: bare soil. IEEE Trans. Geosci. Remote Sens. 1978, GE-16, 286–295. [Google Scholar]
- Ulaby, F.T.; Dubois, P.C.; van Zyl, J. Radar mapping of surface soil moisture. J. Hydrol. 1996, 184, 57–84. [Google Scholar]
- Ulaby, F. T.; Moore, R. K.; Fung, A. K. Microwave Remote Sensing: Active and Passive; Artech House: Boston, MA, 1982; Vol. II. [Google Scholar]
- Wagner, W.; Blöschl, G.; Pampaloni, P.; Calvet, J.-C.; Bizzarri, B.; Wigneron, J.-P.; Kerr, Y. Operational readiness of microwave remote sensing of soil moisture for hydrologic applications. Nordic Hydrology 2007, 38, 1–20. [Google Scholar]
- Moran, M.S.; Peters-Lidard, C.D.; Watts, J.M.; McElroy, S. Estimating soil moisture at the watershed scale with satellite-based radar and land surface models. Can. J. Remote Sensing 2004, 30, 805–826. [Google Scholar]
- Walker, J.P.; Houser, P.R. Requirements of a global near-surface soil moisture satellite mission: accuracy, repeat time, and spatial resolution. Advances in Water Resources 2004, 27, 785–801. [Google Scholar]
- Goodman, J.W. Some fundamental properties of speckle. J. Opt. Soc. Am. 1976, 66, 1145–1150. [Google Scholar]
- Oliver, C.; Quegan, S. Understanding Synthetic Aperture Radar Images; Artech House: Boston London, 1998. [Google Scholar]
- Ulaby, F.T.; Bare, J.E. Look direction modulation function of the radar backscattering coefficient of agricultural fields. Photogrammetric Engineering and Remote Sensing 1979, 45, 1495–1506. [Google Scholar]
- Dobson, M.C.; Ulaby, F.T. Active microwave soil moisture research. IEEE Trans. Geosc. Remote Sens. 1986, 24, 23–36. [Google Scholar]
- Ulaby, F. T.; Moore, R. K.; Fung, A. K. Microwave remote sensing: active and passive; Artech House: Boston, MA, 1986; Vol. III. [Google Scholar]
- Beaudoin, A.; Le Toan, T.; Gwyn, H.J. SAR observation and modeling of the C-band backscatter due to multiscale geometry and soil moisture. IEEE Trans. Geosci. Remote Sens. 1990, 28, 886–894. [Google Scholar]
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. An empirical model and an inversion technique for radar scattering from bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 1992, 30, 370–381. [Google Scholar]
- Fung, A.K. Microwave scattering and emission models and their applications; Artech House: Boston, MA, 1994. [Google Scholar]
- Michelson, D.B. ERS-1 SAR backscattering coefficient from bare fields with different tillage row direction. Int. J. Remote Sens. 1994, 15, 2679–2685. [Google Scholar]
- Rakotoarivony, L.; Taconet, O.; Vidal-Madjar, D.; Bellemain, P.; Benallègue, M. Radar backscattering over agricultural bare soils. Journal of Electromagnetic Waves and Applications 1996, 10, 187–209. [Google Scholar]
- Remond, A.; Beaudoin, A.; King, C. SAR imagery to estimate roughness parameters when modelling runoff risk. Int. J. Remote Sens. 1999, 20, 2613–2625. [Google Scholar]
- Davidson, M.W.J.; Le Toan, T.; Mattia, F.; Satalino, G.; Manninen, T.; Borgeaud, M. On the characterization of agricultural soil roughness for radar remote sensing studies. IEEE Trans. Geosci. Remote Sens. 2000, 38, 630–640. [Google Scholar]
- Davidson, M.W.J.; Mattia, F.; Satalino, G.; Verhoest, N.E.C.; Le Toan, T.; Borgeaud, M.; Louis, J.M.B.; Attema, E. Joint statistical properties of RMS height and correlation length derived from multisite 1-m roughness measurements. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1651–1658. [Google Scholar]
- Mattia, F.; Davidson, M.W.J.; Le Toan, T.; D'Haese, C.M.F.; Verhoest, N.E.C.; Gatti, A.M.; Borgeaud, M. A comparison between soil roughness statistics used in surface scattering models derived from mechanical and laser profilers. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1659–1671. [Google Scholar]
- Mattia, F.; Le Toan, T. Backscattering properties of multi-scale rough surfaces. Journal of Electromagnetic Waves and Applications 1999, 13, 491–526. [Google Scholar]
- Hallikainen, M.T.; Ulaby, F.T.; Dobson, M.C.; El-Rayes, M.A.; Wu, L.K. Microwave dielectric behavior of wet soils, Part I: Empirical models and experimental observations. IEEE Trans. Geosci. Remote Sens. 1985, 23, 25–34. [Google Scholar]
- Dobson, M.C.; Ulaby, F.T.; Hallikainen, M.T.; El-Rayes, M.S. Microwave dielectric behavior of wet soils: II. Dielectric mixing models. IEEE Trans. Geosci. Remote Sens. 1985, 23, 35–46. [Google Scholar]
- Peplinsky, N.R.; Ulaby, F.T.; Dobson, M.C. Dielectric properties of soils in the 0.3-1.3 GHz range. IEEE Trans. Geosci. Remote Sens. 1995, 33, 803–807. [Google Scholar]
- Peplinsky, N.R.; Ulaby, F.T.; Dobson, M.C. Corrections to ‘Dielectric properties of soils in the 0.3-1.3 GHz range’. IEEE Trans. Geosci. Remote Sens. 1995, 33, 1340. [Google Scholar]
- Ulaby, F.T.; Batlivala, P.P. Optimum radar parameters for mapping soil moisture. IEEE Trans. Geosci. Remote Sens. 1976, 14, 81–93. [Google Scholar]
- Fung, A.K.; Chen, K.S. Dependence of the surface backscattering coefficients on roughness, frequency and polarization states. Int. J. Remote Sens. 1992, 13, 1663–1680. [Google Scholar]
- Baghdadi, N.; King, C.; Bourguignon, A.; Remond, A. Potential of ERS and Radarsat data for surface roughness monitoring over bare agricultural fields: application to catchments in Northern France. Int. J. Remote Sens. 2002, 23, 3427–3442. [Google Scholar]
- Holah, N.; Baghdadi, N.; Zribi, M.; Bruand, A.; King, C. Potential of ASAR/ENVISAT for the characterization of soil surface parameters over bare agricultural fields. Remote Sens. Environ. 2005, 96, 78–86. [Google Scholar]
- Hirosawa, H.; Komiyama, S.; Matsozaka, Y. Cross polarized radar backscatter from moist soil. Remote Sens. Environ. 1978, 7, 211–217. [Google Scholar]
- Bradley, G.A.; Ulaby, F.T. Aircraft radar response to soil moisture. Remote Sens. Environ. 1981, 11, 419–438. [Google Scholar]
- Blanchard, A.J.; Newton, R.W.; Tsang, L.; Jean, R.B. Volumetric effects in cross-polarized airborne radar data. IEEE Trans. Geosci. Rem. Sens. 1982, 36, 36–41. [Google Scholar]
- McNairn, H.; Brisco, B. The application of C-band polarimetric SAR for agriculture: a review. Can. J. Remote Sensing 2004, 30, 525–542. [Google Scholar]
- Baghdadi, N.; Cerdan, O.; Zribi, M.; Auzet, V.; Darboux, F.; El Hajj, M.; Bou Kheir, R. Operational performance of current synthetic aperture radar sensors in mapping soil surface characteristics in agricultural environments: application to hydrological and erosion modelling. Hydrol. Proc. 2008, 22, 9–20. [Google Scholar]
- Mattia, F.; Le Toan, T.; Souyris, J.C.; De Carolis, G.; Floury, N.; Posa, F.; Pasquariello, G. The effect of surface roughness on multifrequency polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1997, 33, 915–926. [Google Scholar]
- Bruckler, L.; Wittono, H.; Stengel, P. Near surface moisture estimation from microwave measurements. Remote Sens. Environ. 1988, 26, 101–121. [Google Scholar]
- Chanzy, A. Basic soil surface characteristics derived from active microwave remote sensing. Remote Sensing Reviews 1993, 7, 303–319. [Google Scholar]
- Dobson, M.C.; Ulaby, F.T. Microwave backscatter dependence on surface roughness, soil moisture and soil texture: Part III – Soil tension. IEEE Trans. Geosci. Remote Sens. 1981, 19, 51–61. [Google Scholar]
- Fung, A.K.; Li, Z.; Chen, K.S. Backscattering from a randomly rough dielectric surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 356–369. [Google Scholar]
- Rahman, M.M.; Moran, M.S.; Thoma, D.P.; Bryant, R.; Sano, E.E.; Holifield Collins, C.D.; Skirvin, S.; Kershner, C.; Orr, B.J. A derivation of roughness correlation length for parameterizing radar backscatter models. Int. J. Remote Sens. 2007, 28, 3994–4012. [Google Scholar]
- Baronti, S.; Del Frate, F.; Ferrazzoli, P.; Palosca, S.; Pampaloni, P.; Schiavon, G. SAR polarimetric features of agricultural areas. Int. J. Remote Sens. 1995, 16, 2639–2656. [Google Scholar]
- Ferrazzoli, P.; Palosca, S.; Pampaloni, P.; Schiavion, G.; Sigismondi, S.; Solimini, D. The potential of multifrequency polarimetric SAR in assessing agricultural and arboreous biomass. IEEE Trans. Geosci. Remote Sens. 1997, 35, 5–17. [Google Scholar]
- Hajnsek, I.; Pottier, E.; Cloude, S.R. Inversion of surface parameters from polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 2003, 41, 727–744. [Google Scholar]
- Wever, T.; Henkel, J. Evaluation of the AIRSAR system for soil moisture analysis. Remote Sens. Environ. 1995, 53, 118–122. [Google Scholar]
- Baghdadi, N.; Holah, N.; Zribi, M. Soil moisture estimation using multi-incidence and multi-polarization ASAR SAR data. Int. J. Remote Sens. 2006, 27, 1907–1920. [Google Scholar]
- Srivastava, H.S.; Patel, P.; Manchanda, M.L.; Adiga, S. Use of multi-incidence angle RADARSAT-1 SAR data to incorporate the effects of surface roughness in soil moisture estimation. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1638–1640. [Google Scholar]
- Bryant, R.; Moran, M.S.; Thoma, D.P.; Holifield Collins, C.D.; Skirvin, S.; Rahman, M.; Slocum, K.; Starks, P.; Bosch, D.; González Dugo, M.P. Measuring surface roughness height to parameterize radar backscatter models for retrieval of surface soil moisture. IEEE Geosc Remote Sens. Letters 2007, 4. [Google Scholar]
- Le Toan, T.; Davidson, M.; Mattia, F.; Borderies, P.; Chenerie, I.; Manninen, T.; Borgeaud, M. Improved observation and modeling of bare surfaces for soil moisture retrieval. Earth Obs. Quarterly 1999, 62, 20–24. [Google Scholar]
- Baghdadi, N.; Paillou, P.; Grandjean, G.; Dubois, P.; Davidson, M. Relationship between profile length and roughness variables for natural surfaces. Int. J. Remote Sens. 2000, 21, 3375–3381. [Google Scholar]
- Zhixiong, L.; Nan, C.; Perdok, U.D.; Hoogmoed, W.B. Characterisation of Soil Profile Roughness. Biosystems Engineering 2005, 91, 369–377. [Google Scholar]
- Zribi, M.; Dechambre, M. A new empirical model to retrieve soil moisture and roughness from radar data. Remote Sens. Environ. 2002, 84, 42–52. [Google Scholar]
- Zribi, M.; Ciarletti, V.; Taconet, O. Validation of a rough surface model based on fractional Brownian geometry with SIRC and ERASME radar data over Orgeval site. Remote Sens. Environ. 2000, 73, 65–72. [Google Scholar]
- Zribi, M.; Baghdadi, N.; Holah, N.; Fafin, O.; Guérin, C. Evaluation of a rough soil surface description wih ASAR ENVISAT radar data. Remote Sens. Environ. 2005, 95, 67–76. [Google Scholar]
- Mattia, F.; Satalino, G.; Dente, L.; Pasquariello, G. Using a priori information to improve soil moisture retrieval from ENVISAT ASAR AP data in semiarid regions. IEEE Trans. Geosci. Remote Sens. 2006, 44, 900–912. [Google Scholar]
- Satalino, G.; Mattia, F.; Davidson, M.; Le Toan, T.; Pasquariello, G.; Borgeaud, M. On current limits of soil moisture retrieval from ERS-SAR data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2438–2447. [Google Scholar]
- Boisvert, J.B.; Gwyn, Q.H.K.; Chanzy, A.; Major, D.J.; Brisco, B.; Brown, R.J. Effect of surface soil moisture gradients on modeling radar backscattering from bare fields. Int. J. Remote Sens. 1997, 18, 153–170. [Google Scholar]
- Shi, J.; Wang, J.; Hsu, A.Y.; O'Neill, P.E.; Engman, E.T. Estimation of bare surface soil moisture and surface roughness parameter using L-band SAR image data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1254–1266. [Google Scholar]
- Bindlish, R.; Barros, A.P. Multifrequency soil moisture inversion from SAR measurements with the use of IEM. Remote Sens. Environ. 2000, 71, 61–88. [Google Scholar]
- Baghdadi, N.; Aubert, M.; Cerdan, O.; Franchistéguy, L.; Viel, C.; Martin, E.; Zribi, M.; Desprats, J.F. Operational mapping of soil moisture using synthetic aperture radar data: application to the Touch basin (France). Sensors 2007, 7, 2458–2483. [Google Scholar]
- Leconte, R.; Brissette, F.; Galarneau, M.; Rousselle, J. Mapping near-surface soil moisture with RADARSAT-1 synthetic aperture radar data. Water Resour. Res. 2004, 40, 1–13. [Google Scholar]
- Baghdadi, N.; King, C.; Chanzy, A.; Wigneron, J.P. An empirical calibration of the integral equation model based on SAR data and measurements of soil moisture and surface roughness over bare soils. Int. J. Remote Sensing 2002, 23, 4325–4340. [Google Scholar]
- Baghdadi, N.; Gherboudj, I.; Zribi, M.; Sahebi, M.; King, C.; Bonn, F. Semi-empirical calibration of the IEM backscattering model using radar images and moisture and roughness field measurements. Int. J. Remote Sensing 2004, 25, 3593–3623. [Google Scholar]
- Baghdadi, N.; Holah, N.; Zribi, M. Calibration of Integral Equation Model for SAR data in C-Band and HH and VV polarizations. Int. J. Remote Sens. 2006, 27, 805–816. [Google Scholar]
- Zribi, M.; Taconet, O.; Le Hégerat-Mascle, S.; Vidal-Madjar, D.; Emblauch, C.; Loumagne, C.; Normand, M. Backscattering behavior and simulation comparison over bare soils using SIR-C/X-SAR and ERASME 1994 data over Orgeval. Remote Sens. Environ. 1997, 59, 256–266. [Google Scholar]
- Verhoest, N.E.C.; De Baets, B.; Mattia, F.; Satalino, G.; Lucau, C.; Defourny, P. A possibilistic approach to soil moisture retrieval from ERS synthetic aperture radar backscattering under soil roughness uncertainty. Water Resour. Res. 2007, 43, W07435–WR005295. [Google Scholar]
- Liu, Z.; Meyer, D.J. Study of high SAR backscattering caused by an increase of soil moisture over a sparsely vegetated area: implications for characteristics of backscatter. Int. J. Remote Sens. 2002, 23, 1063–1074. [Google Scholar]
- Rahman, M.M.; Moran, M.S.; Thoma, D.P.; Bryant, R.; Holifield Collins, C.D.; Jackson, T.; Orr, B.J.; Tischler, M. Mapping surface roughness and soil moisture using multi-angle radar imagery without ancillary data. Remote Sensing Environ. 2008, 112, 391–402. [Google Scholar]
- Cognard, A.-L.; Loumagne, C.; Normand, M.; Olivier, P.; Ottlé, C.; Vidal-Madjar, D.; Louahala, S.; Vidal, A. Evaluation of the ERS 1/synthetic aperture radar capacity to estimate surface soil moisture: Two-year results over the Naizin watershed. Water Resour. Res. 1995, 31, 975–982. [Google Scholar]
- Deroin, J.P.; Company, A.; Simonin, A. An empirical model for interpreting the relationship between backscattering and arid land surface roughness as seen with the SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 86–92. [Google Scholar]
- Wang, J.R.; Hsu, A.; Shi, J.C.; O'Neill, P.E.; Engman, E.T. A comparison of soil moisture retrieval models using SIR-C measurements over the Little Washita River watershed. Remote Sens. Environ. 1997, 59, 308–320. [Google Scholar]
- Taconet, O.; Vidal-Madjar, D.; Emblanch, C.; Normand, M. Taking into account vegetation effects to estimate soil moisture from C-band radar measurements. Remote Sens. Environ. 1996, 56, 52–56. [Google Scholar]
- Weimann, A.; Von Schönemark, M.; Schumann, A.; Jorm, P.; Gunter, R. Soil moisture estimation with ERS-1 SAR in the East German loess soil area. Int. J. Remote Sens. 1998, 19, 237–243. [Google Scholar]
- Le Hégerat-Mascle, S.; Zribi, M.; Alem, F.; Weisse, A. Soil moisture estimation from ERS/SAR data: Toward an operational methodology. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2647–2658. [Google Scholar]
- Zribi, M.; Baghdadi, N.; Holah, N.; Fafin, O. New methodology for soil surface moisture estimation and its application to ENVISAT-ASAR multi-incidence data inversion. Remote Sens. Environ. 2005, 96, 485–496. [Google Scholar]
- Quesney, A.; Le Hégerat-Mascle, S.; Taconet, O.; Vidal-Madjar, D.; Wigneron, J.P.; Loumagne, C.; Normand, M. Estimation of watershed soil moisture index from ERS/SAR data. Remote Sens. Environ. 2000, 72, 290–303. [Google Scholar]
- Álvarez-Mozos, J.; Casalí, J.; Gonzalez-Audícana, M.; Verhoest, N.E.C. Correlation between ground measured soil moisture and RADARSAT-1 derived backscatter coefficient over an agricultural catchment of Navarre (North of Spain). Biosyst. Engineering 2005, 92, 119–133. [Google Scholar]
- Engman, E.T.; Chauhan, N. Status of microwave soil moisture measurements with remote sensing. Remote Sens. Environ. 1995, 51, 189–198. [Google Scholar]
- Wang, J.R.; Engman, E.T.; Shiue, J.C.; Rusek, M.; Steinmeier, C. The SIR-B observations of microwave backscatter dependence on soil moisture, surface roughness and vegetation covers. IEEE Trans. Geosci. Remote Sens. 1986, 24, 510–516. [Google Scholar]
- Dubois, P.C.; van Zyl, J.; Engman, E.T. Measuring soil moisture with imaging radars. IEEE Trans. Geosci. Remote Sens. 1995, 33, 915–926. [Google Scholar]
- Moran, M.S.; Hymer, D.C.; Qi, J.; Sano, E.E. Soil moisture evaluation using multitemporal synthetic aperture radar (SAR) in semiarid rangeland. Agric. Forest Meteorol. 2000, 105, 69–80. [Google Scholar]
- Wagner, W.; Pathe, C.; Sabel, D.; Bartsch, A.; Künzer, C.; Scipal, K. Experimental 1 km soil moisture products from ENVISAT ASAR for Southern Africa. Proceedings of ENVISAT Symposium, Montreux, Switzerland; 2007; p. SP-636. [Google Scholar]
- Rombach, M.; Demircan, A.; Mauser, W. Correlation between soil moisture and the backscattering coefficient of ERS-1 data. Proceedings of the second ERS-1 symposium on space at the service of our environment, Hamburg, Germany; 1993; pp. 861–864. [Google Scholar]
- Mohan, S.; Mehta, N.S.; Mehta, R.L.; Patel, P.; Rjak, D.R.; srivastava, H.S.; Das, D.K.; Sharma, S.; Saxena, C.M.; Sudtrodhar, A.K. Soil moisture estimation using ERS-1 SAR data. Proceedings of the second ERS-1 symposium on space at the service of our environment, Hamburg, Germany; 1993; pp. 875–878. [Google Scholar]
- Poncét, F.V.; Hanneman, J.; Prietzsch, C.; Tapkenhinrichs, M. Regionalization of soil physical parameters using ERS- PRI SAR data. Proceedings of the second ERS-1 symposium on space at the service of our environment, Hamburg, Germany; 1993; pp. 879–881. [Google Scholar]
- Moeremans, B.; Dautrebande, S. Use of ERS SAR interferometric coherence and PRI images to evaluate crop height and soil moisture and to identify crops. Proceedings of EUROPTO conference on remote sensing for agriculture, ecosystems and hydrology, Barcelona, Spain; 1998; pp. 9–19. [Google Scholar]
- Dubois, P.C.; van Zyl, J.; Engman, E.T. Corrections to “Measuring soil moisture with imaging radars”. IEEE Trans. Geosci. Remote Sens. 1995, 33, 1340. [Google Scholar]
- Dawson, M. S.; Fung, A. K.; Manry, M. T. Tools for soil moisture retrieval from radar measurements. Proceedings of the International Symposium on Retrieval of Bio- and Geophysical Parameters from SAR Data for Land Applications, Toulouse, France; 1995; pp. 295–305. [Google Scholar]
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. An inversion algorithm to retrieve soil moisture and surface roughness from polarimetric radar observations. Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS'94), Pasadena, California; 1994; pp. 1582–1584. [Google Scholar]
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. Semi-empirical model of the ensemble-averaged differential Meuller matrix for microwave backscattering from bare soil surfaces. IEEE Trans. Geosci. Remote Sens 2002, 40, 1348–1355. [Google Scholar]
- Oh, Y. Quantitative retrieval of soil moisture content and surface roughness from mulitipolarized radar observations of bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 2004, 42, 596–601. [Google Scholar]
- Ji, J.; van der Keur, P.; Thomson, A.; Skriver, H. Soil moisture retrieval using the Danish L- and C-band polarimetric SAR. Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS'96), Lincoln, Nebrasca, USA; 1996; pp. 1300–1302. [Google Scholar]
- van Oevelen, P.J.; Hoekman, D.H. Radar backscatter inversion techniques for estimation of surface soil moisture: EFEDA-Spain and HAPEX-Sahel case studies. IEEE Trans. Geosci. Remote Sens. 1999, 37, 113–123. [Google Scholar]
- Baghdadi, N.; Zribi, M. Evaluation of radar backscatter models IEM, Oh and Dubois using experimental observations. Int. J. Remote Sens. 2006, 27, 3831–3852. [Google Scholar]
- Álvarez-Mozos, J.; Gonzalez-Audícana, M.; Casalí, J. Evaluation of empirical and semi-empirical backscattering models for surface soil moisture estimation. Can. J. Remote Sensing 2007, 33, 176–188. [Google Scholar]
- D'Urso, G.; Minacapilli, M. A semi-empirical approach for surface soil water content estimation from radar data without a-priori information on surface roughness. J. Hydrol. 2006, 321, 297–310. [Google Scholar]
- Fung, A.K.; Chen, K.S. An update of the IEM surface backscattering model. IEEE Geosci. Remote Sens. Letters 2004, 1, 75–77. [Google Scholar]
- Thoma, D.P.; Moran, M.S.; Bryant, R.; Rahman, M.; Holifield Collins, C.D.; Keefer, T.O.; Noriega, R.; Osman, I.; Skirvin, S.; Tischler, M.; Bosch, D.; Starks, P.J.; Peters-Lidard, C. Appropriate scale of soil moisture retrieval from high-resolution radar imagery for bare and minimally vegetated soils. Remote Sensing of Environment 2008, 112, 403–414. [Google Scholar]
- Saillard, M.; Sentenac, A. Rigorous solutions for electromagnetic scattering from rough surfaces. Waves in Random Media 2001, 11, R103–R137. [Google Scholar]
- Elfouhaily, T.M.; Guérin, C. A. A critical survey of approximate scattering wave theories from random rough surfaces. Waves in Random Media 2004, 14, R1–R40. [Google Scholar]
- Zribi, M.; Ciarletti, V.; Taconet, O.; Boissard, P.; Chapron, P.; Rabin, B. Backscattering on soil structure described by plane facets. Int. J. Remote Sens. 2000, 21, 137–153. [Google Scholar]
- Dong, W.P.; Sullivan, P.J.; Stout, K.J. Comprehensive study of parameters for characterizing three dimensional surface topography III: Parameters for characterizing amplitude and some functional properties. Wear 1994, 178, 29–43. [Google Scholar]
- Callens, M.; Verhoest, N.E.C.; Davidson, M.W.J. Parameterization of tillage-induced single-scale soil roughness from 4-m profiles. IEEE Trans. Geosci. Remote Sens. 2006, 44, 878–888. [Google Scholar]
- Rice, S.O. Reflection of electromagnetic waves from slightly rough surfaces. Communications in pure and applied mathematics 1951, 4, 361–378. [Google Scholar]
- Beckman, P.; Spizzichino, A. The scattering of electromagnetic waves from rough surfaces; Pergamon: New York, 1963. [Google Scholar]
- Voronovich, A.G. Small-Slope Approximation in wave scattering from rough surfaces. Sov. Phys. JETP 1985, 62, 65–70. [Google Scholar]
- Voronovich, A.G. Wave scattering from rough surfaces, ser; Springer Series on Wave Phenomena; Springer, 1994. [Google Scholar]
- Chen, K.S.; Wu, T.D.; Tsang, L.; Li, Q.; Shi, J.; Fung, A.K. Emission of rough surfaces calculated by the Integral Equation Method with comparison to three-dimensional moment method simulations. IEEE Trans. Geosci. Remote Sens. 2003, 41, 90–101. [Google Scholar]
- Hsieh, C.; Fung, A.; Nesti, G.; Sieber, A.; Coppo, P. A further study of the IEM surface scattering model. IEEE Trans. Geosci. Remote Sens. 1997, 35, 901–909. [Google Scholar]
- Schanda, E. On the contribution of volume scattering to the microwave backscattered signal from wet snow and wet soil. International Journal of Remote Sensing 1987, 8, 1489–1500. [Google Scholar]
- Mancini, M.; Hoeben, R.; Troch, P.A. Multifrequency radar observations of bare surface soil moisture content: A laboratory experiment. Water Resour. Res. 1999, 35, 1827–1838. [Google Scholar]
- Macelloni, G.; Nesti, G.; Pampaloni, P.; Sigismondi, S.; Tarchi, D.; Lolli, S. Experimental validation of surface scattering and emission models. IEEE Trans. Geosci. Remote Sens. 2000, 38, 459–469. [Google Scholar]
- Licheri, M.; Floury, N.; Borgeaud, M.; Migliaccio, M. On the scattering from natural surfaces: the IEM and the improved IEM. Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS’01), Sidney, Australia; 2001; pp. 2911–2913. [Google Scholar]
- Altese, E.; Bolognani, O.; Mancini, M.; Troch, P.A. Retrieving soil moisture over bare soils from ERS-1 synthetic aperture radar data: Sensitivity analysis based on a theoretical surface scattering model and field data. Water Resour. Res. 1996, 32, 653–662. [Google Scholar]
- Mattia, F.; Le Toan, T.; Davidson, M. An analytical, numerical, and experimental study of backscattering from multiscale soil surfaces. Radio Science 2001, 36, 119–135. [Google Scholar]
- Weimann, A. Inverting a microwave backscattering model by the use of a neural network for the estimation of soil moisture. Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS'98), Seattle, Washington, USA; 1998; pp. 1837–1839. [Google Scholar]
- Bindlish, R.; Barros, A.P. Parameterization of vegetation backscatter in radar-based soil moisture estimation. Remote Sens. Environ. 2001, 76, 130–137. [Google Scholar]
- Shi, J.; Chen, K.S.; Li, Q.; Jackson, T.J.; O'Neill, P.E.; Tsang, L. A parameterized surface reflectivity model and estimation of bare-surface soil moisture with L-band radiometer. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2674–2686. [Google Scholar]
- Wu, T.D.; Chen, K.S.; Shi, J.; Fung, A.K. A transition model for the reflection coefficient in surface scattering. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2040–2050. [Google Scholar]
- Chen, K.S.; Wu, T.D.; Tsay, M.K.; Fung, A.K. A note on the multiple scattering in an IEM model. IEEE Trans. Geosci. Remote Sens. 2000, 38, 249–256. [Google Scholar]
- Wu, T.D.; Chen, K.S. A reappraisal of the validity of the IEM model for backscattering from rough surfaces. IEEE Trans. Geosci. Remote Sens. 2004, 42, 743–753. [Google Scholar]
- Soares, J.V.; Bernard, R.; Vidal-Madjar, D. Spatial and temporal behaviour of a large agricultural area as observed from airborne C-band scatterometer and thermal infrared radiometer. Int. J. Remote Sens. 1987, 8, 981–996. [Google Scholar]
- Sano, E.E.; Moran, M.S.; Huete, A.R.; Miura, T. C- and multiangle Ku-band synthetic aperature radar data for bare soil moisture estimation in agricultural areas. Rem. Sens. Environ. 1998, 64, 77–90. [Google Scholar]
- Taconet, O.; Ciarletti, V. Estimating soil roughness indices on a ridge-and-furrow surface using stereo photogrammetry. Soil Till. Res. 2007, 93, 64–76. [Google Scholar]
- Huang, C.-h.; Bradford, JM. Applications of a laser scanner to quantify soil microtopography. Soil Sci. Soc. Am. J. 1992, 56, 14–21. [Google Scholar]
- Linden, D.R.; Van Doren, D.M. Parameters for characterizing tillage-induced soil surface roughness. Soil Sci. Soc. Am. J. 1986, 50, 1560–1565. [Google Scholar]
- Bertuzzi, P.; Rauws, G.; Courault, D. Testing roughness indices to estimate soil roughness changes due to simulated rainfall. Soil Till. Res. 1990, 17, 87–99. [Google Scholar]
- Mattia, F.; Satalino, G.; Balenzano, A.; Pauwels, A.; Verhoest, N.; Skriver, H. Exploiting L-band SAR Data for the Improvement of Surface Process Modelling. Proceedings of the 5th International Symposium on Retrieval of Bio- and Geophysical Parameters from SAR Data for Land Applications, Bari, Italy; 2007. in press. [Google Scholar]
- Oh, Y.; Kay, Y.C. Condition for precise measurement of soil surface roughness. IEEE Trans. Geosci. Remote Sens. 1998, 36, 691–695. [Google Scholar]
- Jackson, T.J.; McNairn, H.; Weltz, A.; Brisco, B.; Brown, R. First order surface roughness correction of active microwave observations for estimating soil moisture. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1065–1069. [Google Scholar]
- Onstad, C.A.; Zobeck, T.M. Tillage and rainfall effect on random roughness: A review. Soil Tillage Res. 1987, 9, 1–20. [Google Scholar]
- Álvarez-Mozos, J.; Casalí, J.; Gonzalez-Audícana, M.; Verhoest, N.E.C. Assessment of the operational applicability of RADARSAT-1 data for surface soil moisture estimation. IEEE Trans. Geosci., Remote Sens. 2006, 44, 913–924. [Google Scholar]
- Ogilvy, J.A. Theory of wave scattering from random rough surfaces. London, UK; In Inst. Phys.; 1991. [Google Scholar]
- Wickel, A.J.; Jackson, T.J.; Wood, E.F. Multitemporal monitoring of soil moisture with RADARSAT SAR during the 1997 Southern Great Plains hydrology experiment. Int. J. Remote Sens. 2001, 22, 1571–1583. [Google Scholar]
- Ogilvy, A.; Foster, J.M. Rough surfaces: Gaussian or exponential statistics? J. Phys. D: Appl. Phys. 1989, 22, 1243–1251. [Google Scholar]
- Li, Q.; Shi, J.; Chen, K.S. A generalized power law spectrum and its application to the backscattering of soil surfaces based on integral equation model. IEEE Trans. Geosci. Remote Sens. 2002, 40, 271–280. [Google Scholar]
- Zribi, M.; Ciarletti, V.; Taconet, O.; Paillé, J.; Boissard, P.; Chapron, P. Characterisation of the soil structure and microwave backscattering based on numerical three-dimensional surface representation: analysis with a Brownian model. Remote Sens. Environ. 2000, 72, 159–169. [Google Scholar]
- Oh, Y.; Hong, J.-Y. Effect of surface profile length on the backscattering coefficients of bare surfaces. IEEE Trans. Geosci. Remote Sens. 2007, 45, 632–638. [Google Scholar]
- Lehrsch, G.A.; Whisler, F.D.; Römkens, M.J.M. Spatial variation of parameters describing soil surface roughness. Soil Sci. Soc. Am. J. 1988, 52, 311–319. [Google Scholar]
- Wang, J.R.; Engman, E.T.; Mo, T.; Schmugge, T.J.; Shiue, J.C. The effect of soil moisture, surface roughness, and vegetation on L-band emission and backscatter. IEEE Trans. Geosci. Remote Sens. 1987, 25, 825–833. [Google Scholar]
- Kuipers, H. A reliefmeter for soil cultivation studies. Neth. J. Agric. Sci. 1957, 5, 255–262. [Google Scholar]
- Podmore, T.H.; Huggins, L.F. An automated profile meter for surface roughness measurements. Trans ASAE 1981, 24, 663–665. [Google Scholar]
- Römkens, M.J.M.; Singarayar, S.; Gantzer, C.J. An automated non-contact surface profile meter. Soil Till. Res. 1986, 6, 193–202. [Google Scholar]
- Western, A.W.; Grayson, R.B. The Tarrawarra data set: soil moisture patterns, soil characteristics, and hydrological flux measurements. Water Resour. Res. 1998, 34, 2765–2768. [Google Scholar]
- Sano, E.E.; Huete, A.R.; Troufleau, D.; Moran, M.S.; Vidal, A. Relation between ERS-1 synthetic aperture radar data and measurements of surface roughness and moisture content of rocky soils in a semiarid rangeland. Water Resour. Res. 1998, 34, 1491–1498. [Google Scholar]
- Moreno, R.G.; Álvarez, M.C.D.; Alonso, A.T.; Barrington, S.; Requejo, A.S. Tillage and soil type effects on soil roughness at semiaric climatic conditions. Soil Till. Res. 2008, in press. [Google Scholar]
- Burkwell, R.E.; Allmaras, R.R.; Amemiya, M. A field measurement of total porosity and surface microrelief of soils. Soil Sci. Soc. Am. Proc. 1963, 27, 697–700. [Google Scholar]
- Podmore, T.H.; Huggins, L.F. Surface roughness effects on overland flow. Trans. ASAE 1980, 23, 1434–1445. [Google Scholar]
- Wagner, L.E.; Yiming, Y. Digitization of profile meter photographs. Trans. ASAE 1991, 34, 412–416. [Google Scholar]
- Jester, W.; Klik, A. Soil surface roughness measurement-methods, applicability, and surface representation. CATENA 2005, 64, 174–192. [Google Scholar]
- Mendeleyev, V.Y. Dependence of measuring errors of RMS roughness on stylus tip size for mechanical profilers. Appl. Opt 1997, 36, 202–209. [Google Scholar]
- Kwon, K.-H.; Cho, N.-G. Assessing the effects of stylus tip radius on surface roughness measurement by accumulation spectral analysis. International Journal of Precision Engineering 2006, 7, 9–12. [Google Scholar]
- Helming, K.; Römkens, M.J.M.; Prasad, S.N. Surface roughness related processes of runoff and soil loss: a flume study. Soil Sci. Soc. Am. J. 1998, 62, 243–250. [Google Scholar]
- Darboux, F.; Huang, C. An instantaneous-profile laser scanner to measure soil surface microtopography. Soil Science Society of America Journal 2003, 67, 92–99. [Google Scholar]
- Welch, R.T.; Jordan, T.R.; Thomas, A.W. A photogrammetric technique for measuring soil erosion. J. Soil Water Conserv. 1984, 39, 191–194. [Google Scholar]
- Warner, W.S. Mapping a three-dimensional soil surface with handheld 35 mm photography. Soil Tillage Res. 1995, 34, 187–197. [Google Scholar]
- Hancock, G.; Willgoose, G. The production of digital elevation models from experimental model landscapes. Earth Surface Processes and Landforms 2001, 26, 475–490. [Google Scholar]
- Oelze, M.L.; Sabatier, J.M.; Raspect, R. Roughness measurements of soil surfaces by acoustic backscatter. Soil Sci. Soc. Am. J. 2003, 67, 241–250. [Google Scholar]
- Römkens, M.J.M.; Wang, J.Y. Effect of tillage on surface roughness. Trans. Am. Soc. Agric. Eng. 1986, 29, 429–433. [Google Scholar]
- Robichaud, P.R.; Molnau, M. Measuring soil roughness changes with an ultrasonic profiler. Trans. ASAE 1990, 33, 1851–1858. [Google Scholar]
- Archer, D.J.; Wadge, G. On the use of theoretical models for the retrieval of surface roughness from playa surfaces. Proc. of the 2nd International Workshop on Retrieval of Bio- and Geophysical parameters from SAR data for Land Applications, Noordwijk, The Netherlands, October 21-23, 2008.
- D'Haese, C; Verhoest, N; De Troch, F. Comparison and evaluation of two soil surface roughness measuring techniques: The meshboard method and the ESA - CESBIO laserprofiler, internal report.; Laboratory of Hydrology and Water Management: Ghent University, 2000. [Google Scholar]
- Ogilvy, J.A. Computer simulation of acoustic wave scattering from rough surfaces. J. Phys. D: Appl. Phys. 1988, 21, 260–277. [Google Scholar]
- Sayles, R.S.; Thomas, T.R. Surface topography as a nonstationary random process. Nature 1978, 271, 431–434. [Google Scholar]
- Álvarez-Mozos, J.; Verhoest, N.E.C.; Larrañaga, A.; Casalí, J.; González-Audícana, M. Influence of surface roughness spatial variability and temporal dynamics on the retrieval of soil moisture from SAR observations. IEEE Trans. Geosci. Remote Sens. 2008. submitted. [Google Scholar]
- Verhoest, N.E.C.; Troch, P.A.; Paniconi, C.; De Troch, F.P. Mapping basin scale variable source areas from multitemporal remotely sensed observations of soil moisture behavior. Water Resour. Res. 1998, 34, 3235–3244. [Google Scholar]
- Thoma, D.P.; Moran, M.S.; Bryant, R.; Rahman, M.; Holifield Collins, C.D.; Skirvin, S.; Sano, E.E.; Slocum, K. Comparison of four models to determine surface soil moisture from C-band radar imagery in a sparsely vegetated semiarid landscape. Water Resour. Res. 2006, 42, W01418–WR003905. [Google Scholar]
- Idowu, O.J.; Rickson, R.J.; Godwin, R.J. Analysis of surface roughness in relation to soil loss and runoff at high rainfall intensities. Hydrol. Process. 2002, 16, 2339–2345. [Google Scholar]
- Elliot, J.K. An investigation of the change in surface roughness through time on the foreland of austre okstindbreen. Computer and Geosciences 1989, 15, 209–217. [Google Scholar]
- Phillips, J. Spatial analysis of shoreline erosion, Delaware bay, New Jersey. Annals of the Association of American Geographers 1986, 76, 50–62. [Google Scholar]
- Monteith, N.H. The role of surface roughness in runoff. Soil Conserv. J. 1974, 30, 42–45. [Google Scholar]
- Campbell, B.; Shepard, M. Lava flow surface roughness and depolarized radar scattering. Journal of Geoph. Res. 1996, 101, 18941–18952. [Google Scholar]
- Falconer, K. Fractal geometry: Mathematical Foundations and Applications; John Wiley and Sons: New York, 1990. [Google Scholar]
- Feder, J. Fractals; Plenum Press: New York and London, 1988. [Google Scholar]
- Kolmogorov, A. Local structure of turbulence in an incompressible liquid for very large Reynolds numbers. C.R. Acad. Sci. USSR 1941, 30, 299–303. [Google Scholar]
- Mandelbrot, B.; Ness, J.V. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar]
- Church, L. Fractal surface finish. Applied Optics 1988, 27, 1518–1526. [Google Scholar]
- Manninen, A. Multiscale surface roughness and backscattering. Progress in Electromagnetic Research 1997, 16, 175–203. [Google Scholar]
- Manninen, A. Multiscale surface roughness description for scattering modelling of bare soil. Physica A 2003, 319, 535–551. [Google Scholar]
- Davidson, M.; Le Toan, T.; Manninen, T.; Borderies, P.; Chenerie, I.; Rouvier, S.; Bachelier, E.; Mattia, F.; Satalino, G. Final report: Retrieval algorithms for active remote sensing; ESA/ESTEC: Noordwijk, The Netherlands, Tech. rep. 008/96/NL/NB; 2000. [Google Scholar]
- Dierking, W. Quantitative roughness characterization of geological surfaces and implications for radar signature analysis. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2397–2412. [Google Scholar]
- Pardini, G.; Gallart, F. A combination of laser technology and fractals to analyze soil surface roughness. European J. Soil Sci. 1998, 49, 197–202. [Google Scholar]
- Rouvier, S.; Borderies, P.; Chenerie, I.; Souyris, J.C.; Le Toan, T.; Floury, N. Fractal analysis of bidimensional profiles and application to electromagnetic scattering from soils. Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS'96), Lincoln, Nebrasca, USA; 1996; pp. 2167–2169. [Google Scholar]
- Zribi, M.; Paillè, J.; Ciarletti, V.; Taconet, O.; Boissard, P.; Chapronn, M.; Rabin, B. Modelisation of roughness and microwave scattering of bare soil surfaces based on fractal Brownian geometry. Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS'98), Seattle, Washington, USA; 1998; pp. 11399–11408. [Google Scholar]
- Pardini, G. Fractal scaling of surface roughness in artificially weathered smectite-rich soil regholits. Geoderma 2003, 117, 159–167. [Google Scholar]
- Perez-Gutierrez, C.; Martinez-Fernandez, J.; Sanchez, N.; Álvarez-Mozos, J. Modeling of soil roughness using terrestrial laser scanner for soil moisture retrieval. Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS 2007), Barcelona, Spain; 2007; pp. 1877–1880. [Google Scholar]
- Kraus, K.; Karel, W.; Briese, C.; Mandlburger, G. Local Accuracy Measures for Digital Terrain Models. The Photogrammetric Record 2006, 21(116), 342–354. [Google Scholar]
- Davenport, I. J.; Holden, J.; Pentreath, R. J. Derivation of soil surface properties from airborne laser altimetry. Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS'03), Toulouse, France; 2003; pp. 4389–4391. [Google Scholar]
- Davenport, I. J.; Holden, N.; Gurney, R. J. Characterizing errors in airborne laser altimetry data to extract soil roughness. IEEE Trans. Geosc. Remote Sensing 2004, 42, 2130–2141. [Google Scholar]
- Wagner, W.; Ullrich, A.; Ducic, V.; Melzer, T.; Studnicka, N. Gaussian decomposition and calibration of a novel small-footprint full-waveform digitising airborne laser scanner. ISPRS Journal of Photogrammetry and Remote Sensing 2006, 60, 100–112. [Google Scholar]
- Colpitts, B.G. The integral equation model and surface roughness signatures in soil moisture and tillage type determination. IEEE Trans. Geosc. Remote Sens. 1998, 36, 833–837. [Google Scholar]
- Pasquariello, G.; Satalino, G.; Mattia, F.; Casarano, D.; Posa, F.; Souyris, J.C.; Le Toan, T. On the retrieval of soil moisture from SAR data over bare soils. Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS'97), Singapore; 1997; pp. 1272–1274. [Google Scholar]
- Baghdadi, N.; Gaulier, S.; King, C. Retrieving surface roughness and soil moisture from synthetic aperture radar (SAR) data using neural networks. Can. J. Remote Sensing 2002, 28, 701–711. [Google Scholar]
- Fung, A.K.; Dawson, M.S.; Chen, K.S.; Hsu, A.Y.; Engman, E.T.; O'Neill, P.E.; Wang, J. A modified IEM model for scattering from soil surfaces with application to soil moisture sensing. Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS'96), Lincoln, Nebrasca, USA; 1996; pp. 1297–1299. [Google Scholar]
- Schuler, D.L.; Lee, J.-S.; Kasilingam, D.; Nesti, G. Surface roughness and slope measurements using polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 687–698. [Google Scholar]
- Zadeh, L. The concept of a linguistic variable and its application to approximate reasoning, part i. Inf. Sci. 1975, 8, 199–249. [Google Scholar]
- Zadeh, L. The concept of a linguistic variable and its application to approximate reasoning, part ii. Inf. Sci. 1975, 8, 301–357. [Google Scholar]
- Zadeh, L. The concept of a linguistic variable and its application to approximate reasoning, part iii. Inf. Sci. 1975, 9, 43–80. [Google Scholar]
- Verhoest, N.E.C.; De Baets, B.; Vernieuwe, H.; Takagi-Sugeno, A. Fuzzy rule-based model for soil moisture retrieval from SAR under soil roughness uncertainty. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1351–1360. [Google Scholar]
- Santanello, J.A.; Peters-Lidard, C.D.; Garcia, M.E.; Mocko, D.M.; Tischler, M.A.; Moran, M.S.; Thoma, D.P. Using remotely-sensed estimates of soil moisture to infer soil texture and hydraulic properties across a semi-arid watershed. Remote Sensing of Environment 2007, 110, 79–97. [Google Scholar]
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Verhoest, N.E.C.; Lievens, H.; Wagner, W.; Álvarez-Mozos, J.; Moran, M.S.; Mattia, F. On the Soil Roughness Parameterization Problem in Soil Moisture Retrieval of Bare Surfaces from Synthetic Aperture Radar. Sensors 2008, 8, 4213-4248. https://doi.org/10.3390/s8074213
Verhoest NEC, Lievens H, Wagner W, Álvarez-Mozos J, Moran MS, Mattia F. On the Soil Roughness Parameterization Problem in Soil Moisture Retrieval of Bare Surfaces from Synthetic Aperture Radar. Sensors. 2008; 8(7):4213-4248. https://doi.org/10.3390/s8074213
Chicago/Turabian StyleVerhoest, Niko E.C, Hans Lievens, Wolfgang Wagner, Jesús Álvarez-Mozos, M. Susan Moran, and Francesco Mattia. 2008. "On the Soil Roughness Parameterization Problem in Soil Moisture Retrieval of Bare Surfaces from Synthetic Aperture Radar" Sensors 8, no. 7: 4213-4248. https://doi.org/10.3390/s8074213




