Comparing Different Approaches for Mapping Urban Vegetation Cover from Landsat ETM+ Data: A Case Study on Brussels
Abstract
:1. Introduction
2. Study area and data
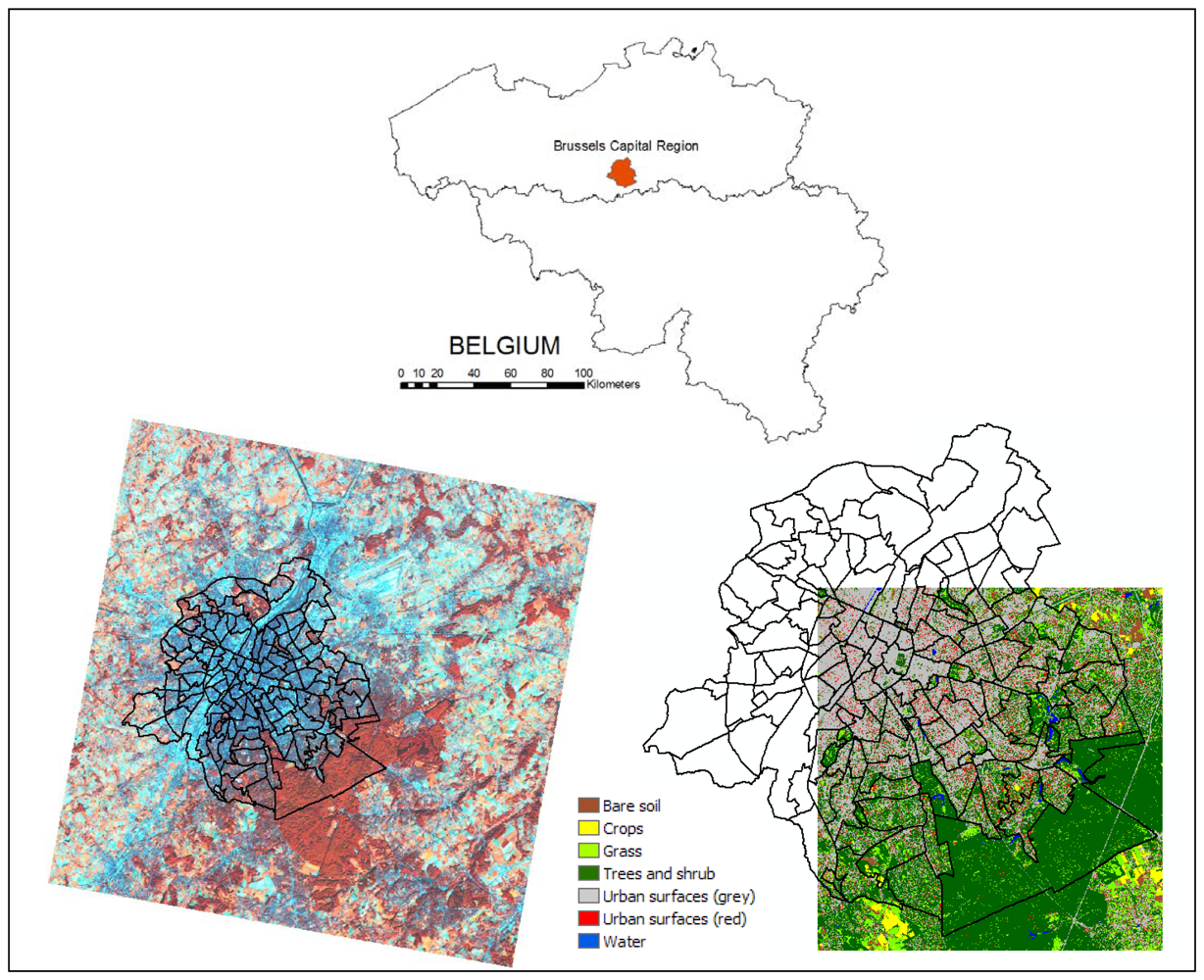
2.1. Study area
2.2. Image and ancillary data
2.3. Training and validation data
3. Methods for estimating per-pixel vegetation fractions
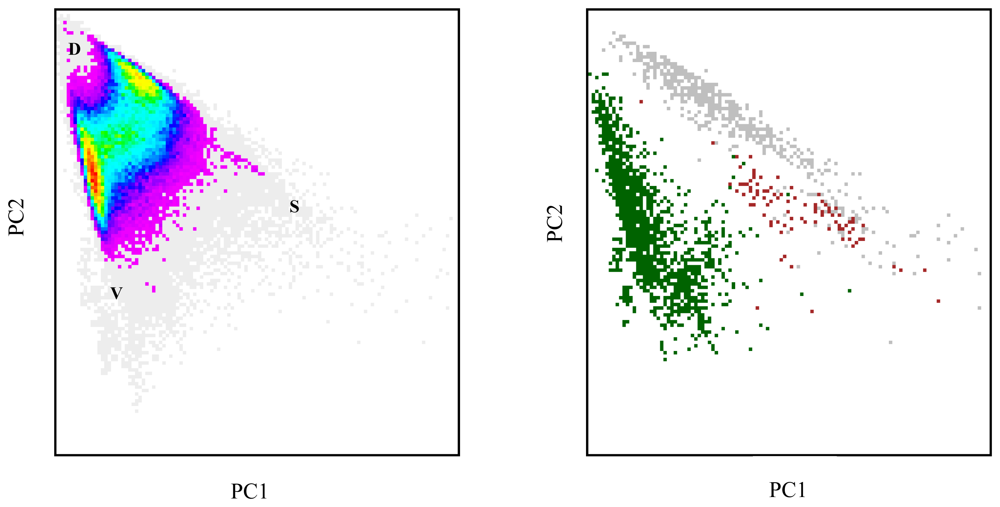
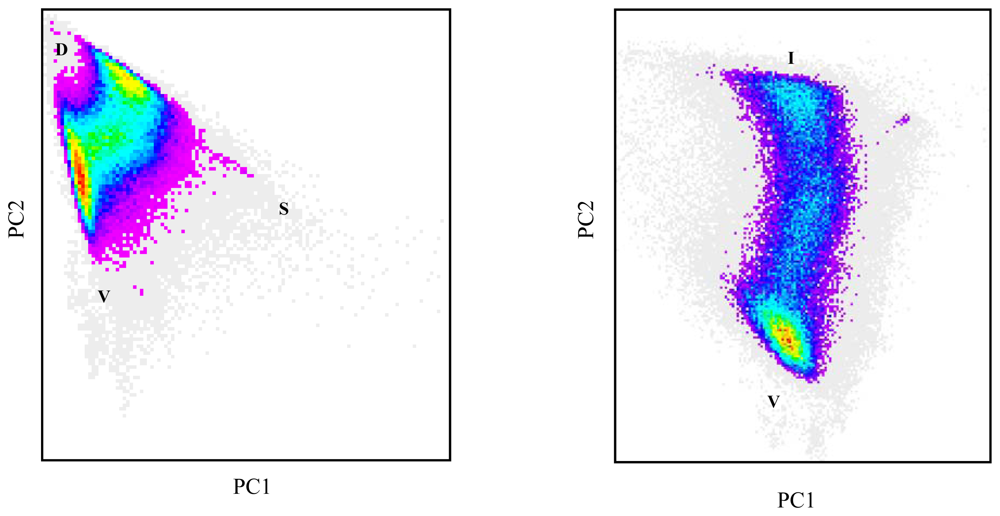
3.1. Linear spectral mixture analysis
3.2. Linear regression analysis
3.3. Unmixing with neural networks
4. Model validation
- N: the total number of pixels in the validation sample
- Pj: the proportion of vegetation inside validation pixel j, derived from the high-resolution classification (ground truth)
- P′j: the proportion of vegetation inside validation pixel j, estimated by the sub-pixel classifier
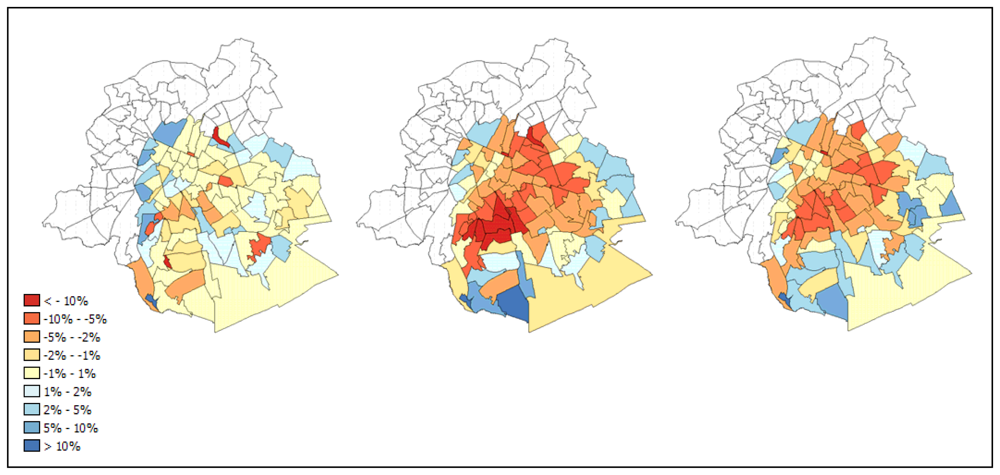
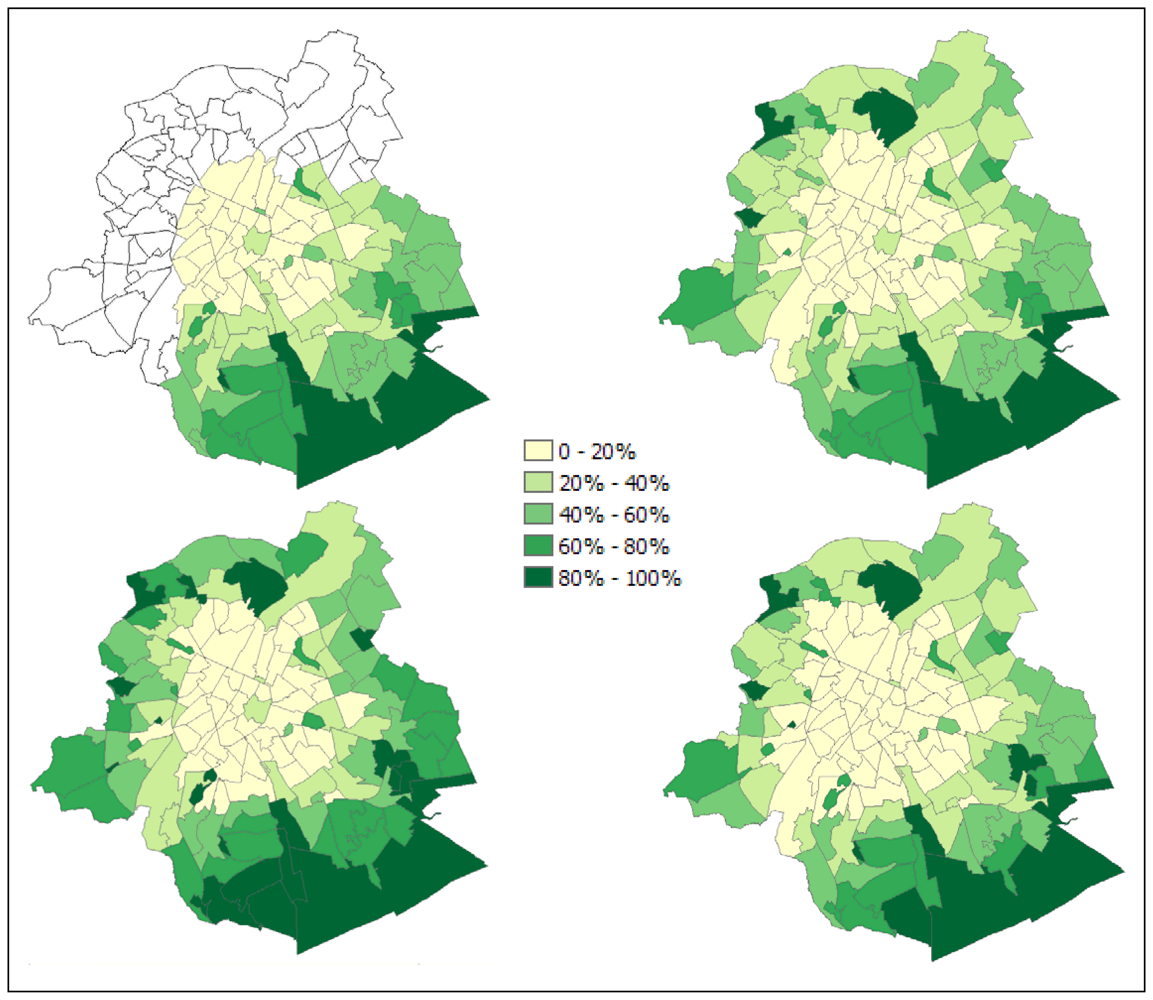
5. Deriving urban green indicators at neighbourhood level
5. Conclusions
Acknowledgments
References
- Martine, G. The State of the World Population 2007; United Nations Population Fund: New York, 2007; p. 1. [Google Scholar]
- UN-HABITAT. The State of the World's Cities Report; Earthscan: London, 2006; p. 216. [Google Scholar]
- Commission of the European Communities, DG Environment. COM(2004)60 Towards a thematic strategy on the urban environment; Commission of the European Communities, 2004; p. 56. [Google Scholar]
- Commission of the European Communities, DG Enterprise and Industry. COM(2005)330 Common actions for growth and employment : the community Lisbon programme; Commission of the European Communities, 2004; p. 56. [Google Scholar]
- de Villers, J. Rapport over de staat van het leefmilieu in Brussel, semi-natuurlijk leefmilieu en openbare groene ruimten; Leefmilieu Brussel – BIM, 2006; pp. 3–8. [Google Scholar]
- Wang, Y.; Zhang, X. A SPLIT model for extraction of subpixel impervious surface information. Photogrammetric Engineering and Remote Sensing 2004, 70, 821–828. [Google Scholar]
- Van der Meer, F. Image classification through spectral unmixing. In Spatial Statistics for Remote Sensing; Stein, A., van der Meer, F., Gorte, B., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999; pp. 185–193. [Google Scholar]
- Wu, C.; Murray, A.T. Estimating impervious surface distribution by spectral mixture analysis. Remote sensing of Environment 2003, 84, 493–505. [Google Scholar]
- Liu, W.; Wu, E.Y. Comparison of non-linear mixture models: sub-pixel classification. Remote Sensing of Environment 2005, 94, 145–154. [Google Scholar]
- Bauer, M.E.; Loffelholz, B.E.; Wilson, B. Estimating and mapping impervious surface area by regression analysis of Landsat imagery. In Remote Sensing of Impervious Surfaces; Weng, Q., Ed.; CRC Press, Taylor & Francis Group: Boca Raton, 2008; pp. 3–19. [Google Scholar]
- Yang, X.; Liu, Z. Use of satellite-derived landscape imperviousness index to characterize urban spatial growth. Computers, Environment and Urban Systems 2005, 29, 524–540. [Google Scholar]
- Foody, G.M.; Lucas, R.M.; Curran, P.J.; Honzak, M. Non-linear mixture modeling without end-members using an artificial neural network. International Journal of Remote Sensing 1997, 18, 937–953. [Google Scholar]
- Carpenter, G.; Gopal, S.; Macomber, S.; Martens, S.; Woodcock, C. A neural network method for mixture estimation for vegetation mapping. Remote sensing of Environment 1999, 70, 138–152. [Google Scholar]
- Liu, W.; Seto, K.; Gopal, S.; Woodcock, C. ART-MMAP: A neural network approach to subpixel classification. IEEE Transactions on Geoscience and Remote Sensing 2004, 42, 1976–1983. [Google Scholar]
- Lee, S.; Lathrop, R.G. Subpixel analysis of Landsat ETM+ using self-organizing map (SOM) neural networks for urban land cover characterization. IEEE Transactions on Geoscience and Remote Sensing 2006, 44, 1642–1654. [Google Scholar]
- Olthof, I.; Fraser, R.H. Mapping Northern land cover fractions using Landsat ETM+. Remote Sensing of Environment 2007, 107, 496–509. [Google Scholar]
- Tottrup, C.; Rasmussen, M.S.; Eklundh, L.; Jönsson, P. Mapping fractional forest cover across the highlands of mainland Southeast Asia using MODIS data and regression tree modelling. International Journal of Remote Sensing 2007, 28, 23–46. [Google Scholar]
- Foody, G.M. Approaches for the production and evaluation of fuzzy land cover classifications from remotely sensed data. International Journal of Remote Sensing 1996, 17, 1317–1340. [Google Scholar]
- Xiao, J.; Moody, A. A comparison of methods for estimating fractional green vegetation cover within a desert-to-upland transition zone in central New Mexico, USA. Remote Sensing of Environment 2005, 98, 237–250. [Google Scholar]
- Hurcom, S.J.; Harrison, A.R. The NDVI and spectral decomposition for semi-arid vegetation abundance estimation. International Journal of Remote Sensing 1998, 19, 3109–3125. [Google Scholar]
- Elmore, A.J.; Mustard, J.F.; Manning, S.J.; Lobell, D.B. Quantifying vegetation change in semiarid environments: precision and accuracy of spectral mixture analysis and the normalized difference vegetation index. Remote Sensing of Environment 2000, 73, 87–102. [Google Scholar]
- Garcia-Haro, F.J.; Gilabert, M.A.; Melia, J. Linear spectral mixture modeling to estimate vegetation amount from optical spectral data. International Journal of Remote Sensing 1996, 17, 3373–3400. [Google Scholar]
- Pu, R.; Xu, B.; Gong, P. Oakwood crown closure estimation by unmixing Landsat TM data. International Journal of Remote Sensing 2003, 24, 4433–4445. [Google Scholar]
- FOD Economie - Algemene Directie Statistiek en Economische Informatie, Dienst Demografie. Bevolking per geslacht en per leeftijdsgroep - Brussels Hoofdstedelijk Gewest (2000-2007). URL: http://www.statbel.fgov.be/figures/d21_nl.asp#2 last accessed March 4th 2008.
- Verslag over de staat van het leefmilieu in Brussel – inleiding; Leefmilieu Brussel – BIM: Brussels, 2006; p. 29.
- Verslag over de staat van het leefmilieu in Brussel – semi-natuurlijk leefmilieu en openbare groene ruimten; Leefmilieu Brussel – BIM: Brussels, 2006; pp. 5–8.
- Irish, R.R. Landsat 7 Science Data Users Handbook; NASA: Greenbelt, MD, 2007. [Google Scholar]
- Van de Voorde, T.; De Genst, W.; Canters, F. Improving pixel-based VHR land-cover classifications of urban areas with post-classification techniques. Photogrammetric Engineering and Remote Sensing 2007, 73, 1017–1027. [Google Scholar]
- Van de Voorde, T.; De Roeck, T.; Canters, F. A comparison of two spectral mixture modelling approaches for impervious surface mapping in urban areas. International Journal of Remote Sensing. accepted.
- Singer, R.B. Near-infrared spectral reflectance of mineral mixtures: Systematic combinations of pyroxenes, olivine and iron oxides. Journal of Geophysical Research 1981, 86, 7967–7982. [Google Scholar]
- Johnson, P.E.; Smith, M.O.; Taylor-George, S.; Adams, J.B. A semiempirical method for analysis of the reflectance spectra for binary mineral mixtures. Journal of Geophysical Research 1983, 88, 3557–3561. [Google Scholar]
- Adams, J.B.; Smith, M.O.; Johnson, P.E. Spectral mixture modelling: a new analysis of rock and soil types at the Viking 1 Lander site. Journal of Geophysical Research 1986, 91, 8098–8112. [Google Scholar]
- Van der Meer, F. Image classification through spectral unmixing. In Spatial Statistics for Remote Sensing; Stein, A., van der Meer, F., Gorte, B., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999; pp. 185–193. [Google Scholar]
- Smith, M.O.; Ustin, S.L.; Adams, J.B.; Gillespie, A.R. Vegetation in deserts: I. A regional measure of abundance from multispectral images. Remote Sensing of Environment 1990, 31, 1–26. [Google Scholar]
- Adams, J.B.; Sabol, D.E.; Kapos, V.; Filho, R. A.; Roberts, D. A.; Smith, M.O.; Gilespie, A.R. Classification of multispectral images based on fractions of endmembers: Application to land cover change in the Brazilian Amazon. Remote Sensing of Environment 1995, 52, 137–154. [Google Scholar]
- Settle, J.J.; Drake, N.A. Linear mixing and the estimation of ground cover proportions. International Journal of Remote Sensing 1993, 14, 1159–1177. [Google Scholar]
- Phinn, S.; Stanford, M.; Scarth, P.; Murray, A.T.; Shyy, P.T. Monitoring the composition of urban environments based on the vegetation-impervious-soil (VIS) model by subpixel analysis techniques. International Journal of Remote Sensing 2002, 23, 4131–4153. [Google Scholar]
- Ji, M.; Jensen, J.R. Effectiveness of subpixel analysis in detecting and quantifying urban imperviousness from Landsat Thematic Mapper imagery. Geocarto International 1999, 14, 33–41. [Google Scholar]
- Small, C. High spatial resolution spectral mixture analysis of urban reflectance. Remote Sensing of Environment 2003, 88, 170–186. [Google Scholar]
- Powell, R.L.; Roberts, D.A.; Dennison, P.E.; Hess, L.L. Sub-pixel mapping of urban land-cover using multiple endmember spectral mixture analysis: Manaus, Brazil. Remote Sensing of Environment 2007, 106, 253–267. [Google Scholar]
- Rashed, T.; Weeks, J.R.; Roberts, D.; Rogan, J.; Powell, R. Measuring the physical composition of urban morphology using multiple endmember spectral mixture models. Photogrammetric Engineering and Remote Sensing 2003, 69, 1011–1020. [Google Scholar]
- Rashed, T.; Weeks, J.R.; Stow, D.; Fugate, D. Measuring temporal composition of urban morphology through spectral mixture analysis: towards a soft approach of change analysis in crowded cities. International Journal of Remote Sensing 2005, 26, 699–718. [Google Scholar]
- Ridd, M.K. Exploring a V–I–S (Vegetation–Impervious Surface–Soil) model for urban ecosystem analysis through remote sensing - Comparative anatomy for cities. International Journal of Remote Sensing 1995, 16, 2165–2185. [Google Scholar]
- Small, C. A global analysis of urban reflectance. International Journal of Remote Sensing 2005, 26, 661–681. [Google Scholar]
- Small, C. The Landsat ETM+ spectral mixing space. Remote Sensing of Environment 2004, 93, 1–17. [Google Scholar]
- Boardman, J.W. Automating spectral unmixing of AVIRIS data using convex geometry concepts. In Fourth Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) Airborne Geoscience Workshop; Green, R. O., Ed.; Jet Propulsion Laboratory: Pasadena, CA, 1993; p. 11. [Google Scholar]
- Wu, C. Normalized spectral mixture analysis for monitoring urban composition using ETM+ imagery. Remote Sensing of Environment 2004, 93, 480–492. [Google Scholar]
- Lu, D.; Weng, Q. Spectral mixture analysis of the urban landscape in Indianapolis with Landsat ETM+ imagery. Photogrammetric Engineering and Remote Sensing 2004, 70, 1053–1062. [Google Scholar]
- Roberts, D.A.; Batista, G.T.; Pereira, J.L.G.; Waller, E.K.; Nelson, B.W. Change identification using multitemporal spectral mixture analysis: applications in Eastern Amazonia. In Remote Sensing Change Detection: Environmental Monitoring Methods and Applications; Lunetta, R.S., Elvidhe, C.D., Eds.; Ann Arbor Press: Ann Arbor, Michigan, 1998; pp. 137–161. [Google Scholar]
- Rogge, D.M.; Rivard, B.; Zhang, J.; Feng, J. Iterative spectral unmixing for optimising per-pixel endmember sets. IEEE Transactions on Geoscience and Remote Sensing 2006, 44, 3725–3736. [Google Scholar]
- Small, C.; Lu, J.W.T. Estimation and vicarious validation of urban vegetation abundance by spectral mixture analysis. Remote Sensing of Environment 2006, 100, 441–456. [Google Scholar]
- Lu, D.; Weng, Q. Use of impervious surface in urban land-use classification. Remote Sensing of Environment 2006, 102, 146–160. [Google Scholar]
- Berk, R.A. Regression Analysis: A Constructive Critique; Sage Publications, 2004. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar]
- Atkinson, P.; Cutler, M.; Lewis, H. Mapping sub-pixel proportional land cover with AVHRR imagery. International Journal of Remote Sensing 1997, 18, 917–935. [Google Scholar]
- Tso, B.; Mather, P.M. Classification Methods for Remotely Sensed Data; Taylor and Francis: London, 2001; pp. 107–110. [Google Scholar]
- Neuralware. NeuralWorks Predict: the complete solution for neural data modelling – user guide; NeuralWare: Carnegie, PA, USA, 2007; Volume 8, pp. 19–20. [Google Scholar]
- Fahlman, S.E.; Lebiere, C. The Cascade-Correlation Learning Architecture. In Advances in Neural Information Processing Systems; Touretzky, D.S., Ed.; Morgan Kaufmann Publisher Inc.: San Fransisco, 1990; Vol. 2, pp. 524–532. [Google Scholar]
- Mather, P.M. Computer Processing of Remotely Sensed Images : An Introduction, 3rd Ed. ed; John Wiley and Sons, 2004. [Google Scholar]
- Song, C. Cross-sensor calibration between Ikonos and Landsat ETM+ for spectral mixture analysis. Geoscience and Remote Sensing Letters 2004, 4, 272–276. [Google Scholar]
- Wilcoxon, F. Individual comparisons by ranking methods. Biometrics 1945, 1, 80–83. [Google Scholar]
- Siegel, S. Non-parametric Statistics for the Behavioral Sciences; McGraw-Hill: New-York, 1956. [Google Scholar]
- De Corte, S.; Sanderson, J.P. Uitwerking van een wijkmonitoring die het hele grondgebied van het Brussels Hoofdstedelijk Gewest bestrijkt; Gewestelijk Secretariaat voor Stedelijke Ontwikkeling (GSSO): Brussels, 2007; p. 21. [Google Scholar]
- De Corte, S.; De Lannoy, W. 99 times Brussels: a typology of the residential environment. In Brusselse thema's 7; Witte, E., Mares, A., Eds.; VUBpress: Brussels, 2001; pp. 517–522. [Google Scholar]
| MAE | ME | Lin. unmixing (VIS) not normalised | Lin. unmixing (VIS) normalised | Lin. unmixing (2 EM) not normalised | Lin. unmixing (2 EM) normalised | Lin. unmixing (SVD) | Lin. unmixing (modified SVD) | Lin. regres. (all bands) not normalised | Lin. regres. (bands 3,4) not normalised | Lin. regres. (bands 2357) normalised | Lin. regres. (band 4) normalised | MLP (VIS) not normalised | MLP (VIS) normalised | MLP (2 EM) not normalised | MLP (2 EM) normalised | MLP (1 EM) not normalised | MLP (1 EM) normalised | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | 0.1322 | 0.1090 | 0.1318 | 0.1070 | 0.3457 | 0.1270 | 0.1196 | 0.1269 | 0.1049 | 0.1124 | 0.1008 | 0.0963 | 0.0966 | 0.1000 | 0.0972 | 0.0949 | ||
| ME | -0.0747 | -0.0457 | -0.0266 | -0.0130 | -0.3246 | -0.0001 | -0.0047 | -0.0055 | -0.0045 | -0.0076 | 0.0079 | 0.0100 | 0.0127 | 0.0122 | 0.0117 | 0.0072 | ||
| Lin. unmixing (VIS) not normalised | 0.1322 | -0.0747 | 1 | 0 | 0.0001 | 0 | 0 | 0.0031 | 0 | 0.518 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Lin. unmixing (VIS) normalised | 0.1090 | -0.0457 | 0 | 1 | 0 | 0.2378 | 0 | 0 | 0 | 0 | 0.0738 | 0 | 0.0799 | 0 | 0 | 0.001 | 0 | 0 |
| Lin. unmixing (2 EM) not normalised | 0.1318 | -0.0266 | 0.0001 | 0 | 1 | 0 | 0 | 0.0349 | 0 | 0.0108 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Lin. unmixing (2 EM) normalised | 0.1070 | -0.0130 | 0 | 0.2378 | 0 | 1 | 0 | 0 | 0 | 0 | 0.0078 | 0 | 0.0097 | 0 | 0 | 0.0002 | 0 | 0 |
| Lin. unmixing (SVD) | 0.3457 | -0.3246 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Lin. unmixing (modified SVD) | 0.1270 | -0.0001 | 0.0031 | 0 | 0.0349 | 0 | 0 | 1 | 0.3035 | 0 | 0 | 0.0017 | 0 | 0 | 0 | 0 | 0 | 0 |
| Lin. regres. (all bands) not normalised | 0.1196 | -0.0047 | 0 | 0 | 0 | 0 | 0 | 0.3035 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Lin. regres, (bands 3,4) not normalised | 0.1269 | -0.0055 | 0.518 | 0 | 0.0108 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Lin. regres. (bands 2357) normalised | 0.1049 | -0.0045 | 0 | 0.0738 | 0 | 0.0078 | 0 | 0 | 0 | 0 | 1 | 0 | 0.0005 | 0 | 0 | 0 | 0 | 0 |
| Lin. regres. (band 4) normalised | 0.1124 | -0.0076 | 0 | 0 | 0 | 0 | 0 | 0.0017 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| MLP (VIS) not normalised | 0.1008 | 0.0079 | 0 | 0.0799 | 0 | 0.0097 | 0 | 0 | 0 | 0 | 0.0005 | 0 | 1 | 0 | 0 | 0.0037 | 0 | 0 |
| MLP (VIS) normalised | 0.0963 | 0.0100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0.0208 | 0 | 0.9259 | 0.0053 |
| MLP (2 EM) not normalised | 0.0966 | 0.0127 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0208 | 1 | 0 | 0 | 0.0039 |
| MLP (2 EM) normalised | 0.1000 | 0.0122 | 0 | 0.001 | 0 | 0.0002 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0037 | 0 | 0 | 1 | 0 | 0 |
| MLP (1 EM) not normalised | 0.0972 | 0.0117 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.9259 | 0 | 0 | 1 | 0.1892 |
| MLP (1 EM) normalised | 0.0949 | 0.0072 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0053 | 0.0039 | 0 | 0.1892 | 1 |
| No brightness normalisation | Brightness normalisation | ||||
|---|---|---|---|---|---|
| ETM+ bands | R2adj | Mean absolute error | ETM+ bands | R2adj | Mean absolute error |
| 1,2,3,4,5,7 | 0.811 | 0.120 | 2,3,5,7 | 0.851 | 0.105 |
| 1,3,4,5,7 | 0.811 | 0.120 | 2,3,4,5,7 | 0.851 | 0.105 |
| 3,4,5,7 | 0.808 | 0.121 | 2,3,4,7 | 0.850 | 0.105 |
| 3,4,7 | 0.800 | 0.123 | 3,4,7 | 0.844 | 0.107 |
| 3,4 | 0.791 | 0.127 | 3,4 | 0.836 | 0.110 |
| 4 | 0.536 | 0.208 | 4 | 0.828 | 0.112 |
| Linear regression | Linear unmixing | MLP | ||
|---|---|---|---|---|
| VIS | SVD | |||
| # neighbourhoods | 95 | 95 | 95 | 95 |
| Correlation | 0.992 | 0.989 | 0.978 | 0.990 |
| Mean absolute error | 0.020 | 0.055 | 0.047 | 0.034 |
| Mean error | 0.000 | -0.053 | -0.029 | -0.014 |
| Standard deviation | 0.031 | 0.035 | 0.041 | 0.041 |
| 95% conf. interval | ± 0.006 | ± 0.007 | ± 0.008 | ± 0.008 |
| # times best predictor with VIS | 63 (66.3%) | 8 (8.4%) | 24 (25.3%) | |
| # times best predictor with SVD | 58 (61.1%) | 18 (18.9%) | 19 (20.0%) | |
| Linear regression | Linear unmixing | MLP | ||
|---|---|---|---|---|
| VIS | SVD | |||
| # neighbourhoods | 145 | 145 | 145 | 145 |
| Total vegetated area (ha) | 7114.63 | 6198.92 | 6848.69 | 7004.95 |
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Van de Voorde, T.; Vlaeminck, J.; Canters, F. Comparing Different Approaches for Mapping Urban Vegetation Cover from Landsat ETM+ Data: A Case Study on Brussels. Sensors 2008, 8, 3880-3902. https://doi.org/10.3390/s8063880
Van de Voorde T, Vlaeminck J, Canters F. Comparing Different Approaches for Mapping Urban Vegetation Cover from Landsat ETM+ Data: A Case Study on Brussels. Sensors. 2008; 8(6):3880-3902. https://doi.org/10.3390/s8063880
Chicago/Turabian StyleVan de Voorde, Tim, Jeroen Vlaeminck, and Frank Canters. 2008. "Comparing Different Approaches for Mapping Urban Vegetation Cover from Landsat ETM+ Data: A Case Study on Brussels" Sensors 8, no. 6: 3880-3902. https://doi.org/10.3390/s8063880




