Impact of Spatial LAI Heterogeneity on Estimate of Directional Gap Fraction from SPOT-Satellite Data
Abstract
:1. Introduction
2. Theoretical framework
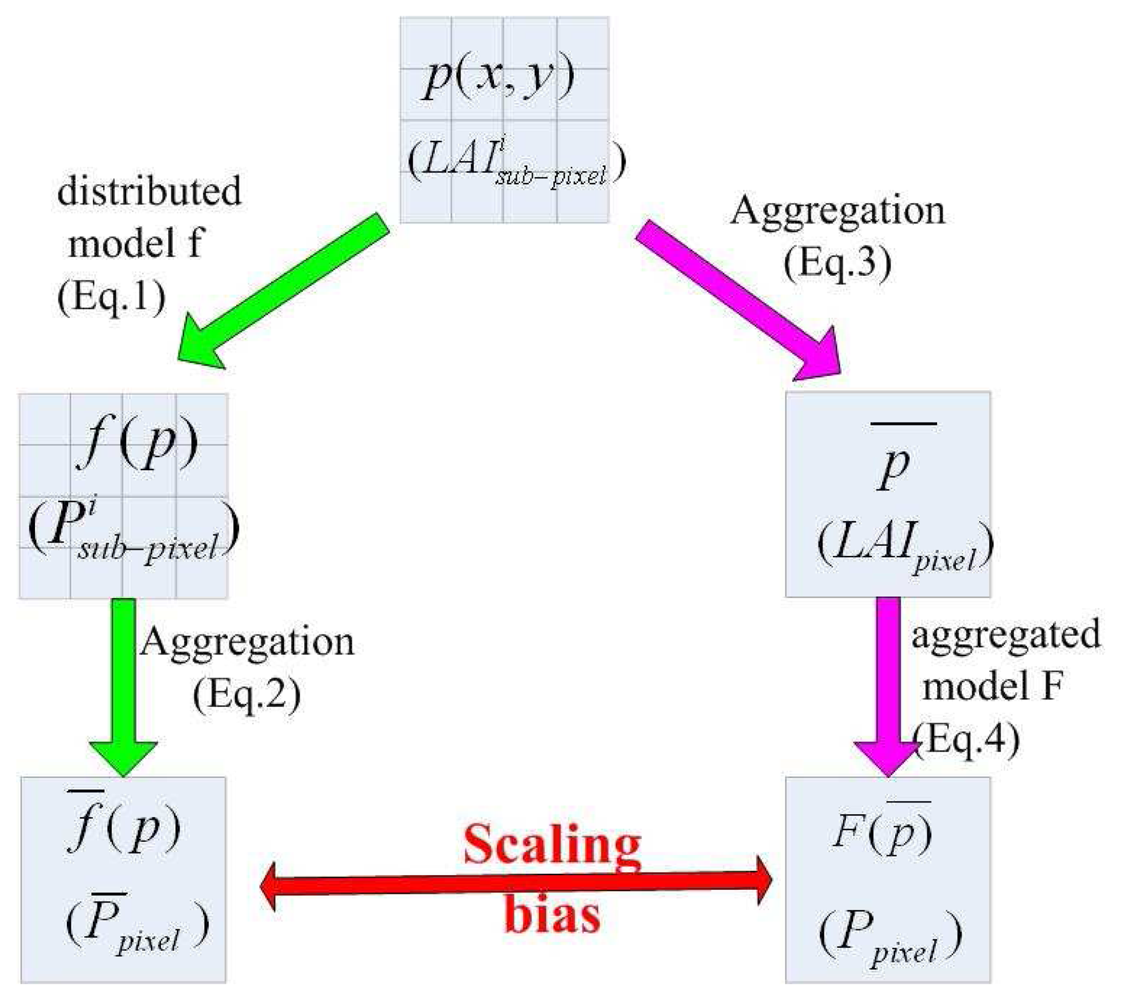
2.1. Up-scaling of directional gap probability
- 1)
- The aggregation of the results which are derived from a distributed model f using distributed input variables. Spatially distributed variables p(x, y) (here ) are input to a distributed model f (here Eq. 1), results of the distributed model f are denoted as f (p) (here ), then the aggregative result f̅(p) (here P̅pixel(θ)) on a larger scale are deduced (Eq. 2) from distributed results;(see left flow chart of Figure 1)
- 2)
- The aggregation of input variables before use in an aggregative model F (here Eq. 3), thereby producing an aggregative result. Spatially distributed input data p(x, y) (here ) are first averaged to p̅ (here LAIpixel) from local scale to a larger scale, then p̅ is input to aggregative model F (Eq. 4), produces aggregative result F(p̅) (here Ppixel(θ)). (see right flowchart of Figure 1)
2.2. Scaling bias of directional gap probability
2.3. Redefinition of clumping index
3. Description of the data
4. Results and Discussion
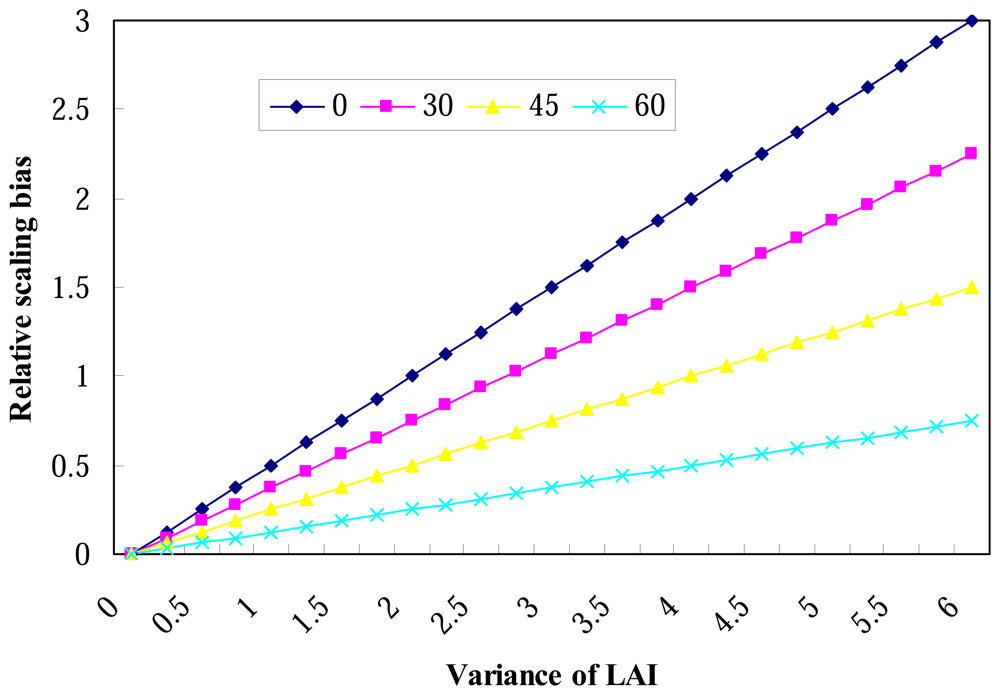
4.1. Simulation of relative scaling bias of gap probability
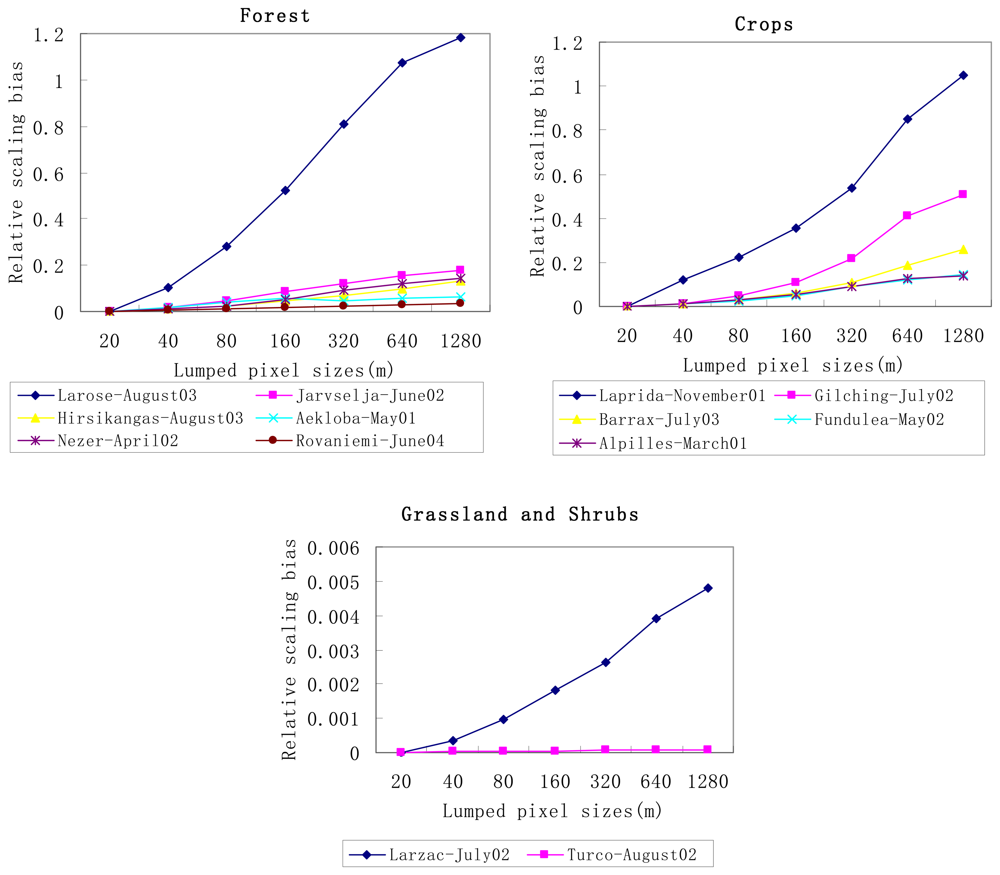
4.2. Spatial scaling bias of gap probability obtained from the VALERI dataset
- 1)
- Beer's law used to retrieve gap probability from LAI (Eq. 1) is assumed without any scaling bias at 20 m spatial resolution, because no satellite data are available to us at the spatial resolution finer than 20m.
- 2)
- Incident beam is assumed to be vertical, i.e. cos(θ) = 1
- 3)
- A spherical leaf angle distribution is assumed, i.e. G=0.5, which is a reasonable assumption for many conifer shoots and closed, broad-leaved canopies (Walter, 2003).
4.3. “Clumping index” Ĉ for VALERI sites
5. Conclusion
- (1)
- relative scaling bias is only dependent on the G function and the spatial heterogeneity of LAI, but independent on the LAI value itself, and
- (2)
- extension of “clumping index” Ĉ is directly proportional to the mean value of LAI and inversely proportional to the spatial heterogeneity of LAI for given G function and direction.
Acknowledgments
References
- Baret, F.; Weiss, M.; Allard, D.; Garrigues, S.; Leroy, M.; Jeanjean, H.; Fernandes, R.; Myneni, R.; Morissette, J.; Privette, J.; Bohbot, H.; Bosseno, R.; Dedieu, G.; Bella, C.D.; Espana, M.; Gond, V.; Gu, X.; Guyon, D.; Lelong, C.; Maisongrande, P.; Mougin, E.; Nilson, T.; Veroustraete, F.; Vintilla, R. in press. Valeri: a network of sites and a methodology for the validation of medium spatial resolution land satellite product. Remote Sensing of Environment. (in press).
- Chen, J.M. Canopy architecture and remote sensing of the fraction of photonsynthetically active radiation absorbed by boreal conifer forests. IEEE Transactions on Geoscience and Remote Sensing 1996, 34, 1353–1368. [Google Scholar]
- Chen, J.M. Spatial scaling of a remotely sensed surface parameter by contexture. Remote Sensing of Environment 1999, 69, 30–42. [Google Scholar]
- Chen, J.M.; Pavlic, G.; Brown, L.; Cihlar, J.; Leblanc, S.G.; White, H.P.; Hall, R.J.; Peddle, D.; King, D.J.; Trofymow, J.A.; Swift, E.; Van der Sanden, J.; Pellikka, P. Derivation and validation of Canada-wide coarse resolution leaf area index maps using high resolution satellite imagery and ground measurements. Remote Sensing of Environment 2002, 80, 165–184. [Google Scholar]
- Chen, J.M.; Menges, C.H.; Leblanc, S.G. Global mapping of the foliage clumping index using multi-angular satellite data. Remote Sensing of Environment 2005, 97(4), 447–457. [Google Scholar]
- Fernandes, R.; Butson, C.; Leblanc, S.; Latifovic, R. Landsat-5 TM and Landsat-7 ETM+ based accuracy assessment of leaf area index products for Canada derived from SPOT-4 VEGETATION data. Canadian Journal of Remote Sensing 2003, 29(2), 241–258. [Google Scholar]
- Francois, C. The potential of directional radiometric temperatures for monitoring soil and leaf temperature and soil moisture status. Remote Sensing of Environment 2002, 80, 122–133. [Google Scholar]
- Francois, C.; Ottle, C.; Prevot, L. Analytical parameterization of canopy directional emissivity and directional radiance in thermal infrared. Application on the retrieval of soil and foliage temperatures using two directional measurements. International Journal of Remote Sensing 1997, 18(12), 2587–2612. [Google Scholar]
- Friedl, M.A.; Davis, F.W.; Michaelsen, J.; Moritz, M.A. Scaling and uncertainty in the relationship between the NDVI and land surface biophysical variables: An analysis using a scene simulation model and data from FIFE. Remote Sensing of Environment 1995, 54, 233–246. [Google Scholar]
- Fuchs, M.; Asrar, G.; Kanemasu, E.; Hipps, L. Leaf area estimates from measurements of photosynthetically active radiation in wheat canopies. Agricultural and Forest Meteorology 1984, 32, 13–22. [Google Scholar]
- Garrigues, S.; Allard, D.; Baret, F.; Weiss, M. Quantifying spatial heterogeneity at the landscape scale using variogram models. Remote Sensing of Environment 2006a, 103, 81–96. [Google Scholar]
- Garrigues, S.; Allard, D.; Baret, F.; Weiss, F. Influence of the spatial heterogeneity on the non-linear estimation of Leaf Area Index from moderate resolution remote sensing data. Remote Sensing of Environment 2006b, 105(4), 286–298. [Google Scholar]
- Hall, F.G.; Huemmrich, K.F.; Goetz, S.J. Satellite remote sensing of surface energy balance: success, failures, and unsolved idles in FIFE. Journal of Geophysical Research 1992, 97, 19 061–19 089. [Google Scholar]
- Jonckheere, I.; Fleck, S.; Nackaerts, K.; Muys, B.; Coppin, P.; Weiss, M.; Baret, F. Methods for leaf area index determination. Part I: Theories, techniques and instruments. Agricultural and Forest Meteorology 2004, 121, 19–35. [Google Scholar]
- Kotz, B.; Schaepman, M.; Morsdorf, F.; Bowyer, P.; Itten, K.; Allgower, B. Radiative transfer modeling within a heterogeneous canopy for estimation of forest fire fuel properties. Remote Sensing of Environment 2004, 92, 332–344. [Google Scholar]
- Leblanc, S.G.; Chen, J.M.; White, H.P.; Latifvic, R. Canadawide foliage clumping index mapping from multi-angular POLDER measurements. Canadian Journal of Remote Sensing 2005, 31(5), 364–376. [Google Scholar]
- Li, Z.-L.; Stoll, M.P.; Zhang, R.H.; Jia, L.; Su, Z. On the separate retrieval of soil and vegetation temperatures from ATSR2 data. Science in China, Series D 2001, 44(2), 97–111. [Google Scholar]
- Menenti, M.; Jia, L.; Li, Z.-L. Multi-angular thermal infrared observations of terrestrial vegetation. In Advances in Land Remote Sensing: System, Modeling, Inversion and Application; Springer Verlag, 2008; pp. 51–93. [Google Scholar]
- Menenti, M.; Jia, L.; Li, Z.-L.; Djepa, V.; Wang, J.; Stoll, M. P.; Su, Z.; Rast, M. Estimation of soil and vegetation temperatures with multiangular thermal infrared observations: the HEIHE, SGP'97, IMGRASS. Journal of Geophysical Research 2001, 106(D11), 11997–12010. [Google Scholar]
- Myneni, R.B.; Nemani, R.R.; Running, E.W. Algorithm for the estimation of global land cover, LAI and FPAR based on radiative transfer models. IEEE Transactions on Geoscience and Remote Sensing 1997, 35, 1380–1393. [Google Scholar]
- Nilson, T. A theoretical analysis of the frequency of gaps in plant stands. Agricultural Meteorology 1971, 8, 25–38. [Google Scholar]
- Norman, J.; Kustas, W.; Humes, K. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agricultural and Forest Meteorology 1995, 77, 263–293. [Google Scholar]
- Nouvellon, Y.; Begue, A.; Moran, M.; Seen, D.; Rambal, S.; Luquet, D.; Chehbouni, G.; Inoue, Y. Par extinction in shortgrass ecosystems: effects of clumping, sky conditions and soil albedo. Agricultural and Forest Meteorology 2000, 105, 21–41. [Google Scholar]
- Pelgrum, H. Spatial Aggregation of Land Surface Characteristics. PhD thesis, Wageningen University, Netherlands, 2000; pp. 33–39. [Google Scholar]
- Pinty, B.; Govron, N.; Widlowski, J.-L.; Lavergne, T.; Verstraete, M. M. Synergy between 1-D and 3-D radiation transfer models to retrieve vegetation canopy properties from remote sensing data. Journal of Geophysical Research 2004, 109, D21205. [Google Scholar]
- Rochdi, N.; Ad, M.; Chelle, R.F. An assessment of needles clumping within shoots when modeling radiative transfer within homogeneous canopies. Remote Sensing of Environment 2006, 102, 116–134. [Google Scholar]
- Smolander, S.; Stenberg, P. A method to account for the shot scale clumping in coniferous canopy reflectance models. Remote Sensing of Environment 2003, 88, 363–373. [Google Scholar]
- Walter, J.-M.N.; Fournier, R.A.; Soudani, K.; Meyer, E. Integrating clumping effects in forest canopy structure: an assessment through hemispherical photographs. Canadian Journal of Remote Sensing 2003, 29(3), 388–410. [Google Scholar]
- Wang, W.-M.; Li, Z.-L. Scaling directional gap probability over heterogeneous land surface: influences on the estimates of component temperatures. Remote Sensing of Environment. (submitted in 2008).
- Wang, W.-M.; Li, Z.-L.; Su, H.-B. Comparison of leaf angle distribution functions: effects on extinction coeffcient and fraction sunlit foliage. Agricultural and Forest Meteorology 2007, 143, 106–122. [Google Scholar]
- Weiss, M.; Baret, F.; Smith, G.J.; Jonckheere, I.; Coppin, P. Review of methods for in situ leaf area index (LAI) determination Part II: Estimation of LAI, errors and sampling. Agricultural and Forest Meteorology 2004, 121, 37–53. [Google Scholar]
- Weiss, M.; Baret, F. Evaluation of canopy biophysical variable retrieval performances from the accumulation of large swath satellite data. Remote Sensing of Environment 1999, 70, 293–306. [Google Scholar]

| Site name | Land cover type | Date | Lat. | Lon. | mLAI | σLAI |
|---|---|---|---|---|---|---|
| Aekloba-May01 | Palm tree plantation | 1/Jun./2001 | 2.63 | 99.58 | 3.54 | 0.671 |
| Alpilles-March01 | Crops | 15/Mar./2001 | 43.81 | 4.74 | 0.93 | 1.15 |
| Barrax-July03 | Cropland | 3/Jul./2003 | 39.07 | -2.10 | 0.97 | 1.41 |
| Fundulea-May02 | Crops | 9/Jun./2002 | 44.41 | 26.59 | 1.53 | 1.30 |
| Gilching-July02 | Crops and forest | 8/Jul./2002 | 48.08 | 11.32 | 5.39 | 1.79 |
| Hirsikangas-August03 | Forest | 2/Aug./2003 | 62.64 | 27.01 | 2.55 | 1.14 |
| Jarvselja-June02 | Boreal forest | 13/Jul./2002 | 58.30 | 27.26 | 4.20 | 1.09 |
| Laprida-November01 | Grassland | 3/Nov./2001 | -36.99 | -60.55 | 5.66 | 2.07 |
| Larose-August03 | Mixed forest | 18/Sep./2003 | 45.38 | -75.21 | 5.87 | 2.00 |
| Larzac-July02 | Grassland | 12/Jul./2002 | 43.94 | 3.12 | 0.81 | 0.20 |
| Nezer-April02 | Pine forest | 21/Apr./2002 | 44.57 | -1.04 | 2.38 | 1.11 |
| Rovaniemi-June04 | Forest | 23/Jul./2004 | 66.46 | 25.35 | 1.25 | 0.52 |
| Turco-August02 | Shrubs | 29/Aug./2002 | -18.24 | -68.19 | 0.04 | 0.03 |
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ma, L.; Li, C.; Tang, B.; Tang, L.; Bi, Y.; Zhou, B.; Li, Z.-L. Impact of Spatial LAI Heterogeneity on Estimate of Directional Gap Fraction from SPOT-Satellite Data. Sensors 2008, 8, 3767-3779. https://doi.org/10.3390/s8063767
Ma L, Li C, Tang B, Tang L, Bi Y, Zhou B, Li Z-L. Impact of Spatial LAI Heterogeneity on Estimate of Directional Gap Fraction from SPOT-Satellite Data. Sensors. 2008; 8(6):3767-3779. https://doi.org/10.3390/s8063767
Chicago/Turabian StyleMa, Lingling, Chuanrong Li, Bohui Tang, Lingli Tang, Yuyin Bi, Beiyan Zhou, and Zhao-Liang Li. 2008. "Impact of Spatial LAI Heterogeneity on Estimate of Directional Gap Fraction from SPOT-Satellite Data" Sensors 8, no. 6: 3767-3779. https://doi.org/10.3390/s8063767






