1. Introduction
Synthetic aperture radar (SAR) becomes an important tool in modern remote sensing for its all-weather, day and night capability to provide high-resolution maps of scene of interest. The demand for radar images is constantly pushing for finer resolutions. This quest for the resolving power has two major consequences [
1-
2]: first, their useful bandwidth should increase in proportion with the resolution in range. Second, the length of the synthetic antenna should increase in proportion with the along-track resolution.
Due to technical limitations, particularly the limited sampling rate of the analog to digital converters, synthetic bandwidth technique [
3-
6] is proposed to solve the hardware challenges of wideband radar. As compared to the commonly used wideband linear frequency modulated (LFM) radar waveform, by adopting stepped-chirp waveform and applying synthetic bandwidth techniques, it is possible to achieve high range resolution while still retaining the advantages of lower instantaneous receiver bandwidth and lower analog-to-digital sampling rate. However, the relative motion between the radar and the target during the period of a pulse cluster is not always negligible. If it is not taken into account, as a consequence, it may result in performance degradations, such as range error, loss in signal-to-noise ratio, and degraded range resolution. Unfortunately, the phase errors resulted from this motion are space-variant. The traditional synthetic bandwidth techniques only compensate these errors corresponding to a specified point target, for example, the scene center. Consequently, the purpose of this paper is to compensate this space-variant phase error.
With respect to the azimuth dimension, high resolution is obtained by coherent integration over a large aperture. The generally linear radar flight trajectory assumption, which is the basis of frequency domain image formation algorithm, is deviated, especially when nonplanar motion (NPM) occurs. Polar format algorithm (PFA) [
7-
8] is a popular high resolution spotlight SAR algorithm due to its efficient NPM compensation capability. However, due to the planar wavefront approximations made in PFA, the data exhibits space-variant phase errors and migration errors, which limit the focused scene size. Then, subaperture algorithm [
9] is proposed. Due to its space-variant phase correction capability, fine resolution imaging of large scene becomes available.
In this paper, a new image formation algorithm which incorporates the synthetic bandwidth technique with subaperture processing is proposed. Instead of traditional pulse synthesis preprocessing, it integrates the pulse synthesis into range subaperture processing. Meanwhile, it is able to compensate the space-variant phase errors caused by the radar motion during the pulse cluster.
2. SAR Signal Modeling
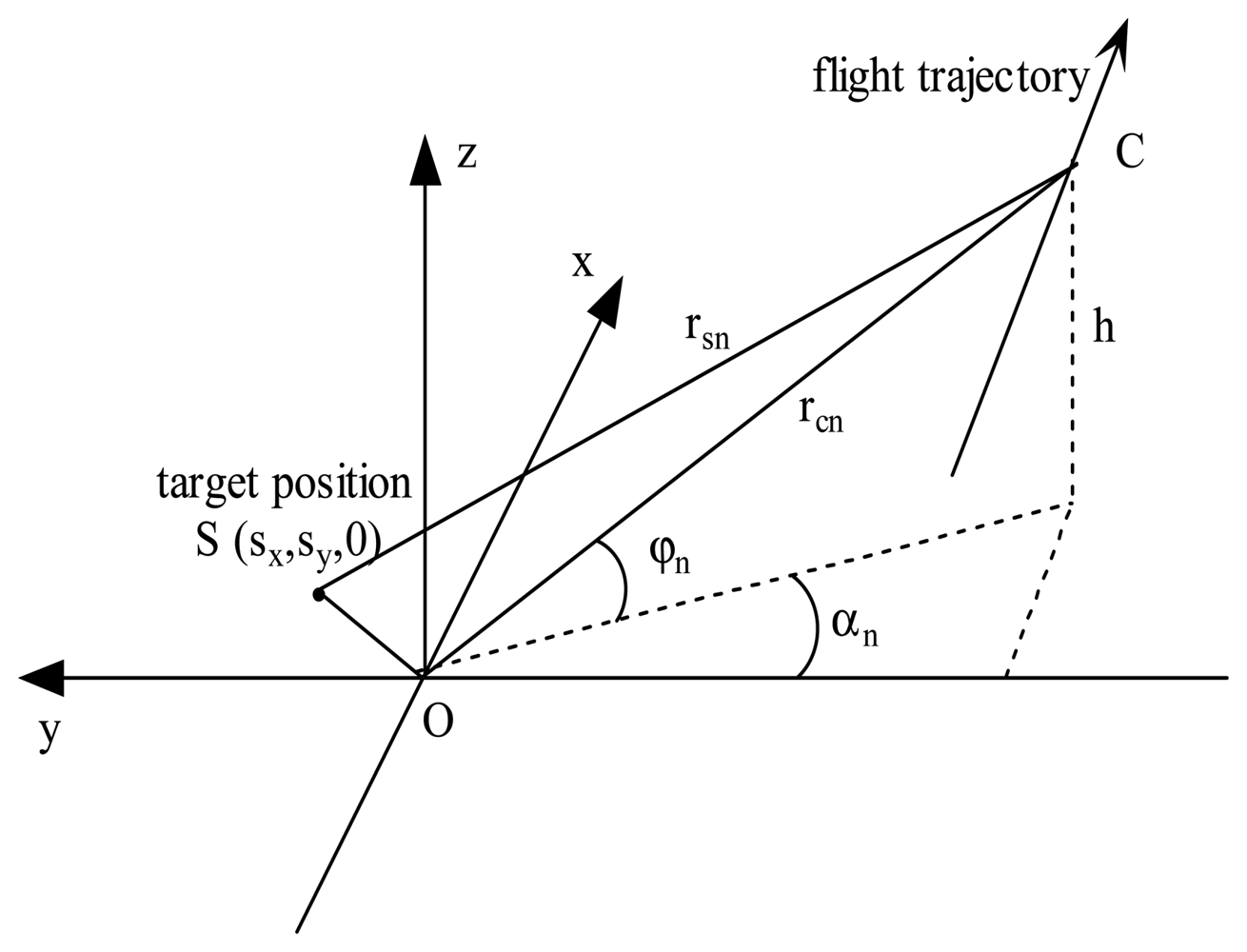
Consider a spotlight SAR operating in the geometry of
Figure 1, for simplicity, we only examine the case in which the sensor travels in a straight line at constant velocity. The central point of the scene is defined as the origin of the coordinate system, and radar antenna phase center (APC) is identified by coordinates (
x,
y,
z). The variable
αn and
φn are the APC's instantaneous squint angle and grazing angle, respectively, at the nth LFM pulse. They equal
α0 and
φ0 at the center of the aperture. The distance from the APC to the scene center is
rcn. In this paper, we account for the broadside mode only, then
α0 = 0. A target scatter is located at (
sx,
sy, 0), and the range from APC to this target is measured by
rsn. After performing dechirp and residual video phase (RVP) elimination on the echo signal of the nth pulse, we can express the Doppler phase history as [
7]
where
RΔ = (
rcn−
rsn) is the differential range,
c is the velocity of light,
f0 is the carrier frequency of the transmitted signal,
γ is the chirp rate,
Ts is the sample interval in fast time,
i is the range sample index with −
I/2≤
i≤
I/2 − 1, and
n is the index value of pulse number with −
N/2 ≤
n ≤
N/2 −1.
The differential range
RΔ can be expressed as [
7]
where
, which is caused by the assumption of planar wavefront. By using the Taylor expansion,
ξ(
n) can be expressed as
ξ (
n) ≈
ε0 +
ε1n +
ε2n2 when the cubic and higher order terms are ignored. Since the coefficients of this polynomial are dependent on the target position, this error is space-variant.
Inserting
Equation (2) into
Equation (1), the sampled signal can be represented as
where
and
.
Performing range resampling formulated by
where
is a constant, we can have the phase history as
For the purpose of clearness and simplicity, we still use
i instead of
í in the following discussion. Then,
Equation (5) is expressed as
If the space sampling position
n satisfied tan
αn =
dαn, where
dα is constant, the range resampled signal can be modeled as
4. Stepped-Chirp based PFOSA (SCPFOSA)
To reduce the transmission bandwidth, and meanwhile to achieve the high range resolution, it is possible to transmit series of narrow-band signals centered at different carrier frequencies. For example, an equivalent wideband LFM chirp can be assembled from lesser-bandwidth chirp segments in the data processing stage. These subchirp signals, which are referred to as a pulse cluster, are transmitted as separate pulses, each with their own carrier frequencies. The carrier frequencies distribute sequentially to keep the spectrums covering the desired bandwidth.
Now assume that each pulse cluster has
K2 chirp segments each with bandwidth
Bs, the carrier frequency of the middle subchirp is
f0, and the step carrier frequency is Δ
f (Δ
f <
Bs). Then the center frequency of the
k2 th (−
K2/2≤
k2 ≤
K2/2−1) subchirp is
f0 +
k2Δ
f. Analogous to
Equation (3), after preprocessing, the
k2th backscattered echo signal in the
nth pulse cluster can be represented by
where
k1 is the range sample index in each chirp segment,
k2 is the chirp segment index, and
n is the cluster index. It is important to note that the grazing angle
φn,k2 and squint angle
αn,k2 vary not only with index
n, which is desirable, but also with
k2, which is undesirable. The latter change of
φn,k2 and
αn,k2 is resulted from the radar motion during the pulse cluster. Neglecting this variation will introduce space-variant phase errors which limit the focused scene size. But in
Equation (12) it does not appear explicitly. To illustrate this effect, we develop a polynomial expression by using Taylor series expansion.
The key to analysis of the characteristics of the
Equation (12) is to have expression for cos
φn,k2 cos
αn,k2 in terms of tan
αn,k2. From the geometry in
Figure.1, it is easy to get the following relationship
where
φ0,0 is the grazing angle at the aperture center corresponding to
αn,k2 = 0.
Since the wavefront curvature error term
ξ(
n,
k2) does not play an important role in this development, it is neglected. Then inserting
Equation (13) into
Equation (12) and perform a Taylor series expansion, we get the signal phase history in
Equation (12) approximated as
where
,
and
.
As before, we assume that the space sampling position
n satisfies tan
αn,k2 =
dα(
nK2+
k2) then
Equation (14) can be divided into two parts
where
Phase term Φbasic contains the basic imaging information. The phase term Φerr, which causes distortion and defocus in range, is the error term introduced by the radar motion during pulse cluster. Due to its dependence on target position (sx, sy), this phase error is space-variant. Analogous to phase error resulted from wavefront curvature, if not compensated, it set the focused scene size limit, and particularly troublesome as resolution approaches the nominal wavelength of the radar.
For
Equation (12), after range resampling, the phase history becomes
where
,
and
.
Comparing with
Equation (6), it is clear to see that in
Equation (17) we get the range subaperture data naturally via the transmission and reception of the chirp segment signals. The difference is that
αn,k2 and
ξ(
n,
k2) varies with index
k2, while in
Equation (6) they keep constant at specified
n.
Insert tan
αn,k2 =
dα(
nK2 +
k2) into
Equation (17), and then divide the azimuth aperture into subapertures
where
ϕerr(
k1,
k2) =
κo [1 +
β0(
k1 +
μ2k2)]
sxdαk2 is the phase error term resulted from radar motion during pulse cluster but after range resampling. Compared with phase error term Φ
err before range resampling, parts of phase error are compensated, and the range position dependence is eliminated.
Analogous to
Equation (11), for
Equation (18), we neglect the constant phase term and wavefront error terms in the subapertures and rearrange the rest terms
where
ϕe1 =
κ0β0sxdαK2Δ
2m2k1,
ϕe2 =
κ0 (1+
β0μ2k2) [
ε1 Δ
2m2 +
ε2 (Δ
2m2)
2], and
ϕe3 =
κ0β0μ2ε0k2 are undesired terms just like those in PFOSA which are introduced by wavefront curvature. While error phase terms
ϕerr(
k1) =
κoβ0sxdαk2k1 and
, the two parts of
ϕerr(
k1,
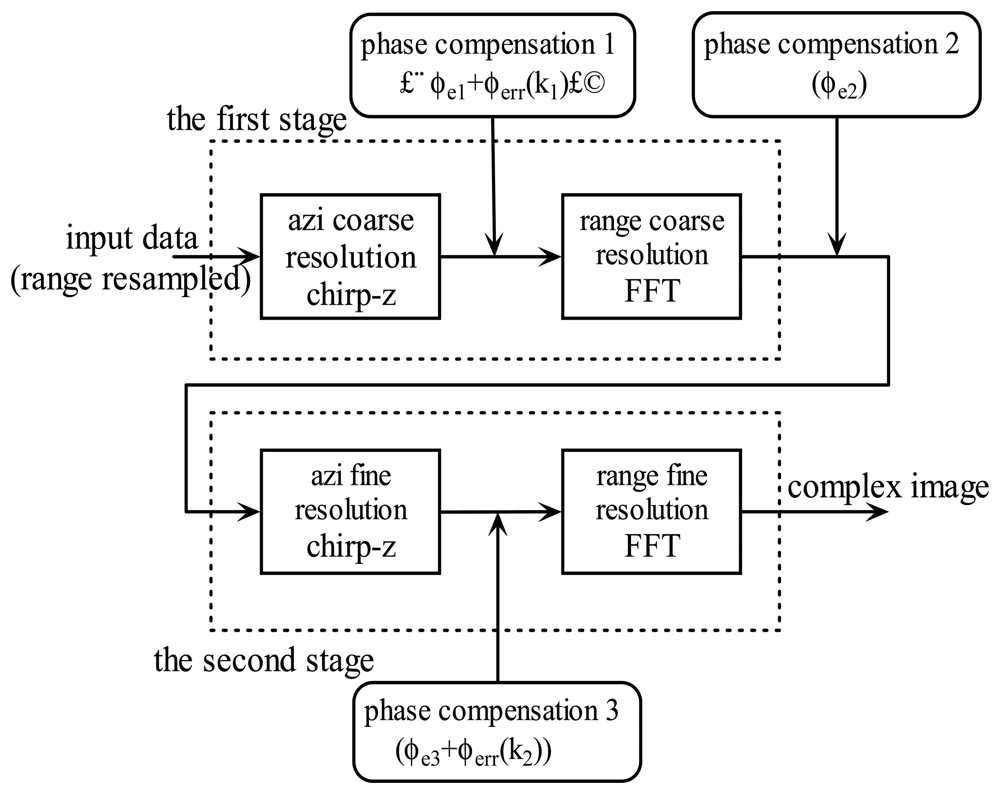
k2), are due to radar motion during the pulse cluster. These error terms are space-variant due to the dependence on azimuth position (range dependence is eliminated owing to range resampling). If these phase errors are not compensated, as a consequence, they result in displacement and defocus in range. Since the coarse location information can be extracted from the coarse resolution images, it is possible to compensate these errors by modifying the classical PFOSA. The new algorithm (we call it SCPFOSA) can be derived from
Equation (19), whose flow chart is illustrated in
figure 2.
Step1: Perform a CZT across m1, get the azimuth coarse resolution estimate sx.
Step2: Use the estimate of sx to compensate the error phase terms ϕe1 and ϕerr (k1), and then perform a FFT across k1 to obtain the range coarse resolution estimate sy.
Step3: Use the estimate of sx and sy to correct the error term ϕe2, then perform a CZT across m2 to get the azimuth fine resolution estimate sx.
Step4: Use the fine resolution estimation of sx and coarse resolution estimate of sy to compensate the error terms ϕe3 and ϕerr (k2), and then perform a FFT across k2 to get the range fine resolution estimate sy. The result is the fine resolution complex SAR image.
5. Simulation Results
In this section, point target simulation is employed to validate the presented algorithm. The waveform parameters are chosen as:
Bs = 250
MHz, Δ
f =100
MHz,
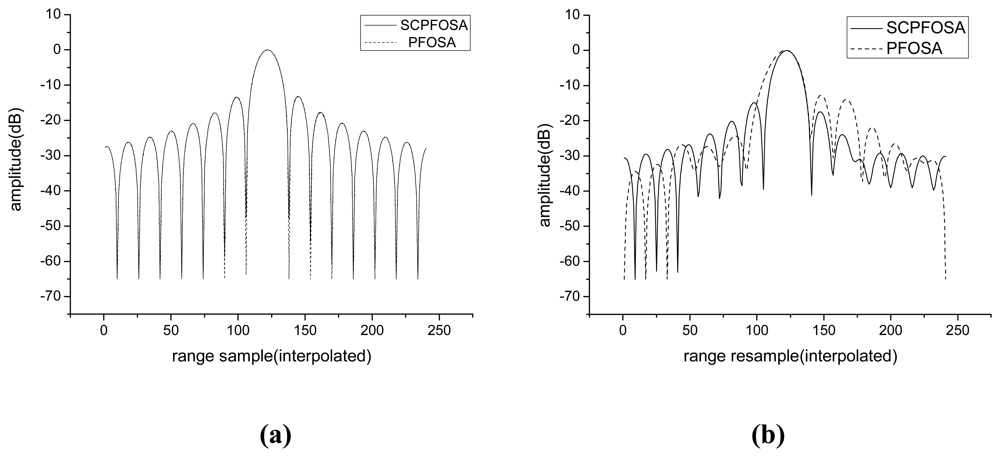
K2 =15. The other parameters are listed as follow: standoff range is 10km, azimuth resolution is 0.1m, and radar forward velocity is 150m/s. Two point targets are simulated, the first one is the scene center point, and the other one is located at azimuth 150m away from the scene center. The new algorithm is evaluated with respect to the classical PFOSA which doesn't compensate the error terms resulted from the use of stepped-chirp signals. In subaperture algorithm, subapertures are overlapped to control the sidelobes; in particular, they are overlapped to control the amplitude to grating lobes due to data decimation. The degree of allowable overlap will depend on the window functions employed, and sidelobe toleration limits. In our paper, the overlap rate is not the problem we are concerned, so we do not employ window function in the simulation. As the phase error term
ϕerr (
k1,
k2) results in distortion and defocus only in the range, we show the range profiles of impulse response function (IRF) for the two simulated targets (
Figure. 3). For scene center point, since the error terms
ϕerr (
k1) and
ϕerr (
k2) are both zeros, the two algorithms have almost the same response. However, for the azimuth displaced point target, the mainlobe of range profile is broadening for PFOSA, since the phase errors caused by motion of radar during pulse cluster are not compensated. While using SCPFOSA, due to the correction of these phase errors, its range profile has improved significantly (mainlobe reduce 12% and peak sidelobe ratio (PSR) reduces about 2.5dB).