Motion Compensation of Moving Targets for High Range Resolution Stepped-Frequency Radar
Abstract
:1. Introduction
2. Signal Model
3. Velocity Estimation and Motion Compensation
3.1. Maximum Likelihood Estimation of the Target Velocity
3.2. The Motion Compensation and Profile Reconstruction Algorithm
- Step 1
- Assume that the number of scatterers is K=1.
- Step 2
- Obtain scatterers' parameters by using SMLE.
- Step 3
- Calculate the MDL(K).
- Step 4
- Assume K=K+1, and repeat Step 2 and Step 3.
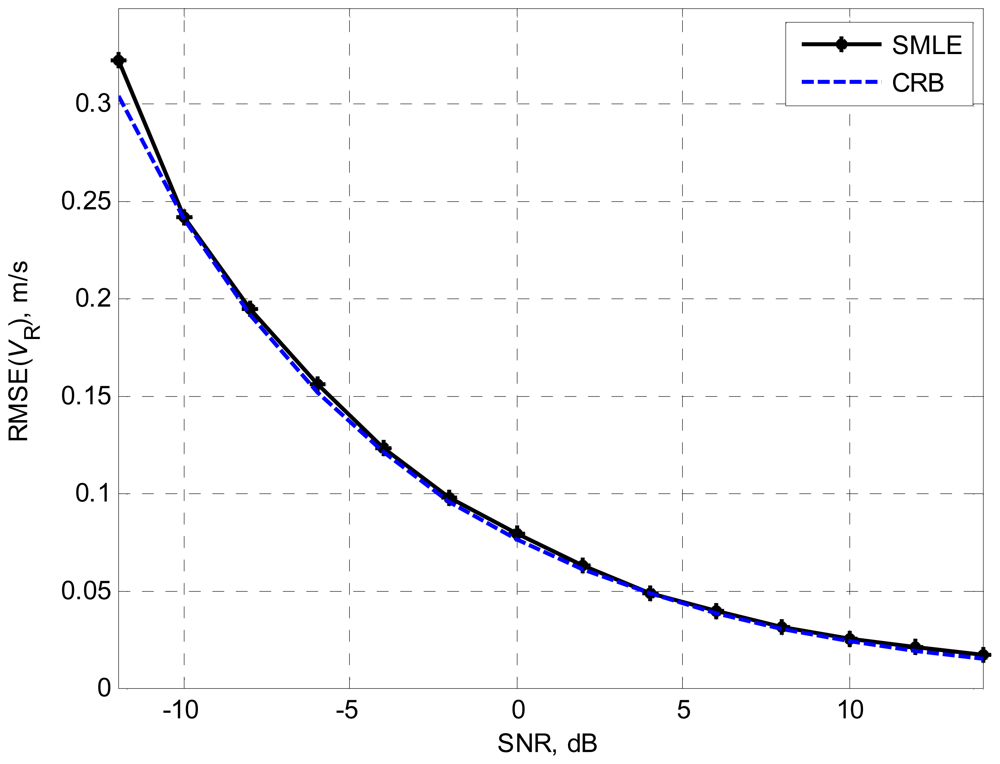
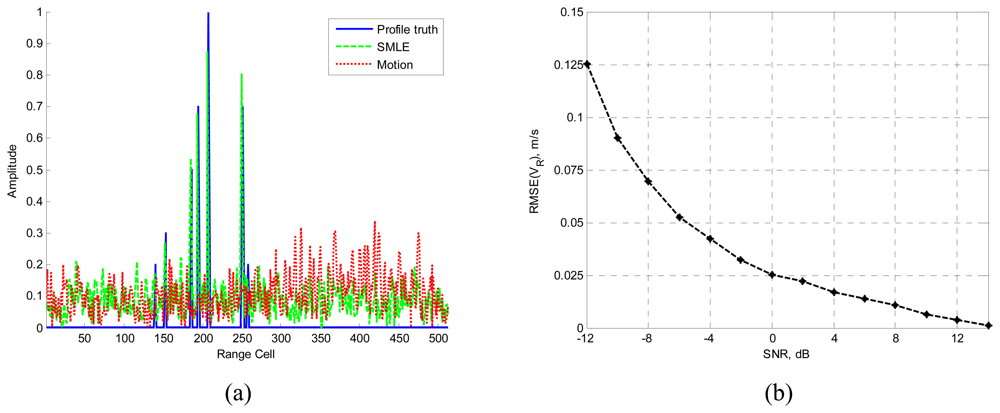
4. Numerical Examples
5. Conclusion
Acknowledgments
References and Notes
- Ruttenberg, K.; Chanzit, L. High range resolution by means of pulse to pulse frequency shifting. EASCON '68 Record 47–51.
- Einstein, T.H. Generation of high resolution radar range profiles and range profile autocorrelation functions using stepped frequency pulse trains. In Project Report TT-54; Massachusetts Institute of Technology: Lincoln Laboratory, 1984; (AD-A149242). [Google Scholar]
- Wehner, D.R. High Resolution Radar; 1987; Artech House: Norwood, MA. [Google Scholar]
- Lei, W.; Long, T.; Han, Y.Q. Moving targets imaging for stepped frequency radar. The 5th International Signal Processing Proceedings 2000, 3, 1851–1855. [Google Scholar]
- Wong, S.K.; Duff, G.; Riseborough, E. Analysis of distortion in the high range resolution profile from a perturbed target. IEE Proceedings – Radar, Sonar and Navigation 2001, 148(6), 353–362. [Google Scholar]
- Temple, M.A.; Sitler, K.L.; Raines, R.A.; Hughes, J.A. High range resolution (HRR) improvement using synthetic HRR processing and stepped-frequency polyphase coding. IEE Proceedings – Radar, Sonar and Navigation 2004, 151(1), 41–47. [Google Scholar]
- Chen, H.; Liu, Y.; Jiang, W.; Guo, G. A new approach for synthesizing the range profile of moving targets via stepped-frequency waveforms. IEEE Geoscience and Remote Sensing Letters 2006, 3(3), 406–409. [Google Scholar]
- Li, G.; Meng, H.D.; Xia, X.G.; Peng, Y.N. Range and velocity estimation of moving targets using multiple stepped-frequency pulse trains. Sensors 2008, 8, 1343–1350. [Google Scholar]
- Schwarz, G. Estimating the dimension of a model. The Annals of Statistics 1978, 6(2), 461–464. [Google Scholar]
- Peleg, S.; Porat, B. The Cramer–Rao lower bound for signals with constant amplitude and polynomial phase. IEEE Transactions on Signal Processing 1991, 39(3), 749–752. [Google Scholar]
- Ristic, B.; Boashash, B. Comments on “The Cramer–Rao lower bounds for signals with constant amplitude and polynomial phase”. IEEE Transaction on Signal Processing 1998, 46(6), 1078–1079. [Google Scholar]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory; 1993; Prentice-Hall. [Google Scholar]
| K | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| MDL | 1100 | 924.99 | 748.11 | 572.3 | 574.9 | 576.12 | 577.36 | 578.7 | 580.14 | 581.6 |
| Parameter | Value |
|---|---|
| Radar center frequency (fc) | 9 GHz |
| Frequency step size (Δf) | 1 MHz |
| Pulse number (N) | 512 |
| Range resolution (ΔR) | 0.293 m |
| Pulse repetition interval (PRI) | 1 ms |
| Pulse width (T) | 0.5 μs |
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Liu, Y.; Meng, H.; Zhang, H.; Wang, X. Motion Compensation of Moving Targets for High Range Resolution Stepped-Frequency Radar. Sensors 2008, 8, 3429-3437. https://doi.org/10.3390/s8053429
Liu Y, Meng H, Zhang H, Wang X. Motion Compensation of Moving Targets for High Range Resolution Stepped-Frequency Radar. Sensors. 2008; 8(5):3429-3437. https://doi.org/10.3390/s8053429
Chicago/Turabian StyleLiu, Yimin, Huadong Meng, Hao Zhang, and Xiqin Wang. 2008. "Motion Compensation of Moving Targets for High Range Resolution Stepped-Frequency Radar" Sensors 8, no. 5: 3429-3437. https://doi.org/10.3390/s8053429




