Experimental-Numerical Comparison of the Cantilever MEMS Frequency Shift in presence of a Residual Stress Gradient
Abstract
:1. Introduction
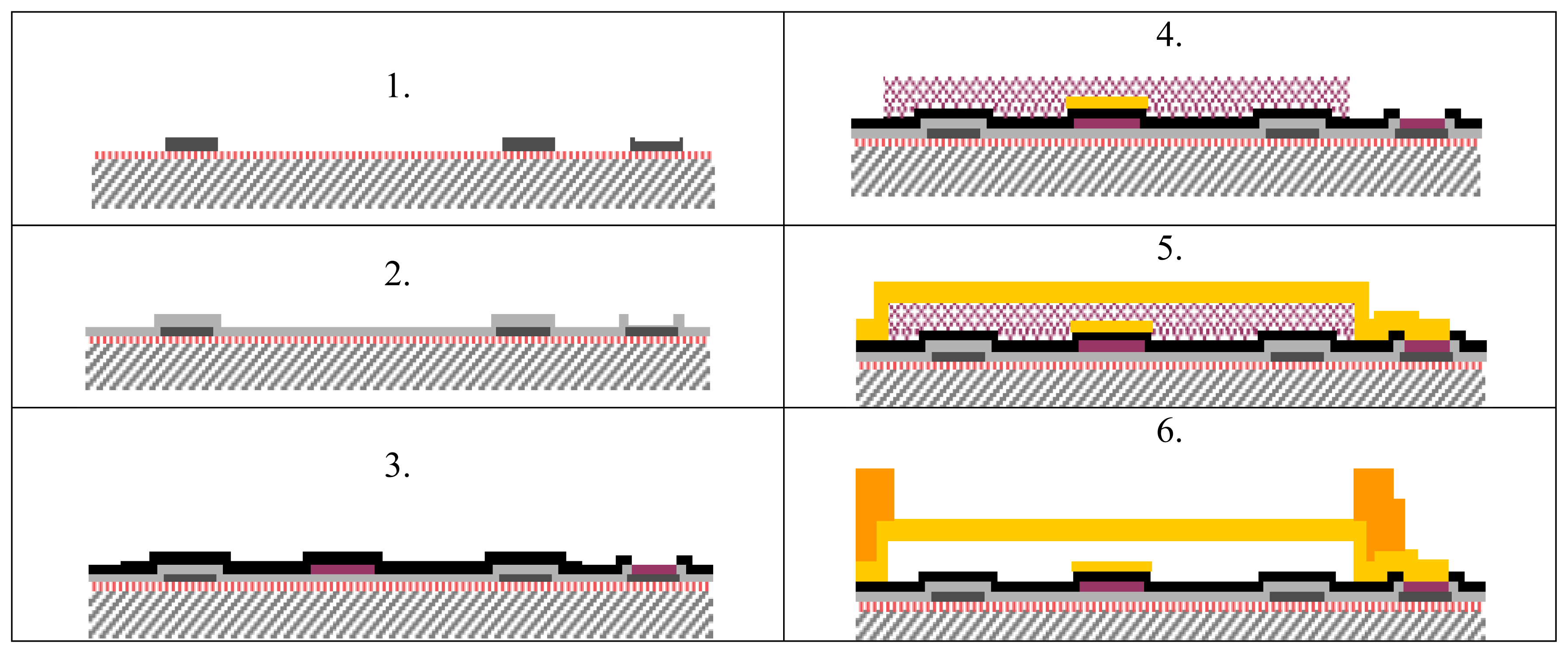
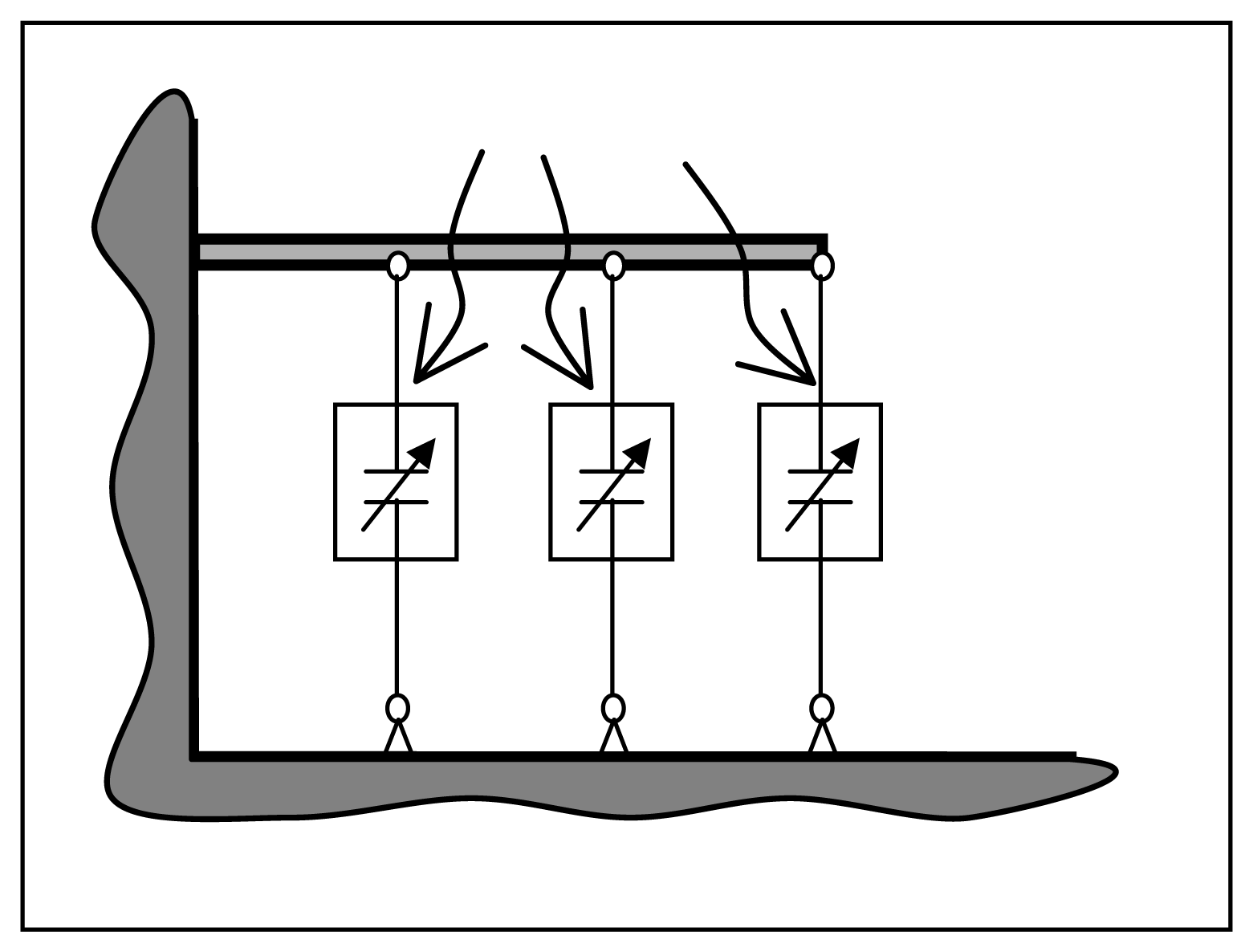
2. Fabrication process and specimen's geometry description
- At first a 1000 nm thick thermal field oxide is grown at 975°C in a wet ambient on a silicon wafer, then a nitrogen annealing at the same temperature is performed. A 630 nm thick polysilicon layer employed for resistors and for actuation lines is deposited by LPCVD and subsequently patterned through dry etching.
- A 300 nm thick silicon oxide is deposited at 718°C, also by LPCVD process and via-holes are opened through dry etching.
- A multi-layer metal for signal lines is sputtered and subsequently patterned by dry etching. Temperature profile: Ti(30nm): 400°C; TiN(50 nm): 400°C; Al/Si+Ti(410/60 nm): ambient temperature; TiN(80 nm): 300°C. A 100 nm thick oxide layer is then deposited at 430°C. In order to define via-holes for opening contacts or to uncover the multimetal line oxide removal is defined with a mask by dry etching.
- A 150 nm gold layer is deposited by PVD and patterned through wet etching. A 3 μm thick sacrificial photoresist layer is deposited and patterned.
- A 1.3 μm thick gold layer is electroplated at 52°C employing a chromium-gold PVD adhesion layer, called seed layer. This is the suspended/movable part of the devices.
- The last deposition step is another gold layer deposited at 52°C used to reinforce the anchors and the suspended parts of the structures. Finally, the structure release is obtained by ashing the sacrificial layer through plasma oxygen etching. At the end of the process a sintering is performed at 190°C.
3. Measurement methods and experimental results
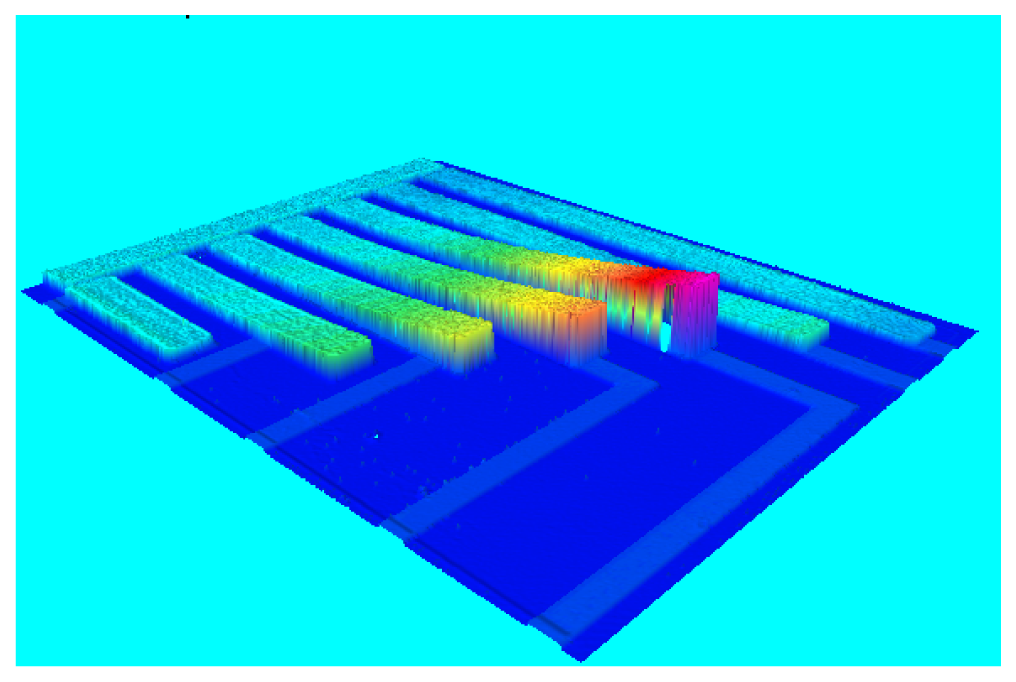
3.1. Profilometry measurements
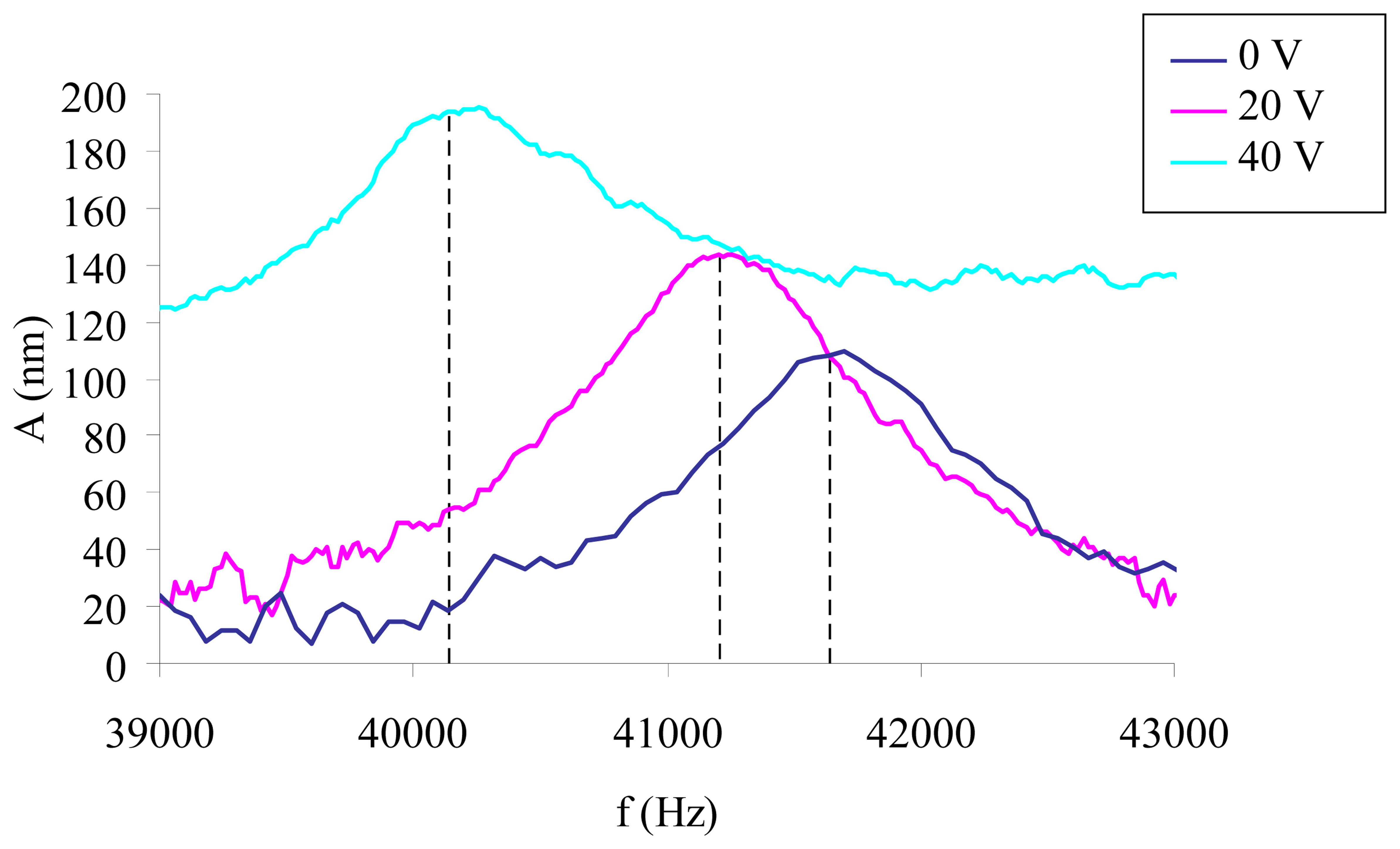
3.2. Out of plane vibration measurements
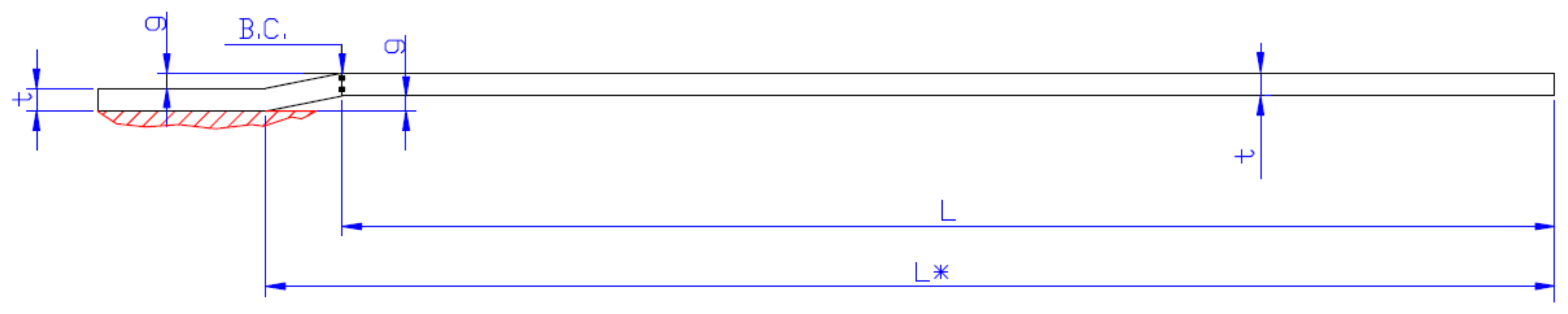
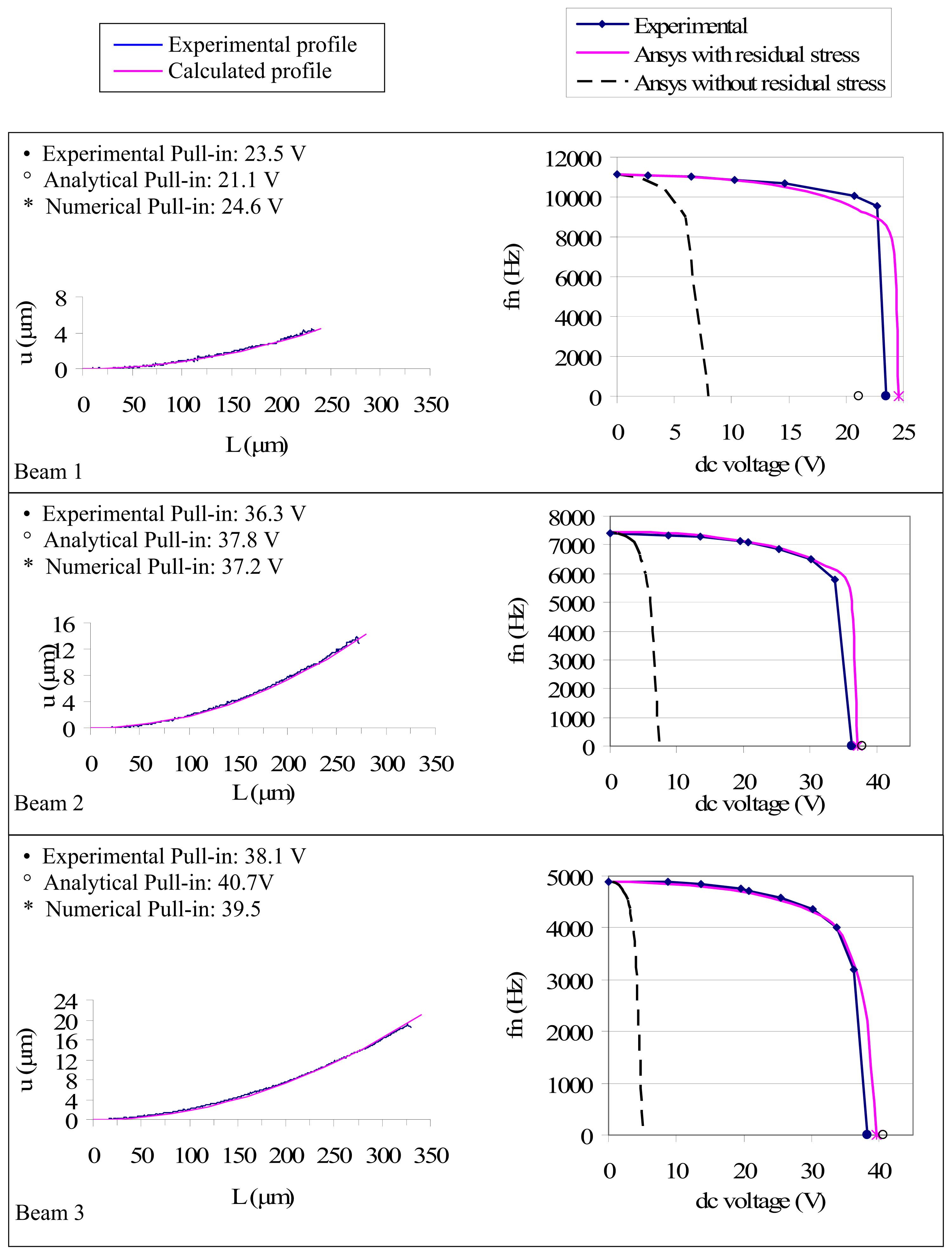
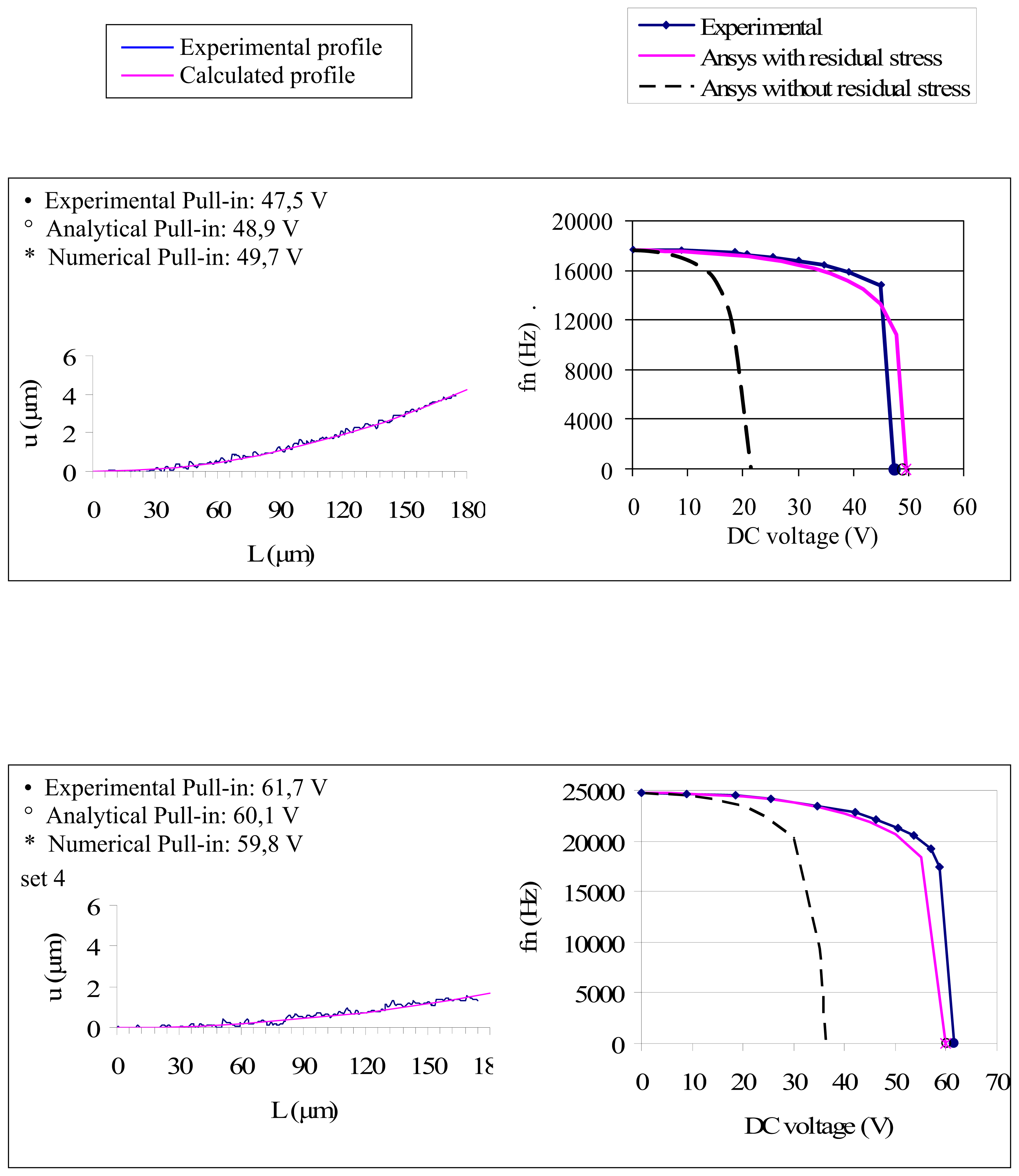
4. Frequency shift: analytical models and residual stress evaluation
4.1. Analytical models
4.2. Numerical models
5. Conclusions
Acknowledgments
References
- Chung, K.; Fang, Y. J.; Cheng, C. M.; Hong, Y. Z.; Wang, C. H. Effect of seed layer stress on the fabrication of monolithic MEMS microstructures. Microsyst. Technol. 2007, 13, 299–304. [Google Scholar]
- Stanec, J. R.; Smith, C. H., III; Chasiotis, I.; Barker, N. S. Realization of low-stress Au cantilever beams. J. Micromech. Microeng. 2007, 17, N7–N10. [Google Scholar]
- Elbrecht, L.; Storm, U.; Catanescu, R.; Binder, J. Comparison of stress measurement techniques in surface micromaching. J. Micromech. Microeng. 1997, 7, 151–154. [Google Scholar]
- Fang, W.; Wickert, J.A. Post buckling of micromaching beams. J. Micromech. Microeng. 1994, 4, 116–122. [Google Scholar]
- Fang, W.; Wickert, J.A. Determining mean and gradient residual stresses in thin films using micromachined cantilevers. J. Micromech. Microeng. 1996, 6, 301–309. [Google Scholar]
- Chung, C.K.; Lin, C.J.; Wu, L.H.; Fang, Y.J.; Hong, Y.Z. Selection of mold materials for electroforming of monolithic two-layer microstructure. Microsyst. Technol. 2004, 10, 467–471. [Google Scholar]
- Kim, J.W.; Yamagata, Y.; Morita, S.; Moriyasu, S.; Ohmori, H.; Higuchi, T. A study on the fabrication of multi-layer microstructure using ELID grinding and the thick photoresist technology. Key Eng. Mater. 2003, 238–239, 19–22. [Google Scholar]
- Zhang, L.X.; Zhao, Y.P. Electromechanical model of RF MEMS switches. Microsyst. Technol. 2003, 9, 420–426. [Google Scholar]
- Nicu, L.; Temple-Boyer, P.; Bergaud, C.; Scheid, E.; Martinez, A. Energy study of buckled micromachined beams for thin-film stress measurements applied to SiO2. J. Micromech. Microeng. 1999, 9, 414–421. [Google Scholar]
- Laconte, J.; Iker, F.; Jorez, S.; Andrè, N.; Proost, J.; Pardoen, T.; Flandre, D.; Raskin, J.P. Thin films stress extraction using micromachined structures and wafer curvature measurements. Microelectron. Eng. 2004, 76, 219–226. [Google Scholar]
- Baek, C.W.; Kim, Y.K.; Ahn, Y.; Kim, Y.H. Measurement of the mechanical properties of electroplated gold thin films using micromachined beam structures. Sens. Actuat. A 2005, 117, 17–27. [Google Scholar]
- Lee, W. S.; Kim, B. K.; Cho, J. H.; Youn, S. K.; Kwon, K. C. Frequency-shifting analysis of electrostatic tunable micromechanical actuator. J. Model. Simul. Microsyst. 2001, 2, 83–88. [Google Scholar]
- Brusa, E.; De Bona, F.; Gugliotta, A.; Somà, A. Modelling and prediction of the dynamic behaviour of microbeams under electrostatic load. Analog Integr. Circ. S. 2004, 40, 155–164. [Google Scholar]
- Van Der Poel Filho, C. J.; Gugliotta, A.; Somà, A.; Pavanello, R. Dynamic Identification of MEMS by Eigensensitivity and Newmark Simulation. Analog Integr. Circ. S. 2005, 44, 155–162. [Google Scholar]
- Brusa, E.; De Bona, F.; Della Schiava, A.; Somà, A. Model synthesis of structural dynamics for electrostatic microactuators. Presented at European micro and nano systems 2004, Paris, 20-21 October, 2004.
- Zhang, Y.; Zhao, Y. An effective method of determining the residual stress gradients in a micro-cantilever. Microsyst. Technol. 2006, 12, 357–364. [Google Scholar]
- Subhadeep, K.; Bagolini, A.; Margesin, B.; Zen, M. Stress and resistivity analysis of electrodeposited gold films for MEMS application. Microelectron. J. 2006, 37. [Google Scholar]
- Margesin, B.; Bagolini, A.; Guamieri, I.; Giacomozzi, F.; Faes, A. Stress characterization of electroplated gold layers for low temperature surface micromachining. Presented at Symposium on Design Test, Integration & Packaging of MEMS-MOEMS, Mandelieu-La Napoule, France, 5-7 May, 2003.
- Zoomsurf 3D User manual Version 1.3; Fogale Nanotech: Nimes, France.
- Ballestra, A.; Brusa, E.; Munteanu, M.G.; Somà, A. Experimental characterization of the static behaviour of microcantilevers electrostatically actuated. Presented at Symposium on Design Test, Integration & Packaging of MEMS-MOEMS, Stresa, Italy, 25-27 April 2007.
- Collenz, A.; De Bona, F.; Gugliotta, A.; Somà, A. Large deflections of microbeams under electrostatic loads. J. Micromech. Microeng. 2004, 14, 365–37. [Google Scholar]
- Petitgrand, S.; Yahiaoui, R.; Danaie, K.; Bosseboeuf, A.; Gilles, J. P. 3D measurement of micromechanical devices vibration mode shapes with a stroboscopic interferometric microscope. Optics and Lasers in Engineering 2001, 36(2), 77–101. [Google Scholar]
- Fang, W.; Wickert, J.A. Determining mean and gradient residual stresses in thin films using micromachined cantilevers. J. Micromech. Microeng. 1996, 6. [Google Scholar]
- Tibeica, C.; Voicu, R.; Bazu, M.; Ilian, V.E.; Vasilache, D.; Galateanu, L.; Pons, P.; Yacine, K.; Flourens, F. Analytical VS. Computational approach of the pull-in voltage of electrostatically actuated micro-bridges. 0-7803-9214-0/05. IEEE 2005. [Google Scholar]
- O’Mahony, C.; Hill, M.; Duane, R.; Mathewson, A. Analysis of electromechanical boundary effects on the pull-in of micromachined fixed-fixed beams. J. Micromech. Microeng. 2003, 13, S75–S80. [Google Scholar]
- Somà, A.; De Pasquale, G. Identification of test structures for Reduced Order Modeling of the squeeze film damping in MEMS. Presented at Symposium on design, test, integration and packaging of mems/moems, 2007, Stresa, Italy, 25-27 April, 2007.
- .
- Osterberg, P.M.; Senturia, S.D. M-Test: a test chip for MEMS material property measurement using electrostatically actuated test structures. J. Microelectromech. Syst. 1997, 6(2). [Google Scholar]
- Gupta, K. J. Electrostatic Pull-in Test Structure Design for in-situ Mechanical Property Measurements of Microelectromechanical Systems (MEMS). Ph.D. dissertation, 1998. [Google Scholar]
- Nemirovsky, Y.; Bochobza-Degani, O. A methodology and model for the pull-in parameters of electrostatic actuators. J. Microelectromech. Syst. 2001, 10(4). [Google Scholar]
Abbreviations
| c | curvature |
| E | elastic modulus |
| f | exitation frequency |
| fc | corrective coefficient for pull-in tension |
| fn | natural frequency |
| g | air-gap |
| g0 | initial gap |
| gm | medium gap |
| I | inertia moment of beam section |
| L | effective length |
| Lc | total length |
| m | mass |
| Mb | bending moment |
| Rc | curvature radius |
| S | surface |
| t | thickness |
| Vac | ac voltage |
| Vdc | dc voltage |
| w | width |
| u | vertical beam deflection |
| z | vertical coordinate along the thickness |
| ε0 | dielectric constant |
| σ0 | planar constant stress |
| σz | coefficient of linear stress variation |
| Ω | stress gradient |

| g (μm) | t (μm) | L (μm) | u (μm) | c (μm-1) | Ω (MPa/μm) | |
|---|---|---|---|---|---|---|
| specimen1 | ||||||
| set1 | 3.0 | 1.78 | 242.4 | 3.81 | 1.30E-04 | 12.8 |
| set2 | 3.0 | 1.68 | 245.0 | 5.30 | 1.77E-04 | 17.4 |
| set3 | 3.0 | 1.75 | 240.0 | 4.67 | 1.62E-04 | 16.0 |
| mean value | 3.0 | 1.73±0.05 | 242.5±2.5 | 4.59±0.74 | 1.56E-04 | 15.4±2.3 |
| specimen2 | ||||||
| set1 | 3.0 | 1.84 | 288.5 | 13.43 | 3.23E-04 | 31.8 |
| set2 | 3.0 | 1.71 | 289.4 | 13.61 | 3.25E-04 | 32.0 |
| set3 | 3.0 | 1.72 | 293.3 | 12.23 | 2.84E-04 | 28.0 |
| mean value | 3.0 | 1.76±0.06 | 290.6±2.7 | 13.09±0.69 | 3.11E-04 | 30.6±2.0 |
| specimen3 | ||||||
| set1 | 3.0 | 1.91 | 340.1 | 19.14 | 3.31E-04 | 32.6 |
| set2 | 3.0 | 1.59 | 343.8 | 18.85 | 3.19E-04 | 31.4 |
| set3 | 3.0 | 1.55 | 340.1 | 14.11 | 2.44E-04 | 24.0 |
| mean value | 3.0 | 1.68±0.18 | 341.3±1.8 | 17.37±2.51 | 2.98E-04 | 29.3±4.3 |
| g (μm) | t (μm) | L (μm) | u (μm) | c (μm-1) | Ω (MPa/μm) | |
|---|---|---|---|---|---|---|
| specimen1 | ||||||
| set4 | 3.0 | 1.78 | 192.8 | 4.16 | 2.23E-04 | 22.0 |
| set5 | 3.0 | 1.77 | 191.4 | 4.65 | 2.53E-04 | 24.9 |
| set6 | 3.0 | 1.74 | 189.6 | 4.23 | 2.35E-04 | 23.1 |
| mean value | 3.0 | 1.76±0.02 | 191.3±1.6 | 4.35 | 2.37E-04 | 23.3 |
| specimen2 | ||||||
| set4 | 3.0 | 2.41 | 191.9 | 2.69 | 1.46E-04 | 14.4 |
| set5 | 3.0 | 2.26 | 192.1 | 2.10 | 1.14E-04 | 11.2 |
| set6 | 3.0 | 2,31 | 192.1 | 2.55 | 1.38E-04 | 13.6 |
| mean value | 3.0 | 2.33±0.07 | 192.0±0.2 | 2.45 | 1.32E-04 | 13.7 |
| specimen3 | ||||||
| set4 | 3.0 | 4.31 | 189.9 | 0 | 0 | 0 |
| set5 | 3.0 | 4.40 | 191.5 | 0 | 0 | 0 |
| set6 | 3.0 | 4.37 | 190.5 | 0 | 0 | 0 |
| mean value | 3.0 | 4.36±0.04 | 190.6±0.8 | 0 | 0 | 0 |
© 2008 by MDPI Reproduction is permitted for non commercial purposes
Share and Cite
Ballestra, A.; Somà, A.; Pavanello, R. Experimental-Numerical Comparison of the Cantilever MEMS Frequency Shift in presence of a Residual Stress Gradient. Sensors 2008, 8, 767-783. https://doi.org/10.3390/s8020767
Ballestra A, Somà A, Pavanello R. Experimental-Numerical Comparison of the Cantilever MEMS Frequency Shift in presence of a Residual Stress Gradient. Sensors. 2008; 8(2):767-783. https://doi.org/10.3390/s8020767
Chicago/Turabian StyleBallestra, Alberto, Aurelio Somà, and Renato Pavanello. 2008. "Experimental-Numerical Comparison of the Cantilever MEMS Frequency Shift in presence of a Residual Stress Gradient" Sensors 8, no. 2: 767-783. https://doi.org/10.3390/s8020767






