The Successive Projection Algorithm (SPA), an Algorithm with a Spatial Constraint for the Automatic Search of Endmembers in Hyperspectral Data
Abstract
:1. Introduction
2. Background
2.1. Spectral endmembers in convex geometry
- Property 1
- Property 2
- Property 3
- For a given point in the simplex, a point with maximum distance must be a vertex of the simplex [27].
- Property 4
- The affine transformation (e.g. orthogonal projection) of a simplex is also a simplex, and endmembers are still located in the vertices of the new simplex after this transformation [14, 26]. In SPA this allows the use of orthogonal subspace projections as the core mechanism for endmember extraction.
2.2. Endmember extraction algorithms based on convex geometry
3. The successive projection algorithm (SPA)
3.1. Spectral similarity and spatial adjacency as selection criteria
3.2. Description of the SPA algorithm
- Step 1: Parameter setting
- Values for the following three parameters must be set: the number of endmembers(m) to find, the spectral angle threshold (t _θ) and the spatial threshold (t _pixel).
- Step 2: Extraction of the first endmember (e⃗1)
- The vector norms of all pixels in the image are calculated to locate the pixel that has the largest norm. According to Property 2, this pixel is at one of the simplex vertices and typically is the brightest pixels in the image cube. The first endmember e⃗1 is then estimated as described in Section 3.1.
- Step 3: Extraction of the second endmember (e⃗2)
- The distances between all pixels and e⃗1 are calculated and the pixel that has the largest distance is located. According to Property 3, this pixel will be at another vertex of the simplex usually corresponding to the darkest object in the scene (e.g. water body or shade). The 2nd endmember, e⃗2, can then be estimated according to section 3.1.
- Step 4: Orthogonal projection and extraction of a new endmember
- An endmember matrix U =[e⃗1, e⃗2] is then constructed using the two previously defined endmembers, and all pixels are projected to the subspace, Sproj, orthogonal to the space spanned by U aswhere p⃗(i,j)_proj and p⃗(i,j) are the projected and original pixel vector at image location (i, j) respectively. O is the projection operator,where I is the identity matrix, and U+ is the pseudo inverse of U, denoted byIn the projected subspace (Sproj), the contribution to the mixtures from endmembers in U is eliminated. According to Property 4, the projected data in the new space still conform to the convexity, that is to say the endmembers are still at the vertices of the simplex. The vector (pixel) with the maximum norm in the projected subspace (Sproj) will correspond to a new endmember (Property 2) in this case e⃗3, and this pixel is located at the apex of the simplex furthest away from the subspace spanned by the previously defined endmembers, e⃗1 and e⃗2.
- Step 5: Complete the search of all endmembers
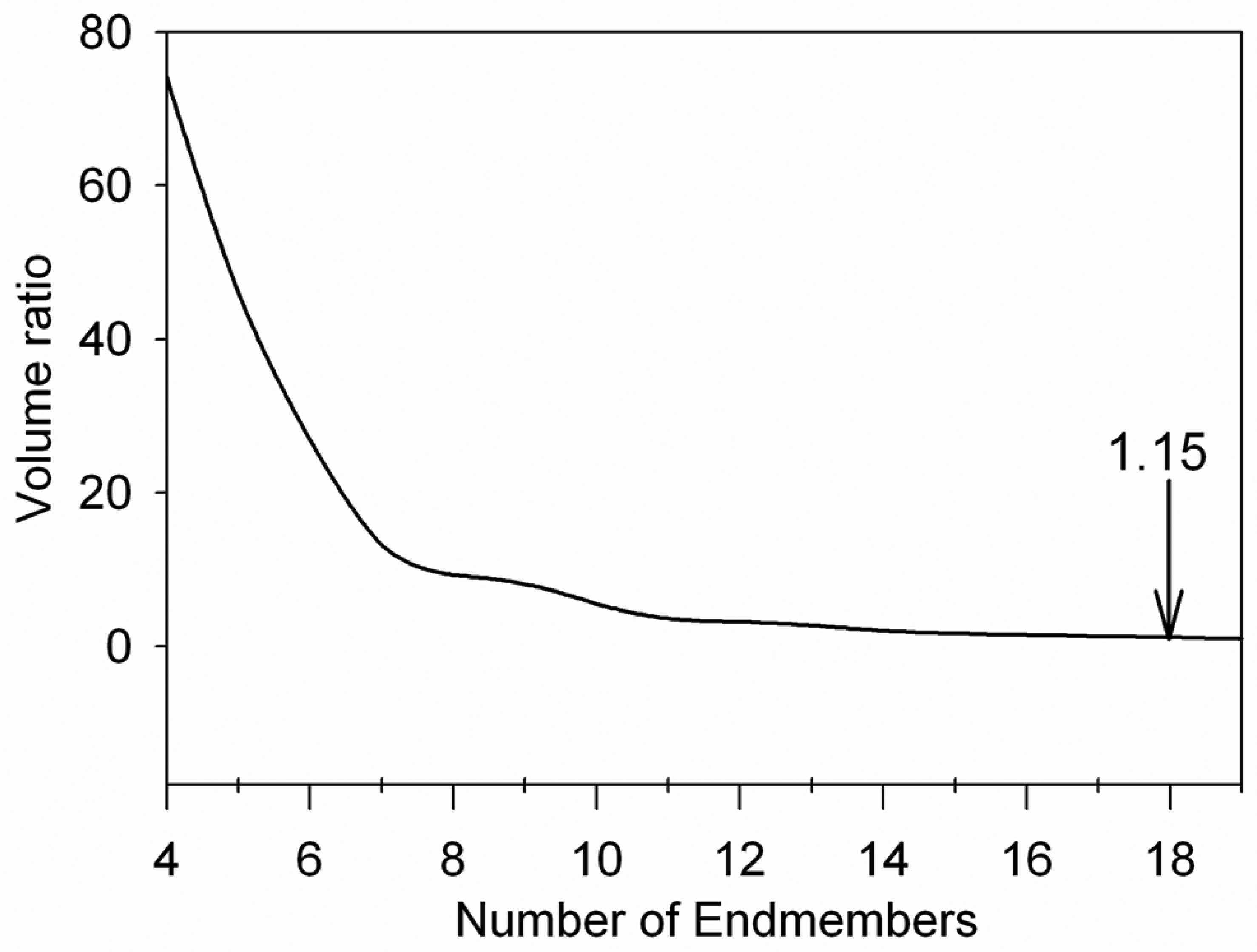
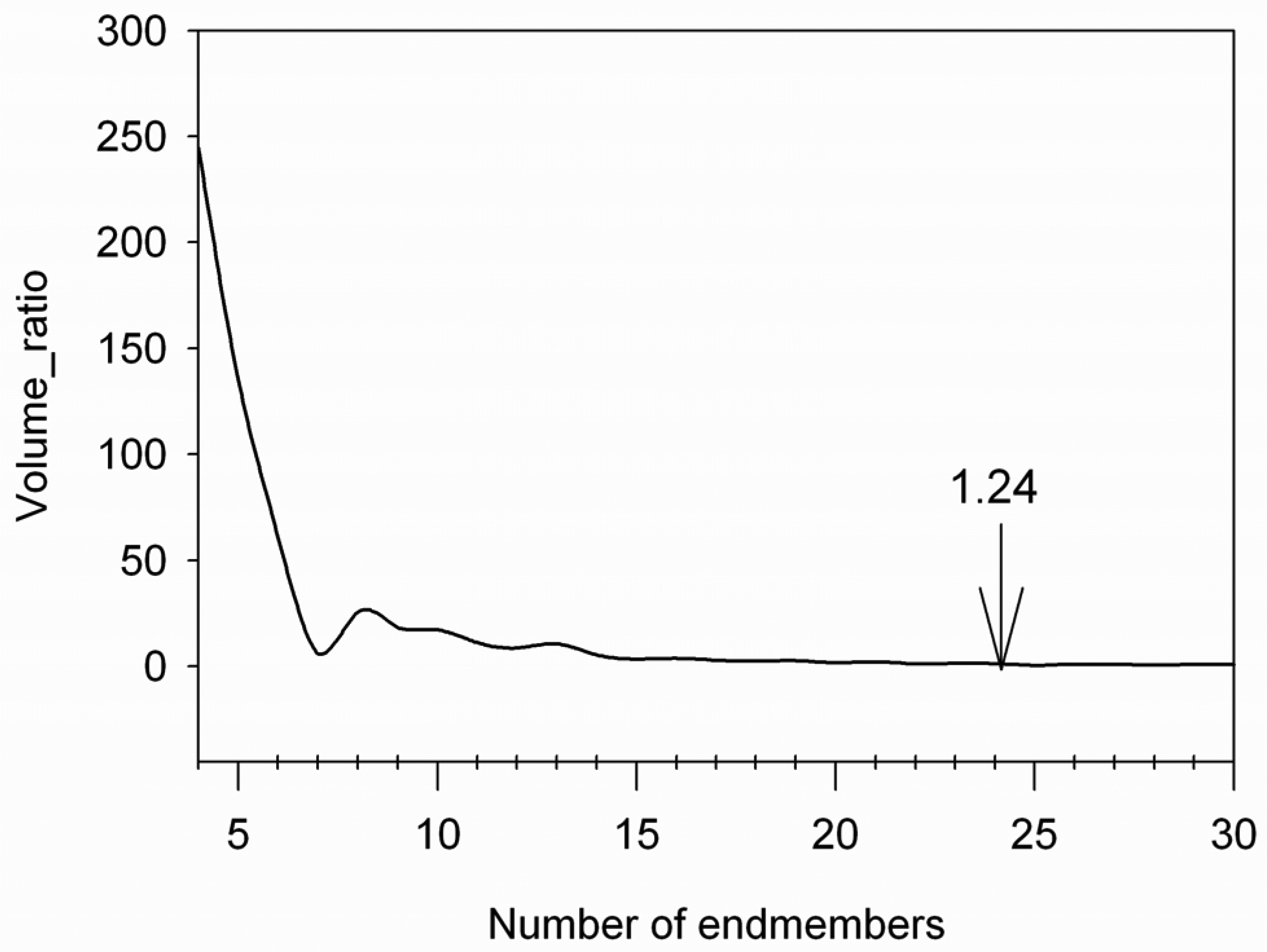
- The endmember matrix, U = [e⃗1, e⃗2, e⃗3], is then updated and Step 4 repeated to define a new endmember. This step is repeated until the predetermined number (m) of endmembers is reached.We calculate the change of the simplex volume with each subspace projection because it provides an insight on the convergence of the algorithm. The volume of the simplex can be calculated only when the simplex has more than 3 vertices. According to Property 1, the complete endmember set defines a simplex with the maximum volume, assuming that a simplex can fit the hyperspectral data perfectly. Thus, as a new endmember is estimated from the data, a new vertex is added to the simplex defined by the previous endmembers, and the volume of the simplex increases until the requested number of endmembers is reached. The volume increase is determined by the spectral contrast between the current endmember and the previously defined endmember set. Assuming data with m endmembers, if Cl–1 and Cl denote the simplexes defined by the current endmember set, {e⃗1,e⃗2, ⋯, e⃗l-1, e⃗l} and the previous endmember set {e⃗1,e⃗2, ⋯,e⃗l-1}, the ratio of the volumes of Cl and Cl–1 can be calculated asAs endmembers are selected (e.g. the value of l is approaching m), the ν_ratiol decreases and theoretically converges to 1.0 if the simplex can fit the hyperspectral data very well [32]. The noise level and the complexity of the data will impact how quickly the volume ratio (ν_ratiol) converges and whether it converges to 1.0.
4. Description of the test data
4.1. AVIRIS data for Cuprite
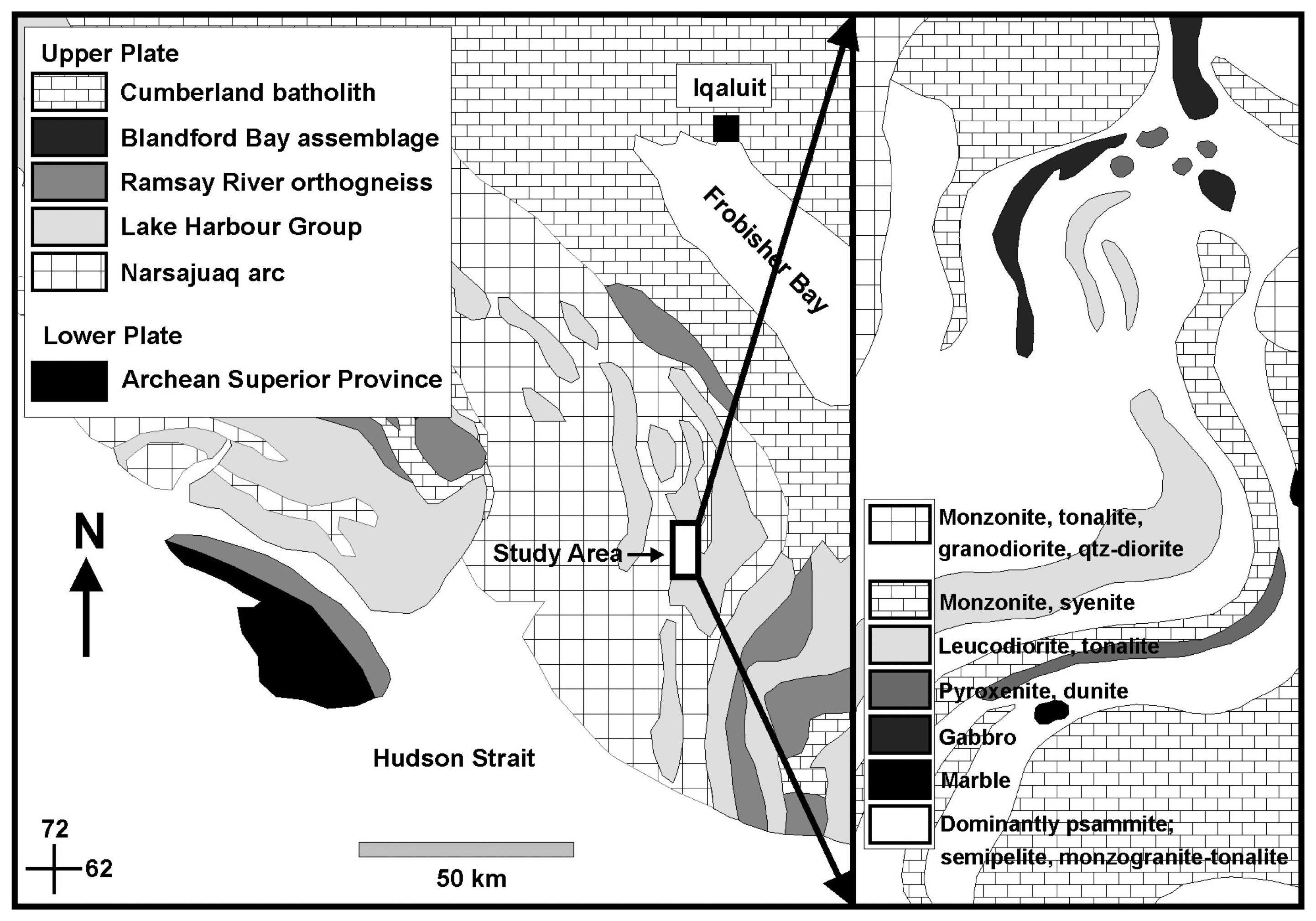
4.2. Probe-1 data for Baffin Island
5. Results
5.1. AVIRIS data for Cuprite
Comparison with PPI endmembers validated in the literature
Merits of the spatial constraint
Changes in simplex volume
5.2. Probe-1 data for Baffin Island
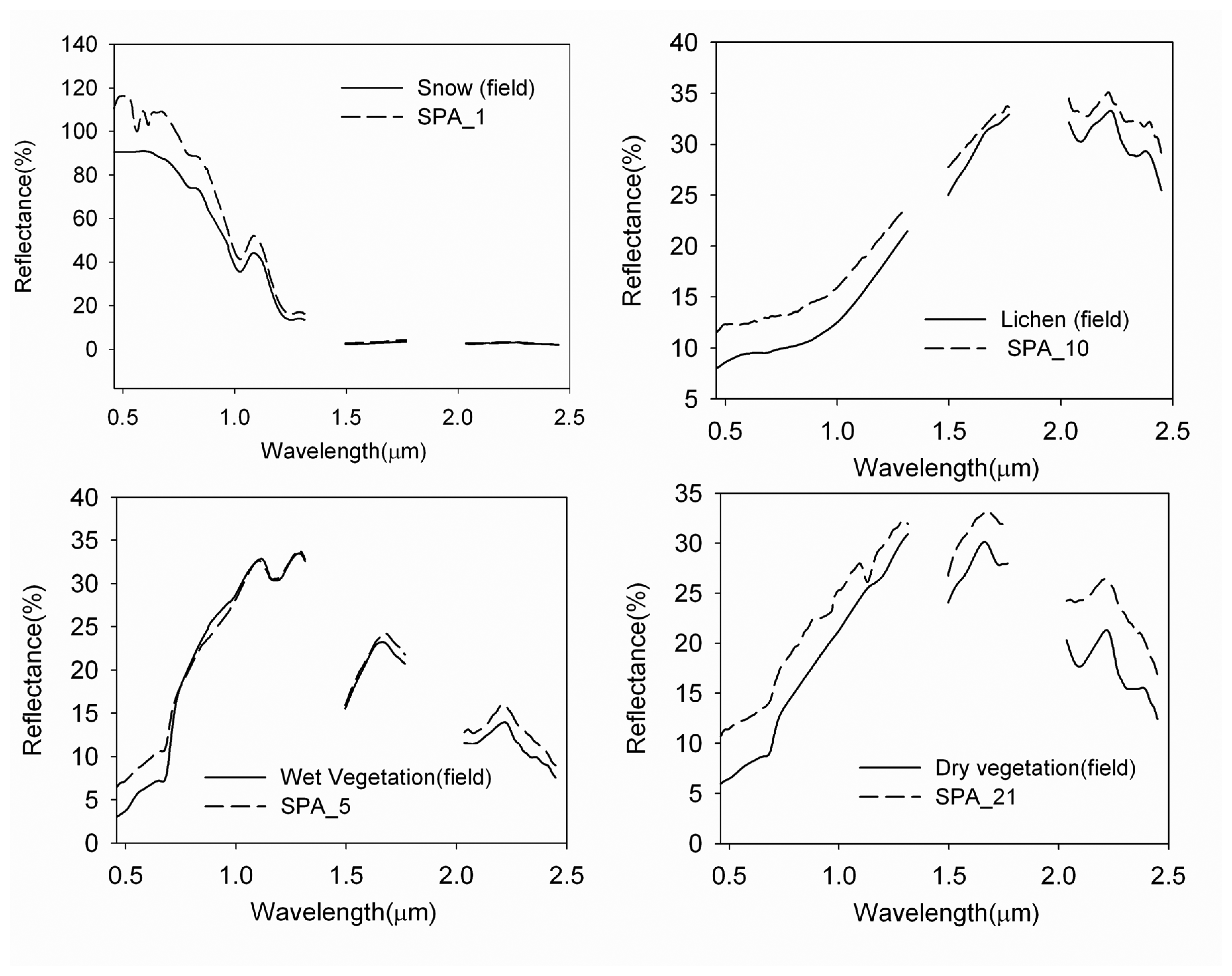
Comparison with spectra collected in the field
Comparison with IEA image endmembers
Changes in simplex volume
6. Discussion and future work
Acknowledgments
References and Notes
- Clark, R.N.; Gallagher, A.J.; Swayze, G.A. Material absorption band depth mapping of imaging spectrometer data using a complete band shape least-squares fit with library reference spectra. In Proceedings 2ndAirborne Visible/Infrared Imaging Spectrometer (AVIRIS) Workshop; JPL Publication; Volume 90-54, 1990; pp. 176–186. [Google Scholar]
- Kruse, F. A.; Huntington, J. H. The 1995 Geology AVIRIS Group Shoot. Proceedings of the Sixth Annual JPL Airborne Earth Science Workshop, JPL publication 96-4 1996, 1, 155–166. [Google Scholar]
- Ben-Dor, E.; Kruse, F.A. Surface mineral mapping of Makhtesh Ramon Negev, Israel using GER 63 channel scanner data. International Journal of Remote Sensing 1995, 16, 3529–3553. [Google Scholar]
- Mustard, J.F.; Pieters, C.M. Abundance and distribution of ultramafic microbreccia in Moses Rock dike: Quantitative application of mapping spectroscopy. Journal of Geophysical Research 1987, 92(B10), 10376–10390. [Google Scholar]
- Murphy, R.J. Mapping of jasperiod in the Cedar Mountains, Utah, U.S.A., using imaging spectrometer data. International Journal of Remote Sensing 1995, 16, 1021–1041. [Google Scholar]
- Bierwirth, P.; Blewett, R.; Huston, D. Finding new mineral prospects with HYMAP: early results from a hyperspectral remote-sensing case study in the west Pilbara. AGSO Research Newsletter. 31 November 1999. http://www.ga.gov.au/pdf/Corp0038.pdf.
- Asner, G.P.; Heidebrecht, K.B. Spectral unmixing of vegetation, soil and dry carbon cover in arid regions: comparing multispectral and hyperspectral observations. International Journal of Remote Sensing 2002, 23, 3939–3958. [Google Scholar]
- Neville, R.A.; Levesque, J.; Staenz, K.; Nadeau, P.; Hauff, P.; Borstad, G.A. Spectral unmixing of hyperspectral imagery for mineral exploration: comparison of results from SFSI and AVIRIS. Canadian Journal of Remote Sensing 2003, 29, 99–110. [Google Scholar]
- Adams, J.B.; Gillespie, A. R. Remote sensing of landscapes with spectral images: A physical modeling approach; Cambridge University Press: New York, 2006; p. 362. [Google Scholar]
- Boardman, J. W.; Kruse, F. A.; Green, R. O. Mapping target signatures via partial unmixing of AVIRIS data. In Summaries, Fifth JPL Airborne Earth Science Workshop; JPL Publication 95-1, 1995; vol. 1, pp. 23–26. [Google Scholar]
- Boardman, J.W. Automating spectral unmixing of AVIRIS data using convex geometry concepts. Summaries of the fourth Annual JPL airborne Geoscience Workshop, JPL Publication 93-26 1993, vol. 1, 11–14. [Google Scholar]
- Winter, M. E. N-FINDR: An algorithm for fast autonomous spectral end-member determination in hyperspectral data. Descour, M. R., Shen, S. S., Eds.; Imaging Spectrometry V; In Proceedings of SPIE; vol. 3753, 1999; Denver, USA; pp. 266–275. [Google Scholar]
- Neville, R. A.; Staenz, K.; Szeredi, T.; Lefebvre, J.; Hauff, P. Automatic endmember extraction from hyperspectral data for mineral exploration. In Proceedings of Fourth International Airborne Remote Sensing Conference and Exhibition / 21st Canadian Symposium on Remote Sensing; vol. 2, Ottawa, Canada, 1999; pp. 891–897. [Google Scholar]
- Nascimento, J.M.P.; Dias, J.M.B. Vertex component analysis: a fast algorithm to unmix hyperspectral data. IEEE Transactions on Geoscience and Remote Sensing 2005, 43, 898–910. [Google Scholar]
- Bajorski, P.; Schott, J.; Ientilucci, E. Comparison of Basis-Vector Selection Methods for Target and Background Subspaces as Applied to Subpixel Target Detection. Shen, S. S., Lewis, P. E., Eds.; In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery X, Proceedings of SPIE; vol. 5425, Orlando, USA, 2004; pp. 97–108. [Google Scholar]
- Gruninger, J. H.; Ratkowski, A. J.; Hoke, M. L. The sequential maximum angle convex cone (SMACC) endmember model. Shen, S. S., Lewis, P. E., Eds.; In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery X, Proceedings of SPIE; Volume 5425, Orlando, USA, 2004; pp. 1–14. [Google Scholar]
- Berman, M.; Kiiveri, H.; Lagerstrom, R.; Ernst, A.; Dunne, R.; Huntington, J. 2004. ICE: An automated statistical approach to identifying endmembers in hyperspectral images. IEEE Transactions on Geoscience and Remote Sensing 2004, 42, 2085–2095. [Google Scholar]
- Chang, C.-I.; Wu, C.-C.; Liu, W.-W.; Ouyang, Y.-C. A new growing method for simplex-based endmember extraction algorithm. IEEE Transactions on Geoscience and Remote Sensing 2006, 44, 2804–2819. [Google Scholar]
- Miao, L.; Qi, H. Endmember extraction from highly mixed data using minimum volume constrained nonnegative matrix factorization. IEEE Transactions on Geoscience and Remote Sensing 2007, 45, 765–777. [Google Scholar]
- Bowles, J. H.; Palmadesso, P. J.; Antoniades, J. A.; Baumback, M. M.; Rickard, L. J. Use of filter vectors in hyperspectral data analysis. Strojnik, M., Andresen, B. F., Eds.; In Infrared Spaceborne Remote Sensing, Proceedings of SPIE; vol. 2553, San Diego, USA, 1995; pp. 148–157. [Google Scholar]
- Howes, D. J.; Clare, P. E.; Oxford, W. J.; Murphy, S. Endmember selection techniques for improved spectral unmixing. Shen, S. S., Lewis, P. E., Eds.; In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery X, Proceedings of SPIE, vol. 5425; Orlando, USA; vol. 5425, 2004; pp. 65–76. [Google Scholar]
- Rogge, D.; Rivard, B.; Zhang, J.; Harris, J.; Feng, J.; Sanchez, A. Integration of spatial-spectral information for the improved extraction of endmembers. Remote Sensing of Environment 2007, 110, 287–303. [Google Scholar]
- Haskell, K.H.; Hanson, R. J. An algorithm for linear least squares problems with equality and non-negativity constraints. Mathematical Programming 1981, 21, 98–118. [Google Scholar]
- Shimabukuro, Y.E.; Smith, J.A. The least squares mixing models to generate fraction images derived from remote sensing on multispectral Data. IEEE Transactions on Geoscience and Remote Sensing 1991, 29, 16–20. [Google Scholar]
- Bajorski, P. Stepwise simplex projection method for the selection of endmembers in hyperspectral images. Shen, S. S., Lewis, P. E., Eds.; In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XI, Proceedings of SPIE; Volume 5806, Orlando, USA, 2005; pp. 318–329. [Google Scholar]
- Gritzmann, P.; Klee, V. On the Complexity of Some Basic Problems in Computational Convexity: II. Volume and Mixed Volumes. In Technical Report TR94 -31; DIMACS, Rutgers University: New Brunswick, NJ, 1994. [Google Scholar]
- Winter, M. E. A proof of the N-FINDR algorithm for the automated detection of end-members in a hyperspectral image. Shen, S. S., Lewis, P. E., Eds.; In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XI, Proceedings of SPIE; Orlando, USA; Vol. 5425, 2004; pp. 31–41. [Google Scholar]
- Lee, K. A subpixel scale target detection algorithm for hyperspectral imagery. PhD. dissertation, Rochester Institute of Technology, 54 Lomb Memorial Drive, Rochester, NY, 2003. [Google Scholar]
- Green, A.A.; Berman, M.; Switzer, P.; Craig, M.D. A transformation for ordering multispectral data in terms of image quality with implications for noise removal. IEEE Transactions on Geoscience and Remote Sensing 1988, 26, 65–74. [Google Scholar]
- Plaza, A.; Martinez, P.; Perez, R.; Plaza, J. A quantitative and comparative analysis of endmember extraction algorithms from hyperspectral data. IEEE Transactions on Geoscience and Remote Sensing 2004, 42, 650–663. [Google Scholar]
- Plaza, A.; Chang, C. An improved N-FINDER algorithm in Implementation. Shen, S. S., Lewis, P. E., Eds.; In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XI, Proceedings of SPIE; vol. 5806, Orlando, USA, 2005; pp. 298–306. [Google Scholar]
- Turner, J.F., II; Zhang, J.; O'Connor, A. A spectral identity mapper for chemical image analysis. Applied spectroscopy 2004, 58, 1308–1317. [Google Scholar]
- Grande, B.; Manne, R. Use of convexity for finding pure variables in two-way data from mixtures. Chemometrics and intelligent laboratory systems 2000, 50, 19–33. [Google Scholar]
- Gao, B.C.; Goetz, A.F.H. Column atmospheric water vapor and vegetation liquid water retrievals from airborne imaging spectrometer data. Journal of Geophysical Research 1990, 95, 3549–3564. [Google Scholar]
- Boardman, J. W. Post-ATREM polishing of AVIRIS apparent reflectance data using EFFORT: a lesson in accuracy versus precision. In Summaries of the Seventh JPL Airborne Earth Science Workshop; JPL Publication 99-17, 1998; vol. 1, p. 53. [Google Scholar]
- Abrams, M.J.; Ashley, R.P.; Rowan, L.C.; Goetz, A.F.H.; Kahle, A.B. Mapping of hydrothermal alteration in the Cuprite Mining District, Nevada, using aircraft scanner images for the spectral region 0.46–2.36μm. Geology 1977, 5, 713–718. [Google Scholar]
- Kruse, F.A.; Kierein-Young, K. S.; Boardman, J. W. Mineral mapping at Cuprite, Nevada with a 63 channel imaging spectrometer. Photogrammetric Engineering and Remote Sensing 1990, 56, 83–92. [Google Scholar]
- Hook, S.J.; Rast, M. Mineralogic mapping using Airborne Visible Infrared Imaging Spectrometer (AVIRIS), Shortwave Infrared (SWIR) data acquired over Cuprite, Nevada. Green, R.O., Ed.; In Proceedings of the Second Airborne Visible Infrared Imaging Spectrometer (AVIRIS) Workshop, JPL Publication 90-54; 1990; pp. 199–207. [Google Scholar]
- Clark, R.N.; Swayze, G.A.; Gallagher, A. Mapping Minerals with Imaging Spectroscopy. U.S. Geological Survey, Office of Mineral Resources Bulletin 1993, 2039, 141–150. [Google Scholar]
- Swayze, G.A.; Clark, R.N.; Kruse, F.; Sutley, S.; Gallagher, A. Ground-Truthing AVIRIS Mineral Mapping at Cuprite, Nevada. Summaries of the Third Annual JPL Airborne Geosciences Workshop, Volume 1: AVIRIS Workshop. JPL Publication 92-14 1992, 47–49. [Google Scholar]
- Lewry, J.F.; Stauffer, M.R. The early Proterozoic Trans-Hudson Orogen of North America; Geological Association of Canada, 1990; Vol. 37, p. 505. [Google Scholar]
- St-Onge, M.R.; Wodicka, N.; Lucas, S.B. Geology of McKeller Bay-Wight Inlet – Frobisher Bay area, southern Baffin Island, Northwest Territories: Current Research, 1998-C. Geological Survey of Canada 1999, 43–53. [Google Scholar]
- St-Onge, M.R.; Wodicka, N.; Scott, D.J. Review of crustal architecture and evolution in the Ungava Peninsula – Baffin Island area: connection to the lithoprobe ECSOOT transect. Canadian Journal of Earth Sciences 2002, 39, 589–610. [Google Scholar]
- Clark, R.N.; Swayze, G.A.; Livo, K.E.; Kokaly, R.F.; Sutley, S.J.; Dalton, J.B.; McDougal, R.R.; Gent, C.A. Imaging spectroscopy: Earth and planetary remote sensing with the USGS Tertracorder and expert systems. Journal of Geophysical Research 2003, 108(E12), 5-1–5-14. [Google Scholar]
- Clark, R. N. Chapter 1: Spectroscopy of Rocks and Minerals, and Principles of Spectroscopy. In in Manual of Remote Sensing, Volume 3, Remote Sensing for the Earth Sciences; Rencz, A.N., Ed.; John Wiley and Sons: New York, 1999. [Google Scholar]
- Barducci, A.; Mecocci, A. Theoretical and experimental assessment of noise effects on least-squares spectral unmixing of hyperspectral images. Optical Engineering 2005, 44, 087008-1–087008-17. [Google Scholar]
- Chang, C.-I. Hyperspectral imaging : Techniques for spectral detection and classification; Plenum Publishing Co., 2003; p. 370p. [Google Scholar]




| SPA endmember | PPI-endmember (“truth”) |
|---|---|
| SPA_1, SPA-17 | Silicate (bright) |
| SPA_16 | Silica (dark) |
| SPA_4 | Alunite 1 (2.16 μm) |
| SPA_12, SPA_15 | Alunite 2(2.18 μm) |
| SPA_8 | Buddingtonite |
| SPA_3, SPA_14 | Kaolinite |
| SPA_6 | Calcite |
| SPA_5 | Zeolite |
| SPA_7, SPA_10, SPA_11, SPA_13 | Muscovite/illite |
| *SPA_9 | Na |
| **SPA_2, SPA_18, SPA_19 | Na |
| SPA Endmember | Label |
|---|---|
| 1, 4, 8, 9, 13, 14, 15, 17, 19, 20, 24, 26, 27 | Snow |
| 2 | Water |
| 3 | Felsic (Granite/varnish) |
| 5 | Vegetation (wet) |
| 6 | Marble |
| 7 | Shade |
| 10, 18, 25, 29 | Lichen |
| 11 | Peridotite |
| 12 | Fe-metasediment |
| 16 | Clay-metasediment |
| 21 | Dry vegetation |
| 22 | Quartzite |
| 23 | Marble (low albedo) |
| 28 | Quartzite (low albedo) |
| 30 | Peridotite |
| Rock_type | IEA endmember | SPA endmember |
|---|---|---|
| Felsic (Granite/varnish) | IEA_3 | SPA_3 |
| Marble | IEA_7, IEA_22 (Similar but differ in amplitude) | SPA_6, SPA_23 (Similar but differs in amplitude) |
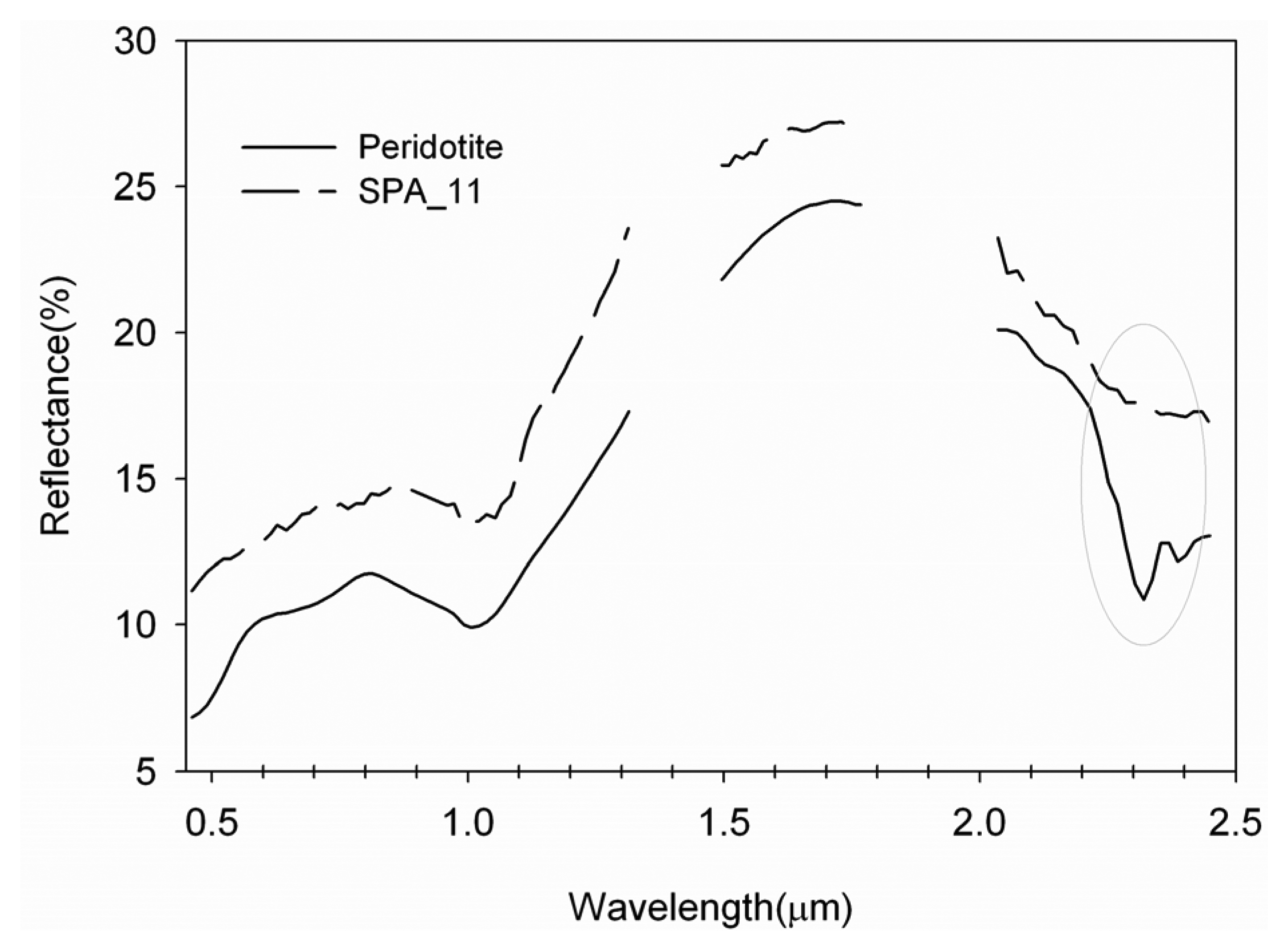
| Peridotite | IEA_14 | *SPA_11, SPA_30 |
| Fe-metasediment | IEA_19 | SPA_12 |
| Clay-metasediment | IEA_13 | SPA_16 |
| Metasediment | IEA_28 | Missing |
| Quartzite | IEA_30 | SPA_22, SPA_28 (Similar but differs in amplitude) |
© 2008 by MDPI Reproduction is permitted for noncommercial purposes.
Share and Cite
Zhang, J.; Rivard, B.; Rogge, D.M. The Successive Projection Algorithm (SPA), an Algorithm with a Spatial Constraint for the Automatic Search of Endmembers in Hyperspectral Data. Sensors 2008, 8, 1321-1342. https://doi.org/10.3390/s8021321
Zhang J, Rivard B, Rogge DM. The Successive Projection Algorithm (SPA), an Algorithm with a Spatial Constraint for the Automatic Search of Endmembers in Hyperspectral Data. Sensors. 2008; 8(2):1321-1342. https://doi.org/10.3390/s8021321
Chicago/Turabian StyleZhang, Jinkai, Benoit Rivard, and D. M. Rogge. 2008. "The Successive Projection Algorithm (SPA), an Algorithm with a Spatial Constraint for the Automatic Search of Endmembers in Hyperspectral Data" Sensors 8, no. 2: 1321-1342. https://doi.org/10.3390/s8021321




