Effects of van der Waals Force and Thermal Stresses on Pull-in Instability of Clamped Rectangular Microplates
Abstract
:1 Introduction
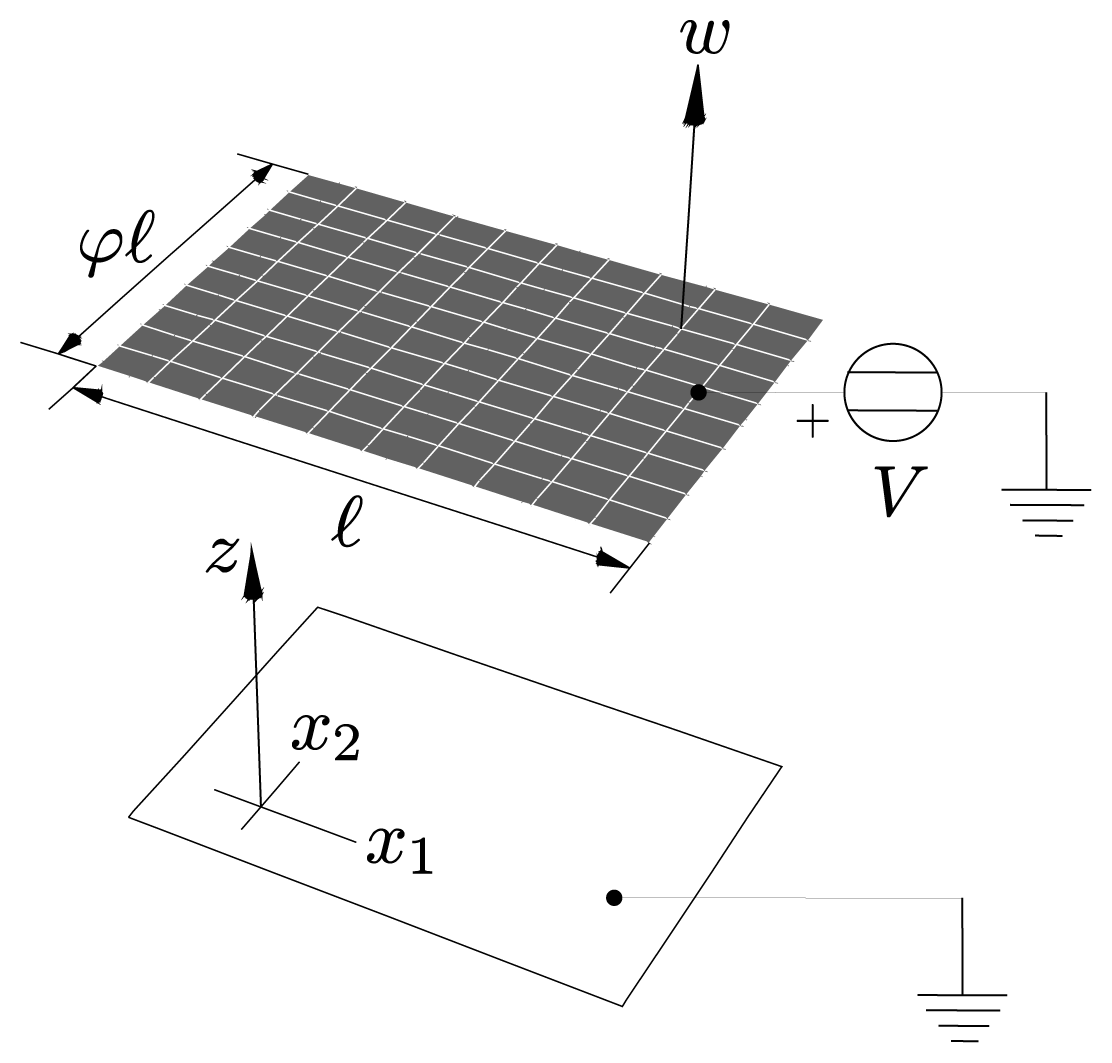
2 Problem statement
3 Reduced-order model
3.1 Basis functions for in-plane displacement
3.2 Relation between ξ, and ζ
3.3 Governing equations of the reduced-order model
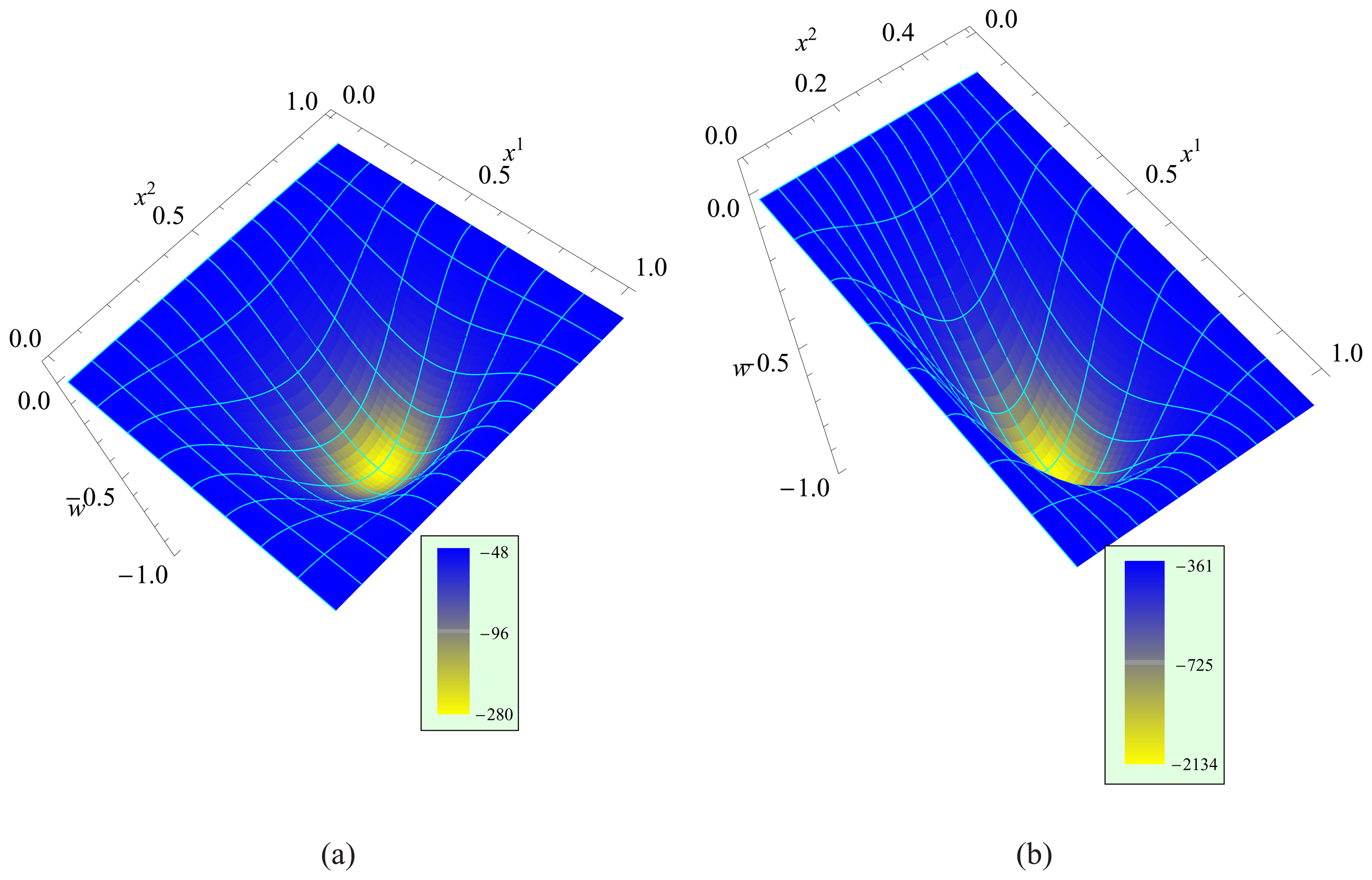
3.4 Extraction of pull-in parameters from the static problem
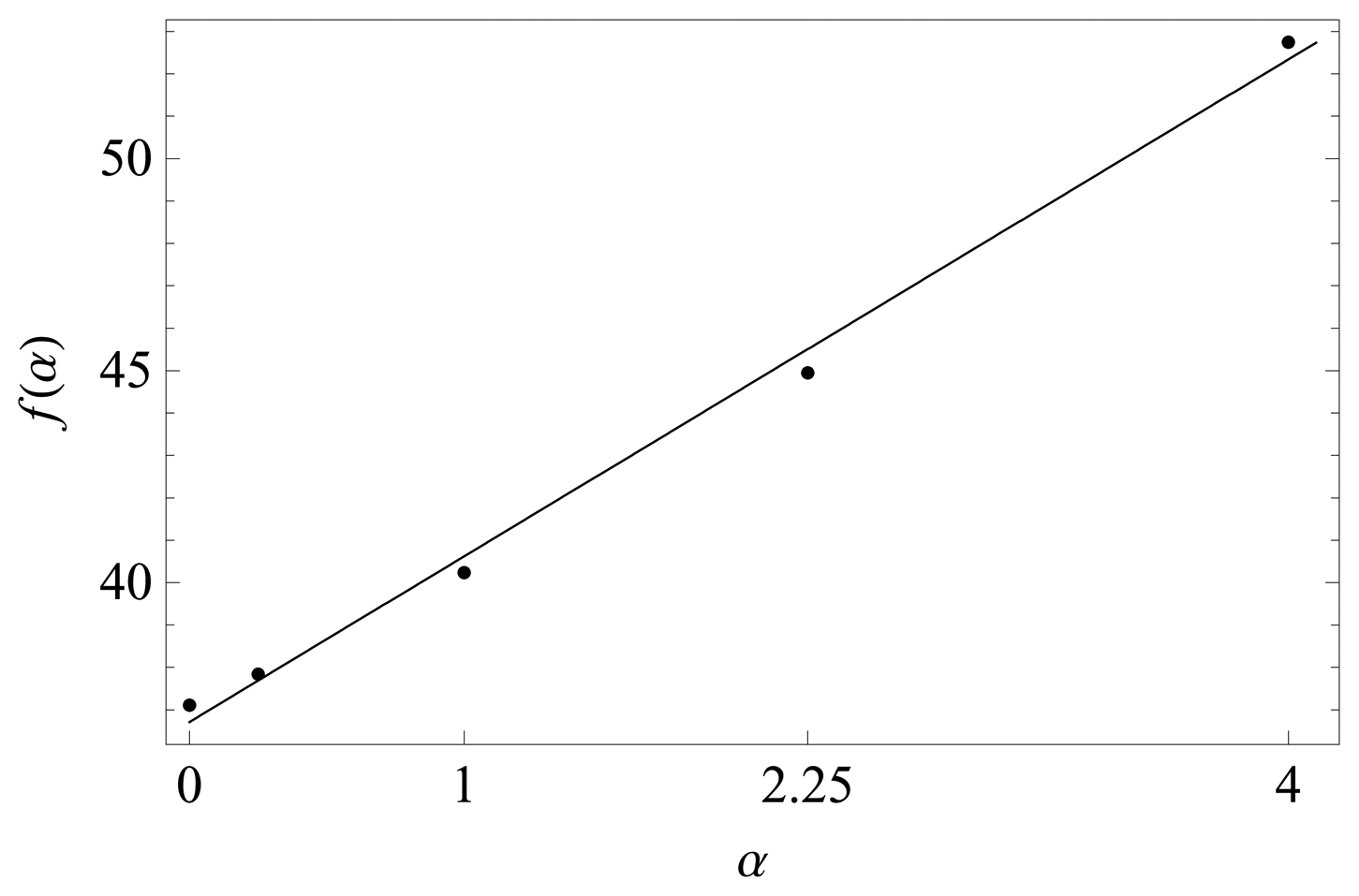
3.5 Buckling thermal stress parameter from the static problem
3.6 Extraction of pull-in parameters from the linear eigenvalue problem
4 Results and discussion
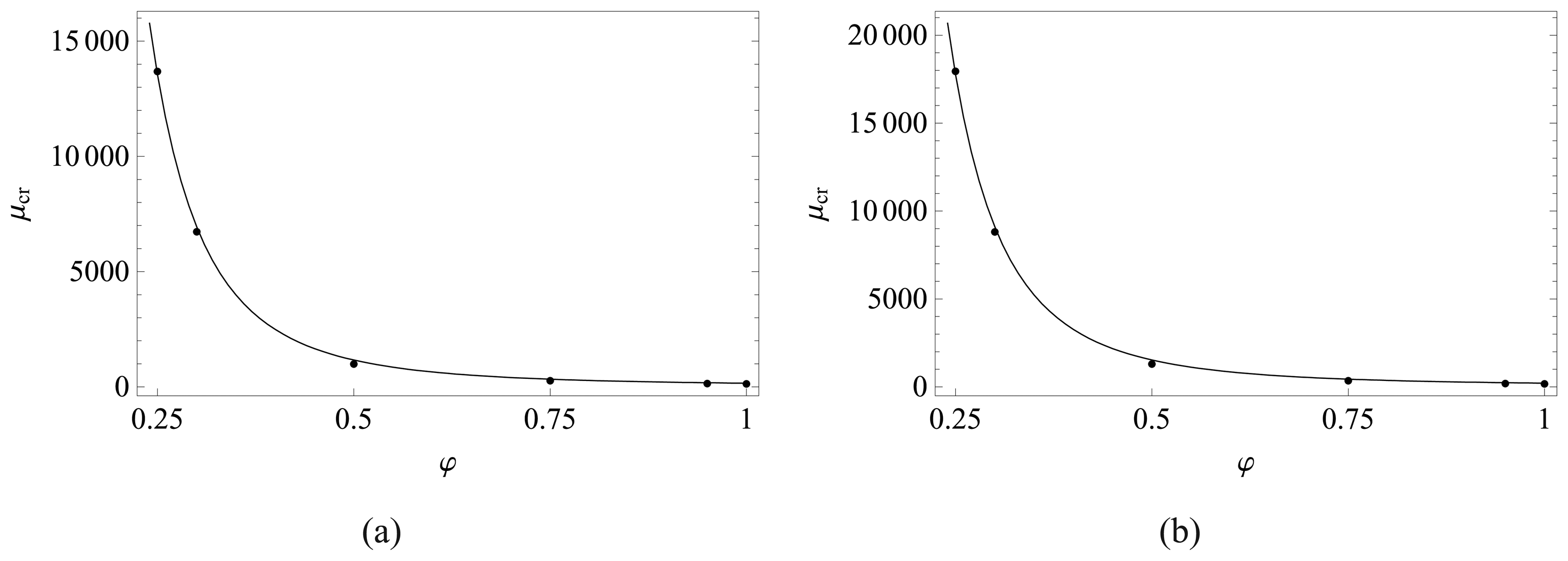
4.1 Critical value of van der Waals force parameter
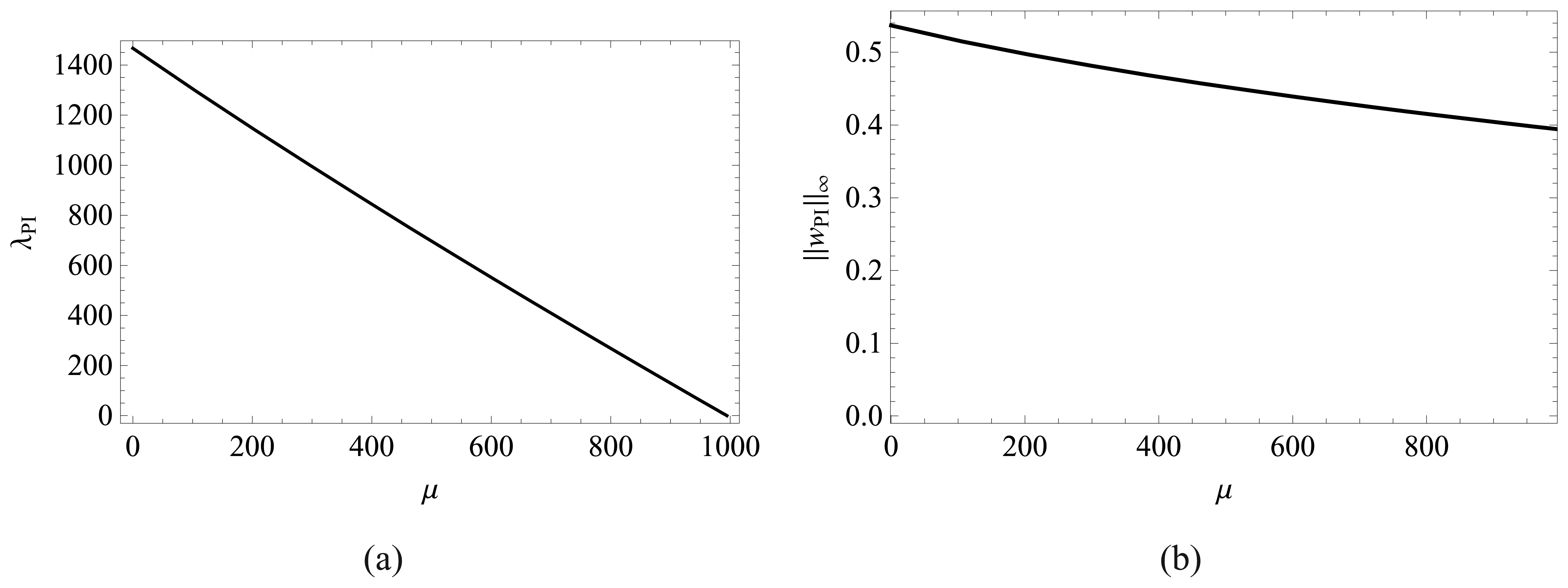
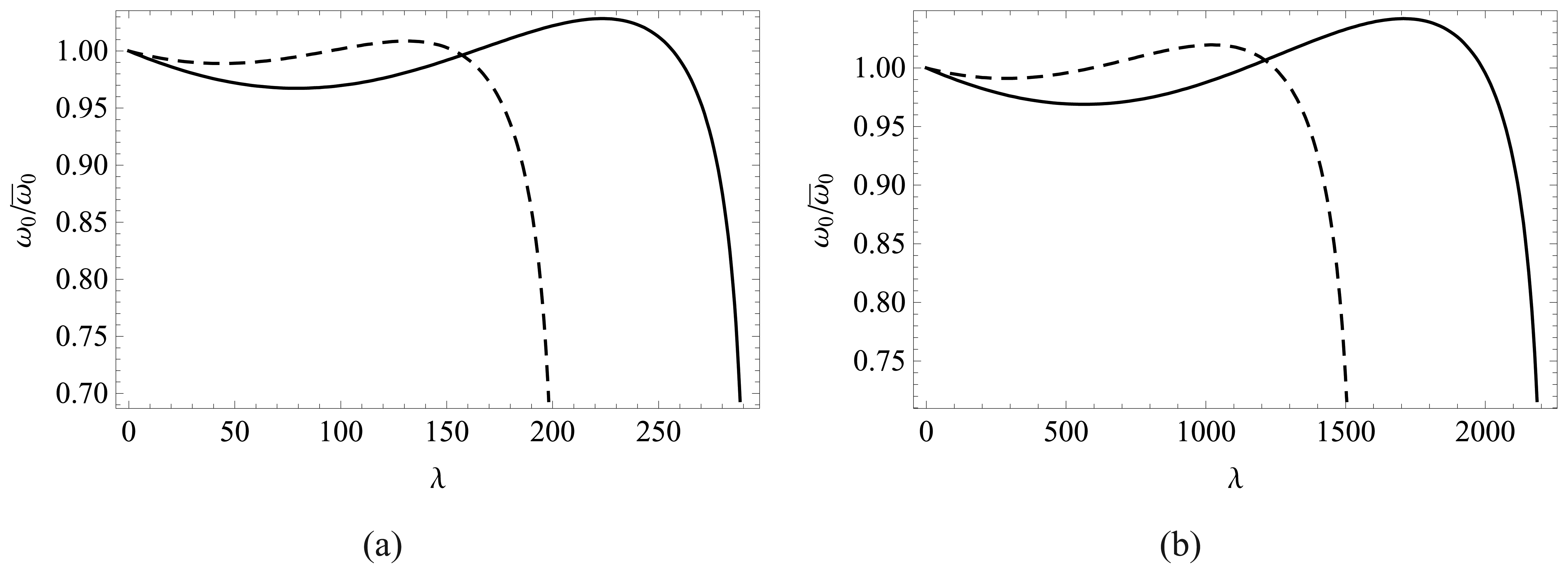
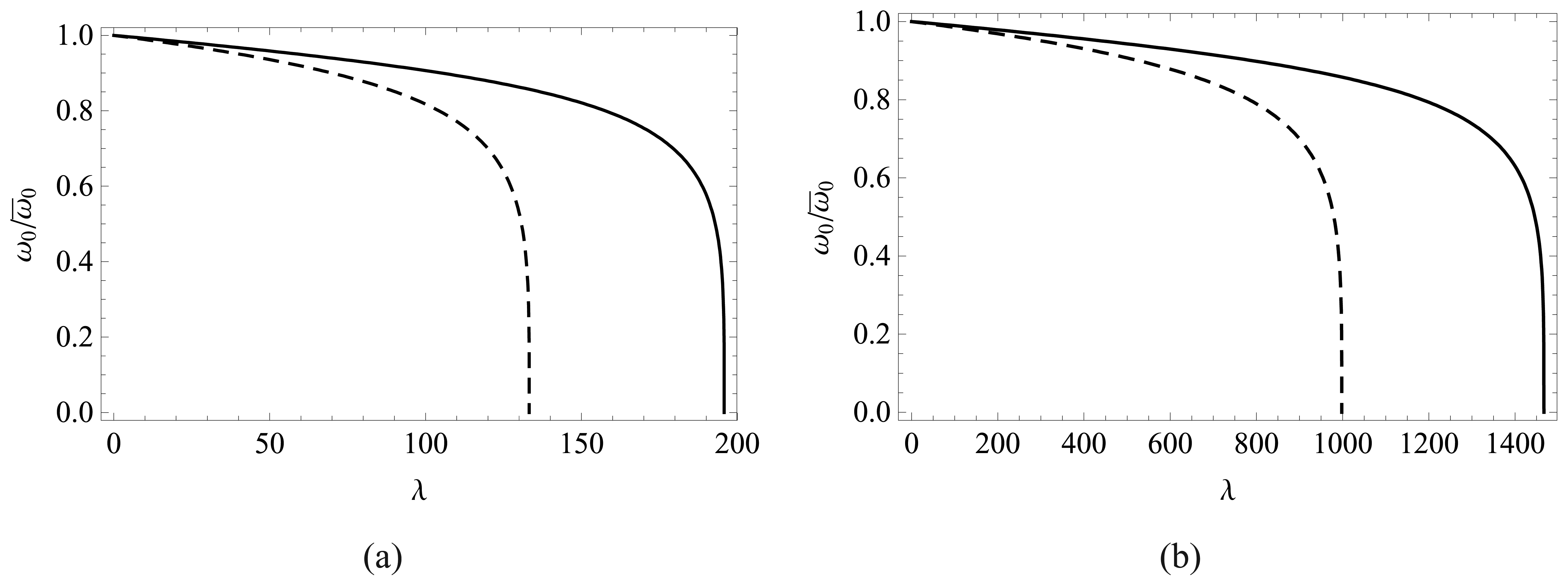
4.2 Effect of van der Waals force on pull-in parameters
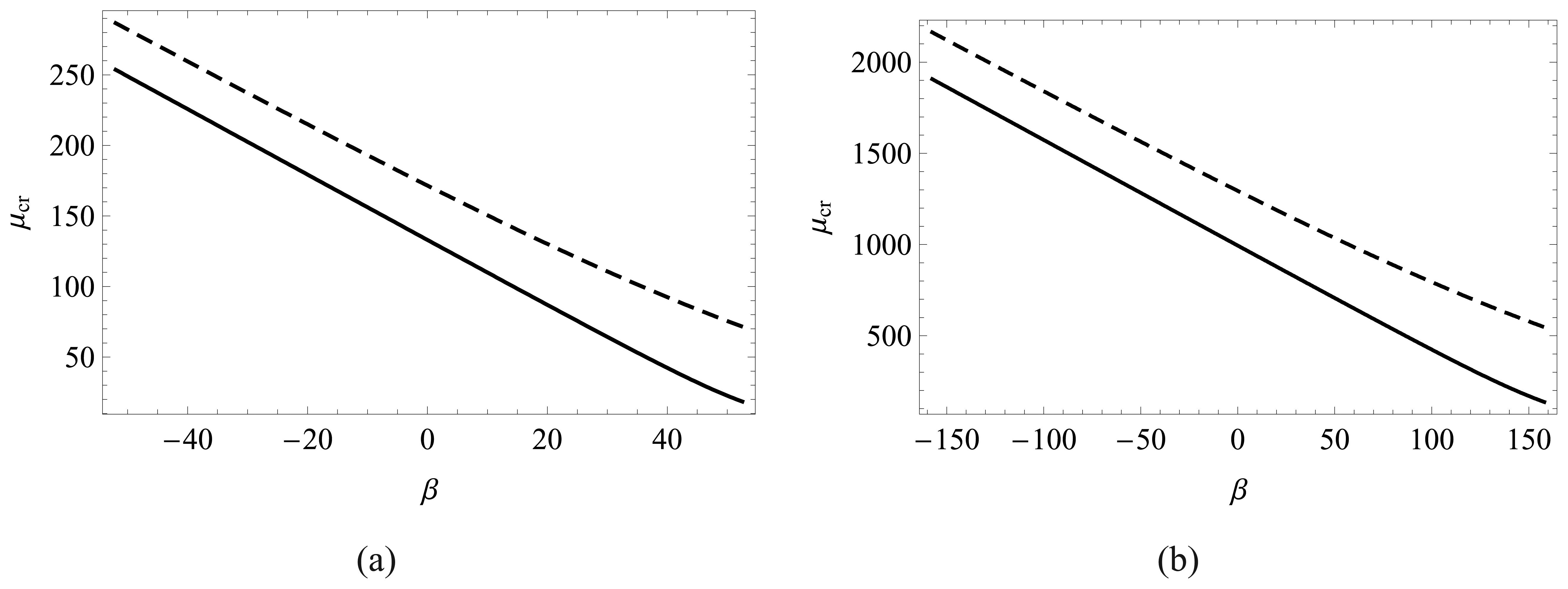
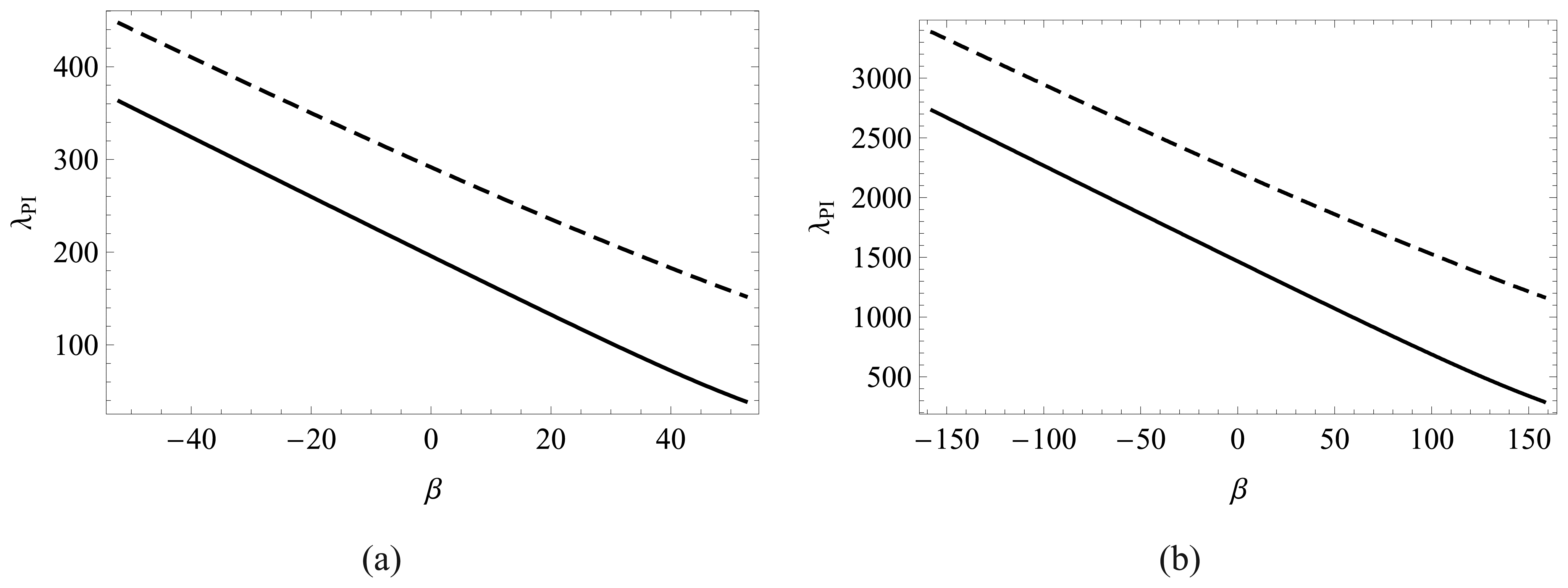
4.3 Effect of thermal stress on pull-in and critical van der Waals force parameters
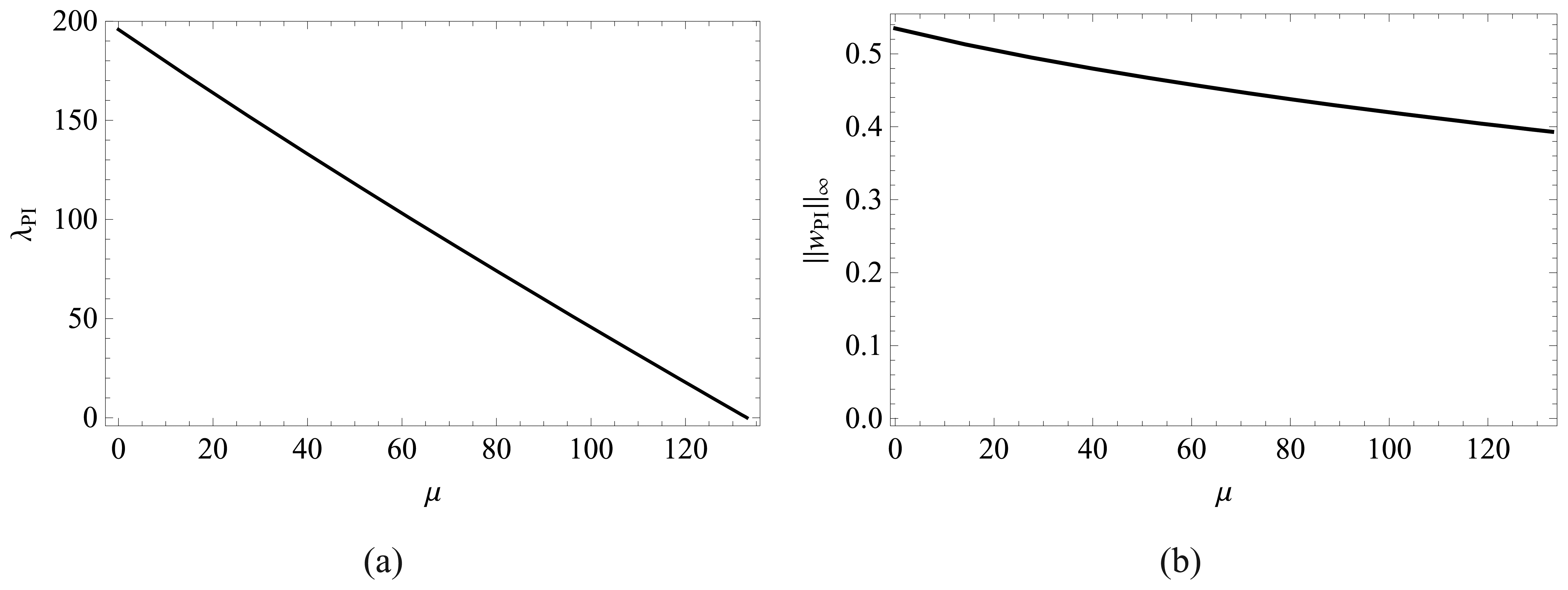
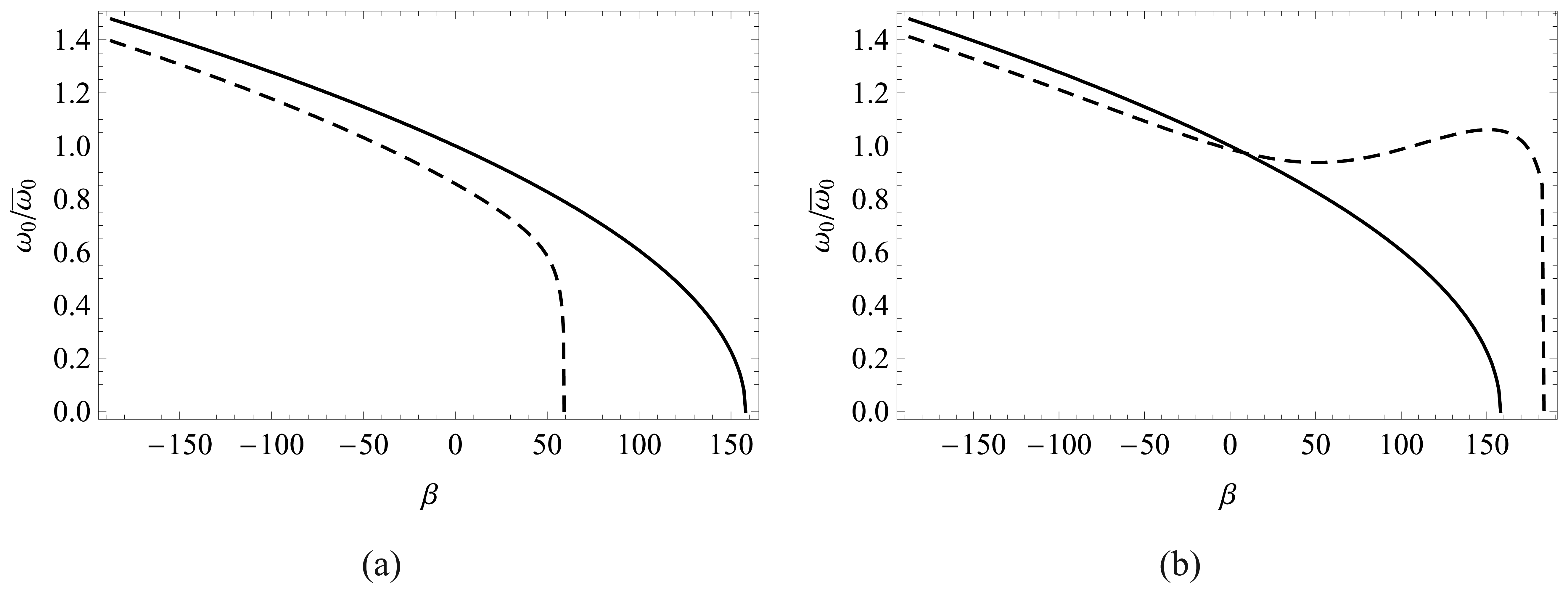
4.4 Pull-in parameters from the analysis of frequencies of a deformed plate
4.5 Effect of thermal stress on the fundamental frequency of predeformed plates
5 Conclusions
Acknowledgments
References
- Abeysinghe, D. C.; Dasgupta, S.; Jackson, H. E.; Boyd, J. T. Novel MEMS pressure and temperature sensors fabricated on optical fibers. Jornal of Micromechanics and Microengineering 2002, 72, 229–235. [Google Scholar]
- Burns, D.; Zook, J.; Horning, R.; Herb, W.; Guckel, H. Sealed-cavity resonant microbeam pressure sensor. Sensors and Actuators A 1995, 48(3), 179–186. [Google Scholar]
- Gupta, R. K.; Senturia, S. D. Pull-in time dynamics as a measure of absolute pressure, Proceedings IEEE International Workshop on Microelectromechanical Systems (MEMS′97), Nagoya, Japan, January 1997; pp. 290–294.
- Howe, R. T.; Muller, R. S. Resonant-microbridge vapor sensor. IEEE Transactions on Electronics Devices 1986, 33, 499–Wo506. [Google Scholar]
- Osterberg, P. M.; Senturia, S. D. M-TEST: A test chip for MEMS material property measurement using electrostatically actuated test structures. Journal of Microelectromechanical Systems 1997, 6(2), 107–118. [Google Scholar]
- Nguyen, C. T. C.; Katehi, L. P. B.; Rebeiz, G. M. Micromachined devices for wireless communications. Proceedings of the IEEE 1998, volume 86, 1756–1768. [Google Scholar]
- Xie, W. C.; Lee, H. P.; Lim, S. P. Nonlinear dynamic analysis of MEMS switches by nonlinear modal analysis. Nonlinear Dynamics 2003, 31, 243–256. [Google Scholar]
- Batra, R. C.; Porfiri, M.; Spinello, D. Review of modeling electrostatically actuated microelec-tromechanical systems. Smart Materials and Structures 2007, 16, R23–R31. [Google Scholar]
- Pelesko, J. A.; Bernstein, D. H. Modeling MEMS and NEMS; Chapman & Hall: Boca Raton, Fla, November 2002; Chapter 7. [Google Scholar]
- Taylor, G. I. The coalescence of closely spaced drops when they are at different electric potentials. Proceedings of the Royal Society A 1968, 306, 423–434. [Google Scholar]
- Nathanson, H. C.; Newell, W. E.; Wickstrom, R. A.; Davis, J. R. The resonant gate transistor. IEEE Transactions on Electron Devices 1967, 14(3), 117–133. [Google Scholar]
- Hung, E. S.; Senturia, S. D. Extending the travel range of analog-tuned electrostatic actuators. Journal of Microelectromechanical Systems 1999, 8(4), 497–505. [Google Scholar]
- Tilmans, H. A.; Legtenberg, R. Electrostatically driven vacuum-encapsulated polysilicon res-onators: Part I. Design and fabrication. Sensors and Actuators A 1994, 45, 57–66. [Google Scholar]
- Pelesko, J.; Triolo, A. Nonlocal problems in MEMS device control. Journal of Engineering Mathematics 2001, 41(4), 345–366. [Google Scholar]
- Timoshenko, S. Theory of ElasticityMcGraw-Hill Companies: New York, 3rd edition; 1970. [Google Scholar]
- Francais, O.; Dufour, I. Normalized abacus for the global behavior of diaphragms: pneumatic, electrostatic, piezoelectric or electromagnetic actuation. Journal of Modeling and Simulation of Microsystems 1999, 2, 149–160. [Google Scholar]
- Ng, T. Y.; Jiang, T. Y.; Lam, K. Y.; Reddy, J. N. A coupled field study on the non-linear dynamic characteristics of an electrostatic micropump. Journal of Sound and Vibration 2004, 273, 989–1006. [Google Scholar]
- Zhao, X.; Abdel-Rahman, E. M.; Nayfeh, A. H. A reduced-order model for electrically actuated microplates. Journal of Micromechanics and Microengineering 2004, 14(7), 900–906. [Google Scholar]
- Vogl, G. W.; Nayfeh, A. H. A reduced-order model for electrically actuated clamped circular plates. Journal of Micromechanics and Microengineering 2005, 15, 684–690. [Google Scholar]
- Batra, R. C.; Porfiri, M.; Spinello, D. Reduced-order models for microelectromechanical rect-angular and circular plates incorporating the Casimir force. International Journal of Solids and Structures. Accepted.
- Batra, R. C.; Porfiri, M.; Spinello, D. Vibrations and pull-in instabilities of microelectromechanical von Kármán elliptic plates incorporating the Casimir force. Journal of Sound and Vibration. In press.
- Porfiri, M. Vibrations of parallel arrays of electrostatically actuated microplates. Journal of Sound and Vibration 2008. In press. [Google Scholar]
- Juillard, J.; Colinet, E. Modelling of nonlinear circular plates using modal analysis: simulation and model validation. Journal of Micromechanics and Microengineering 2006, 16, 448–456. [Google Scholar]
- Mansfield, E. H. The bending & stretching of platesCambridge University Press: Cambridge; New York, 2nd edition; 1989; Chapter 9. [Google Scholar]
- Pelesko, J. A. Mathematical modeling of electrostatic MEMS with tailored dielectric properties. SIAM Journal of Applied Mathematics 2002, 62(3), 888–908. [Google Scholar]
- Pelesko, J. A.; Bernstein, D. H.; McCuan, J. Symmetry and symmetry breaking in electrostatic MEMS. In Proceedings of Modeling and Simulation of Microsystems; pp. 304–307. San Fran-cisco: CA, USA, February 2003. [Google Scholar]
- Pelesko, J. A.; Chen, X. Y. Electrostatic deflections of circular elastic membranes. Journal of Electrostatics 2003, 57, 1–12. [Google Scholar]
- Batra, R. C.; Porfiri, M.; Spinello, D. Analysis of electrostatic MEMS using meshless local Petrov-Galerkin (MLPG) method. Engineering Analysis with Boundary Elements 2006, 30(11), 949–962. [Google Scholar]
- Batra, R. C.; Porfiri, M.; Spinello, D. Effects of Casimir force on pull-in instability in micromem-branes. Europhysics Letters 2007, 77, 20010. [Google Scholar]
- Lamoreaux, S. K. The Casimir force: background, experiments, and applications. Reports on progress in Physics 2005, 68, 201–236. [Google Scholar]
- Bordag, M.; Mohideen, U.; Mostepanenko, V.M. New developments in the Casimir effect. Physics reports 2001, 353, 1–205. [Google Scholar]
- Lifshitz, E.M. The theory of molecular attractive forces between solids. Soviet Physics JETP 1956, 2, 73–83. [Google Scholar]
- Klimchitskaya, G. L.; Mohideen, U.; Mostepanenko, V. M. Casimir and van der Waals forces between two plates or a sphere (lens) above a plate made of real metals. Physical Review A 2000, 61, 062107. [Google Scholar]
- Lin, W.-H.; Zhao, Y.-P. Influence of damping on the dynamical behavior of the electrostatic parallel-plate and torsional actuators with intermolecular forces. Sensors 2007, 7, 3012–3026. [Google Scholar]
- Zhu, Y.; Espinosa, H. D. Reliability of capacitive RF MEMS switches at high and low temperatures. International Journal of RF and Microwave Computer-Aided Engineering 2004, 14, 317–328. [Google Scholar]
- Nayfeh, A. H.; Younis, M. I. Modeling and simulations of thermoelastic damping in microplates. Journal of Micromechanics and Microengineering 2004, 14, 1711–1717. [Google Scholar]
- Nakhaie Jazar, G. Mathematical modeling and simulation of thermal effects in flexural microcan-tilever resonator dynamics. Journal of Vibration and Control 2006, 12(2), 139–163. [Google Scholar]
- Zhu, Y.; Espinosa, H. D. Effect of temperature on capacitive RF MEMS switch performance-a coupled-field analysis. Journal of Micromechanics and Microengineering 2004, 14, 1270–1279. [Google Scholar]
- Rocha, L. A.; Cretu, E.; Wolffenbuttel, R. F. Compensation of temperature effects on the pull-in voltage of microstructures. Sensors and Actuators A 2004, 115, 351–356. [Google Scholar]
- Nieminen, H.; Ermolov, V.; Silanto, S.; Nybergh, K.; Ryhänen, T. Design of a temperature-stable RF MEM capacitor. Journal of Microelectromechanical Systems 2004, 13, 705–714. [Google Scholar]
- Landau, L. D.; Lifshitz, E. M. Theory of elasticity.; Pergamon Press: New York, 1986. [Google Scholar]
- Batra, R. C. Elements of Continuum Mechanics.; AIAA: American Institute of Aeronautics and Astronautics: Reston, VA, 2005. [Google Scholar]
- Krylov, S.; Seretensky, S. Higher order correction of electrostatic pressure and its influence on the pull-in behavior of microstructures. Journal of Micromechanics and Microengineering 2006, 16, 1382–1396. [Google Scholar]
- Bordag, M. Casimir effect for a sphere and a cylinder in front of a plane and corrections to the proximity force theorem. Physical Review D 2006, 73, 125018. [Google Scholar]
- Gies, H.; Klingmuller, K. Casimir effect for curved geometries: Proximity-Force-Approximation validity limits. Physical Review Letters 2006, 96, 220401. [Google Scholar]
- Israelachvili, J. N. Intermolecular and Surface Forces.Academic Press: London, 2nd edition; 1991. [Google Scholar]
- Laliotis, A.; Maurin, I.; Todorov, P.; Hamdi, I.; Dutier, G.; Yarovitski, A.; Saltiel, S.; Gorza, M.-P; Fichet, M.; Ducloy, M.; Bloch, D. Testing the distance-dependence of the van der waals interaction between an atom and a surface through spectroscopy in a vapor nanocell. Proceedings ofSPIE 14th International School on Quantum Electronics: Laser Physics and Applications, Peter A. Atanasov, Tanja N. Dreischuh, Sanka V. Gateva, Lubomir M. Kovachev, Editors, 660406 (Mar. 5, 2007) 2007, volume 6604. [Google Scholar]
- Zhao, Y.-P.; Wang, L. S.; Yu, T. X. Mechanics of adhesion in MEMS-a review. Journal of Adhesion Science & Technology 2003, 17(4), 519–546. [Google Scholar]
- Israelachvili, J. N.; Tabor, D. The measurement of van der Waals dispersion forces in the range 1.5 to 130 nm. Proc. R. Soc. London, Ser A 1972, 331, 19–38. [Google Scholar]
- Meirovitch, L. Analytical methods in vibrations.; Macmillan: New York, 1967. [Google Scholar]
- Tilmans, H. A.; Legtenberg, R. Electrostatically driven vacuum-encapsulated polysilicon res-onators: Part II. Theory and performance. Sensors and Actuators A 1994, 45(1), 67–84. [Google Scholar]
- Abdel-Rahman, E. M.; Younis, M. I.; Nayfeh, A. H. Characterization of the mechanical behavior of an electrically actuated microbeam. Journal of Micromechanics and Microengineering 2002, 12(6), 759–766. [Google Scholar]
- Batra, R. C.; Porfiri, M.; Spinello, D. Electromechanical model of electrically actuated narrow microbeams. Journal of Microelectromechanical Systems 2006, 15(5), 1175–1189. [Google Scholar]
- Batra, R. C.; Porfiri, M.; Spinello, D. Vibrations of narrow microbeams predeformed by an electric field. Journal of Sound and Vibration 2008, 309(3), 600–612. [Google Scholar]
- Batra, R. C.; Porfiri, M.; Spinello, D. Capacitance estimate for electrostatically actuated narrow microbeams. Micro & Nano Letters 2006, 1(2), 71–73. [Google Scholar]
- Arenas, J. P. On the vibration analysis of rectangular clamped plates using the virtual work principle. Journal of Sound and Vibration 2003, 266(4), 912–918. [Google Scholar]
- *In the literature [31–33], the Casimir force, see Equation (7), is usually termed the retarded van der Waals, whereas the van der Waals force, see Equation (8), is called the nonretarded van der Waals. This nomenclature better illustrates the common physical nature of these surface forces.

© 2008 by MDPI Reproduction is permitted for noncommercial purposes.
Share and Cite
Batra, R.C.; Porfiri, M.; Spinello, D. Effects of van der Waals Force and Thermal Stresses on Pull-in Instability of Clamped Rectangular Microplates. Sensors 2008, 8, 1048-1069. https://doi.org/10.3390/s8021048
Batra RC, Porfiri M, Spinello D. Effects of van der Waals Force and Thermal Stresses on Pull-in Instability of Clamped Rectangular Microplates. Sensors. 2008; 8(2):1048-1069. https://doi.org/10.3390/s8021048
Chicago/Turabian StyleBatra, Romesh C., Maurizio Porfiri, and Davide Spinello. 2008. "Effects of van der Waals Force and Thermal Stresses on Pull-in Instability of Clamped Rectangular Microplates" Sensors 8, no. 2: 1048-1069. https://doi.org/10.3390/s8021048




