Airborne Laser Scanning of Forest Stem Volume in a Mountainous Environment
Abstract
:1. Introduction
2. Study area and data
2.1 Study area
2.2 Airborne laser scanner data
2.3. Forest inventory data
3. Data pre-processing
3.1. ALS data pre-processing
3.2. Co-registration of the forest inventory data to the ALS data
4. Stem volume estimation
4.1. Multiplicative stem volume model
4.2. Regression analyses
4.3. Correction of the logarithmic transformation bias
4.4. Validation of the stem volume model
5. Results
5.1. Sample plot size
5.2. Effects of different ALS point densities and acquisition times
6. Discussion
6.1. Stem volume model
6.2. Forest inventory data
7. Conclusions
Acknowledgments
References
- Kraus, K.; Karel, W.; Briese, C.; Mandlburger, G. Local Accuracy Measures for Digital Terrain Models. The Photogrammetric Record 2006, 21(116), 342–354. [Google Scholar]
- Chen, Q.; Gong, P.; Baldocchi, D.; Xie, G. Filtering airborne laser scanning data with morphological methods. Photogrammetric Engineering and Remote Sensing 2007, 73(2), 175–185. [Google Scholar]
- Kobler, A.; Pfeifer, N.; Ogrinc, P.; Todorovski, L.; Oštir, K.; Džeroski, S. Repetitive interpolation: A robust algorithm for DTM generation from Aerial Laser Scanner Data in forested terrain. Remote Sensing of Environment 2007, 108(1), 9–23. [Google Scholar]
- Flood, M. Laser Altimetry: From Science to Commercial Lidar Mapping. Photogrammetric Engineering & Remote Sensing 2001, 11, 1209–1217. [Google Scholar]
- Wehr, A.; Lohr, U. Airborne laser scanning - an introduction and overview. ISPRS Journal of Photogrammetry & Remote Sensing 1999, 54, 68–82. [Google Scholar]
- Axelsson, P. Processing of laser scanner data - algorithms and applications. Photogrammetry & Remote Sensing 1999, 54, 138–147. [Google Scholar]
- Wagner, W.; Hollaus, M.; Briese, C.; Ducic, V. 3D vegetation mapping using small-footprint full-waveform airborne laser scanners. International Journal of Remote Sensing 2007, in press. [Google Scholar]
- Goodwin, N. R.; Coops, N. C.; Culvenor, D. S. Development of a simulation model to predict LiDAR interception in forested environments. Remote Sensing of Environment 2007. [Google Scholar] [CrossRef]
- Sithole, G.; Vosselman, G. Experimental comparison of filter algorithms for bare-Earth extraction from airborne laser scanning point clouds. ISPRS Journal of Photogrammetry & Remote Sensing 2004, 59(1-2), 85–101. [Google Scholar]
- Kraus, K.; Pfeifer, N. Determination of terrain models in wooded areas with airborne laser scanner data. ISPRS Journal of Photogrammetry & Remote Sensing 1998, 53(4), 193–203. [Google Scholar]
- Dubayah, R.; Drake, J. Lidar Remote Sensing for Forestry. Journal of Forestry 2000, 98, 44–46. [Google Scholar]
- Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LIDAR remote sensing of forest structure. Progress in Physical Geography 2003, 27(1), 88–106. [Google Scholar]
- Næsset, E.; Gobakken, T.; Holmgren, J.; Hyyppä, H.; Hyyppä, J.; Maltamo, M.; Nilsson, M.; Olsson, H.; Persson, Å; Söderman, U. Laser scanning of forest resources: the Nordic experience. Scandinavian Journal of Forest Research 2004, 19(6), 482–499. [Google Scholar]
- Lee, A. C.; Lucas, R. M. A LiDAR-derived canopy density model for tree stem and crown mapping in Australian forests. Remote Sensing of Environment 2007. [Google Scholar] [CrossRef]
- Evans, D. L.; Roberts, S. D.; Parker, R. C. LiDAR - A new tool for forest measurements? Forestry Chronicle 2006, 82(2), 211–218. [Google Scholar]
- Packalen, P.; Maltamo, M. Predicting the plot volume by tree species using airborne laser scanning and aerial photographs. Forest Science 2006, 52(6), 611–622. [Google Scholar]
- Hyyppä, J.; Hyyppä, H.; Litkey, P.; Yu, X.; Haggrén, H.; Rönnholm, P.; Pyysalo, U.; Pitkänen, J.; Maltamo, M. Algorithms and Methods of Airborne Laser Scanning for Forest Measurements. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences 2004, XXXVI(Part 8/W2), 82–89. [Google Scholar]
- Næsset, E. Estimating Timber Volume of Forest Stands Using Airborne Laser Scanner Data. Remote Sensing of Environment 1997, 61(2), 246–253. [Google Scholar]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sensing of Environment 2002, 80(1), 88–99. [Google Scholar]
- Næsset, E. Practical Large-scale Forest Stand Inventory Using a Smallfootprint Airborne Scanning Laser. Scandinavian Journal of Forest Research 2004, 19(2), 164–179. [Google Scholar]
- Hollaus, M.; Wagner, W.; Eberhöfer, C.; Karel, W. Accuracy of large-scale canopy heights derived from LiDAR data under operational constraints in a complex alpine environment. ISPRS Journal of Photogrammetry & Remote Sensing 2006, 60(5), 323–338. [Google Scholar]
- Shiver, B. D.; Borders, B. E. Sampling techniques for forest resource inventory; John Wiley & Sons Inc.: New York, 1996; p. 368. [Google Scholar]
- Wagner, W.; Eberhöfer, C.; Hollaus, M.; Summer, G. Robust Filtering of Airborne Laser Scanner Data for Vegetation Analysis. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences 2004, XXXVI(Part 8/W2), 56–61. [Google Scholar]
- Keylwerth, R. Ein Beitrag zur qualitativen Zuwachsanalyse. Holz als Roh- und Werkstoff 1954, 12, 41–44. [Google Scholar]
- Prodan, M. Holzmeßlehre; Sauerländer: Frankfurt am Main, 1965; p. 644. [Google Scholar]
- Pollanschütz, J. Formzahlfunktionen der Hauptbaumarten Österreichs. Allgemeine Forstzeitung 1974, 85(12), 341–343. [Google Scholar]
- Süß, H. Programm zur Auswertung von betrieblichen Forstinventuren mittels Winkelzählproben, Institute of Forest growth and Yield research; University of Natural Resources and Applied Life Sciences: Vienna, 1984. [Google Scholar]
- Sterba, H. Holzmesslehre [Forest measurements]. Vorlesungsunterlagen. In Heft 3 der Berichte aus der Abteilung Holzmesskunde und Inventurfragen. Institut für forstliche Ertragslehre; Universität für Bodenkultur: Wien, 1991; p. 169. [Google Scholar]
- Kager, H. Discrepancies between overlapping laser scanner strips - simultaneous fitting of aerial laser scanner strips. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences 2004, XXXV(Part B/1), 555–560. [Google Scholar]
- Briese, C.; Pfeifer, N.; Dorninger, P. Applications of the Robust Interpolation for DTM Determination. Proceedings of Photogrammetric Computer Vision (PCV′02), ISPRS Commission III. In: International Archives of Photogrammetry and Remote Sensing, Graz, Austria; 2002; XXXIV / 3A, pp. 55–61. [Google Scholar]
- Pfeifer, N.; Stadler, P.; Briese, C. Derivation of Digital Terrain Models in the SCOP++ Environment. Proceedings of OEEPE Workshop on Airborne Laserscanning and Interferometric SAR for Detailed Digital Elevation Models, 1.-3. March 2001, Stockholm, Sweden; 2001; p. 13 pp. [Google Scholar]
- Nilsson, M. Estimation of Tree Heights and Stand Volume Using an Airborne Lidar System. Remote Sensing of Environment 1996, 56(1), 1–7. [Google Scholar]
- Beauchamp, J. J.; Olson, J. S. Corrections for bias in regression estimates after logarithmic transformation. Ecology 1973, 54(6), 1403–1407. [Google Scholar]
- Snowdon, P. A ratio estimator for bias correction in logarithmic regressions. Canadian Journal of Forest Research 1991, 21, 720–724. [Google Scholar]
- Baskerville, G. L. Use of logarithmic regression in the estimation of plant biomass. Canadian Journal of Forest Research 1972, 2, 49–53. [Google Scholar]
- Sprugel, D. G. Correcting for bias in log-transformed allometric equations. Ecology 1983, 64(1), 209–210. [Google Scholar]
- Popescu, S. C.; Wynne, R. H.; Scrivani, J. A. Fusion of small-footprint lidar and multispectral data to estimate plot-level volume and biomass in deciduous and pine forests in Virginia, U.S.A. Forest Science 2004, 50(4), 551–565. [Google Scholar]
- Mutlu, M.; Popescu, S. C.; Stripling, C.; Spencer, T. Mapping surface fuel models using lidar and multispectral data fusion for fire behavior. Remote Sensing of Environment 2007. [Google Scholar] [CrossRef]
- Wulder, M. A.; Han, T.; White, J. C.; Sweda, T.; Tsuzuki, H. Integrating profiling LIDAR with Landsat data for regional boreal forest canopy attribute estimation and change characterization. Remote Sensing of Environment 2007, 110(1), 123–137. [Google Scholar]
- Reitberger, J.; Krzystek, P.; Heurich, M. Full-waveform analysis of small footprint airborne laser scanning data in the Bavarian forest national park for tree species classification. Proceedings of International Workshop on 3D Remote Sensing in Forestry, Vienna, Austria, 14-15. Feb., 2006; pp. 218–227.
- Næsset, E. Effects of different flying altitudes on biophysical stand properties estimated from canopy height and density measured with a small-footprint airborne scanning laser. Remote Sensing of Environment 2004, 91(2), 243–255. [Google Scholar]
- Næsset, E. Assessing sensor effects and effects of leaf-off and leaf-on canopy conditions on biophysical stand properties derived from small-footprint airborne laser data. Remote Sensing of Environment 2005, 98(2-3), 356–370. [Google Scholar]
- Gaveau, D. L. A.; Hill, R. A. Quantifying canopy height underestimation by laser pulse penetration in small-footprint airborne laser scanning data. Canadian Journal of Remote Sensing 2003, 29(5), 650–657. [Google Scholar]
- Hyyppä, H.; Yu, X.; Hyyppä, J.; Kaartinen, H.; Kaasalainen, S.; Honkavaara, E.; Rönnholm, P. Factors affecting the quality of DTM generation in forested areas. Proceedings of ISPRS WG III/3, III/4, V/3 Workshop “ Laser scanning 2005”, Enschede, the Netherlands, September 12-14, 2005; pp. 97–102.
- Koukal, T. Nonparametric Assessment of Forest Attributes by Combination of Field Data of the Austrian Forest Inventory and Remote Sensing Data. In Institut für Vermessung, Fernerkundung und Landinformation; Department für Raum, Landschaft und Infrastruktur; vol. Dissertation, Vienna; Universität für Bodenkultur Wien, 2004; p. 115. [Google Scholar]
- Wagner, W.; Ullrich, A.; Ducic, V.; Melzer, T.; Studnicka, N. Gaussian decomposition and calibration of a novel small-footprint full-waveform digitising airborne laser scanner. ISPRS Journal of Photogrammetry & Remote Sensing 2006, 60(2), 100–112. [Google Scholar]
- Donoghue, D. N. M.; Watt, P. J.; Cox, N. J.; Wilson, J. Remote sensing of species mixtures in conifer plantations using LiDAR height and intensity data. Remote Sensing of Environment 2007. doi: 1.1016/j.rse.2007.02.032. [Google Scholar]
- Kaasalainen, S.; Ahokas, E.; Hyyppä, J.; Suomalainen, J. Study of Surface Brightness From Backscattered Laser Intensity: Calibration of Laser Data. IEEE Geoscience and Remote Sensing Letters 2005, 2(3), 255–259. [Google Scholar]
- Höfle, B.; Pfeifer, N. Correction of laser scanning intensity data: Data and model-driven approaches. ISPRS Journal of Photogrammetry & Remote Sensing 2007, in press. [Google Scholar]
- 1. http://www.stand-montafon.at/forstfonds. Last accessed June 2007.
- 2. http://web.bfw.ac.at/i7/oewi.oewi0002. Last accessed June 2007.
- 4. http://www.R-project.org. Last accessed June 2007.

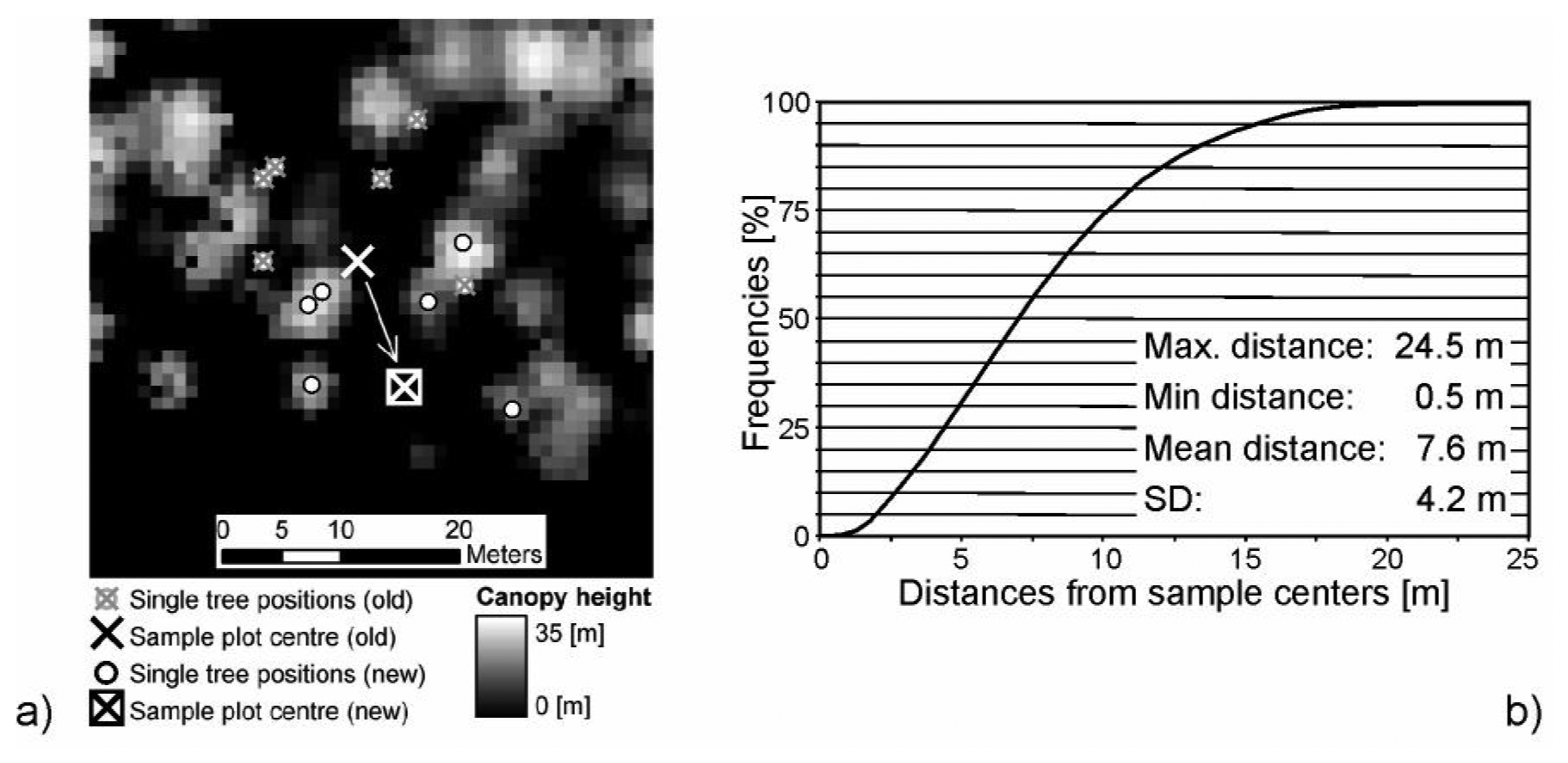
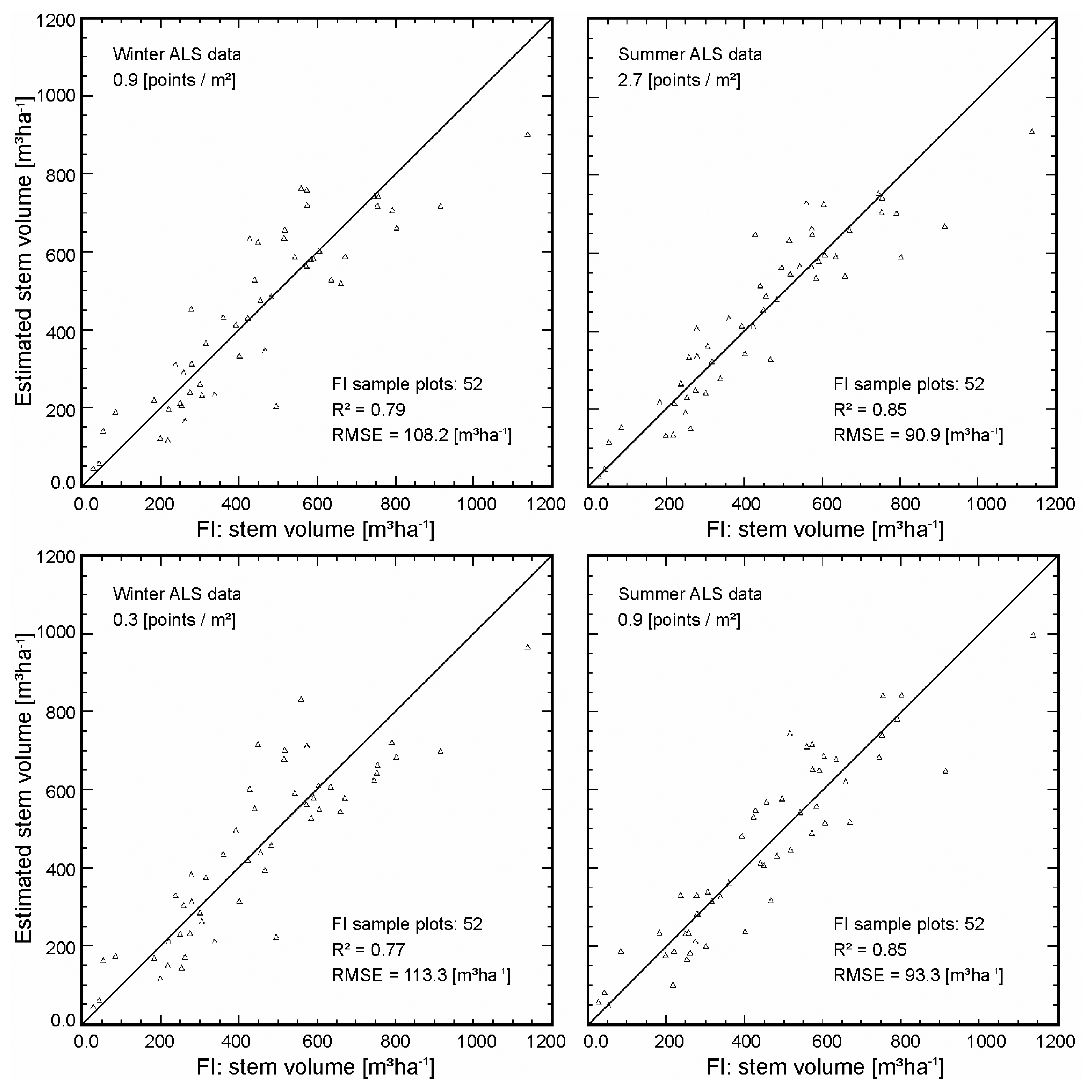
| Variable | Data | MIN | MAX | MEAN | SD |
|---|---|---|---|---|---|
| Diameter at breast height [cm] | All: 1,373 trees | 10.0 | 127.0 | 48.2 | 18.5 |
| Co-registered: 925 trees | 10.0 | 127.0 | 47.6 | 18.8 | |
| - W: 853 trees | 10.0 | 127.0 | 46.8 | 18.9 | |
| - S: 559 trees | 10.0 | 127.0 | 51.1 | 18.8 | |
| -W&S: 485 trees | 10.0 | 127.0 | 50.0 | 19.1 | |
| Tree height [m] | All: 1,373 trees | 5.4 | 43.8 | 27.7 | 6.8 |
| Co-registered: 925 trees | 5.4 | 42.2 | 27.0 | 6.8 | |
| - W: 853 trees | 5.4 | 42.2 | 27.1 | 7.0 | |
| - S: 559 trees | 7.0 | 42.2 | 27.7 | 6.6 | |
| -W&S: 485 trees | 7.0 | 42.2 | 28.1 | 6.8 | |
| Number of trees per plot | All: 143 plots | 1 | 29 | 9.8 | 5.4 |
| Co-registered: 103 plots | 1 | 22 | 8.8 | 4.6 | |
| - W: 92 plots | 1 | 22 | 9.3 | 4.6 | |
| - S: 64 plots | 1 | 22 | 8.7 | 4.3 | |
| -W&S: 52 plots | 1 | 22 | 9.3 | 4.4 | |
| Number of trees per ha | All: 143 plots | 8 | 1,876 | 414 | 392 |
| Co-registered: 103 plots | 11 | 1,876 | 393 | 395 | |
| - W: 92 plots | 11 | 1,876 | 429 | 406 | |
| - S: 64 plots | 11 | 1,602 | 309 | 316 | |
| -W&S: 52 plots | 18 | 1,602 | 352 | 335 | |
| Mean diameter at breast height per plot [cm] | All: 143 plots | 11.0 | 78.0 | 49.0 | 14.0 |
| Co-registered: 103 plots | 11.0 | 77.3 | 48.5 | 14.1 | |
| - W: 92 plots | 11.0 | 77.3 | 47.7 | 14.3 | |
| - S: 64 plots | 21.0 | 77.3 | 51.9 | 13.6 | |
| -W&S: 52 plots | 21.0 | 77.3 | 51.3 | 13.9 | |
| Mean tree height per plot [cm] | All: 143 plots | 6.0 | 42.1 | 26.9 | 6.5 |
| Co-registered: 103 plots | 9.5 | 38.6 | 26.2 | 6.4 | |
| - W: 92 plots | 9.5 | 38.6 | 26.6 | 6.5 | |
| - S: 64 plots | 11.3 | 38.0 | 27.1 | 6.1 | |
| -W&S: 52 plots | 11.3 | 38.0 | 27.7 | 6.2 | |
| Calculated stem volume [m3 ha-1] | All: 143 plots | 10.7 | 1,398.0 | 472.8 | 293.8 |
| Co-registered: 103 plots | 15.7 | 1,137.7 | 423.4 | 239.0 | |
| - W: 92 plots | 15.7 | 1,137.7 | 440.2 | 241.9 | |
| - S: 64 plots | 23.0 | 1,137.7 | 415.9 | 230.0 | |
| -W&S: 52 plots | 27.0 | 1,137.7 | 446,6 | 231.9 | |
| Sample plot size | Parameter | |||||||
|---|---|---|---|---|---|---|---|---|
| κ | RE | R2 | RMSE [m3ha−1] | Cross-validation [m3ha−1] | ||||
| MIN | MAX | MEAN | SD | |||||
| Ø18 m | lnvstem,fi = 4.861837 - 0.419251 lnh10,l + 0.857076 lnd6,f - 0.123035 lnd9,l | |||||||
| 19.9 | 1.025544 | 0.84* | 0.354* | -1.151* | 1.442* | 0.000* | 0.376* | |
| 0.83** | 101.4** | -253.1** | 267.1** | 0.0** | 104.0** | |||
| Ø20 m | lnvstem,fi = 3.178314 - 0.027323 lnd2,f + 0.262734 lnd7,f + 0.526734 lnd6,l | |||||||
| 29.0 | 1.039258 | 0.81* | 0.379* | -1.612* | 1.397* | 0.001* | 0.410* | |
| 0.82** | 101.5** | -264.9** | 291.0** | -0.1** | 105.0** | |||
| Ø22 m | lnvstem,fi = 3.090095 - 0.031669 lnd,2f + 0.609494 lnd6,f + 0.204359 lnd7,l | |||||||
| 29.0 | 1.033626 | 0.83* | 0.361* | -1.794* | 1.088* | 0.001* | 0.385* | |
| 0.83** | 99.1** | -255.2** | 272.3** | 0.0** | 102.1** | |||
| Ø24 m | lnvstem,fi = 4.662327 - 0.901615 lnh0,f + 0.523643 lnh30,l + 0.812855 lnd6,f | |||||||
| 27.2 | 1.017166 | 0.85* | 0.343* | -1.773* | 0.936* | -0.002* | 0.365* | |
| 0.84** | 96.8** | -254.7** | 204.1** | -0.3** | 100.0** | |||
| Ø26 m | lnvstem,fi = 4.662327 - 0.901615 lnh0,l + 0.523643 lnh40,l + 0.812855 lnd6,f | |||||||
| 24.5 | 1.019927 | 0.84* | 0.355* | -1.908* | 0.767* | -0.001* | 0.375* | |
| 0.82** | 103.9** | -338.4** | 282.1** | -0.3** | 107.5** | |||
| Time | κ | CF | R2 | RMSE [m3ha−1] | Cross-validation [m3ha-1] | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| MIN | MAX | MEAN | SD | |||||||
| Percentage of thinning: 0% | ||||||||||
| A | lnvstem,fi = 4.662327 - 0.901615 lnh0,f + 0.523643 lnh30,l + 0.812855 lnd6,f | |||||||||
| 27.2 | 1.017166 | 0.91* | 0.343* | -1.773* | 0.936* | -0.002* | 0.365* | |||
| 0.84** | 96.8** | -254.7** | 204.1** | -0.3** | 100.0** | |||||
| W | lnvstem,fi = 5.621786 - 1.120663 lnh0,f + 0.553731 lnd4,f + 0.761191 lnd6,f | |||||||||
| 19.7 | 1.012892 | 0.84* | 0.351* | -1.290* | 0.949* | -0.004* | 0.379* | |||
| 0.81** | 110.4** | -249.2** | 300.5** | -0.4** | 114.8** | |||||
| S | lnvstem,fi = 2.955974 + 0.102221 lnh90,f - 0.001293 lnd3,l + 0.729716 lnd6,l + 0.099115 lnhcv,l | |||||||||
| 21.7 | 1.046855 | 0.76* | 0.410* | -2.128* | 0.719* | 0.001* | 0.445* | |||
| 0.82** | 97.9** | -385.7** | 317.5** | 0.8** | 110.7** | |||||
| W&S | W | lnvstem,fi = 4.824553 - 0.399229 lnh0,f + 0.094519 lnh80,f - 0.012827 lnd2,f + 0.696564 lnd6,f | ||||||||
| 20.3 | 1.021042 | 0.81* | 0.327* | -1.097* | 1.134* | 0.006* | 0.384* | |||
| 0.79** | 108.2** | -224.7** | 332.0** | 1.6** | 120.0** | |||||
| S | lnvstem,fi = 3.892341 - 0.217090 lnh0,f + 0.047210 lnh80,f + 0.775024 lnd6,f | |||||||||
| 14.9 | 1.018094 | 0.89* | 0.248* | -0.887* | 0.607* | -0.002* | 0.273* | |||
| 0.85** | 90.9** | -242.1** | 258.9** | -0.6** | 97.2** | |||||
| Percentage of thinning: 66% | ||||||||||
| A | lnvstem,fi = 2.818110 - 0.074578 lnd0,f + 0.282504 lnd7,f + 0.606238 lnd6,l | |||||||||
| 24.5 | 1.026639 | 0.84* | 0.356* | -1.7996* | 0.968* | 0.000* | 0.375* | |||
| 0.82** | 104.4** | -268.5** | 311.9** | -0.1** | 106.7** | |||||
| W | lnvstem,fi = 2.960790 - 0.035852 lnd2,l + 0.610804 lnd6,l + 0.270893 lnd8,l | |||||||||
| 18.6 | 1.025183 | 0.80* | 0.387* | -1.514* | 1.795* | -0.001* | 0.411* | |||
| 0.77** | 117.5** | -297.7** | 410.2** | -0.2** | 122.7** | |||||
| S | lnvstem,fi = 3.124630 + 0.129229 lnh90,f + 0.014617 lnd3,l + 0.682713 lnd6,l + 0.065367 lnhcv,l | |||||||||
| 21.7 | 1.048572 | 0.74* | 0.425* | -2.092* | 1.051* | 0.000* | 0.460* | |||
| 0.82** | 99.9** | -370.9** | 309.2** | 0.2** | 111.3** | |||||
| W&S | W | lnvstem,fi = 3.472091 + 0.295300 lnh0,f - 0.510809 lnh30,f + 0.589993 lnh70,f - 0.098405 lnd2,f + 0.483818 lnd6,f | ||||||||
| 28.3 | 1.021042 | 0.80* | 0.333* | -1.259* | 1.047* | 0.003* | 0.402* | |||
| 0.77** | 113.3** | -304.0** | 317.0** | 0.0** | 127.1** | |||||
| S | lnvstem,fi = 2.925126 + 0.250145 lnh0,f + 0.492056 lnh80,f - 0.148622 lnd2,f + 0.353557 lnd5,f | |||||||||
| 25.8 | 1.010784 | 0.85* | 0.293* | -1.251* | 0.940* | -0.011* | 0.363* | |||
| 0.85** | 93.3** | -276.4** | 282.0** | -2.4** | 104.0** | |||||
© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purpose.
Share and Cite
Hollaus, M.; Wagner, W.; Maier, B.; Schadauer, K. Airborne Laser Scanning of Forest Stem Volume in a Mountainous Environment. Sensors 2007, 7, 1559-1577. https://doi.org/10.3390/s7081559
Hollaus M, Wagner W, Maier B, Schadauer K. Airborne Laser Scanning of Forest Stem Volume in a Mountainous Environment. Sensors. 2007; 7(8):1559-1577. https://doi.org/10.3390/s7081559
Chicago/Turabian StyleHollaus, Markus, Wolfgang Wagner, Bernhard Maier, and Klemens Schadauer. 2007. "Airborne Laser Scanning of Forest Stem Volume in a Mountainous Environment" Sensors 7, no. 8: 1559-1577. https://doi.org/10.3390/s7081559




