Cluster-based Dynamic Energy Management for Collaborative Target Tracking in Wireless Sensor Networks
Abstract
:1. Introduction
2. Problem Formulation
2.1. Multi-sensor detection model
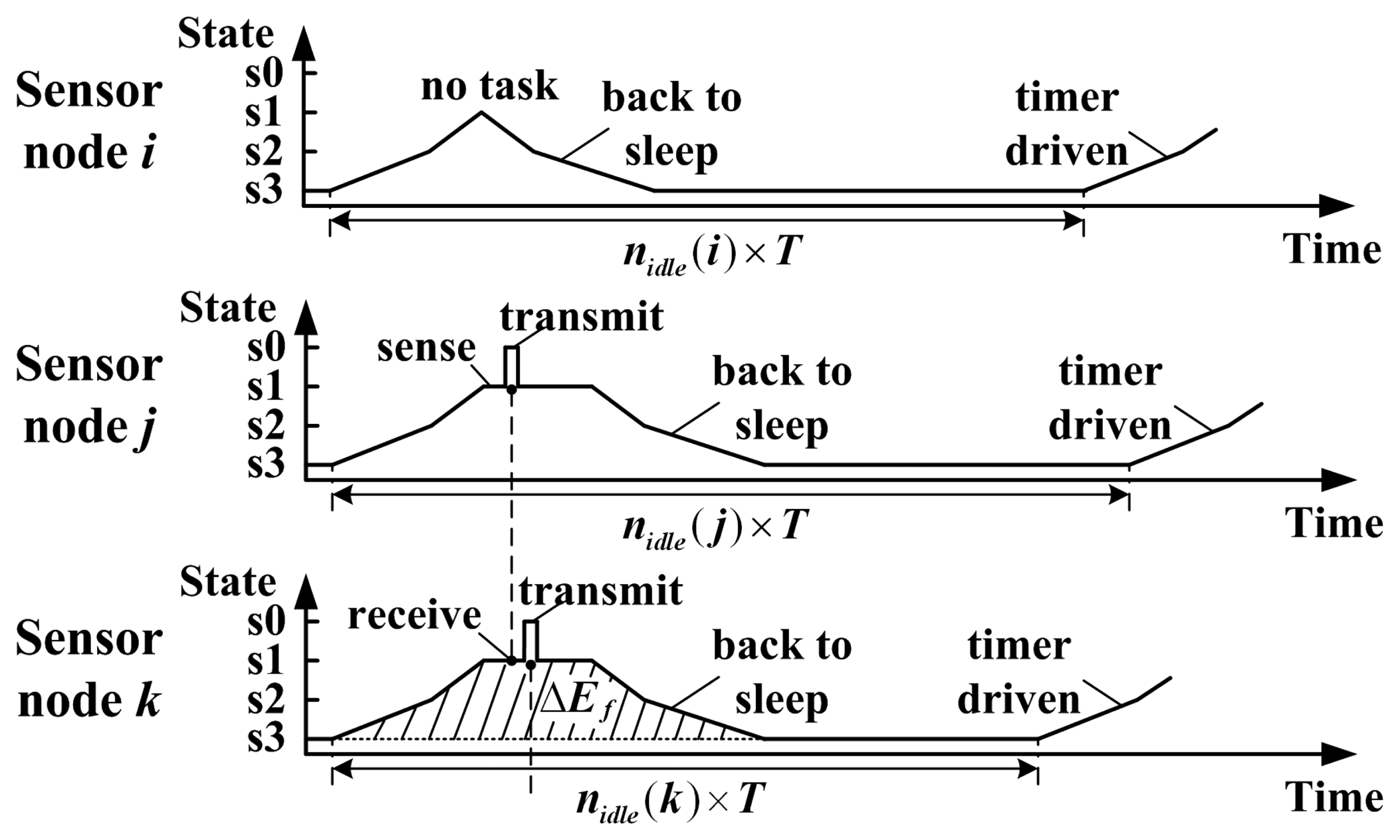
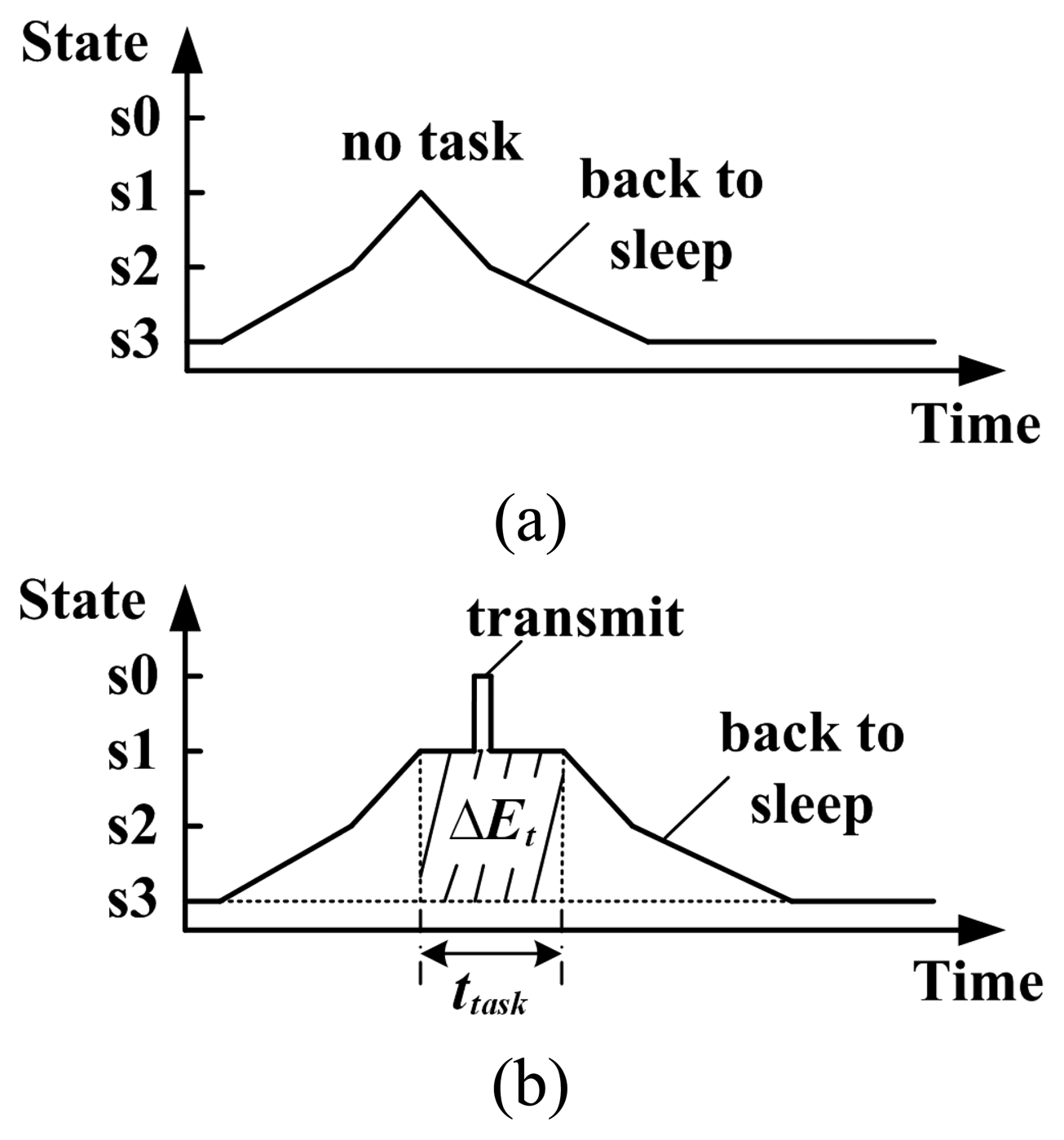
2.2. Energy consumption model
- (a)
- State s0All the components of sensor node are active. Data acquisition, reception and transmission are enabled. Sensor nodes can accomplish target detection and data forwarding tasks in this state. Assume that the power consumption in state s0 is 42 mW+ψTx , where the extra power consumption for data transmission is denoted by ψTx . The propagation distance between sensor nodes i and j can be denoted as di,j . Then transmission cost between the sensor nodes is calculated as ψTx =α1r+α2di,j2r, where r denotes the data rate, α1 denotes the electronics energy expended in transmitting one bit of data, and α2 > 0 is a constant related to the radio energy [14].
- (b)
- State s1Compared to state s0, the data transmission is disabled in state s1 . Sensor node can receive orders from the sink node in this state. Assume the power consumption ψ1 = 42 mW.
- (c)
- State s2In this state, only the sensing component is active. It is the transitional state to deeper sleep state. Assume the power consumption ψ2 = 22 mW.
- (d)
- State s3This is the deepest sleep state, which consumes the lowest power ψ3 = 2 mW. The sensing, processing, memory and communication components are inactive in this state. Sensor nodes in this state can only be wakened by its own timer.
3. Cluster-based Dynamic Energy Management
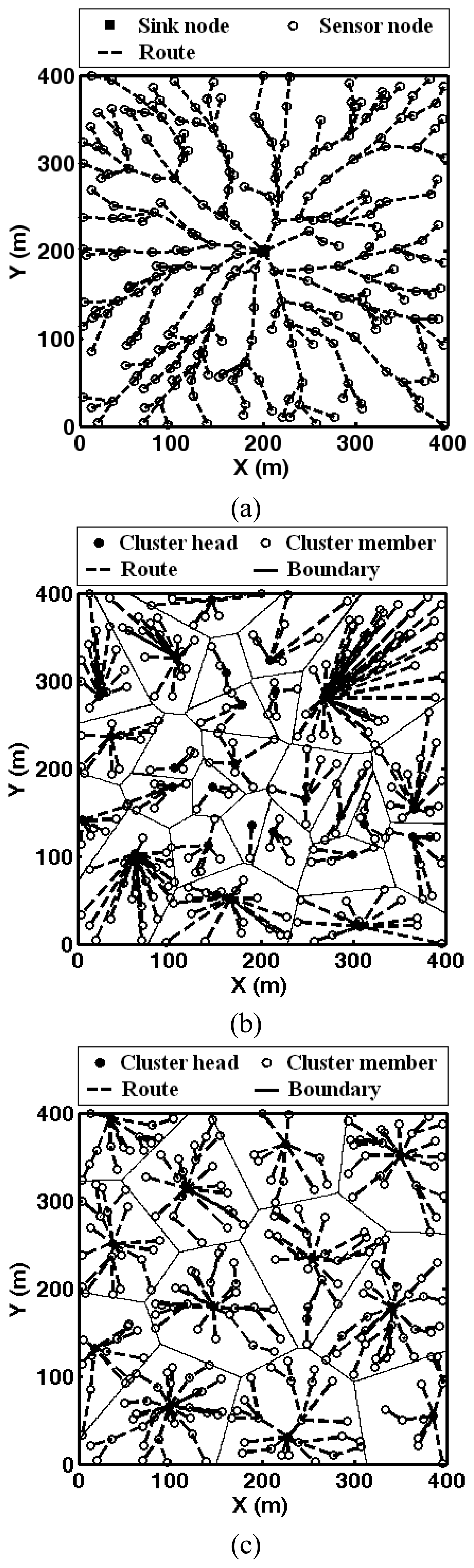
3.1. Distributed adaptive clustering with intra-cluster optimal routing
- Step 1:
- Each sensor node i generates a number ai:where Rand(1) denotes a random number in [0,1] , AC (1) = Ø. If the set of cluster heads in round rC is BC(rC), thenIf AC (rC) = I, then AC (rC + 1) = Ø.
- Step 2:
- Sensor nodes broadcast their number with the same communication range Rh. After receiving the numbers from the neighboring sensor nodes {ak}, each sensor node i set Flaghead(i) as:If Flaghead (i) =1, the sensor node i is regarded as a cluster head.
- Step 3:
- Existing cluster heads send their announcement with range Rh . For sensor node j, if it can receive the announcement, set Flagmember (j) =1; otherwise, set Flagmember (j) = 0.
- Step 4:
- If the condition that Flaghead (k) =1 or Flagmember (k) =1 is satisfied for all the sensor nodes, then stop this process and form the clusters as LEACH does; otherwise, the set of sensor nodes which have not satisfied the condition continue to execute Step 2.
- (a)
- Cluster head, considered as the destination node, is denoted by p0 and the set of cluster members is denoted by P ={p1, p2,…, pn};
- (b)
- According to Section 2.2, the edge weight between pi and pj is:
- (c)
- Variable Di represents estimate of the lowest cost from pi to p0. It converges to the real value after iterations;
- (d)
- The set of cluster members that find the lowest cost paths is denoted by Q.
- (i)
- Initialize the network:
- (ii)
- Search for the next sensor node with the lowest cost path to p0 . For pi ∉ Q , if Di satisfies:the lowest cost path of pi is found, update Q:If Q = P , then search is completed; otherwise, continue searching.
- (iii)
- Update Dj for all pj ∉ Q according to the result of step (ii):Continue to execute step (ii).
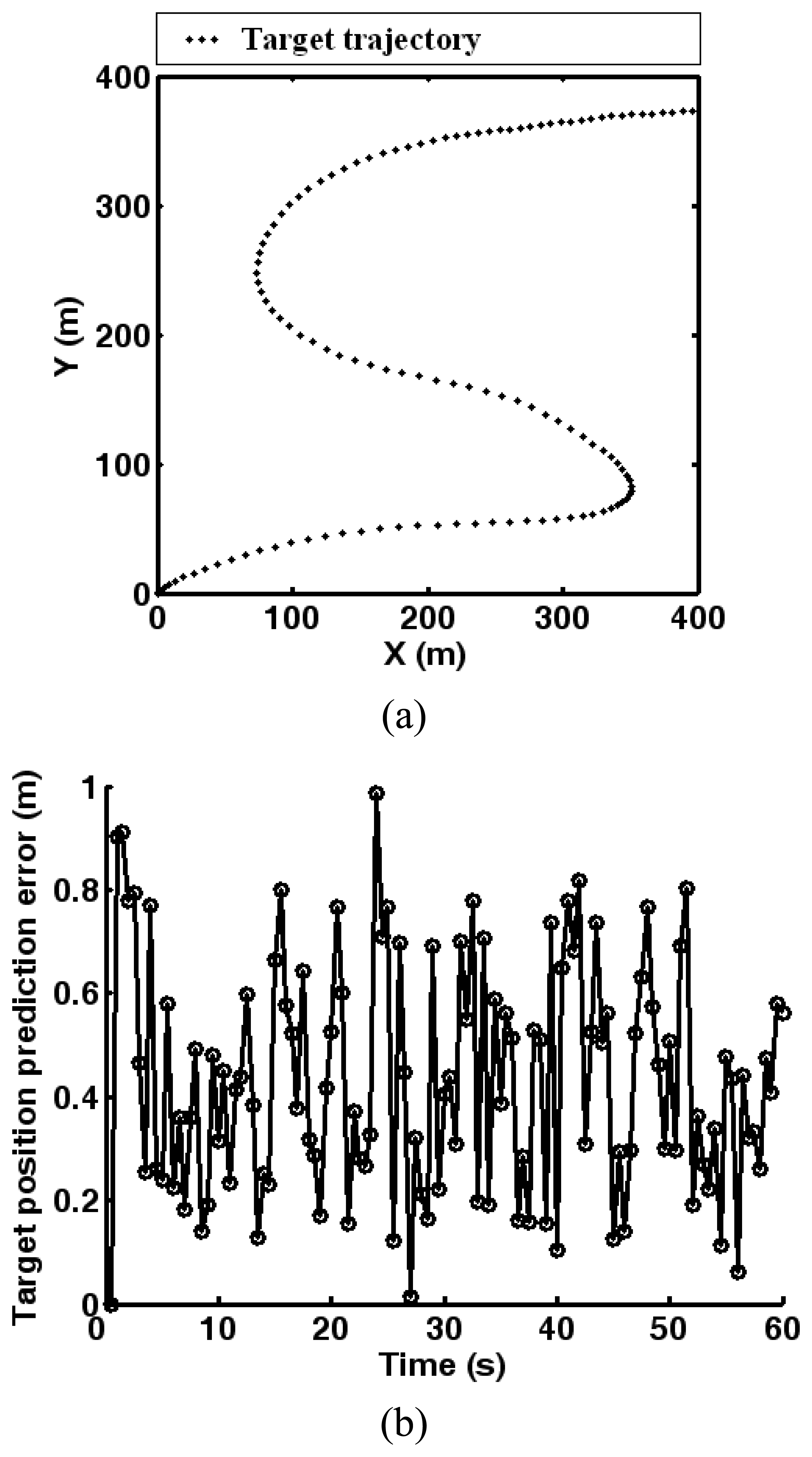
3.2. Dynamic awakening mechanism
- (a)
- InitializationGenerate the particle set according to the target position probability distribution p(X (0)):where X (k) is the target position estimation in the k - th sensing instant. Accordingly, Xi (k) = [xi (k), yi (k) ]T is the target position estimation for particle i. In addition, Ns is the number of particles. Then, the importance weight of particle i is set as:
- (b)
- IterationsSample each particle as:where F is the process noise. The target velocity is estimated according to the displacement, while the target acceleration is estimated according to the displacement increment. Then, evaluate the importance weights up to a normalizing constant and then normalize importance weights.
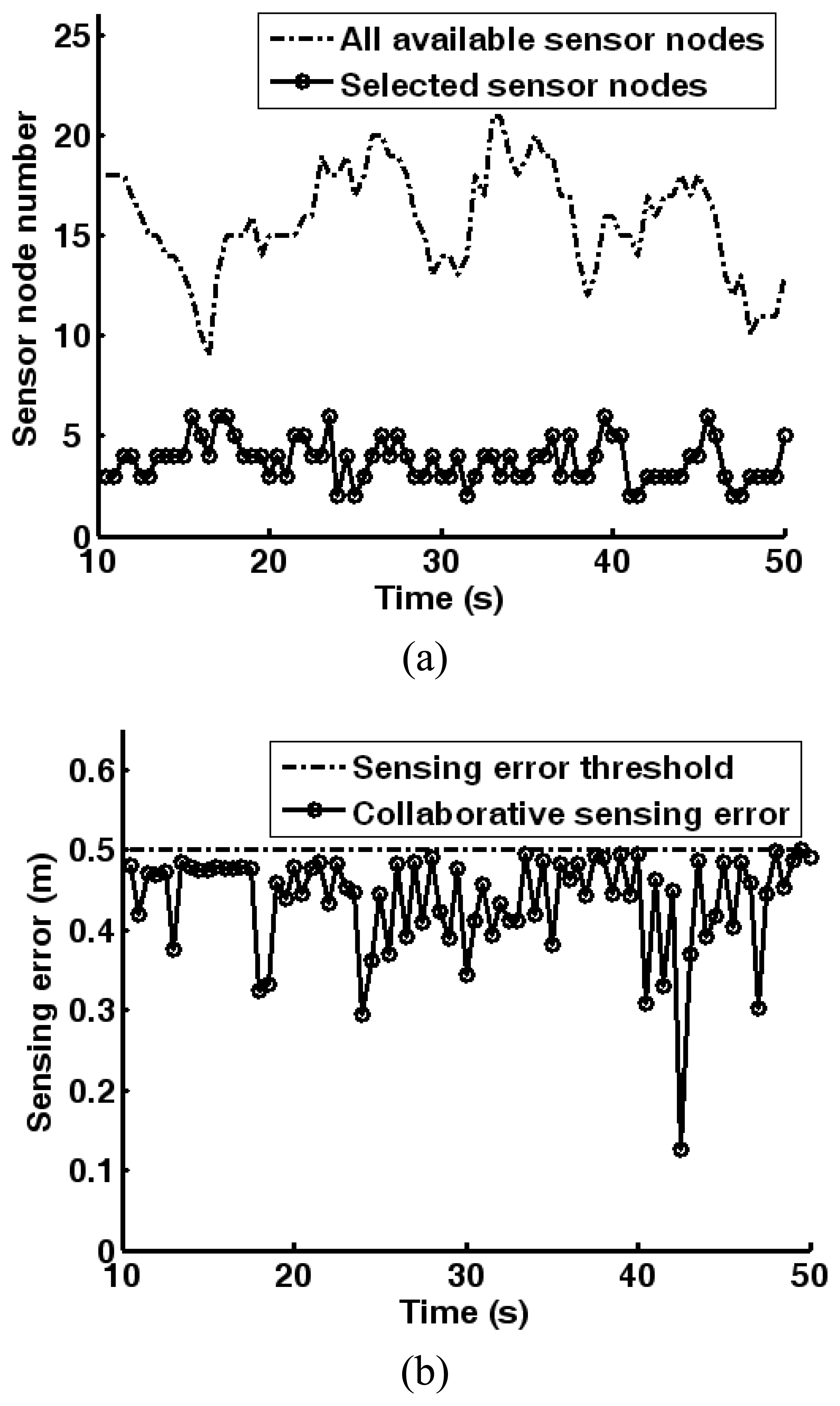
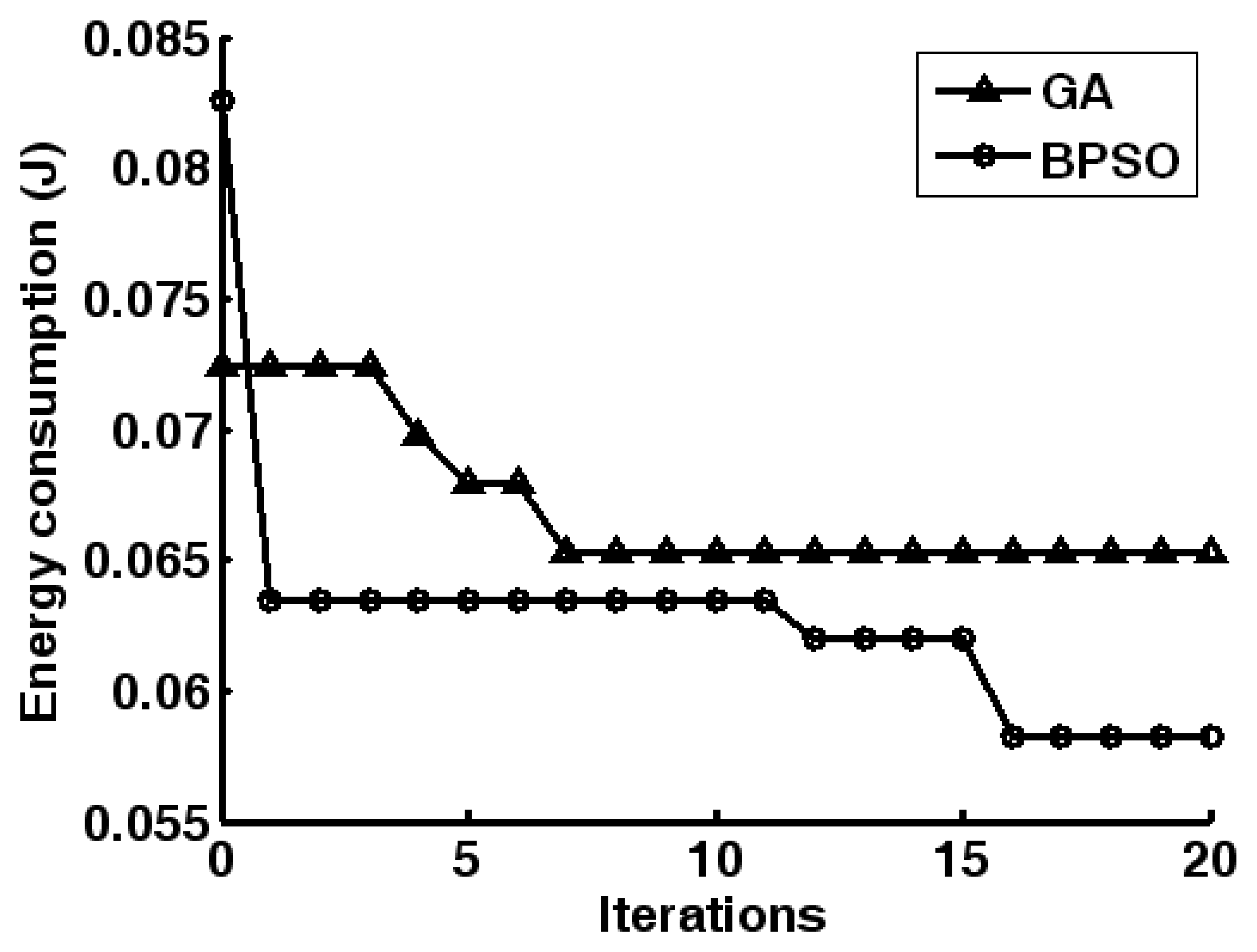
3.3. Sensor node selection optimization
4. Experimental Results
4.1. Experiment environment
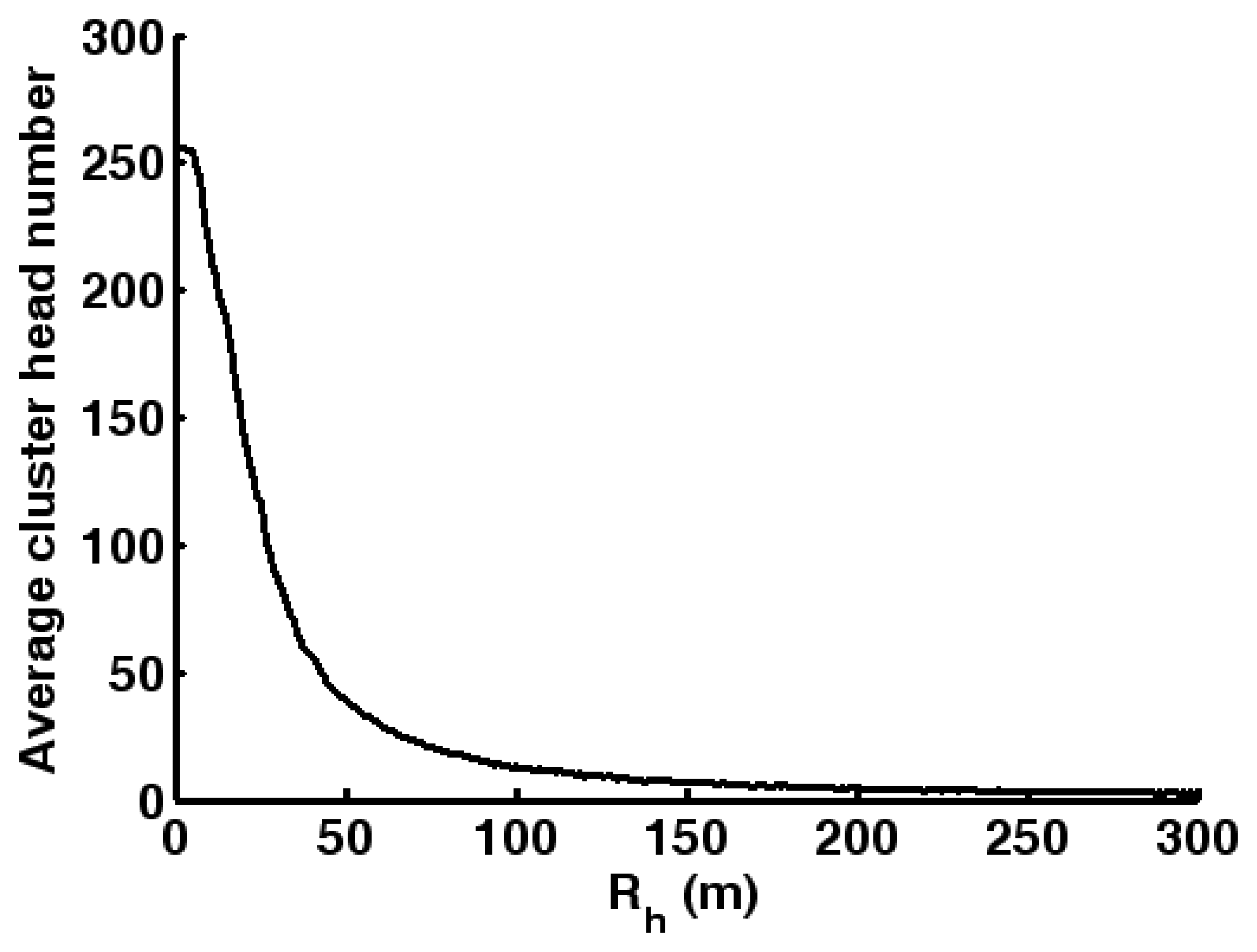
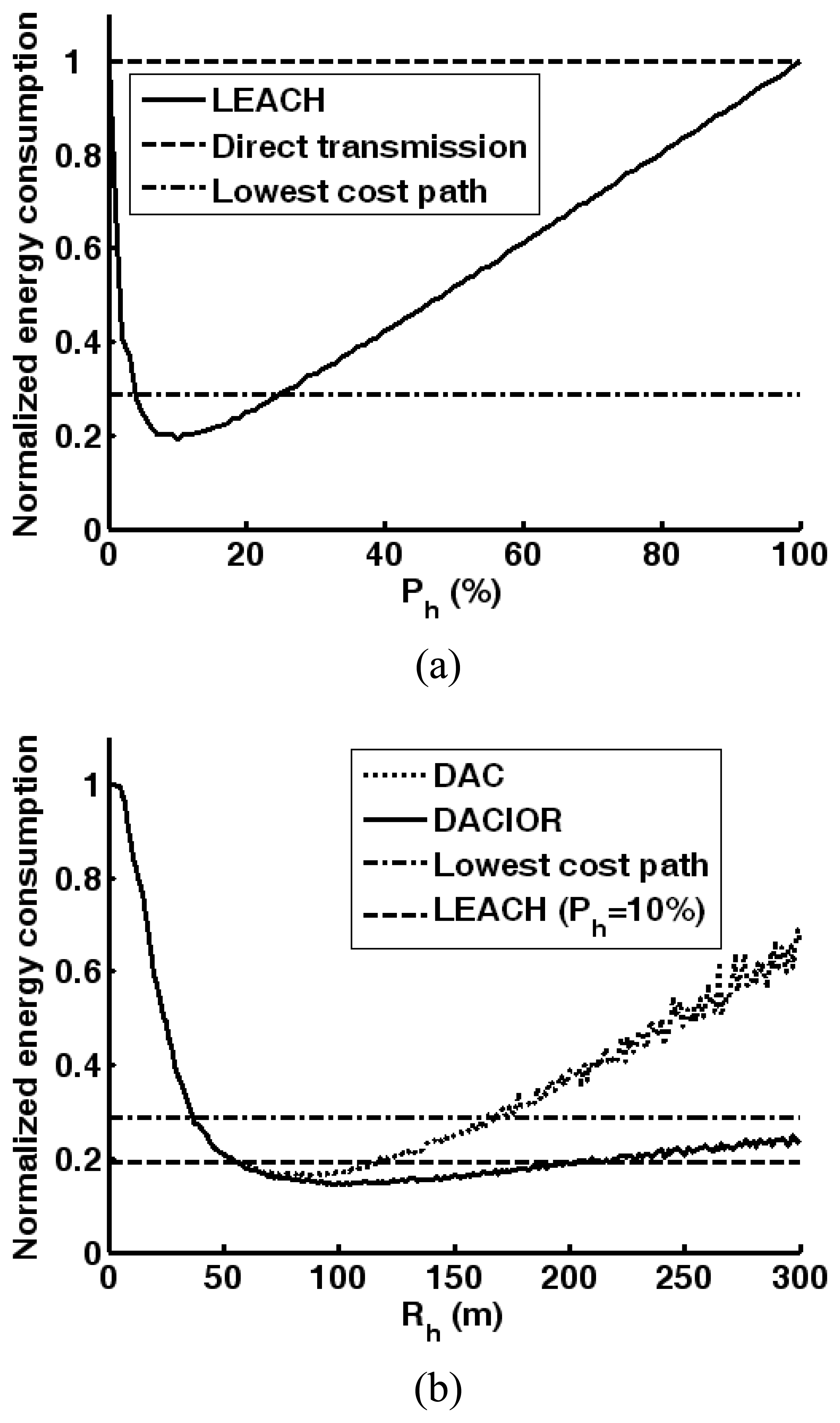
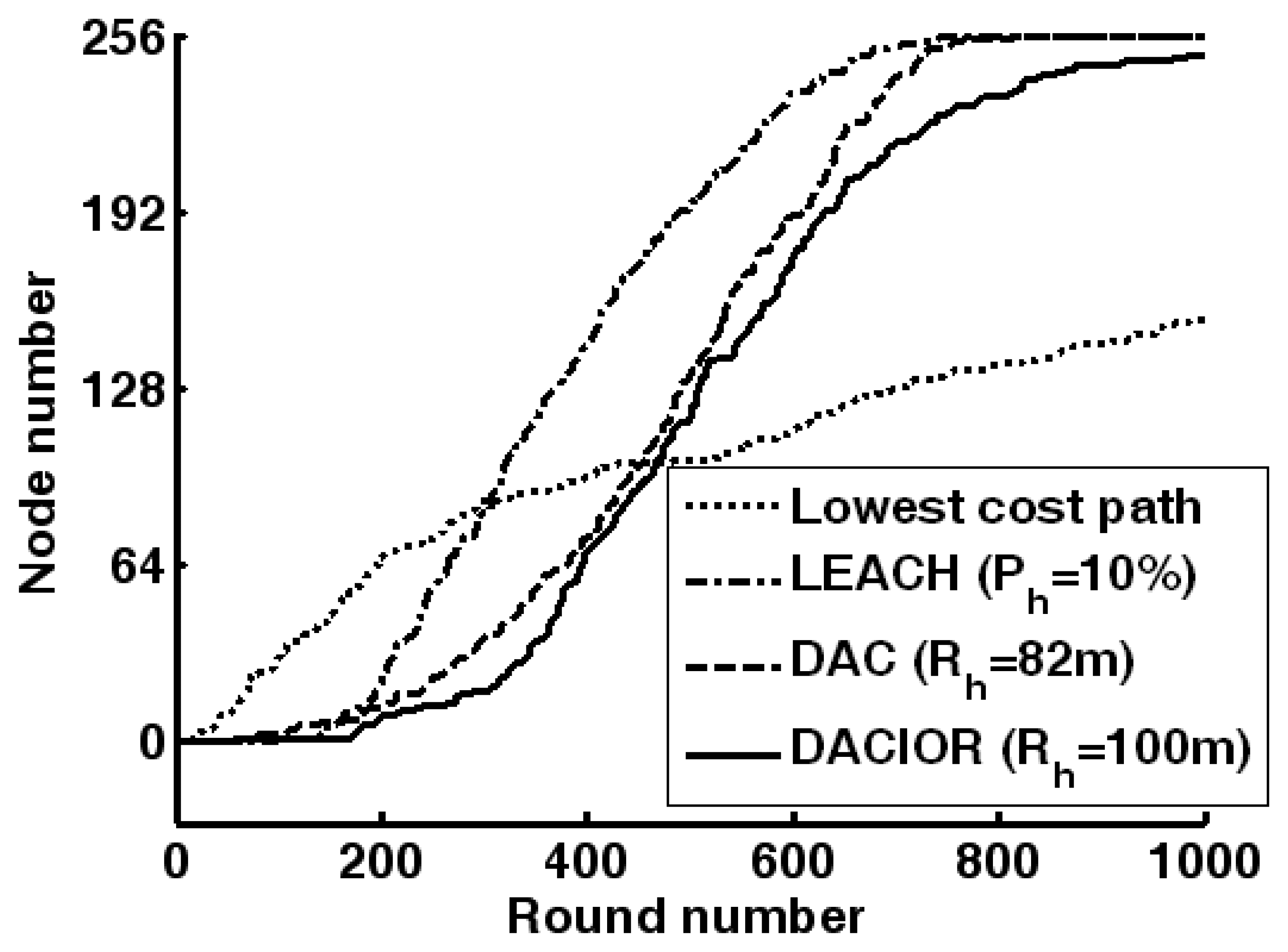
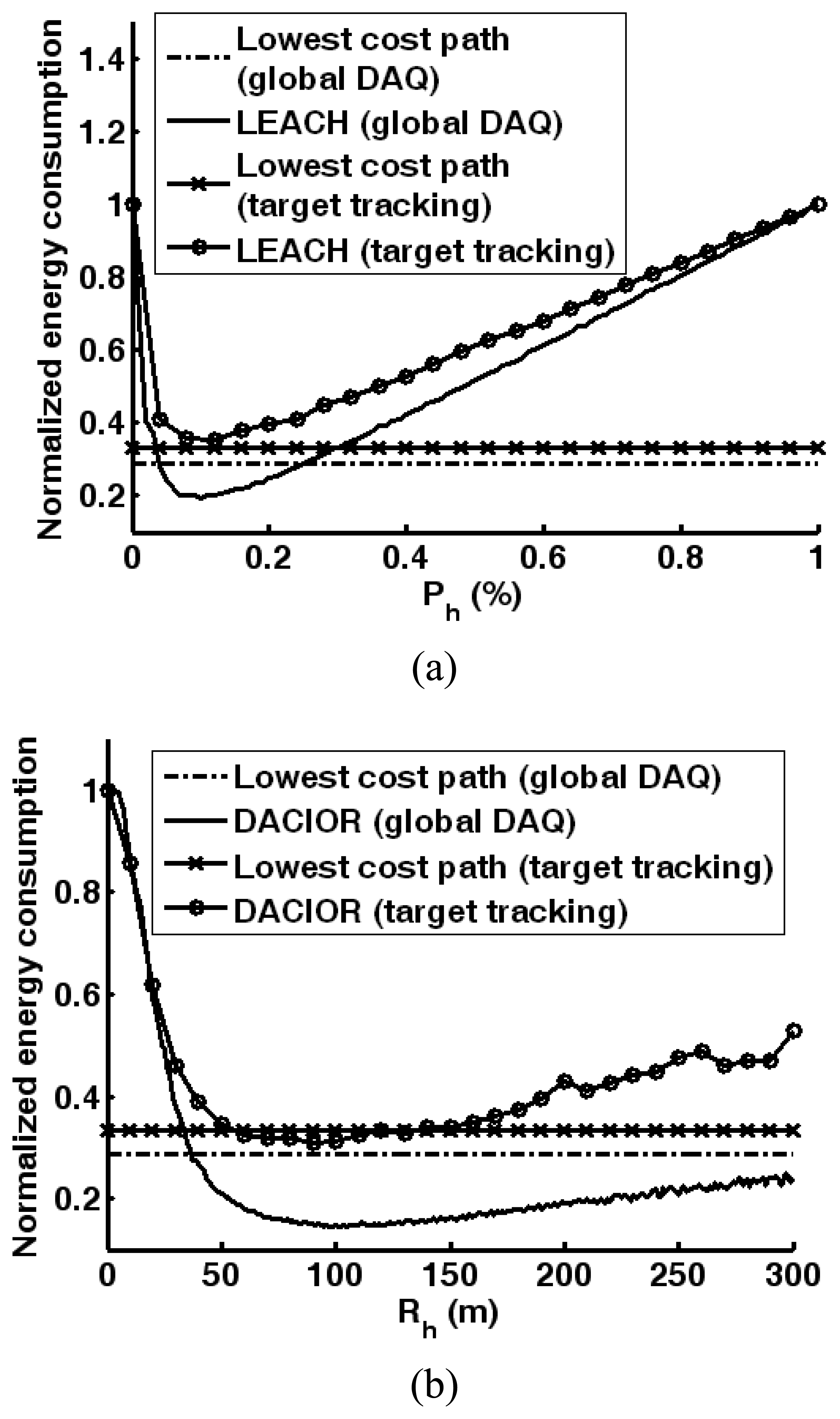
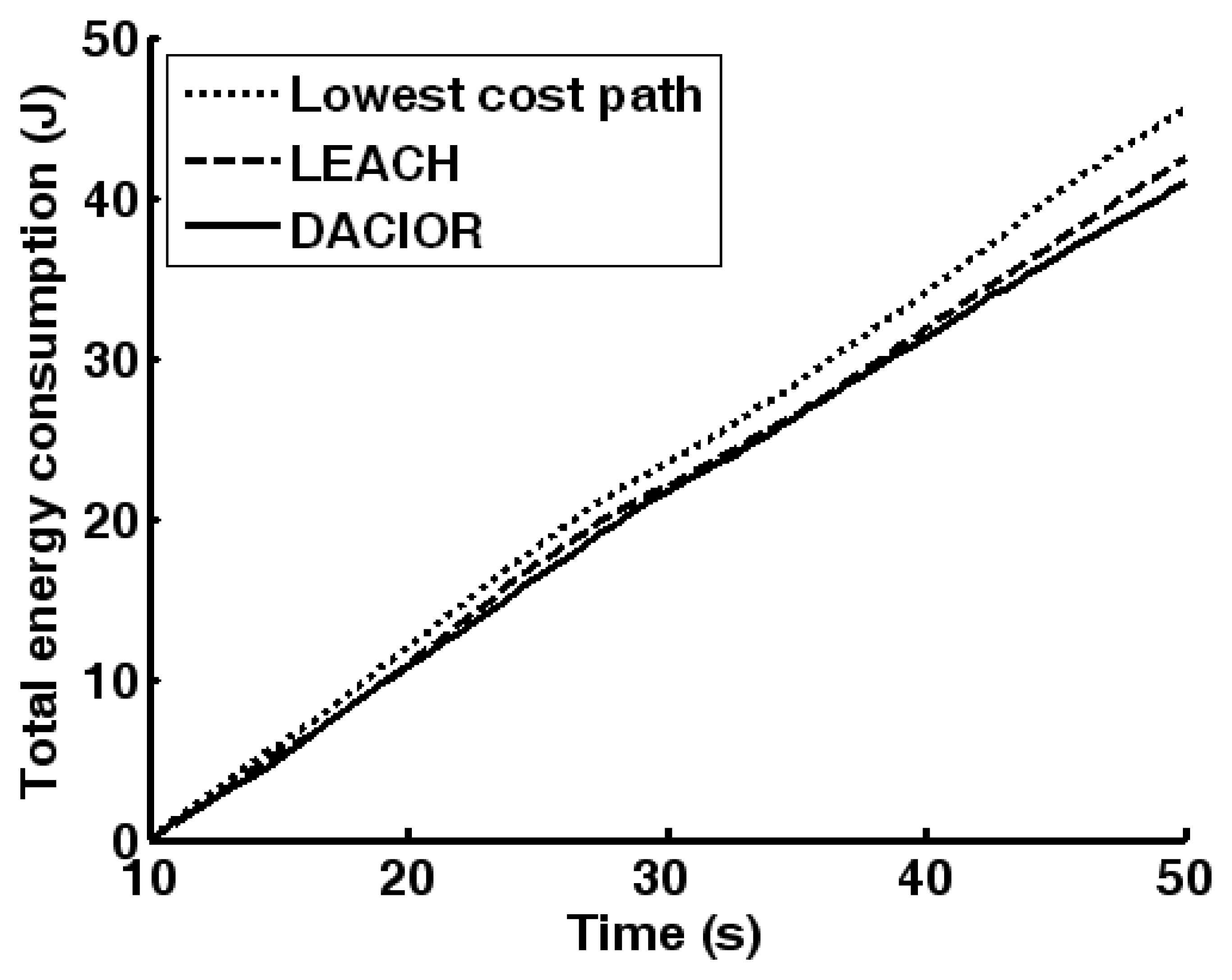
4.2. Simulations of cluster-based dynamic energy management
5. Conclusions
Acknowledgments
References and Notes
- Tan, H.O.; Korpeoglu, I. Power efficient data gathering and aggregation in wireless sensor networks. Proceedings of ACM International Conference on Management of Data; 2003; 32, pp. 66–71. [Google Scholar]
- Younis, O.; Krunz, M.; Ramasubramanian, S. Node clustering in wireless sensor networks: recent developments and deployment challenges. IEEE Network. 2006, 20, 20–25. [Google Scholar]
- Heinzelman, W.R.; Chandrakasan, A. Energy-efficient communication protocol for wireless microsensor networks. Proceedings of International Conference on System Sciences; 2000; pp. 1–10. [Google Scholar]
- Anjeshwar, A.M.; Agrawal, D.P. TEEN: A routing protocol for enhanced efficiency in wireless sensor networks. Proceedings of Parallel and Distributed Processing Symposium; 2001; pp. 2009–2015. [Google Scholar]
- Lindsey, S.; Raghavendra, C.; Sivalingam, K.M. Data gathering algorithms in sensor networks using energy metrics. IEEE Transactions on Parallel and Distributed Systems. 2002, 13, 924–935. [Google Scholar]
- Sinha, A.; Chandrakasan, A. Dynamic Power Management in Wireless Sensor Networks. IEEE Design & Test of Computers. 2001, 18, 62–74. [Google Scholar]
- Sudhakar, T.D. Supply restoration in distribution networks using Dijkstra's algorithm. Proceedings of IEEE International Conference on Power System Technology; 2004; 1, pp. 640–645. [Google Scholar]
- Wang, X.; Wang, S.; Ma, J. An improved particle filter for target tracking in sensor system. Sensors. 2007, 7, 144–156. [Google Scholar]
- Hu, F.; Cao, X.; May, C. Optimized scheduling for data aggregation in wireless sensor networks. Proceedings of IEEE International Conference on Networking, Sensing and Control; 2005; 2, pp. 557–561. [Google Scholar]
- Wang, X.; Wang, S.; Ma, J. Dynamic deployment optimization in wireless sensor networks. Lecture Notes in Control and Information Sciences. 2006, 344, 182–187. [Google Scholar]
- Wang, X.; Jiang, A.; Wang, S. Mobile agent based wireless sensor network for intelligent maintenance. Lecture Notes in Computer Science. 2005, 3645, 316–325. [Google Scholar]
- Zhao, F.; Shin, J. Information-driven dynamic sensor collaboration for tracking applications. IEEE Signal Processing Magazine. 2002, 19, 61–72. [Google Scholar]
- Oshman, Y.; Davidson, P. Optimization of observer trajectories for bearings-only target localization. IEEE Transactions on Aerospace and Electronic Systems. 1999, 35, 892–902. [Google Scholar]
- Chhetri, A.S.; Morrell, D. Energy efficient target tracking in a sensor network using non-myopic sensor scheduling. Proceedings of International Conference on Information Fusion; 2005; pp. 558–565. [Google Scholar]
- Sobrinho, J.L. Algebra and algorithms for QoS path computation and hop-by-hop routing in the Internet. IEEE/ACM Transactions on Networking. 2002, 10, 541–550. [Google Scholar]
- Yang, L.; Feng, C. Adaptive tracking in distributed wireless sensor networks. Proceedings of IEEE International Symposium and Workshop on Engineering of Computer Based Systems; 2006; pp. 103–111. [Google Scholar]
- Yu, Y.; Cheng, Q. Particle filters for maneuvering target tracking problem. Signal Processing. 2006, 80, 195–203. [Google Scholar]
- Jourdan, D.B.; Weck, O.L. Layout optimization for a wireless sensor network using a multi-objective genetic algorithm. Proceedings of IEEE Vehicular Technology Conference; 2004; 5, pp. 2466–2470. [Google Scholar]
- Ting, T.O. A novel approach for unit commitment problem via an effective hybrid particle swarm optimization. IEEE Transactions on Power Systems. 2006, 21, 411–418. [Google Scholar]
- Jin, X.; Zhao, J.; Sun, Y. Distribution network reconfiguration for load balancing using binary particle swarm optimization. Proceedings of International conference on Power System Technology; 2004; pp. 507–510. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Fuzzy adaptive particle swarm optimization. Proceedings of Congress on Evolutionary Computation; 1999; pp. 1945–1950. [Google Scholar]


© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Wang, X.; Ma, J.-J.; Wang, S.; Bi, D.-W. Cluster-based Dynamic Energy Management for Collaborative Target Tracking in Wireless Sensor Networks. Sensors 2007, 7, 1193-1215. https://doi.org/10.3390/s7071193
Wang X, Ma J-J, Wang S, Bi D-W. Cluster-based Dynamic Energy Management for Collaborative Target Tracking in Wireless Sensor Networks. Sensors. 2007; 7(7):1193-1215. https://doi.org/10.3390/s7071193
Chicago/Turabian StyleWang, Xue, Jun-Jie Ma, Sheng Wang, and Dao-Wei Bi. 2007. "Cluster-based Dynamic Energy Management for Collaborative Target Tracking in Wireless Sensor Networks" Sensors 7, no. 7: 1193-1215. https://doi.org/10.3390/s7071193



