Development of a Space-charge-sensing System
Abstract
:1. Introduction
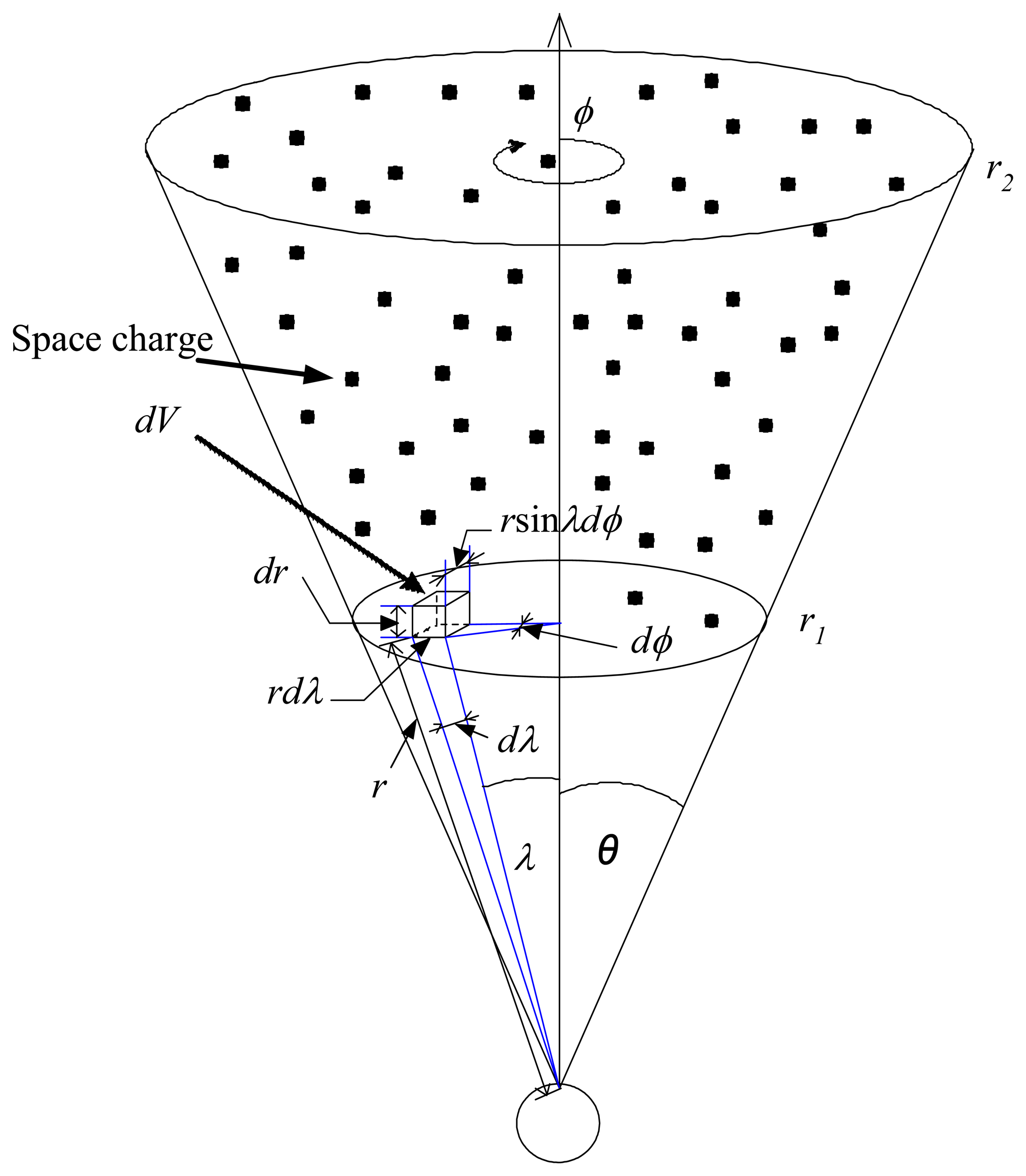
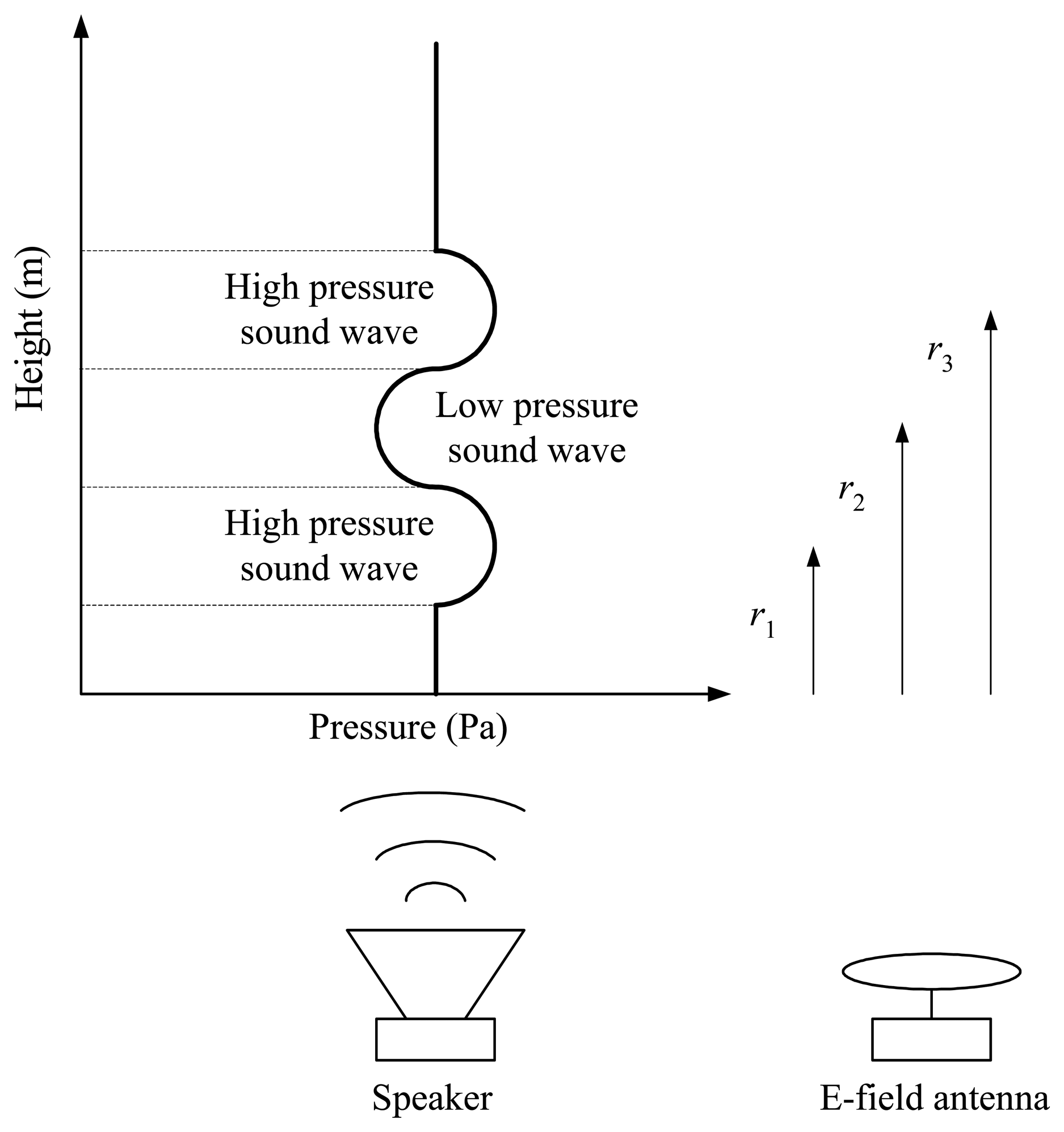
2. Theoretical Background
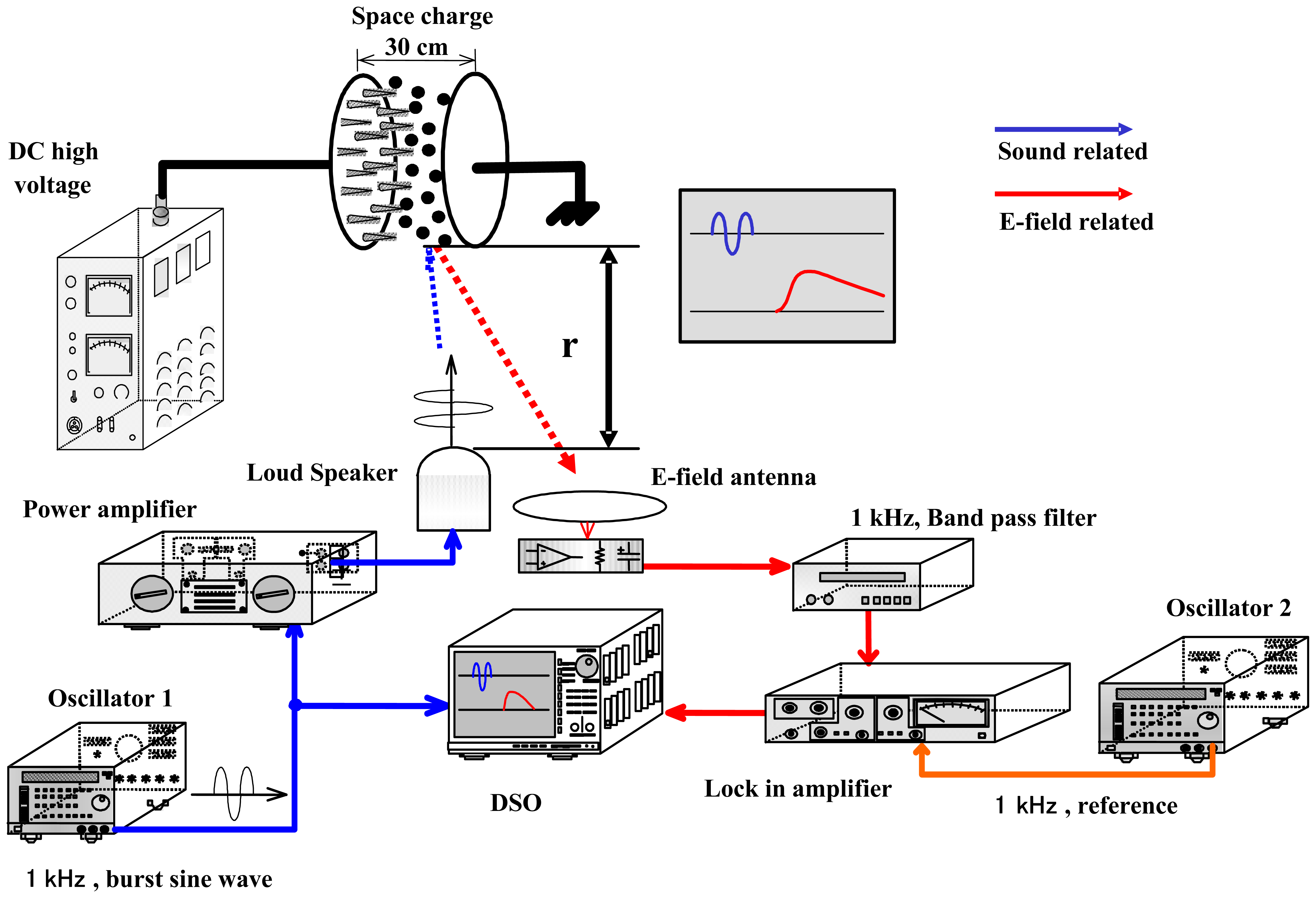
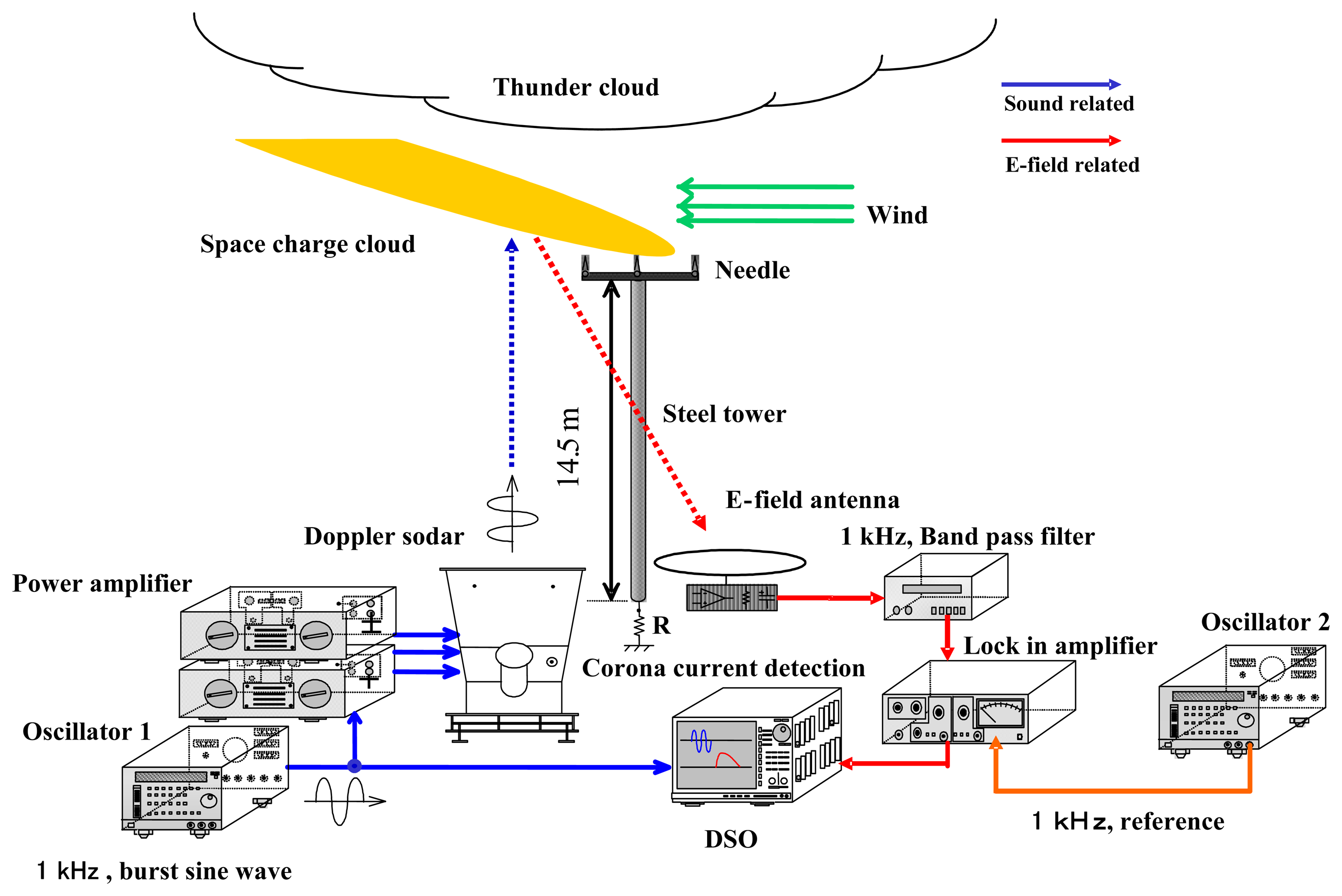
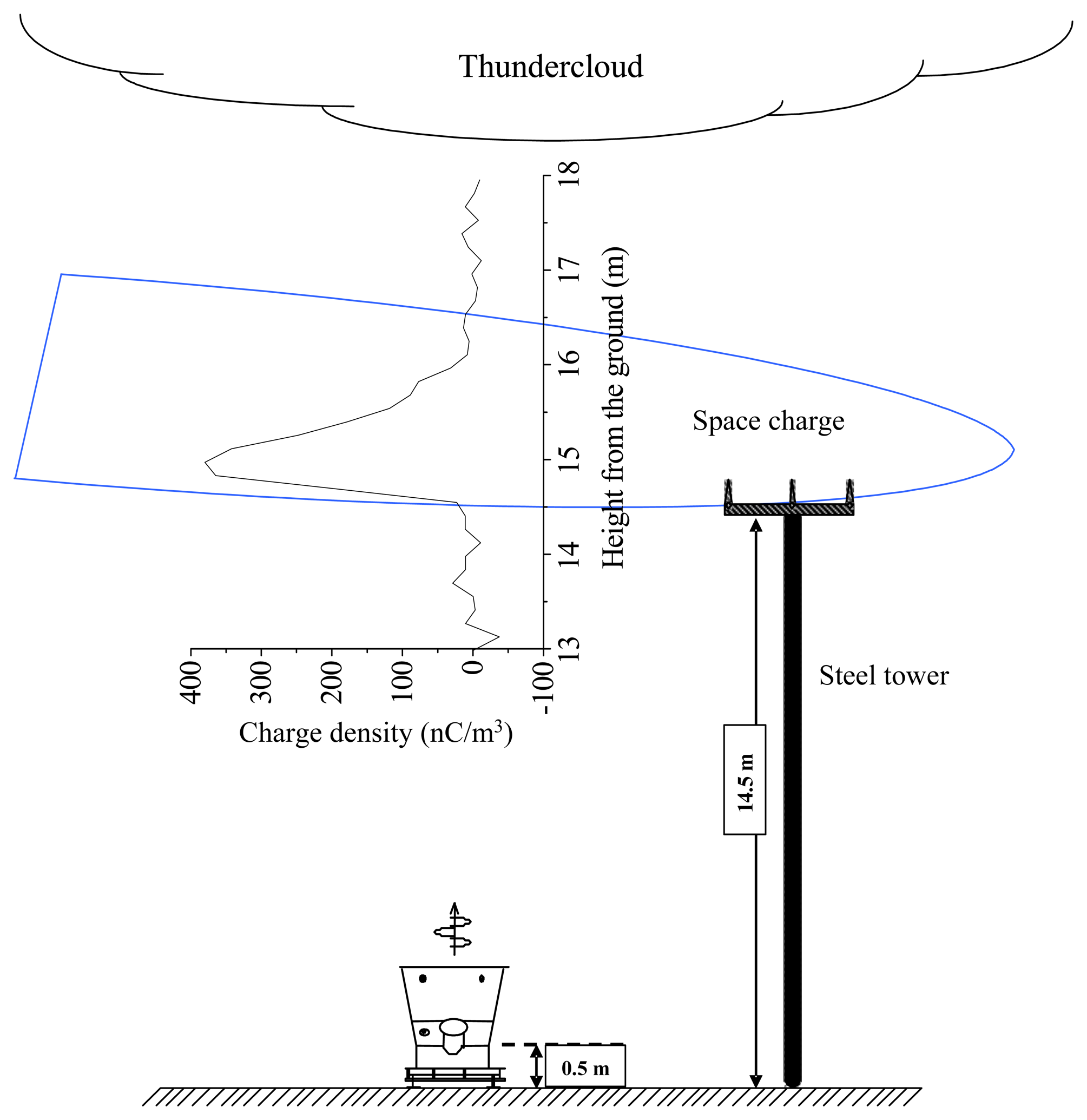
3. Experimental Set-up
4. Results
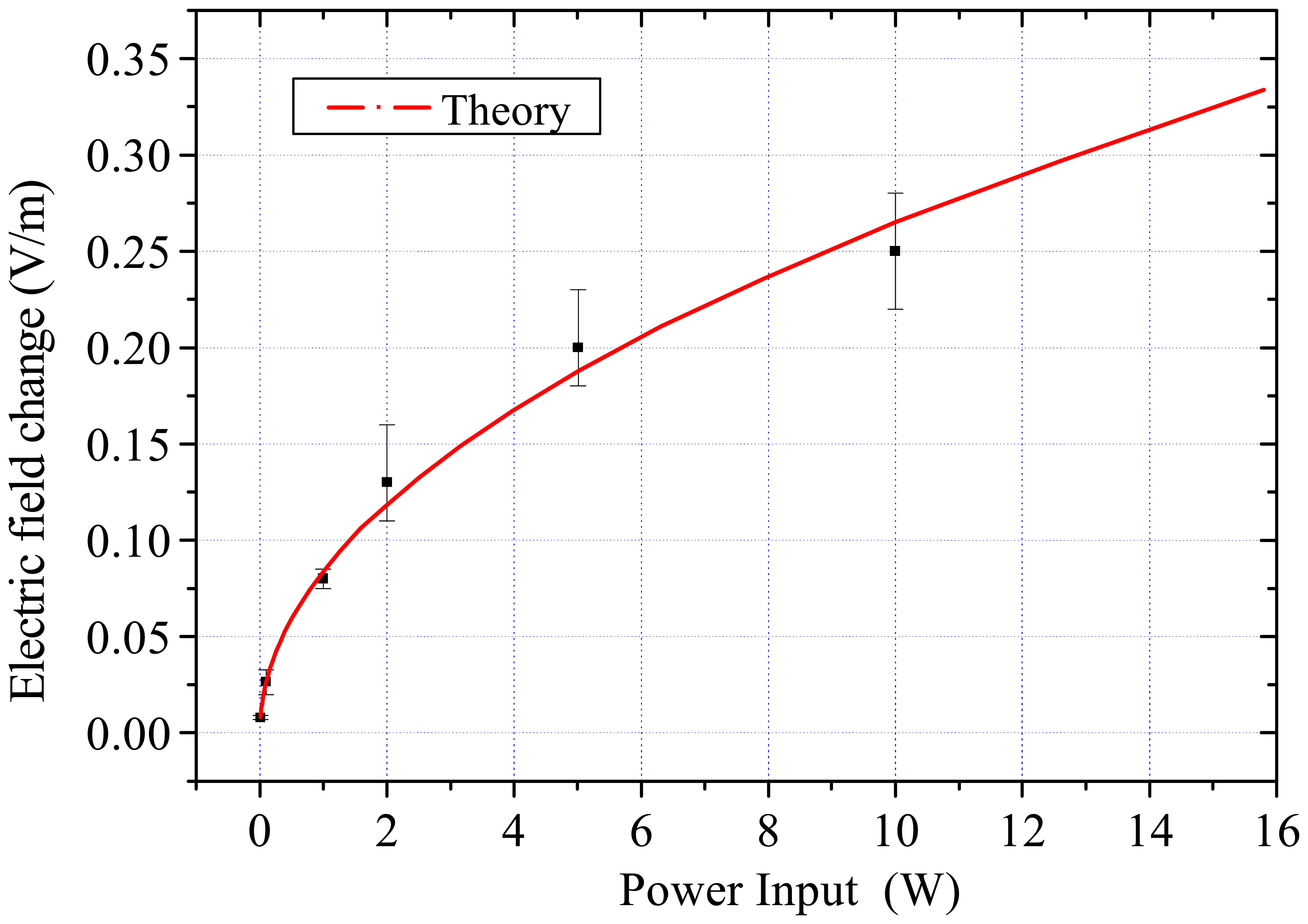
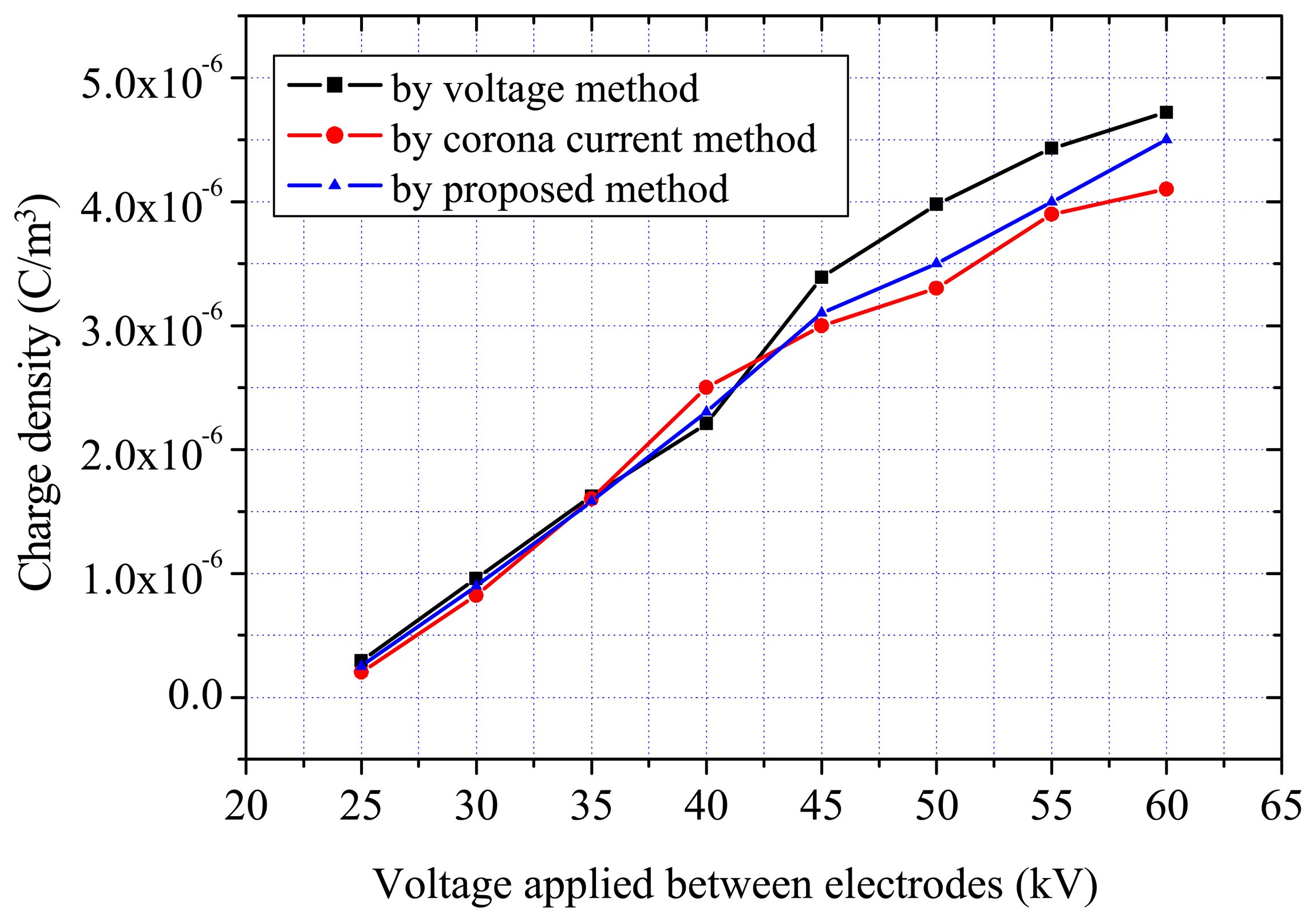
4.1 Results obtained in laboratory experiments
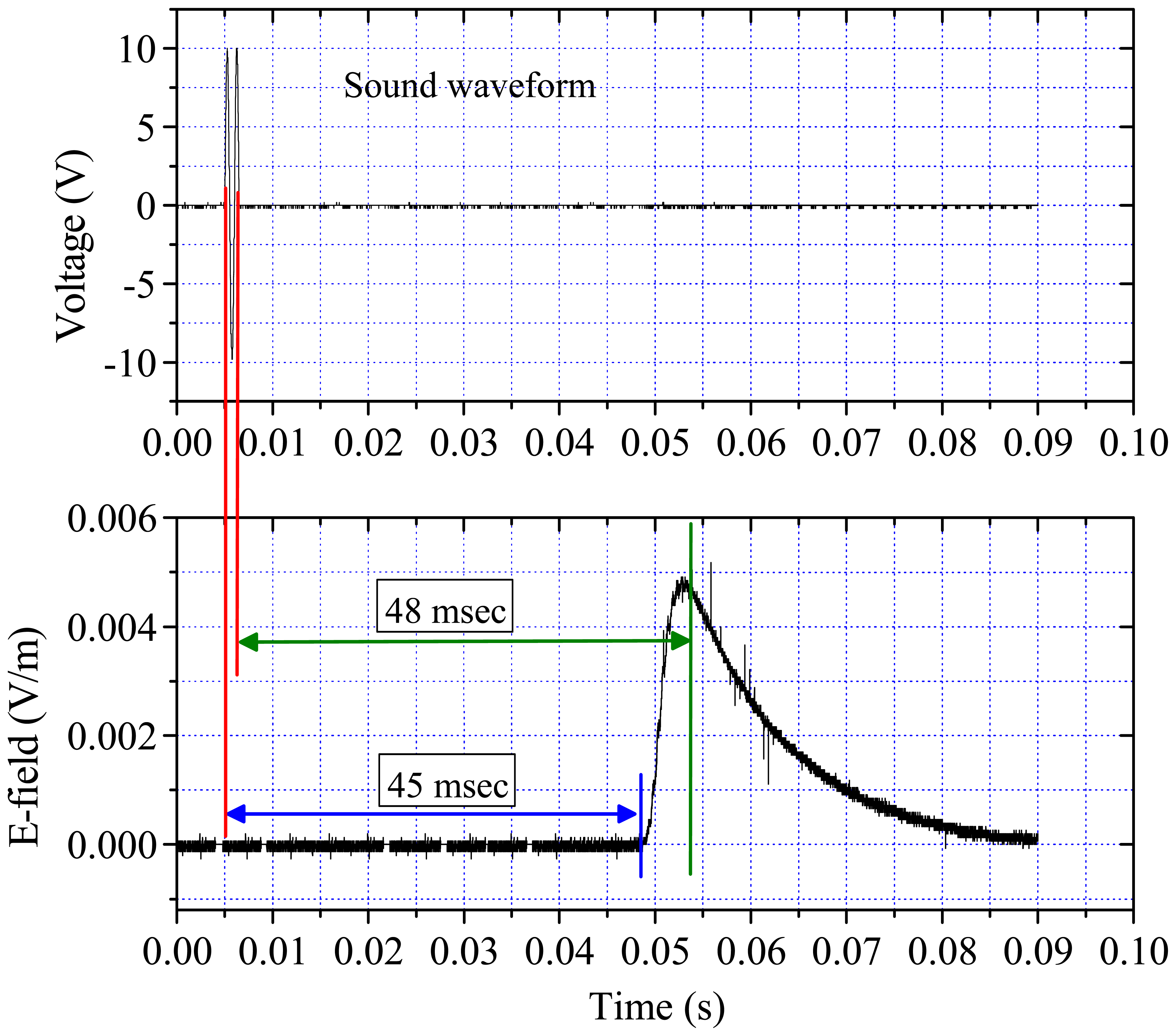
4.2 Results obtained in field experiments
5. Concluding Remarks
Acknowledgments
Appendix A Equations relating sound wave to electric field
- P = the entire pressure (Pa)
- P0 = the atmospheric pressure in steady state (1.013×105 Pa)
- A = amplitude of sound pressure (Pa)
- γ = the ratio of specific heat at constant pressure to constant volume (1.402)
- α = the attenuation constant
- ω = the angular frequency of the sound wave
- K = the wave number
- r = the propagation distance of the sound wave (m)
- c = the speed of sound (331.5 m s-1)
- f = the frequency of the sound wave (Hz)
- λ = wavelength (m)
- ρ = the air density (kg m-3)
- ρ0 = the air density in steady state (1.293 kg m-3)
- ρe = space charge density (C m-3)
- ρe0 = space charge density in steady state (1 nC m-3)
- A = amplitude of sound pressure (Pa)
- W = the sound power (Watt)
- S = area (m2)
- I = the sound intensity (Watt m-2)
References
- Bradley, W. E. Aircraft soundings of potential gradient, space charge and conduction current, and their relation to precipitation. J. Atmospheric Sciences 1968, 25, 863–870. [Google Scholar]
- Chauzy, S.; Medale, J. C.; Prieur, S.; Soula, S. Multilevel measurements of the electric field underneath a thundercloud, 1. A new system and the associated data processing. J. Geophys. Res. 1991, 96(D12), 22319–223326. [Google Scholar]
- Fahy, F. J. Sound Intensity; Elsevier Applied Science: London, U.K., 1989. [Google Scholar]
- Lauren, E. K.; Austin, R. F.; Alan, B. C.; James, V. S. Fundamentals of acoustics; John Willey & Sons: New York, 1982. [Google Scholar]
- Siscoe, G. L. On the possibility of measuring atmospheric space charge by use of sound waves. J. Geophys. Res. 1971, 76(18), 4153–4159. [Google Scholar]
- Soula, S.; Chauzy, S. Multilevel measurements of the electric field underneath a thundercloud, 2. Dynamical evolution of a ground space charge layer. J. Geophys. Res. 1991, 96(D12), 22327–22336. [Google Scholar]
- Marshall, T. C.; Rust, W. D. Two types of vertical electrical structures in stratiform precipitation regions of mesoscale convective systems. Bull. American Meteor. Soc. 1993, 74, 2159–2170. [Google Scholar]
- Tatsuoka, K. Electric field measurement by rocket under the thunderclouds. Proceedings of the 7th International Symposium on High Voltage Engineering, Dresden, Germany, Aug 26-30, 1991.
- Wang, D.; Morisita, S.; Yoshihasi, H.; Chen, M.; Takagi, N.; Watanabe, T. Remote sensing of space charge distribution with sound wave and radio wave. National Convention of the IEE Japan 1997. Paper No. 1728. [Google Scholar]
- Winn, W. P.; Moore, C. B. Electric field measurements in thunderclouds. J. Geophys. Res. 1971, 76(21), 5003–5071. [Google Scholar]

| Frequency band | 150 – 6000 Hz |
| Beam width | 16° |
| Input power | 900 W |
| Drive impedance | 4Ω |
| Height | 2.1 m |
© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Hazmi, A.; Takagi, N.; Wang, D.; Watanabe, T. Development of a Space-charge-sensing System. Sensors 2007, 7, 3058-3070. https://doi.org/10.3390/s7123058
Hazmi A, Takagi N, Wang D, Watanabe T. Development of a Space-charge-sensing System. Sensors. 2007; 7(12):3058-3070. https://doi.org/10.3390/s7123058
Chicago/Turabian StyleHazmi, Ariadi, Nobuyuki Takagi, Daohong Wang, and Teiji Watanabe. 2007. "Development of a Space-charge-sensing System" Sensors 7, no. 12: 3058-3070. https://doi.org/10.3390/s7123058




