Planar Array Sensor for High-speed Component Distribution Imaging in Fluid Flow Applications
Abstract
:1. Introduction
2. System design
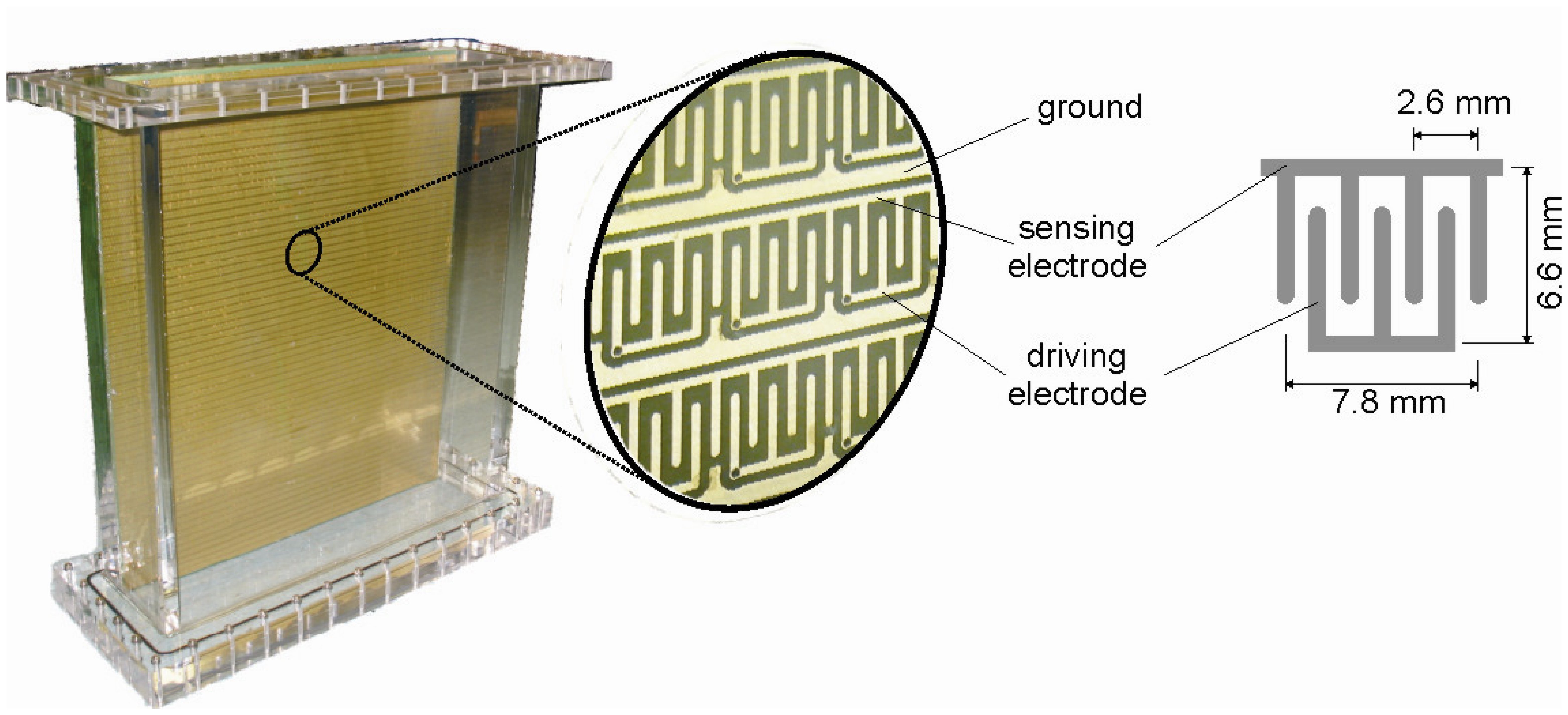
2.1. Interdigital array sensor
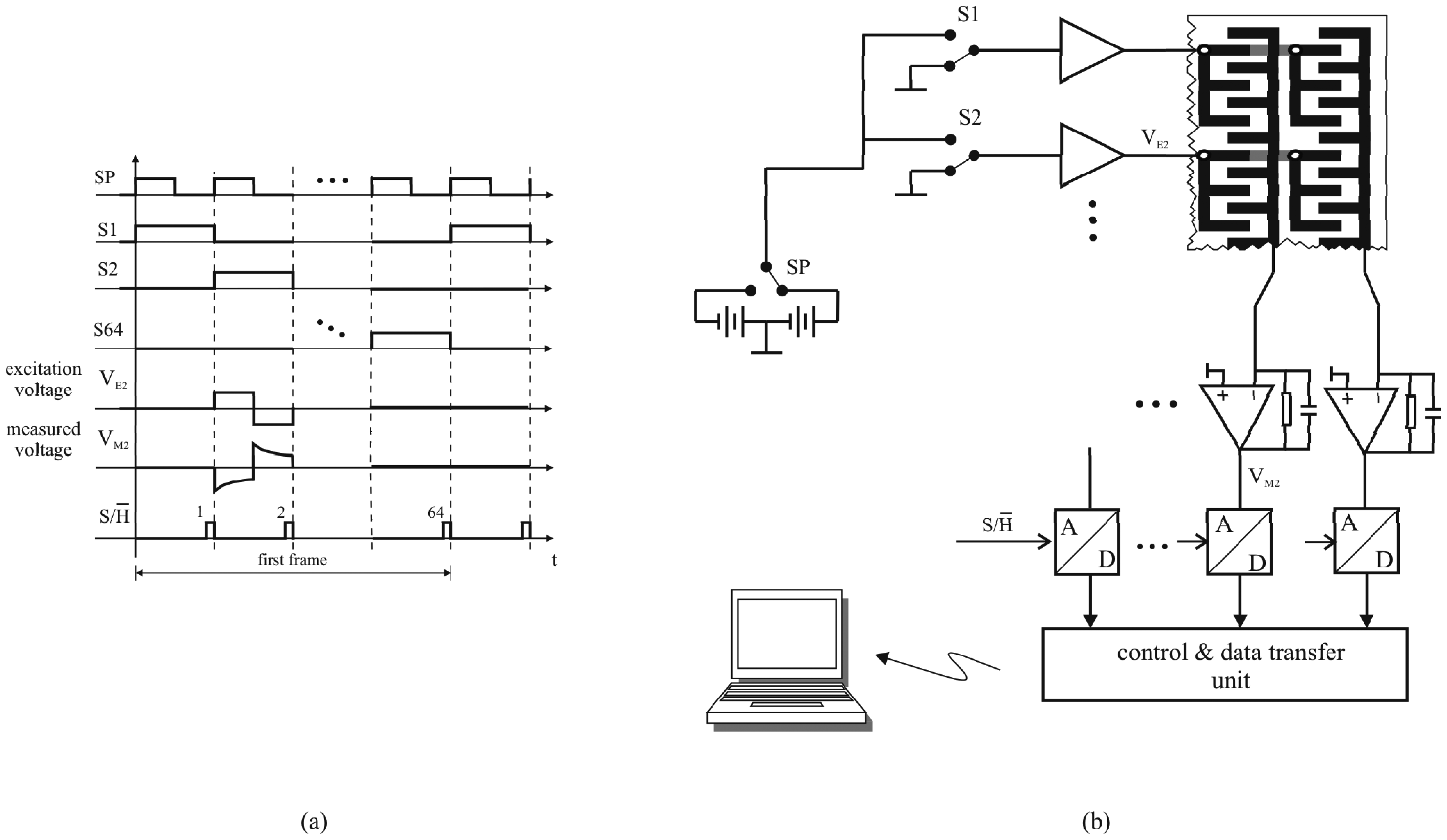
2.2. Measuring electronics
3. Interpreting the measured data
4. Sensor evaluation
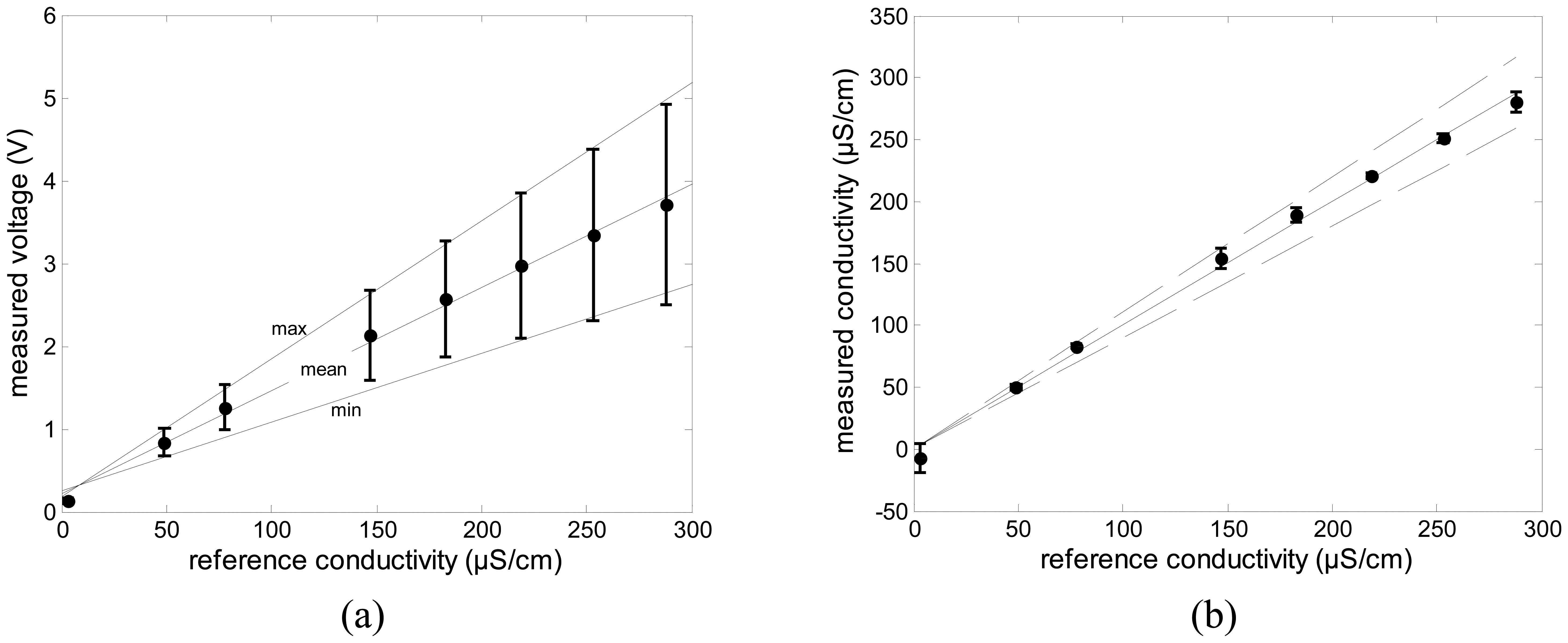
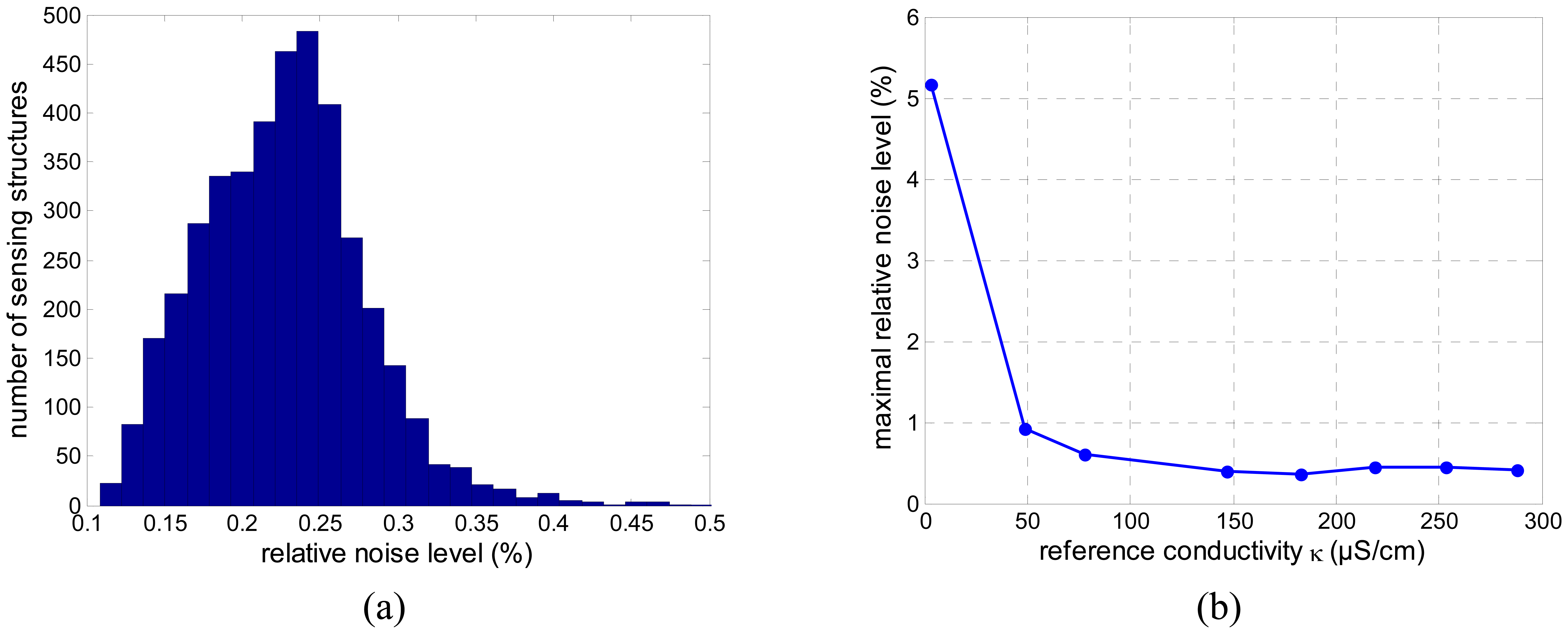
4.1. Accuracy in electrical conductivity measurement
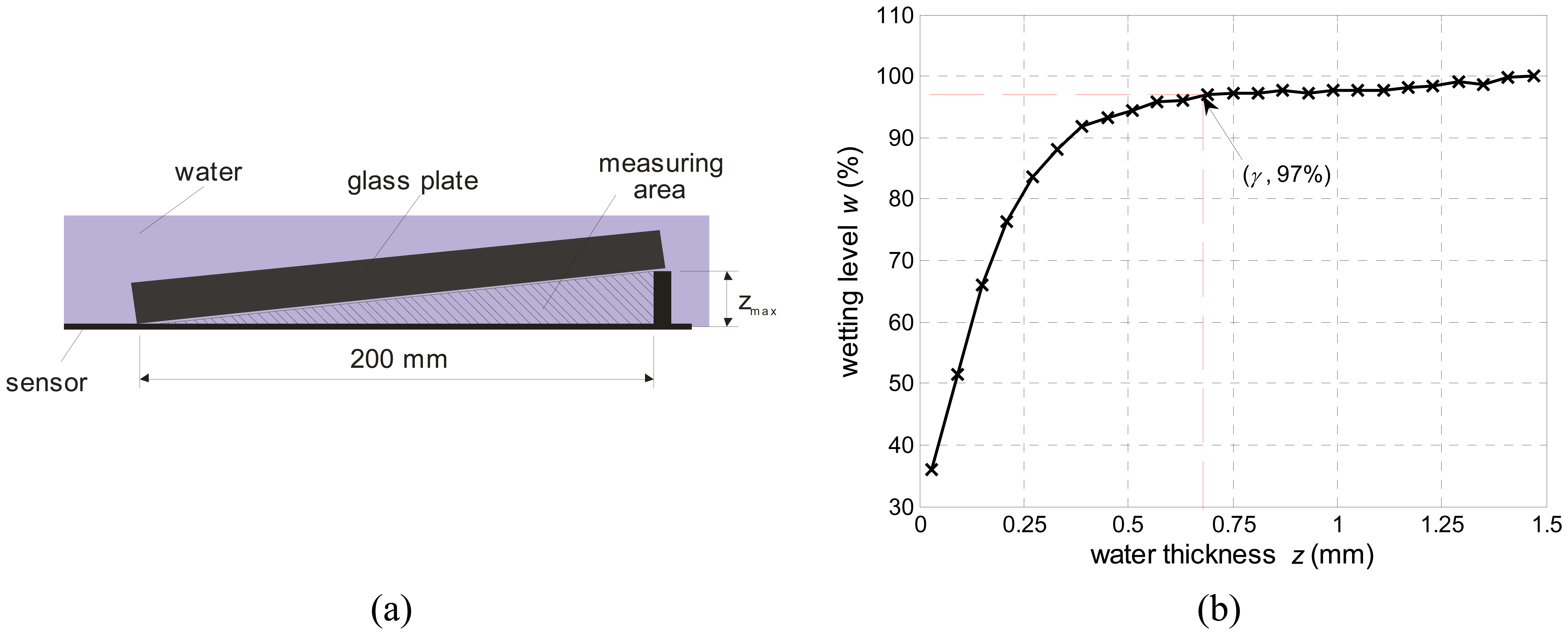
4.2. Depth sensitivity
5. Flow measurement
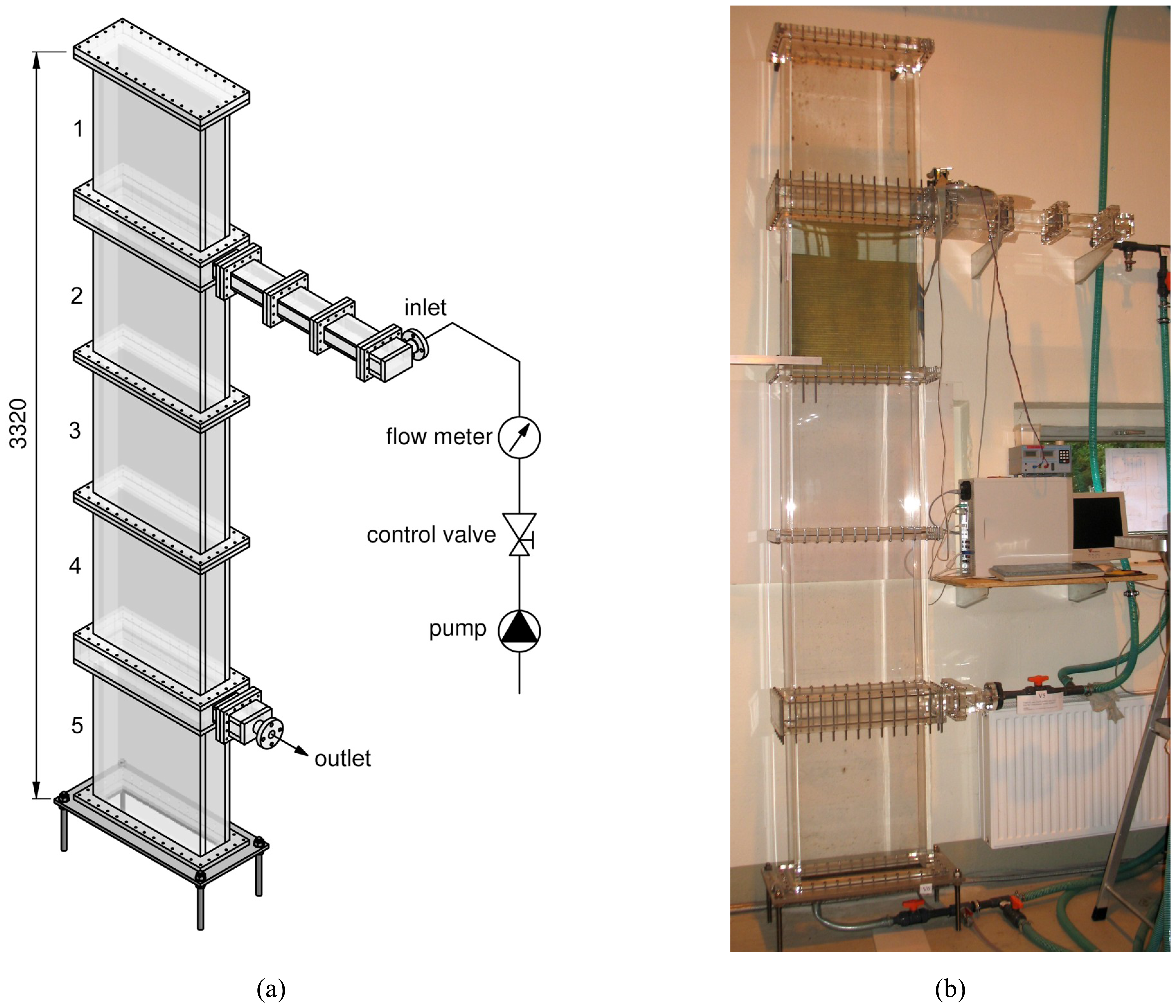
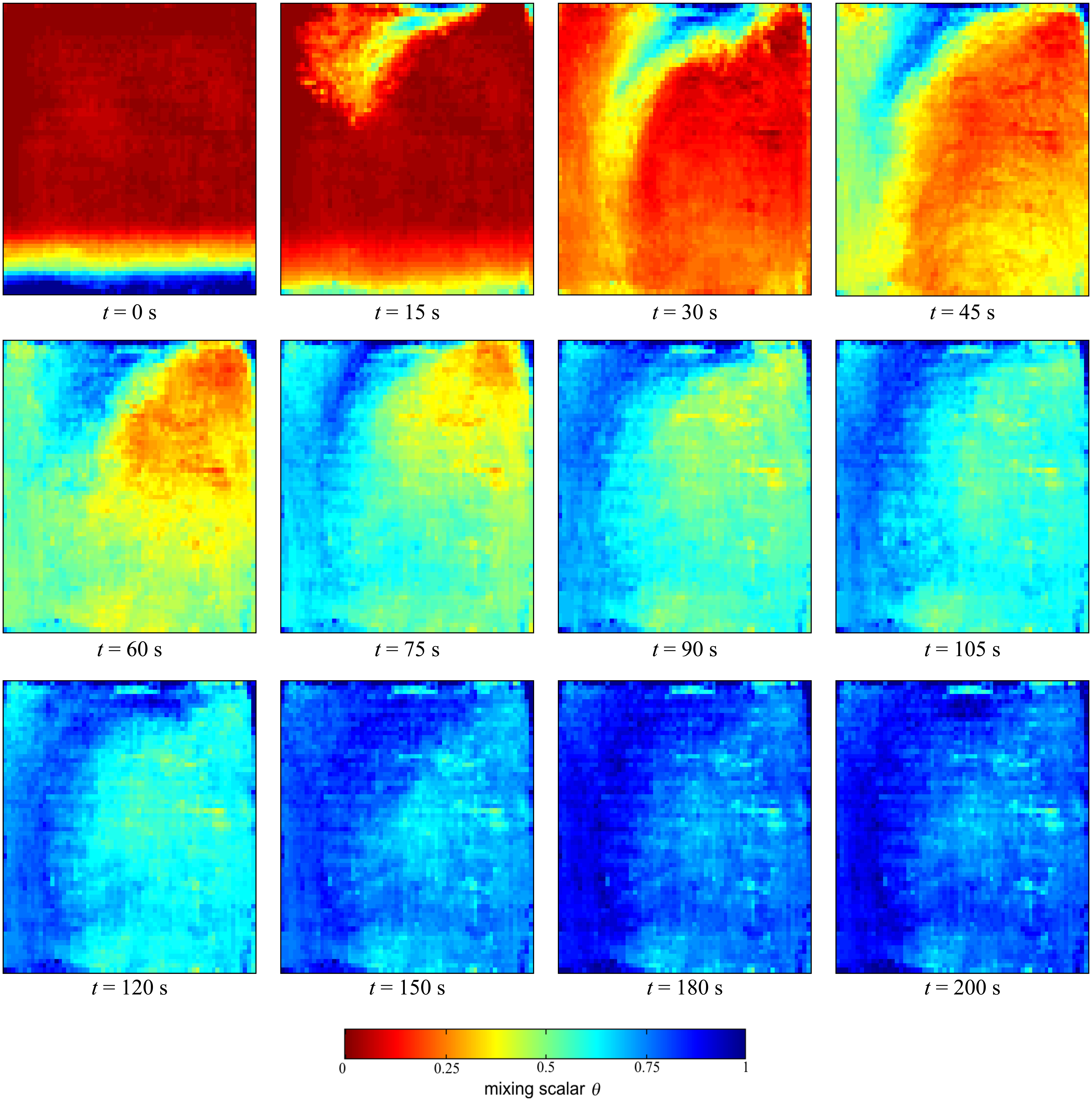
5.1. Buoyancy-driven flow
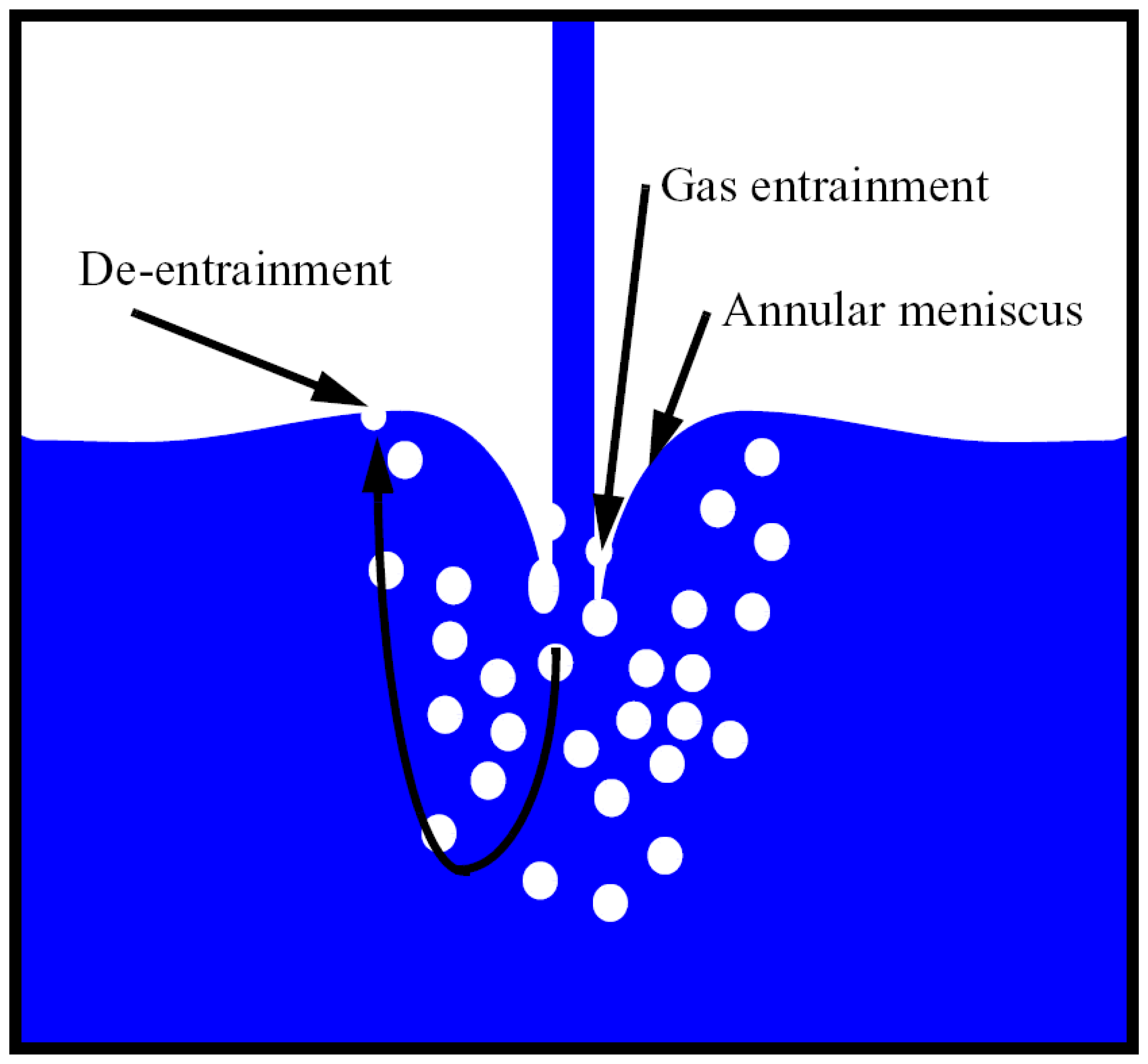
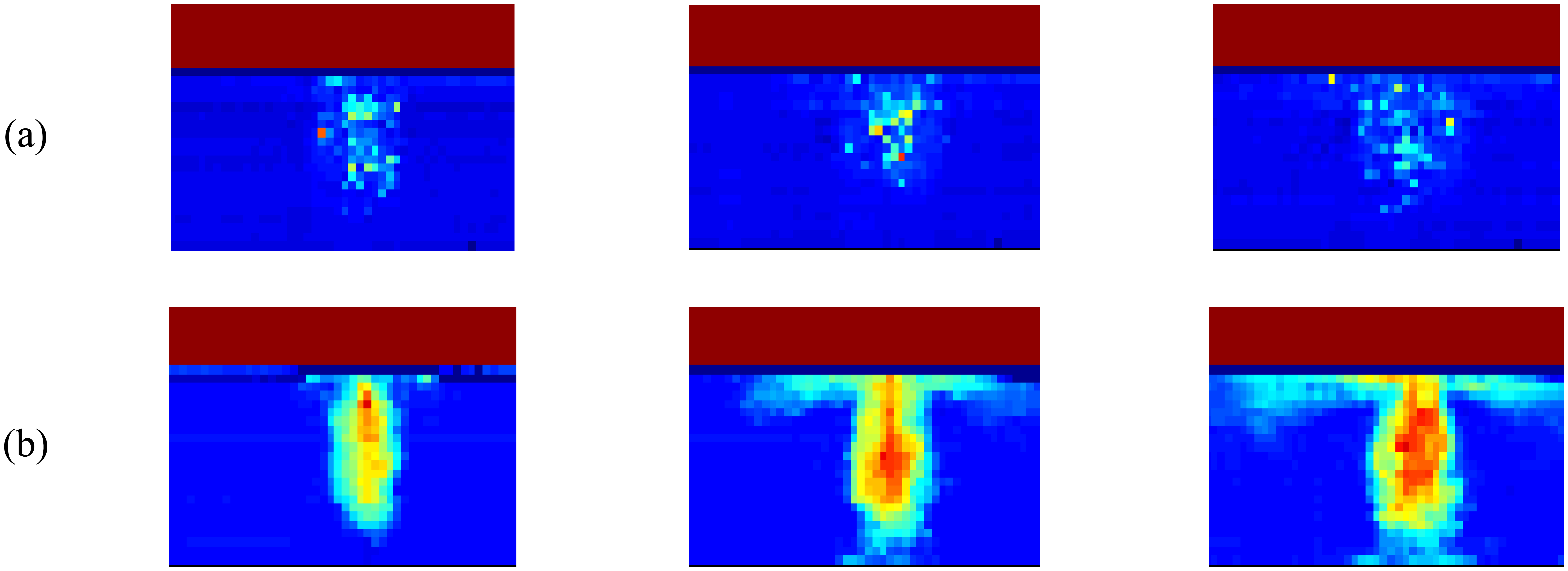
5.2. Plunging jet
5. Conclusions
Acknowledgments
References and Notes
- Mamishev, A.V.; Sundara-Rajan, K.; Yang, F.; Du, Y.; Zahn, M. Interdigital sensors and transducers. Proceedings of the IEEE 2004, 92, 808–845. [Google Scholar]
- Mukhopadhyay, S. C. Novel Planar Electromagnetic Sensors: Modeling and Performance Evaluation. Sensors 2005, 5, 546–579. [Google Scholar]
- Kaatze, U.; Feldman, Y. Broadband dielectric spectrometry of liquids and biosystems. Measurement Science and Technology 2006, 17, R17–R35. [Google Scholar]
- Wittstock, G. Sensor arrays and array sensors. Analytical and Bioanalytical Chemistry 2002, 372, 16–17. [Google Scholar]
- Gardner, J.W.; Pike, A.; de Rooij, N. F.; Koudelka-Hep, M.; Clerc, P.A.; Hierlemann, A.; Opel, W.G. Integrated array sensor for detecting organic solvents. Sensors and Actuators B 1995, 26-27, 135–139. [Google Scholar]
- Hermes, T.; Bühner, M.; Bücher, S.; Sundermeier, C.; Dumschat, C.; Borchardt, M.; Cammann, K.; Knoll, M. An amperometric microsensor array with 1024 individually addressable elements for two-dimensional concentration mapping. Sensors and Actuators B 1994, 21, 33–37. [Google Scholar]
- Wang, H.X.; Yin, W.; Yang, W.Q.; Beck, M.S. Optimum design of segmented capacitance sensing array for multi-phase interface measurement. Measurement Science and Technology 1996, 7, 79–86. [Google Scholar]
- Li, X.B.; Larson, S.D.; Zyuzin, A.S.; Mamishev, A.V. Design Principles for Multichannel Fringing Electric Field Sensors. IEEE Sensors 2006, 6, 434–440. [Google Scholar]
- Prasser, H.M.; Böttger, A.; Zschau, J. A New Electrode-Mesh Tomograph for Gas-Liquid Flows. Flow Measurement and Instrumentation 1998, 9, 111–119. [Google Scholar]
- Prasser, H.M.; Zschau, J.; Peters, D.; Pietzsch, G.; Taubert, W.; Trepte, M. Fast wire-mesh sensors for gas-liquid flows – Visualization with up to 10,000 frames per second. Proceedings of ICAPP, Hollywood, Florida; 2002. Paper No. 1055. [Google Scholar]
- ISO Guide to the expression of uncertainty in measurement (GUM); ISO Publishing, 1995.
- Rohde, U.; Kliem, S.; Höhne, T.; Karlsson, R.; Hemström, B.; Lillington, J.; Toppila, T.; Elter, J.; Bezrukov, Y. Fluid mixing and flow distribution in the reactor circuit, measurement data base. Nuclear Engineering and Design 2005, 235, 421–443. [Google Scholar]
- Prasser, H.-M.; Grunwald, G.; Höhne, T.; Kliem, S.; Rohde, U.; Weiss, F.-P. Coolant mixing in a pressurized water reactor: deboration transients, steam-line breaks, and emergency core cooling injection. Nuclear Technology 2003, 143, 37–56. [Google Scholar]
- Höhne, T.; Kliem, S.; Bieder, U. Modeling of a buoyancy-driven flow experiment at the ROCOM test facility using the CFD-codes CFX-5 and TRIO_U. Nuclear Engineering and Design 2006, 12, 1309–1325. [Google Scholar]
- Lucas, D.; Bestion, D.; Bodèle, E.; Scheuerer, M.; D'Auria, F.; Mazzini, D.; Smith, B.; Tiselj, I.; Martin, A.; Lakehal, D.; Seynhaeve, J.-M.; Kyrki-Rajamäki, R.; Ilvonen, M.; Macek, J. On the simulation of two-phase flow pressurized thermal shock (PTS). 12th International Topical Meeting on Nuclear Reactor Thermal Hydraulics (NURETH-12), Pittsburgh, Pennsylvania, U.S.A., Sept 30 - Oct 4, 2007. Paper No. 035.
- Lucas, D. (Ed.) Review Identification of relevant PTS-scenarios, state of the art of modeling and needs for model improvements. 6th Euratom Framework Program NURESIM. Deliverable D2.1.1. 2005. Available at: http://www.nuresim.com/Documents/Document%20Library/SP2%20-%20Thermalhydraulics/Reports/D2.1.1_final.pdf.
- Reungoat, D.; Riviere, N.; Faure, J.P. 3C PIV and PLIF measurement in turbulent mixing - Round jet impingement. Journal of Visualization 2007, 10, 99–110. [Google Scholar]
- Bonetto, F.; Lahey, R.T., Jr. An experimental study on air carry-under due to a plunging liquid jet. International Journal of Multiphase Flow 1993, 19, 281–294. [Google Scholar]
- Chanson, H.; Manasseh, R. Air Entrainment Processes in a Circular Plunging Jet: Void-Fraction and Acoustic Measurements. Journal of Fluids Engineering 2003, 125, 910–921. [Google Scholar]
© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Da Silva, M.J.; Sühnel, T.; Schleicher, E.; Vaibar, R.; Lucas, D.; Hampel, U. Planar Array Sensor for High-speed Component Distribution Imaging in Fluid Flow Applications. Sensors 2007, 7, 2430-2445. https://doi.org/10.3390/s7102430
Da Silva MJ, Sühnel T, Schleicher E, Vaibar R, Lucas D, Hampel U. Planar Array Sensor for High-speed Component Distribution Imaging in Fluid Flow Applications. Sensors. 2007; 7(10):2430-2445. https://doi.org/10.3390/s7102430
Chicago/Turabian StyleDa Silva, Marco Jose, Tobias Sühnel, Eckhard Schleicher, Roman Vaibar, Dirk Lucas, and Uwe Hampel. 2007. "Planar Array Sensor for High-speed Component Distribution Imaging in Fluid Flow Applications" Sensors 7, no. 10: 2430-2445. https://doi.org/10.3390/s7102430



