Multi-agent Negotiation Mechanisms for Statistical Target Classification in Wireless Multimedia Sensor Networks
Abstract
:1. Introduction
2. Related Work
2.1. Multi-agent architecture of WSNs
2.2. Multi-agent negotiation
2.3. Statistical dimension reduction and classification
3. Negotiation Mechanisms for Target Classification
3.1. Hierarchical multi-agent architecture for WMSNs
3.2. Agent reasoning model and communication language
3.3. Two phase negotiation mechanisms
3.3.1. Phase one: task allocation
- Objective 1:
- A negotiation should be bounded by time, which means whether successful or not, a negotiation should complete within a predefined time window.
- Objective 2:
- Each step of the negotiation should be fast, so that the negotiation process that consists of multiple steps will be finished quickly.
- Objective 3:
- A negotiation should be kept short, that is, the number of iterations should be minimized.
- Objective 4:
- The negotiation-related messages should be kept short so as to reduce loss and improve communication speed.
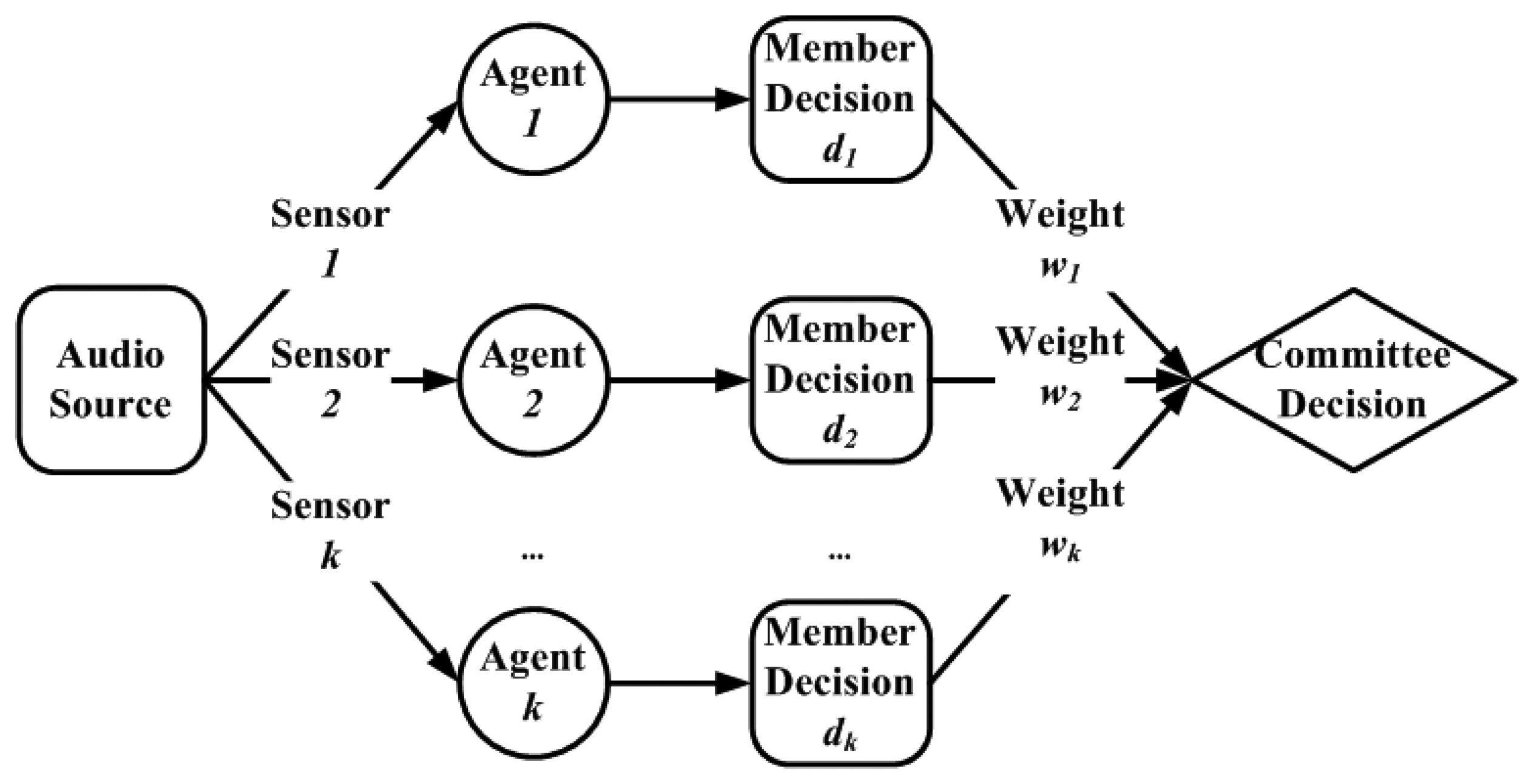
3.3.2. Phase two: combination of individual decisions
4. Statistical Dimension Reduction and Classification
4.1 Feature extraction
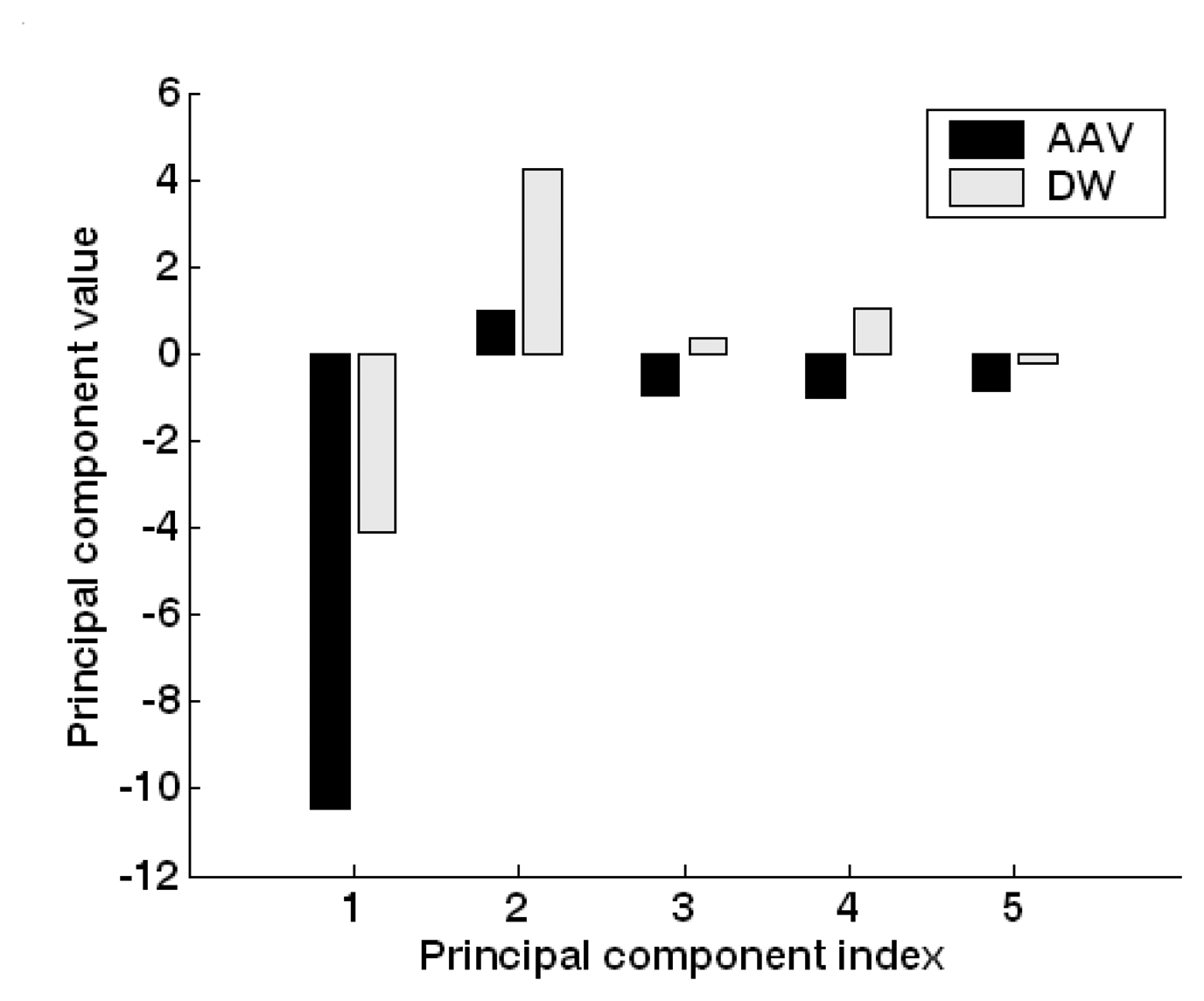
4.2. PCA dimension reduction
4.3. Gaussian process classification
 (0,K) with the mean of 0. The covariance matrix K is parameterized by θ which is generally referred to as hyper-parameter. In other words, the covariance matrix is defined by its elements Kij = k(xi,xj, θ), where k is a covariance function. Following Bayes' rule, the posterior distribution of the latent function for given θ and D can be expressed as [32]
(0,K) with the mean of 0. The covariance matrix K is parameterized by θ which is generally referred to as hyper-parameter. In other words, the covariance matrix is defined by its elements Kij = k(xi,xj, θ), where k is a covariance function. Following Bayes' rule, the posterior distribution of the latent function for given θ and D can be expressed as [32]
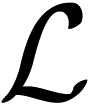 (f) = In p(y∣ f) and
(f) = In p(y∣ f) and
5. Experiments
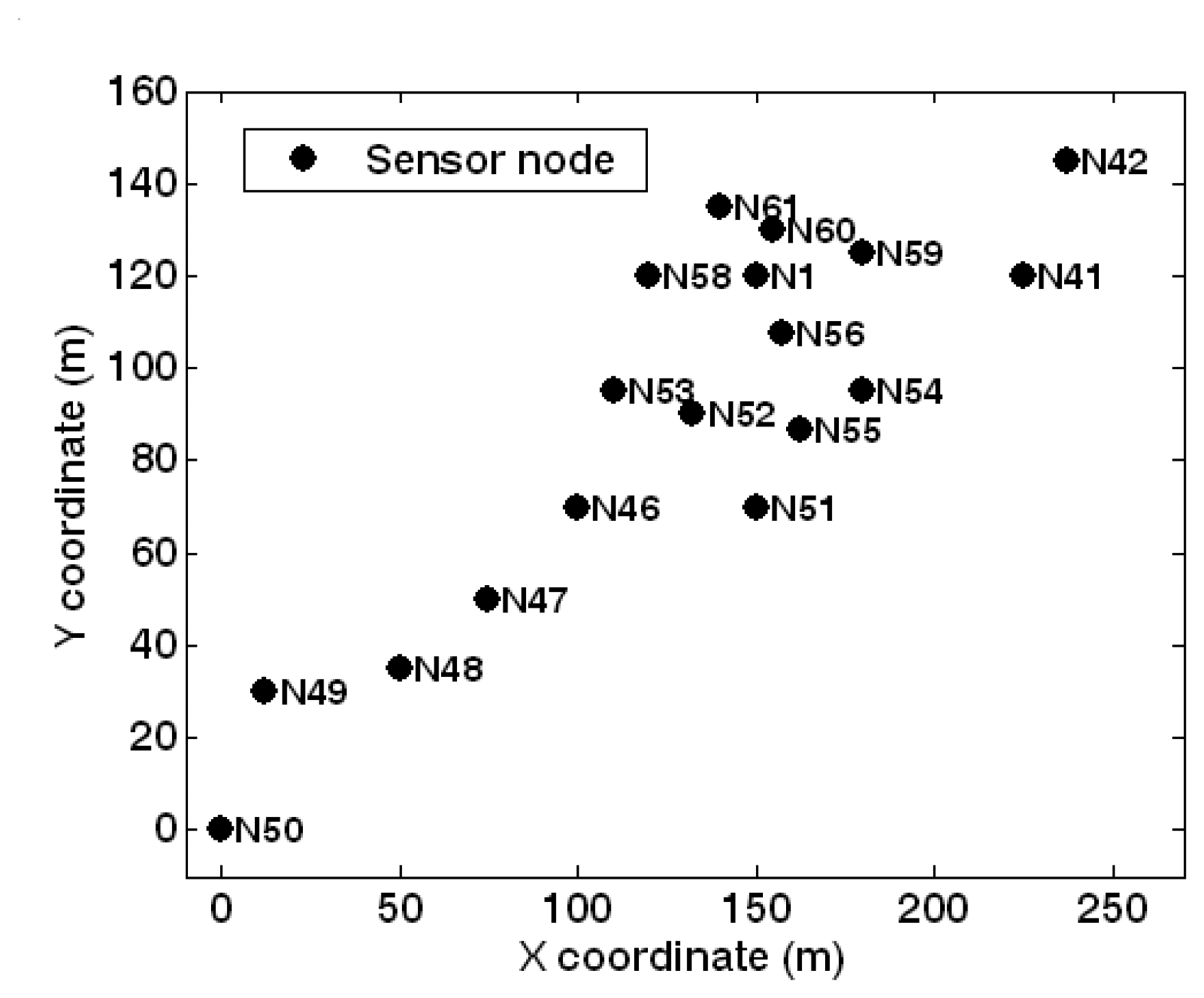
5.1. Experimental setup
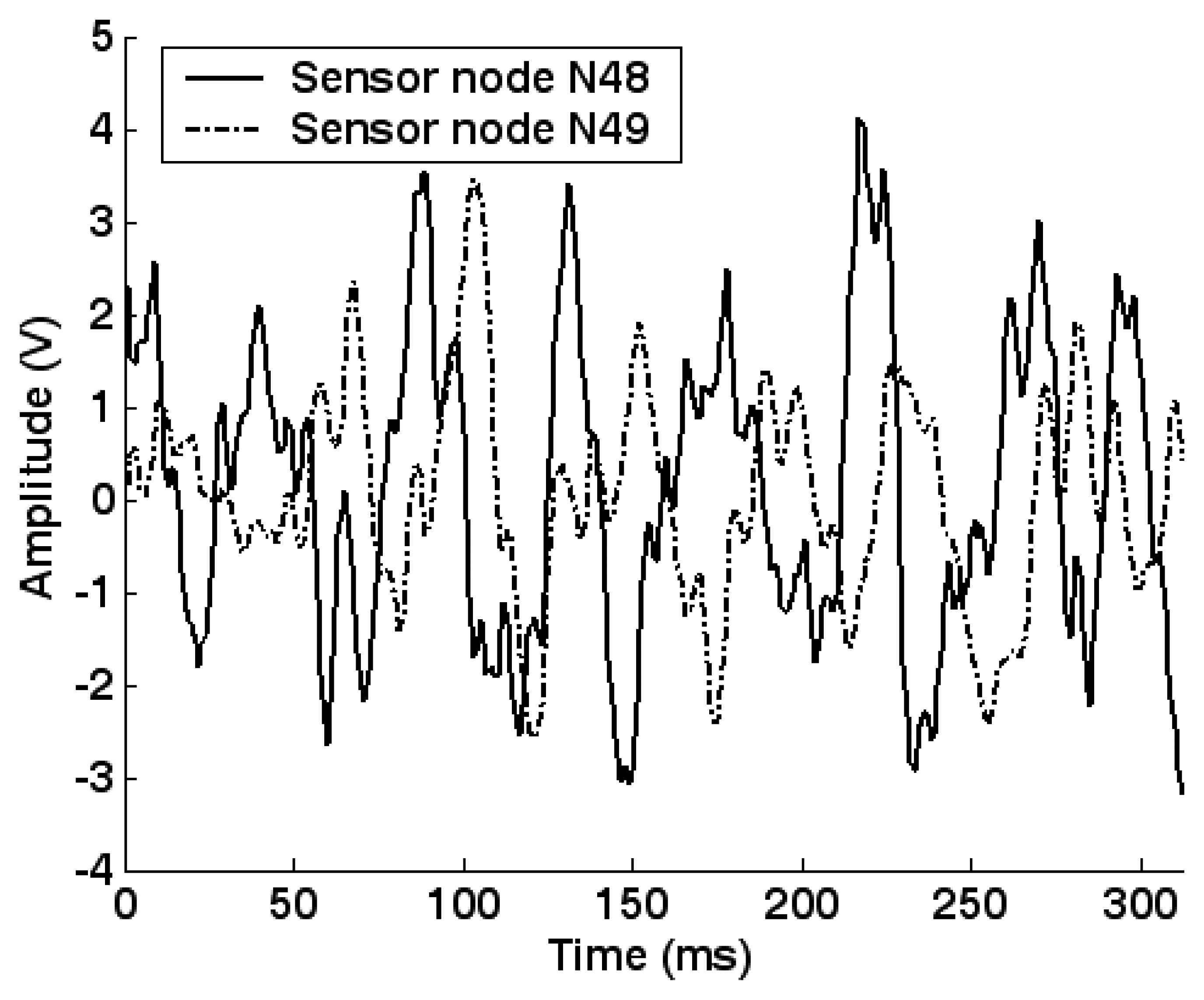
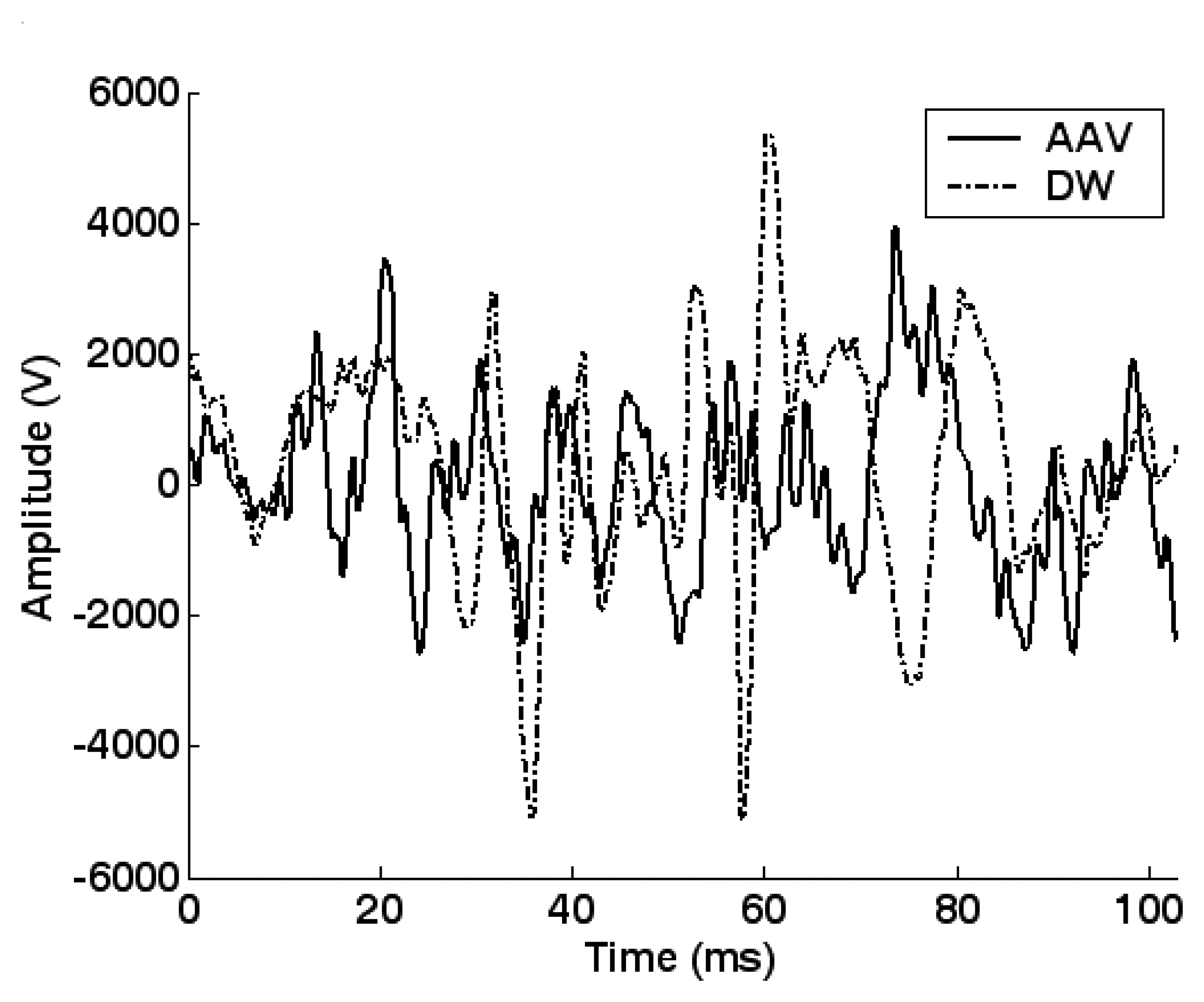
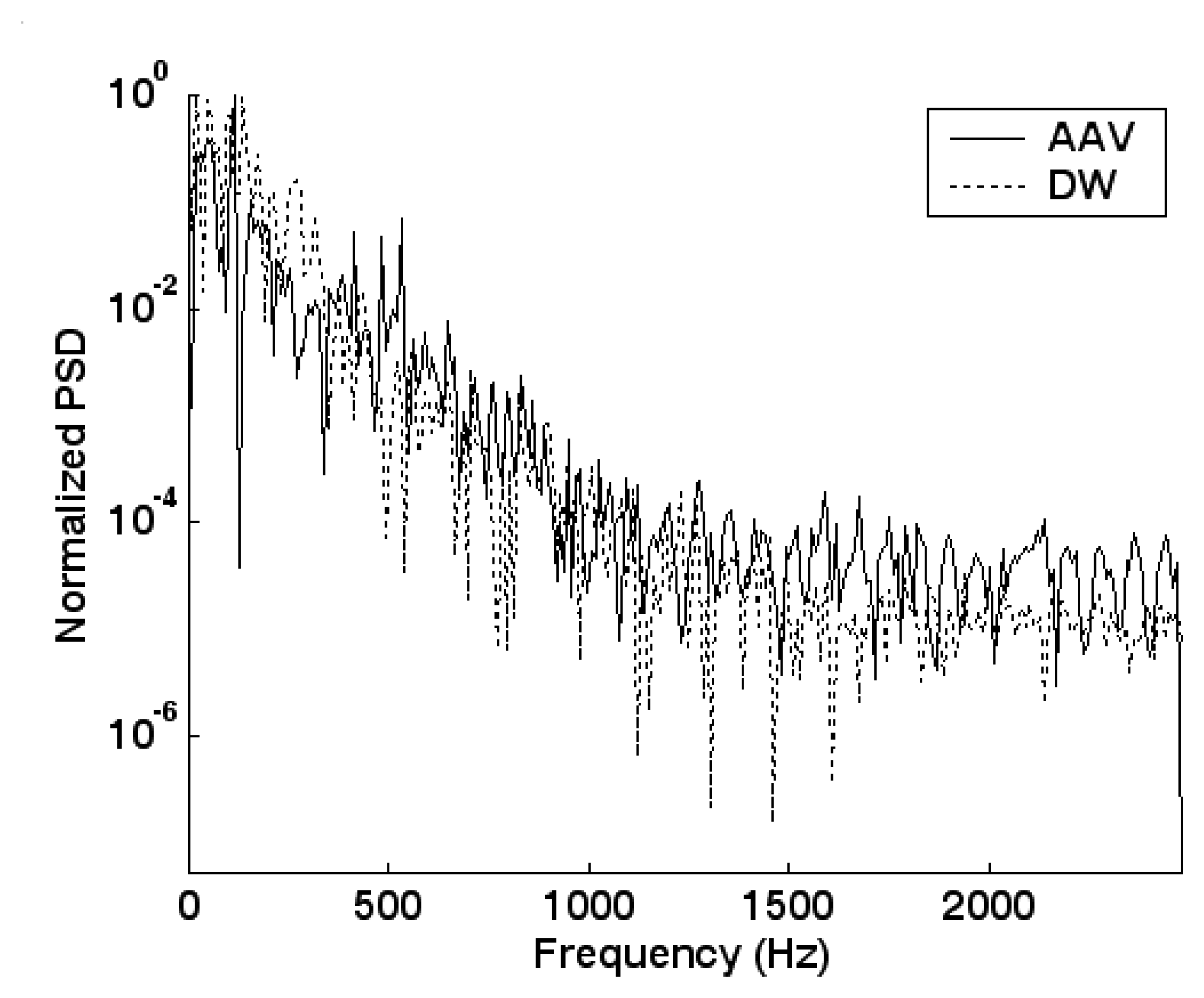
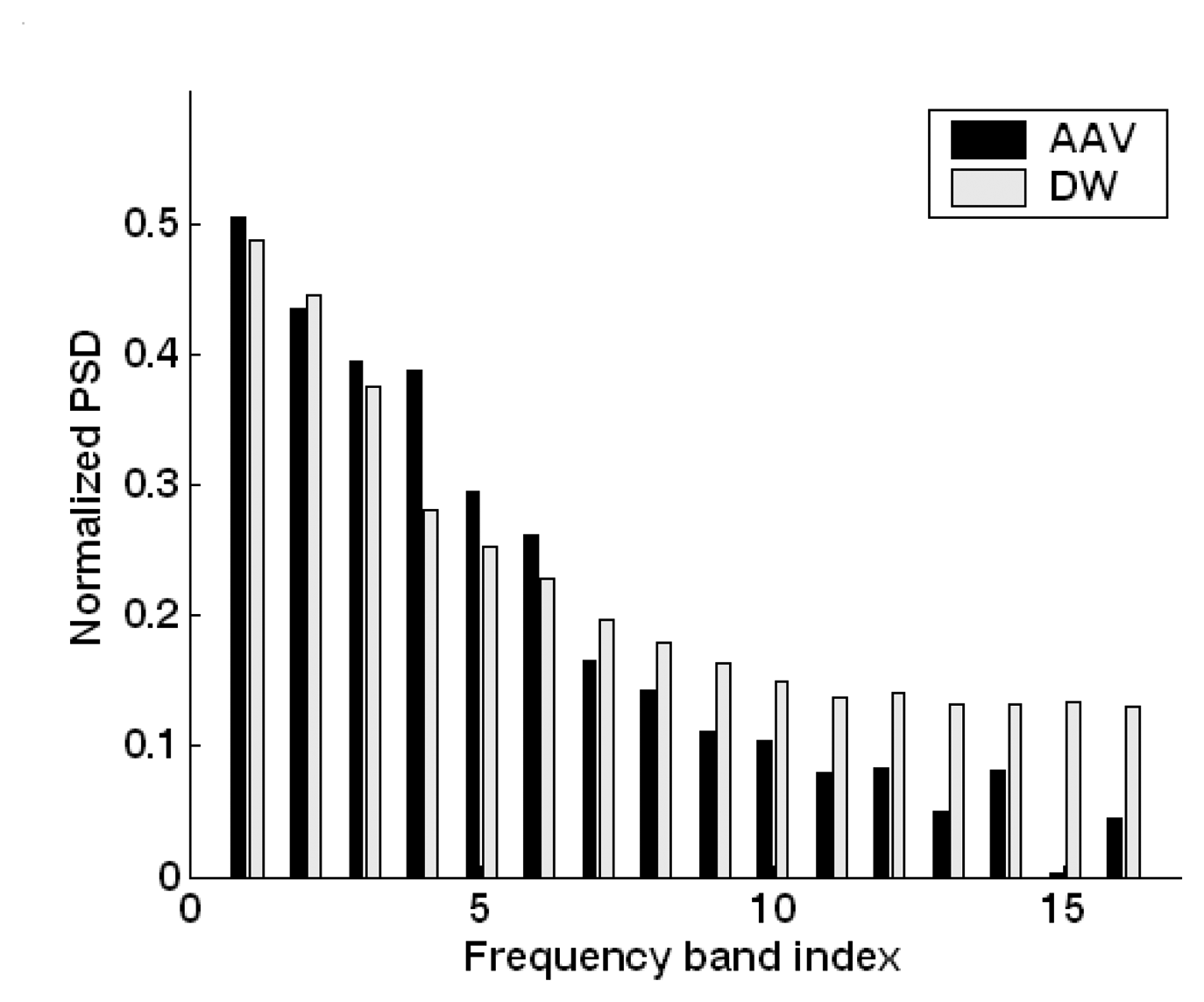
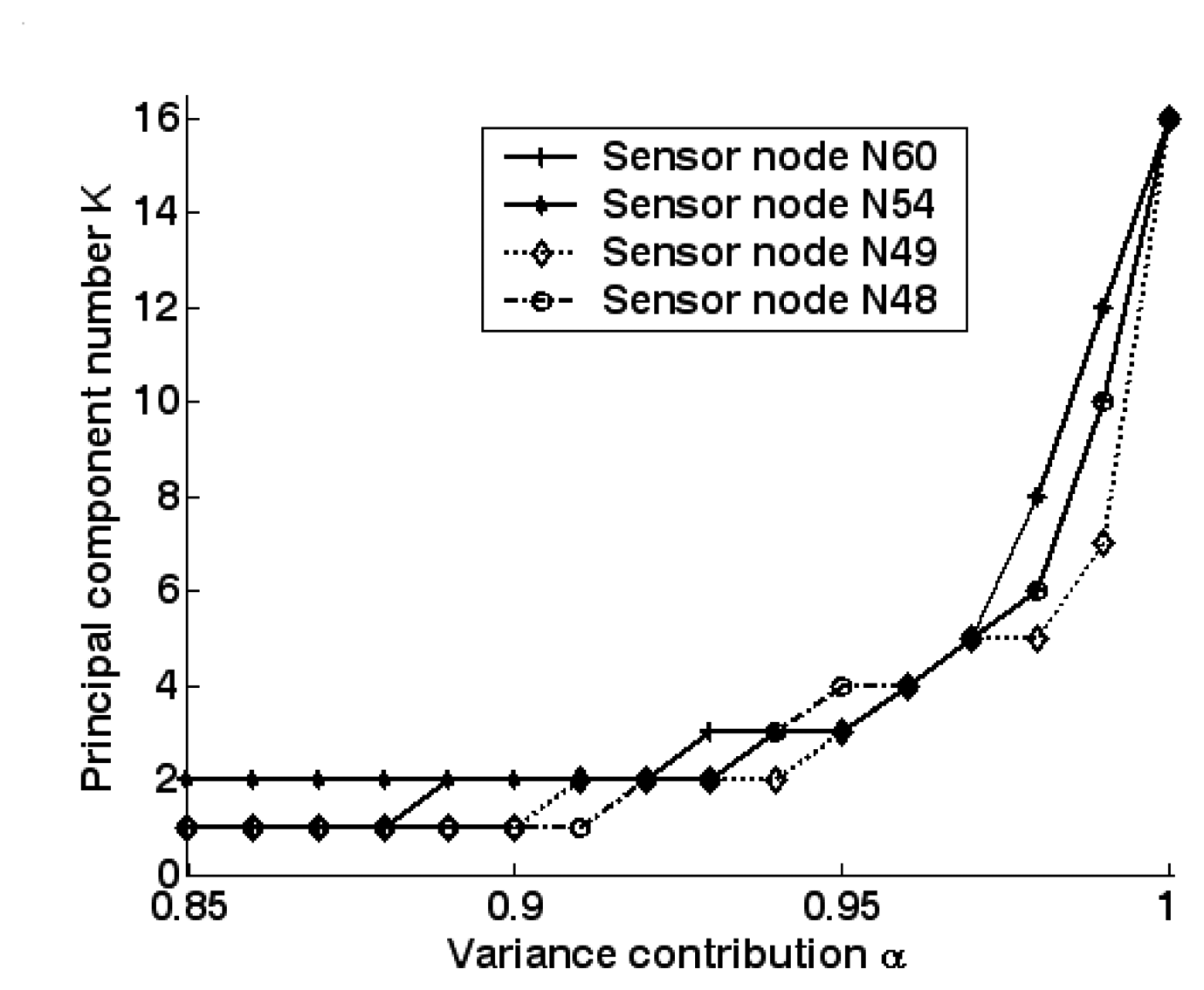
5.2. Feature extraction and dimension reduction
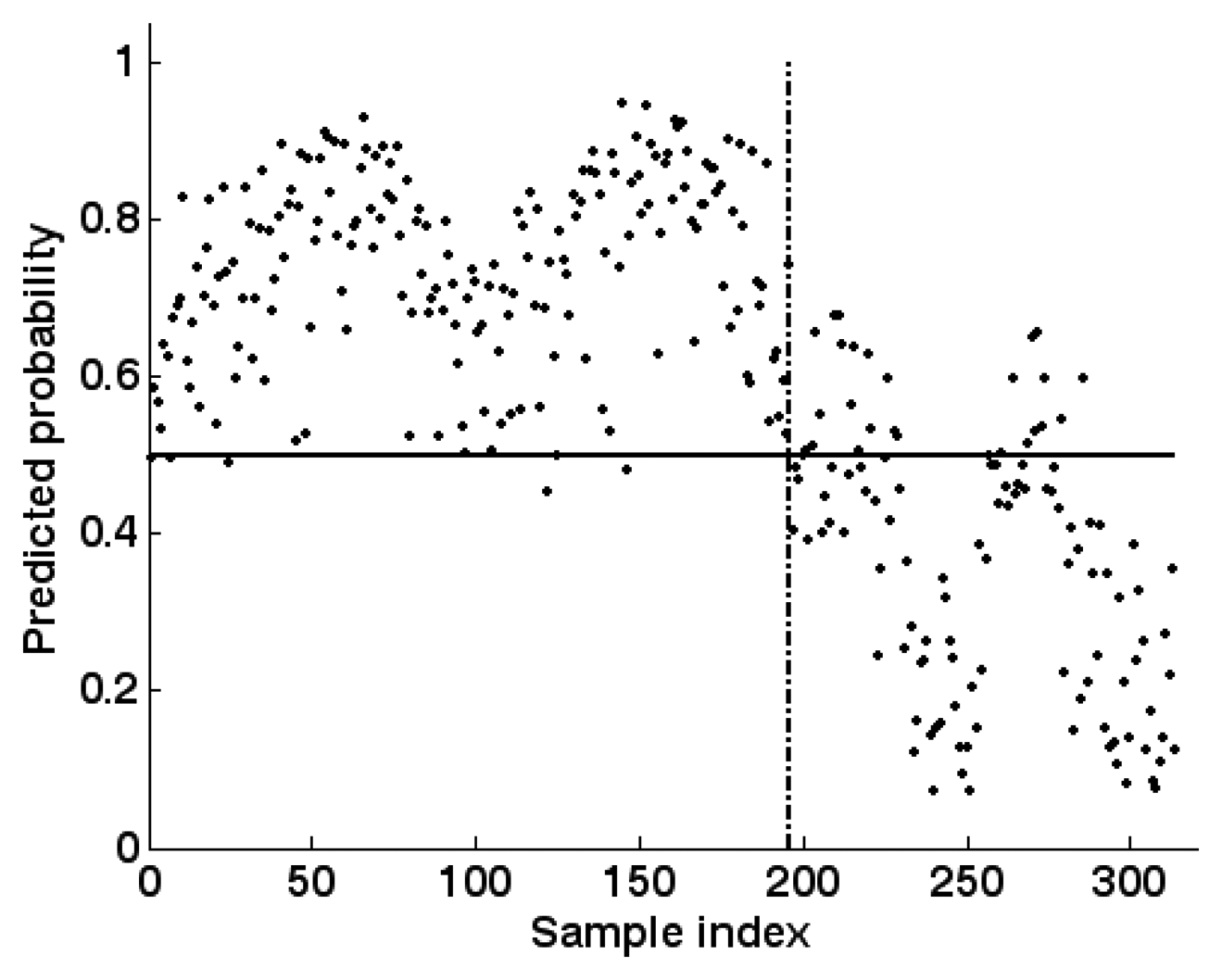
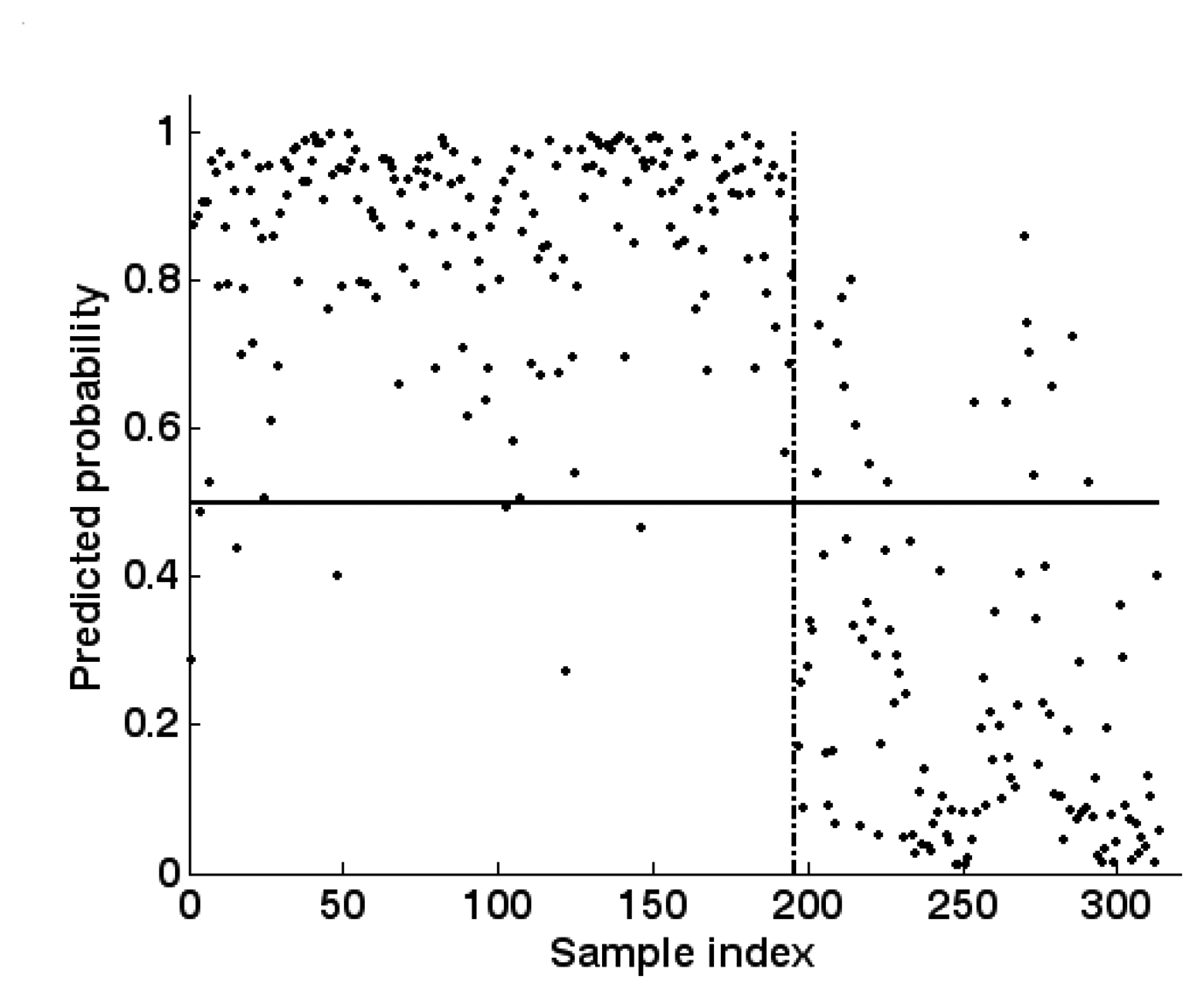
5.3. Training and testing of GPC
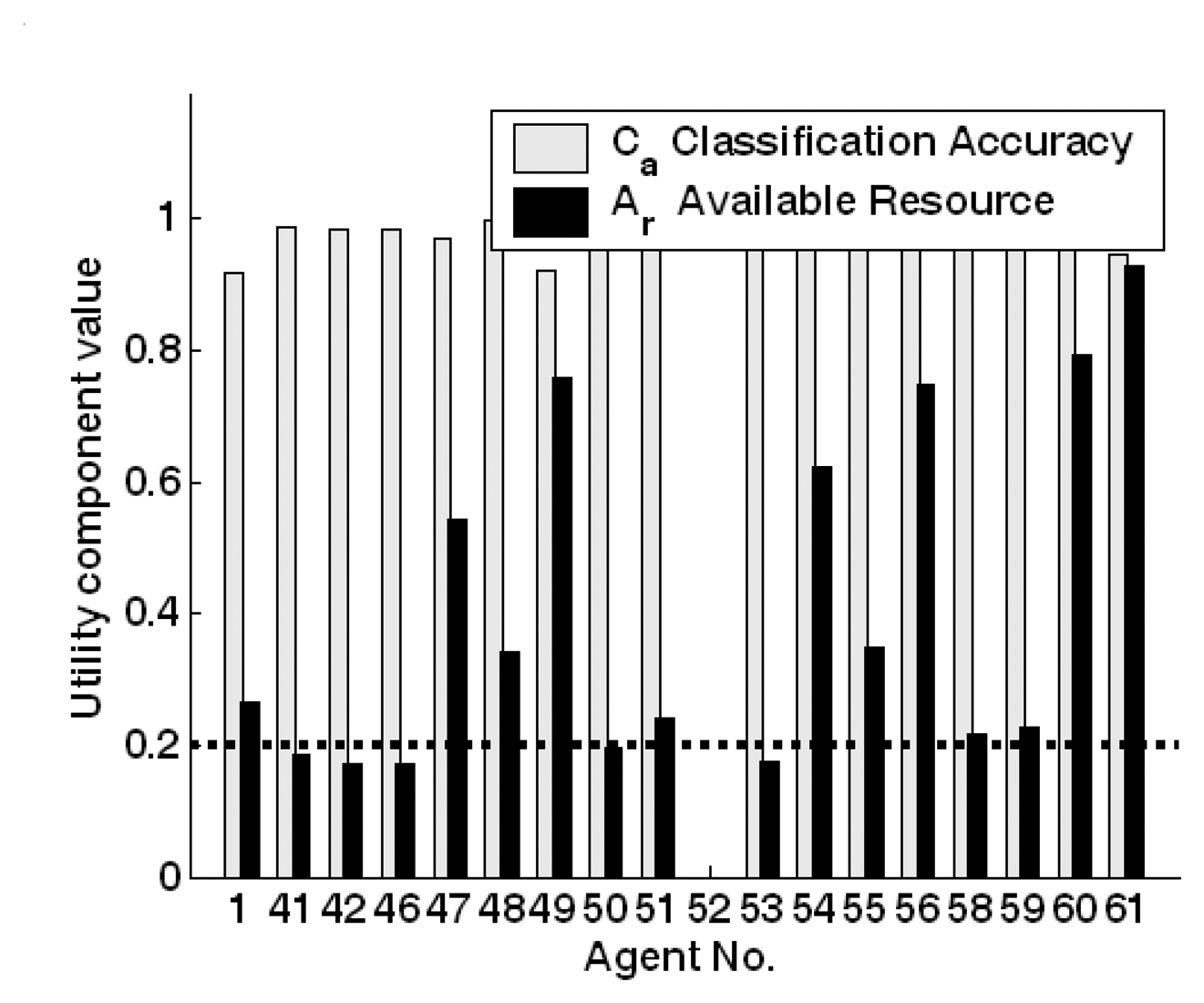
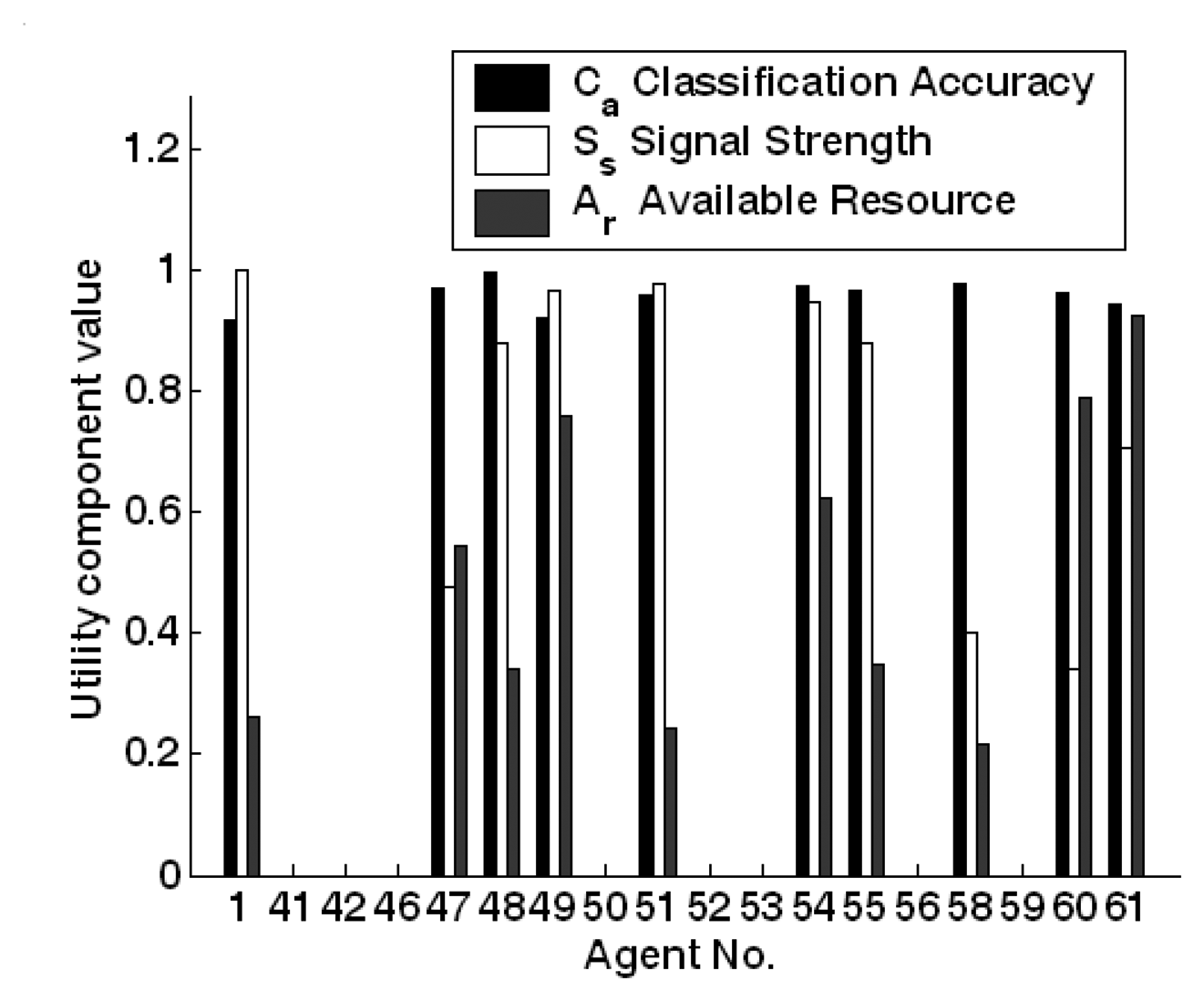
5.4. OSDMIA mechanism for target classification
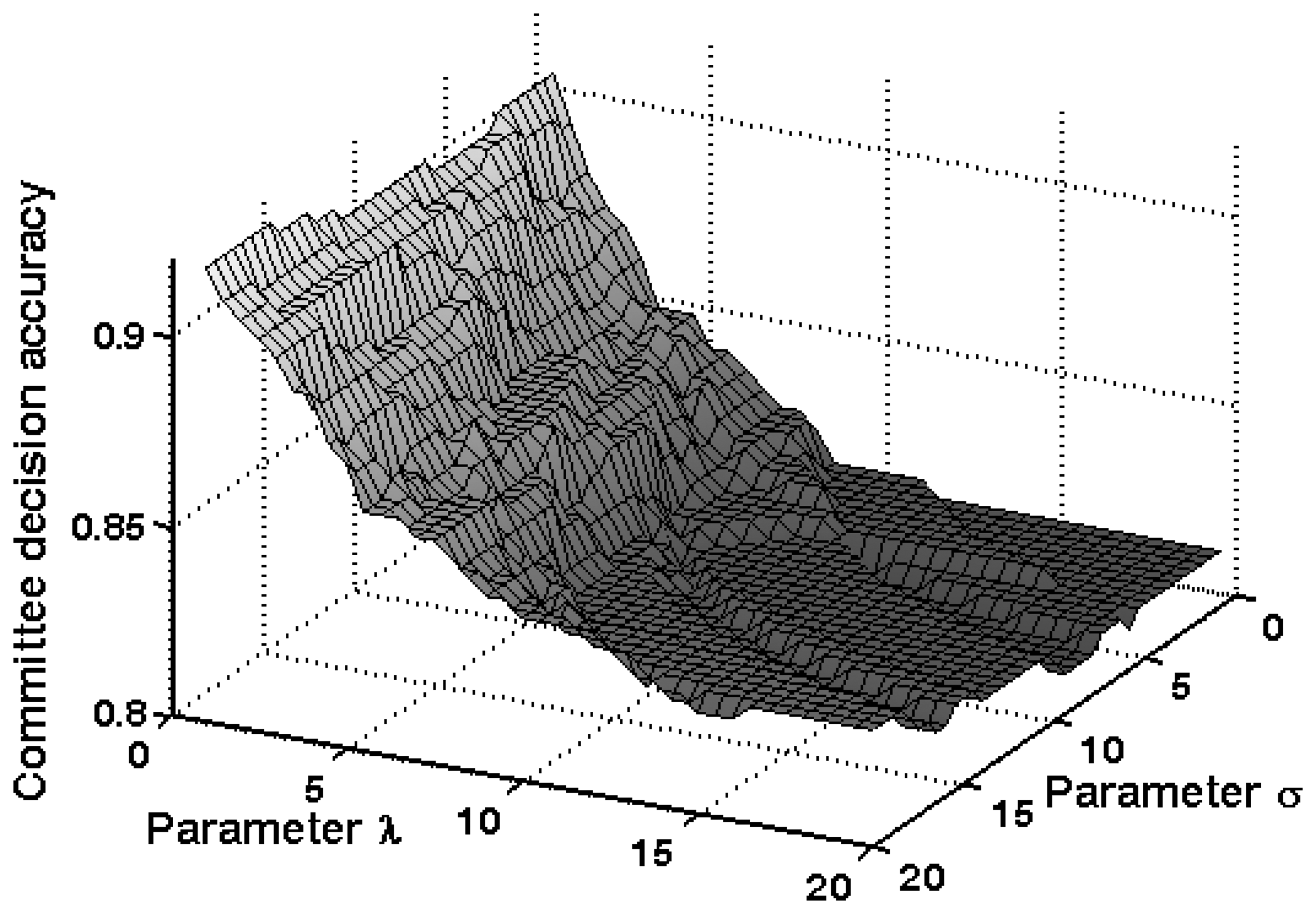
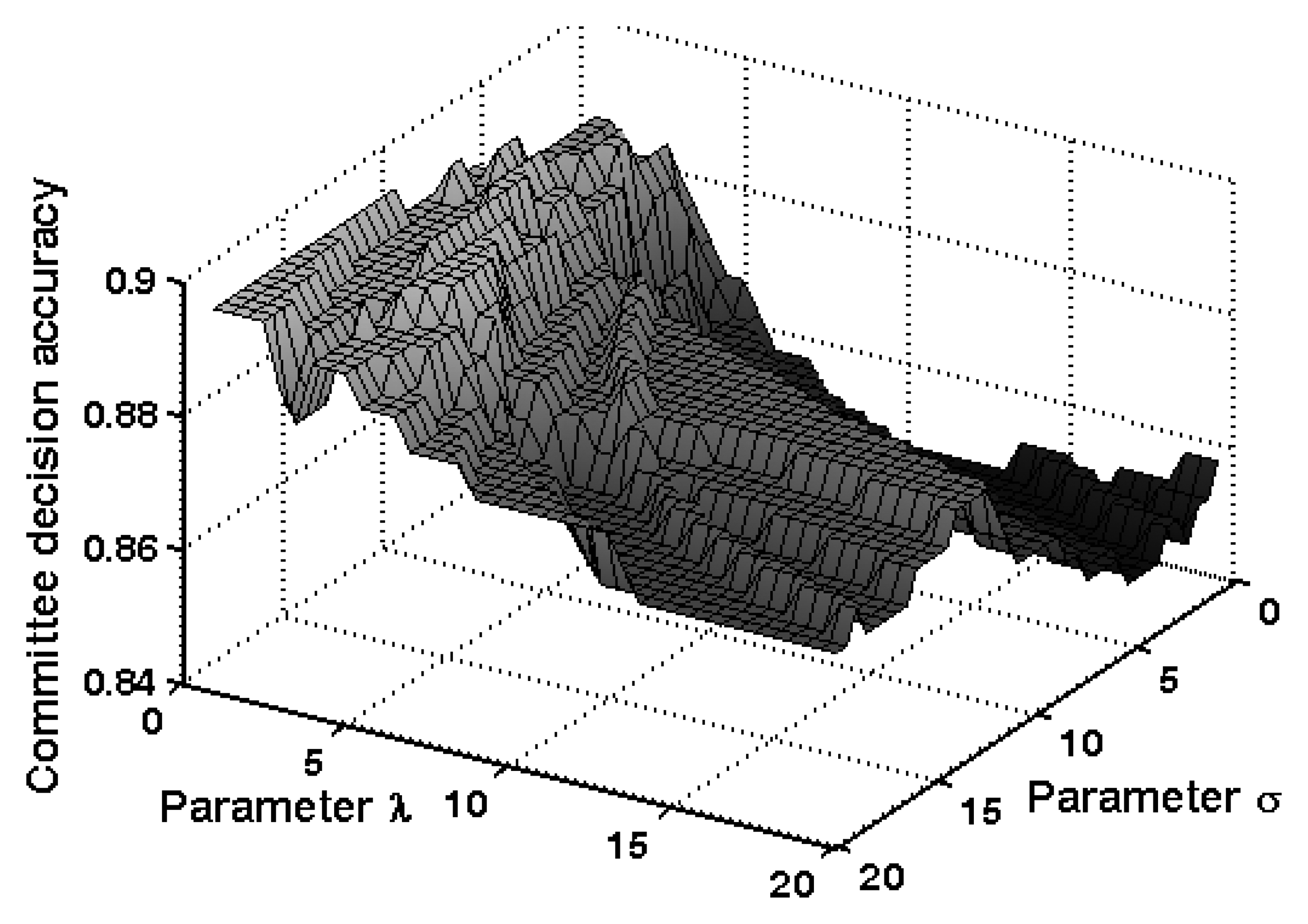
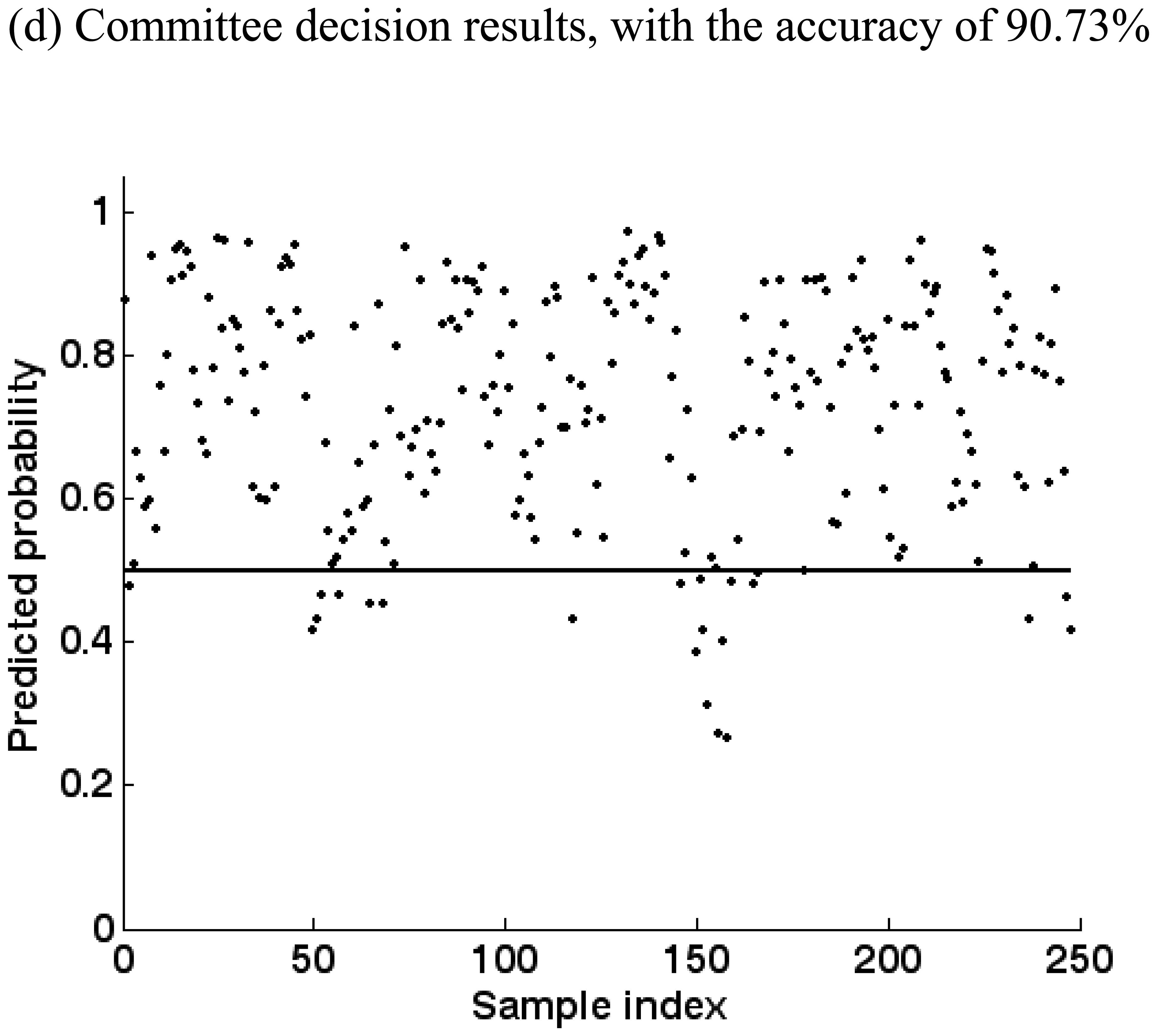
5.5. Committee decision mechanism
6. Conclusions and Future Work
Acknowledgments
References and Notes
- Baronti, P.; Pillai, P.; Chook, V.W.C. Wireless sensor networks: A survey on the state of the art and the 802.15.4 and ZigBee standards. Computer Communication 2007, 30, 1655–1695. [Google Scholar]
- Akyildiz, I.F.; Su, W.L.; Sankarasubramaniam, Y.; Cayirci, E. A Survey on sensor networks. IEEE Communications Magazine 2002, 40(8), 102–114. [Google Scholar]
- Akyildiz, I.F.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. Wireless sensor networks: a survey. Computer Networks 2002, 38, 393–422. [Google Scholar]
- Lédeczi, Á.; Nádas, A.; Völgyesi, P. Countersniper system for urban warfare. ACM Transactions on Sensor Networks 2005, 1(2), 153–177. [Google Scholar]
- Li, D.; Wong, K.; Hu, Y. Detection, classification and tracking of targets in distributed sensor networks. IEEE Signal Processing Magazine 2002, 19(2), 17–30. [Google Scholar]
- Wang, N.; Zhang, N.Q.; Wang, M.H. Wireless sensors in agriculture and food industry—Recent development and future perspective. Computers and Electronics in Agriculture 2006, 50, 1–16. [Google Scholar]
- Cayirci, E.; Tezcan, H.; Dogan, Y.; Coskun, V. Wireless sensor networks for underwater surveillance systems. Ad Hoc Networks 2006, 4, 431–446. [Google Scholar]
- Paek, J.; Chintalapudi, K.; Govindan, R. A wireless sensor network for structural health monitoring: performance and experience. Proceedings of the Second IEEE Workshop on Embedded Networked Sensors; 2005; pp. 1–10. [Google Scholar]
- Krishnamurthy, L.; Adler, R.; Buonadonna, P. Design and deployment of industrial sensor networks: experiences from a semiconductor plant and the North Sea. Proc. of the 3rd International Conference on Embedded Networked Sensor Systems; 2005; pp. 64–75. [Google Scholar]
- Shnayder, V.; Chen, B.R.; Lorincz, K. Sensor networks for medical care; Technical Report TR-08-05; Division of Engineering and Applied Sciences, Harvard University, 2005. [Google Scholar]
- Akyildiz, I.F.; Melodia, T.; Chowdhury, K.R. A survey on wireless multimedia sensor networks. Computer Networks 2007, 51, 921–960. [Google Scholar]
- Wang, X.; Bi, D.W.; Ding, L.; Wang, S. Agent collaborative target localization and classification in wireless sensor networks. Sensors 2007, 7(8), 1359–1386. [Google Scholar]
- Lesser, V.R. Cooperative multiagent systems: a personal view of the state of the art. IEEE Transactions on Knowledge and Data Engineering 1999, 11(1), 133–142. [Google Scholar]
- Marsh, D.; Tynan, R.; O'Kane, D. Autonomic wireless sensor networks. Engineering Applications of Artificial Intelligence 2004, 17, 741–748. [Google Scholar]
- Sandhu, J.S.; Agogino, A.M.; Agogino, A.K. Wireless sensor networks for commercial lighting control: decision making with multi-agent systems. AAAI Workshop on Sensor Networks 2004. [Google Scholar]
- Marsh, D.; O'Kane, D.; O'Hare, G.M.P. Agents for wireless sensor network power management. Proceedings of the 2005 International Conference on Parallel Processing Workshops; 2005; pp. 413–418. [Google Scholar]
- Liu, Z.Y.; Wang, Y.G. A secure agent architecture for sensor networks,”. Proc. of the 2003 International Conference on Artificial Intelligence - Intelligent Pervasive Computing Workshop (IC-AI'03); 2003. [Google Scholar]
- Shakshuki, E.; Ghenniwa, H.; Kamel, M. Agent-based system architecture for dynamic and open environments. Journal of Information Technology and Decision Making 2003, 2(1), 105–133. [Google Scholar]
- Shakshuki, E.; Hussain, S.; Matin, A.W.; Matin, A.R. Agent-based peer-to-peer layered architecture for data transfer in wireless sensor networks. Proc. of 2006 IEEE International Conference on Granular Computing; 2006; pp. 490–493. [Google Scholar]
- Patricio, M.A.; Carbo, J.; Perez, O.; Garcia, J.; Molina, J.M. Multi-agent framework in visual sensor networks. EURASIP Journal on Advances in Signal Processing 2007, 2007, 1–21. [Google Scholar]
- Lau, R.Y.K. Towards genetically optimised multi-agent multi-issue negotiations. Proceedings of the 38th Annual Hawaii International Conference on System Sciences; 2005; pp. 35c–35c. [Google Scholar]
- Fatima, S.; Wooldridge, M.; Jennings, N.R. Optimal negotiation of multiple issues in incomplete information settings. Proceedings of the Third International Joint Conference on Autonomous Agents and Multiagent Systems; 2004; pp. 1080–1087. [Google Scholar]
- Ito, T.; Hattori, H.; Klein, M. Multi-issue negotiation protocol for agents: exploring nonlinear utility spaces. Proceedings of the Twentieth International Joint Conference on Artificial Intelligence (IJCAI07); 2007; pp. 1347–1353. [Google Scholar]
- Kraus, S. Mutli-agents systems and applications; New York, NY; Springer-Verlag New York, Inc, 2001; pp. 150–172. [Google Scholar]
- Collins, J.; Gini, M.; Mobasher, B. Multi-agent negotiation using combinatorial auctions with precedence constraints; Technical Report 02-009; Department of Computer Science and Engineering, University of Minnesota, 2002. [Google Scholar]
- Bartolini, C.; Preist, C. A generic software framework for automated negotiation; Technical Report HPL-2002-2; HP Labs, 2002. [Google Scholar]
- Rahwan, I.; McBurney, P.; Sonenberg, L. Towards a theory of negotiation strategy (a preliminary report). Proceedings of the 5th Workshop on Game Theoretic and Decision Theoretic Agents (GTDT-2003); 2003; pp. 73–80. [Google Scholar]
- Soh, L.K.; Tsatsoulisa, C. Real-time negotiation model and a multi-agent sensor network implementation. Autonomous Agents and Multi-Agent Systems 2005, 11, 215–271. [Google Scholar]
- Mainland, G.; Parkes, D.C.; Welsh, M. Decentralized, adaptive resource allocation for sensor networks,”, Proceedings of the 2nd conference on Symposium on Networked Systems Design and Implementation - Volume 2; 2005.
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; Massachusetts London; the MIT Press, 2006; pp. 2–72. [Google Scholar]
- Seeger, M. Gaussian processes for machine learning. International Journal of Neural Systems 2004, 14(2), 1–38. [Google Scholar]
- Kuss, M.; Rasmussen, C.E. Assessing approximate inference for binary Gaussian process classification. Journal of Machine Learning Research 2005, 6, 1679–1704. [Google Scholar]
- Gibbs, M.N.; Mackay, D.J.C. Variational Gaussian process classifiers. IEEE Transactions on Neural Networks 2000, 11(6), 1458–1464. [Google Scholar]
- Opper, M.; Winther, O. Gaussian processes for classification: mean-field algorithms. Neural Computation 2000, 12(11), 2655–2684. [Google Scholar]
- Kim, H.C.; Hahramani, Z.B. Bayesian Gaussian process classification with the EM-EP algorithm. IEEE Transactions on Pattern Analysis and Machine Intelligence 2006, 28(12), 1948–1959. [Google Scholar]
- Kim, H.C.; Kim, D.J.; Ghahramani, Z.B. Appearance-based gender classification with Gaussian processes. Pattern Recognition Letters 2006, 27, 618–626. [Google Scholar]
- Chu, W.; Ghahramani, Z.B.; Falciani, F. Biomarker discovery in microarray gene expression data with Gaussian processes. Bioinformatics 2005, 21(16), 3385–3393. [Google Scholar]
- Williams, D.P. Gaussian process classification using image deformation. Proc. of IEEE International Conference on Acoustics, Speech and Signal Processing, 2007. ICASSP 2007; 2007; Volume 2, pp. 605–608. [Google Scholar]
- Murillo-Fuentes, J. J.; Caro, S.; Perez-Cruz, F. Gaussian processes for multiuser detection in CDMA receivers. In Advances in Neural Information Processing Systems; Weiss, Y., Scholkopf, B., Platt, J., Eds.; Cambridge, MA; The MIT Press, 2006; pp. 939–946. [Google Scholar]
- Huynh, Q.Q.; Cooper, L.N.; Intrator, N. Classification of underwater mammals using feature extraction based on time-frequency analysis and BCM theory. IEEE Transactions on Signal Processing 1998, 46(5), 1202–1207. [Google Scholar]
- Ishizuka, K.; Miyazaki, N. Speech feature extraction method representing periodicity and aperiodicity in sub bands for robust speech recognition. Proceedings of Acoustics, Speech, and Signal Processing, 2004 (ICASSP'04); 2004; Volume 1, pp. 141–144. [Google Scholar]
- Lee, C.; Hyun, D.; Choi, E. Optimizing feature extraction for speech recognition. IEEE Transactions on Speech and Audio Processing 2003, 11(1), 80–87. [Google Scholar]
- Carreira-Perpinan, M.A. A review of dimension reduction techniques; Technical Report CS-96-09; Department of Computer Science, University of Sheffield, 1997. [Google Scholar]
- Fodor, I.K. A survey of dimension reduction techniques; Technical Report UCRL. ID-148494; Lawrence Livermore National Laboratory, 2002. [Google Scholar]
- Hu, J.; Si, J.; Olson, B.P.; He, J.P. Feature detection in motor cortical spikes by principal component analysis. IEEE Transactions on Neural Systems and Rehabilitation Engineering 2005, 13(3), 256–262. [Google Scholar]
- Polat, K.; Günes, S. An expert system approach based on principal component analysis and adaptive neuro-fuzzy inference system to diagnosis of diabetes disease. Digital Signal Processing 2007, 17, 702–710. [Google Scholar]
- Ye, Z.M.; Auner, G. Principal component analysis approach for biomedical sample identification. Proc. 2004 IEEE International Conference on of Systems, Man and Cybernetics; 2004; Volume 2, pp. 1348–1353. [Google Scholar]
- Wang, B.H.; Bangham, J.A. PCA based shape descriptors for shape retrieval and the evaluations. Proceedings of 2006 International Conference on Computational Intelligence and Security; 2006; Volume 2, pp. 1401–1406. [Google Scholar]
- Zubko, V.; Kaufman, Y.J.; Burg, R.I.; Martins, J.V. Principal component analysis of remote sensing of aerosols over oceans. IEEE Transactions on Geoscience and Remote Sensing 2007, 45(3), 730–745. [Google Scholar]
- Rao, A.S.; Georgeff, M.P. BDI agents: from theory to practice. Proc. of First International Conference on Multi-agent Systems; 1995; pp. 312–319. [Google Scholar]
- Thangarajah, J.; Lin, P.; Harland, J. Representation and reasoning for goals in BDI agents. Proceedings of the Twenty-Fifth Australasian Computer Science Conference (ASCS2002); 2002; pp. 259–245. [Google Scholar]
- Georgeff, M.P.; Pell, B.; Pollack, M.E.; Tambe, M.; Wooldridge, M. The Belief-Desire-Intention model of agency. Proceedings of the 5th International Workshop on Intelligent Agents V, Agent Theories, Architectures, and Languages; 1998; pp. 1–10. [Google Scholar]
- Braubach, L.; Pokahr, A.; Lamersdorf, W.; Moldt, D. Goal representation for BDI agent systems. Second International Workshop on Programming Multiagent 2004, 9–20. [Google Scholar]
- Labrou, Y.; Finin, T.; Peng, Y. The current landscape of agent communication languages. IEEE Intelligent Systems 1999, 14(2), 45–52. [Google Scholar]
- Pokahr, A.; Braubach, L.; Lamersdorf, W. Jadex: implementing a BDI-infrastructure for JADE agents. EXP In Search of Innovation (Special Issue on JADE) 2003, 3(3), 76–85. [Google Scholar]
- Bordini, R.; Dastani, M.; Dix, J. Jadex: A BDI Reasoning Engine. In Multi-Agent Programming; Springer Science+Business Media Inc., 2005; pp. 149–174. [Google Scholar]
- Bellifemine, F.; Poggi, A.; Rimassa, G. Developing multiagent systems with JADE. Proceedings of the 7th International Workshop Agent Theories Architectures and Languages; 2000; pp. 89–103. [Google Scholar]
- Jennings, N.R. An agent-based approach for building complex software systems. Communications of the ACM 2001, 44(4), 35–41. [Google Scholar]
- Wooldridge, M. Introduction to Multiagent Systems; New York, NY; John Wiley & Sons, Inc., 2001. [Google Scholar]
- Rahwan, I. Interest-based negotiation in multi-agent systems. PhD thesis, Dept. of Information Systems, the University of Melbourne, 2004. [Google Scholar]
- Shi, M.H.; Amine, B. Committee machine with over 95% classification accuracy for combustible gas identification, Proc. of the 13th IEEE International Conference on Electronics, Circuits and Systems, 2006. ICECS ′06; 2006; pp. 862–865.
- Tang, H.M.; Lyu, M.R.; King, I. Face recognition committee machines: dynamic vs. static structures. Proceedings of 12th International Conference on Image Analysis and Processing; 2003; pp. 121–126. [Google Scholar]
- Haykin, S. Neural Networks; New Jersey; Prentice Hall, 1999; pp. 392–435. [Google Scholar]
- Marco, F.D.; Yu, H.H. Vehicle classification in distributed sensor networks. Journal of Parallel and Distributed Computing 2004, 64, 826–838. [Google Scholar]

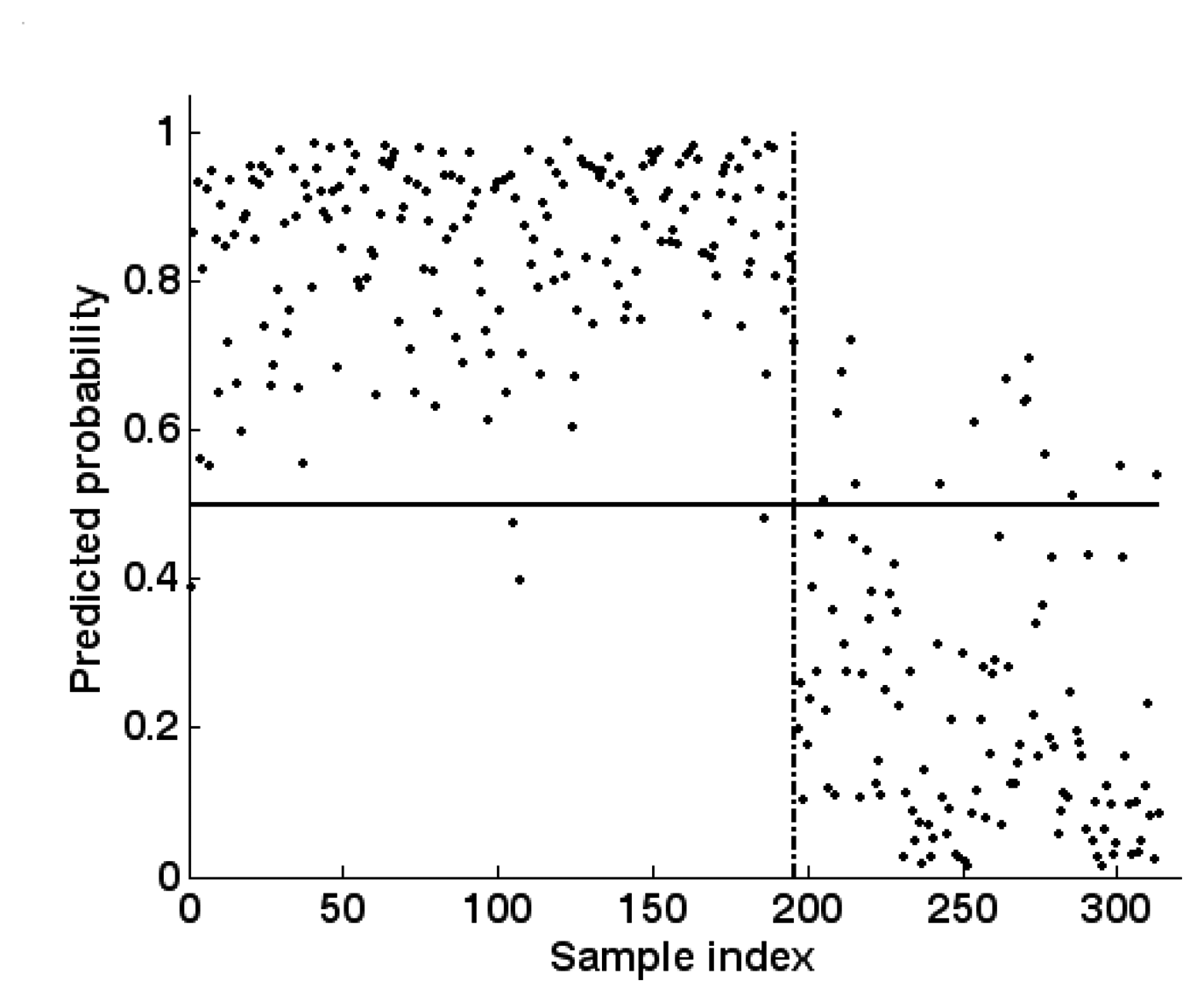
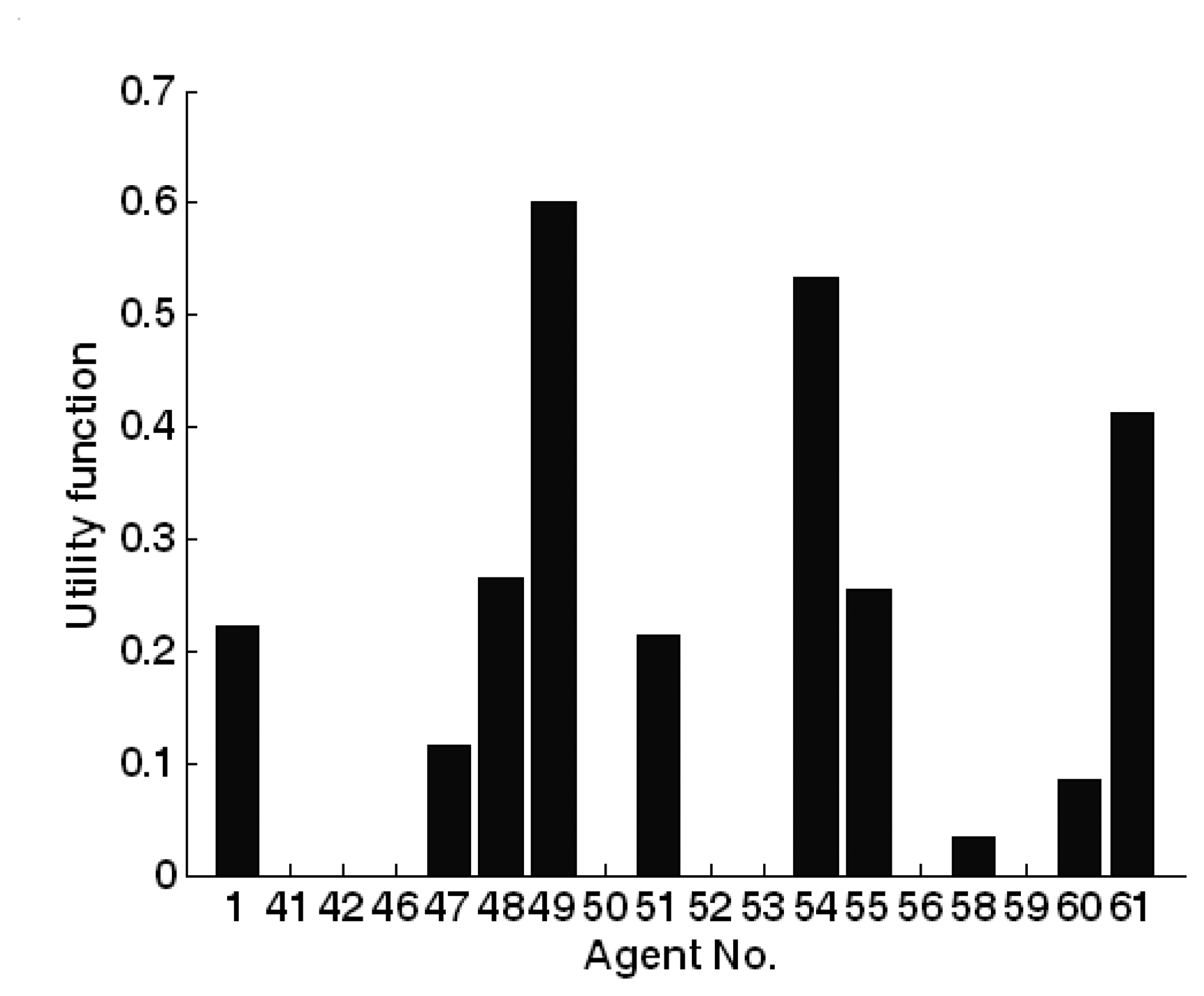
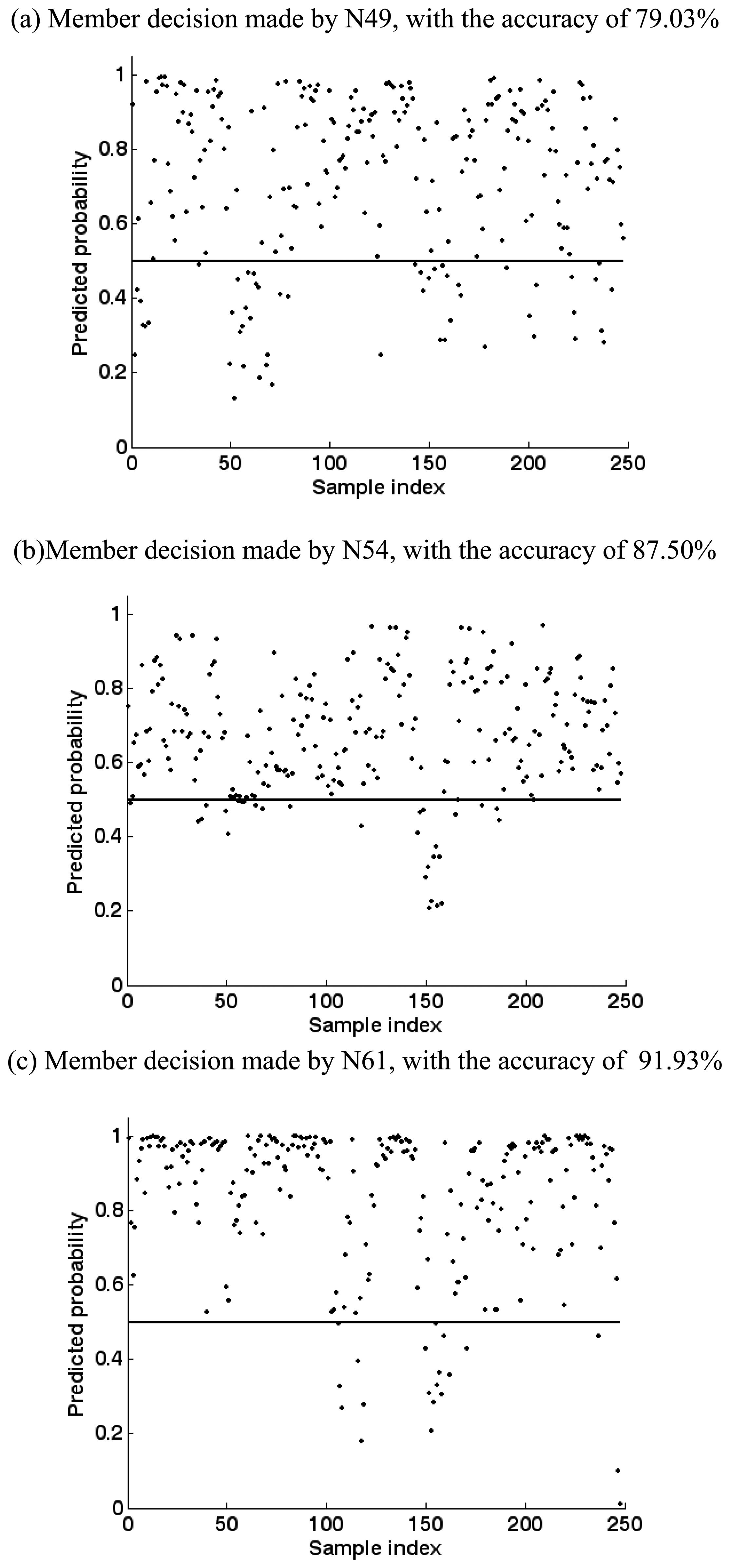
| Committee Member | Member Decision di | Weight Component | Member Weight CaSs | Committee Decision D | |
|---|---|---|---|---|---|
| Ca | Ss | ||||
| N49 | 0.3911 | 0.9204 | 1.0000 | 0.9204 | 0.6293 |
| N54 | 0.6750 | 0.9746 | 0.9824 | 0.9574 | |
| N61 | 0.8837 | 0.9440 | 0.7310 | 0.6900 | |
© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Xue, W.; Bishop, D.-w.; Ding, L.; Wang, S. Multi-agent Negotiation Mechanisms for Statistical Target Classification in Wireless Multimedia Sensor Networks. Sensors 2007, 7, 2201-2237. https://doi.org/10.3390/s7102201
Xue W, Bishop D-w, Ding L, Wang S. Multi-agent Negotiation Mechanisms for Statistical Target Classification in Wireless Multimedia Sensor Networks. Sensors. 2007; 7(10):2201-2237. https://doi.org/10.3390/s7102201
Chicago/Turabian StyleXue, Wang, Dao-wei Bishop, Liang Ding, and Sheng Wang. 2007. "Multi-agent Negotiation Mechanisms for Statistical Target Classification in Wireless Multimedia Sensor Networks" Sensors 7, no. 10: 2201-2237. https://doi.org/10.3390/s7102201





