1. Introduction
Unfortunately, the highest fatality rates per year in car accident statistics are attributed to rollover crashes [
1]. In fact, this type of crash accounts for about 40% of passenger vehicle fatalities. This is why today's cars are designed with the highest priority placed on passenger safety.
On the question of what the causes for this kind of crash are. It has been shown that tall, narrow vehicles with high center of gravity are bound to roll over if they are involved in single-vehicle crashes. In addition, excessive speed, alcohol consumption, poor roads and environmental factors, among others, are all contributory factors to rollover crashes.
Therefore, with this scenario in mind, no one would dispute the need to improve the design of the sensors used for industrial measurements [
2-
22]. This is why in the last decades researchers from all around the world have been working hard to invent intelligent devices consisting of not only sensors, but also advanced materials [
23] and microprocessors, among other devices, that incorporate a certain amount of intelligence to the sensors themselves, transforming them into better prepared measuring systems [
24-
47].
Nevertheless, the process of improving the performance of sensors is not an easy task. Actually, we have to deal with disturbances and/or interferences whose characteristics we have little or no prior knowledge of, and we have to use efficient methods of estimation, prediction and control in order to get clear information about the physical magnitude or process that we want to measure or control [
38-
47].
In short, this paper shows the improvement of the real-time response of a sensor to measure the rollover angle of a car under performance tests. Furthermore, this system can be easily integrated into technologies that aim to improve the comfort and safety of the passengers in most of today's cars. Electronic stability control, variable ride-height suspension and rollover airbag systems are examples of the above mentioned technologies.
1. Accelerometers
2.1. Principles
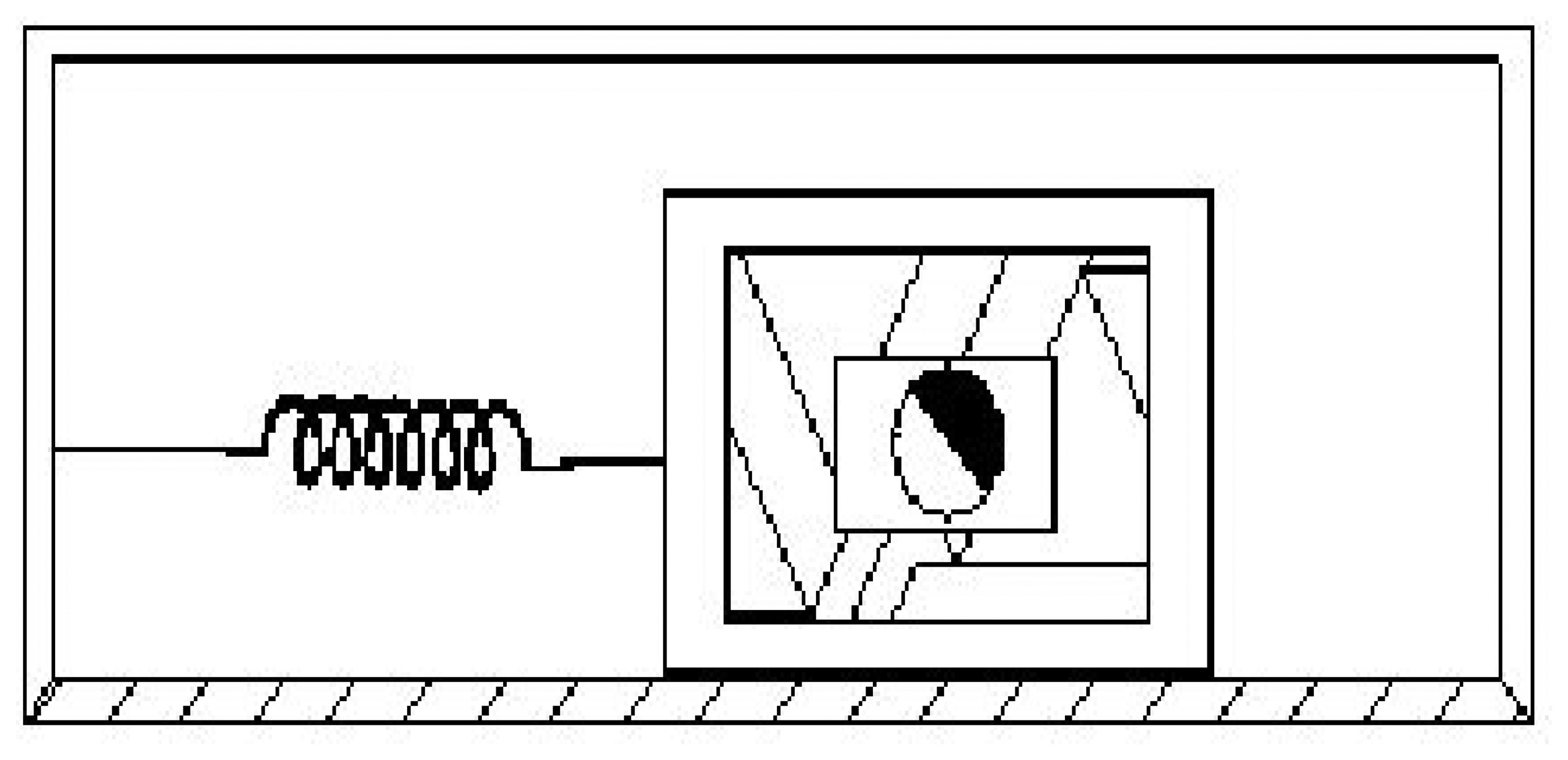
In the industrial world, the most common design of sensors to measure acceleration is the accelerometer design based on a combination of Newton's law of mass acceleration and Hooke's law of spring action.
Figure 1 shows the basic spring-mass system accelerometer. Such a mass is connected to the base by a spring that is in its unextended state and exerts no force on the mass. In addition, the mass is free to slide on the base [
20].
According to Johnson [
20], if the seismic mass m, is undergoing an acceleration a, then there must be a force F acting on the mass and given by F
1 = m·a. In addition, the spring of spring constant k is extended (or stretched) from its equilibrium position for a distance Δx, with a force F
2 (opposite to F
1) acting on the spring and given by F
2 = k · Δx. This condition is described by equating Newton's and Hooke's laws. Thus, the measurement of acceleration is reduced to a measurement of spring extension (linear displacement):
The spring-mass principle applies to many common accelerometer designs, but most designs differ from each other in how they carry out the measurement of the displacement of the spring.
In analyzing the time domain performance of the spring-mass system and carrying out the impulse response analysis, it can be seen that such a system exhibits oscillations at a natural frequency with damping:
where f
osc is the frequency of oscillation, f
N is the natural frequency and ζ is the dimensionless damping ratio.
At this point, it is important to point out that the greater the friction associated with the seismic mass and the base, the sooner the mass settles to equilibrium. That is to say, as the friction increases, the damping becomes greater and the response will reach zero sooner. In addition, if the spring-mass system is underdamped, the mass will swing back and forth with decreasing amplitude. In this case, the frequency of oscillation is given by
Eq. (2). However, if the friction tends to zero (lossless case), the seismic mass will oscillate at some characteristic natural frequency (see
Eq. (3)).
2.1 Types of accelerometers and the selection of the sensor
There is a wide variety of accelerometers that could be used in various applications depending on the requirements of range, natural frequency, damping, temperature, size, weight, hysteresis, low noise, and so on. Piezoelectric accelerometers, piezoresistive accelerometers, variable capacitance accelerometers, linear variable differential transformers (LVDT), variable reluctance accelerometers, potentiometric accelerometers, gyroscopes used for sensing acceleration, strain gauges accelerometers, among others, are some of the numerous accelerometers.
In this paper, we are interested in measuring steady-state accelerations. That is to say, we are interested in a measure of acceleration that may vary in time but that is nonperiodic [
20]. In this application, the frequency at which the acceleration changes is low (< 50 Hz).
Generally speaking, the accelerometers should have the following characteristics:
- 1)
Adequate range to cover expected acceleration magnitudes.
- 2)
A natural frequency higher than twice the frequency at which the measured acceleration changes.
Therefore, taking into consideration the above statements, in this paper the Analog Devices dual-axis accelerometer ADXL202 was used. Such a sensor is a low cost, low power, complete 2-axis accelerometer with a measurement range of ± 2g and sensitivity 312 mV/g, where g is the gravitational acceleration (9.81m/s2). Also, this sensor can measure both dynamic acceleration (e.g., vibration) and static acceleration (e.g., gravity). Furthermore, the bandwidth of such an accelerometer may be set from 0.01 Hz to 5 kHz, and the typical noise floor is
allowing signals below 5 mg to be resolved for bandwidths below 60 Hz.
2. Rollover sensor system and mathematical modeling
In order to obtain an approximation of the model of the system, it is usually assumed that the movement of the car's center of gravity can be discarded [
48,
49]. That is to say, it is assumed that the car has a stiff suspension. Thus, the movement of the car's center of gravity owing to the flexibility of the suspension is disregarded.
Figure 2 shows the mechanical model of the system. In such a figure the car is seen from the front. Furthermore, experience tells us that the influence that the movement of the car's center of gravity exerts on the measure of both the acceleration of the car in the y direction and the acceleration of the car in the z direction (see
Fig. 2) can be discarded.
In
Fig. 2 a dual-axis accelerometer is situated at the car's center of gravity with one of its axes sensing the acceleration in the y direction and the other in the z direction. Also, T represents the track width, r is the radius of the curvature of the path of motion, F
c is the centrifugal force, h is the height of the car's center of gravity, and F
yl and F
yr are friction forces that prevent the car from sliding off of the road. In addition, W represents the weight of the car, β is the degree of inclination of the curve in the road, N
l is the normal force between the left front tire and the ground, and N
r is the normal force between the right front tire and the ground. Furthermore, the total forces in the y and z axis are
where F
y is the total force in the y axis, F
z is the total force in the z axis, v is the longitudinal speed of the car, m is the mass of the car, g is the gravitational acceleration, a
y is the acceleration in the y direction and a
z is the acceleration in the z direction.
Therefore, analyzing the mechanical model shown in
Fig. 2, it can be said that the car is bound to roll over if the vector indicating the force F
t strikes the ground at any point lying to the right of the center of the front right wheel. What is more, it can also be said that
Eq. (4) and
Eq. (5) are the orthogonal projections of F
t on the y and z axis, respectively; and that the car will roll over if
Equations (8) and
(9) can be obtained by using standard techniques of classical mechanics and vector analysis [
50,
51].
3. General considerations of noise characterization
Basically, it can be said that the sources of disturbances or interferences are many, but the most important are those caused by the mechanical and electrical systems that today's cars have, and by poor roads and environmental factors. As a matter of fact, the designer has to deal with vibrations of the framework, chassis, front axle, rear axle, and engine. In addition, the noise generated by the vertical movement, yaw, pitch, roll, and forces and moments on each wheel has to be taken into consideration as noise affecting the signal of interest.
According to Aparicio et al. [
49], the mechanical vibrations have the following eigenfrequencies:
- 1)
1 Hz < eigenfrequencies < 3 Hz. Vibrations of the framework and the car sprung masses, vertical movement, yaw, roll and pitch.
- 2)
4 Hz < eigenfrequencies < 8 Hz. Vibrations of the wheels at low speed.
- 3)
10 Hz < eigenfrequencies < 20 Hz. Vibrations of the car sprung and unsprung masses at medium and high speed. Also, vibrations of the engine, framework, chassis, front and rear axle, etc.
- 4)
eigenfrequencies > 20 Hz. Vibrations caused by direct actions, vibrations of the tires, etc.
The above vibrations are considered to be mechanical disturbances affecting the measurements. In addition, in order to reflect real vehicle driving conditions, the variable road characteristics are treated as a random process [
52-
54]. Moreover, there are other noise sources that are generated by the car's electrical systems. Such noises and/or interferences are a mixture of random signals that fluctuate rapidly in an unpredictable manner and interfere with limited band spectrum.
4. Design of the adaptive filter
5.1. Introduction
The idea of canceling or diminishing the unwanted information without causing damage to the relevant signal is very complex, and the more the noise and the relevant signal share the same frequency spectrum, the less the designer can remove the unwanted information by using classical filters. In fact, when the unwanted information and the relevant signal share the same (or a very similar) frequency spectrum, the use of classical filters should be discarded [
55-
60]. When this happens, it is often said that the signal is buried in a broad-band noise background.
According to Anderson and Moore [
60], the classical approach to filtering postulates that the useful signals lie in one frequency band and unwanted signals, normally termed noise, lie in another, though on occasions there can be overlap. And when this happens, it is very difficult to eliminate small-magnitude disturbance or interference, and the background noise causes serious difficulties. In addition, the use of fixed filters with very sharp cut-off regions can introduce problems such as: additional delays, overshoots, undesirable amplification at some frequency range, and so on. Butterworth filters, Chebyshev filters and elliptical filters are some of the landmarks in the body of classical filter design theory.
In addition, the earliest statistical ideas of Wiener and Kolmogorov [
61,
62] relate to processes with statistical properties which do not change with time, i.e., to stationary processes. For such processes, it proved possible to relate the statistical properties of the useful signal and unwanted noise to their frequency domain properties. The assumption that the underlying signal and noise processes are stationary is crucial to the Wiener and Kolmogorov theory. Nevertheless, this is a drawback of such a theory.
The Wiener-Kolmogorov theory is inadequate to deal with problems in which the relevant signal and/or the noise are not stationary processes. This is the case under study. Therefore, a new theory, the Kalman filter theory [
55-
60], was developed in the late 1950s and early 1960s to deal with situations in which nonstationarity of the signal and/or noise is intrinsic to the problem. The optimal adaptive filter proposed in this paper is based on the Kalman filtering theory.
Therefore, taking into consideration the above statments, it is recommended that designers use optimal signal processing techniques to cancel noise and interference that are usually very hard to cancel using the classical approach to filtering. These reasons, among others, justify the need to apply optimal filtering [
60].
What is more, due to the characteristics of the noise corrupting the important information, it is recommended that such an optimal filter be implemented as an adaptive filter [
63-
67]. In short, an adaptive filter is a filter with a mechanism for adjusting its own parameters automatically by using a recursive algorithm at the same time that it is in active interaction with the environment. In addition, all this happens in such a way that the performance of the adaptive filter is continuously improved according to a specified performance criterion (or cost function) which has been previously established by the designer.
Taking into consideration the above statements and the need to use an optimal adaptive filter with low computational burden, good numerical behavior, robustness, ease of implementation, a satisfactory rate of convergence and good round-off error rejection characteristics, a recursive least-squares (RLS) lattice algorithm was chosen to carry out the process of optimal estimation of the relevant signal [
65-
69]. In the present paper, the application of such an adaptive filter is an interference or noise canceller [
64,
66,
70], and a block diagram representation of it is shown in
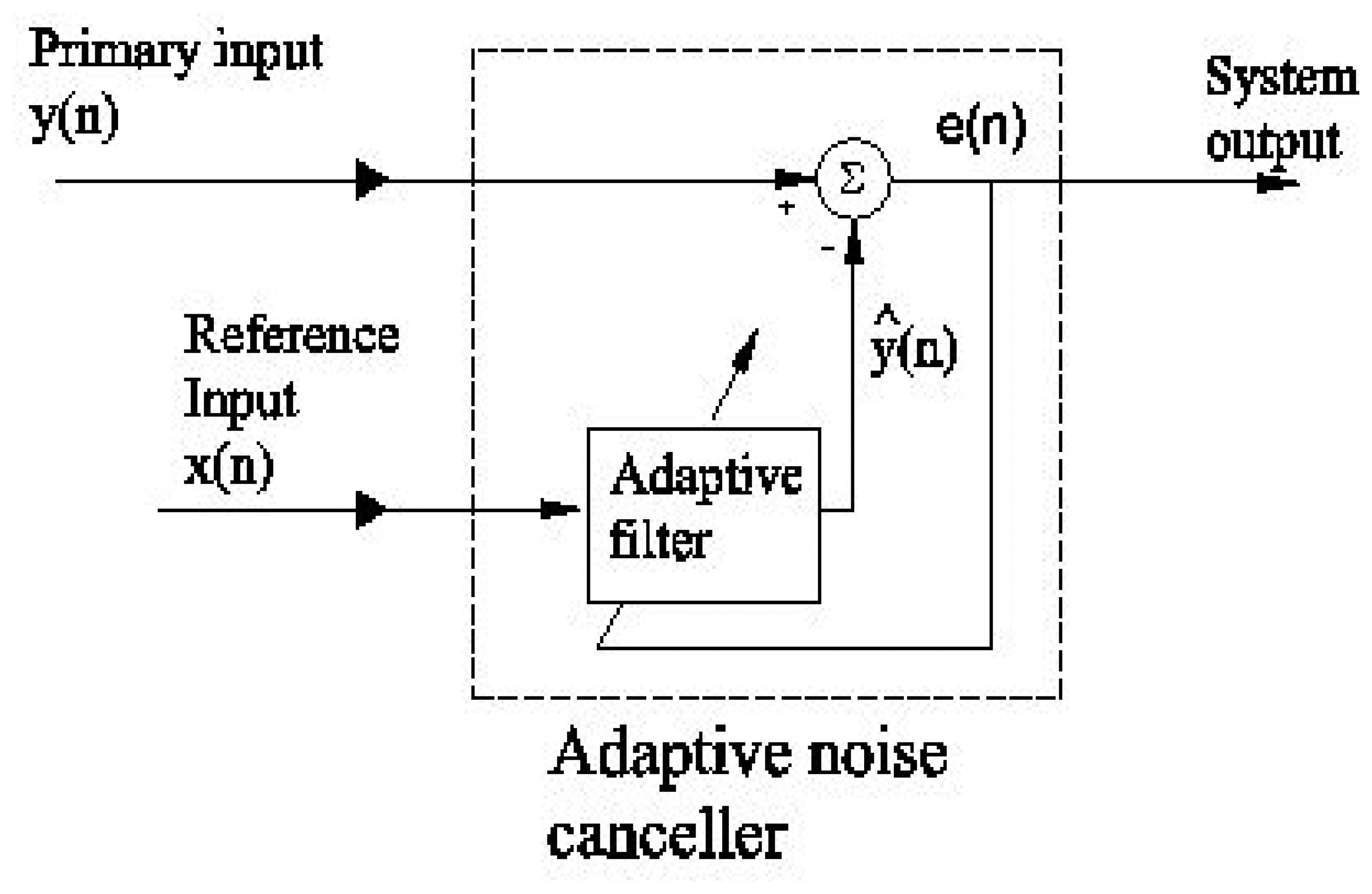
Fig. 3. Furthermore, a summary of it follows.
5.2. Summary of the RLS lattice algorithm (from Haykin [66])
5.2.1 Introduction
According to Haykin [
66], this algorithm is based on a priori estimation errors, and the reflection and joint-process estimation coefficients are all derived directly. The algorithm is called the RLS lattice algorithm using a priori estimation errors with error feedback. To derive this algorithm, we may proceed in one of two ways (among others):
- 1)
Apply the squaring procedure to an extended form of square-root adaptive filtering algorithms for exponentially weighted RLS estimation (QR-RLS). The QR-RLS algorithm, or, more precisely, the QR decomposition-based RLS algorithm (QRD-RLS), derives its name from the fact that the computation of the least-squares weight vector in a finite-duration impulse response (FIR) filter implementation of the adaptive filtering algorithm is accomplished by working directly with the incoming data matrix via QR decomposition [
71], rather than working with the (time-average) correlation matrix of the input data as in the standard RLS algorithm. Accordingly, the QRD-RLS algorithm is numerically more stable than the standard RLS algorithm.
- 2)
Apply Kalman filter theory [
55-
60,
66,
67] in conjunction with the covariance Kalman filtering algorithm for the special unforced dynamical model of the state-space model of the RLS filter for an exponential weighting factor greater than zero and lower than or equal to one [
66].
In this paper, it is followed procedure 2) because this is insightful and fairly straightforward. In addition, this algorithm, naturally enough, has both advantages and disadvantages.
On the one hand, as the updating of the reflection and regression coefficients is performed directly, the numerical behavior of the RLS lattice algorithm using a priori estimation errors with error feedback is very good. The good numerical behavior of this algorithm is one of its strength in the case under study. This issue is very important for us because of the effects of quantization, or round-off, errors that arise when adaptive filters are implemented digitally. In short, the quantization process has the effect of causing the performance of a digital implementation of the algorithm to deviate from the ideal (i.e., infinite-precision) form of the adaptive filtering algorithm. In addition, the nature of this deviation is influenced by a combination of the following factors:
- a)
The design details of the adaptive filtering algorithm
- b)
The degree of ill conditioning (i.e., the eigenvalue spread) in the underlying correlation matrix that characterizes the input data
- c)
The form of numerical computation (fixed point or floating point) employed
Understanding the numerical properties of adaptive filtering algorithms helps the designers to meet design specifications.
Another advantage of the RLS lattice algorithm using a priori estimation errors with error feedback is the high quality of the estimation of unknown parameters of the stochastic model of the physical process under study. This is another very important strength of this algorithm.
On the other hand, the input data and internal calculations are all quantized to a finite precision that is determined by design and cost considerations. The cost of a digital implementation of an algorithm is influenced by the number of bits (i.e., the precision) available for performing the numerical computations associated with the algorithm. In general, the cost of implementation increases with the number of bits employed.
Another disadvantage of this algorithm is that, generally speaking, algorithms based on Kalman filtering algorithms have no good long-term stability. However, this problem can be solved by reinitializing the algorithm at any appropriate interval of time, whether fixed or variable.
On balance, although there are disadvantages, experience tells us that the RLS lattice algorithm using a priori estimation errors with error feedback is one of the best that the designers can use when estimating unknown parameters of the stochastic models of many physical process.
5.2.2 The RLS lattice algorithm using a priori estimation errors with error feedback
5.2.2.1. Initialization
To initialize the algorithm, at time n = 0, set
where δ is a small positive constant, Φ is the forward prediction-error energy, Θ is the backward prediction-error energy, r is the order of the least-squares predictor and r = 1, 2, …, R, where R is the final order of the least-squares predictor. In addition, γ is the forward reflection coefficient, π is the backward reflection coefficient, and κ is the conversion factor.
For each instant n ≥ 1, generate the zeroth-order variables:
where the constant λ, 0 < λ ≤ 1, is the forgetting factor and its typical values used are the real numbers in the range from 0.99 to 1, η is the forward a priori prediction error, β is the backward a priori prediction error, and x is the reference input.
For joint-process estimation, at time n = 0, set
At each instant
n ≥ 1, generate the zeroth-order variable
where σ is the tap-weight vector of the transversal filter. It contains R + 1 taps. Also, y is the primary input and ε is the system output.
5.2.2.2. Predictions
For n = 1, 2, 3,…, compute the various order updates in the sequence r = 1, 2, …, R.
5.2.2.3. Filtering
For n = 1, 2, 3,…, compute the various order updates in the sequence r = 1, 2, …, R + 1:
where the asterisk denotes
complex conjugation.
Before moving on to the calibration of the system, it is important to point out that, as stated in the initialization step, the output of the filtering process (ε
R+1) is the system output (see
Fig. 3). Moreover, the outputs of the lattice predictor (η
R and β
R) are the variables used in this paper to obtain the cost function (see Section 7).
5. Calibration of the system
Before moving on to the results of the experiment, it is important to carry out the calibration of the sensor presented in this paper, so that the costumer can have an estimation of the uncertainty of measurement of the system [
72-
76].
In this paper, a computer-controlled platform was used to generate the reference signals for the calibration process of the intelligent sensor. In addition, an inclinometer was used as the working standard in this research.
Specifically, a TESA ClinoBEVEL1 inclinometer was used, which, in order to guarantee the traceability of the measurements carried out in the experiment, was calibrated by the National Accreditation Body of Spain. Also, the result of such a calibration was an uncertainty of measurement of ±0.02°, where the superscript ° represents degrees.
Furthermore, the previously mentioned uncertainty estimate represents an expanded uncertainty expressed at approximately the 95% level of confidence using a coverage factor of k = 2. The calibration steps carried out in the laboratory experiments are described below.
First, the zero of the computer-controlled platform is adjusted. In short, the angle of inclination of the computer-controlled platform is set at 0° and the inclinometer (or working standard in this paper) is situated on the surface of the platform. Then angle of inclination of the computer-controlled platform is adjusted until the inclinometer reads 0°. After that, the system is allowed to stabilize for approximately 15 minutes, and the zero is readjusted if necessary.
Second, the inclination of the platform is increased step by step from 0° to 45°, which is the working range, and the working standard is used to guarantee that the platform inclination is at the desired calibration point. Consequently, a measurement is carried out by the system under calibration at the calibration point and the result of this measurement is written in a table specifically prepared to satisfactorily record this information. Here, the calibration points are the following: 0°, 5°, 10°, 15°, 20°, 25°, 30°, 35°, 40° and 45°.
Third, once the platform has reached the 45° of inclination, this is decreased step by step to 0°, and also one measurement is carried out at each of the i'th calibration points. Note that this step is performed similarly to the second step except that the movement of the platform is in the opposite direction.
Fourth, when the platform reaches the 0° of inclination, this is again increased and the processes explained in the second and third steps are repeated for four more times.
In the end, a record of 100 measurements is obtained. What is more, such measurements are well organized in groups of 10 measurements carried out at each one of the 10 calibration points.
Fifth, the expanded uncertainty of the system at the
i'th calibration point is
with a coverage factor of k = 2. Furthermore, u
ws is the uncertainty of measurement of the working standard using a coverage factor of k = 1, s
i is the experimental standard deviation of the p measurements (p = 10) taken by the measuring instrument of the computer-controlled platform at the
i'th calibration point, and c
i is the difference between the mean of such measurements and the conventional true value indicated by the working standard at the
i'th calibration point.
Sixth, the uncertainty of the system is the maximum among the ten Ui values obtained in step five.
Finally, the calibration of the system was carried out following the above mentioned steps and its expanded uncertainty was ±0.10° using a coverage factor of k = 2, the laboratory temperature was 20°C ± 1°C. Furthermore, the repeatability was 0.04°, the non-linearity was 0.03° and the sensitivity was 1000.2 m°/°. Moreover, the response characteristic of this system is completely linear.
6. Results of the experiment
Generally speaking, in order to get the best information about the complex dynamics of cars, several accelerometers, speedometers, inclinometers, dynamometers, position sensors, etc., should be used and placed in the most important sections of the car under performance tests. However, the instrumentation of a car is sometimes expensive. For this reason, in this paper, the use of the optimal adapative filtering algorithm presented in previous sections was proposed to carry out the real-time measure of the rollover angle of a car under performace tests. The knowledge of this information by car drivers can save millions of lives every year [
1]. Therefore, this section is devoted to showing the results of the laboratory experiments.
The optimal estimation of the filter parameters is obtained from experimental curves, which have been obtained by ensemble-averaging the mean-squared error (MSE) of the filter over 360 independent trials of the experiment.
In addition, after studying the bandwidth of the relevant signal, a sampling frequency of 500 Hz was chosen. Furthermore, the signal treatment was carried out by using a laptop computer and the National Instruments Data Acquisition Card DAQCard-700, both placed in the car under performance tests. Moreover, a computer-controlled platform was used to generate the reference signals or desired responses necessary to test the sensor.
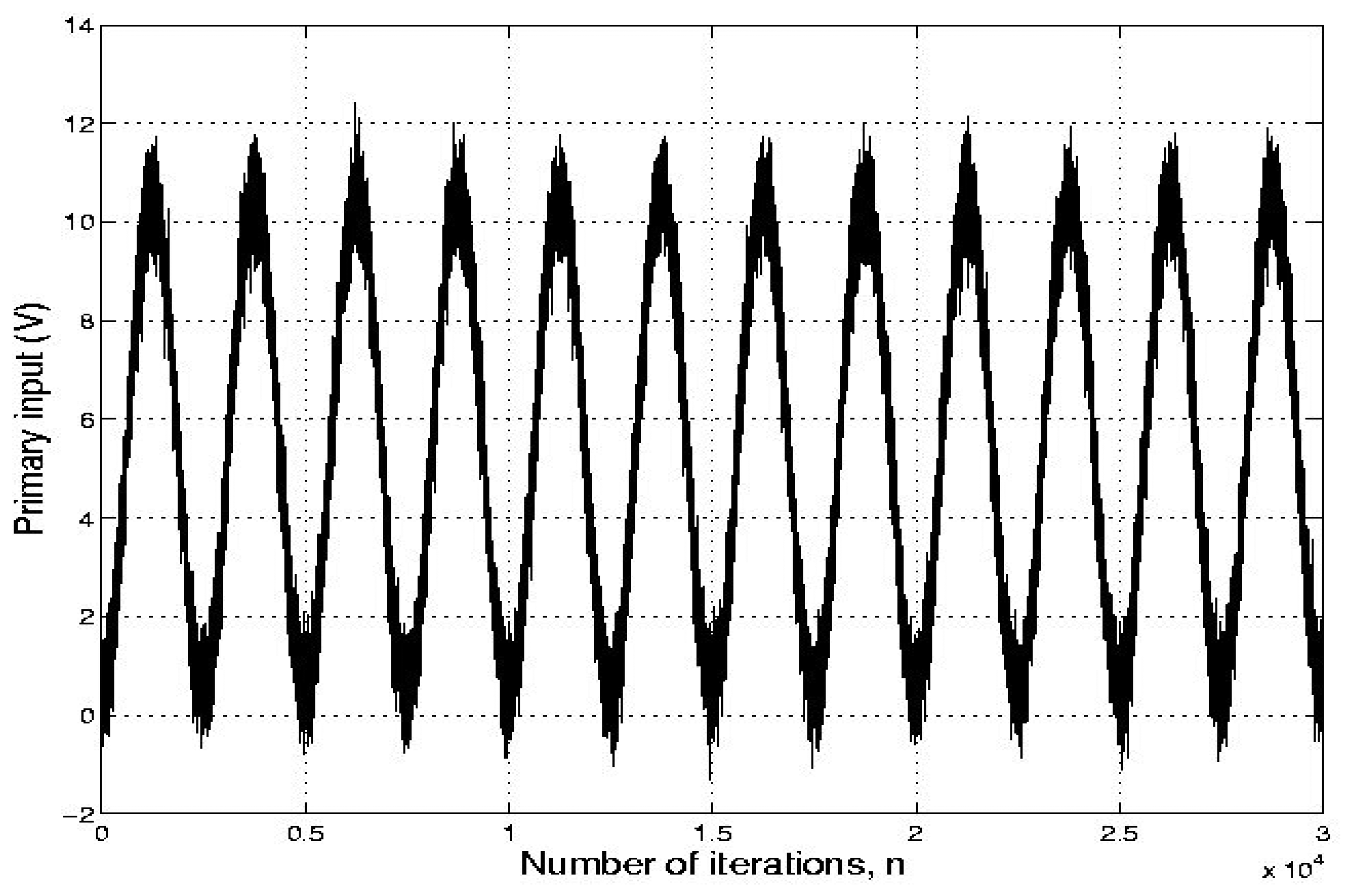
Fig. 4 shows a typical signal coming from the sensor (i.e., the primary input). In addition, the reference input is a signal that is uncorrelated with the relevant signal but correlated in some way with its noise. The reference signal consists of additive noise coming from another accelerometer placed close to the dual-axis accelerometer that is carrying out the measurements.
In addition, and
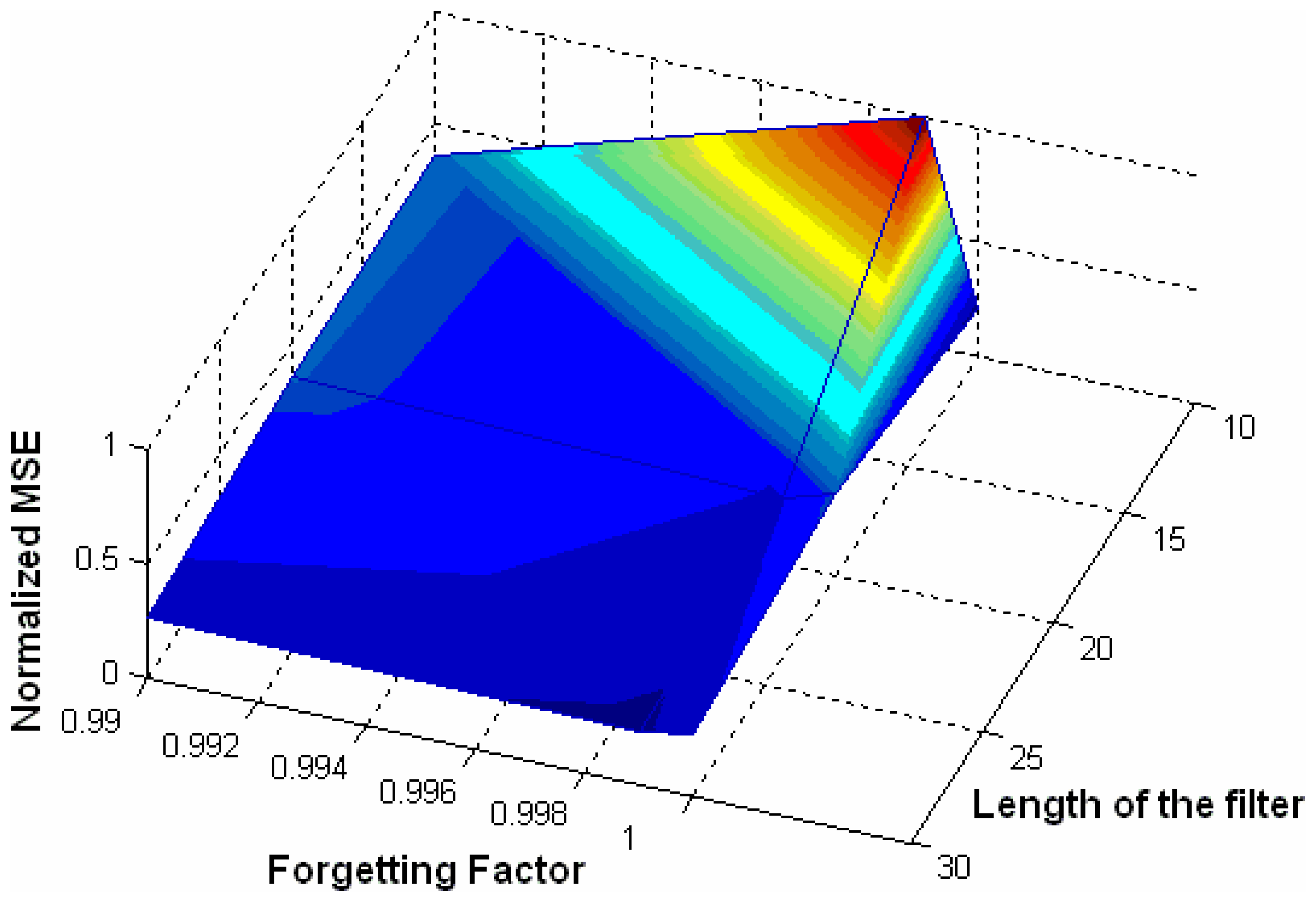
Table 1 shows the normalized ensemble-averaged mean-squared error of the filter (i.e., the cost function) over 360 independent trials of the experiment. Such independent trials were carried out in the following way: 40 independent trials were done for each one of the nine possible combinations of the variables shown in
Table 1, the length (or number of taps) of the filter (R + 1) and the forgetting factor (λ).
What is more, the values of R were chosen in accordance with the idea of implementing an adaptive filter with a small number of adaptive weights. Furthermore, experience tells us that the values of us λ should be the ones in the range from 0.99 to 1. In the case under study, if λ is lower than 0.99, the system is unstable.
The cost function is
where E is the expectation operator. Moreover,
Fig. 5 shows the normalized mean-squared performance surface for the system.
Here, it is important to point out that one may use a large number of adaptive weights, that is to say a large number of taps of the filter, but doing so could cause problems due to weight-vector noise. Such problems diminish the detection ability of the main signal due to spurious peaks, which may be confused with the signal of interest. What is more, infinite length of the weight-vector is the ideal solution but in digital signal processing high-order filters increase the computational burden and therefore the speed of the required processor. In addition, high-order filters require increased software complexity, which increases coding and debugging time [
65]. For this reason, this paper is focused on finding an estimate of the optimal filter using a small number of taps of the filter.
In accordance with the above mentioned statements and the information shown in
Fig. 5 and
Table 1,
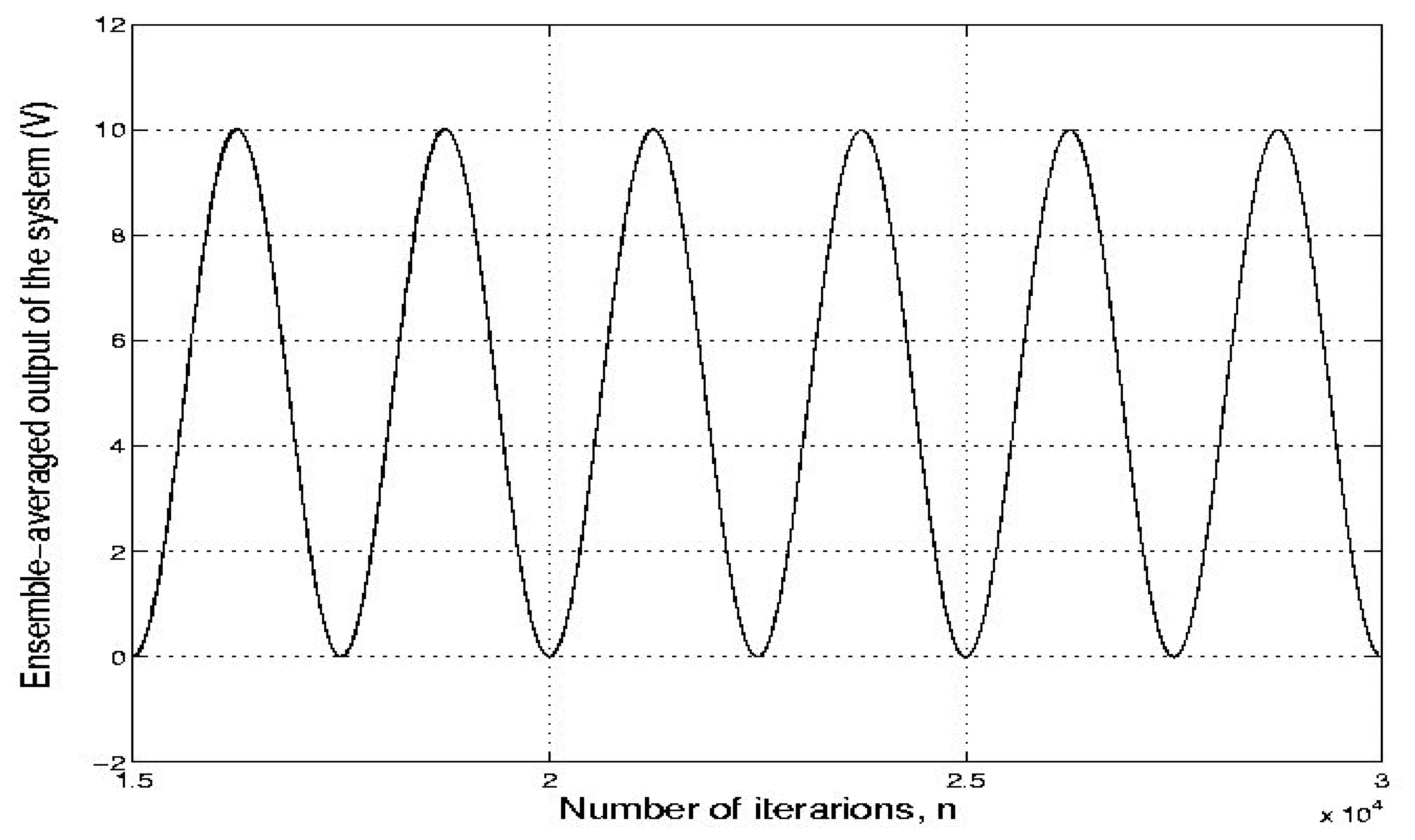
Fig. 6 shows the ensemble-averaged output of the system versus n curve over 200 independent trials of the experiment from n = 15000 to n=30000, where R = 9 and λ = 1.
Moreover,
Fig. 7 shows the power spectral density (PSD) of the electrical signals shown in
Figs. 4 and
6. The signal-to-noise ratio (SNR) of the primary input is approximately 18.6 dB, and the SNR at the system output is 45.3 dB. Therefore, a SNR improvement of approximately 26.7 dB was achieved, which is a good performance factor for judging the quality of the filter.
The experimental results presented in this paper show that the adaptive noise canceller significantly reduced the noise corrupting the relevant information while leaving the important information relatively unchanged from a practical viewpoint.
7. Conclusions
To conclude, in this paper a sensor to measure the rollover angle of a car under performance tests with low uncertainty and easy to implement in today's cars has been presented. Such a sensor is an optimal estimator of the rollover angle of today's cars, and has been designed and tested under laboratory conditions.
The results show that despite the signals coming from real physical systems being corrupted by noise and interferences, and that the behavior of such systems is affected negatively by undesirable disturbances, the use of optimal signal processing techniques can bring satisfactory results. In addition, it is important to stress that the system designed in this paper is easy to implement and was built by using low-cost components, which makes the use of this technology affordable to car manufacturers. The system does not need expensive sensors to work satisfactorily, which is a very important factor to be taken into consideration when constructing non-luxury cars. What is more, the system is well suited for use in automotive applications, not only in those addressing rollover, but also in others addressing stability and occupant protection, which are also safety-related problems.
In this paper, the application of the adaptive filter was as an adaptive noise (or interference) canceller, but there are others where it is recommended that we use an adaptive line enhancer device. That is to say, the same adaptive filter designed here but with the input being a delay version of the desired response, so that the system can predict the relevant signal, which is typically buried in a corrupted environment.
Last but not least, the use of this paper's design method can bridge the gap between intelligent signal processing methods and the design of sensors and actuators for a wide range of applications. The reality is that only by the fusion of these concepts can the designer find the way clear to build the intelligent sensors that today's cars need.