A Novel Method for the Dynamic Coefficients Identification of Journal Bearings Using Kalman Filter
Abstract
:1. Introduction
2. Test Rig and Rotor Modeling
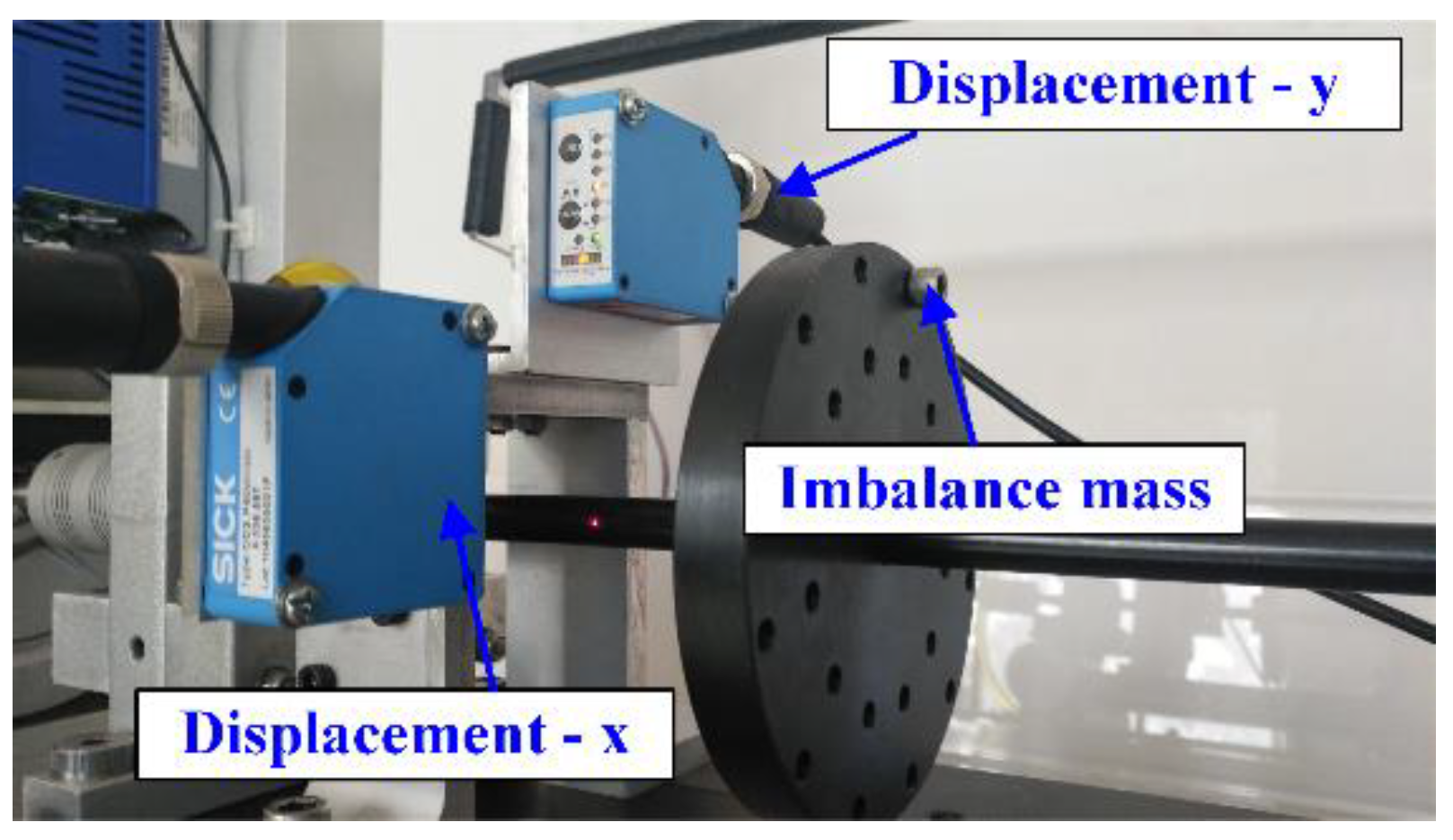
2.1. Test Rig
2.2. Modeling
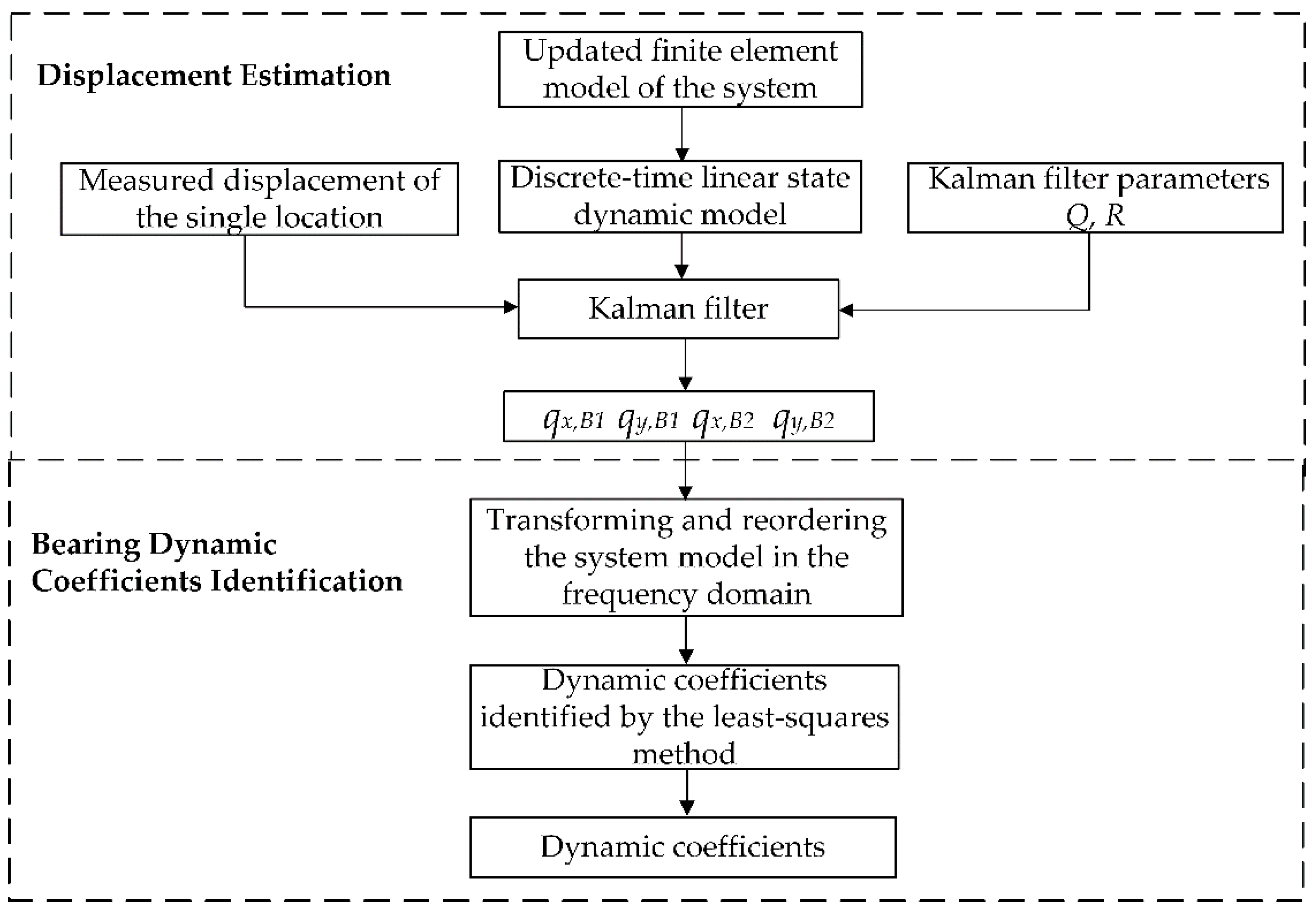
3. Proposed Method
3.1. Displacement Estimation
3.2. Bearing Dynamic Coefficients Identification
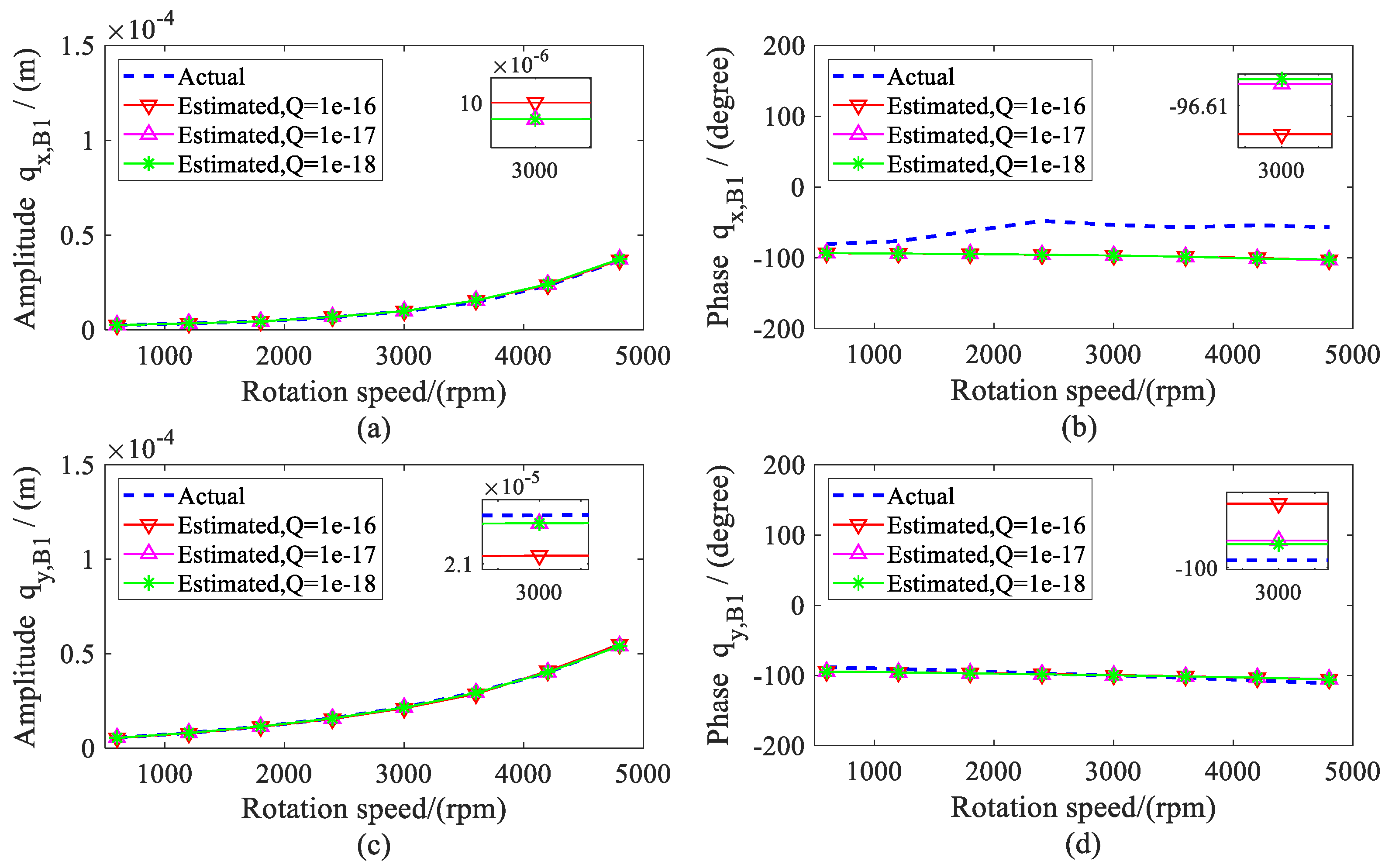
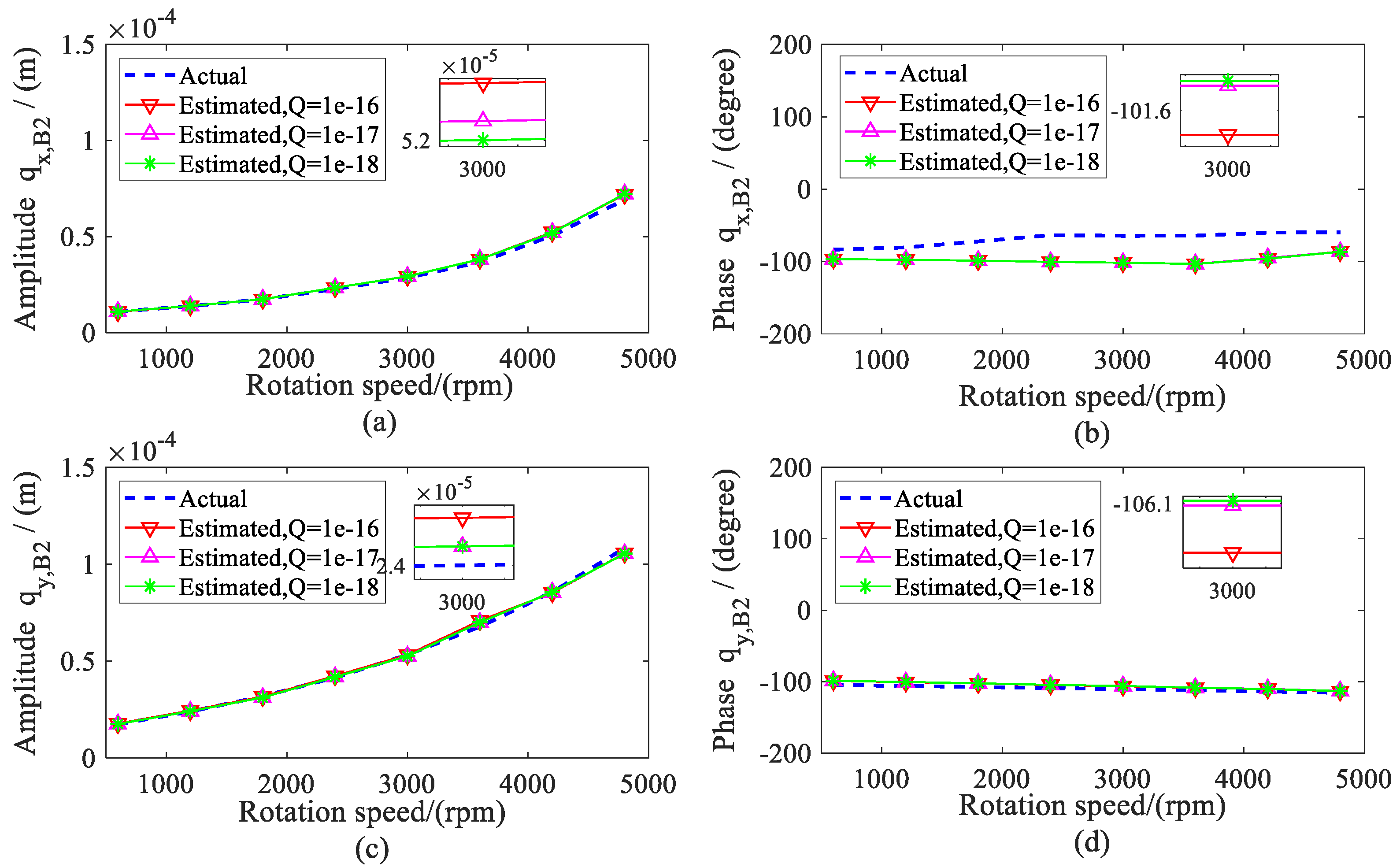
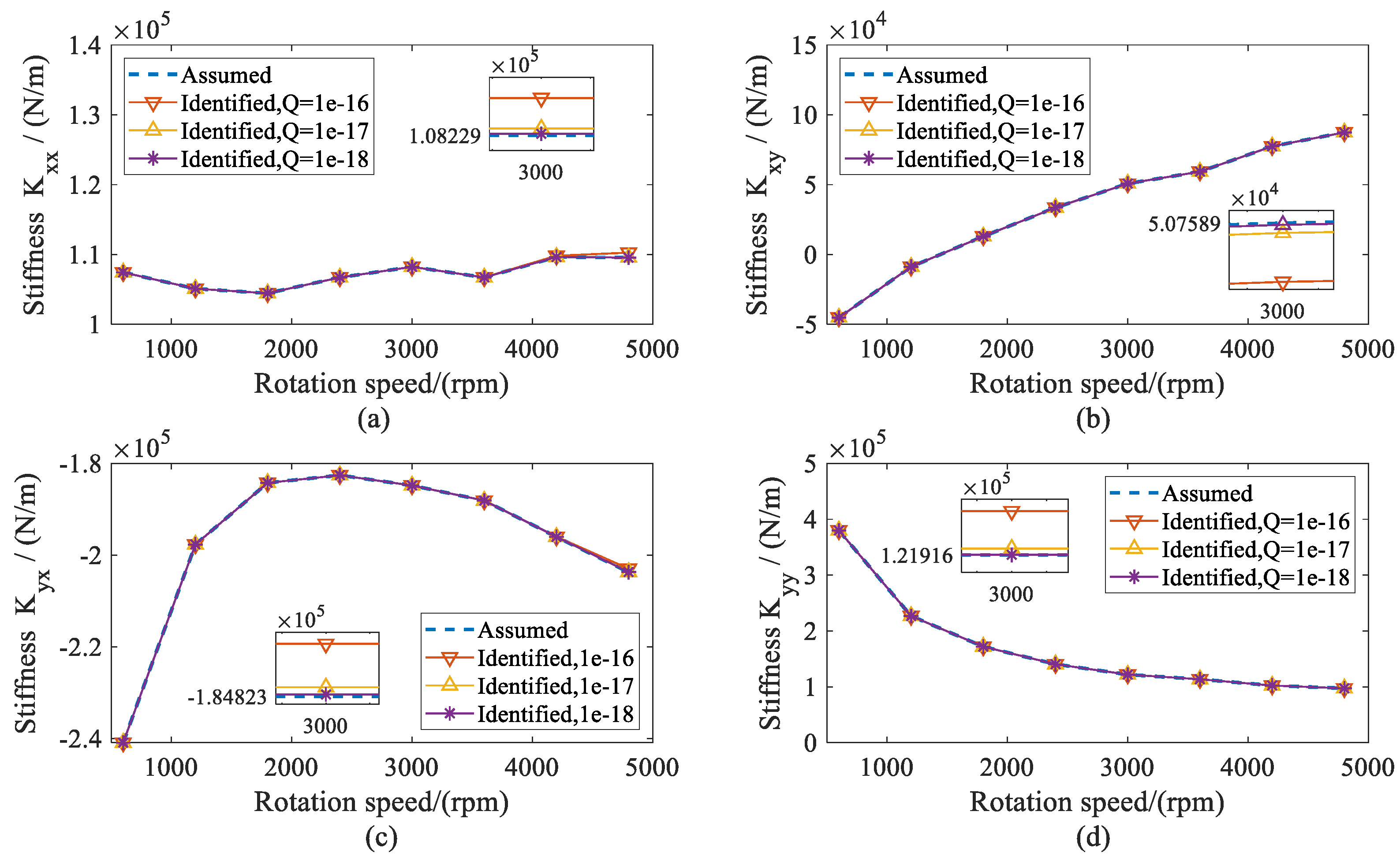
4. Simulations
5. Experimental Analysis
5.1. Experimental Description
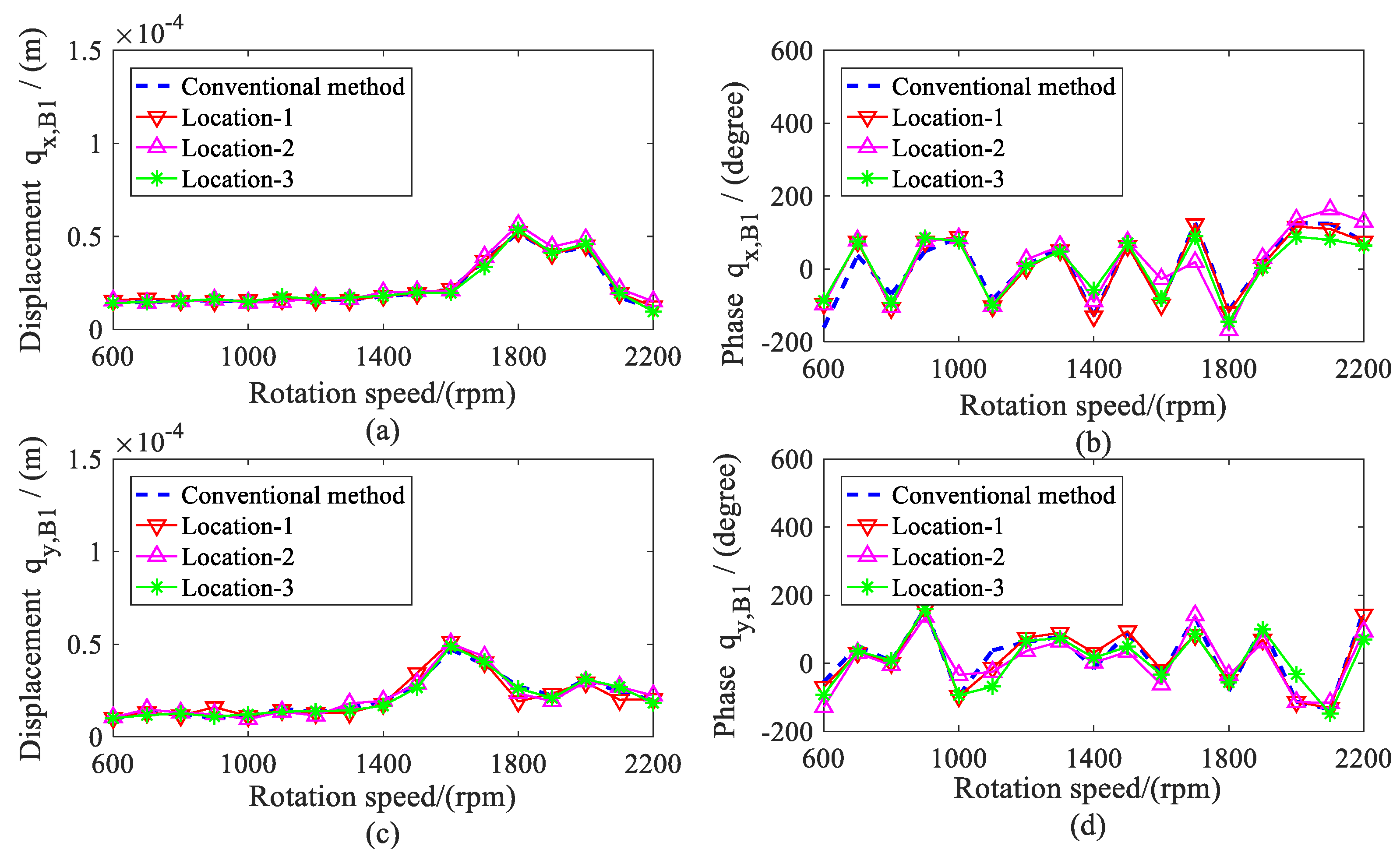
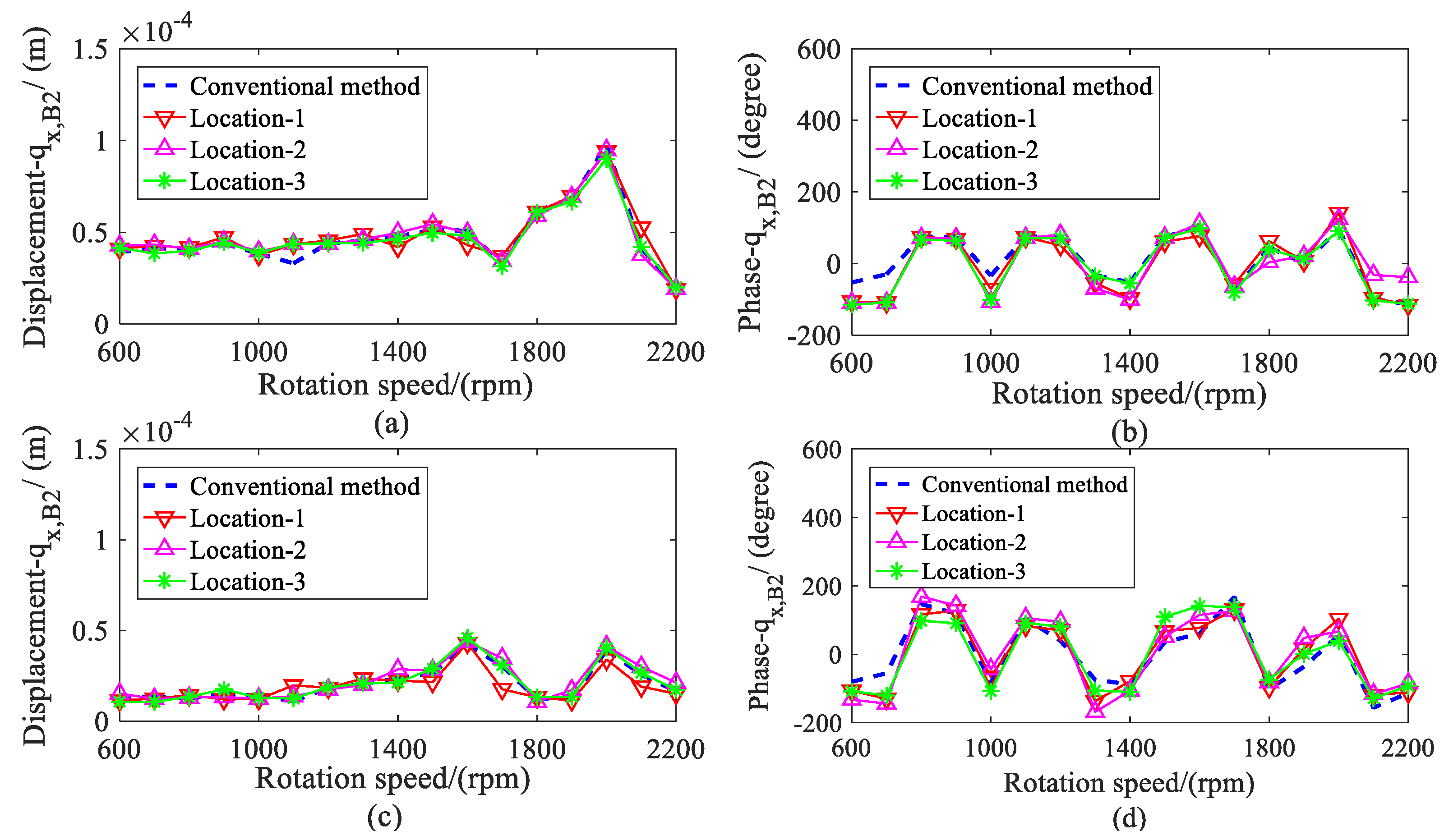
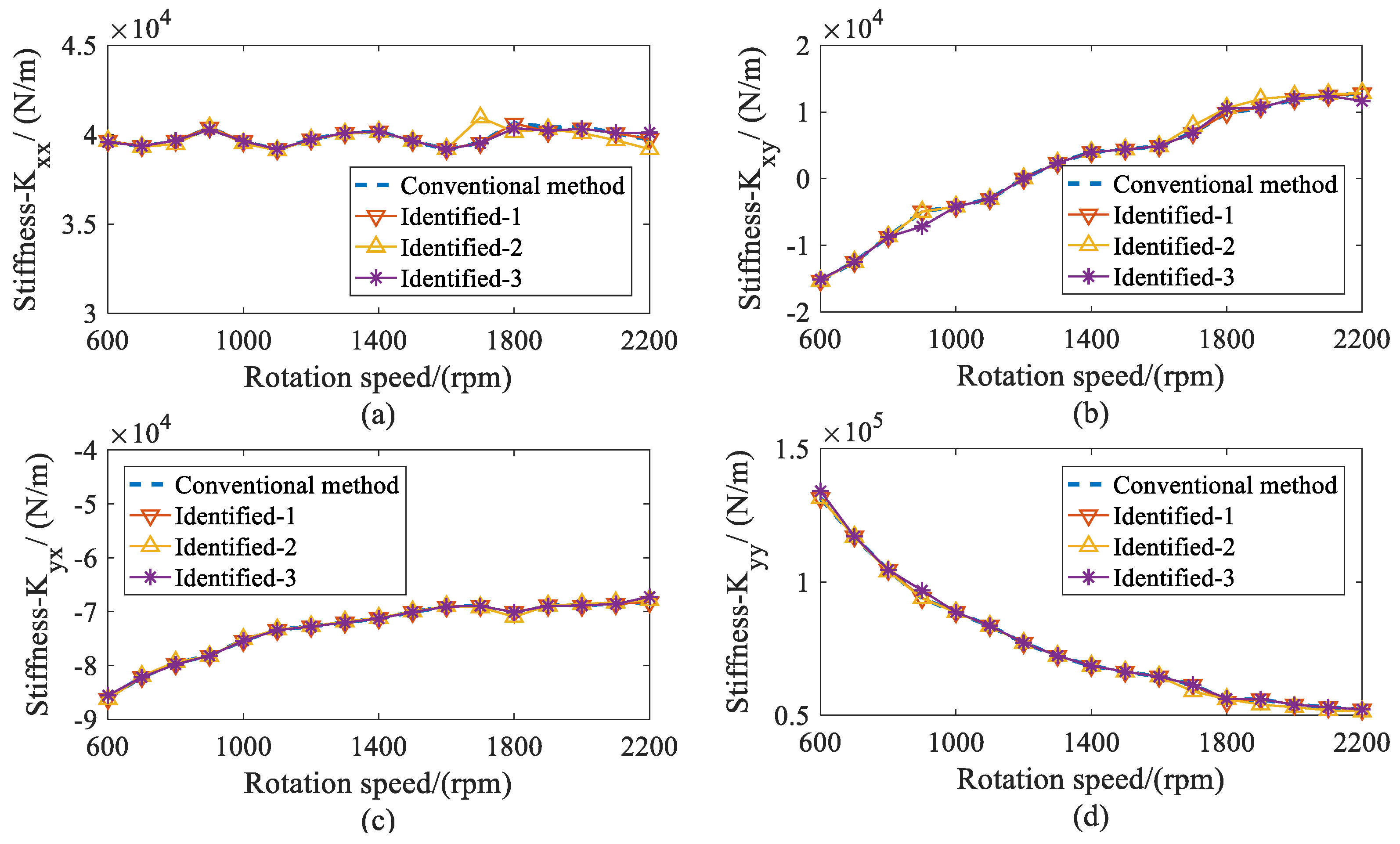
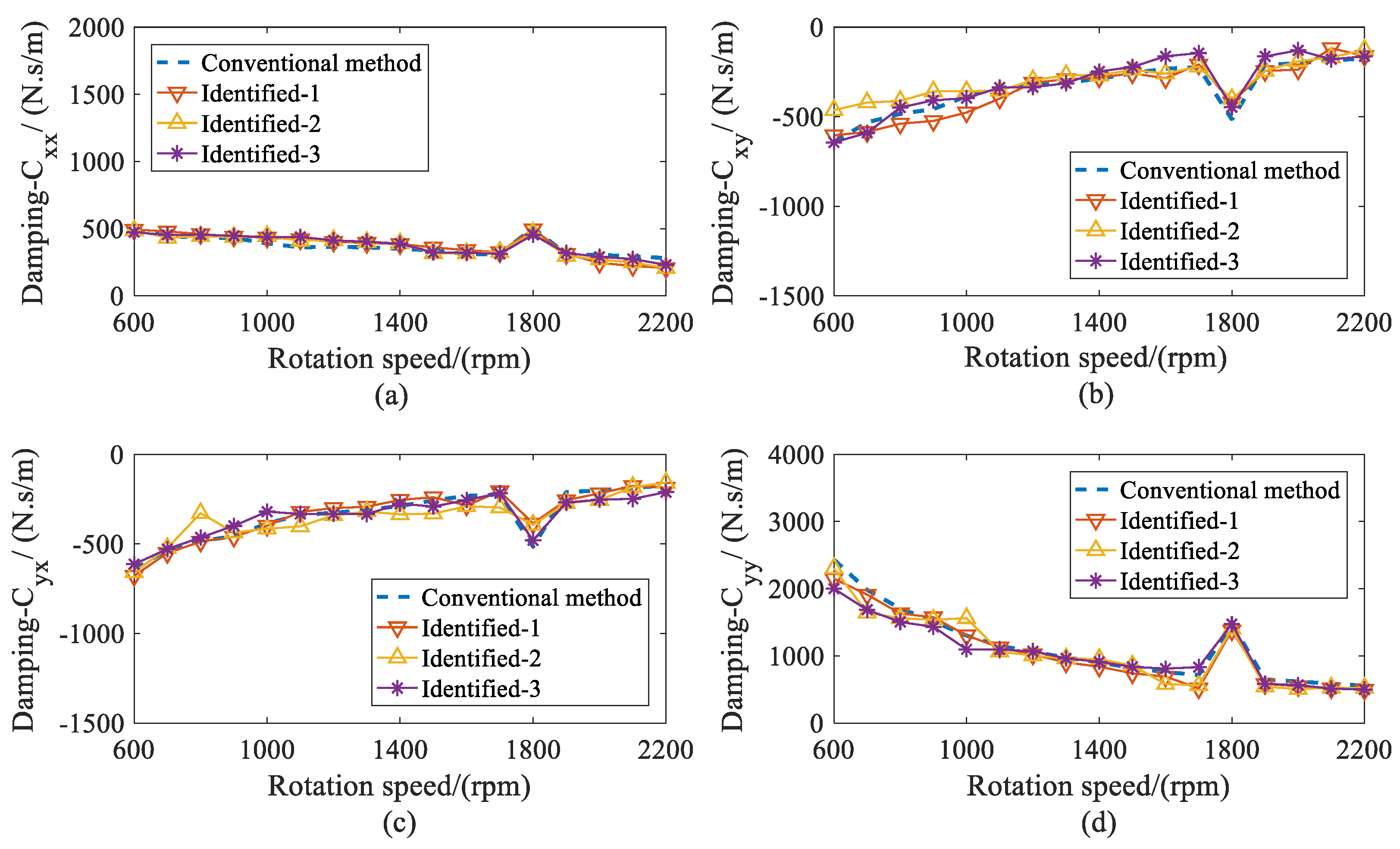
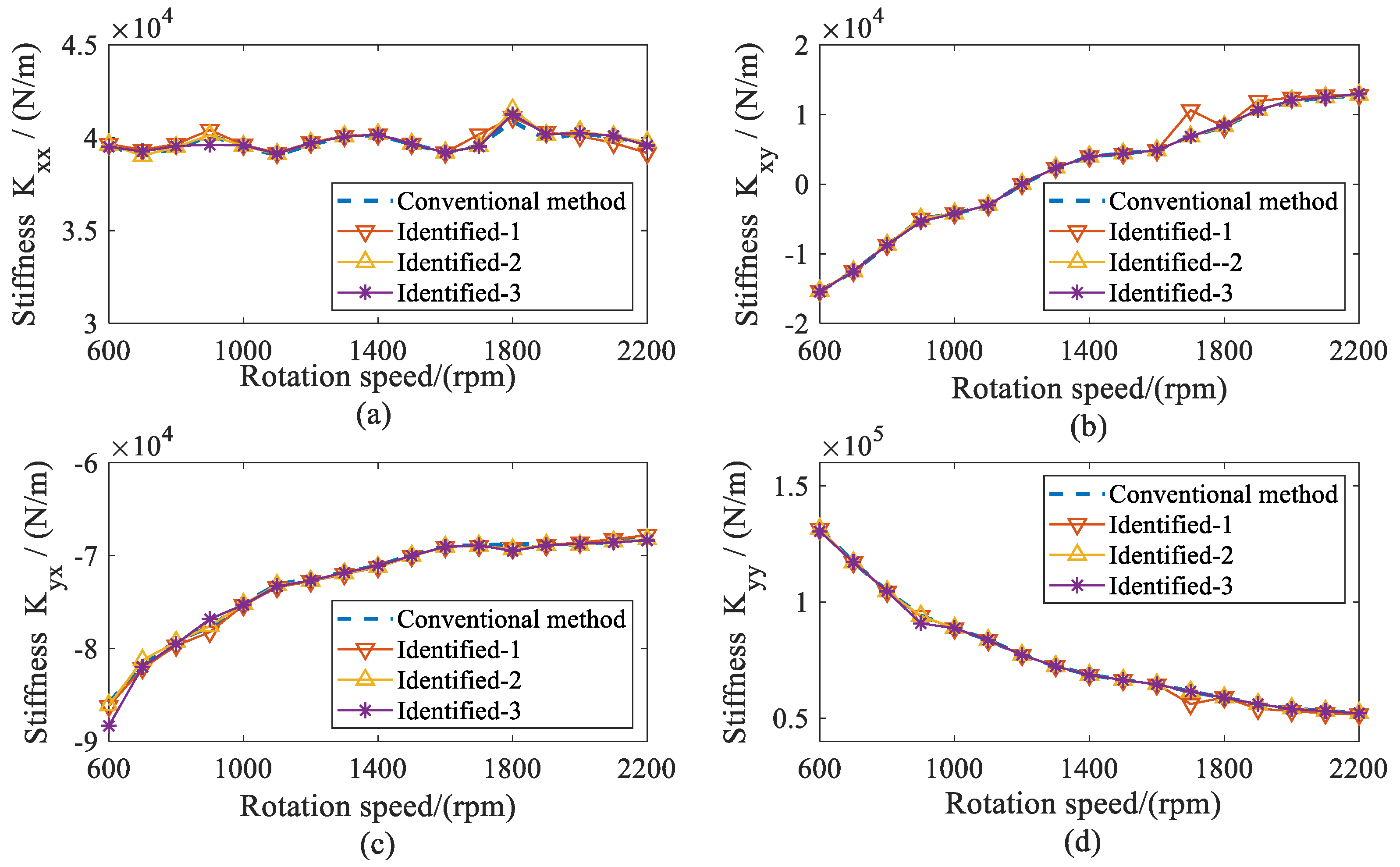
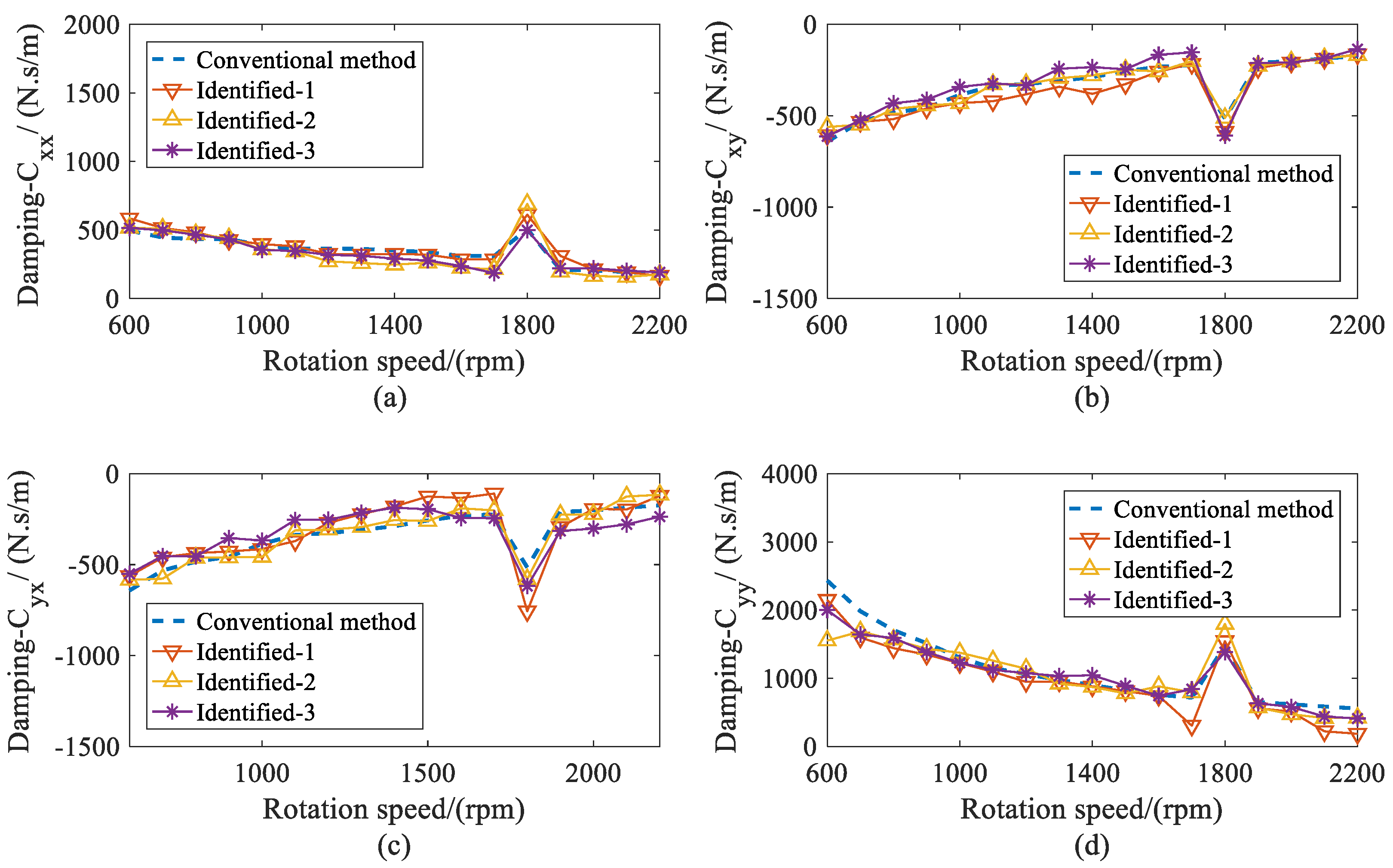
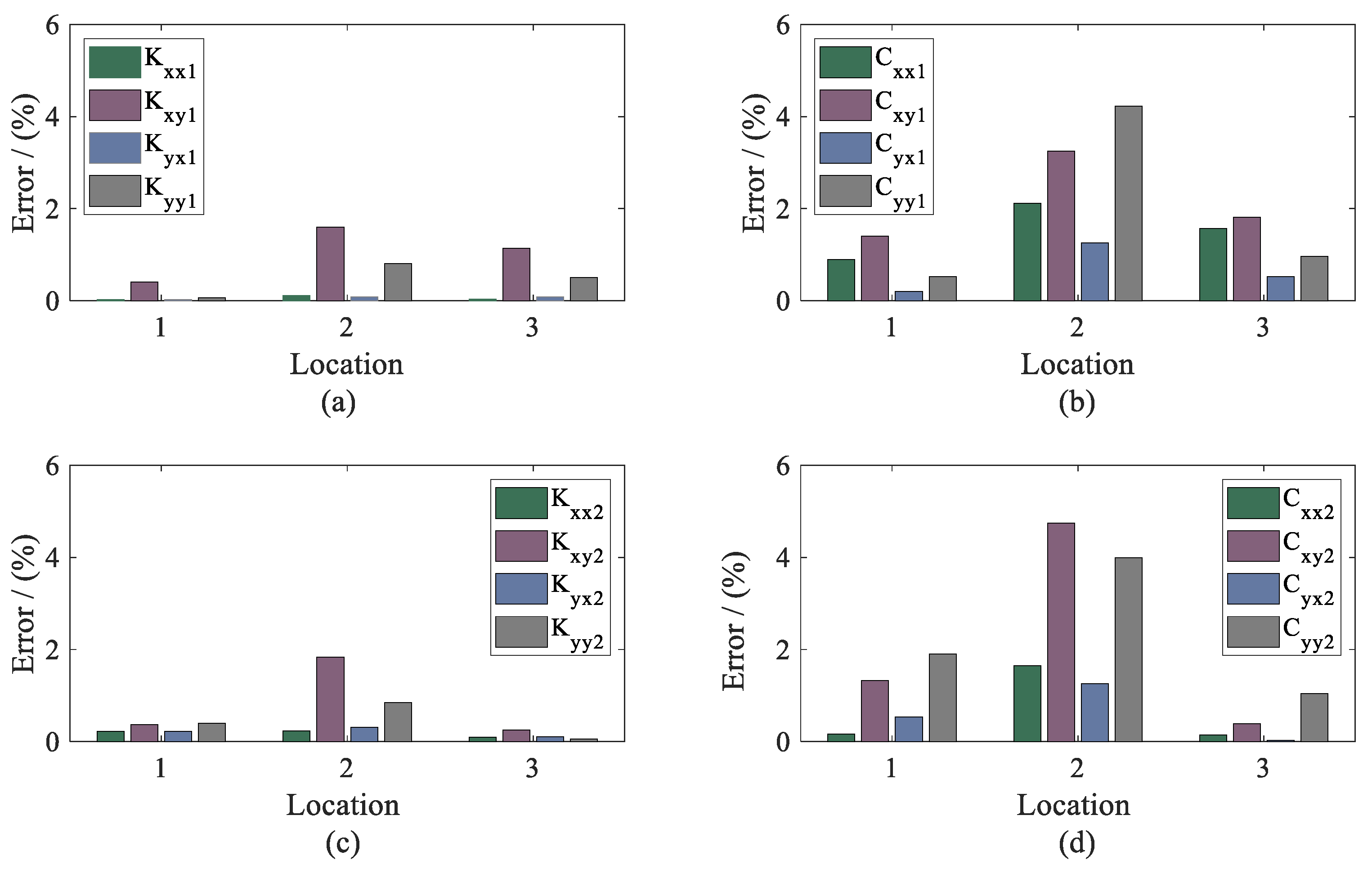
5.2. Results and Discussions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Snyder, T.; Braun, M. Comparison of Perturbed Reynolds Equation and CFD Models for the Prediction of Dynamic Coefficients of Sliding Bearings. Lubricants 2018, 6, 5. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Zhang, S.; Ma, L. Stiffness and damping coefficients for journal bearing using the 3D transient flow calculation. J. Mech. Sci. Technol. 2017, 31, 2083–2091. [Google Scholar] [CrossRef]
- Dyk, Š.; Rendl, J.; Byrtus, M. Dynamic coefficients and stability analysis of finite-length journal bearings considering approximate analytical solutions of the Reynolds equation. Tribol. Int. 2019, 130, 229–244. [Google Scholar] [CrossRef]
- Merelli, C.E.; Barilá, D.O.; Vignolo, G.G.; Quinzani, L.M. Dynamic Coefficients of Finite Length Journal Bearing. Evaluation Using a Regular Perturbation Method. Int. J. Mech. Sci. 2019, 151, 251–262. [Google Scholar] [CrossRef] [Green Version]
- Tiwari, R.; Lees, A.W.; Friswell, M.I. Identification of Speed-Dependent Bearing Parameters. J. Sound Vib. 2002, 254, 967–986. [Google Scholar] [CrossRef] [Green Version]
- Tiwari, R.; Chakravarthy, V. Simultaneous identification of residual imbalances and bearing dynamic parameters from impulse responses of rotor–bearing systems. Mech. Syst. Signal Process. 2006, 20, 1590–1614. [Google Scholar] [CrossRef]
- Qiu, Z.L.; Tieu, A.K. Identification of sixteen force coefficients of two journal bearings from impulse responses. Wear 1997, 212, 206–212. [Google Scholar] [CrossRef]
- Tiwari, R.; Lees, A.W.; Friswell, M.I. Identification of dynamic bearing parameters: A review. Shock Vib. Dig. 2004, 36, 99–124. [Google Scholar] [CrossRef]
- Tieu, A.K.; Qiu, Z.L. Identification of sixteen dynamic coefficients of two journal bearings from experimental imbalance response. Wear 1994, 177, 63–69. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, J.; Di, L.; Zhao, C. Active magnetic bearings dynamic parameters identification from experimental rotor unbalance response. Mech. Syst. Signal Process. 2016, 83, 228–240. [Google Scholar] [CrossRef]
- Tiwari, R.; Chakravarthy, V. Simultaneous estimation of the residual imbalance and bearing dynamic parameters from the experimental data in a rotor-bearing system. Mech. Mach. Theory 2009, 44, 792–812. [Google Scholar] [CrossRef]
- Han, F.; Guo, X.; Gao, H. Bearing parameter identification of rotor-bearing system based on Kriging surrogate model and evolutionary algorithm. J. Sound Vib. 2013, 332, 2659–2671. [Google Scholar] [CrossRef]
- Li, K.; Liu, J.; Han, X. Identification of oil-film coefficients for a rotor-journal bearing system based on equivalent load reconstruction. Tribol. Int. 2016, 104, 285–293. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.H.; Yang, B.S.; Tan, A.C.C. Bearing parameter identification of rotor–bearing system using clustering-based hybrid evolutionary algorithm. Struct. Multidiscip. Optim. 2007, 33, 493–506. [Google Scholar] [CrossRef]
- Tyminski, N.C.; Tuckmantel, F.W.S.; Cavalca, K.L.; De Castro, H.F. Bayesian inference applied to journal bearing parameter identification. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 2983–3004. [Google Scholar] [CrossRef]
- Chen, C.; Jing, J.; Cong, J.; Dai, Z. Identification of dynamic coefficients in circular journal bearings from imbalance response and complementary equations. J. Eng. Tribol. 2019, 233, 1016–1028. [Google Scholar]
- Santiago, O.D.; Andres, L.S. Experimental Identification of Bearing Dynamic Force Coefficients in a Flexible Rotor—Further Developments. Tribol. Lubr. Technol. 2007, 50, 114–126. [Google Scholar] [CrossRef]
- Li, Q.; Wang, W.; Weaver, B. Model-Based Interpolation-Iteration Method for Bearing Coefficients Identification of Operating Flexible Rotor-Bearing System. Int. J. Mech. Sci. 2017, 131, 471–479. [Google Scholar] [CrossRef]
- Ma, C.K.; Lin, D.C. Input forces estimation of a cantilever beam. Inverse Probl. Eng. 2000, 8, 511–528. [Google Scholar] [CrossRef]
- Loh, C.H.; Yang, J.N. Input force identification using Kalman filter techniques: Application to soil-pile interaction. Int. Soc. Opt. Eng. 2008, 6932, 1–12. [Google Scholar]
- Song, X.; Zhang, Y.; Liang, D. Load Identification for a Cantilever Beam Based on Fiber Bragg Grating Sensors. Sensors 2017, 17, 1733. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shrivastava, A.; Mohanty, A.R. Estimation of single plane unbalance parameters of a rotor-bearing system using Kalman filtering based force estimation technique. J. Sound Vib. 2018, 418, 184–199. [Google Scholar] [CrossRef]
- Gao, F.; Lu, Y. A Kalman-filter based time-domain analysis for structural damage diagnosis with noisy signals. J. Sound Vib. 2006, 297, 916–930. [Google Scholar] [CrossRef]
- Pan, C.T.; Ji, C.; Li, W.F.; Wen, T.H. An input estimation approach to on-line two-dimensional inverse heat conduction problems. Numer. Heat Transf. 1996, 29, 345–363. [Google Scholar]
- Aljoumani, B.; Sanchez-Espigares, J.; Wessolek, G. Estimating Pore Water Electrical Conductivity of Sandy Soil from Time Domain Reflectometry Records Using a Time-Varying Dynamic Linear Model. Sensors 2018, 18, 4403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Odry, A.; Fuller, R.; Rudas, I.J.; Odry, P. Kalman filter for mobile-robot attitude estimation: Novel optimized and adaptive solutions. Mech. Syst. Signal Process. 2018, 110, 569–589. [Google Scholar] [CrossRef]
- Battistelli, G.; Chisci, L. Stability of consensus extended Kalman filter for distributed state estimation. Automatica 2016, 68, 169–178. [Google Scholar] [CrossRef]
- Azam, S.E.; Chatzi, E.; Papadimitriou, C. A dual Kalman filter approach for state estimation via output-only acceleration measurements. Mech. Systems Signal Process. 2015, 60–61, 866–886. [Google Scholar] [CrossRef]
- Karimipour, H.; Dinavahi, V. Extended Kalman Filter-Based Parallel Dynamic State Estimation. IEEE Trans. Smart Grid 2015, 6, 1539–1549. [Google Scholar] [CrossRef]
- Manganiello, P.; Ricco, M.; Petrone, G.; Monmasson, E.; Spagnuolo, G. Dual-Kalman-filter-based identification and real-time optimization of PV systems. IEEE Trans. Ind. Electron. 2015, 62, 7266–7275. [Google Scholar] [CrossRef]
- Gao, S.; Liu, Y.; Wang, J. The Joint Adaptive Kalman Filter (JAKF) for Vehicle Motion State Estimation. Sensors 2016, 16, 1103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reichbach, N.; Kuperman, A. Recursive-Least-Squares-Based Real-Time Estimation of Supercapacitor Parameters. IEEE Trans. Energy Convers. 2016, 31, 1–3. [Google Scholar] [CrossRef]
- Zhao, S.X.; Zhou, H.; Meng, G.; Zhu, J. Experimental identification of linear oil-film coefficients using least-mean-square method in time domain. J. Sound Vib. 2005, 287, 809–825. [Google Scholar] [CrossRef]
- Nelson, H.D. A Finite Rotating Shaft Element Using Timoshenko Beam Theory. J. Mech. Des. 1980, 102, 793–803. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Kim, H.; Jang, G.; Ha, H. A generalized Reynolds equation and its perturbation equations for fluid dynamic bearings with curved surfaces. Tribol. Int. 2012, 50, 6–15. [Google Scholar] [CrossRef]




| Property | Value |
|---|---|
| Rotor Shaft diameter, R | 0.01265 m |
| Maximum rotation speed, Ω | 6000 rpm |
| Mass, m | 0.86 kg |
| Length of rotor, L | 0.85 m |
| Density | 7800 kg/m3 |
| Rigid discs Inner diameter | 0.01265 m |
| Outer diameter | 0.08 m |
| Thickness | 0.015 m |
| Bearing Diameter | 0.01265 m |
| Length to diameter ratio | 1 |
| Radical clearance of bearings | 5 × 10−5 m |
| Order | Initial Model (Hz) | Measured (Hz) | Updated Model (Hz) |
|---|---|---|---|
| 1 | 69.26 | 62.86 | 62.86 |
| 2 | 129.75 | 110.20 | 110.55 |
| 3 | 287.31 | 279.14 | 279.14 |
| 4 | 378.53 | 361.27 | 362.99 |
| Property | Mass (kg) | Radius (m) | Phase (°) |
|---|---|---|---|
| Node 8 | = 0.004 | r2 = 0.063 | 90 |
| Property | Mass (kg) | Radius (m) | Phase (°) |
|---|---|---|---|
| Node 4 | = 0.0025 | r1 = 0.063 | 0 |
| Node 8 | = 0.0050 | r2 = 0.063 | 90 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, Y.; Shi, Z.; Zhang, H.; Zhen, D.; Gu, F. A Novel Method for the Dynamic Coefficients Identification of Journal Bearings Using Kalman Filter. Sensors 2020, 20, 565. https://doi.org/10.3390/s20020565
Kang Y, Shi Z, Zhang H, Zhen D, Gu F. A Novel Method for the Dynamic Coefficients Identification of Journal Bearings Using Kalman Filter. Sensors. 2020; 20(2):565. https://doi.org/10.3390/s20020565
Chicago/Turabian StyleKang, Yang, Zhanqun Shi, Hao Zhang, Dong Zhen, and Fengshou Gu. 2020. "A Novel Method for the Dynamic Coefficients Identification of Journal Bearings Using Kalman Filter" Sensors 20, no. 2: 565. https://doi.org/10.3390/s20020565






