Kalman Filtering for Attitude Estimation with Quaternions and Concepts from Manifold Theory
Abstract
:1. Introduction
2. Quaternions Describing Orientations
2.1. Quaternions
2.2. Quaternions Representing Rotations
2.3. Distributions of Unit Quaternions
- f is a bijection,
- f is continuous,
- its inverse function is continuous.
2.4. Transition Maps
3. Manifold Kalman Filters
3.1. Manifold Extended Kalman Filter
3.2. Manifold Unscented Kalman Filter
4. Simulation Results
4.1. Performance Metric
4.2. Simulation Scheme
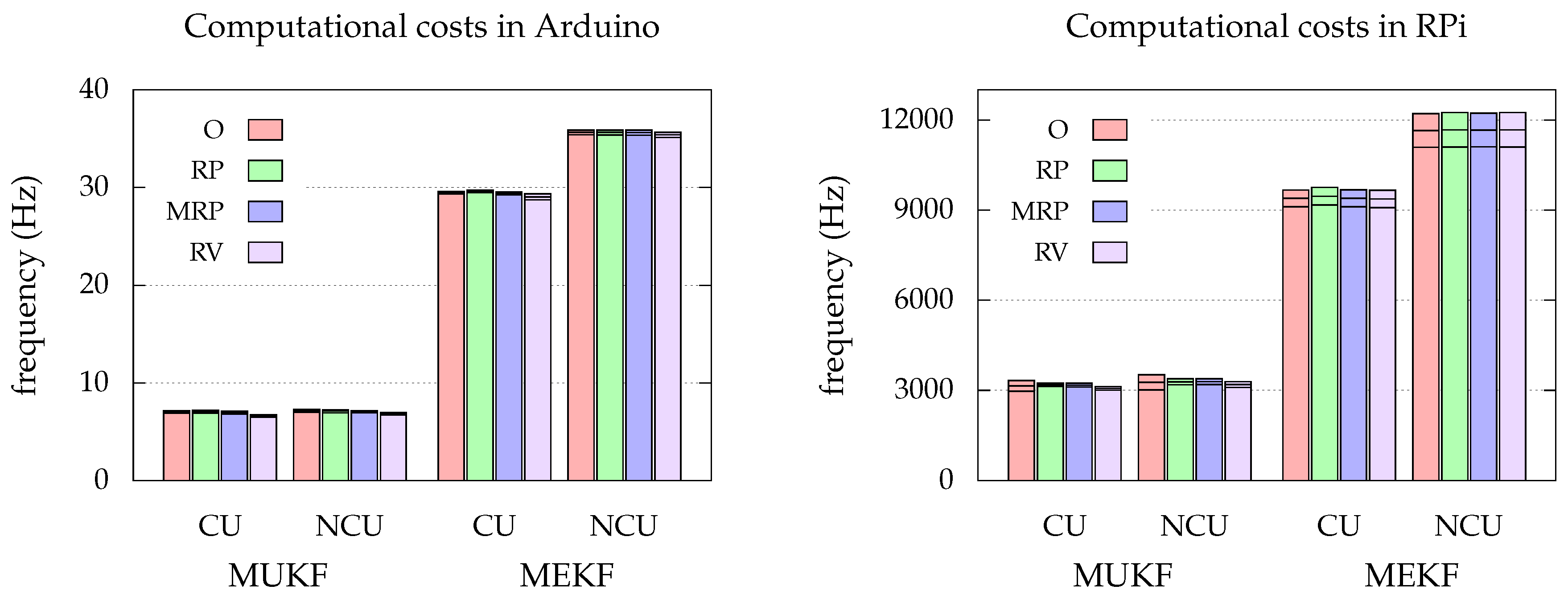
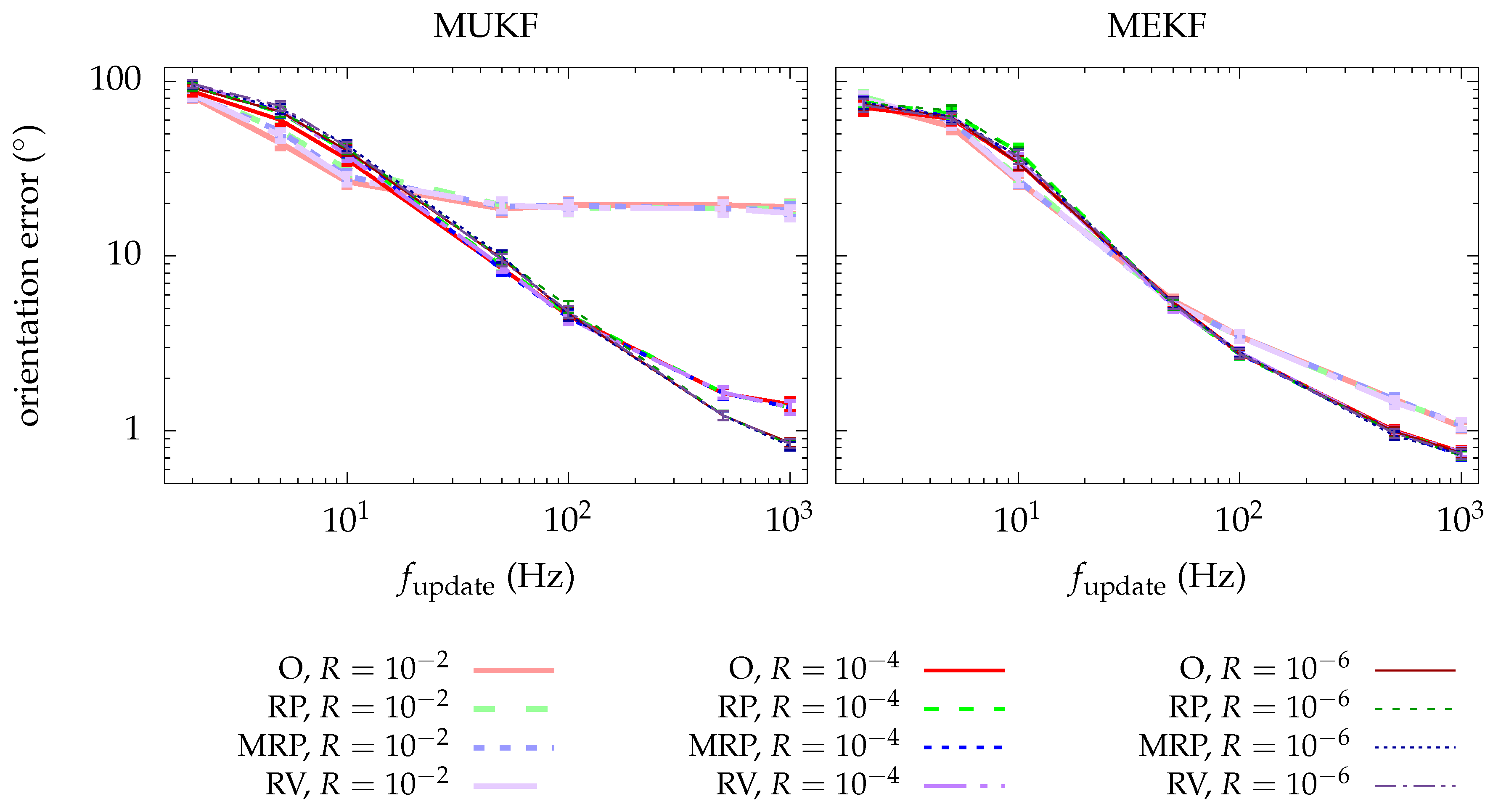
4.3. Results
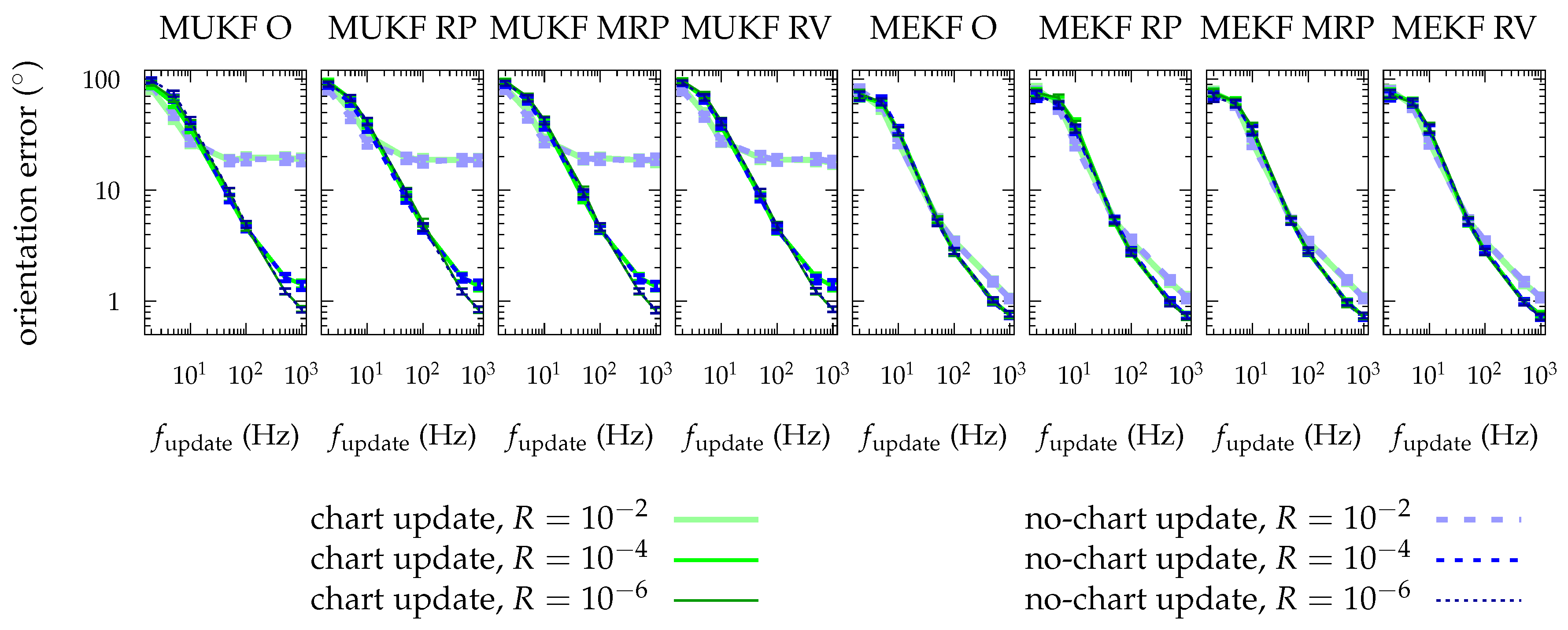
4.3.1. Chart Choice
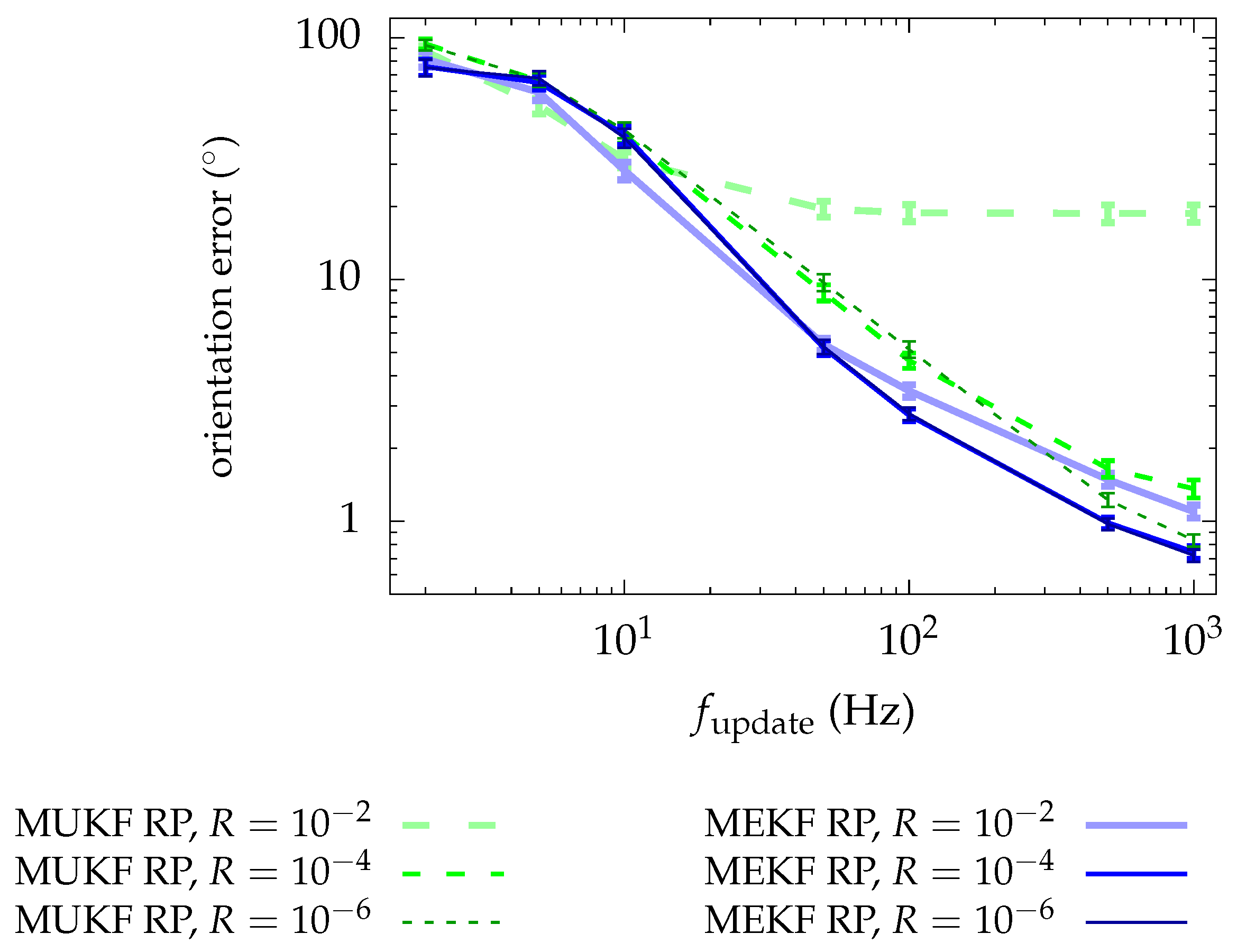
4.3.2. MEKF vs. MUKF
4.3.3. Chart Update vs. No Chart Update
5. Conclusions
- There is no chart that presents a clear advantage over the others, but the RP chart has some characteristics that motivate us to prefer it.
- The MEKF is preferable to the MUKF due to its lower computational cost and its greater accuracy in orientation estimation.
- The “chart update” is not necessary for the MKF in practice.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| EKF | Extended Kalman Filter |
| UKF | Unscented Kalman Filter |
| MKF | Manifold Kalman Filter |
| MEKF | Manifold Extended Kalman Filter |
| MUKF | Manifold Unscented Kalman Filter |
| O | Orthographic |
| RP | Rodrigues Parameters |
| MRP | Modified Rodrigues Parameters |
| RV | Rotation Vector |
Appendix A. Derivation of Transition Maps
Appendix A.1. Orthographic
Appendix A.2. Rodrigues Parameters
Appendix A.3. Modified Rodrigues Parameters
Appendix A.4. Rotation Vector
Appendix B. Details in the Derivation of the MEKF
Appendix B.1. State Prediction
Appendix B.1.1. Evolution of the Expected Value of the State
Appendix B.1.2. Evolution of the State Covariance Matrix
Appendix B.2. Measurement Prediction
Appendix B.2.1. Expected Value of the Measurement Prediction
Appendix B.2.2. Covariance Matrix of the Measurement Prediction
Appendix C. Derivation of the T-matrices
Appendix C.1. Orthographic
Appendix C.2. Rodrigues Parameters
Appendix C.3. Modified Rodrigues Parameters
Appendix C.4. Rotation Vector
References
- Crassidis, J.L.; Markley, F.L.; Cheng, Y. Survey of nonlinear attitude estimation methods. J. Guid. Control Dyn. 2007, 30, 12–28. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. New Extension of the Kalman Filter to Nonlinear Systems; AeroSense’97; International Society for Optics and Photonics: Bellingham, WA, USA, 1997; pp. 182–193. [Google Scholar]
- Shuster, M.D. A survey of attitude representations. Navigation 1993, 8, 439–517. [Google Scholar]
- Stuelpnagel, J. On the parametrization of the three-dimensional rotation group. SIAM Rev. 1964, 6, 422–430. [Google Scholar] [CrossRef]
- Lefferts, E.J.; Markley, F.L.; Shuster, M.D. Kalman filtering for spacecraft attitude estimation. J. Guid. Control Dyn. 1982, 5, 417–429. [Google Scholar] [CrossRef]
- Crassidis, J.L.; Markley, F.L. Unscented filtering for spacecraft attitude estimation. J. Guid. Control Dyn. 2003, 26, 536–542. [Google Scholar] [CrossRef]
- Markley, F.L. Attitude error representations for Kalman filtering. J. Guid. Control Dyn. 2003, 26, 311–317. [Google Scholar] [CrossRef]
- Hall, J.K.; Knoebel, N.B.; McLain, T.W. Quaternion attitude estimation for miniature air vehicles using a multiplicative extended Kalman filter. In Proceedings of the 2008 IEEE/ION Position, Location and Navigation Symposium, Monterey, CA, USA, 5–8 May 2008; IEEE: Piscataway, NJ, USA; pp. 1230–1237. [Google Scholar]
- VanDyke, M.C.; Schwartz, J.L.; Hall, C.D. Unscented Kalman filtering for spacecraft attitude state and parameter estimation. Adv. Astronaut. Sci. 2004, 118, 217–228. [Google Scholar]
- Markley, F.L. Multiplicative vs. additive filtering for spacecraft attitude determination. Dyn. Control Syst. Struct. Space 2004, 6, 311–317. [Google Scholar]
- Crassidis, J.L.; Markley, F.L. Attitude Estimation Using Modified Rodrigues Parameters. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19960035754.pdf (accessed on 1 January 2019).
- Bar-Itzhack, I.; Oshman, Y. Attitude determination from vector observations: Quaternion estimation. IEEE Trans. Aerosp. Electr. Syst. 1985, AES-21, 128–136. [Google Scholar] [CrossRef]
- Mueller, M.W.; Hehn, M.; D’Andrea, R. Covariance correction step for kalman filtering with an attitude. J. Guid. Control Dyn. 2016, 40, 2301–2306. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. Unscented filtering and nonlinear estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef]
- Gramkow, C. On averaging rotations. J. Math. Imag. Vision 2001, 15, 7–16. [Google Scholar] [CrossRef]
- LaViola, J.J. A comparison of unscented and extended Kalman filtering for estimating quaternion motion. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003; IEEE: Piscataway, NJ, USA, 2003; Volume 3, pp. 2435–2440. [Google Scholar]
- Xie, L.; Popa, D.; Lewis, F.L. Optimal and Robust Estimation: With an Introduction to Stochastic Control Theory; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
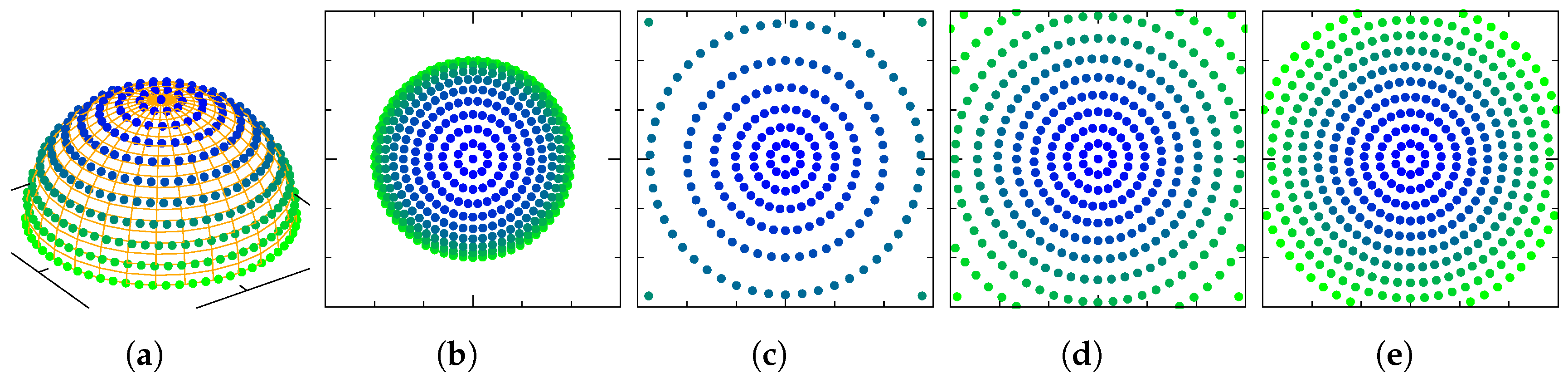

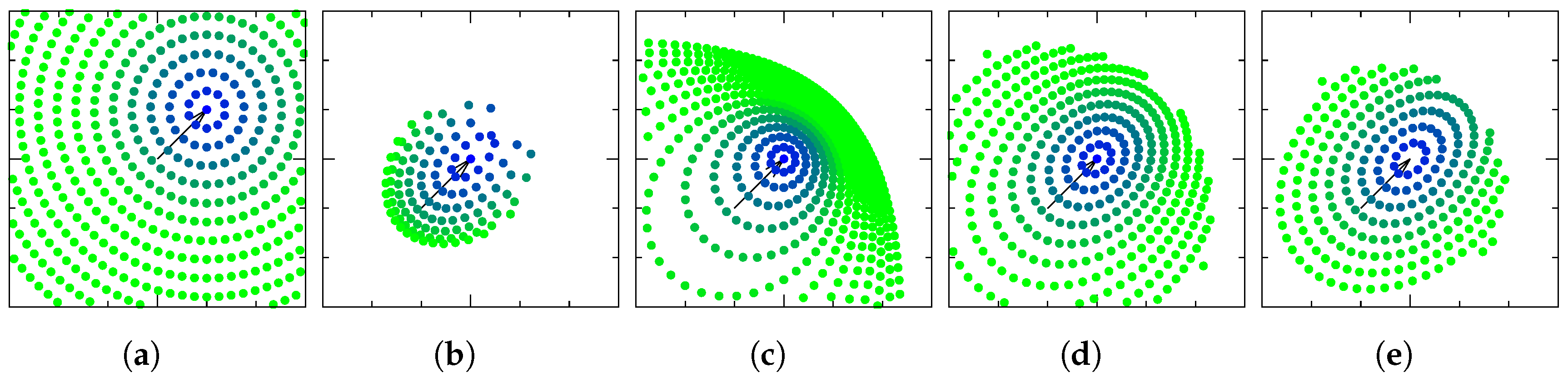
| Representation | Parameters | Continuous | Non-Singular | Linear Evolution Equation |
|---|---|---|---|---|
| Euler angles | 3 | ✗ | ✗ | ✗ |
| Axis-angle | 3–4 | ✗ | ✗ | ✗ |
| Rotation matrix | 9 | ✓ | ✓ | ✓ |
| Unit quaternion | 4 | ✓ | ✓ | ✓ |
| Chart | Domain | Image | ||
|---|---|---|---|---|
| O | ||||
| RP | ||||
| MRP | ||||
| RV |
| Chart | Transition Map |
|---|---|
| O | |
| RP | |
| MRP | |
| RV | , with |
| Chart | Matrix | Domain |
|---|---|---|
| O | ||
| RP | ||
| MRP | ||
| RV |
| Parameter | Value |
|---|---|
| Tsim | |
| dtdtsim | 100 |
| 1000 | |
| R | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernal-Polo, P.; Martínez-Barberá, H. Kalman Filtering for Attitude Estimation with Quaternions and Concepts from Manifold Theory. Sensors 2019, 19, 149. https://doi.org/10.3390/s19010149
Bernal-Polo P, Martínez-Barberá H. Kalman Filtering for Attitude Estimation with Quaternions and Concepts from Manifold Theory. Sensors. 2019; 19(1):149. https://doi.org/10.3390/s19010149
Chicago/Turabian StyleBernal-Polo, Pablo, and Humberto Martínez-Barberá. 2019. "Kalman Filtering for Attitude Estimation with Quaternions and Concepts from Manifold Theory" Sensors 19, no. 1: 149. https://doi.org/10.3390/s19010149
APA StyleBernal-Polo, P., & Martínez-Barberá, H. (2019). Kalman Filtering for Attitude Estimation with Quaternions and Concepts from Manifold Theory. Sensors, 19(1), 149. https://doi.org/10.3390/s19010149






