Complete Tri-Axis Magnetometer Calibration with a Gyro Auxiliary
Abstract
:1. Introduction
2. Error Model
2.1. Magnetic Field Distortions
2.2. Sensor Errors
3. Calibration Algorithm Development
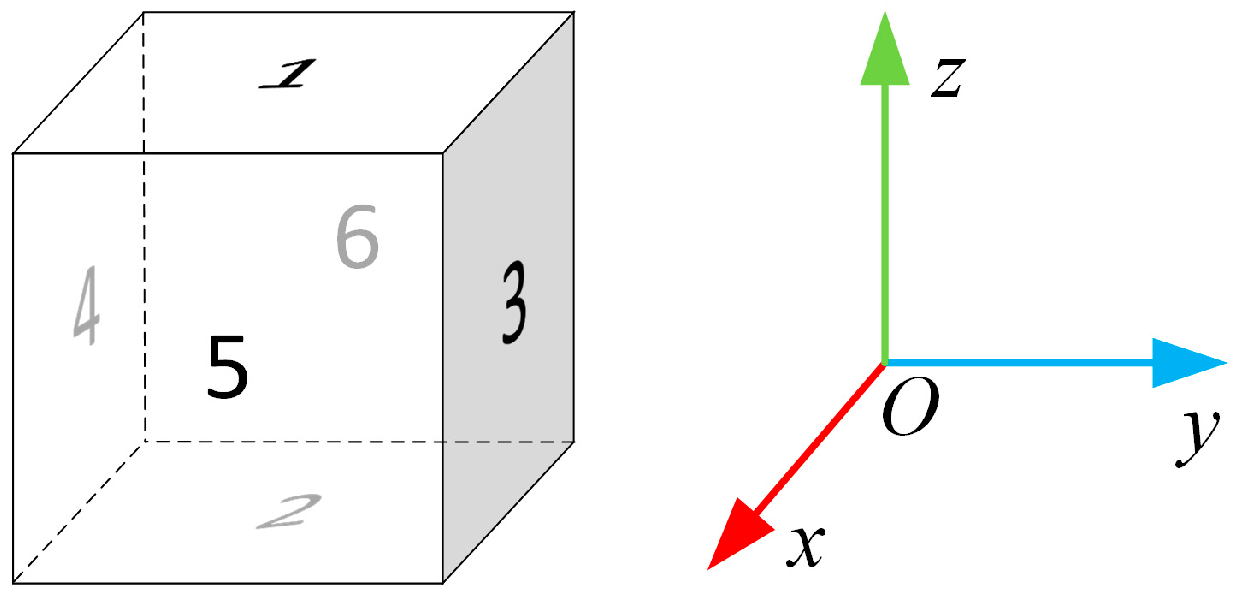
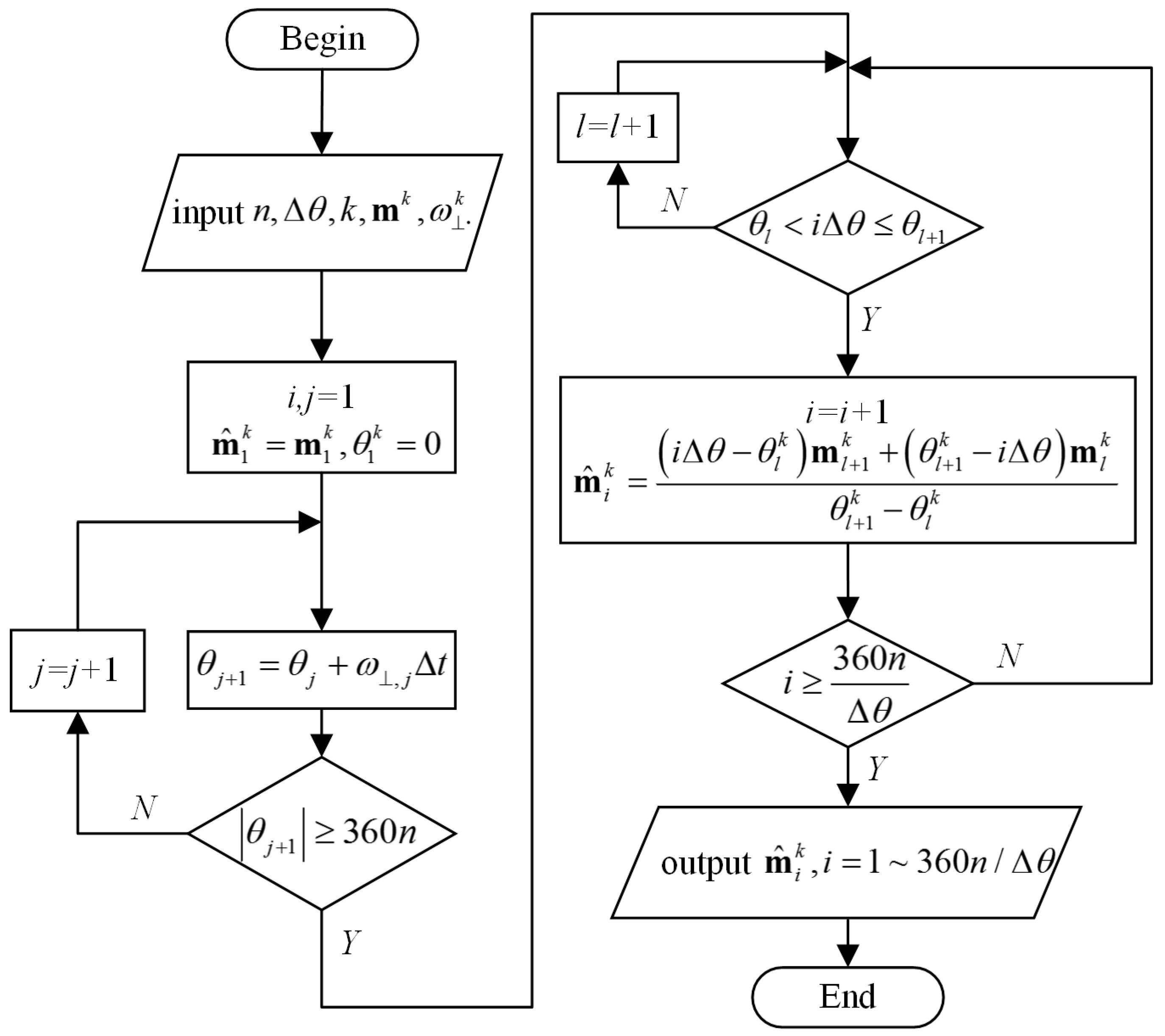
3.1. Magnetometer Interpolation Output Calculation
3.2. Error Coefficient Calculation
- By linear operation of Equations (2), (5)–(15), b is solved:
- By linear operation of Equations (2), (5)–(7), is solved:
- By linear operation of Equations (8)–(11), is solved:
- By linear operation of Equations (12)–(15), is solved:
4. Calibration Error Analysis
4.1. Gyro Bias
4.2. Gyro Misalignment
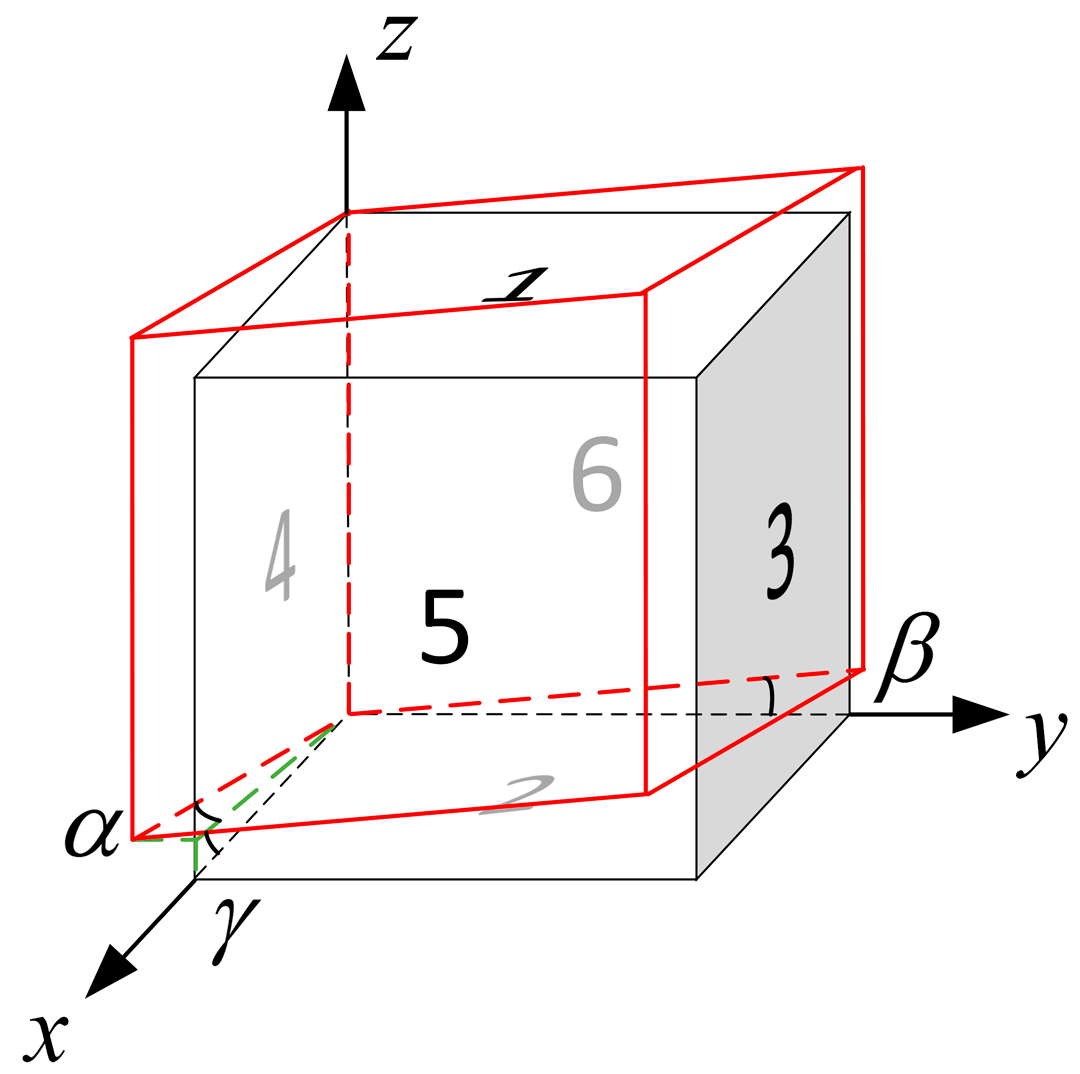
4.3. Non-Orthogonality of Cuboid Frame
4.4. Rotation Deviation
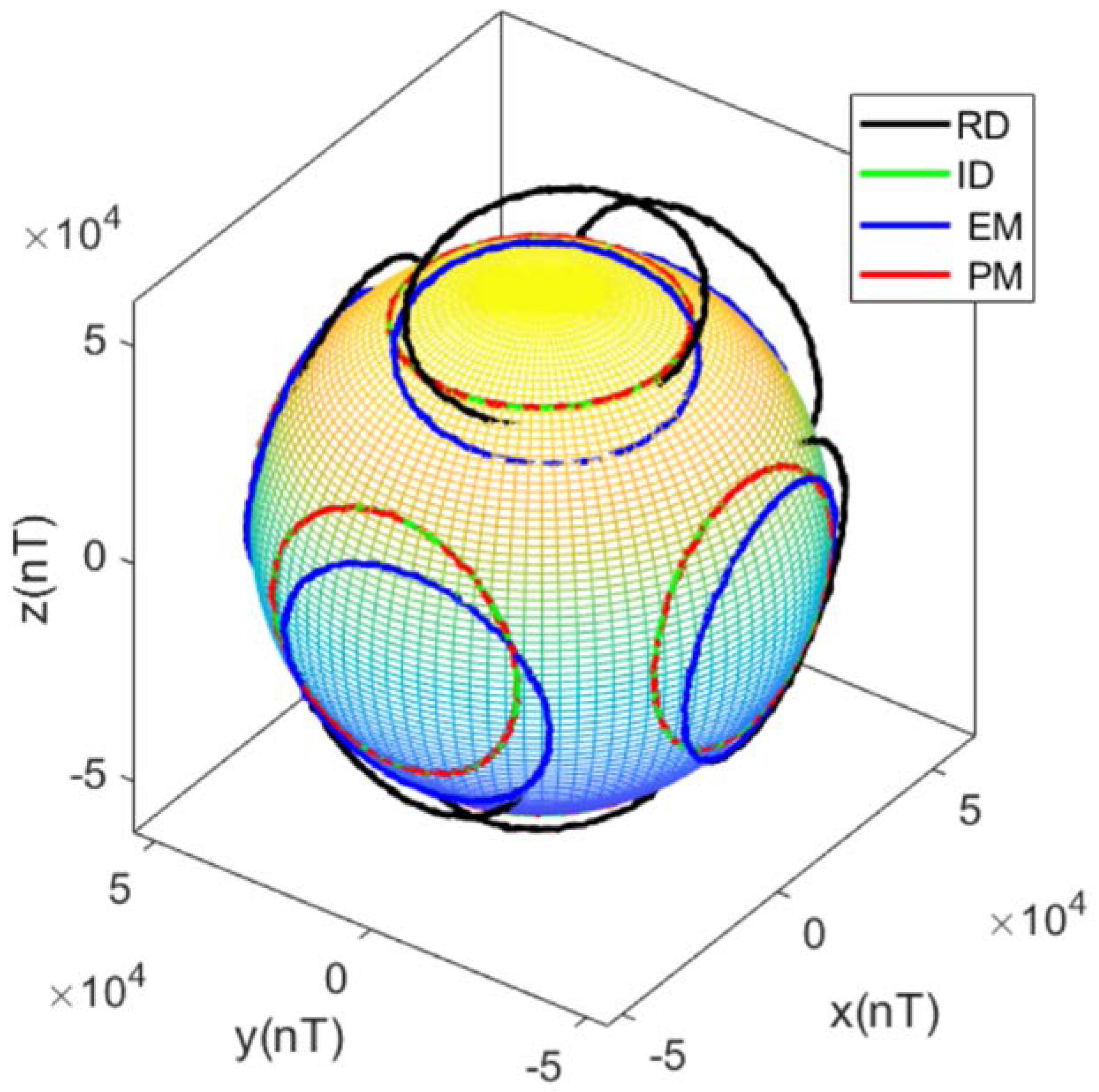
5. Simulation
5.1. Error Condition 1
5.2. Error Condition 2
6. Experiment
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Algorithm Complete Tri-Axis Magnetometer Calibration with a Gyro Auxiliary |
| function [K,b,Mint]=MagCal_YD(MGdata,n,dA,dt,ht) |
| % K: total error coefficient matrix |
| % b: total bias error vector |
| % Mint: tri-axis magnetometer interpolation outputs |
| % MGdata: j x l x k matrix of tri-axis gyro and magnetometer outputs |
| % j is the j-th sample point |
| % l=1~6, represent the x-, y-, z-axis gyro outputs with unit of degree/s, and x-, y-, z-axis magnetometer outputs, respectively. |
| % k=1~6, represent the sensor direction of z-axis upward, z-axis downward, y-axis upward, y-axis downward, x-axis upward, x-axis downward, respectively. |
| % n: number of rotations, n>=1. |
| % dA: angular interval with unit of degree. 360/dA must be an integer. |
| % dt: sampling period, with unit of s. |
| % ht: the geomagnetic field component perpendicular to the table. If ht is unknow, set ht=0. |
| %% step 1: Magnetometer Interpolation Output Calculation |
| AR=360*n; |
| ni= AR/dA; |
| Mint=zeros(AR/dA,3,6); |
| num=length(MGdata(:,1,1)); |
| angle=zeros(3*num,6); |
| for k=1:6 |
| i=1;j=1;l=1; |
| while abs(angle(j,k))<AR |
| angle(j+1,k)=angle(j,k)+MGdata(j,4-floor(0.5*k+0.5),k)*dt; |
| j=j+1; |
| end |
| if angle(j,k)>0 |
| angle(1:j,k)=angle(1:j,k); |
| else |
| angle(1:j,k)=-angle(1:j,k); |
| end |
| Mint(1,:,k)=MGdata(1,4:6,k); |
| while i<(AR/dA) |
| if angle(l,k)<(i)*dA && angle(l+1,k)>=(i)*dA |
| Mint(i+1,:,k)=(i*dA-angle(l,k))/(angle(l+1,k)-angle(l,k))*MGdata(l+1,4:6,k)+(angle(l+1,k)-i*dA)/(angle(l+1,k)-angle(l,k))*MGdata(l,4:6,k); |
| i=i+1; |
| else |
| l=l+1; |
| end |
| end |
| end |
| %% step 2: Error Coefficient Calculation |
| if ht==0 |
| ht=1*(sum(Mint(:,3,1))-sum(Mint(:,3,2))+sum(Mint(:,2,3))-sum(Mint(:,2,4))+sum(Mint(:,1,5))-sum(Mint(:,1,6)))/(ni*6); |
| end |
| bx=sum(sum(Mint(:,1,:)))/(ni*6); |
| by=sum(sum(Mint(:,2,:)))/(ni*6); |
| b=sum(sum(Mint(:,3,:)))/(ni*6); |
| b=[bx;by;bz]; |
| K=zeros(3,3); |
| K(:,3)=(sum(Mint(:,1:3,1))-sum(Mint(:,1:3,2)))'/(ni*2*ht); |
| K(:,2)=(sum(Mint(:,1:3,3))-sum(Mint(:,1:3,4)))'/(ni*2*ht); |
| K(:,1)=(sum(Mint(:,1:3,5))-sum(Mint(:,1:3,6)))'/(ni*2*ht); |
| end |
References
- Ali, A.; Siddharth, S.; Syed, Z. Swarm optimization-based magnetometer calibration for personal handheld devices. Sensors 2012, 12, 12455–12472. [Google Scholar] [CrossRef]
- Gebre-Egziabher, D.; Elkaim, G.H.; Powell, J.D.; Parkinson, B.W. A non-linear, two-step estimation algorithm for calibrating solid-state strapdown magnetometers. In Proceedings of the 8th International Conference on Navigation Systems, St. Petersburg, Russia, 27–31 May 2001; pp. 200–299. [Google Scholar]
- Bowditch, N. The American Practical Navigator; Defense Mapping Agency, Hydrographic/Topographic Center: Bethesda, MD, USA, 1995.
- Merayo, J.M.G.; Brauer, P.; Primdahl, F. Scalar calibration of vector magnetometers. Meas. Sci. Technol. 2000, 11, 120. [Google Scholar] [CrossRef]
- Secer, G.; Barshan, B. Improvements in deterministic error modeling and calibration of inertial sensors and magnetometers. Sens. Actuator. A 2016, 247, 522–538. [Google Scholar] [CrossRef]
- Risbo, T.; Brauer, P.; Merayo, J.M.G.; Nielsen, O.V.; Petersen, J.R.; Primdahl, F.; Richter, I. Ørsted pre-flight magnetometer calibration mission. Meas. Sci. Technol. 2003, 14, 674. [Google Scholar] [CrossRef]
- Petrucha, V.; Kaspar, P. Calibration of a Triaxial Fluxgate Magnetometer and Accelerometer with an Automated Non-Magnetic Calibration System. In Proceedings of the 2009 IEEE Sensors, Christchurch, New Zealand, 25–28 October 2009; pp. 1510–1513. [Google Scholar]
- Zikmund, A.; Janosek, M.; Ulvr, M. Precise calibration method for triaxial magnetometers not requiring earth’s field compensation. IEEE Trans. Instrum. Meas. 2015, 64, 1242–1247. [Google Scholar] [CrossRef]
- Kliment, T.; Praslička, D.; Draganová, K.; Blažek, J. Gradient methodology for 3-axis magnetometer scalar calibration. J. Electr. Eng. 2015, 66, 157–160. [Google Scholar]
- Caruso, M.J. Applications of Magnetoresistive Sensors in Navigation Systems; SAE Technical Paper 970602; SAE International: Warrendale, PA, USA, 1997. [Google Scholar] [CrossRef]
- Gebre-Egziabher, D.; Elkaim, G.H.; David Powell, J. Calibration of strapdown magnetometers in magnetic field domain. J. Aerosp. Eng. 2006, 19, 87–102. [Google Scholar] [CrossRef]
- Foster, C.C.; Elkaim, G.H. Extension of a two-step calibration methodology to include nonorthogonal sensor axes. IEEE Trans. Aerosp. Electron. Syst. 2008, 44. [Google Scholar] [CrossRef]
- Renaudin, V.; Afzal, M.H.; Lachapelle, G. Complete triaxis magnetometer calibration in the magnetic domain. J. Sens. 2010, 2010. [Google Scholar] [CrossRef]
- Wu, Y.; Shi, W. On calibration of three-axis magnetometer. IEEE Sens. J. 2015, 15, 6424–6431. [Google Scholar] [CrossRef]
- Olivares, A.; Ruiz-Garcia, G.; Olivares, G. Automatic determination of validity of input data used in ellipsoid fitting MARG calibration algorithms. Sensors 2013, 13, 11797–11817. [Google Scholar] [CrossRef] [PubMed]
- Kok, M.; Hol, J.D.; Schon, T.B.; Gustafsson, F.; Luinge, H. Calibration of a magnetometer in combination with inertial sensors. In Proceedings of the 15th International Conference on Information Fusion, Singapore, 9–12 July 2012; pp. 787–793. [Google Scholar]
- Vasconcelos, J.F.; Elkaim, G.; Silvestre, C.; Oliveira, P.; Cardeira, B. Geometric approach to strapdown magnetometer calibration in sensor frame. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1293–1306. [Google Scholar] [CrossRef]
- Li, X.; Li, Z. A new calibration method for tri-axial field sensors in strap-down navigation systems. Meas. Sci. Technol. 2012, 23, 2852–2855. [Google Scholar] [CrossRef]
- Salehi, S.; Mostofi, N.; Bleser, G. A practical in-field magnetometer calibration method for IMUs. In Proceedings of the IROS Workshop on Cognitive Assistive Systems, Vilamoura, Algarve, Portugal, 7 October 2012; pp. 39–44. [Google Scholar]
- Ammann, N.; Derksen, A.; Heck, C. A novel magnetometer-accelerometer calibration based on a least squares approach. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 577–585. [Google Scholar]
- Liu, Y.X.; Li, X.S.; Zhang, X.J. Novel calibration algorithm for a three-axis strapdown magnetometer. Sensors 2014, 14, 8485–8504. [Google Scholar] [CrossRef] [PubMed]
- Kok, M.; Schön, T.B. Maximum likelihood calibration of a magnetometer using inertial sensors. IFAC Proc. Vol. 2014, 47, 92–97. [Google Scholar] [CrossRef]
- Kok, M.; Schön, T.B. Magnetometer calibration using inertial sensors. IEEE Sens. J. 2016, 16, 5679–5689. [Google Scholar] [CrossRef]
- Han, K.; Han, H.; Wang, Z. Extended Kalman Filter Based Gyroscope Aided Magnetometer Calibration for Consumer Electronic Devices. IEEE Sens. J. 2016, 99, 1. [Google Scholar] [CrossRef]
- Troni, G.; Whitcomb, L.L. Adaptive Estimation of Measurement Bias in Three-Dimensional Field Sensors with Angular Rate Sensors: Theory and Comparative Experimental Evaluation. In Proceedings of the Robotics: Science and Systems, Berlin, Germany, 24–28 June 2013. [Google Scholar]
- Chulliat, A.; Macmillan, S.; Alken, P.; Beggan, C.; Nair, M.; Hamilton, B.; Woods, A.; Ridley, V.; Maus, S.; Thomson, A. The US/UK World Magnetic Model for 2015–2020; Technical Report; National Geophysical Data Center, NOAA: Boulder, CO, USA, 2015.


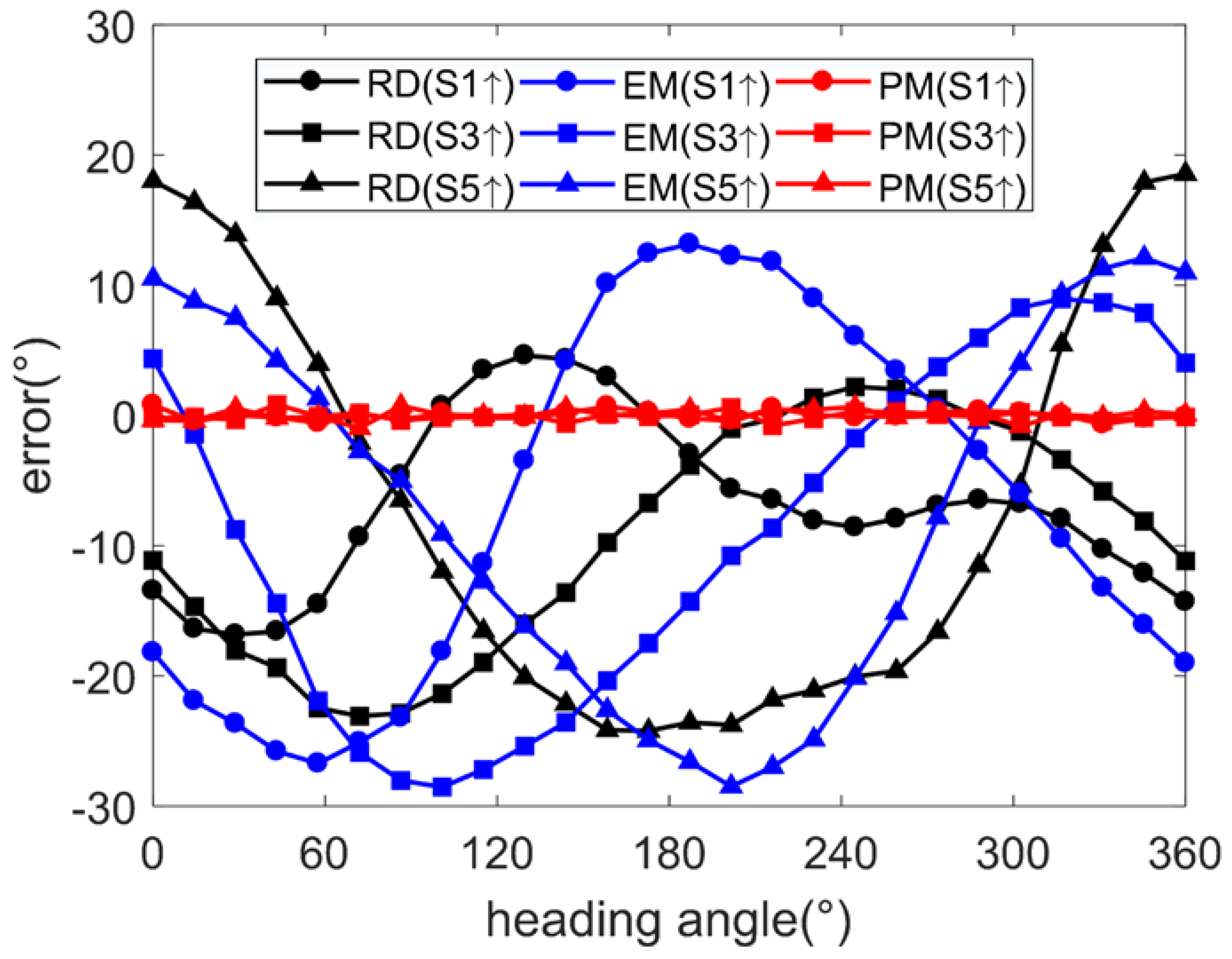
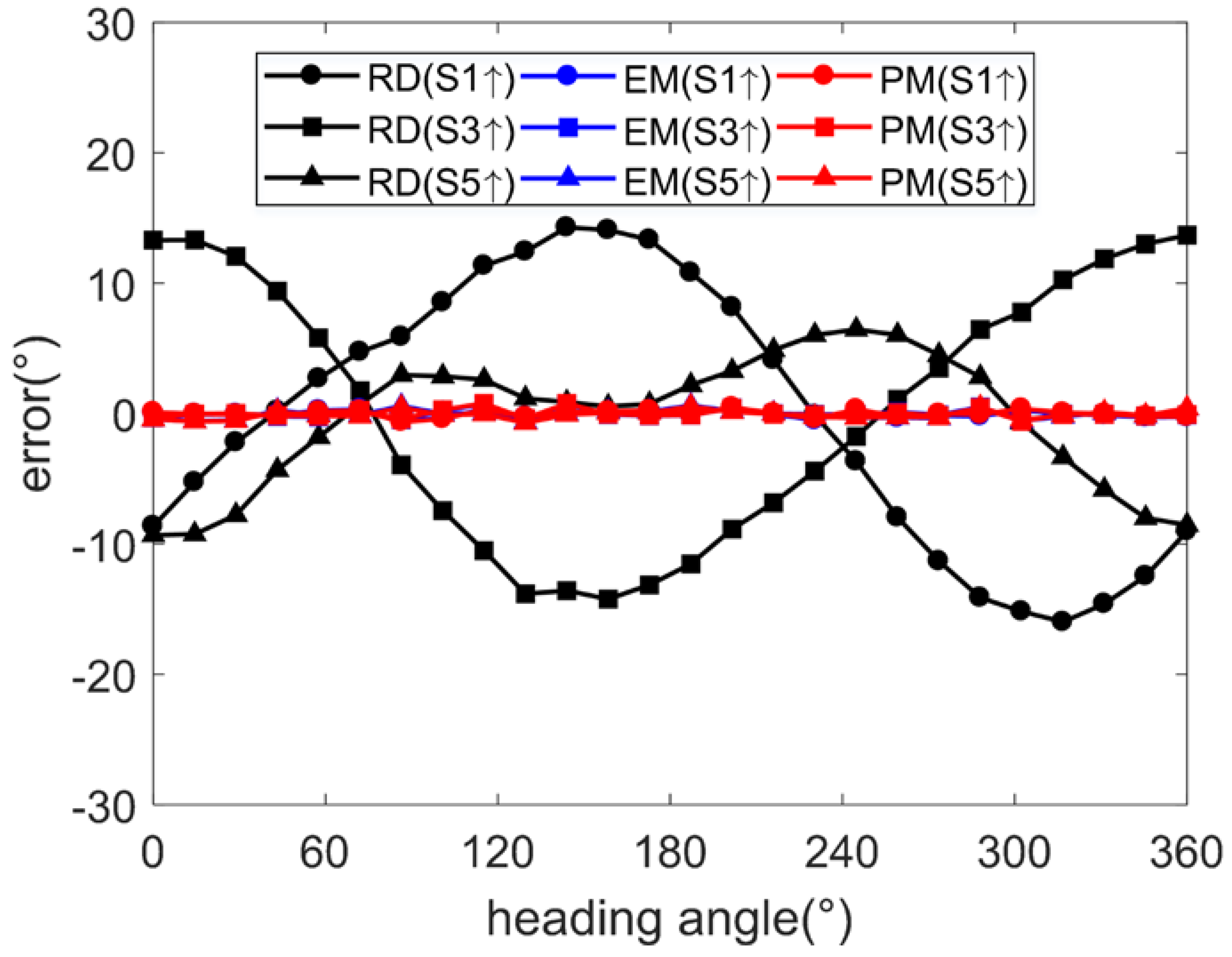



| Error | Value | Error | Value |
|---|---|---|---|
| Calibration Method | Side 1 Upwards (°) | Side 3 Upwards (°) | Side 5 Upwards (°) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| E | σ | max | E | σ | max | E | σ | max | |
| Raw | −6.61 | 6.32 | 17.60 | −9.38 | 8.71 | 23.44 | −7.70 | 15.20 | 24.95 |
| EM | −6.46 | 13.84 | 27.00 | −9.31 | 13.04 | 28.80 | −7.76 | 13.84 | 28.38 |
| PM | −0.01 | 0.44 | 1.36 | −0.03 | 0.37 | 1.13 | 0.05 | 0.40 | 1.29 |
| Calibration Method | Side 1 Upwards (°) | Side 3 Upwards (°) | Side 5 Upwards (°) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| E | σ | max | E | σ | max | E | σ | max | |
| Raw | −0.03 | 10.08 | 16.18 | −0.03 | 9.92 | 14.90 | −0.03 | 4.71 | 9.44 |
| EM | −0.02 | 0.41 | 1.37 | −0.03 | 0.38 | 1.08 | −0.03 | 0.37 | 1.19 |
| PM | −0.03 | 0.41 | 1.34 | −0.03 | 0.38 | 1.07 | −0.01 | 0.39 | 1.36 |
| Calibration Method | Step 1 | Step 2 | Total |
|---|---|---|---|
| EM | 0.3549s | 0.0012s | 0.3561s |
| PM | 0.0161s | 0.0014s | 0.0175s |
| Calibration Method | Side 1 Upwards (°) | Side 3 Upwards (°) | Side 5 Upwards (°) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| E | σ | max | E | σ | max | E | σ | max | |
| Raw | −2.14 | 5.00 | 12.03 | 1.42 | 2.83 | 6.17 | 3.82 | 11.04 | 16.01 |
| EM | 0.18 | 0.97 | 2.58 | 0.53 | 2.12 | 4.14 | 0.26 | 2.32 | 3.68 |
| PM | −0.11 | 0.45 | 1.63 | 0.32 | 0.49 | 1.66 | −0.10 | 0.34 | 1.17 |
| Calibration Method | Step 1 | Step 2 | Total |
|---|---|---|---|
| EM | 0.2177s | 0.0011s | 0.2188s |
| PM | 0.0163s | 0.0011s | 0.0174s |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, D.; You, Z.; Li, B.; Duan, W.; Yuan, B. Complete Tri-Axis Magnetometer Calibration with a Gyro Auxiliary. Sensors 2017, 17, 1223. https://doi.org/10.3390/s17061223
Yang D, You Z, Li B, Duan W, Yuan B. Complete Tri-Axis Magnetometer Calibration with a Gyro Auxiliary. Sensors. 2017; 17(6):1223. https://doi.org/10.3390/s17061223
Chicago/Turabian StyleYang, Deng, Zheng You, Bin Li, Wenrui Duan, and Binwen Yuan. 2017. "Complete Tri-Axis Magnetometer Calibration with a Gyro Auxiliary" Sensors 17, no. 6: 1223. https://doi.org/10.3390/s17061223







