Evaluation and Comparison of the Processing Methods of Airborne Gravimetry Concerning the Errors Effects on Downward Continuation Results: Case Studies in Louisiana (USA) and the Tibetan Plateau (China)
Abstract
:1. Introduction
2. The Semi-Parametric Method Combined with the Regularization
2.1. The Inverse Poisson’s Integral
2.2. The Semi-Parametric Method
2.3. The Regularization Method
2.4. The Semi-Parametric Method Combined with Regularization
- is generated by the natural cubic splines using Equations (12) and (13).
- and the initial value of are added into Equation (17) to calculate .
- and are added into Equation(16) to estimate the systematic error .
- Airborne gravity disturbances subtract to get the airborne gravity disturbances without the systematic errors.
- The airborne gravity disturbances without the systematic errors are brought into Equation (19) to calculate .
- Finally, the ground gravity disturbances are obtained by Equation (21).
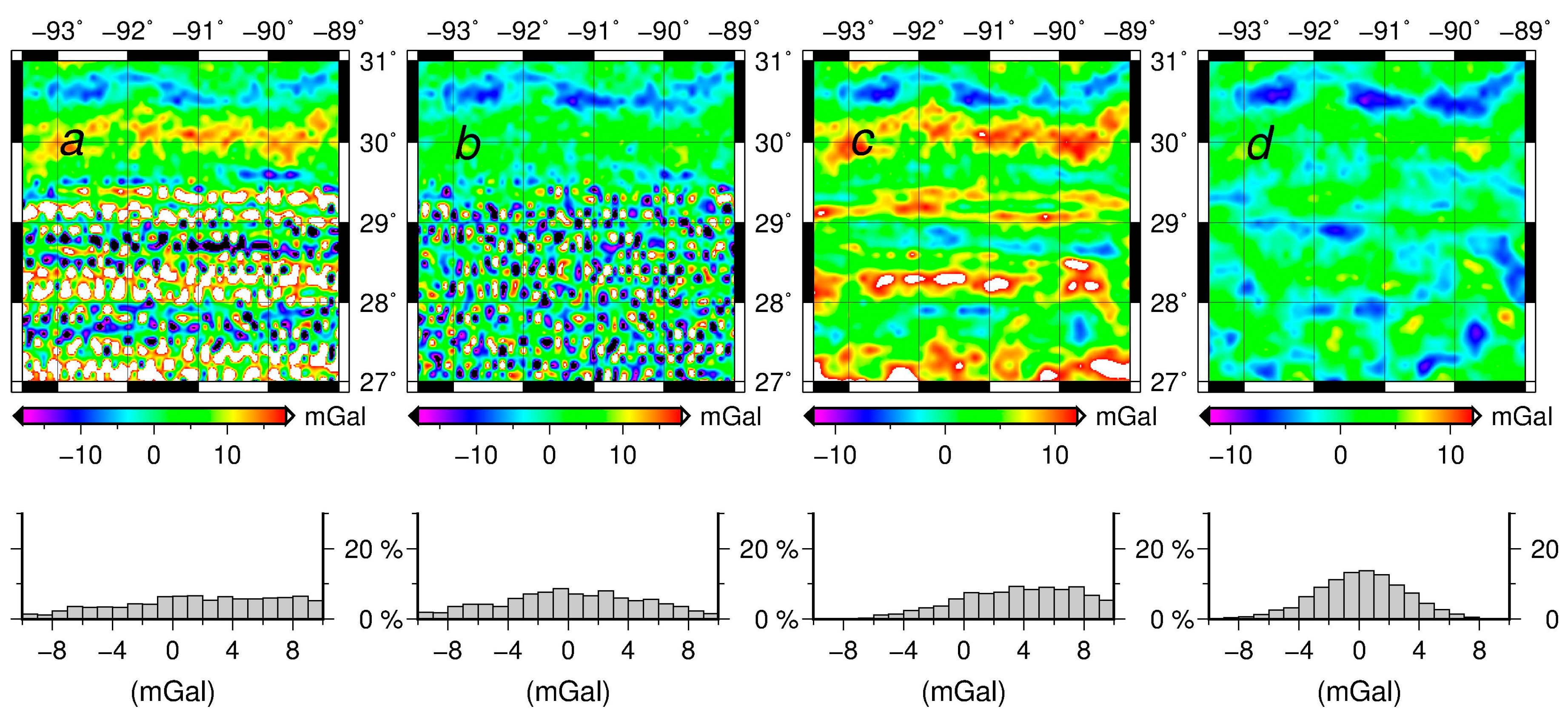
3. The Louisiana Project: The Experimental Results
- Case a:
- The inverse Poisson’s integral
- Case b:
- The semi-parametric method
- Case c:
- The regularization
- Case d:
- The semi-parametric method combined with regularization
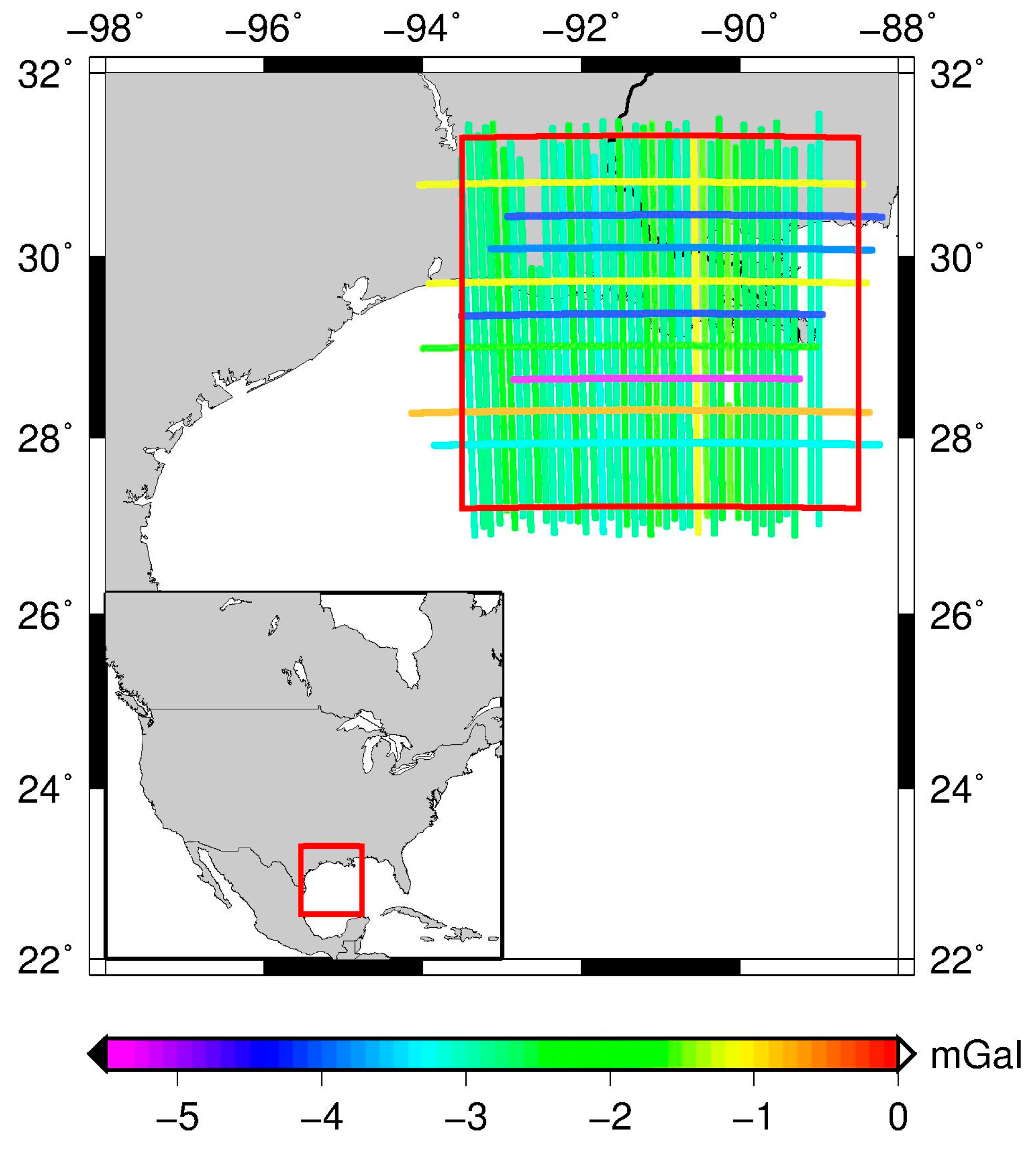
3.1. The Data Description
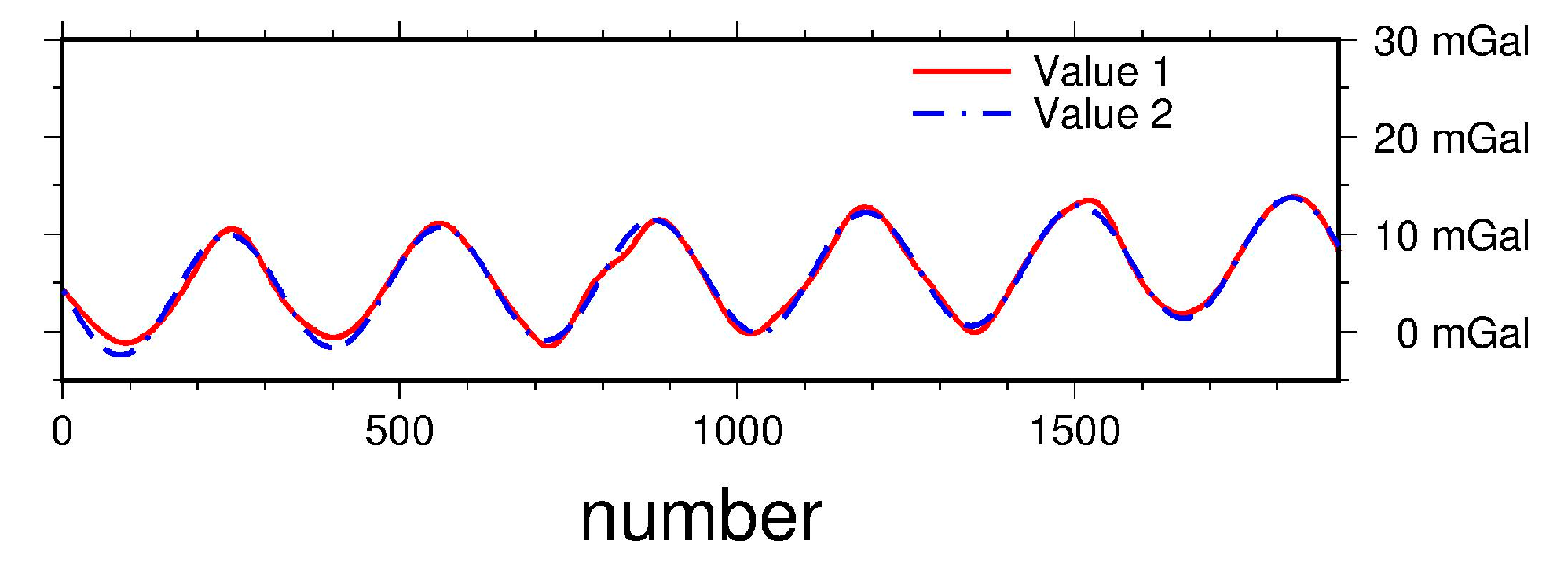
3.2. The Test Results and the Analysis
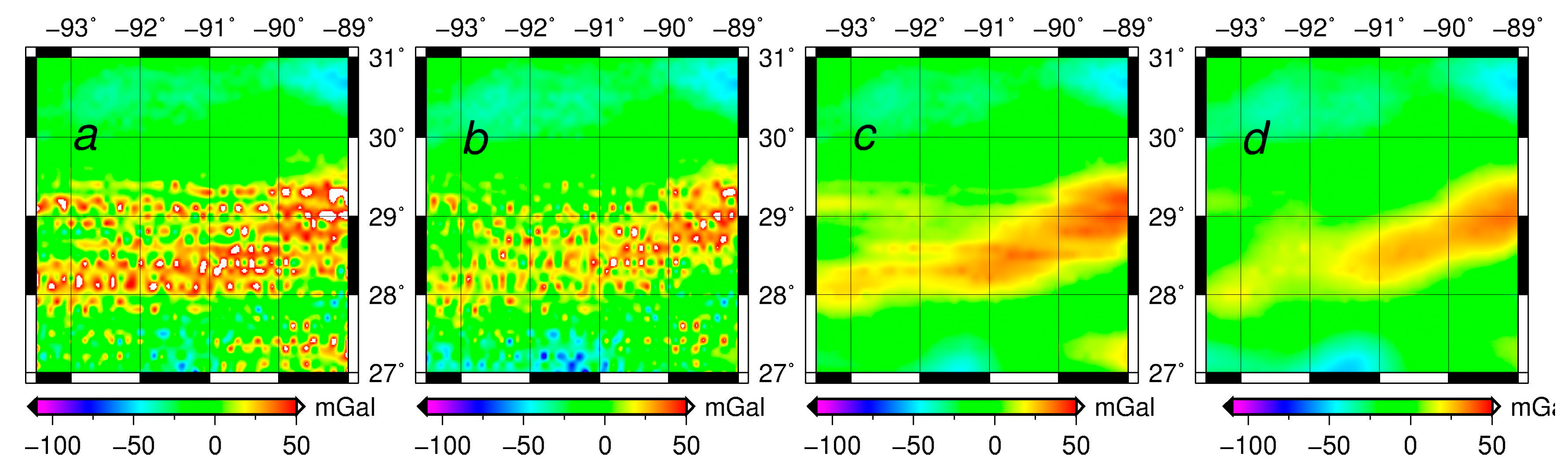
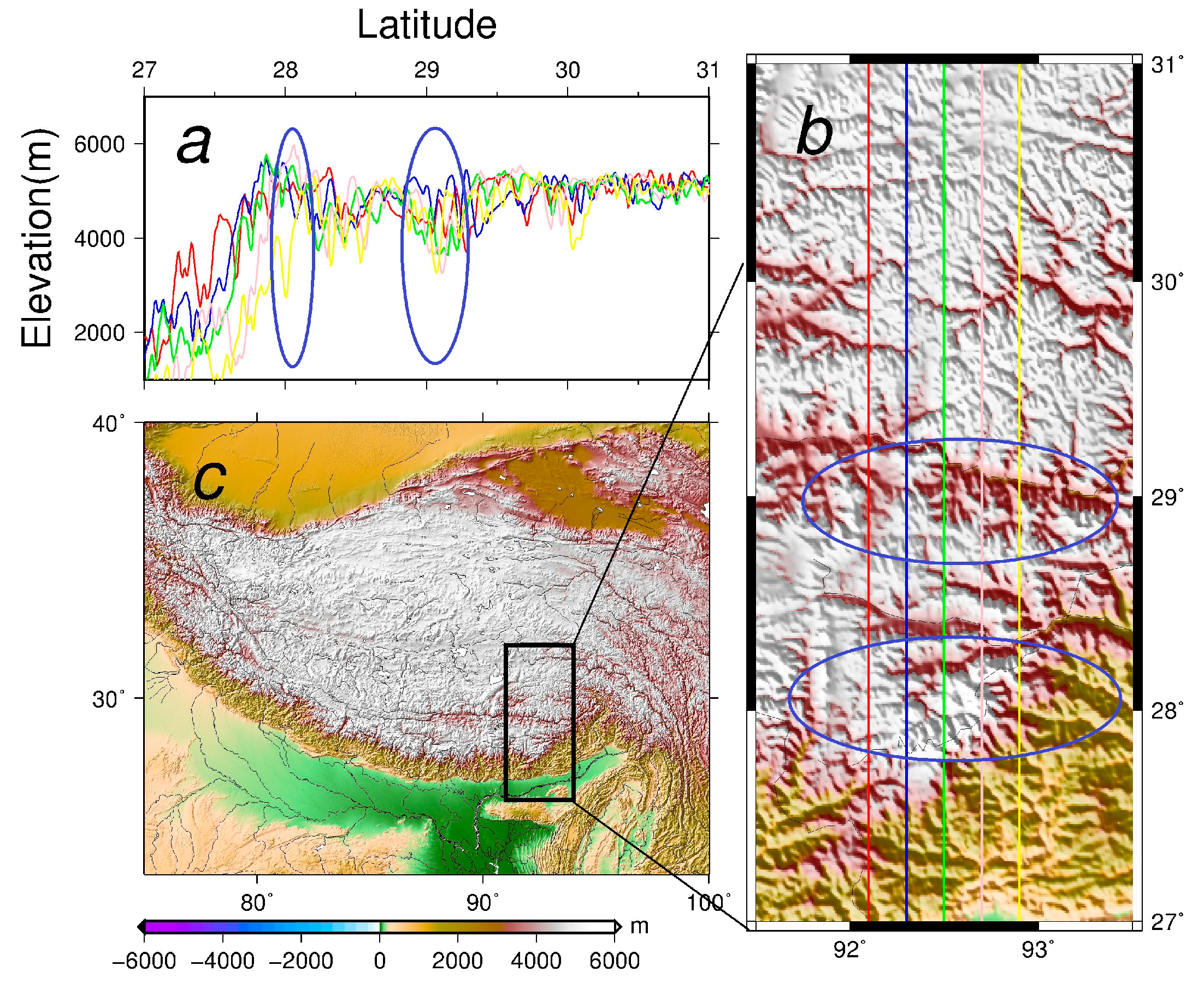
4. The Tibetan Plateau Experimental Results
4.1. Data Description
4.2. Test Results and the Analysis
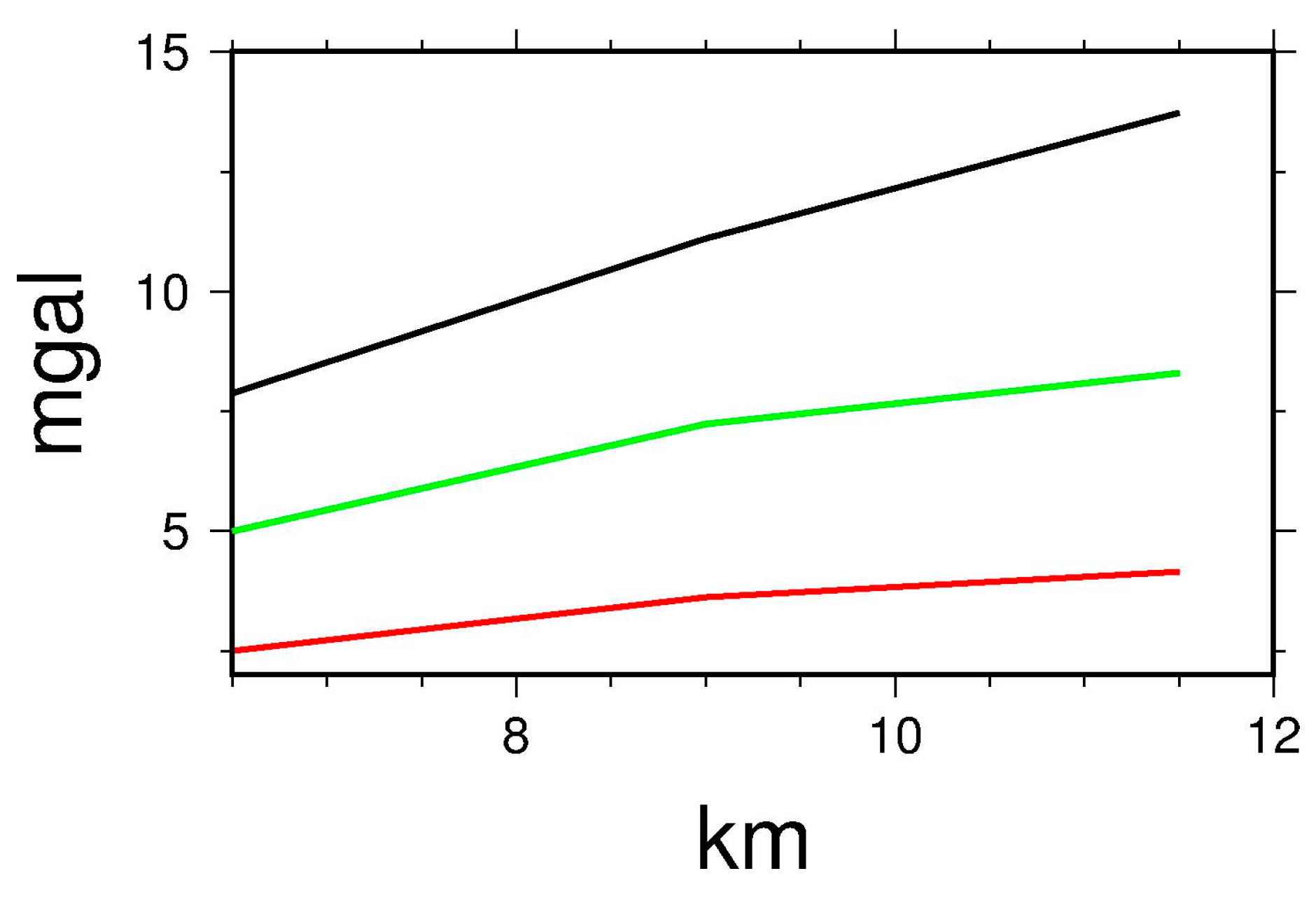
4.3. Test and Analysis of the Influence of the Flight Altitude
5. Analysis of the Relationship between the Downward Continuation Errors and the Flight Altitudes of the Tibetan Plateau
6. Summary and Concluding Remarks
- We have used four different methods for solving the inverse Poisson’s integral, and found that the semi-parametric method combined with the regularization is the best. The RMS of the difference between the signals downward continued from the flight altitude compared to the ground original EGM08 values is smallest.
- The airborne gravity data in Louisiana and the simulated data for the Tibetan Plateau both prove that the proposed method works effectively. In addition, the proposed method is not only best for the downward continuation of the measured aero gravimetric data, but also could improve the airborne gravity data accuracy for the parts of the airborne surveys which are poorly determined.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Forsberg, R.; Olesen, A.V.; Alshamsi, A.; Gidskehaug, A.; Ses, S.; Kadir, M.; Peter, B. Airborne Gravimetry Survey for the Marine Area of the United Arab Emirates. Mar. Geod. 2012, 35, 221–232. [Google Scholar] [CrossRef]
- Hwang, C.W.; Hsiao, Y.S.; Shih, H.C.; Yang, M.; Chen, K.H.; Forsberg, R.; Olesen, A.V. Geodetic and geophysical results from a Taiwan airborne gravity survey: Data reduction and accuracy assessment. J. Geophys. Res. Solid Earth 2007, 112, 1–14. [Google Scholar] [CrossRef]
- Forsberg, R.; Olesen, A.; Bastos, L.; Gidskehaug, A.; Meyer, U.; Timmen, L. Airborne geoid determination. Earth Planets Space 2000, 52, 863–866. [Google Scholar] [CrossRef]
- Bell, R.E.; Blankenship, D.D.; Finn, C.A.; Morse, D.L.; Scambos, T.A.; Brozena, J.M.; Hodge, S.M. Influence of Subglacial Geology on the Onset of a West Antarctic Ice Stream from Aerogeophysical Observations. Nature 1998, 394, 58–62. [Google Scholar] [CrossRef]
- Schwarz, K.; Li, Y.C. What can airborne gravimetry contribute to geoid determination? J. Geophys. Res. Solid Earth 1996, 101, 17873–17881. [Google Scholar] [CrossRef]
- Brozena, J.M. A Preliminary-Analysis of the Nrl Airborne Gravimetry System. Geophysics 1984, 49, 1060–1069. [Google Scholar] [CrossRef]
- Huang, C.H.; Hwang, C.; Hsiao, Y.S.; Wang, Y.M.; Roman, D.R. Analysis of Alabama Airborne Gravity at Three Altitudes: Expected Accuracy and Spatial Resolution from a Future Tibetan Airborne Gravity Survey. Terr. Atmos. Ocean. Sci. 2013, 24, 551–563. [Google Scholar] [CrossRef]
- Hwang, C.W.; Hsiao, Y.S.; Shih, H.C. Data reduction in scalar airborne gravimetry: Theory, software and case study in Taiwan. Comput. Geosci. UK 2006, 32, 1573–1584. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Moritz, H. Physical Geodesy; Springer: Berlin, Germany, 2006. [Google Scholar]
- Wang, X.T.; Xia, Z.R.; Shi, P.; Sun, Z.M. A comparison of different downward continuation methods for airborne gravity data. Chin. J. Geophys. 2004, 47, 1017–1022. [Google Scholar] [CrossRef]
- Sun, Z. Theory, Methods and Applications of Airborne Gravimetry. Ph.D. Thesis, Information Engineering University, Zhengzhou, China, 2004. [Google Scholar]
- Martinec, Z. Stability investigations of a discrete downward continuation problem for geoid determination in the Canadian Rocky Mountains. J. Geod. 1996, 70, 805–828. [Google Scholar] [CrossRef]
- Tscherning, C.C. Advanced Physical Geodesy. Eos Trans. Am. Geophys. Union 1982, 63, 514. [Google Scholar] [CrossRef]
- Carly, W.; Theresa, D. NGS_GRAV-D_Data_Block_CS01_User Manual. 2012. Available online: ftp://ftp.ngs.noaa.gov/pub/grav-d/CS01/ (accessed on 24 May 2017).
- Sans O, F.; Sideris, M.G. The Downward Continuation Approach: A Long-Lasting Misunderstanding in Physical Geodesy. In Geodetic Boundary Value Problem: The Equivalence between Molodensky’s and Helmert’s Solutions; Springer: Berlin, Germany, 2017; pp. 39–46. [Google Scholar]
- Vaníček, P.; Novák, P.; Sheng, M.; Kingdon, R.; Janák, J.; Foroughi, I.; Martinec, Z.; Santos, M. Does Poisson’s downward continuation give physically meaningful results? Stud. Geophys. Geod. 2017, 1–18. [Google Scholar] [CrossRef]
- Sampietro, D.; Capponi, M.; Mansi, A.H.; Gatti, A.; Marchetti, P.; Sansò, F. Space-Wise approach for airborne gravity data modelling. J. Geod. 2017, 91, 535–545. [Google Scholar] [CrossRef]
- Bolkas, D.; Fotopoulos, G.; Braun, A. On the impact of airborne gravity data to fused gravity field models. J. Geod. 2016, 90, 561–571. [Google Scholar] [CrossRef]
- Jiang, T.; Wang, Y.M. On the spectral combination of satellite gravity model, terrestrial and airborne gravity data for local gravimetric geoid computation. J. Geod. 2016, 90, 1405–1418. [Google Scholar] [CrossRef]
- Smith, D.A.; Holmes, S.A.; Li, X.; Guillaume, S.E.B.; Wang, Y.M.; Bürki, B.; Roman, D.R.; Damiani, T.M. Confirming regional 1 cm differential geoid accuracy from airborne gravimetry: The Geoid Slope Validation Survey of 2011. J. Geod. 2013, 87, 885–907. [Google Scholar] [CrossRef]
- Wang, X.; Shi, P.; Zhu, F. Regularization Methods and Spectral Decomposition for the Downward Continuation of Airborne Gravity Data. Acta Geod. Cartogr. Sin. 2004, 1, 6. [Google Scholar]
- Becker, D.; Nielsen, J.E.; Ayres-Sampaio, D.; Forsberg, R.; Becker, M.; Bastos, L. Drift reduction in strapdown airborne gravimetry using a simple thermal correction. J. Geod. 2015, 89, 1133–1144. [Google Scholar] [CrossRef]
- Wei, M.; Schwarz, K.P. Flight test results from a strapdown airborne gravity system. J. Geod. 1998, 72, 323–332. [Google Scholar] [CrossRef]
- Carly, W.; Theresa, D. NGS_GRAV-D_Data_Block_CS02_User Manual. 2012. Available online: ftp://ftp.ngs.noaa.gov/pub/grav-d/CS02/ (accessed on 24 May 2017).
- Xiong, P. Semiparametric model and its application in survey data processing. Surv. Rev. 2006, 38, 406–411. [Google Scholar] [CrossRef]
- Fessler, J.A. Nonparametric Fixed-Interval Smoothing of Nonlinear Vector-Valued Measurements. IEEE Trans. Signal Process. 1991, 39, 907–913. [Google Scholar] [CrossRef]
- Fessler, J.A. Nonparametric Fixed-Interval Smoothing with Vector Splines. IEEE Trans. Signal Process. 1991, 39, 852–859. [Google Scholar] [CrossRef]
- Green, P.J. Penalized likelihood for general semi-parametric regression models. Int. Stat. Rev. 1987, 55, 245–259. [Google Scholar] [CrossRef]
- Reinsch, C.H. Smoothing by spline functions. Numer. Math. 1967, 10, 177–183. [Google Scholar] [CrossRef]
- Rice, J.; Rosenblatt, M. Integrated mean squared error of a smoothing spline. J. Approx. Theory 1981, 33, 353–369. [Google Scholar] [CrossRef]
- Rice, J.; Rosenblatt, M. Smoothing splines: Regression, derivatives and deconvolution. Ann. Stat. 1983, 11, 141–156. [Google Scholar] [CrossRef]
- Schoenberg, I.J. Spline functions and the problem of graduation. Proc. Natl. Acad. Sci. USA 1964, 52, 947–950. [Google Scholar] [CrossRef] [PubMed]
- Wahba, G. Smoothing noisy data with spline functions. Numer. Math. 1975, 24, 383–393. [Google Scholar] [CrossRef]
- Whittaker, E.T. On a new method of graduation. Proc. Edinburgh Math. Soc. 1922, 41, 63–75. [Google Scholar]
- Engle, R.F.; Granger, C.W.; Rice, J.; Weiss, A. Semiparametric estimates of the relation between weather and electricity sales. J. Am. Stat. Assoc. 1986, 81, 310–320. [Google Scholar] [CrossRef]
- Jian-cheng, L.; Jun-yong, C.; Jin-sheng, N.; Ding-Bo, C. The Earth’Gravity Field Approximation Theory and China’s 2000 Quasi-Geoid Determination; Wuhan University Press: Wuhan, China, 2003. [Google Scholar]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Bruinsma, S.L.; Förste, C.; Abrikosov, O.; Lemoine, J.; Marty, J.; Mulet, S.; Rio, M.; Bonvalot, S. ESA’s satellite-only gravity field model via the direct approach based on all GOCE data. Geophys. Res. Lett. 2014, 41, 7508–7514. [Google Scholar] [CrossRef]
- Gilardoni, M.; Reguzzoni, M.; Sampietro, D. GECO: A global gravity model by locally combining GOCE data and EGM2008. Stud. Geophys. Geod. 2016, 60, 228–247. [Google Scholar] [CrossRef]
- Fecher, T.; Pail, R.; Gruber, T.; GOCO Consortium. GOCO05c: A New Combined Gravity Field Model Based on Full Normal Equations and Regionally Varying Weighting. Surv. Geophys. 2017, 38, 571–590. [Google Scholar] [CrossRef]

| EGM08 | DIR-R5 | TIM-R5 | GOCO 05C | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| North-South lines | −2.474 | 0.445 | −2.339 | 4.940 | −2.381 | 4.872 | −2.434 | 1.651 |
| West-East lines | −2.873 | 1.668 | −3.018 | 5.486 | −3.077 | 5.459 | −2.893 | 2.258 |
| Items | Values |
|---|---|
| Altitude (m) | 11 088 |
| Number of Crossovers | 361 |
| RMS of Residuls (mgal) | 1.8 |
| Std of Resduals (mgal) | 1.8 |
| Mean Crossover Difference (mgal) | −0.19 |
| RMS Error (mgal) | 1.28 |
| Max | Min | Mean | RMS | |
|---|---|---|---|---|
| The inverse Poisson’s integral | 117.154 | −57.081 | 6.858 | 19.331 |
| The semi-parametric model | 64.589 | −61.587 | 0.141 | 14.167 |
| The regularization | 18.543 | −8.554 | 4.255 | 6.060 |
| The semi-parametric method combined with the regularization | 9.689 | −9.722 | 0.110 | 2.922 |
| Max | Min | Mean | Std | |
|---|---|---|---|---|
| Simulated values | 13.713 | −2.436 | 5.621 | 4.598 |
| Estimated values | 13.789 | −1.548 | 5.751 | 4.478 |
| Differences | 1.612 | −1.506 | −0.129 | 0.558 |
| Max | Min | Mean | RMS | |
|---|---|---|---|---|
| The inverse Poisson’s integral | 143.684 | −53.674 | 6.212 | 22.908 |
| The semi-parametric model | 70.838 | −56.561 | −0.440 | 19.223 |
| The regularization | 73.519 | −53.697 | 1.686 | 20.002 |
| The semi-parametric method combined with the regularization | 70.939 | −56.596 | −0.429 | 19.139 |
| Max | Min | Mean | RMS | |
|---|---|---|---|---|
| The inverse Poisson’s integral | 27.832 | −19.121 | 4.364 | 8.366 |
| The semi-parametric model combined with the regularization | 24.913 | −19.865 | −0.022 | 6.428 |
| Max | Min | Mean | RMS | |
|---|---|---|---|---|
| The inverse Poisson’s integral | 59.829 | −44.107 | 4.466 | 16.673 |
| The semi-parametric model combined with the regularization | 56.830 | −47.562 | −0.157 | 15.669 |
| Altitude (m) | REE | SEE | |
|---|---|---|---|
| 2 mgal (Std) | 4 mgal (Std) | ||
| 6500 | 2.495 | 4.991 | 7.873 |
| 9000 | 3.618 | 7.236 | 11.108 |
| 11,500 | 4.013 | 8.027 | 13.726 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Q.; Strykowski, G.; Li, J.; Pan, X.; Xu, X. Evaluation and Comparison of the Processing Methods of Airborne Gravimetry Concerning the Errors Effects on Downward Continuation Results: Case Studies in Louisiana (USA) and the Tibetan Plateau (China). Sensors 2017, 17, 1205. https://doi.org/10.3390/s17061205
Zhao Q, Strykowski G, Li J, Pan X, Xu X. Evaluation and Comparison of the Processing Methods of Airborne Gravimetry Concerning the Errors Effects on Downward Continuation Results: Case Studies in Louisiana (USA) and the Tibetan Plateau (China). Sensors. 2017; 17(6):1205. https://doi.org/10.3390/s17061205
Chicago/Turabian StyleZhao, Qilong, Gabriel Strykowski, Jiancheng Li, Xiong Pan, and Xinyu Xu. 2017. "Evaluation and Comparison of the Processing Methods of Airborne Gravimetry Concerning the Errors Effects on Downward Continuation Results: Case Studies in Louisiana (USA) and the Tibetan Plateau (China)" Sensors 17, no. 6: 1205. https://doi.org/10.3390/s17061205
APA StyleZhao, Q., Strykowski, G., Li, J., Pan, X., & Xu, X. (2017). Evaluation and Comparison of the Processing Methods of Airborne Gravimetry Concerning the Errors Effects on Downward Continuation Results: Case Studies in Louisiana (USA) and the Tibetan Plateau (China). Sensors, 17(6), 1205. https://doi.org/10.3390/s17061205





