Figure 1.
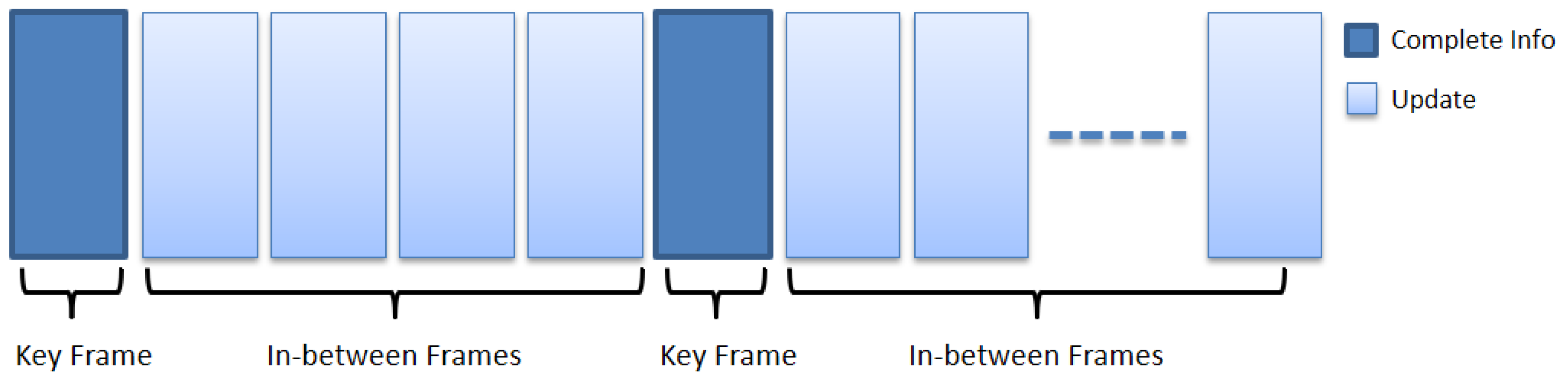
The structure of the key frame concept.
Figure 1.
The structure of the key frame concept.
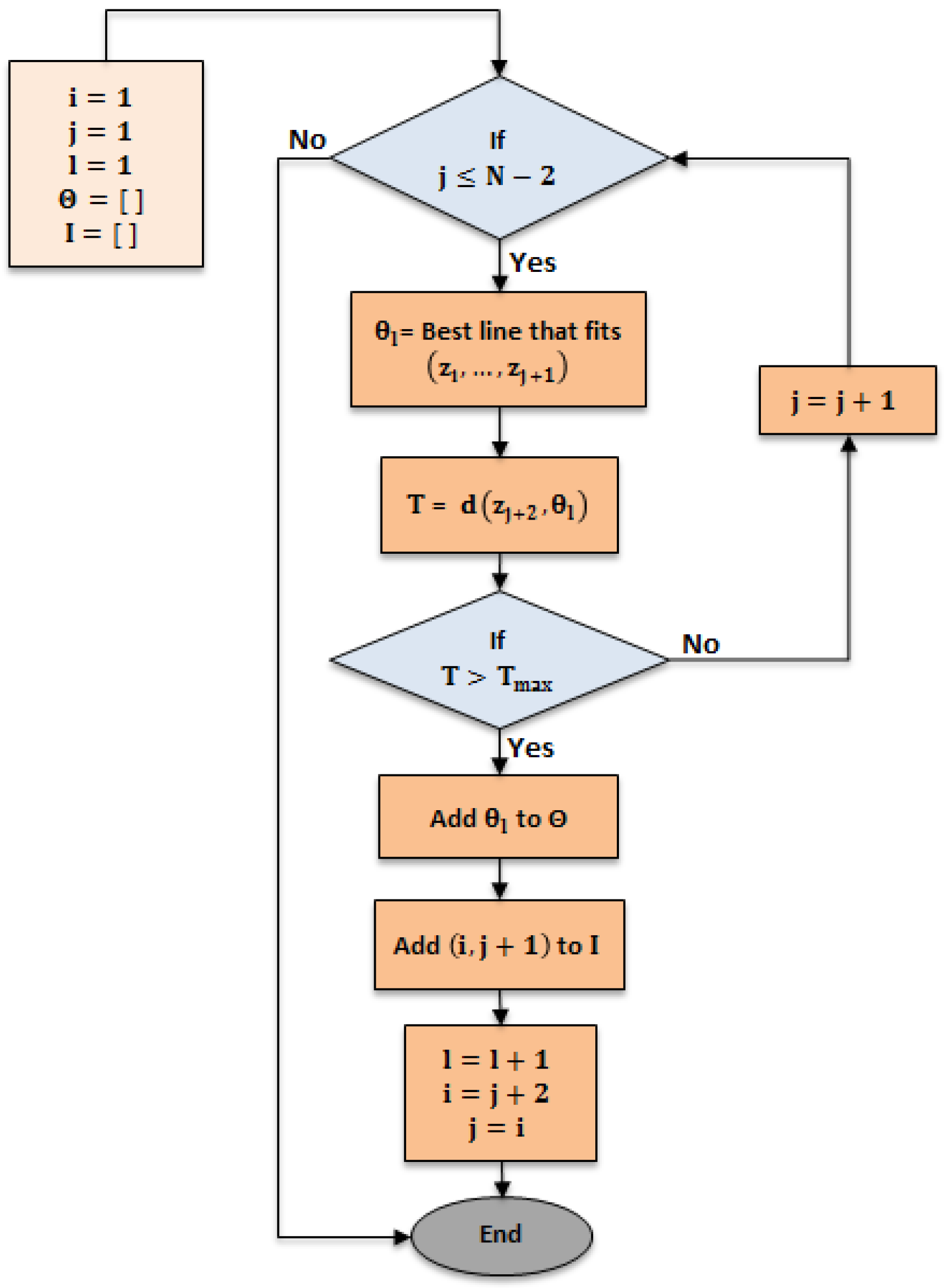
Figure 2.
Alternating structure of the proposed algorithm between the RKF and ICP methods.
Figure 2.
Alternating structure of the proposed algorithm between the RKF and ICP methods.
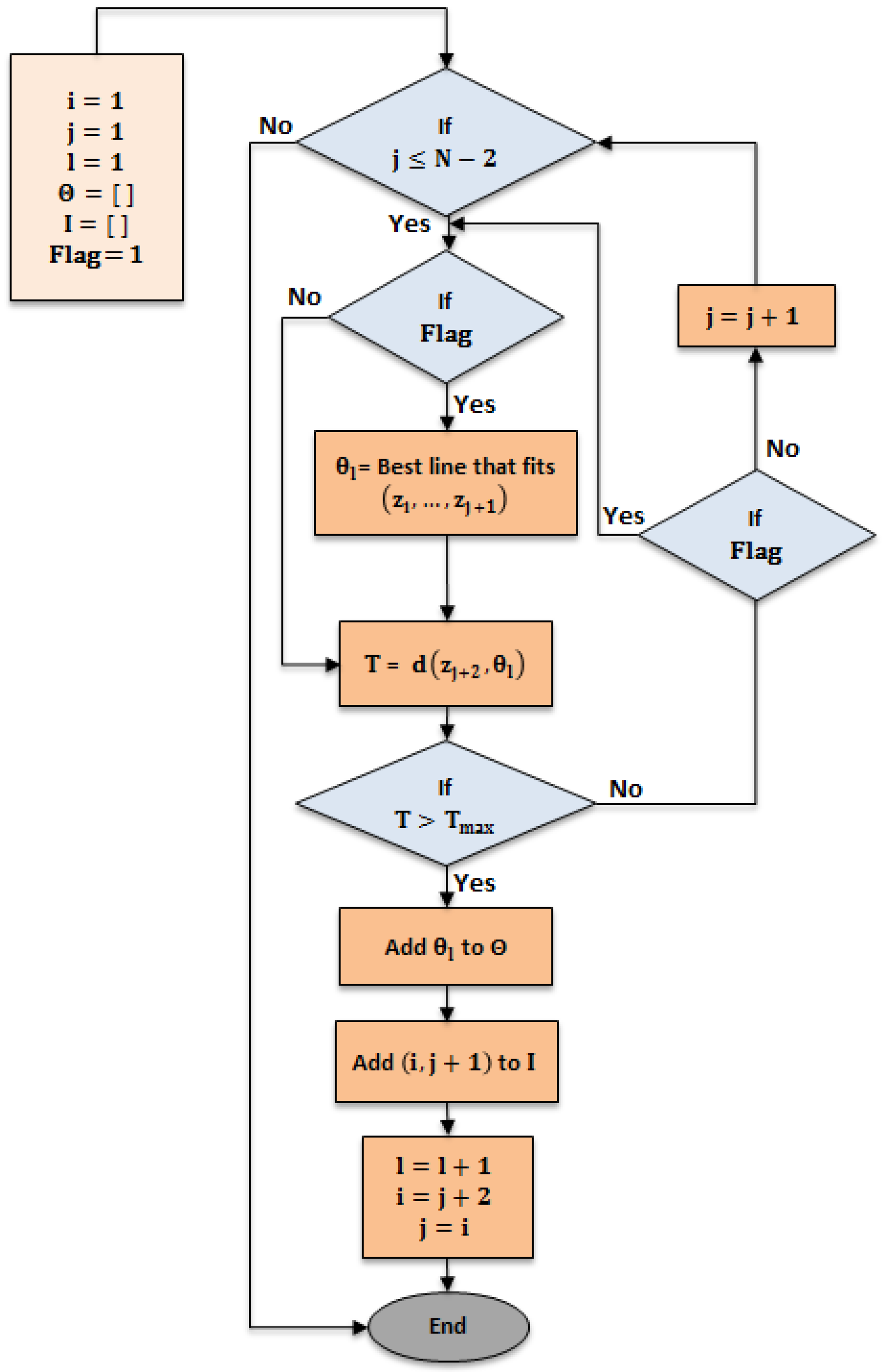
Figure 3.
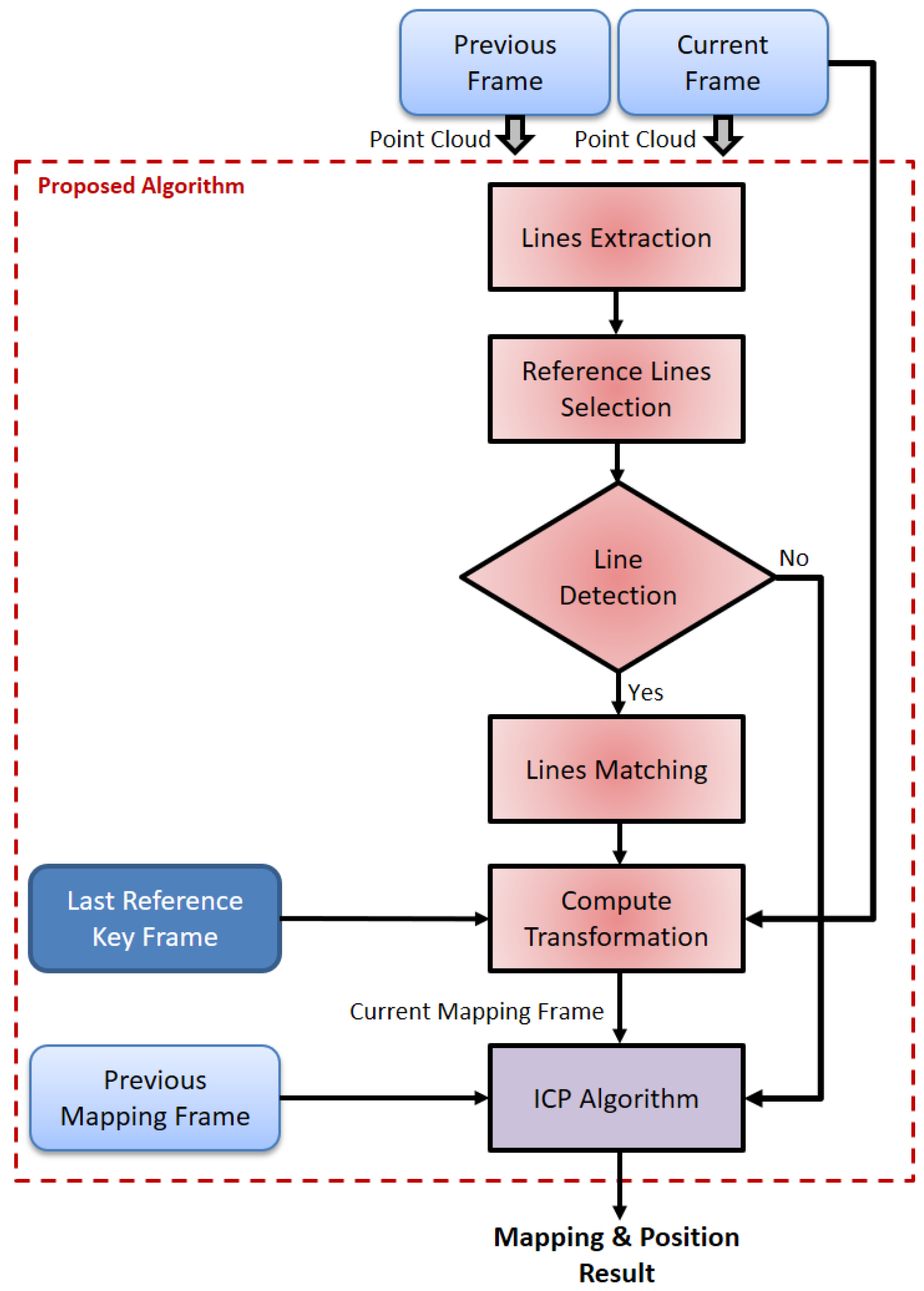
Overall structure of the proposed algorithm.
Figure 3.
Overall structure of the proposed algorithm.
Figure 4.
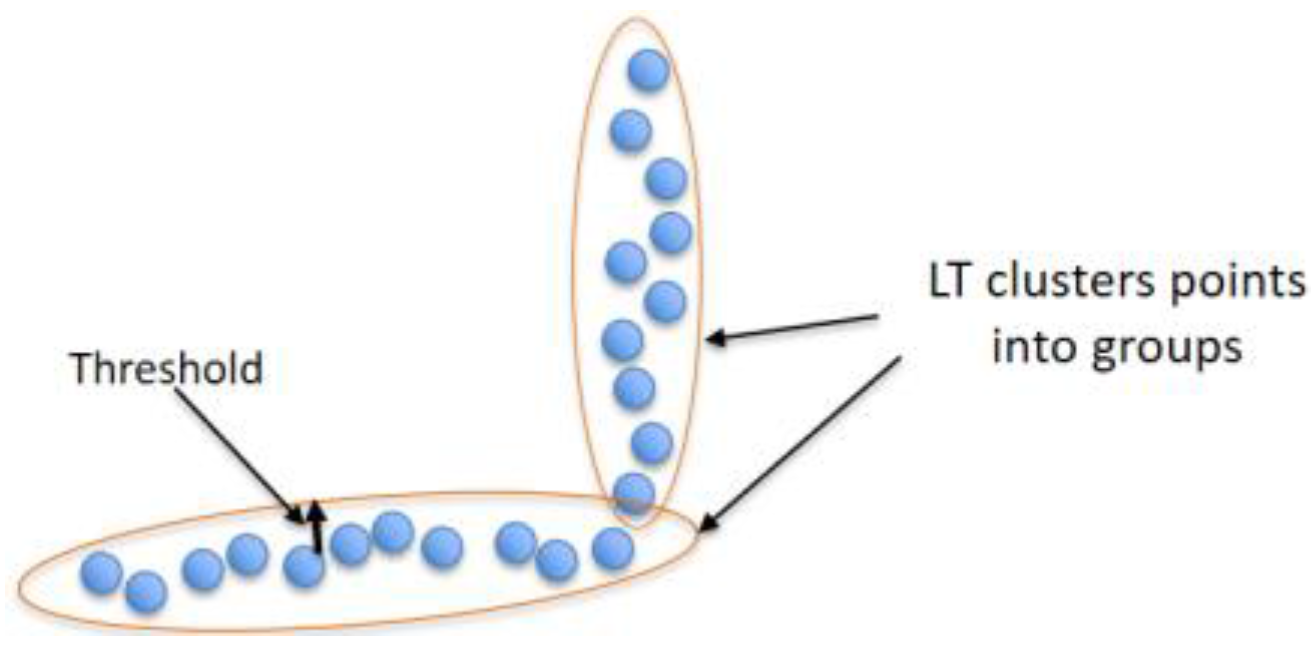
The role of line tracking (LT) algorithm.
Figure 4.
The role of line tracking (LT) algorithm.
Figure 5.
Detection behavior of the laser scanner range finder.
Figure 5.
Detection behavior of the laser scanner range finder.
Figure 6.
Line tracking algorithm (LT).
Figure 6.
Line tracking algorithm (LT).
Figure 7.
Adjusted line tracking algorithm (ALT).
Figure 7.
Adjusted line tracking algorithm (ALT).
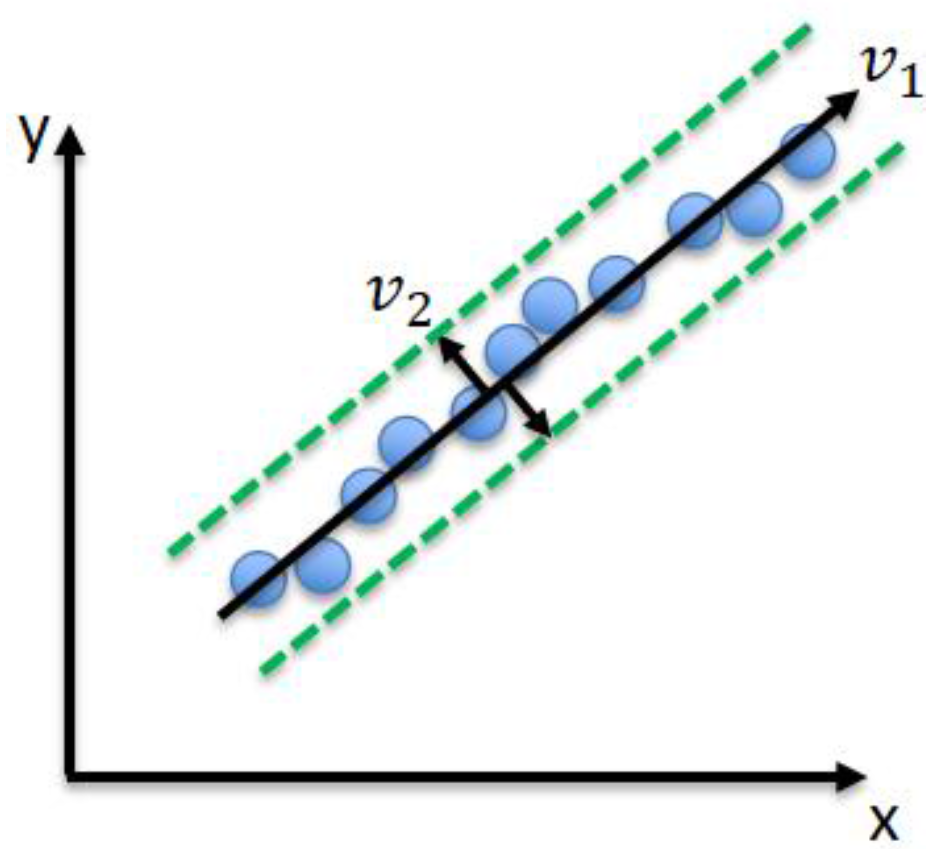
Figure 8.
Principle component analysis (PCA).
Figure 8.
Principle component analysis (PCA).
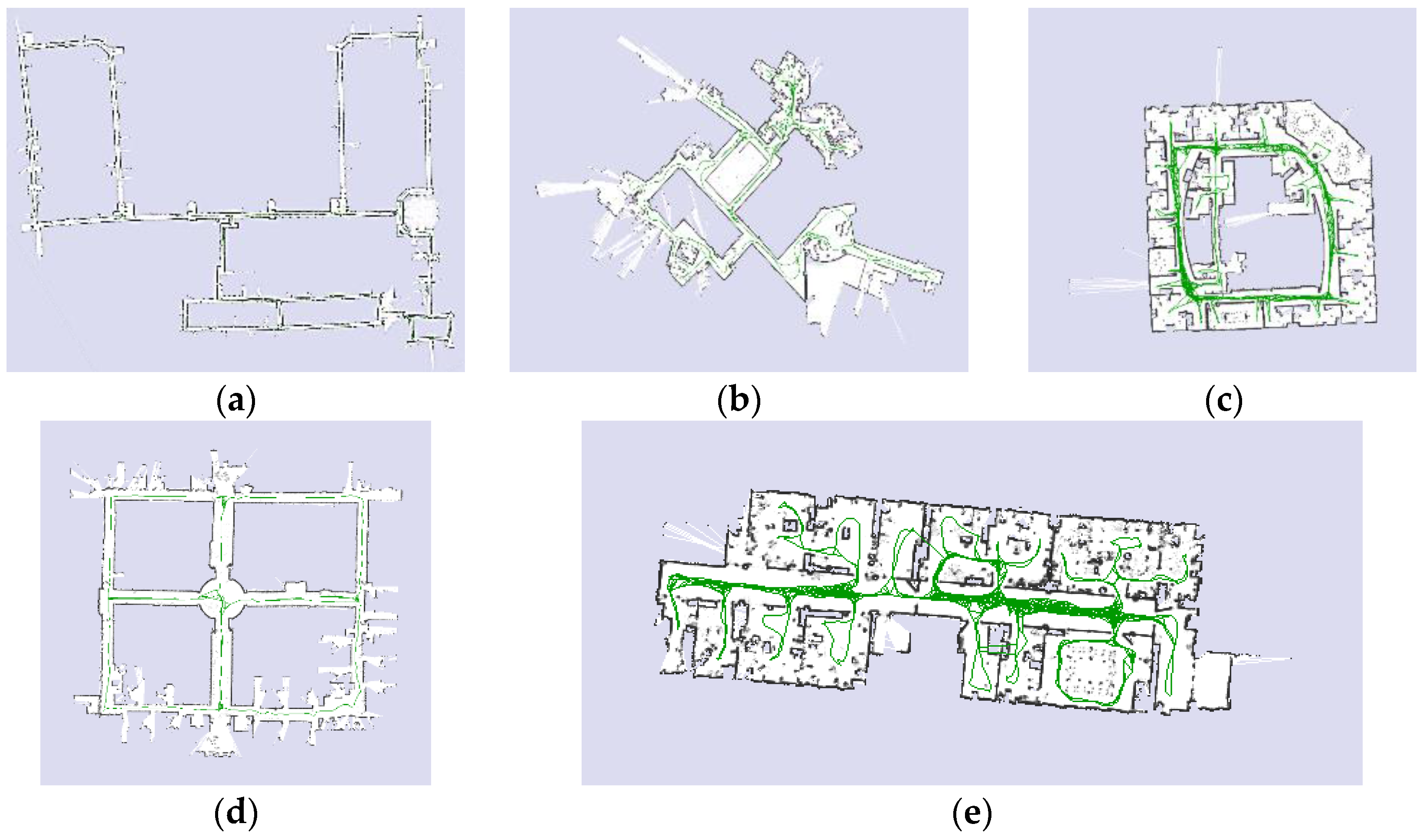
Figure 9.
Maps for different data sets are used: (a) MIT Killian Court; (b) MIT CSAIL Building; (c) Intel Research Lab Seattle; (d) ACES Building at the University of Texas; (e) building 079 University of Freiburg.
Figure 9.
Maps for different data sets are used: (a) MIT Killian Court; (b) MIT CSAIL Building; (c) Intel Research Lab Seattle; (d) ACES Building at the University of Texas; (e) building 079 University of Freiburg.
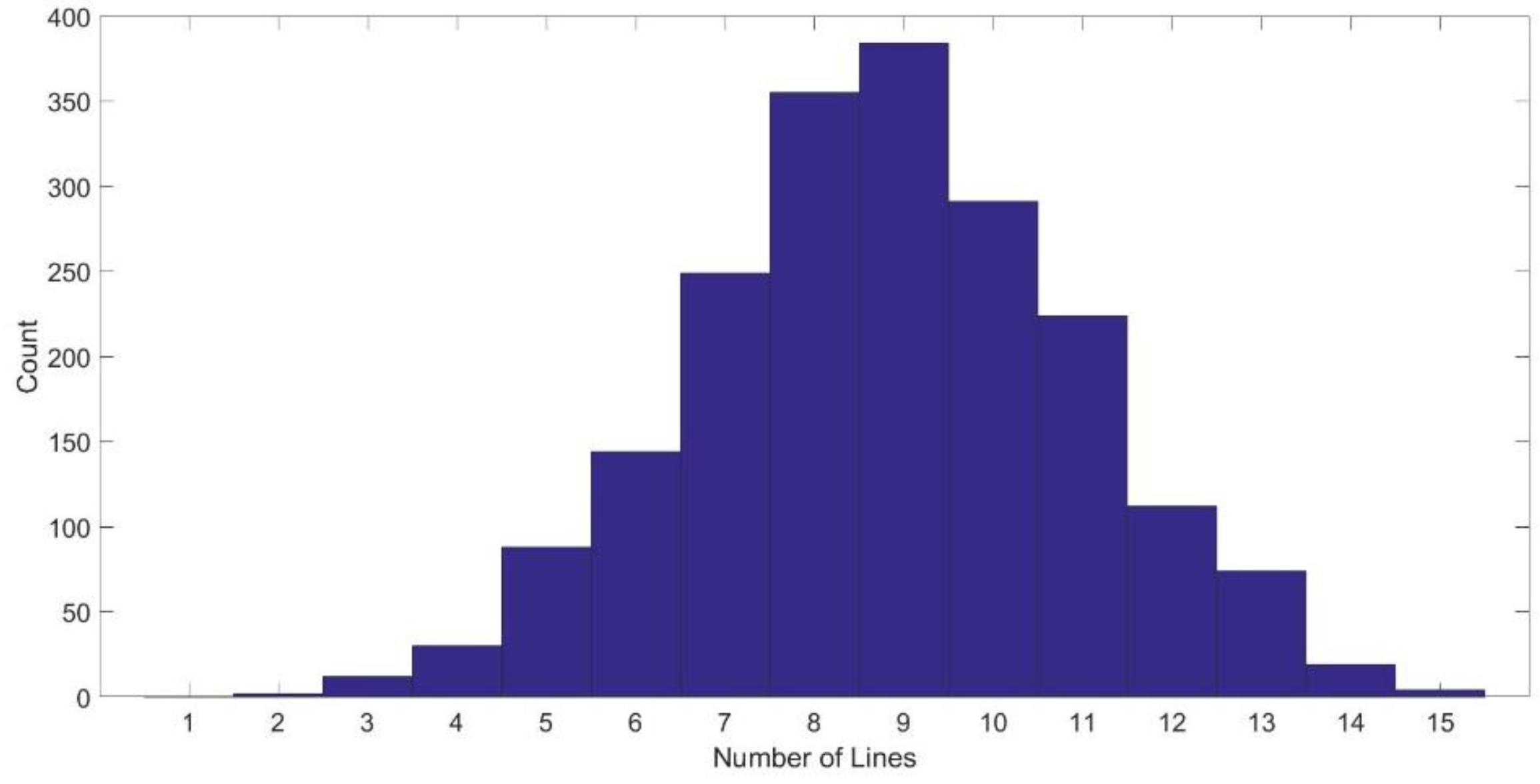
Figure 10.
Histogram of number of lines detected in the MIT CSAIL Building dataset.
Figure 10.
Histogram of number of lines detected in the MIT CSAIL Building dataset.
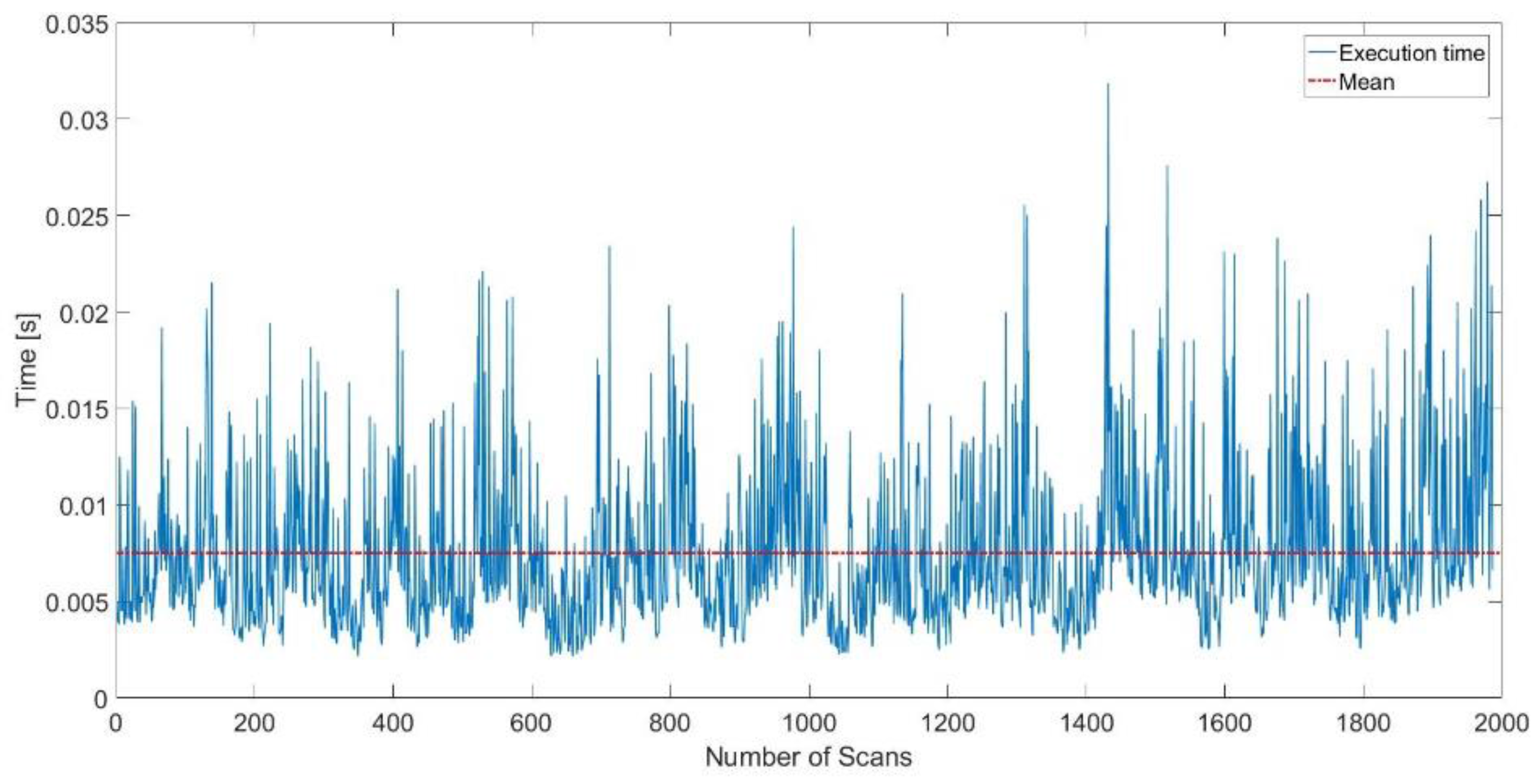
Figure 11.
Execution time of the lines extraction in the MIT CSAIL Building dataset.
Figure 11.
Execution time of the lines extraction in the MIT CSAIL Building dataset.
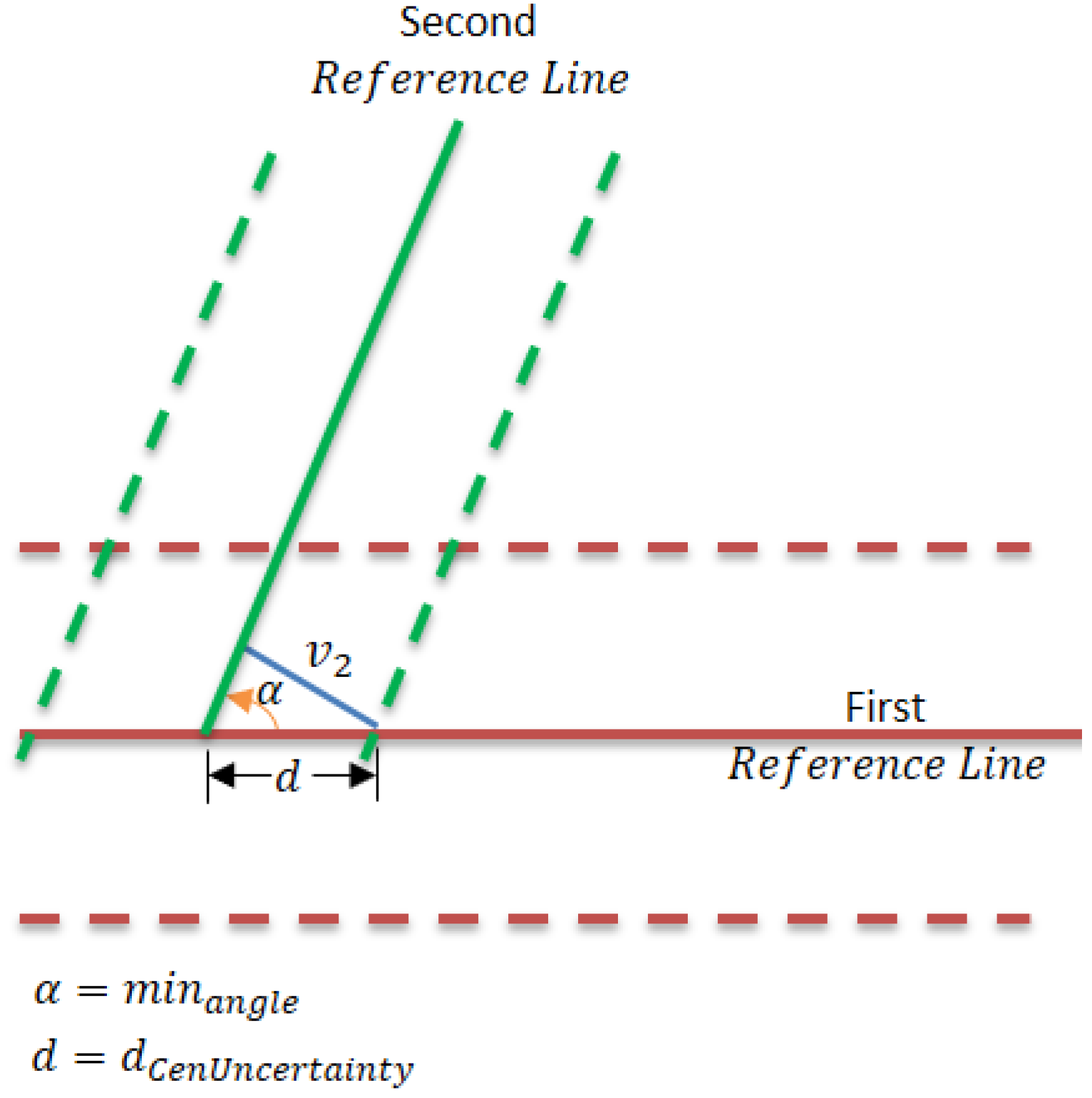
Figure 12.
Setting min angle between two reference lines.
Figure 12.
Setting min angle between two reference lines.
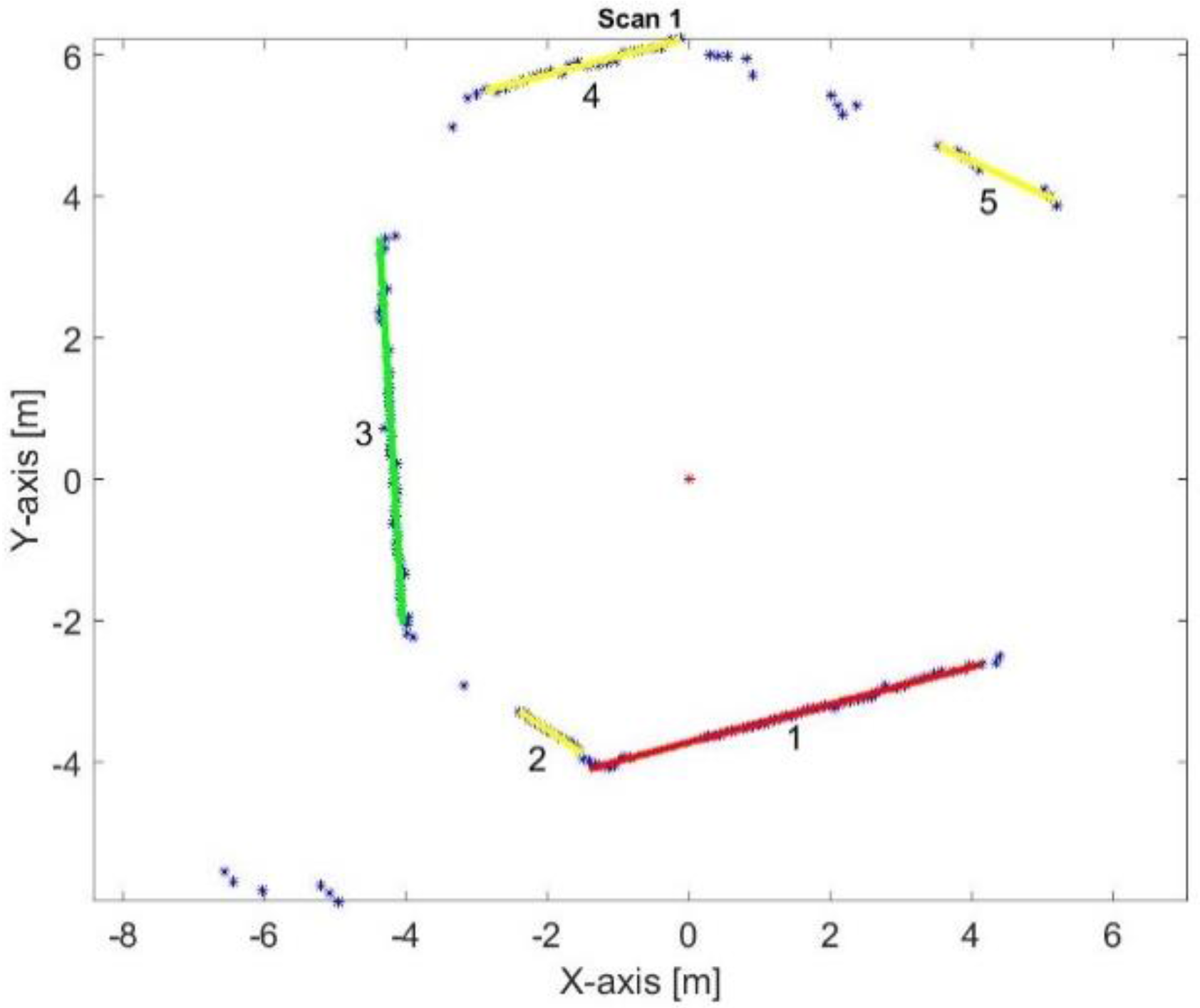
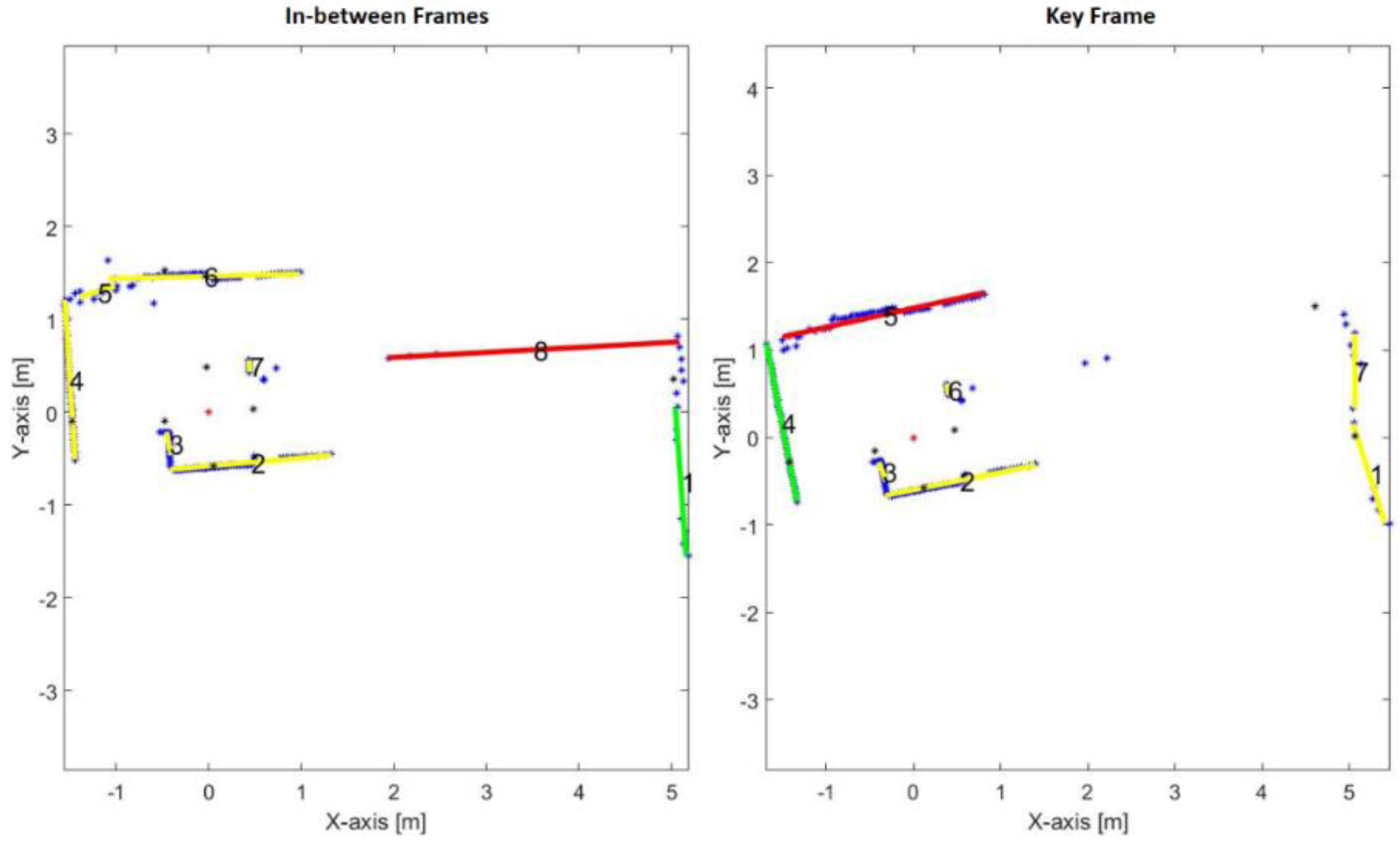
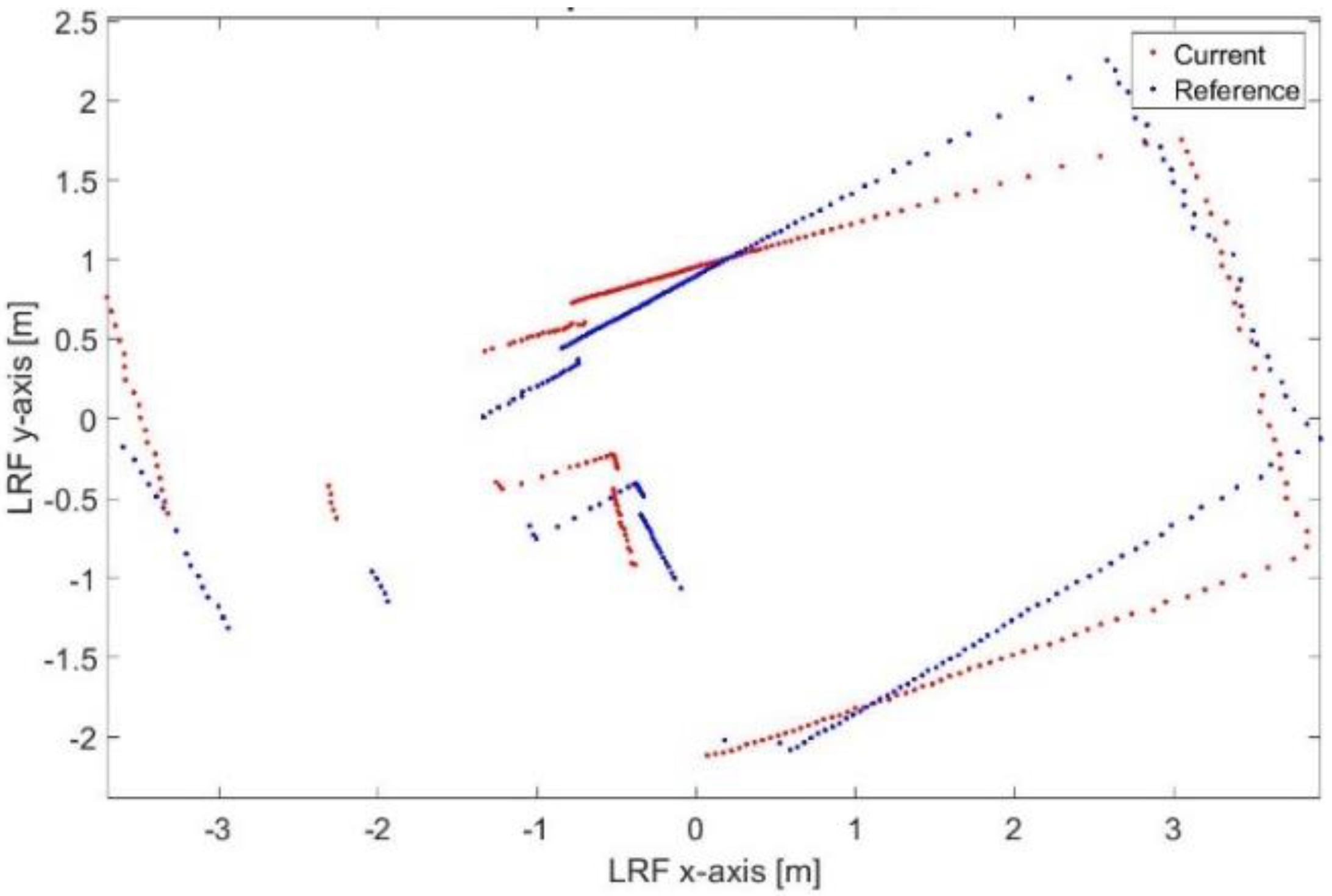
Figure 13.
Two reference lines of the first key frame.
Figure 13.
Two reference lines of the first key frame.
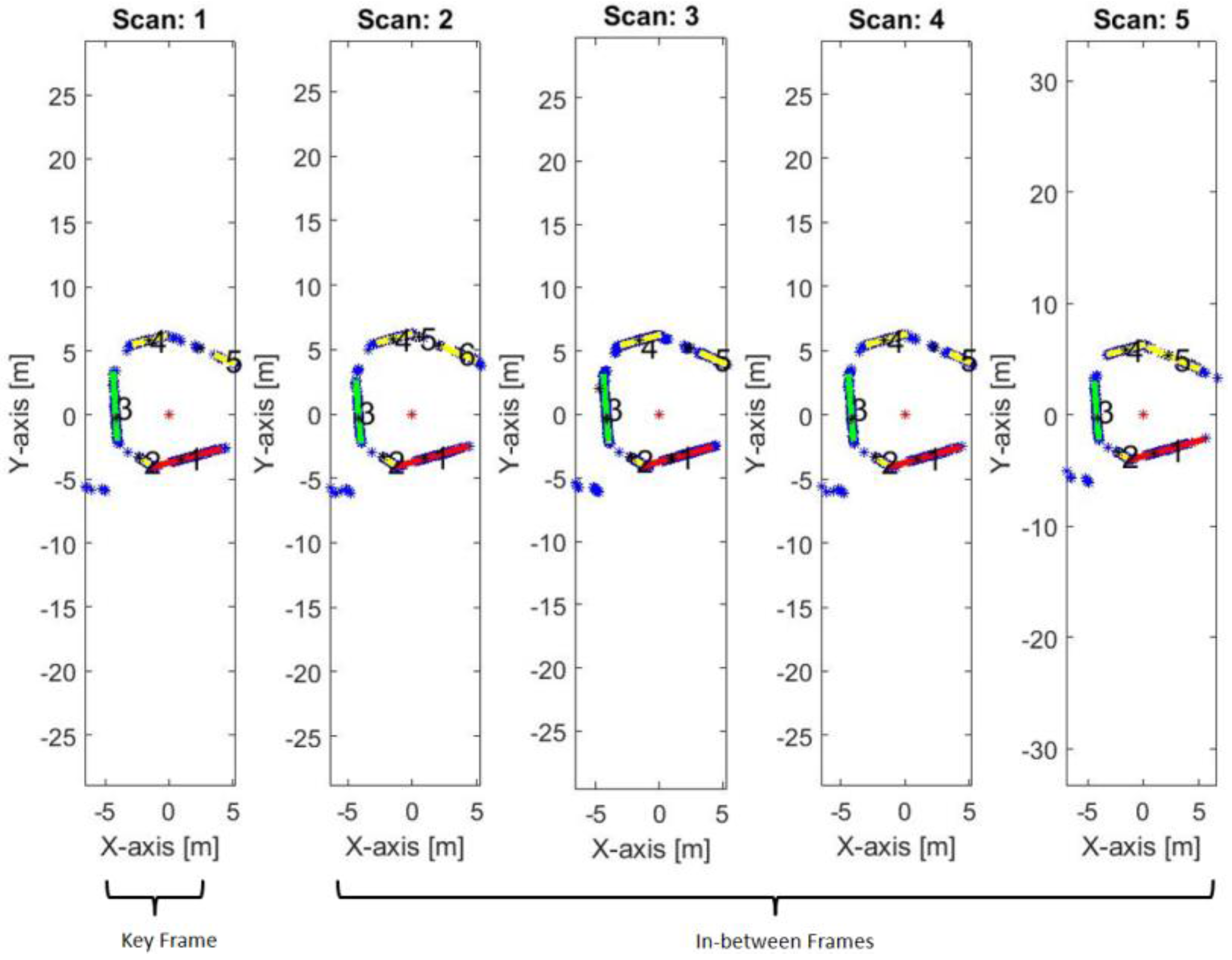
Figure 14.
The first key frame and the successive in-between frames.
Figure 14.
The first key frame and the successive in-between frames.
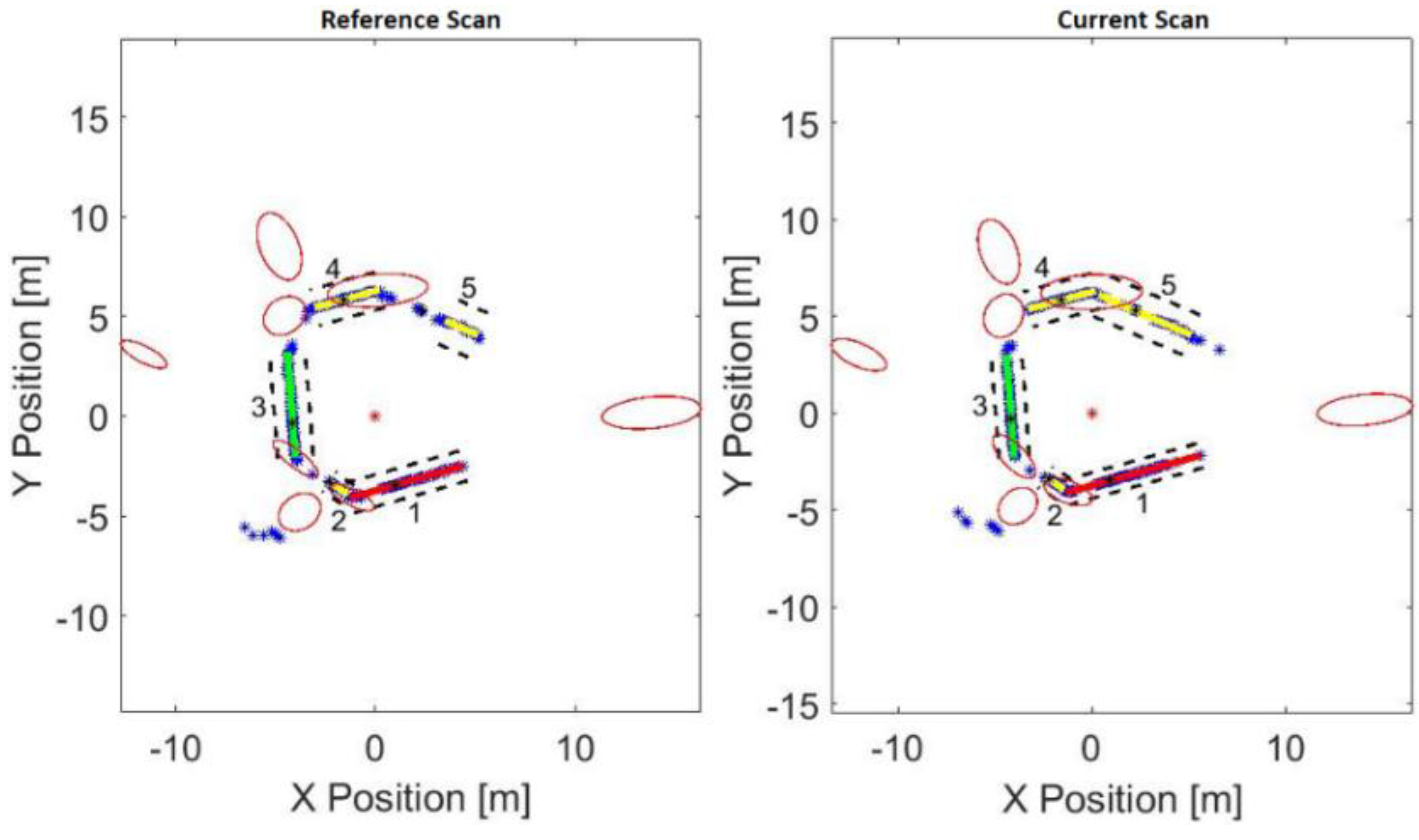
Figure 15.
Corners detection and its confidence ellipsoid region.
Figure 15.
Corners detection and its confidence ellipsoid region.
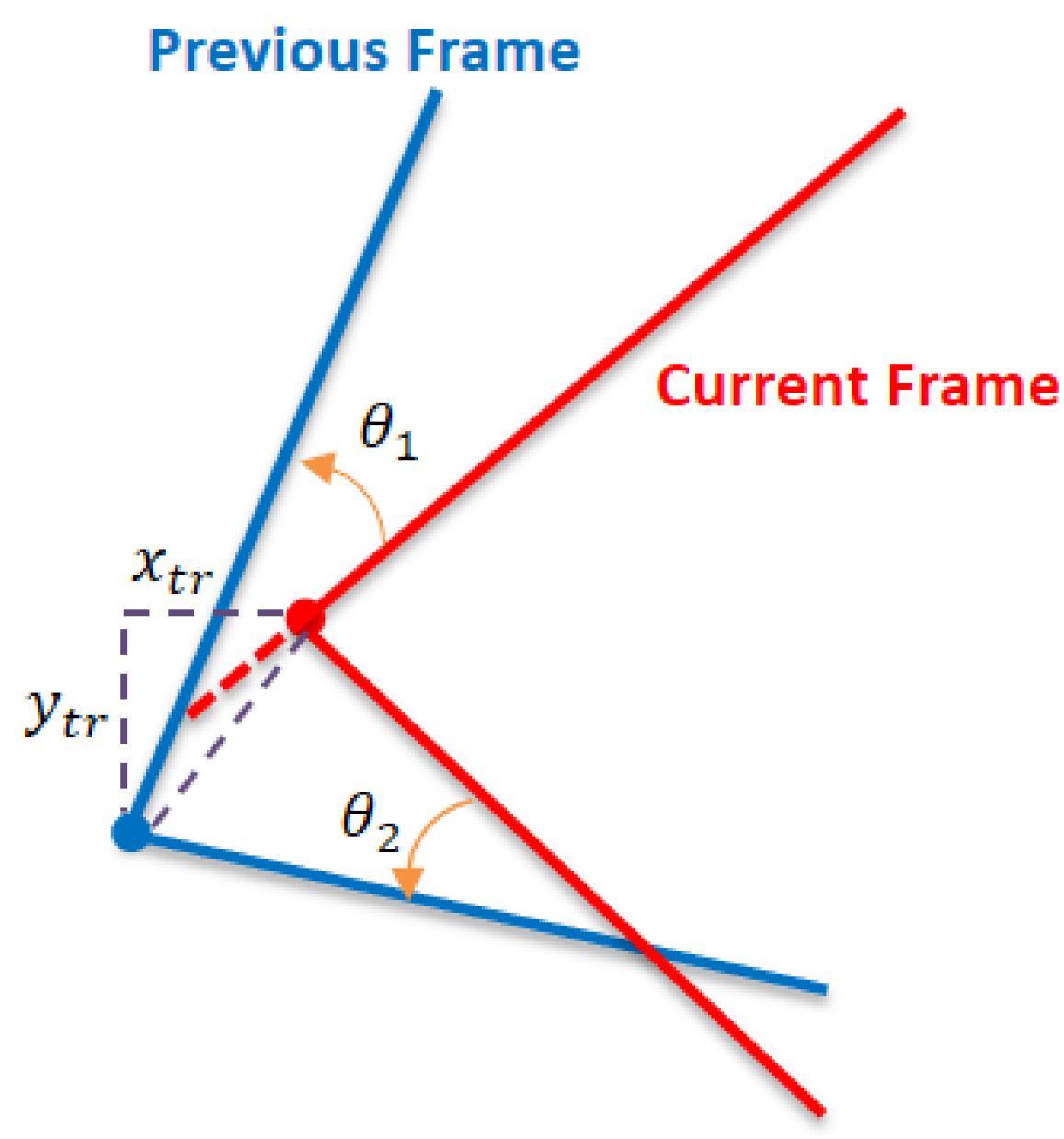
Figure 16.
Line registration algorithm.
Figure 16.
Line registration algorithm.
Figure 17.
Swapping process between the old and new reference lines.
Figure 17.
Swapping process between the old and new reference lines.
Figure 18.
Swapping result between old and new reference lines.
Figure 18.
Swapping result between old and new reference lines.
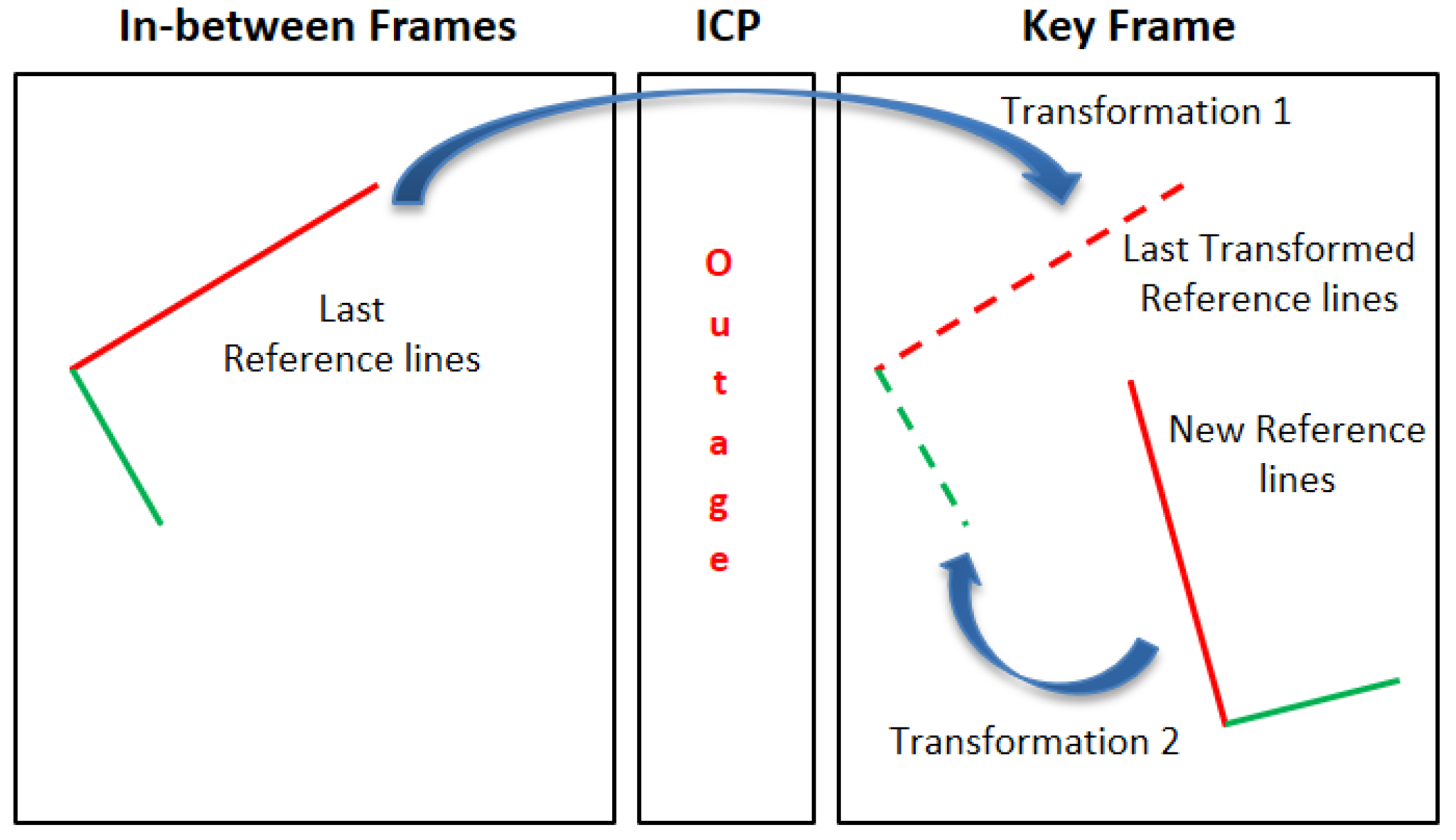
Figure 19.
Last reference lines transformation after the lines outage period.
Figure 19.
Last reference lines transformation after the lines outage period.
Figure 20.
The aerial platform equipped with the laser scanner range finder.
Figure 20.
The aerial platform equipped with the laser scanner range finder.
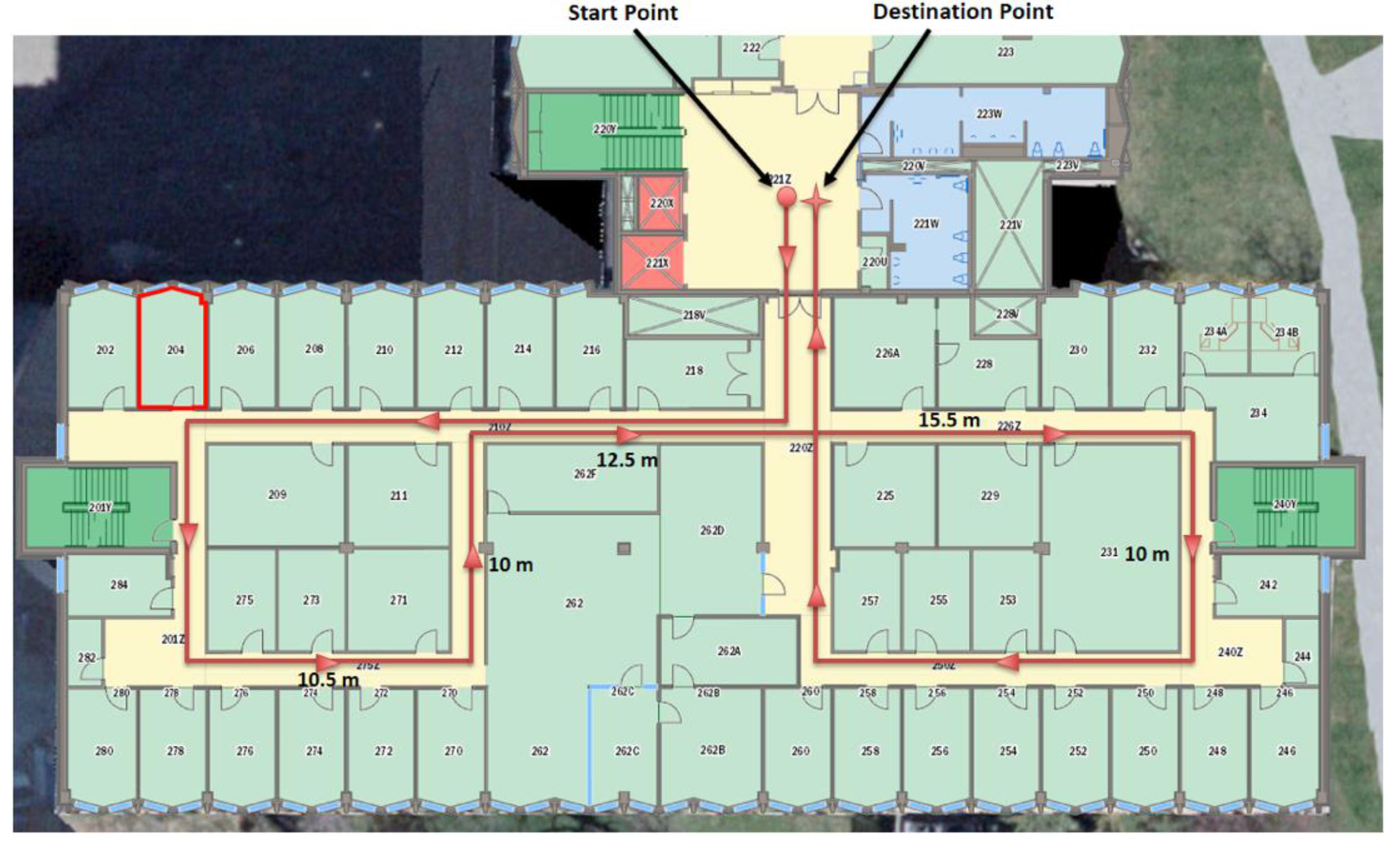
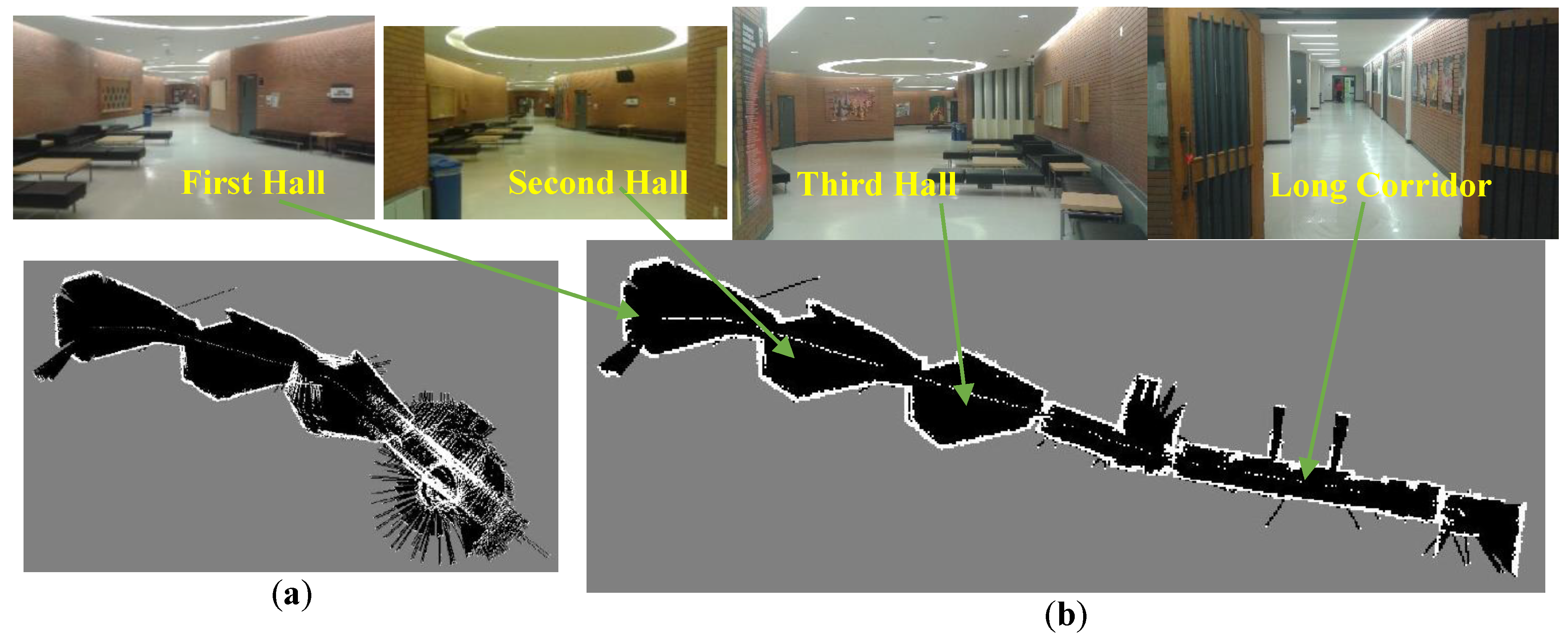
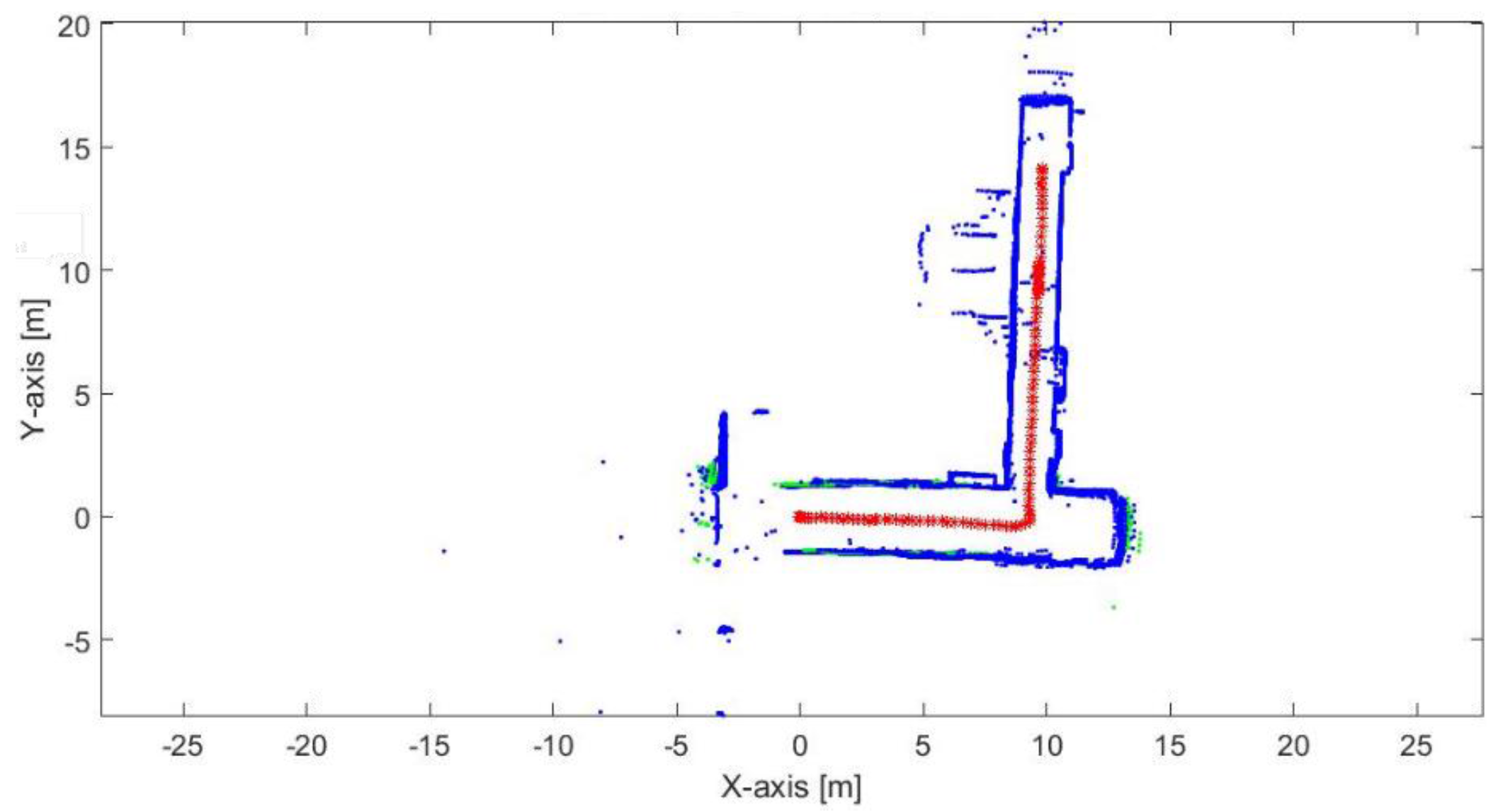
Figure 21.
Map representation of the dataset I.
Figure 21.
Map representation of the dataset I.
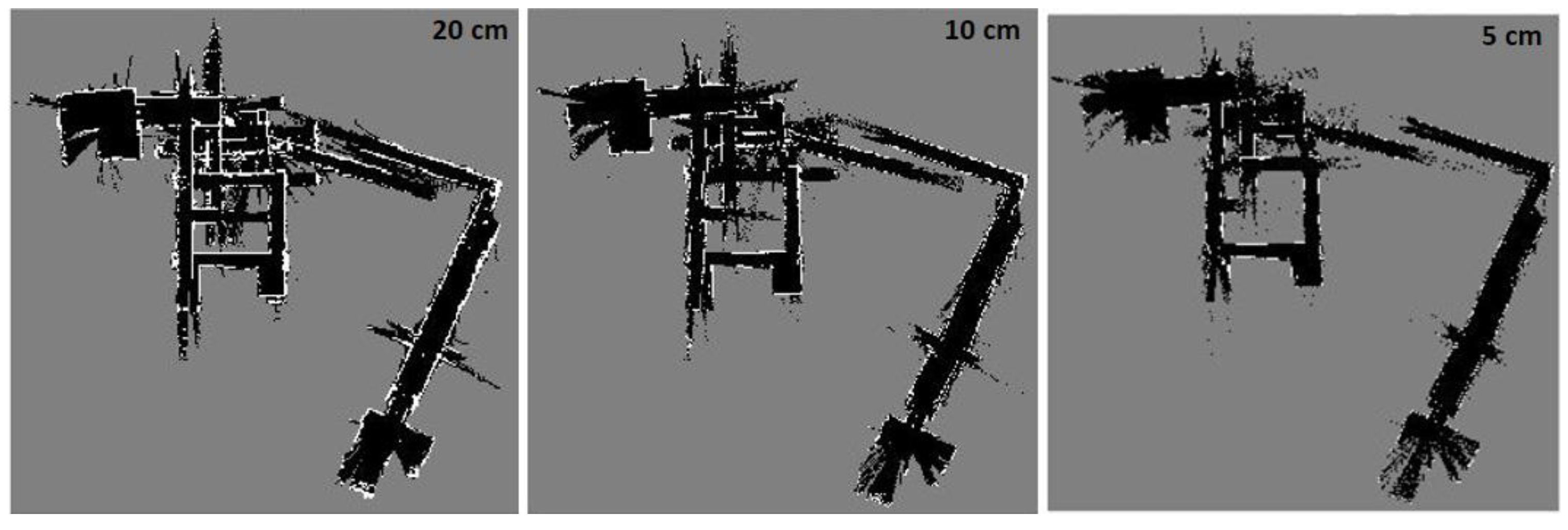
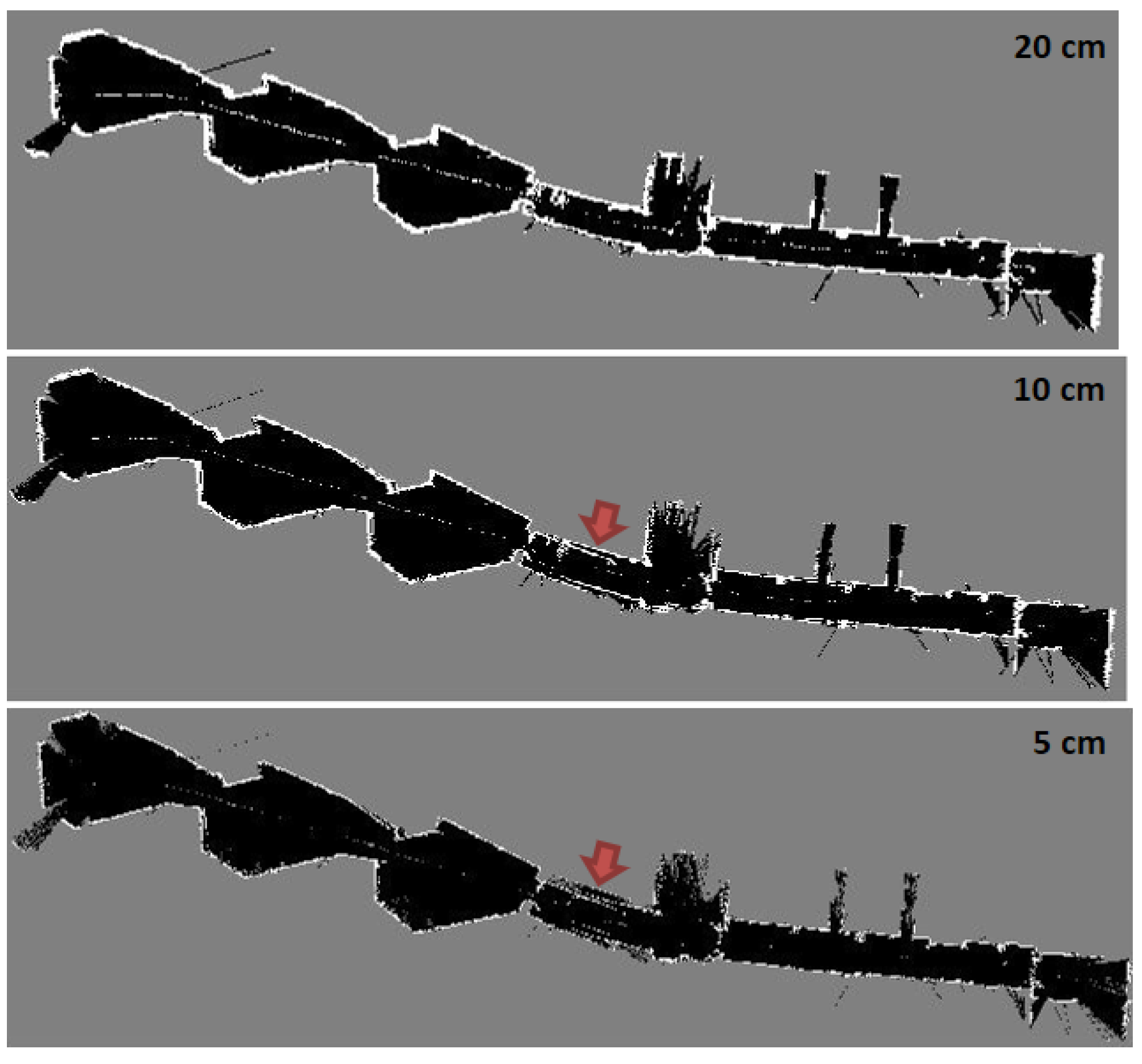
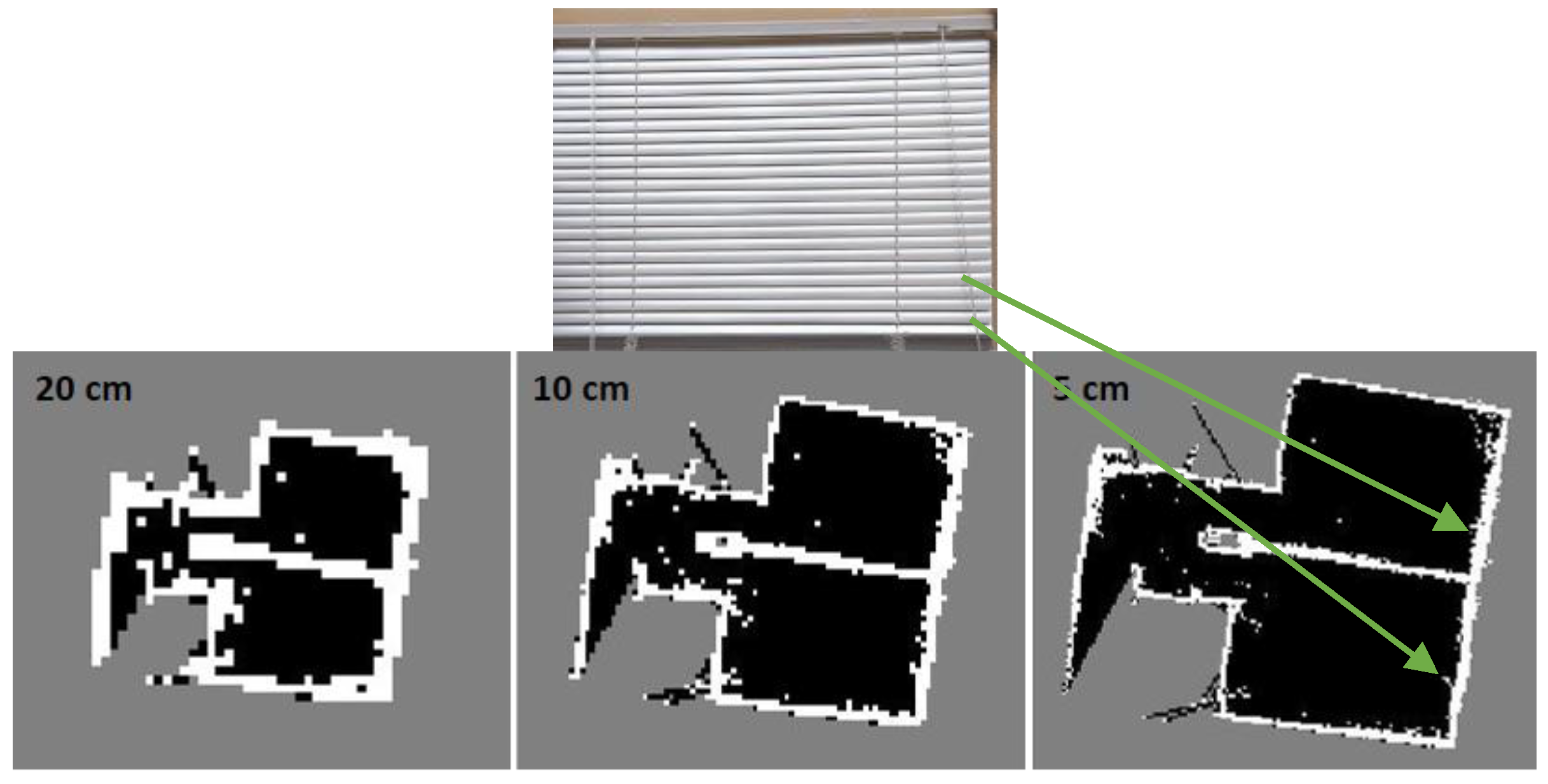
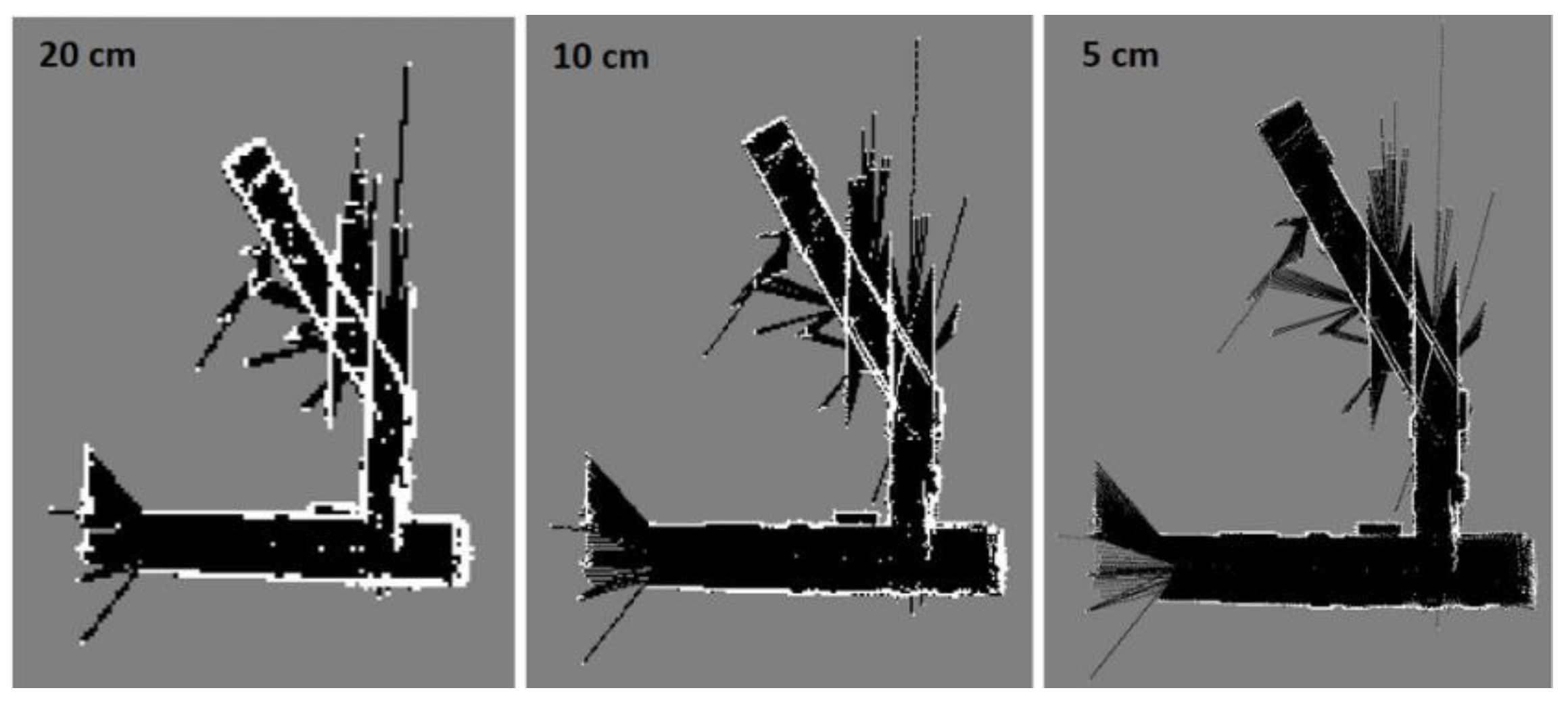
Figure 22.
Hector SLAM three level multi-resolution map representation result using grid cell dimensions 20, 10 and 5 cm.
Figure 22.
Hector SLAM three level multi-resolution map representation result using grid cell dimensions 20, 10 and 5 cm.
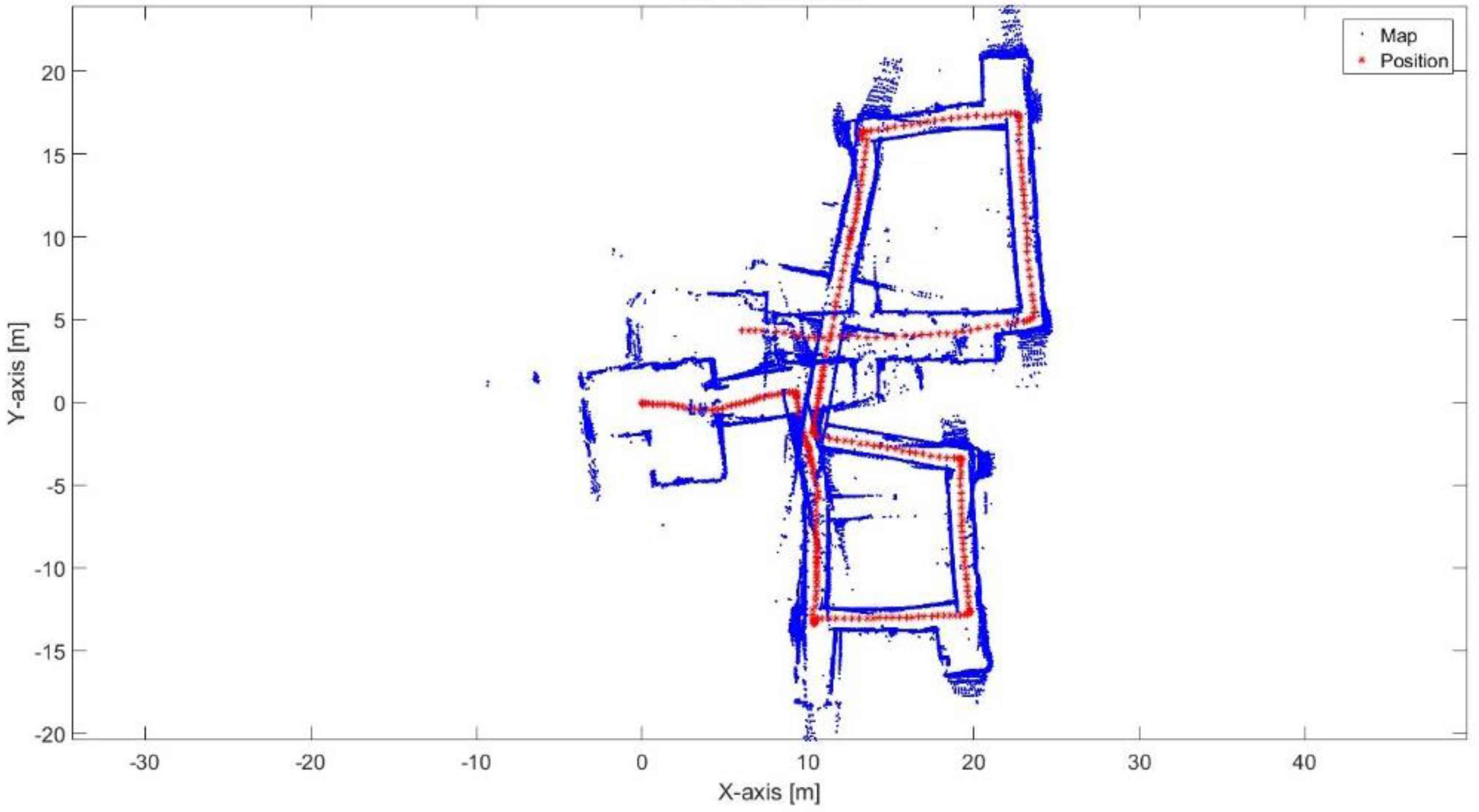
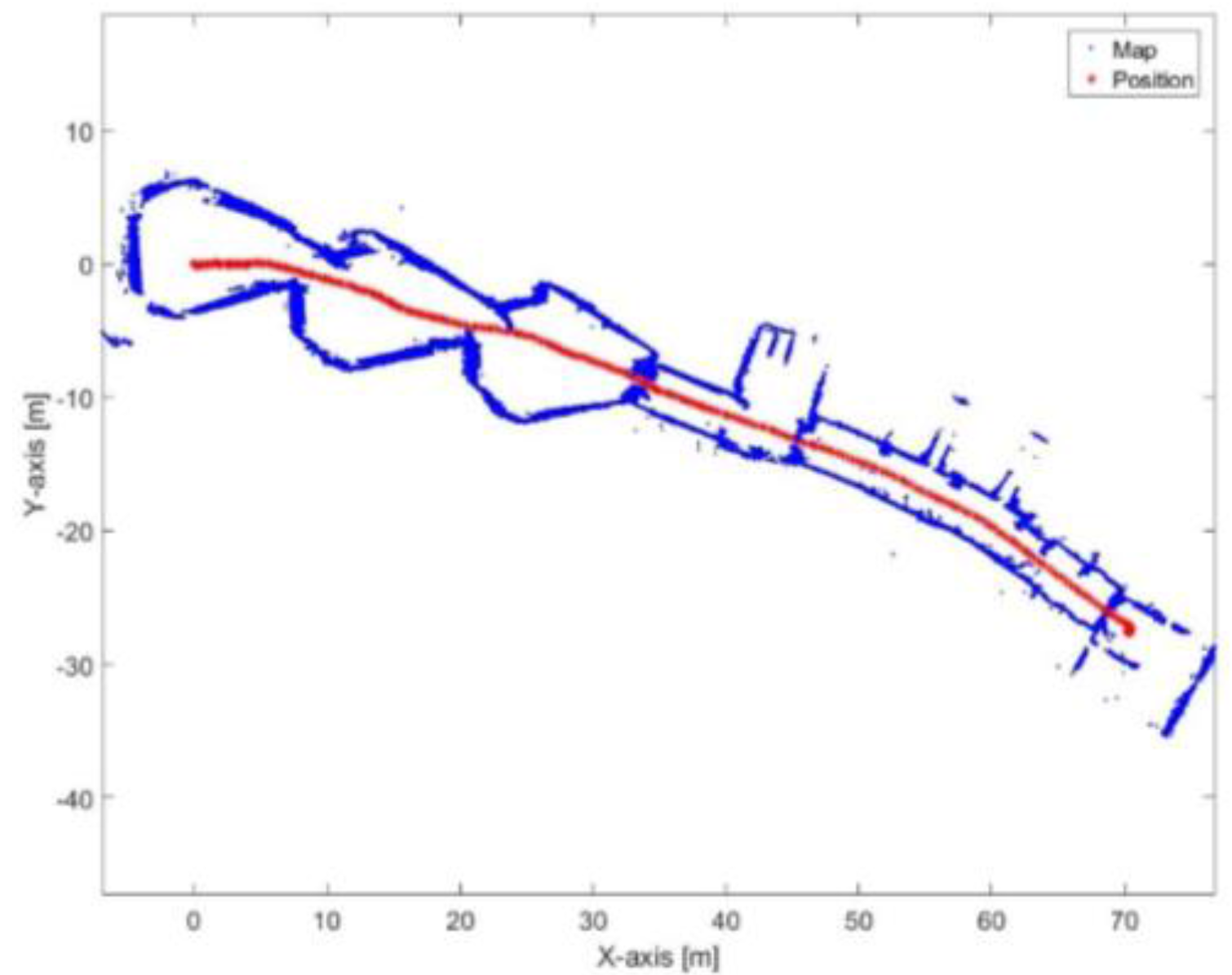
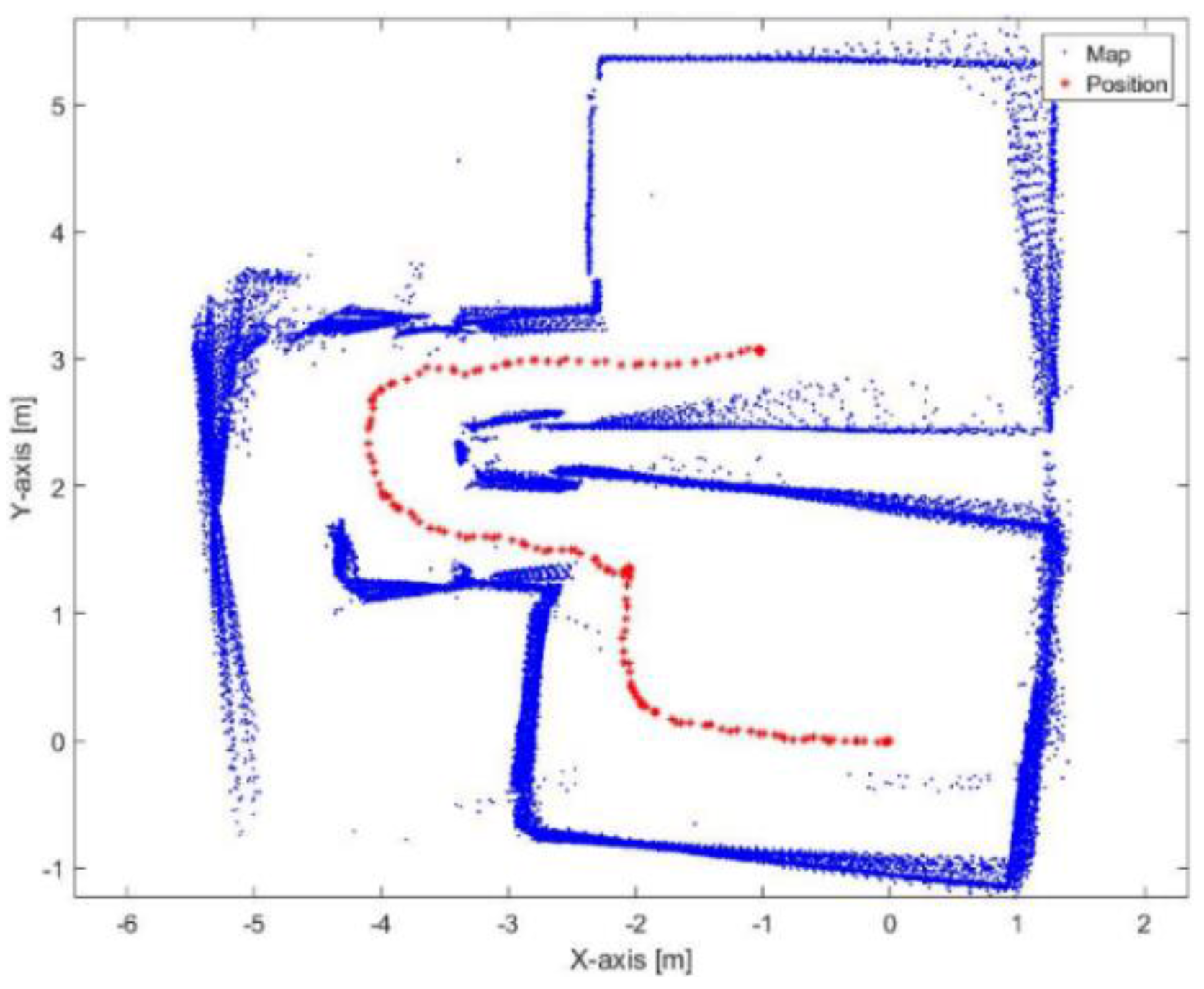
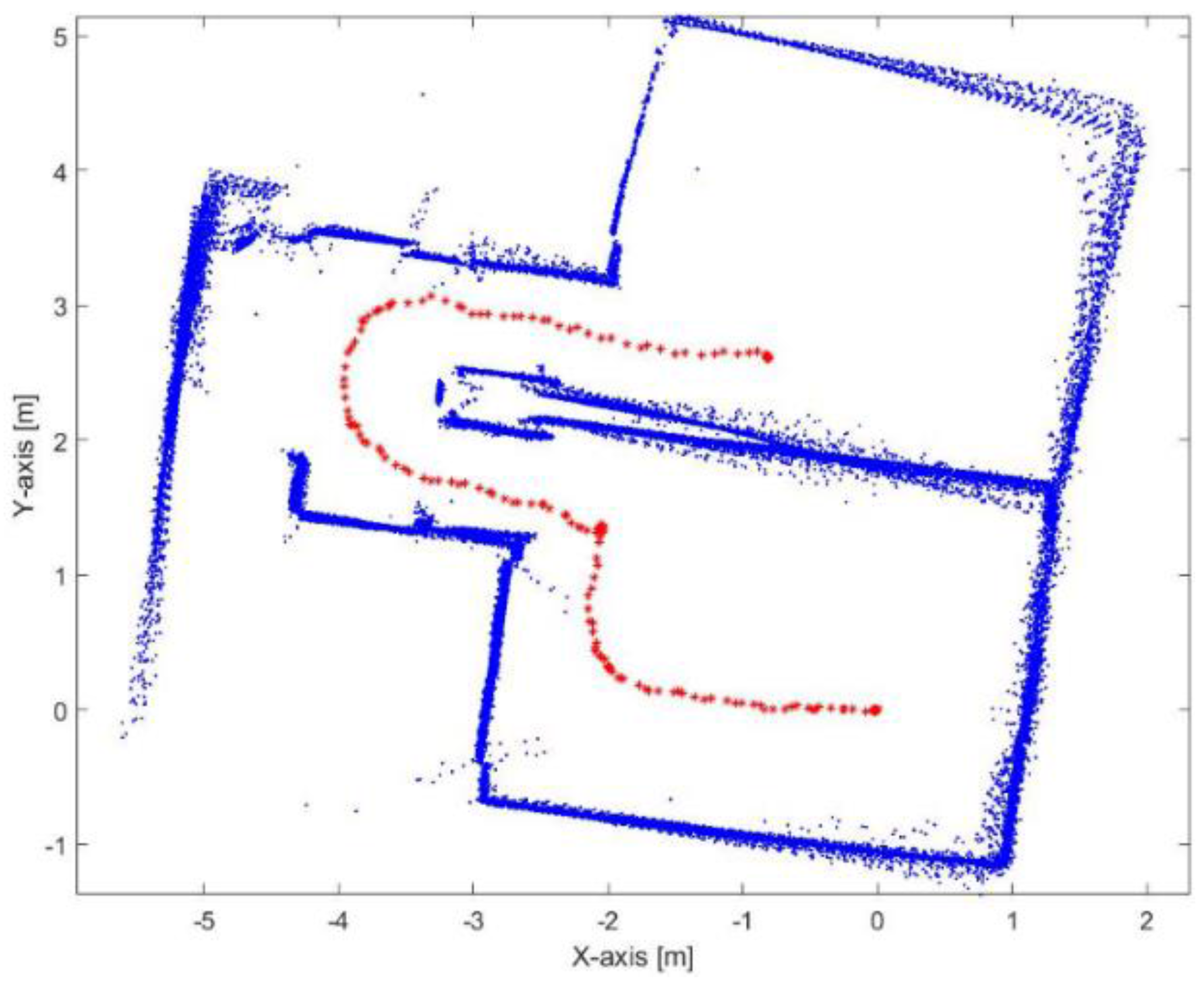
Figure 23.
Mapping and position results for the ICP algorithm.
Figure 23.
Mapping and position results for the ICP algorithm.
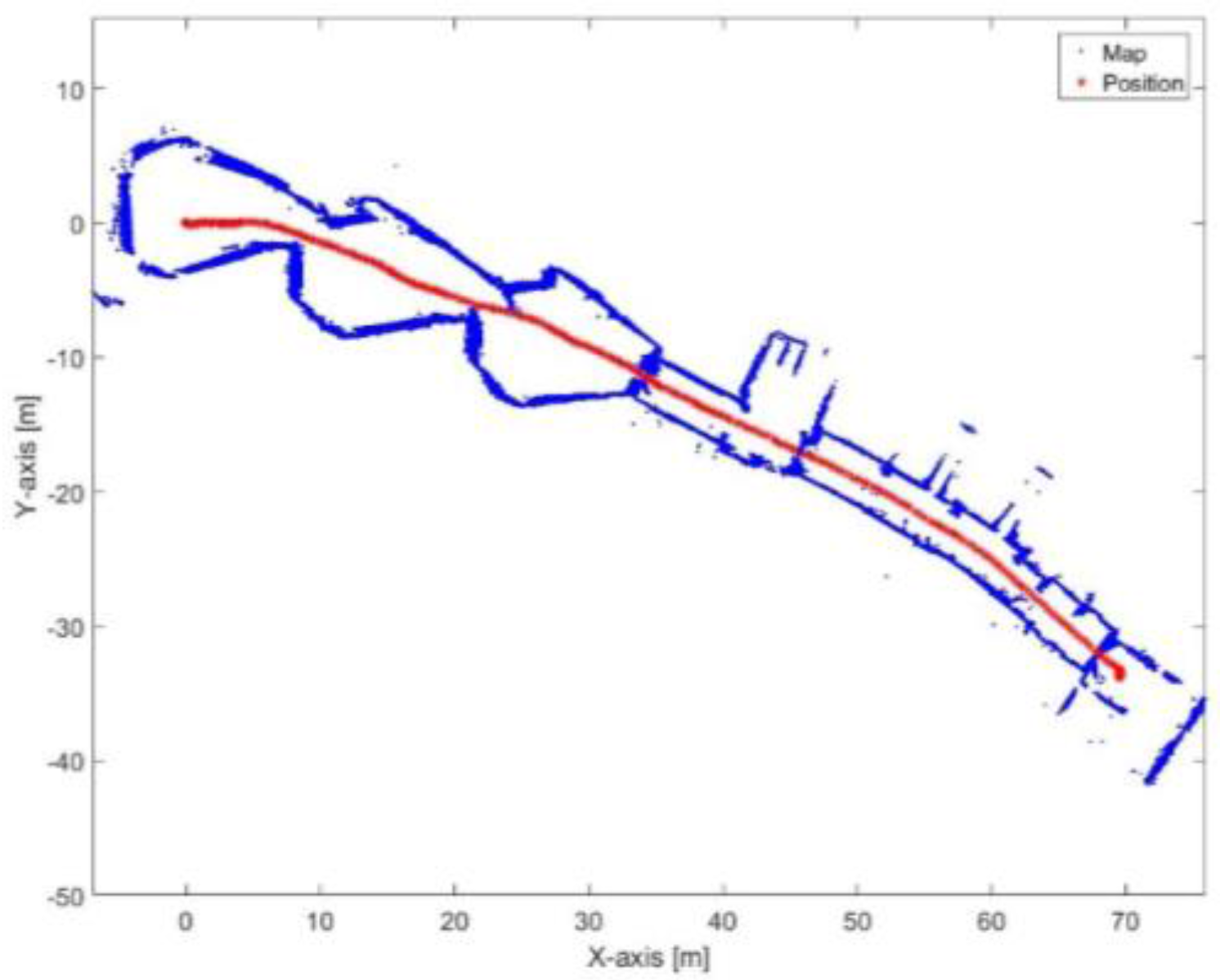
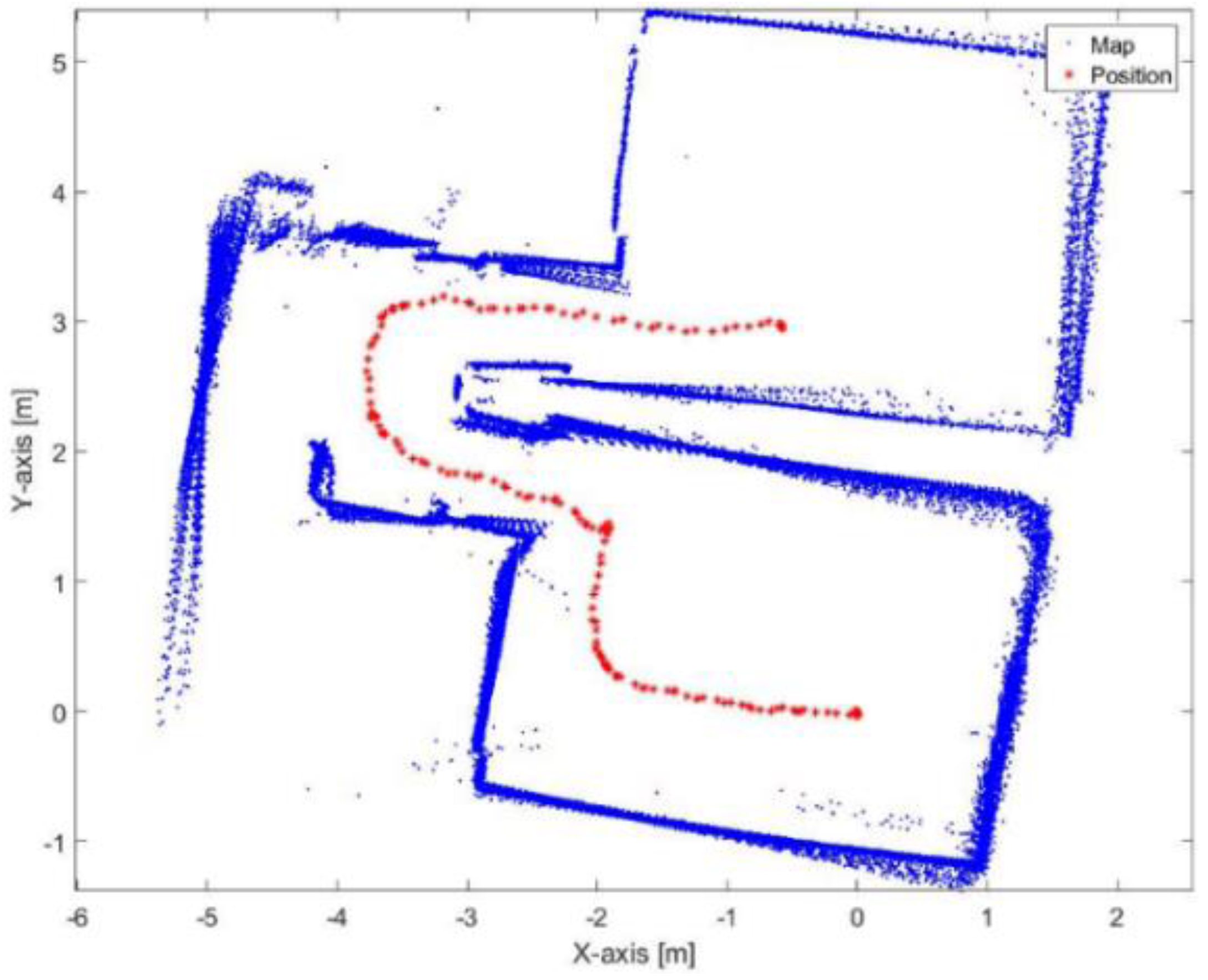
Figure 24.
Mapping and position results for the proposed algorithm.
Figure 24.
Mapping and position results for the proposed algorithm.
Figure 25.
Single level hector SLAM mapping results using different grid cell dimensions: (a) 10 cm; (b) 20 cm.
Figure 25.
Single level hector SLAM mapping results using different grid cell dimensions: (a) 10 cm; (b) 20 cm.
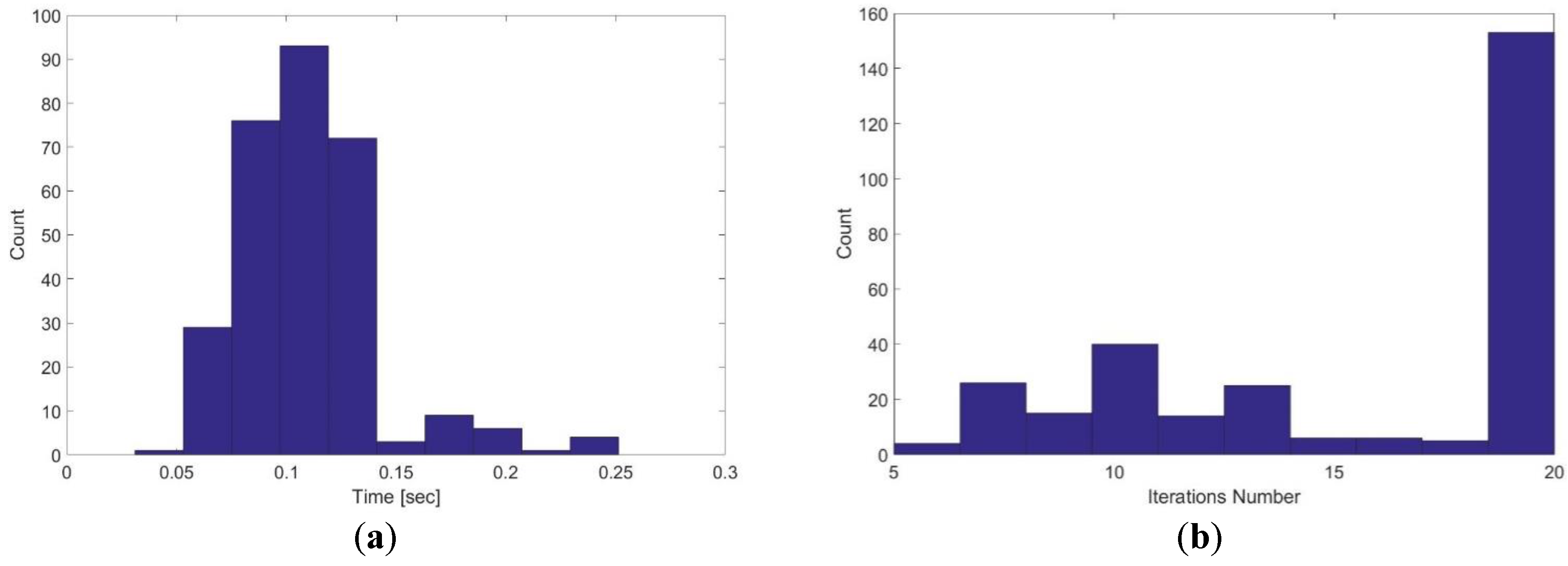
Figure 26.
Single level hector SLAM using 20 cm grid cell dimension: (a) Execution time; (b) iterations number.
Figure 26.
Single level hector SLAM using 20 cm grid cell dimension: (a) Execution time; (b) iterations number.
Figure 27.
Three level multi-resolution map representation result using grid cell dimensions 20, 10 and 5 cm.
Figure 27.
Three level multi-resolution map representation result using grid cell dimensions 20, 10 and 5 cm.
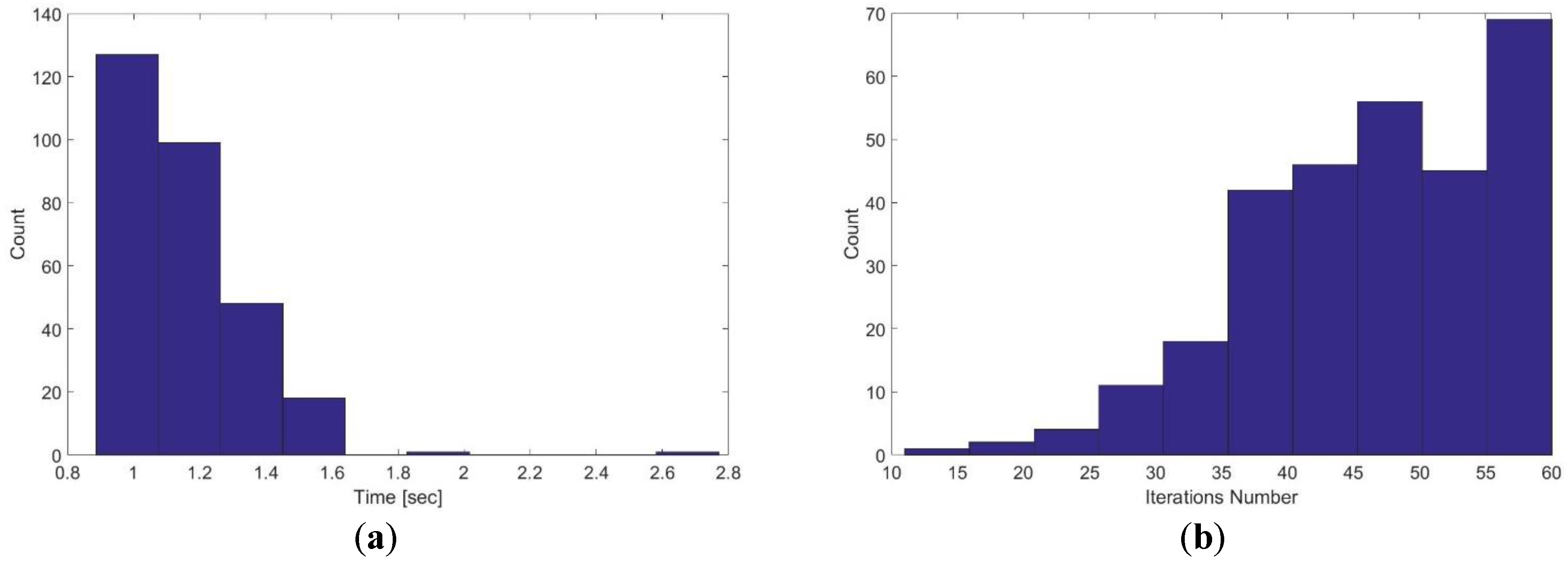
Figure 28.
Execution time and iterations number for three level multi-resolution map representation with 20, 10 and 5 cm grid cell dimensions. (a) Execution time; (b) iterations number.
Figure 28.
Execution time and iterations number for three level multi-resolution map representation with 20, 10 and 5 cm grid cell dimensions. (a) Execution time; (b) iterations number.
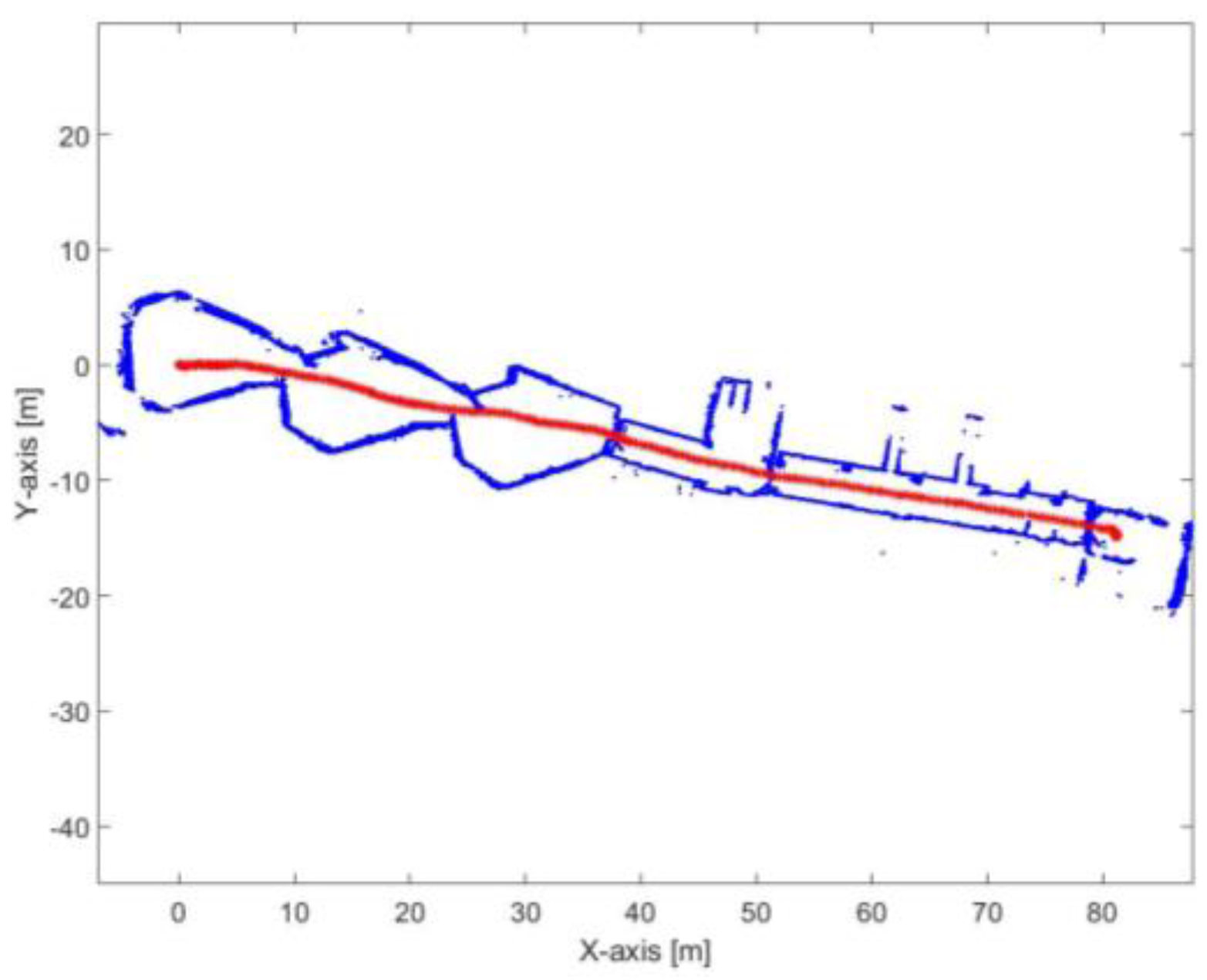
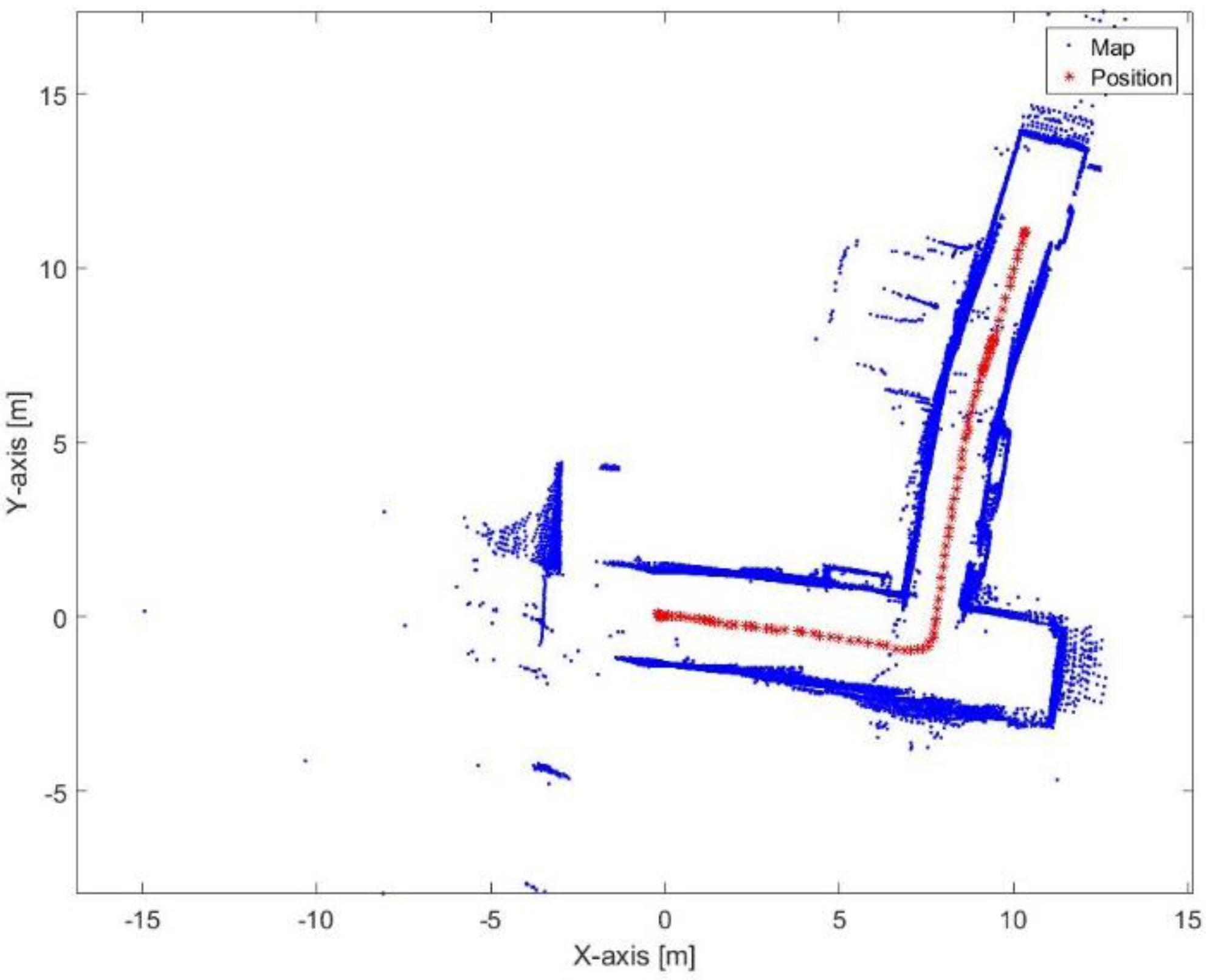
Figure 29.
Mapping and position results for the ICP algorithm.
Figure 29.
Mapping and position results for the ICP algorithm.
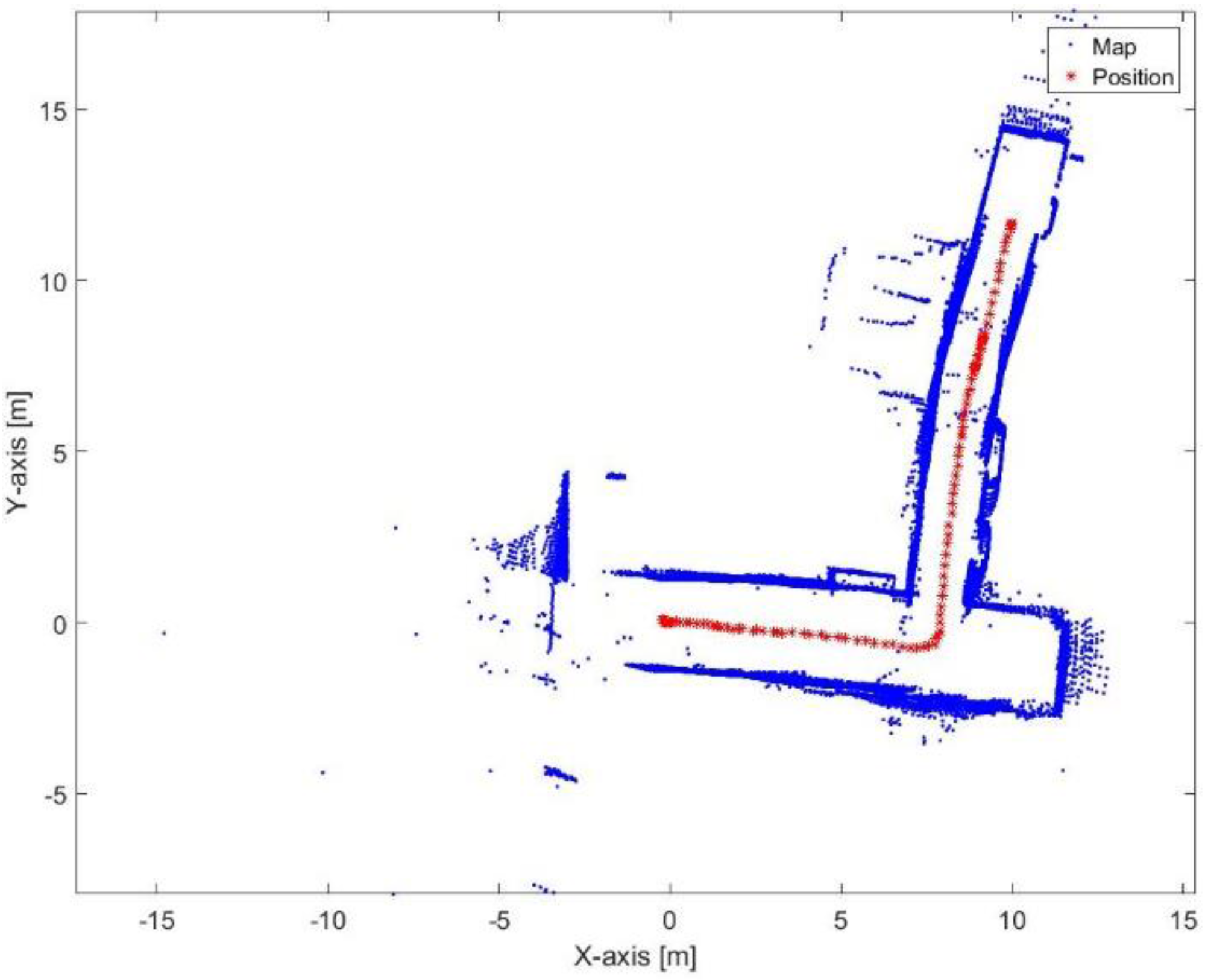
Figure 30.
Mapping and position results using adjusted corners registration.
Figure 30.
Mapping and position results using adjusted corners registration.
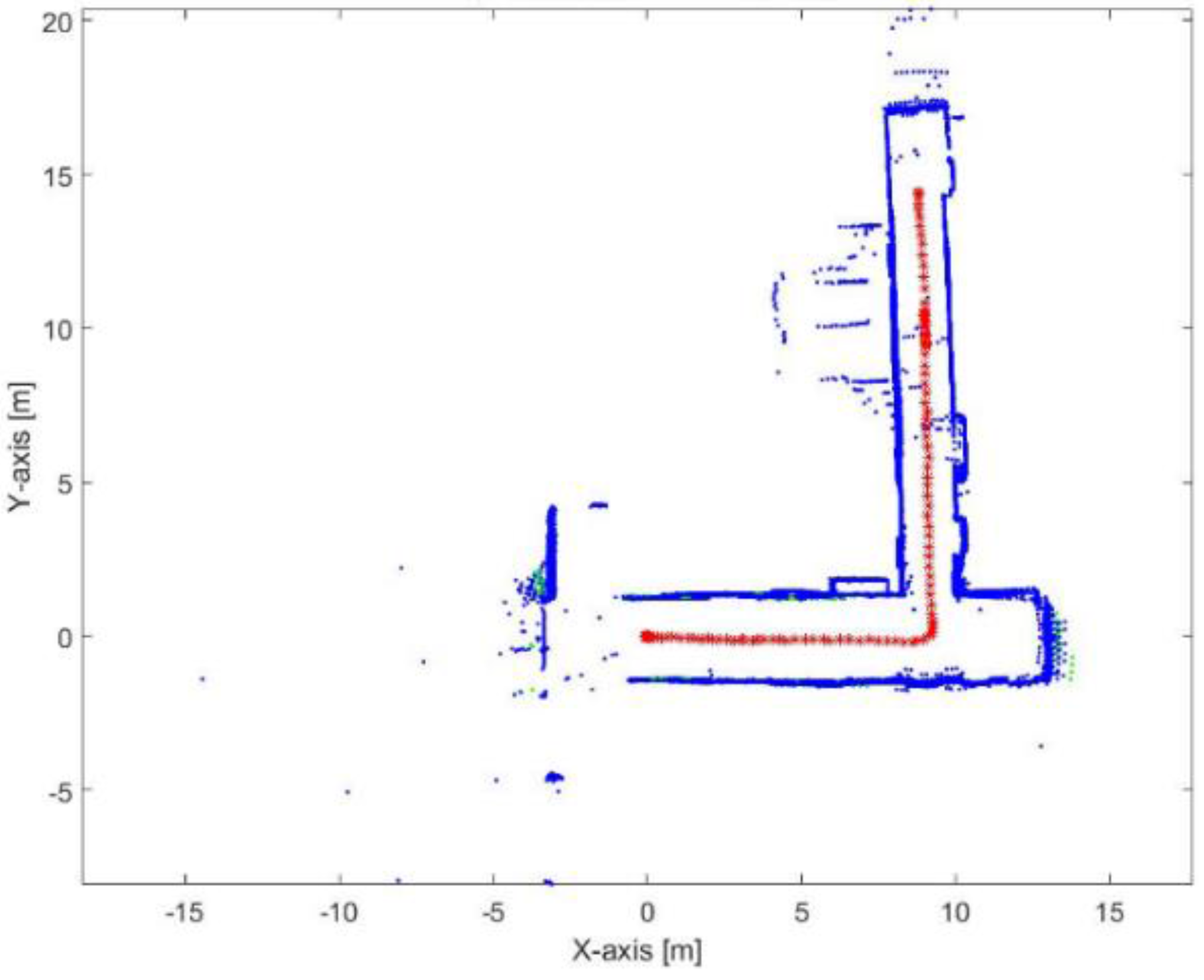
Figure 31.
Mapping and position results for the proposed algorithm.
Figure 31.
Mapping and position results for the proposed algorithm.
Figure 32.
Three level multi-resolution map representation result using grid cell dimensions 20, 10 and 5 cm.
Figure 32.
Three level multi-resolution map representation result using grid cell dimensions 20, 10 and 5 cm.
Figure 33.
Mapping and position results for the ICP algorithm.
Figure 33.
Mapping and position results for the ICP algorithm.
Figure 34.
Mapping and position results for the adjusted corners registration.
Figure 34.
Mapping and position results for the adjusted corners registration.
Figure 35.
Failure of the proposed scan matching algorithm in one of the in-between frames w.r.t the successive frame.
Figure 35.
Failure of the proposed scan matching algorithm in one of the in-between frames w.r.t the successive frame.
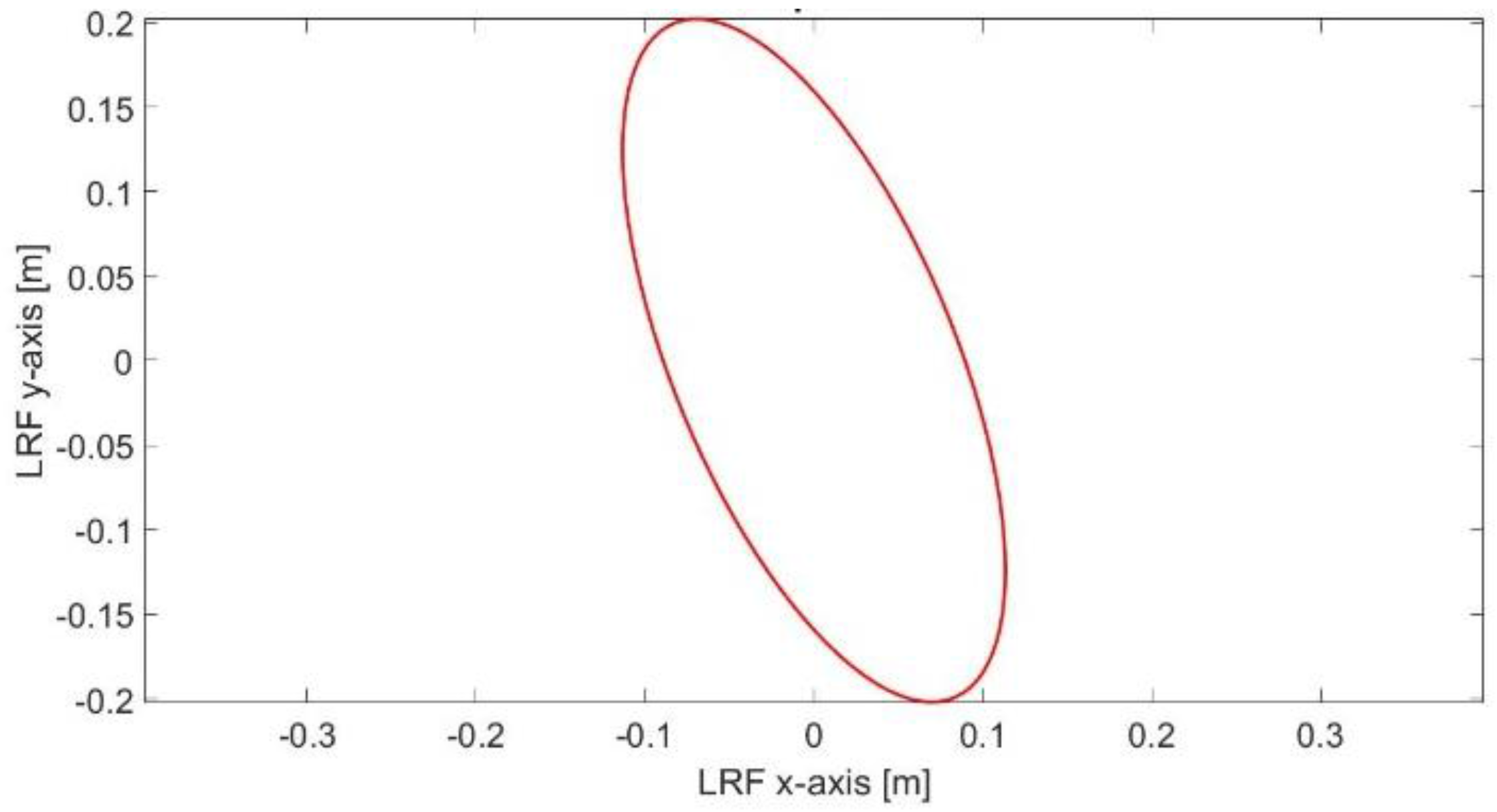
Figure 36.
One sigma ellipse of the scan matching error.
Figure 36.
One sigma ellipse of the scan matching error.
Figure 37.
Mapping and position results for the proposed algorithm.
Figure 37.
Mapping and position results for the proposed algorithm.
Figure 38.
Three level multi-resolution map representation result using grid cell dimensions 20, 10 and 5 cm.
Figure 38.
Three level multi-resolution map representation result using grid cell dimensions 20, 10 and 5 cm.
Figure 39.
Mapping and position results for the ICP algorithm.
Figure 39.
Mapping and position results for the ICP algorithm.
Figure 40.
Mapping and position results for the adjusted corners registration.
Figure 40.
Mapping and position results for the adjusted corners registration.
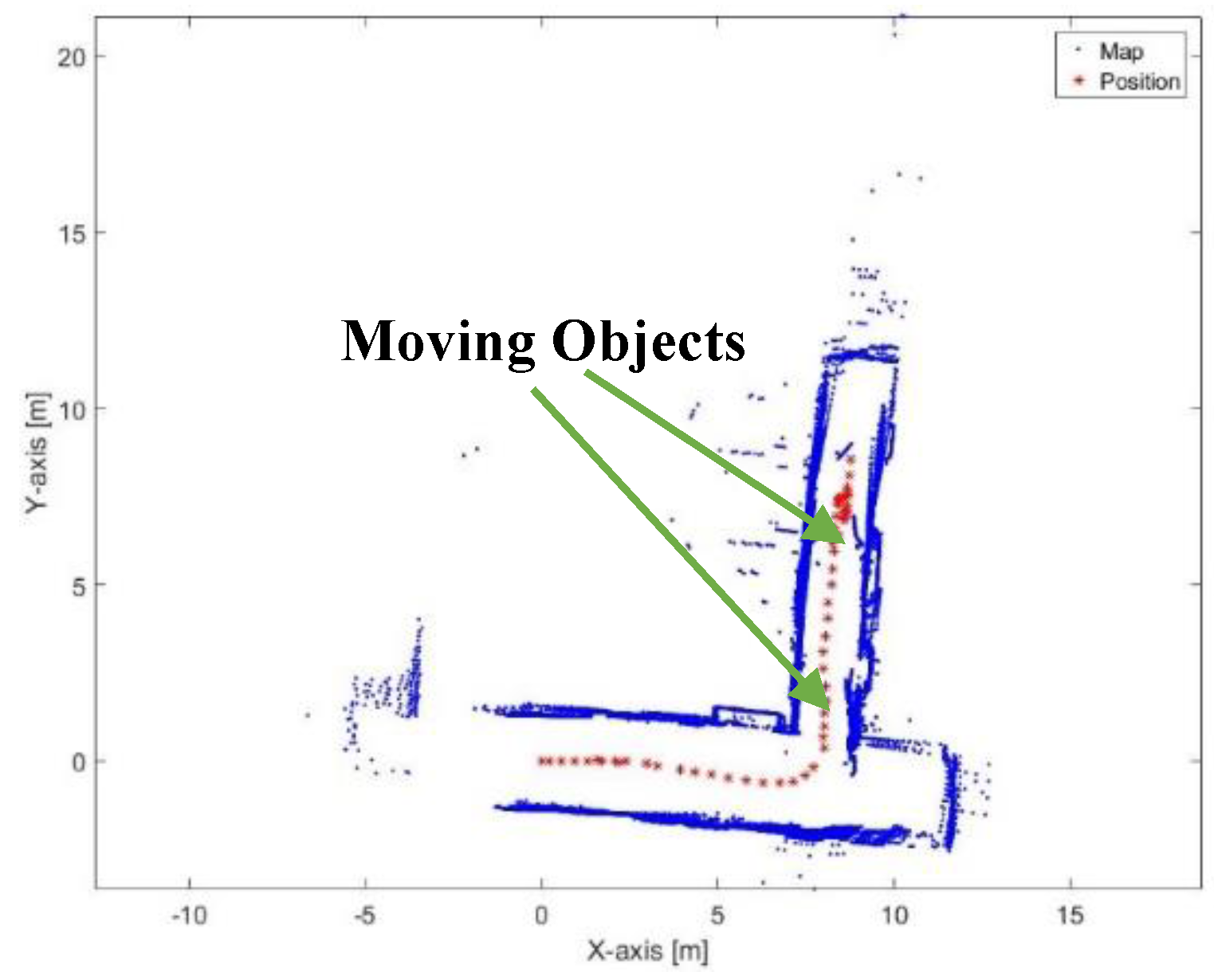
Figure 41.
Mapping and position results for the proposed algorithm.
Figure 41.
Mapping and position results for the proposed algorithm.
Figure 42.
Three level multi-resolution map representation result using grid cell dimensions 20, 10 and 5 cm.
Figure 42.
Three level multi-resolution map representation result using grid cell dimensions 20, 10 and 5 cm.
Figure 43.
Mapping and position results for the ICP algorithm.
Figure 43.
Mapping and position results for the ICP algorithm.
Figure 44.
Mapping and position results for the adjusted corners registration.
Figure 44.
Mapping and position results for the adjusted corners registration.
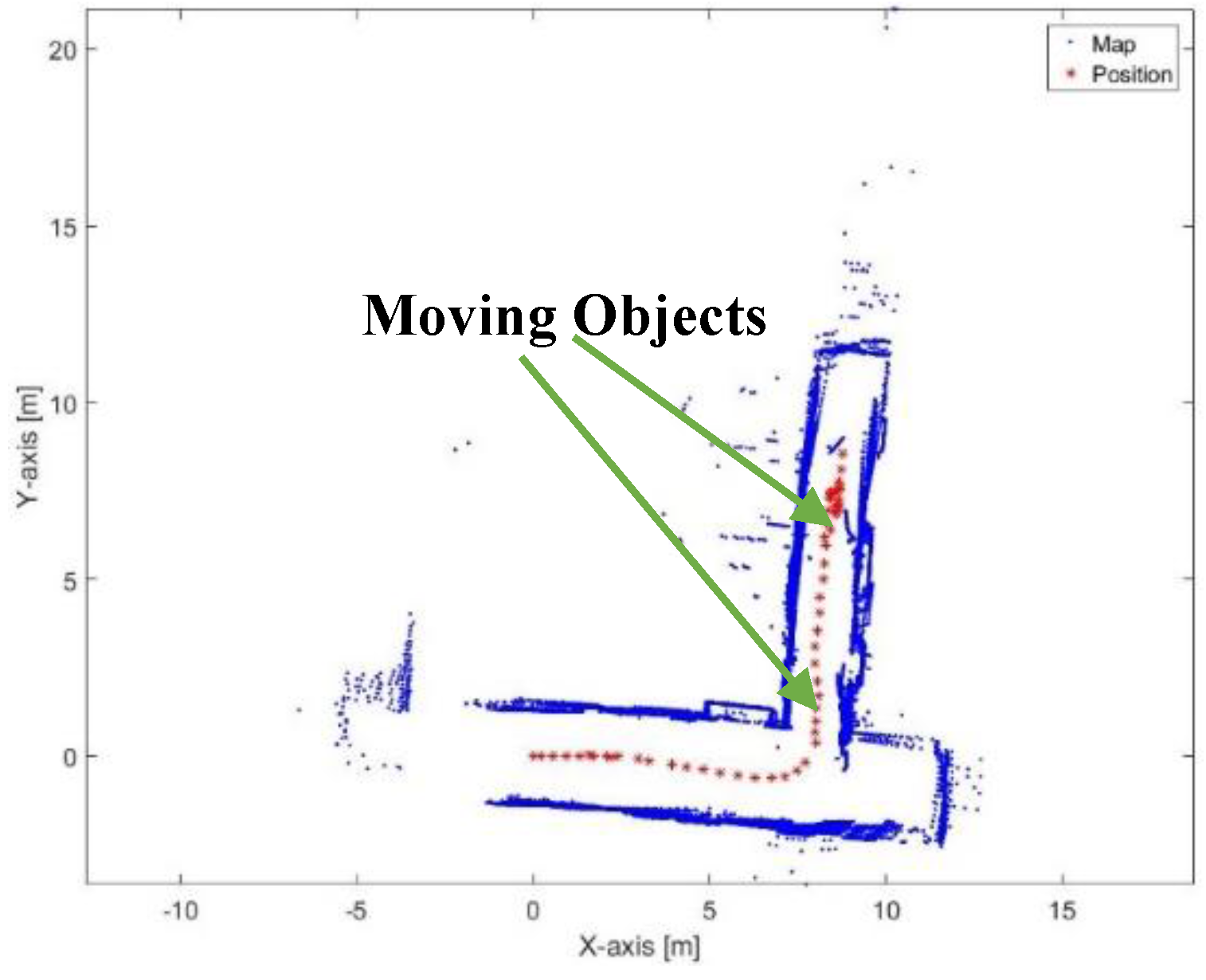
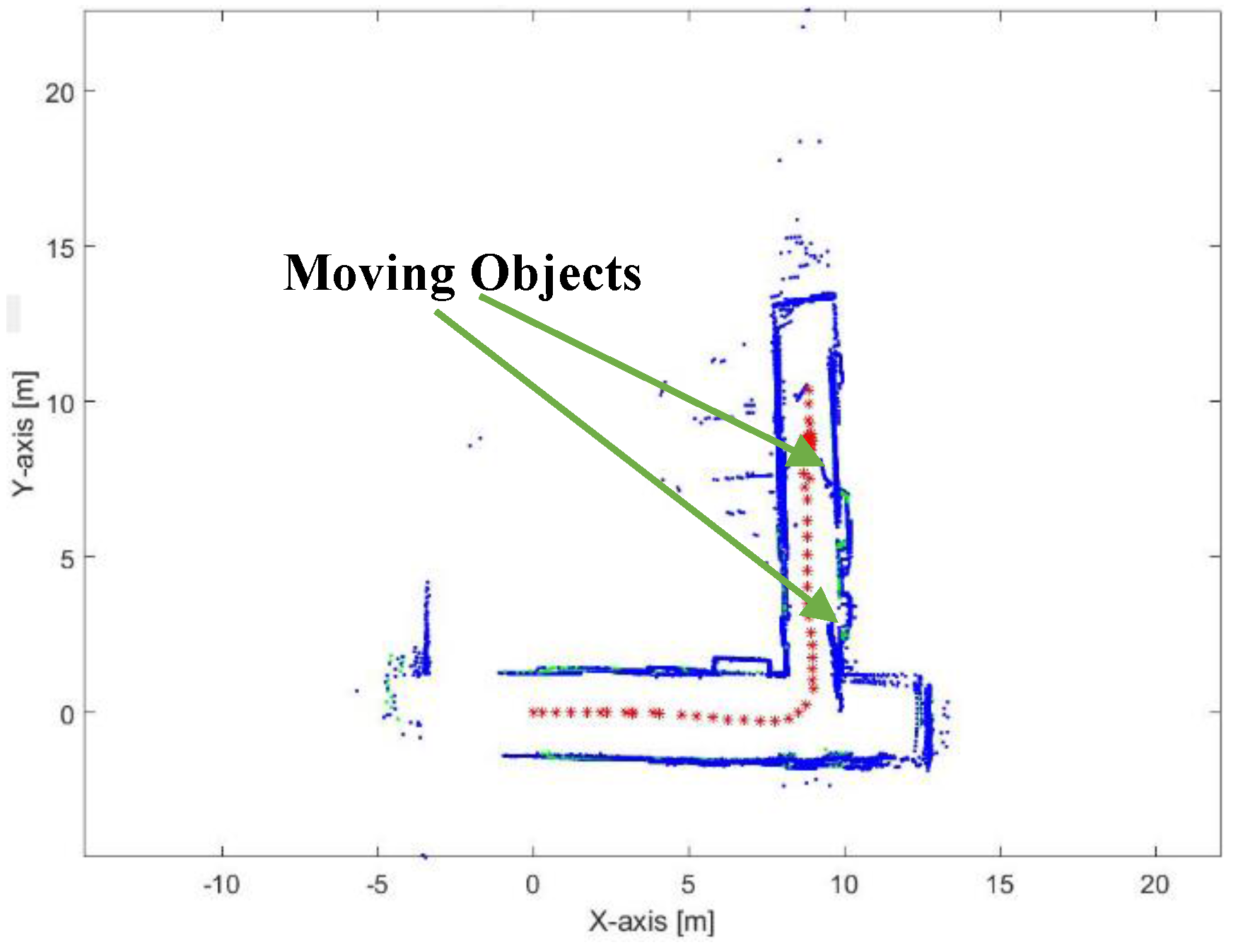
Figure 45.
Mapping and position results for the proposed algorithm.
Figure 45.
Mapping and position results for the proposed algorithm.
Figure 46.
Mapping and position results for the proposed algorithm after changing values of the thresholds.
Figure 46.
Mapping and position results for the proposed algorithm after changing values of the thresholds.
Table 1.
Standard deviations of the laser scanner range finder according to the detection range.
Table 1.
Standard deviations of the laser scanner range finder according to the detection range.
| Detection Range [m] | Standard Deviation [cm] |
|---|
| Less than 1 | 0.34 |
| Less than 2 | 0.73 |
| Less than 3 | 1.79 |
| Less than 4 | 3.27 |
| Less than 5 | 3.92 |
| Less than 6 | 5.44 |
Table 2.
Line availability and extraction time for different data sets.
Table 2.
Line availability and extraction time for different data sets.
| Dataset Name | MIT Killian | MIT CSAIL | Intel Lab | ACES Building | Freiburg Building |
|---|
| Number of scans | 17,481 | 1989 | 13,632 | 7375 | 4496 |
| Mean number of lines | 4.24 | 8.80 | 4.10 | 4.21 | 8.86 |
| Percentage of more than three lines | 88.2% | 99.9% | 81.3% | 84.8% | 99.8% |
| Mean execution time [ms] | 3.7 | 8.9 | 3.4 | 4.0 | 7.4 |
Table 3.
Computed parameters of the extracted lines of the first key frame.
Table 3.
Computed parameters of the extracted lines of the first key frame.
| Line Number | Coefficient of Determination | Adjusted Coefficient of Determination | Number of Data Points | Line Length [m] |
|---|
| 1 | 0.9940 | 0.9937 | 51 | 5.7 |
| 2 | 0.9755 | 0.9706 | 13 | 1.0 |
| 3 | 0.8689 | 0.8631 | 48 | 5.4 |
| 4 | 0.9749 | 0.9722 | 22 | 2.8 |
| 5 | 0.9713 | 0.9598 | 8 | 1.8 |
Table 4.
The environment status and contribution for each experimental dataset.
Table 4.
The environment status and contribution for each experimental dataset.
| Dataset Name | Environment Status | Contribution |
|---|
| Dataset I | Static | Corridors, loopback, glass objects |
| Dataset II | Static | Brick walls, glass objects, Corridors |
| Dataset III | Static | Aluminum curtains, Sharp rotation |
| Dataset IV | Static | Glass objects, corridors |
| Dataset V | Dynamic | Glass objects, corridors, moving objects |
Table 5.
Mean execution time and number of iterations for multi-resolution map representation with different levels and grid cell dimensions.
Table 5.
Mean execution time and number of iterations for multi-resolution map representation with different levels and grid cell dimensions.
| Level | Cell Dimension [cm] | Mean Execution Time [s] | Mean Iterations Number |
|---|
| 1 | 20 | 0.11 | 15.7 |
| 2 | 10, 5 | 0.80 | 33.5 |
| 3 | 20, 10, 5 | 1.15 | 47 |