Assessing Human Activity in Elderly People Using Non-Intrusive Load Monitoring
Abstract
:1. Introduction
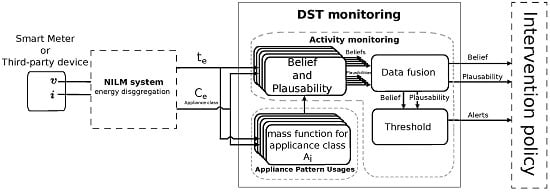
2. Model Description
Basic Belief Assignments and Weighing
3. Experimental Results
3.1. Datasets, Preprocessing, and Selection of the Training Samples
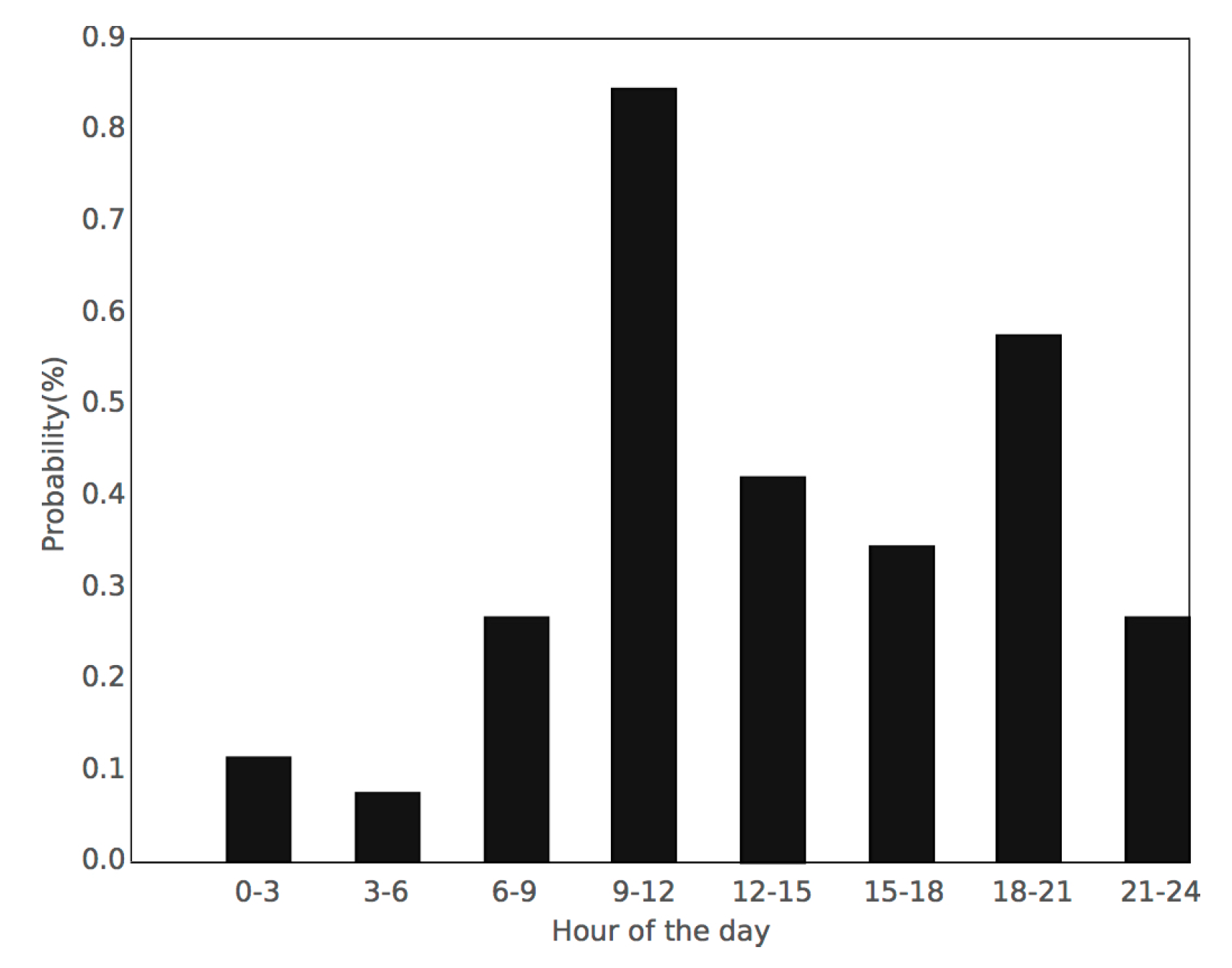
3.2. Definition of Parameters and Constants in DST
3.3. The Benchmark’s Model
3.4. Analysis of DST and GMM Scores
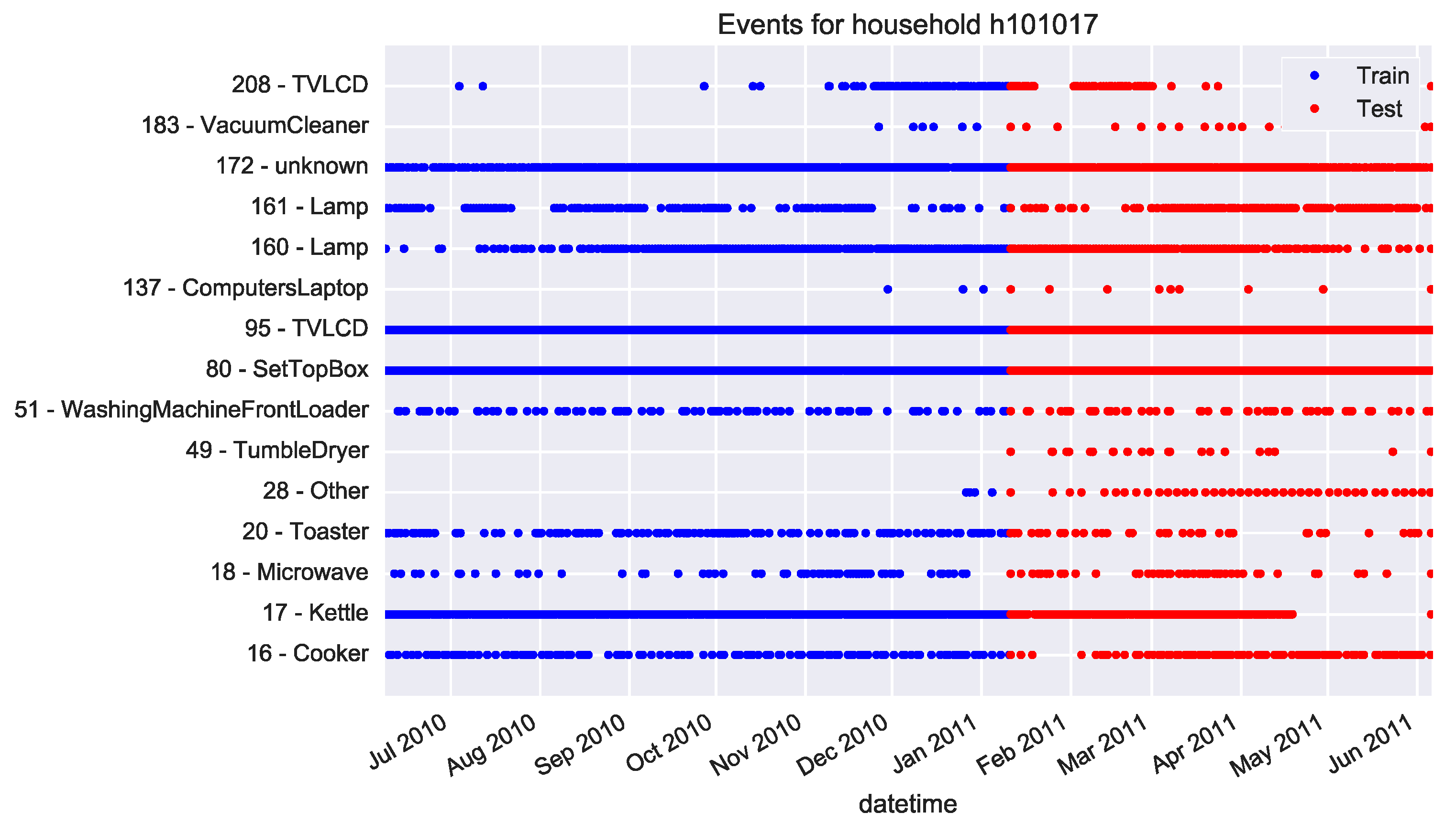
3.4.1. Single Pensioner Household No. 101017 in the HES Dataset
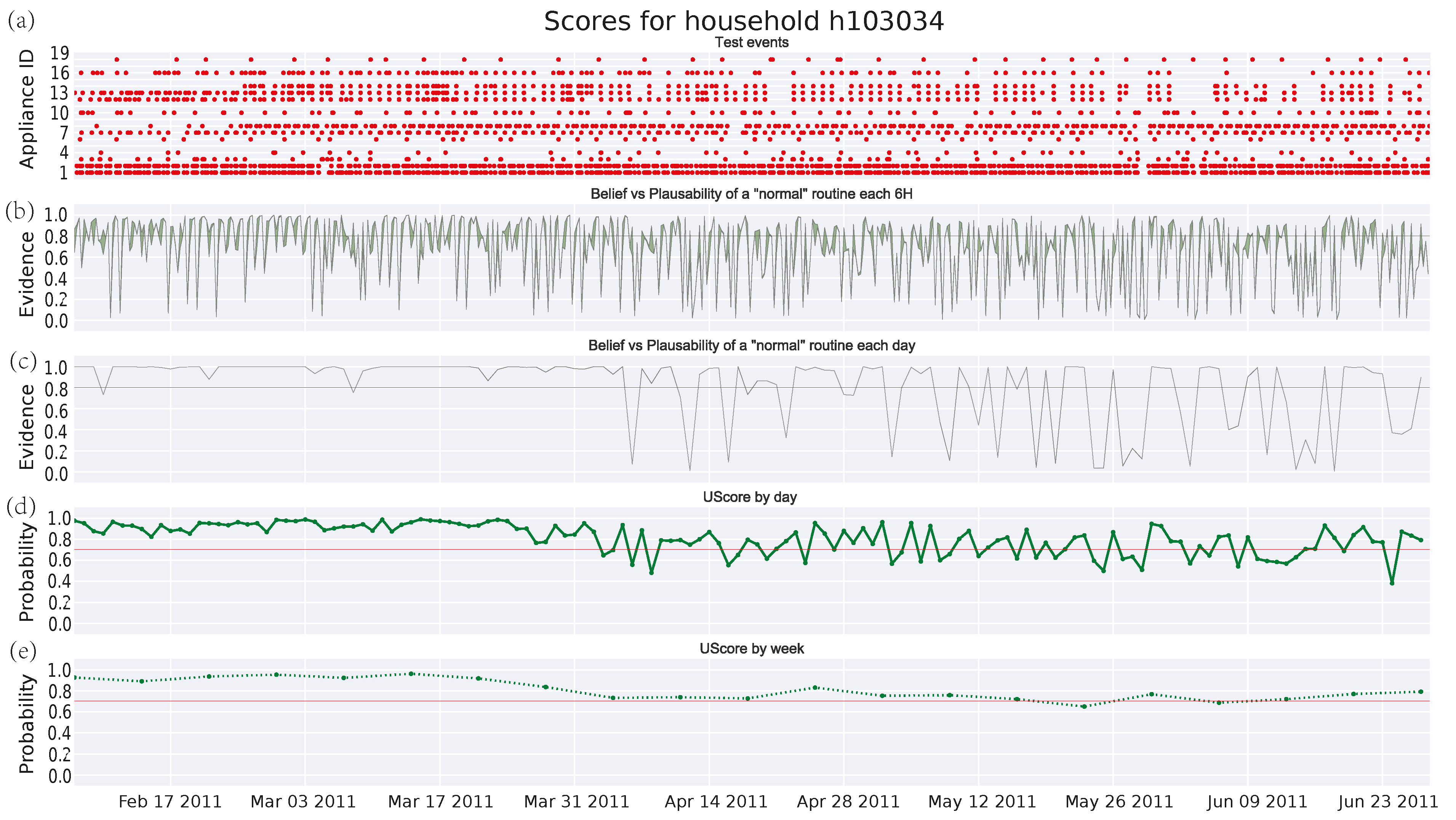
3.4.2. Single Pensioner Household No. 103034 in the HES Dataset
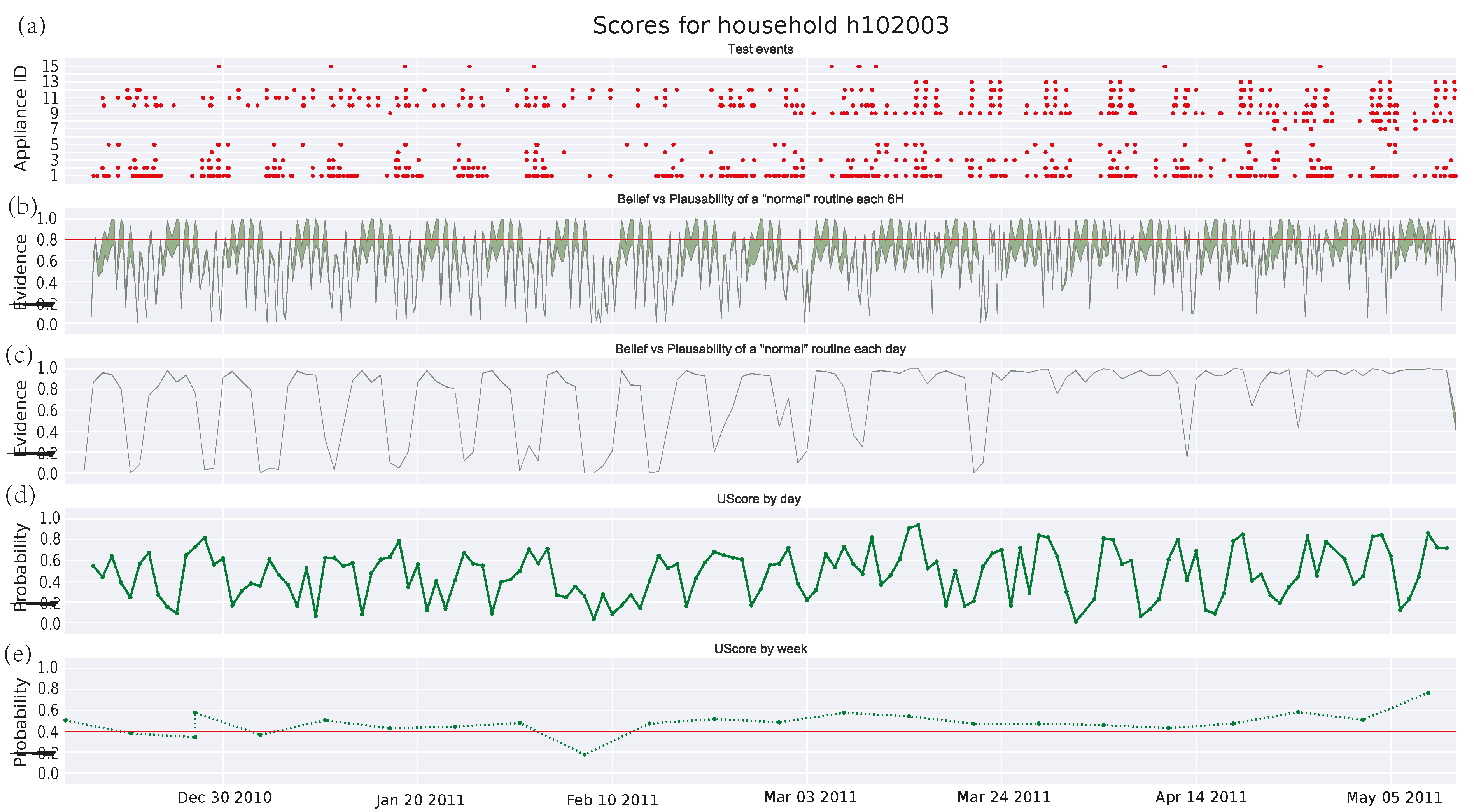
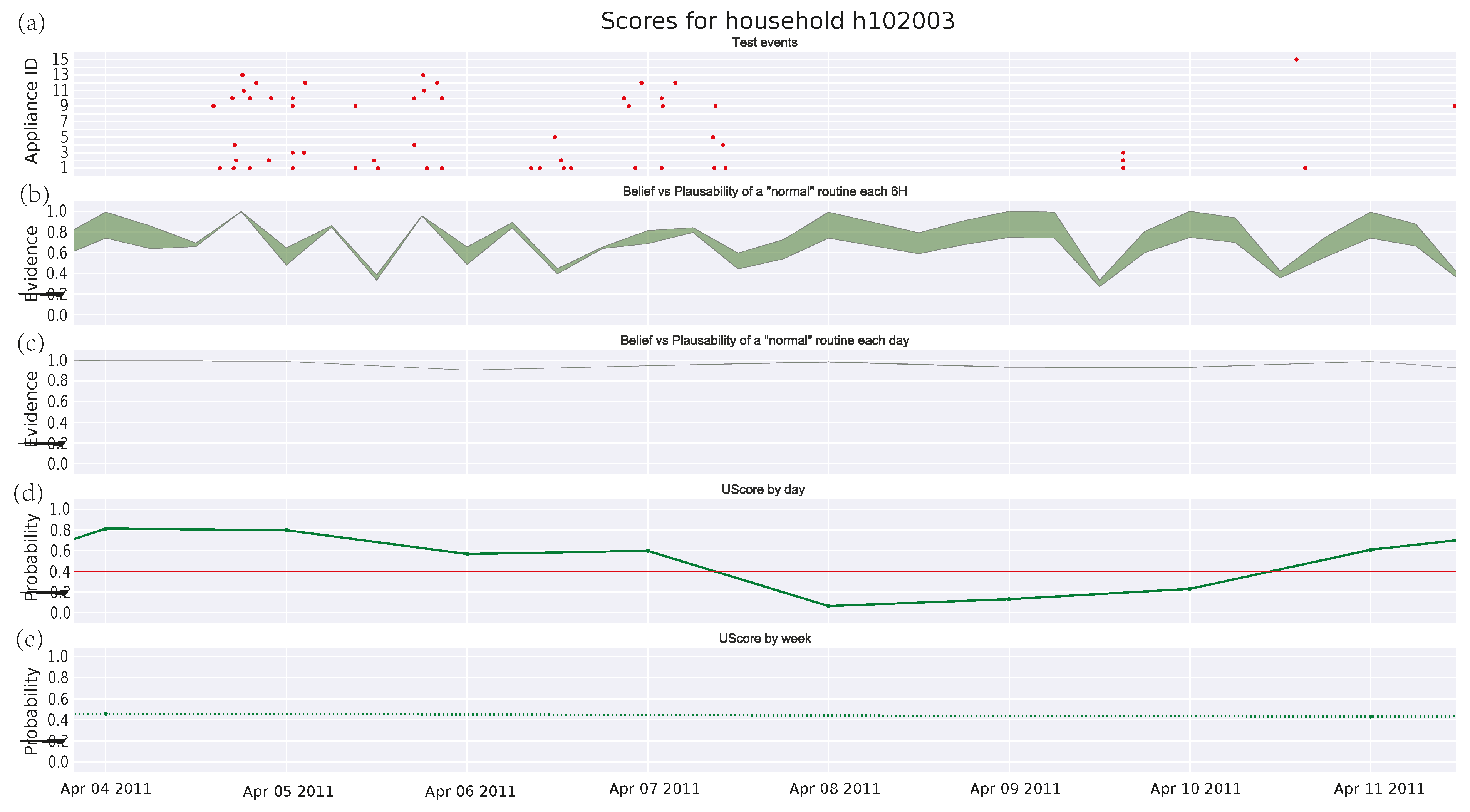
3.4.3. Single Pensioner Household No. 102003 in the HES Dataset
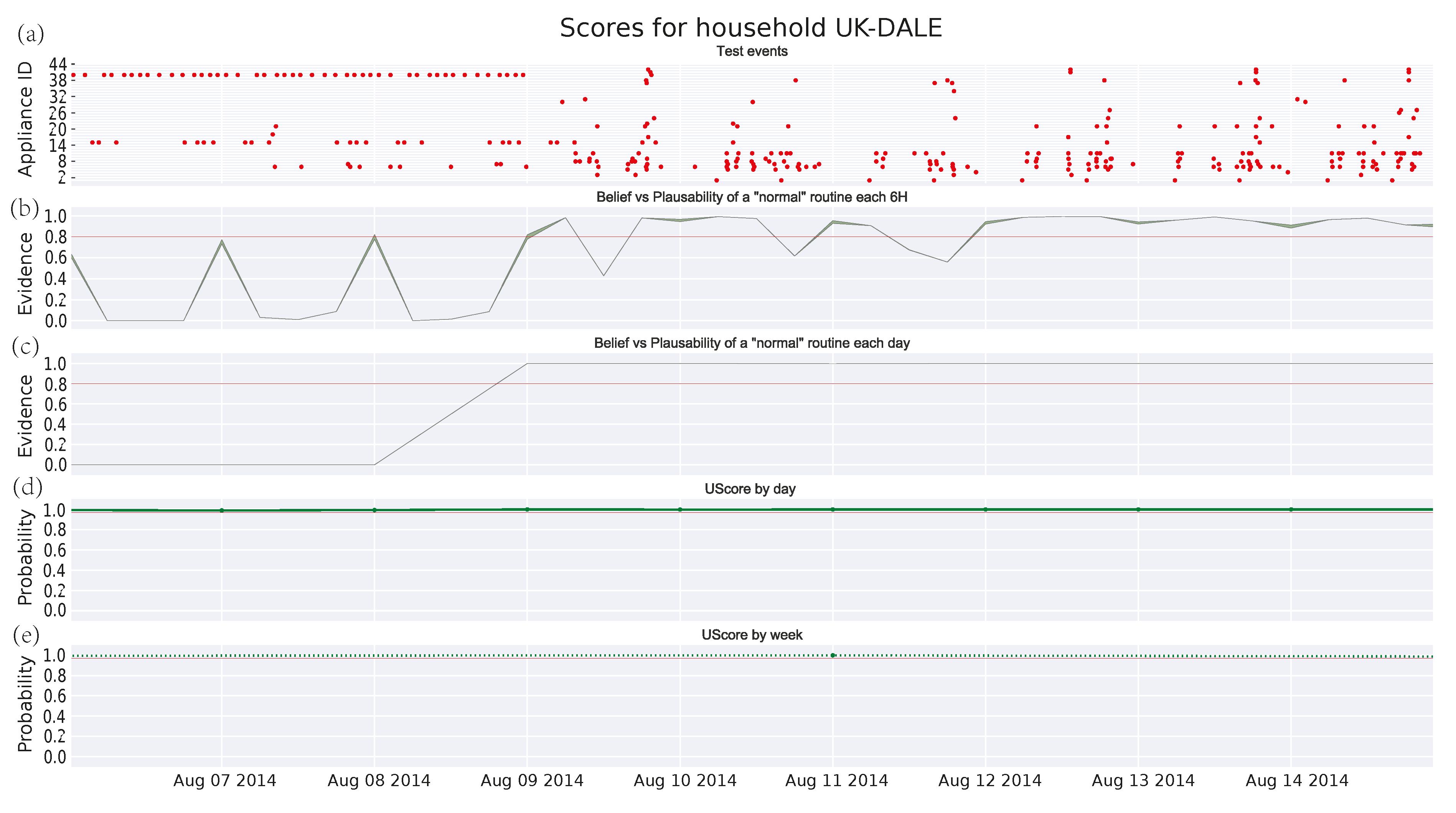
3.4.4. Family House in UKDALE Dataset
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Debes, C.; Merentitis, A.; Sukhanov, S.; Niessen, M.; Frangiadakis, N.; Bauer, A. Monitoring activities of daily living in smart homes. IEEE Signal Process. Mag. 2016, 33, 81–94. [Google Scholar] [CrossRef]
- Scanaill, C.N.; Carew, S.; Barralon, P.; Noury, N.; Lyons, D.; Lyons, G.M. A review of approaches to mobility telemonitoring of the elderly in their living environment. Ann. Biomed. Eng. 2006, 34, 547–563. [Google Scholar] [CrossRef] [PubMed]
- Ghamari, M.; Janko, B.; Sherratt, R.S.; Harwin, W.; Piechockic, R.; Soltanpur, C. A survey on wireless body area networks for ehealthcare systems in residential environments. Sensors 2016, 16, 831. [Google Scholar] [CrossRef] [PubMed]
- Patel, S.; Park, H.; Bonato, P.; Chan, L.; Rodgers, M. A review of wearable sensors and systems with application in rehabilitation. J. Neuroeng. Rehabil. 2012, 9, 21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lou, C.; Li, R.; Li, Z.; Liang, T.; Wei, Z.; Run, M.; Yan, X.; Liu, X. Flexible graphene electrodes for prolonged dynamic ECG monitoring. Sensors 2016, 16, 1833. [Google Scholar] [CrossRef] [PubMed]
- Katz, S.; Ford, A.B.; Moskowitz, R.W.; Jackson, B.A.; Jaffe, M.W. Studies of illness in the aged. The index of ADL: A standardized measure of biological and psychosocial function. J. Am. Med. Assoc. 1963, 185, 914–919. [Google Scholar] [CrossRef]
- LaPlante, M.P. The classic measure of disability in activities of daily living is biased by age but an expanded IADL/ADL measure is not. J. Gerontol. Ser. B Psychol. Sci. Soc. Sci. 2010, 65, 720–732. [Google Scholar] [CrossRef] [PubMed]
- Kautz, H.; Etzioni, O.; Fox, D.; Weld, D. Foundations of Assisted Cognition Systems; Technical Report; Department of Computer Science & Engineering, University of Washington: Seattle, WA, USA, 2003; pp. 1–25. [Google Scholar]
- Lim, J.; Jang, H.; Jang, J.; Park, S. Daily activity recognition system for the elderly using pressure sensors. In Proceedings of the 2008 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–24 August 2008; pp. 5188–5191.
- Moufawad El Achkar, C.; Lenoble-Hoskovec, C.; Paraschiv-Ionescu, A.; Major, K.; Büla, C.; Aminian, K. Physical behavior in older persons during daily life: Insights from instrumented shoes. Sensors 2016, 16, 1225. [Google Scholar] [CrossRef] [PubMed]
- Massot, B.; Noury, N.; Gehin, C.; McAdams, E. On designing an ubiquitous sensor network for health monitoring. In Proceedings of the 2013 IEEE 15th International Conference on e-Health Networking, Applications & Services (Healthcom), Lisbon, Portugal, 9–12 October 2013; pp. 310–314.
- Rashidi, P.; Cook, D.J.; Holder, L.B.; Schmitter-Edgecombe, M. Discovering activities to recognize and track in a smart environment. IEEE Trans. Knowl. Data Eng. 2011, 23, 527–539. [Google Scholar] [CrossRef] [PubMed]
- Kakde, A.; Gulhane, V. Real time composite user activity modelling using hybrid approach for recognition. In Proceedings of the 2015 IEEE International Conference on Electrical, Computer and Communication Technologies (ICECCT), Coimbatore, India, 5–7 March 2015; Volume 32248, pp. 1–6.
- Tapia, E.M.; Intille, S.S.; Larson, K. Activity recognition in the home using simple and ubiquitous sensors. Pervasive Comput. 2004, 3001, 158–175. [Google Scholar]
- Chen, B.; Fan, Z.; Cao, F. Activity recognition based on streaming sensor data for assisted living in smart homes. In Proceedings of the 2015 International Conference on Intelligent Environments (IE), Prague, Czech Republic, 15–17 July 2015; pp. 124–127.
- Hoque, E.; Stankovic, J. AALO: Activity recognition in smart homes using Active Learning in the presence of Overlapped activities. In Proceedings of the 2012 6th International Conference on Pervasive Computing Technologies for Healthcare (PervasiveHealth), San Diego, CA, USA, 21–24 May 2012; pp. 139–146.
- Oliver, E.H.N.; Garg, A. Layered representations for human activity recognition. In Proceedings of the 4th IEEE International Conference on Multimodal Interfaces, Pittsburgh, PA, USA, 14–16 October 2002; pp. 3–8.
- Hong, X.; Nugent, C.; Mulvenna, M.; McClean, S.; Scotney, B.; Devlin, S. Evidential fusion of sensor data for activity recognition in smart homes. Pervasive Mob. Comput. 2009, 5, 236–252. [Google Scholar] [CrossRef]
- Nugent, C.D.; Hong, X.; Hallberg, J.; Finlay, D.; Synnes, K. Assessing the impact of individual sensor reliability within smart living environments. In Proceedings of the IEEE International Conference on Automation Science and Engineering (CASE 2008), Washington, DC, USA, 23–26 August 2008; pp. 685–690.
- Noury, N.; Quach, K.A.; Berenguer, M.; Bouzi, M.J.; Teyssier, H. A feasibility study of using a smartphone to monitor mobility in elderly. In Proceedings of the 2012 IEEE 14th International Conference on e-Health Networking, Applications and Services (Healthcom), Beijing, China, 10–13 October 2012; pp. 423–426.
- Sprint, G.; Cook, D.; Fritz, R.; Schmitter-Edgecombe, M. Detecting health and behavior change by analyzing smart home sensor data. In Proceedings of the 2nd IEEE International Conference on Smart Computing (SMARTCOMP 2016), St. Louis, MO, USA, 18–20 May 2016; pp. 1–3.
- Dawadi, P.N.; Cook, D.J.; Schmitter-Edgecombe, M. Modeling patterns of activities using activity curves. Pervasive Mob. Comput. 2016, 28, 51–68. [Google Scholar] [CrossRef] [PubMed]
- Noury, N.; Berenguer, M.; Teyssier, H.; Bouzid, M.J.; Giordani, M. Building an index of activity of inhabitants from their activity on the residential electrical power line. IEEE Trans. Inf. Technol. Biomed. 2011, 15, 758–766. [Google Scholar] [CrossRef] [PubMed]
- Noury, N.; Quach, K.A.; Berenguer, M.; Teyssier, H.; Bouzid, M.J.; Goldstein, L.; Giordani, M. Remote follow up of health through the monitoring of electrical activities on the residential power line—Preliminary results of an experimentation. In Proceedings of the 11th International Conference on e-Health Networking, Applications and Services (Healthcom 2009), Sydney, Australia, 16–18 December 2009; pp. 9–13.
- Zhang, X.; Kato, T.; Matsuyama, T. Learning a context-aware personal model of appliance usage patterns in smart home. In Proceedings of the 2014 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Kuala Lumpur, Malaysia, 20–23 May 2014; pp. 73–78.
- Bonfigli, R.; Squartini, S.; Fagiani, M.; Piazza, F. Unsupervised algorithms for non-intrusive load monitoring: An up-to-date overview. In Proceedings of the 2015 IEEE 15th International Conference on Environment and Electrical Engineering (EEEIC), Rome, Italy, 10–13 June 2015; pp. 1175–1180.
- Zoha, A.; Gluhak, A.; Imran, M.A.; Rajasegarar, S. Non-intrusive load monitoring approaches for disaggregated energy sensing: A survey. Sensors 2012, 12, 16838–16866. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parson, O.; Ghosh, S.; Weal, M.; Rogers, A. An unsupervised training method for non-intrusive appliance load monitoring. Artif. Intell. 2014, 217, 1–19. [Google Scholar] [CrossRef]
- Kelly, J.; Knottenbelt, W. Neural NILM. In Proceedings of the 2nd ACM International Conference on Embedded Systems for Energy-Efficient Built Environments, Seoul, Korea, 4–5 November 2015; pp. 55–64.
- Anderson, K.D.; Berges, M.E.; Ocneanu, A.; Benitez, D.; Moura, J.M.F. Event detection for non intrusive load monitoring. In Proceedings of the 38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 3312–3317.
- De Baets, L.; Ruyssinck, J.; Deschrijver, D.; Dhaene, T. Event detection in NILM using cepstrum smoothing. In Proceedings of the 3rd International Workshop on Non-Intrusive Load Monitoring, Vancouver, BC, Canada, 14–15 May 2016.
- Wild, B.; Barsim, K.S.; Yang, B. A new unsupervised event detector for non-intrusive load monitoring. In Proceedings of the 2015 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Orlando, FL, USA, 14–16 December 2015; pp. 73–77.
- Gao, J.; Kara, E.C.; Giri, S.; Berges, M. A feasibility study of automated plug-load identification from high-frequency measurements. In Proceedings of the 2015 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Orlando, FL, USA, 14–16 December 2015; pp. 220–224.
- Hassan, T.; Javed, F.; Arshad, N. An empirical investigation of V-I trajectory based load signatures for non-intrusive load monitoring. IEEE Trans. Smart Grid 2014, 5, 870–878. [Google Scholar] [CrossRef]
- Song, H.; Kalogridis, G.; Fan, Z. Short paper: Time-dependent power load disaggregation with applications to daily activity monitoring. In Proceedings of the 2014 IEEE World Forum on Internet of Things (WF-IoT), Seoul, Korea, 6–8 March 2014; pp. 183–184.
- Alcalá, J.; Parson, O.; Rogers, A. Detecting anomalies in activities of daily living of elderly residents via energy disaggregation and cox processes. In Proceedings of the 2nd ACM International Conference on Embedded Systems for Energy-Efficient Built Environments, Seoul, Korea, 4–5 November 2015.
- Fleury, A.; Vacher, M.; Noury, N. SVM-based multimodal classification of activities of daily living in health smart homes: Sensors, algorithms, and first experimental results. IEEE Trans. Inf. Technol. Biomed. 2010, 14, 274–283. [Google Scholar] [CrossRef] [PubMed]
- Nikamalfard, H.; Zheng, H.; Wang, H.; Jeffers, P.; Mulvenna, M.; McCullagh, P.; Martin, S.; Wallace, J.; Augusto, J.; Carswell, W.; et al. Knowledge discovery from activity monitoring to support independent living of people with early dementia. In Proceedings of the 2012 IEEE-EMBS International Conference on Biomedical and Health Informatics (BHI), Hong Kong, China, 5–7 January 2012; Volume 25, pp. 910–913.
- Alcalá, J.; Ureña, J.; Hernández, Á. Activity supervision tool using non-intrusive load monitoring systems. In Proceedings of the IEEE 20th Conference on Emerging Technologies & Factory Automation (ETFA), Luxembourg, 8–11 September 2015.
- NILM-wiki. NILM datasets. Available online: http://wiki.nilm.eu/index.php?title=NILM_datasets (accesed on 1 February 2017).
- Batra, N.; Kelly, J.; Parson, O.; Dutta, H.; Knottenbelt, W.; Rogers, A.; Singh, A.; Srivastava, M. NILMTK: An open source toolkit for non-intrusive load monitoring categories and subject descriptors. In Proceedings of the 5th International Conference on Future Energy Systems (ACM e-Energy), Cambridge, UK, 11–13 June 2014; pp. 1–4.
- Beckel, C.; Kleiminger, W.; Cicchetti, R.; Staake, T.; Santini, S. The ECO data set and the performance of non-intrusive load monitoring algorithms. In Proceedings of the 1st ACM Conference on Embedded Systems for Energy-Efficient Buildings, Memphis, TN, USA, 3–6 November 2014; pp. 80–89.
- NILM-wiki. Companies Offering NILM Products and Services. Available online: http://wiki.nilm.eu/index.php?title=Companies_offering_NILM_products_and_services (accesed on 1 February 2017).
- Rakowsky, U.K. Fundamentals of the Dempster-Shafer theory and its applications to reliability modeling. Int. J. Reliab. Qual. Saf. Eng. 2007, 14, 579–601. [Google Scholar] [CrossRef]
- Zimmermann, J.-P.; Evans, M.; Lineham, T.; Griggs, J.; Surveys, G.; Harding, L.; King, N.; Roberts, P. Household Electricity Survey: A Study of Domestic Electrical Product Usage; Intertek: London, UK, 2012; p. 600. [Google Scholar]
- Kelly, J.; Knottenbelt, W. The UK-DALE dataset, domestic appliance-level electricity demand and whole-house demand from five UK homes. Sci. Data 2015, 2, 150007. [Google Scholar] [CrossRef] [PubMed]
- Cook, D.J.; Crandall, A.S.; Thomas, B.L.; Krishnan, N.C. CASAS: A smart home in a box. Computer 2013, 46, 62–69. [Google Scholar] [CrossRef] [PubMed]


| BBAs for X in | BBAs for Y in | |
|---|---|---|
| 0.89 | 0.89 | 0.92 | |
| 0.08 | 0.08 | 0.1 | |
| 0.02 | 1 | 1 |
| Appliance Label | ||||
|---|---|---|---|---|
| Appliance ID | Household no. 101017 | Household no. 103034 | Household no. 102003 | Family House |
| 1 | Cooker | Kettle | Cooker | Boiler |
| 2 | Kettle | Microwave | Kettle | Solar thermal station |
| 3 | Microwave | Toaster | Microwave | Washer drier |
| 4 | Toaster | Cooker extractor fan | Toaster | Dish washer |
| 5 | Washing machine | Cooker extractor fan | Television | |
| 6 | Tumble dryer | Washing machine | Light 1 | |
| 7 | Washing Machine | DVD player | TV-LCD | HTPC |
| 8 | Set Top Box | TV-CRT | TV-LCD 2 | Kettle |
| 9 | TV-LCD | VCR | Computer desktop | Toaster |
| 10 | Laptop | Lamp 1 | Computer monitor | Fridge freezer |
| 11 | Lamp 1 | Lamp 2 | Printer inkjet | Microwave |
| 12 | Lamp 2 | Lamp 3 | Lamp 1 | Computer monitor |
| 13 | Lamp 4 | Lamp 2 | Breadmaker | |
| 14 | Vacuum cleaner | Lamp 3 | Audio amplifier | |
| 15 | TV-LCD | Vacuum cleaner | Lamp 4 | Light 2 |
| 16 | Lamp 5 | Soldering iron | ||
| 17 | Ethernet switch | |||
| 18 | Vaccuum cleaner | Vaccum cleaner | ||
| 19 | Light 3 | |||
| 20 | Light 4 | |||
| 21 | Light 5 | |||
| 22 | Light 6 | |||
| 23 | Active subwoofer | |||
| 24 | Light 7 | |||
| 25 | Radio | |||
| 26 | Light 8 | |||
| 27 | Phone charger | |||
| 28 | Light 9 | |||
| 29 | Phone charger 2 | |||
| 30 | Light 10 | |||
| 31 | Coffee maker | |||
| 32 | Radio 2 | |||
| 33 | Phone charger 3 | |||
| 34 | Hair dryer | |||
| 35 | Hair straighteners | |||
| 36 | Clothes iron | |||
| 37 | Oven | |||
| 38 | Light 11 | |||
| 39 | Baby monitor | |||
| 40 | Light 12 | |||
| 41 | Light 13 | |||
| 42 | Computer desktop | |||
| 43 | Fan | |||
| 44 | Printer | |||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alcalá, J.M.; Ureña, J.; Hernández, Á.; Gualda, D. Assessing Human Activity in Elderly People Using Non-Intrusive Load Monitoring. Sensors 2017, 17, 351. https://doi.org/10.3390/s17020351
Alcalá JM, Ureña J, Hernández Á, Gualda D. Assessing Human Activity in Elderly People Using Non-Intrusive Load Monitoring. Sensors. 2017; 17(2):351. https://doi.org/10.3390/s17020351
Chicago/Turabian StyleAlcalá, José M., Jesús Ureña, Álvaro Hernández, and David Gualda. 2017. "Assessing Human Activity in Elderly People Using Non-Intrusive Load Monitoring" Sensors 17, no. 2: 351. https://doi.org/10.3390/s17020351