Testing of the 4SM Method in the Gulf of California Suggests Field Data Are not Needed to Derive Satellite Bathymetry
Abstract
:1. Introduction
2. Materials and Methods
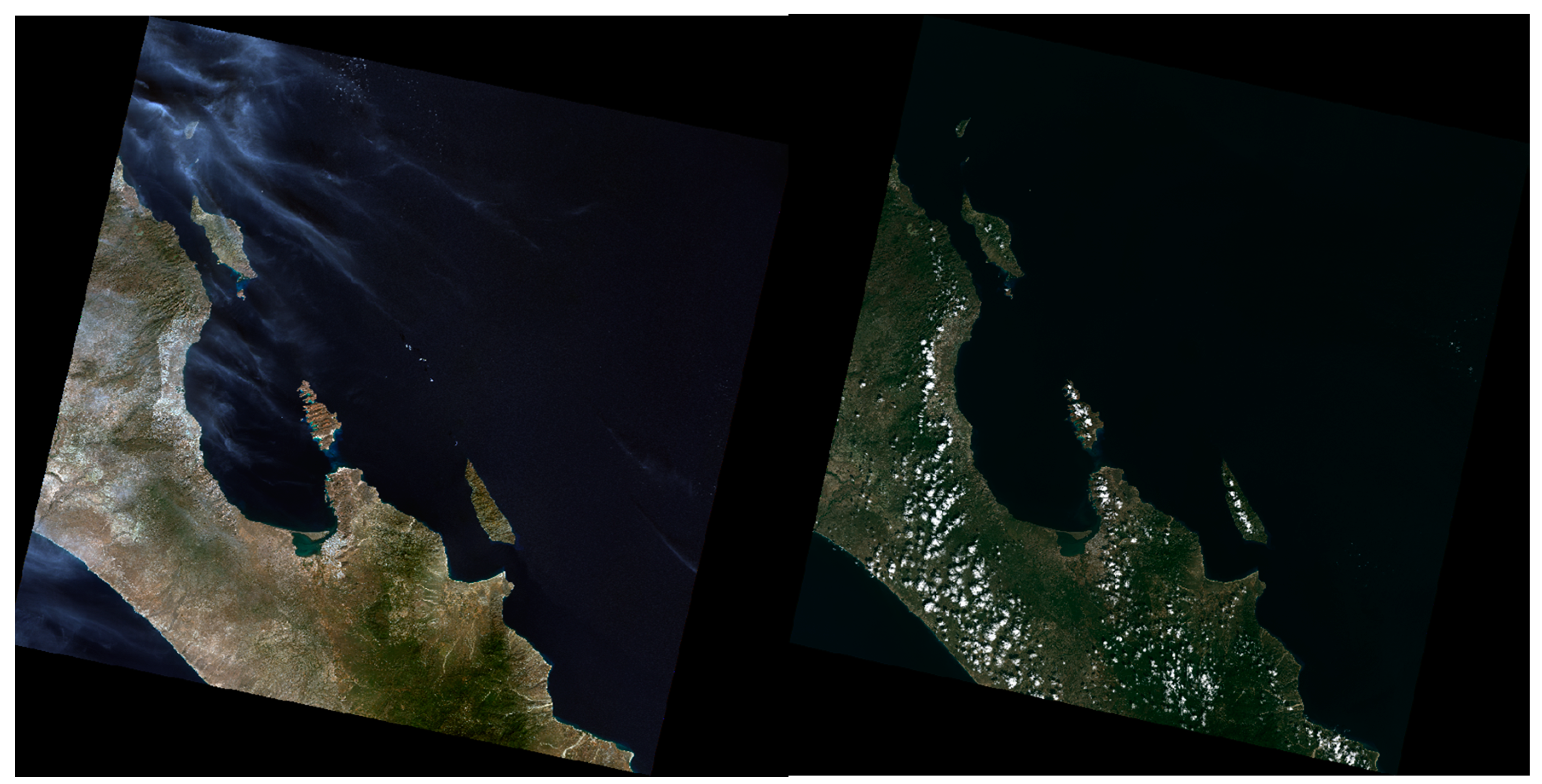
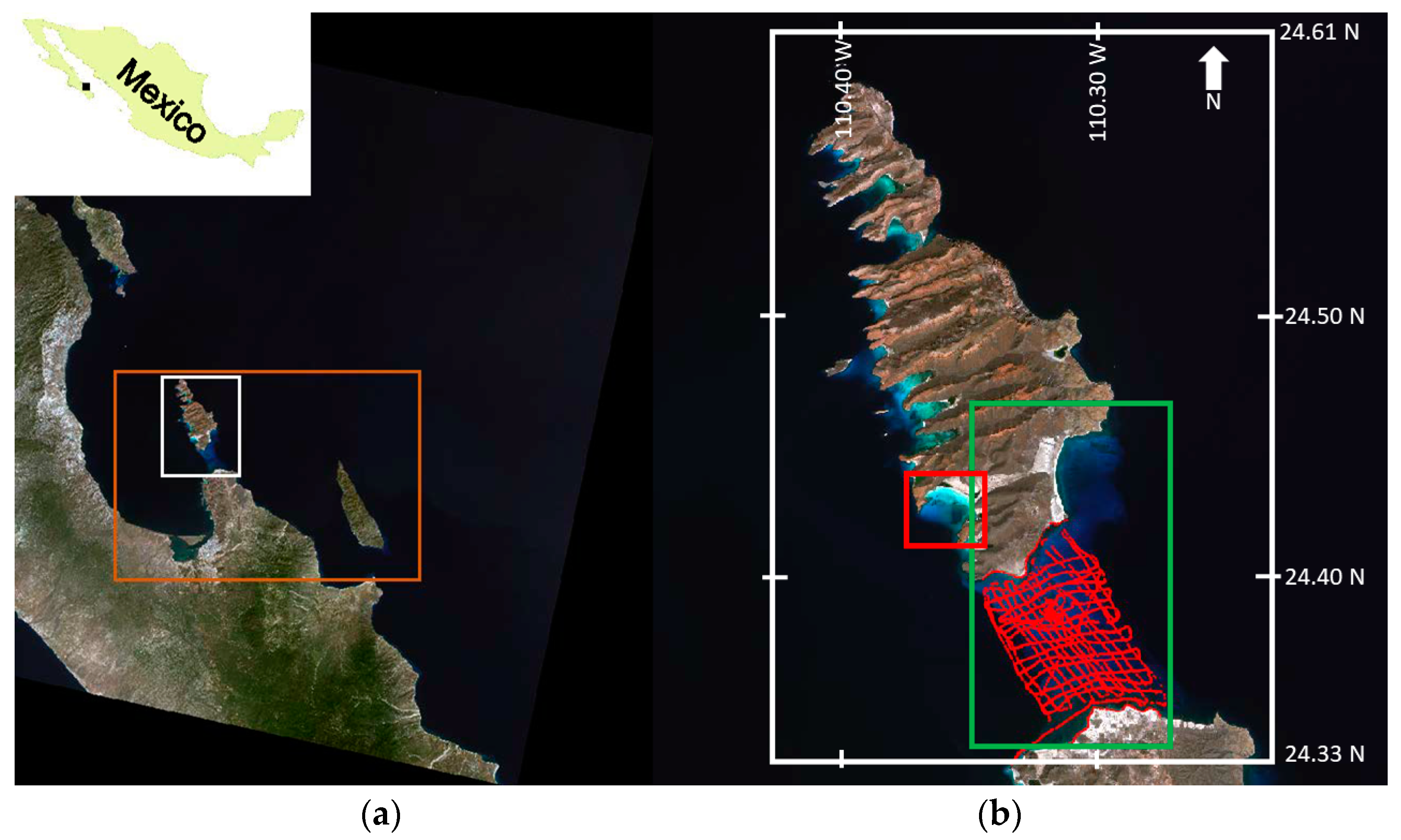
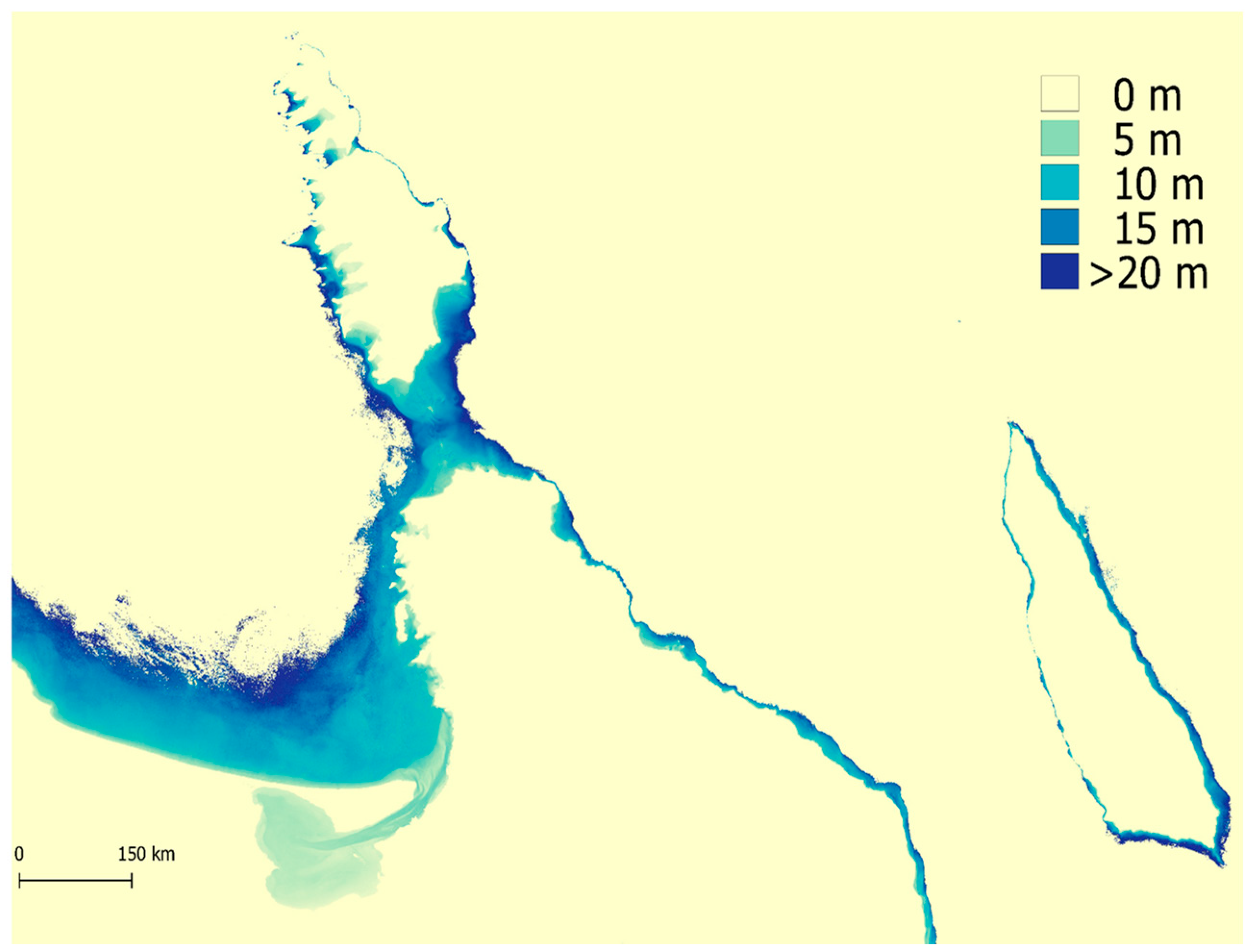
2.1. Study Area
2.2. Radiative Transfer Equation
2.3. Image Resources Preparation
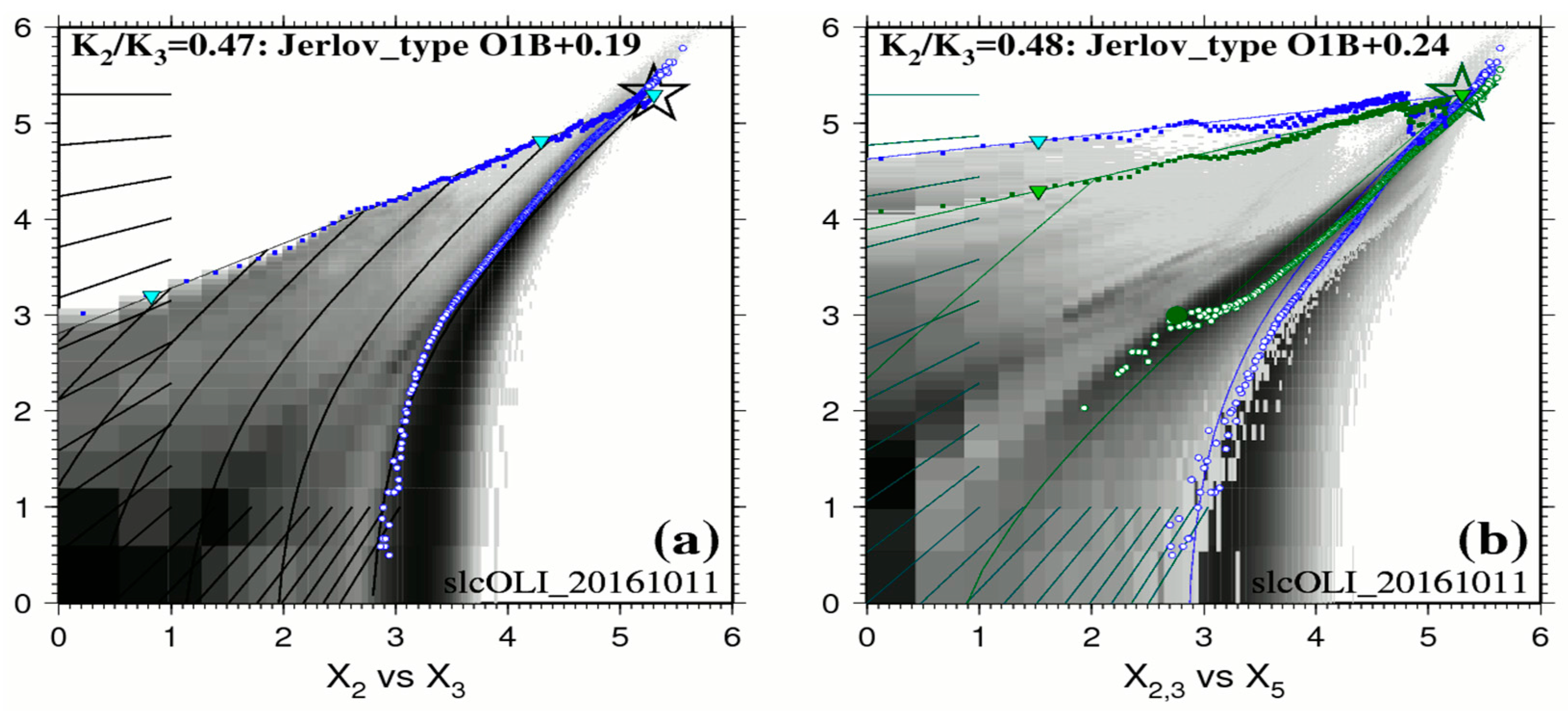
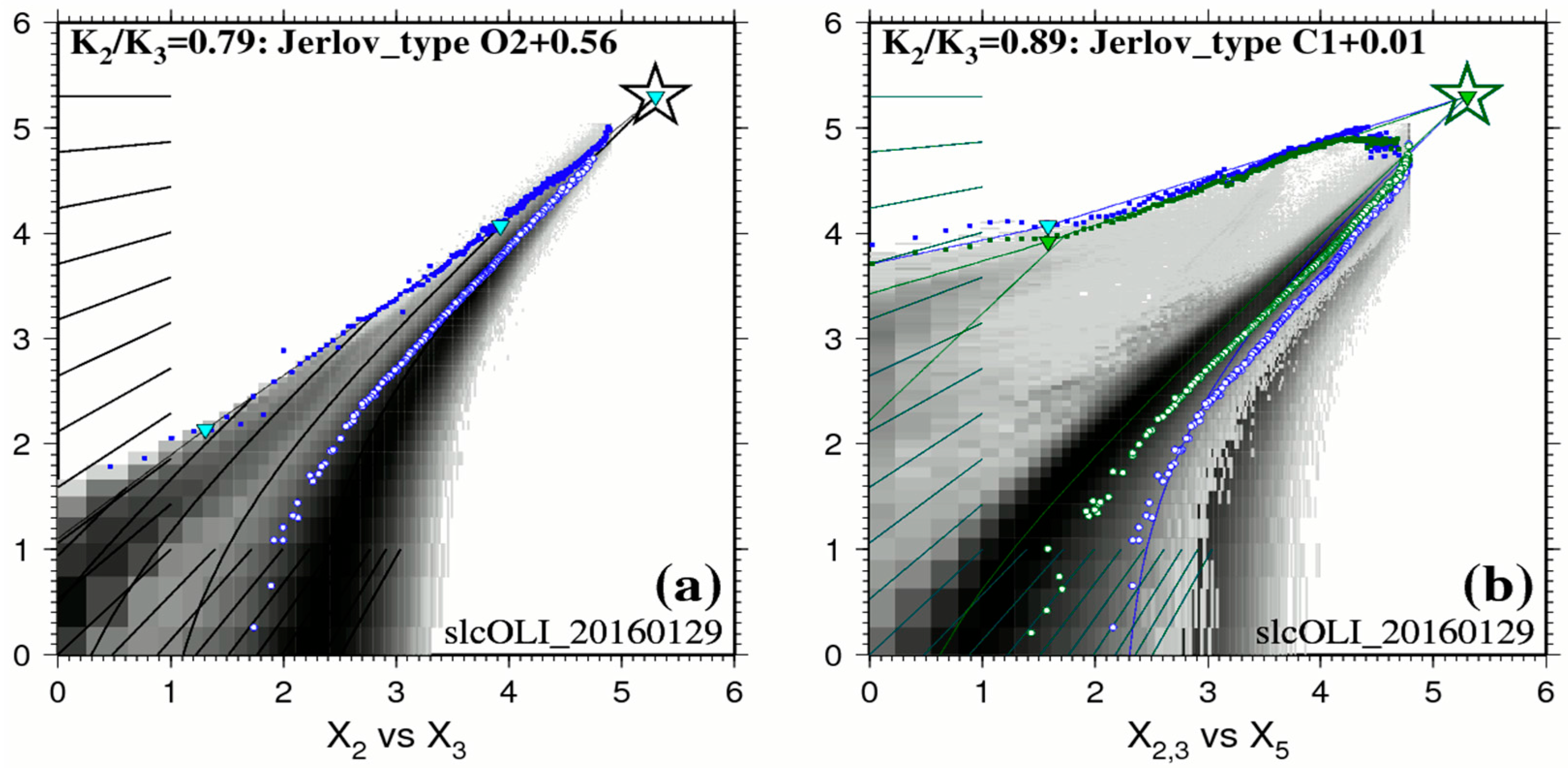
2.4. Optical Calibration of the Simplified RTE in 4SM
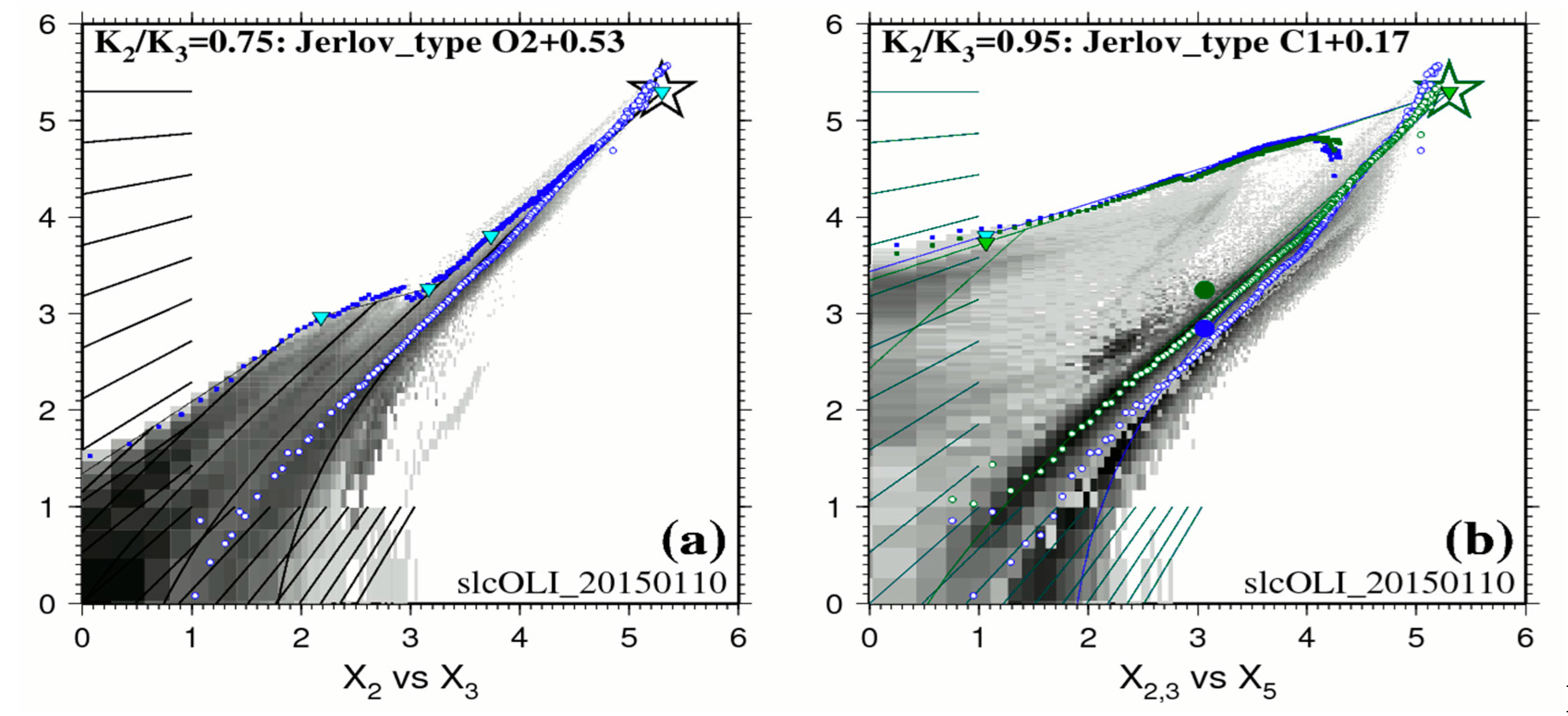
- 0–5 m depth range: on that day, the BPL pixels in Figure 2a clearly display along a straight line over the 0–5 m depth range for the pair Blue/Green. The ratio Kblue/Kgreen for this surficial layer is estimated at 0.95; this denotes a water type C1 + 0.17 of Jerlov. The BPL pixels in Figure 2b display along two straight lines for the pairs Blue/Red and Green/Red; these two straight lines have virtually the same slope. Diffuse attenuation coefficients in units of m−1 are estimated at Kblue = 0.272, Kgreen = 0.285, and Kred = 0.774. Please note that 0.272/0.285 = 0.95;
- 5–10 m depth range: Figure 2a seems to exhibit a progressive change in water quality over the 5–10 m depth range;
- 10–25 m depth range: on that day, the BPL pixels in Figure 2a clearly display along a straight line over the 10–25 m depth range. The ratio Kblue/Kgreen for this deeper layer is estimated at 0.75; this denotes a water type OII + 0.53 of Jerlov. Diffuse attenuation coefficients in units of m−1 are estimated at Kblue = 0.173, Kgreen = 0.232.
- In case of locally increased attenuation coefficient K (phytoplankton), retrieved depth would be under-estimated accordingly, unless a stratified waters model is specified as shown in Figure 2 in the 0–5 m depth range;
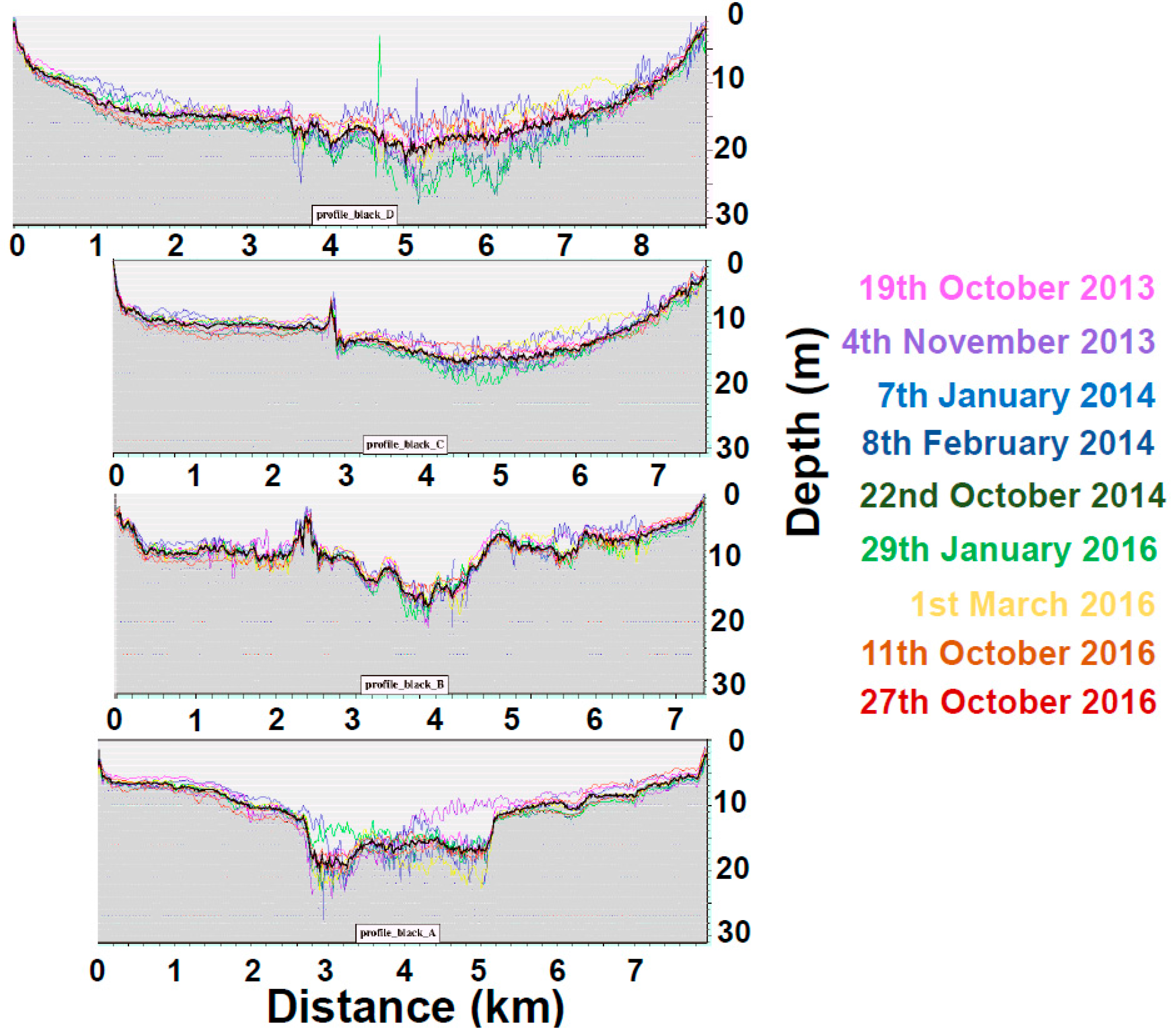
- In case of locally increased sediment turbidity (sediment resuspension), water leaving reflectance would be increased accordingly, therefore retrieved depth would be under-estimated, like shown between 4 and 5 km on Profile A in Figure 3.
2.5. Depth Retrieval in 4SM
2.6. Combining Depths in 4SM
2.7. Groundtruthed DTM
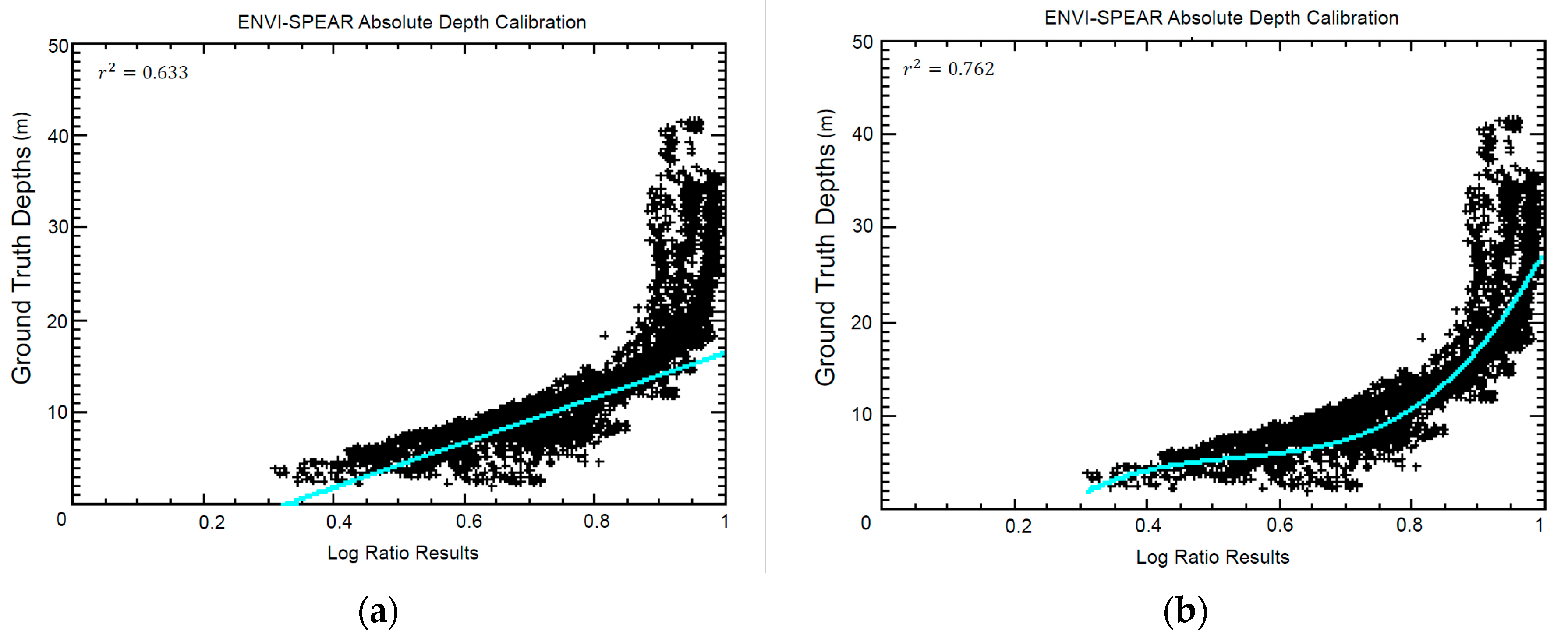
2.8. Depth Retrieval in ENVI-SPEAR Tool
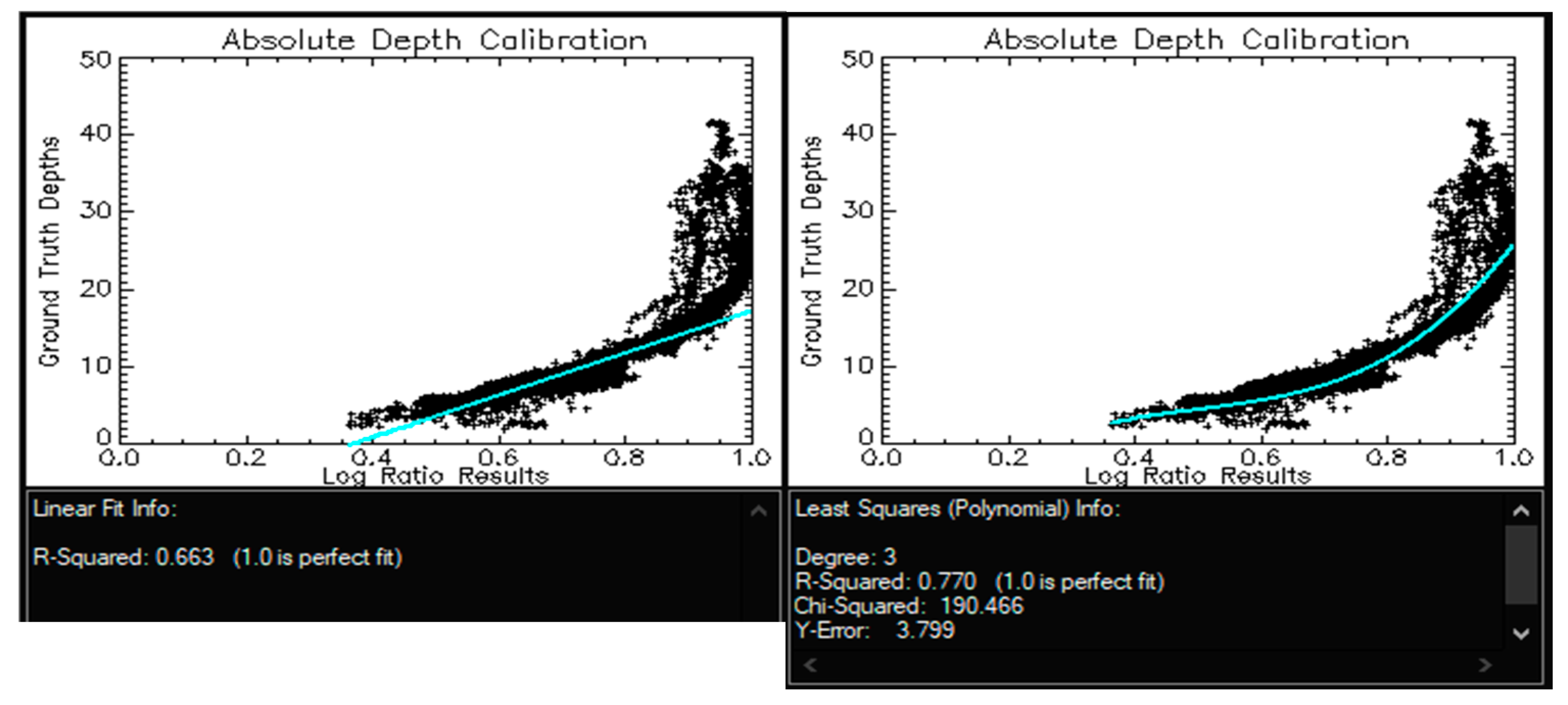
2.9. Groundtruthing Regressions and Comparisons
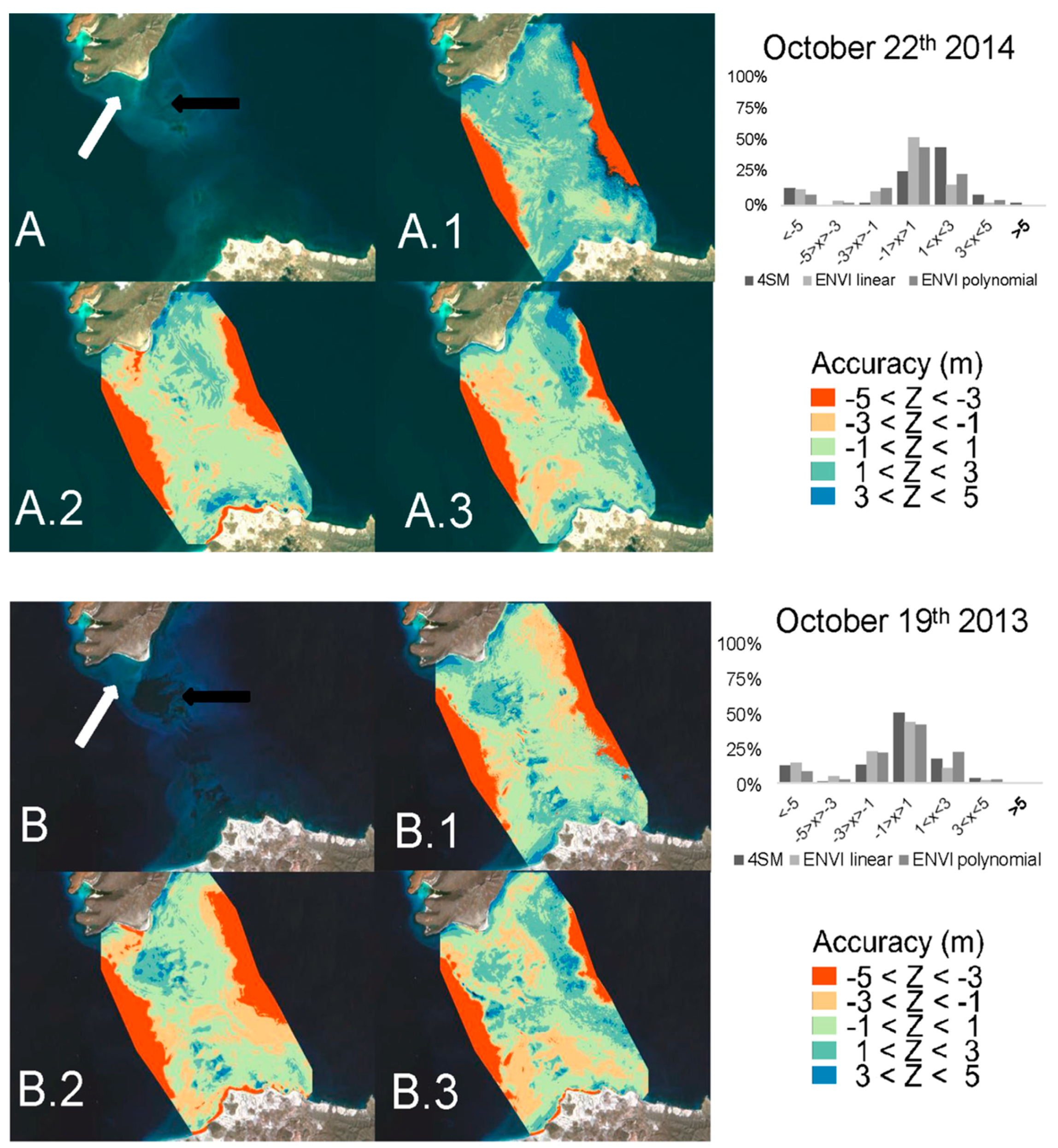
3. Results
3.1. Seatruth Regressions
3.2. Accuracy Assessment
3.3. Depth Residuals
4. Discussion
4.1. San Lorenzo Channel’s Conditions
4.2. Models Comparison
4.3. The 4SM Method
5. Conclusions
- 4SM is independent on field data to achieve the optical calibration;
- its accuracy is equally valid, and in some case better, compared to the accepted and widely used Stumpf’s algorithm;
- it provides a priori important insight on the optical properties of the water column (spectral K, i.e., water quality), and also on the hydrological conditions;
- it uses all bands with significant bottom detection and delivers computed depths, and water column corrected spectral bottom reflectance;
- it provides all valuable information that allows to explore and monitor large coastal areas in a more efficient and cheaper way in terms of resources and time.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A


Appendix B
Appendix C
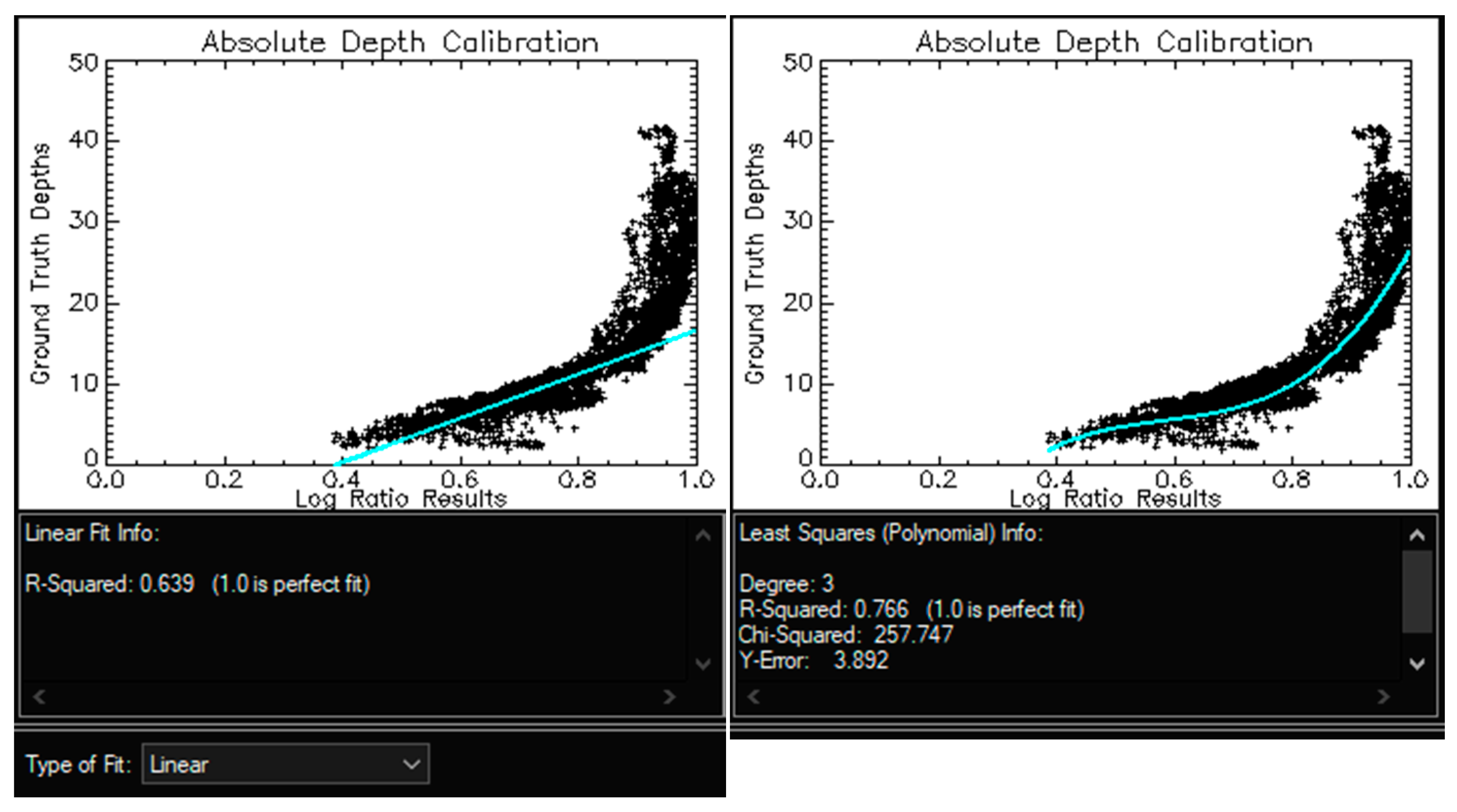
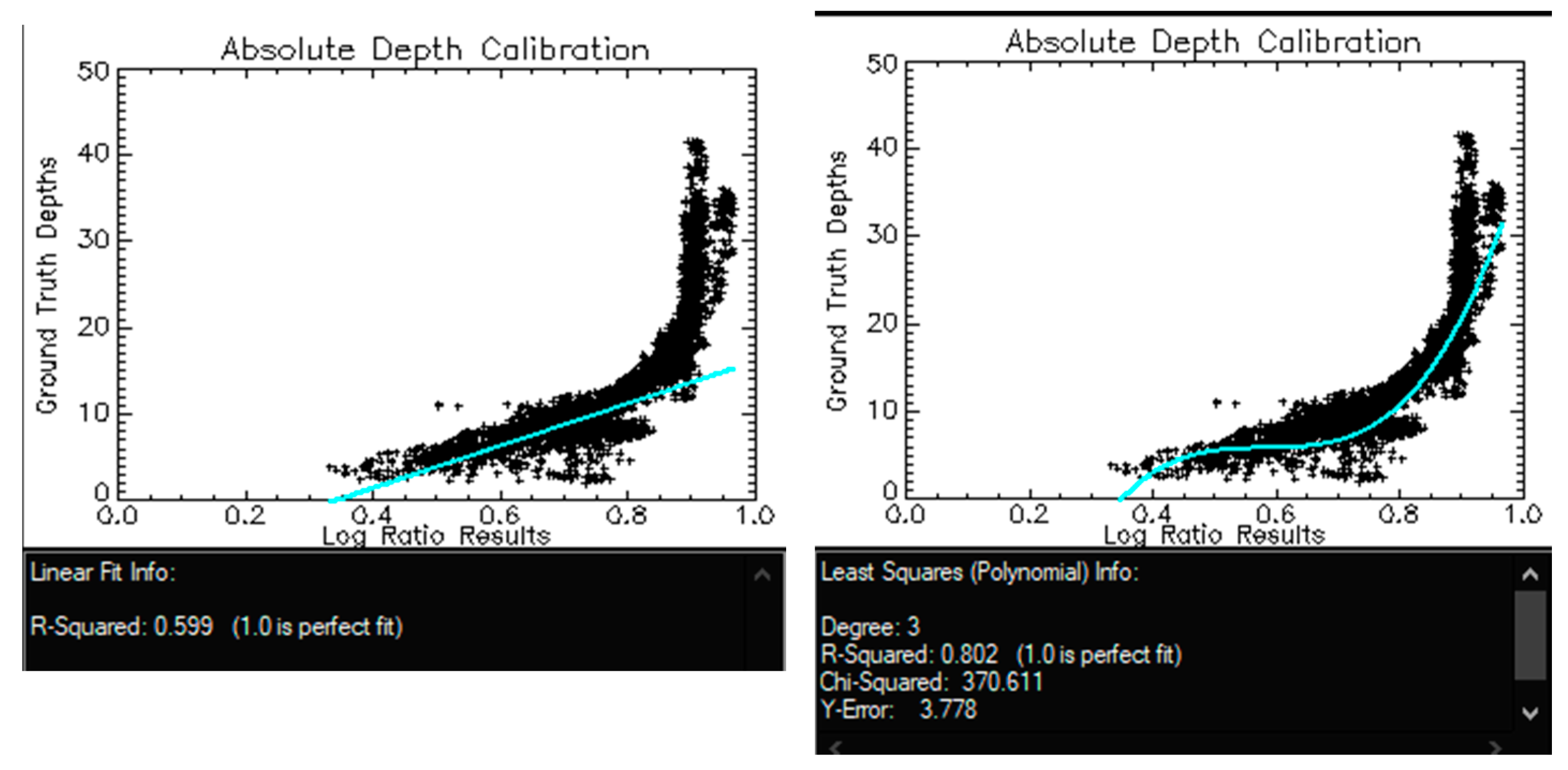
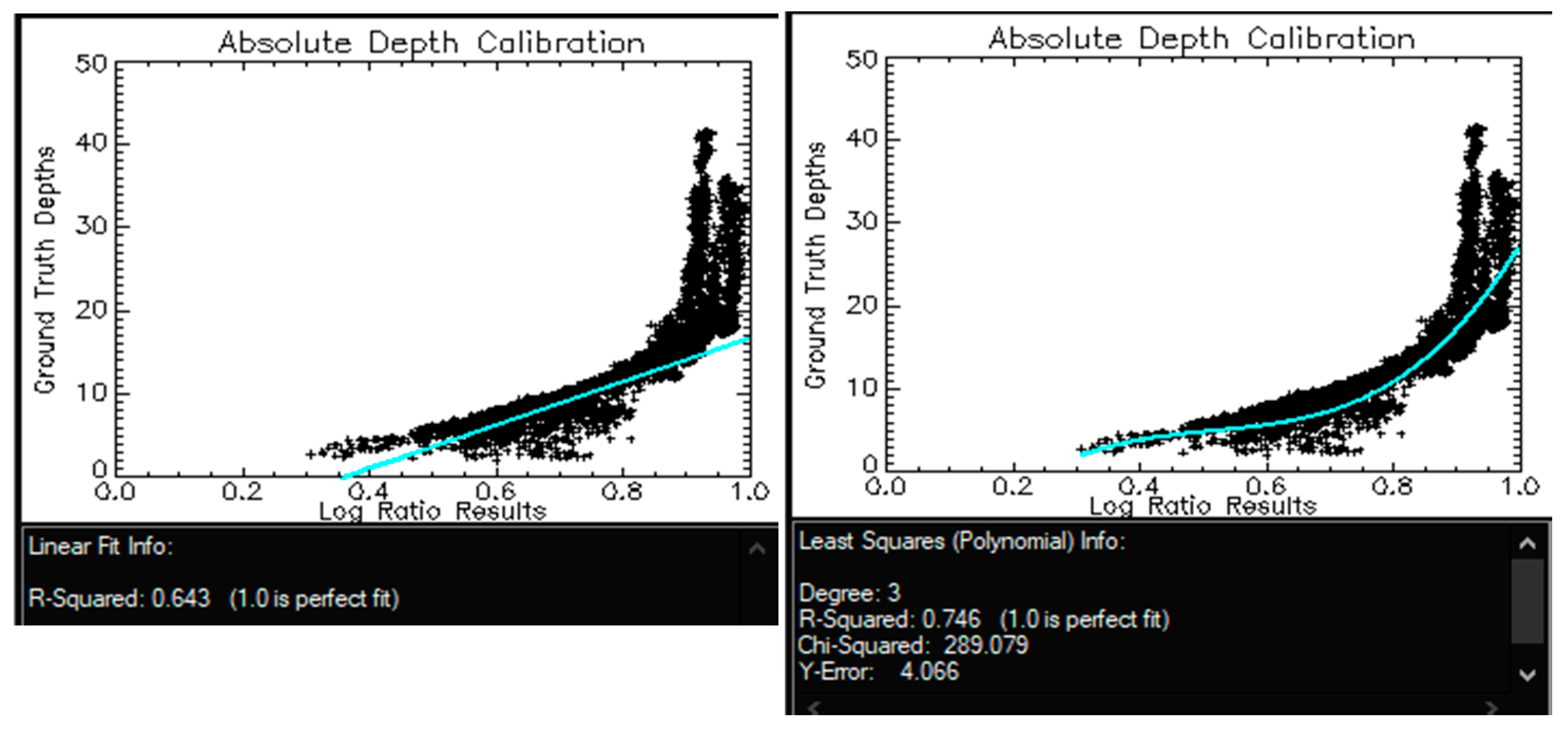
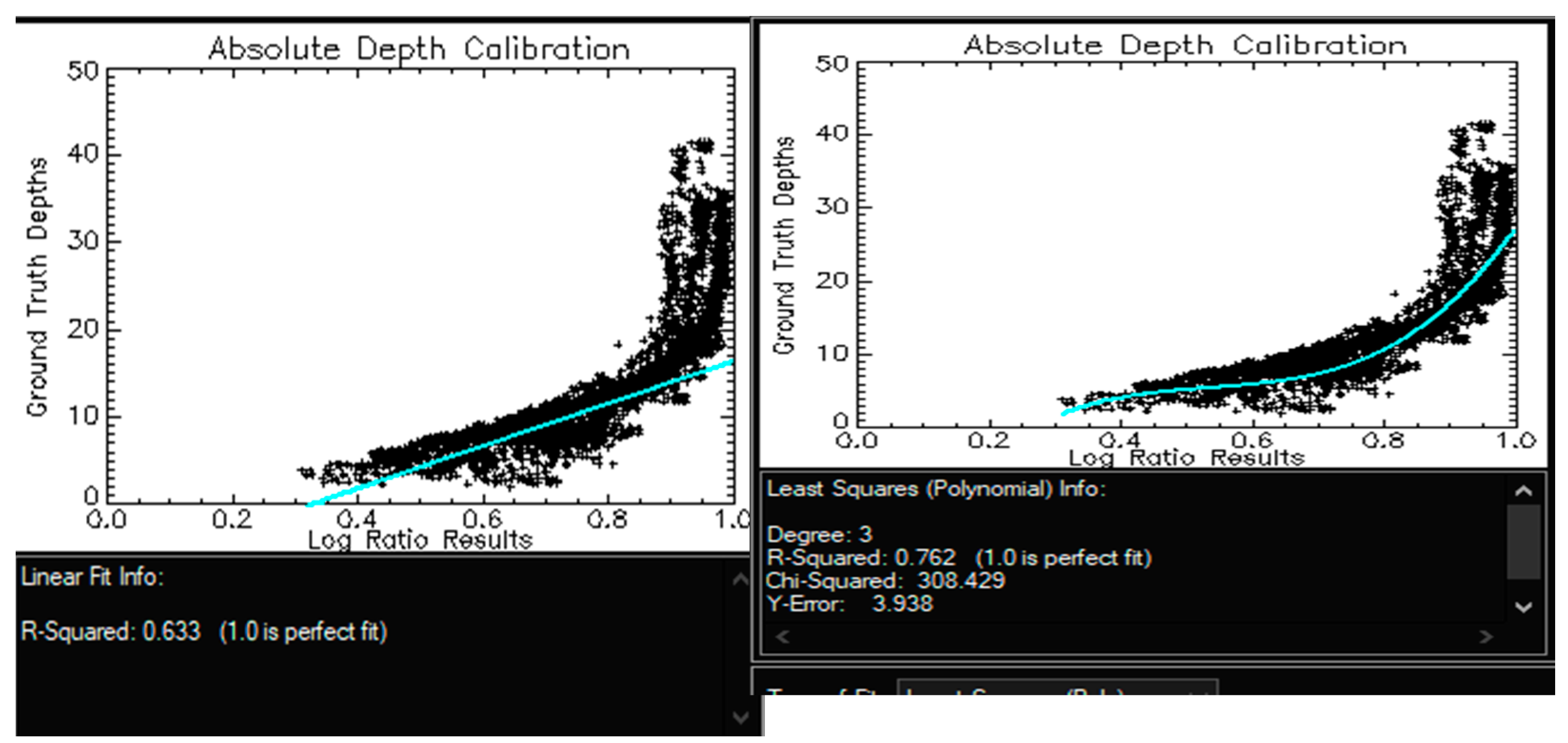
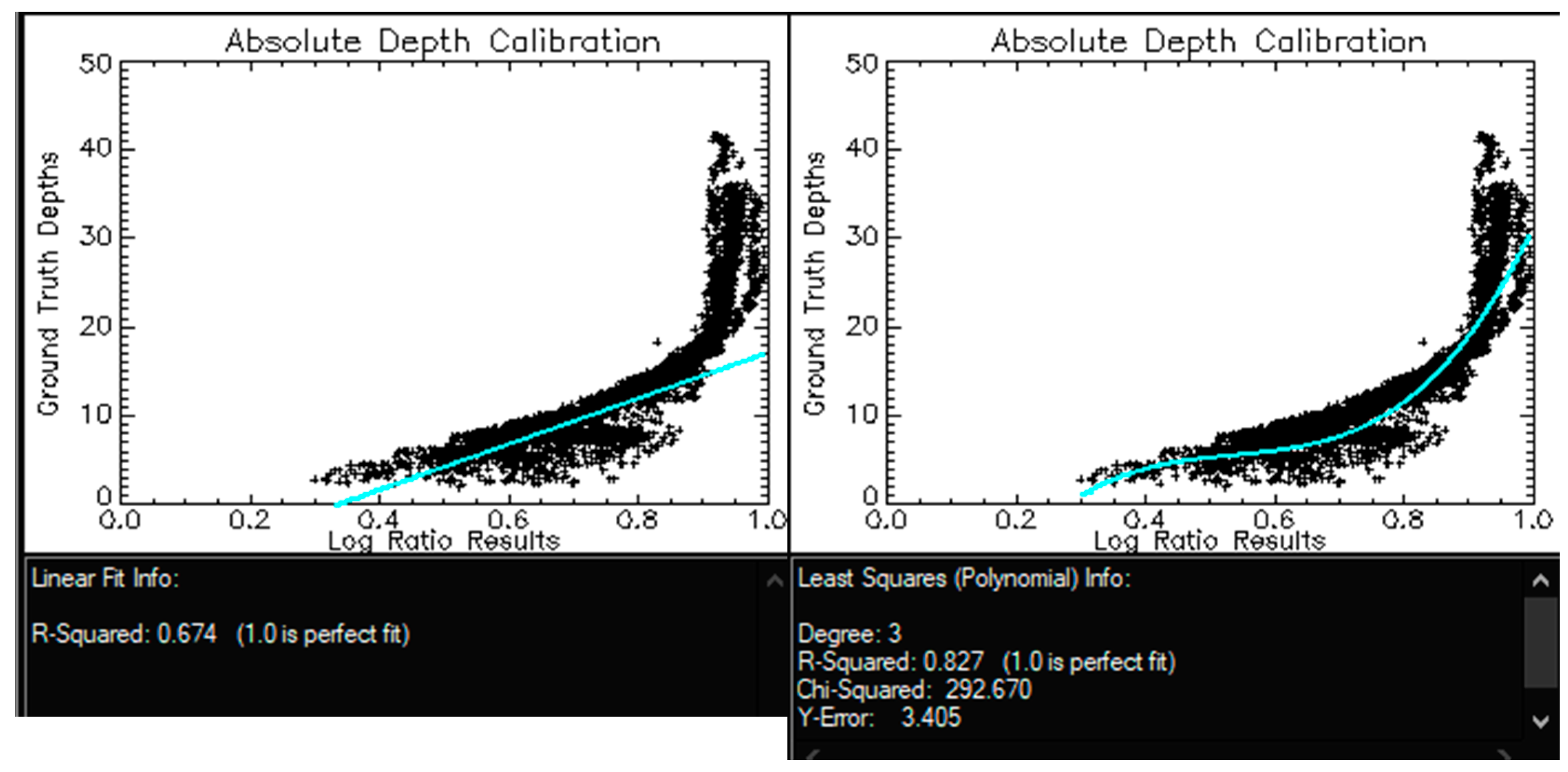
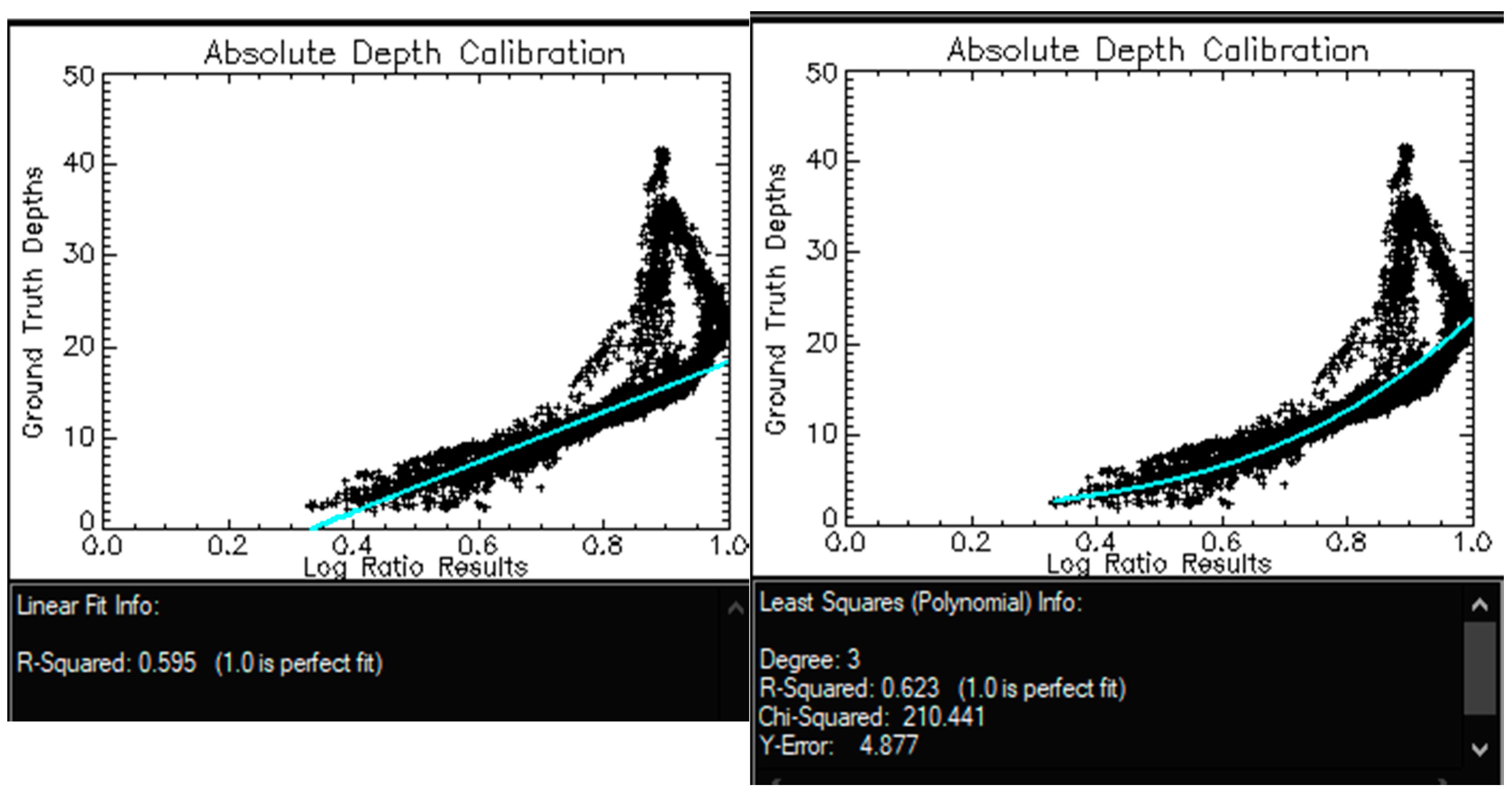
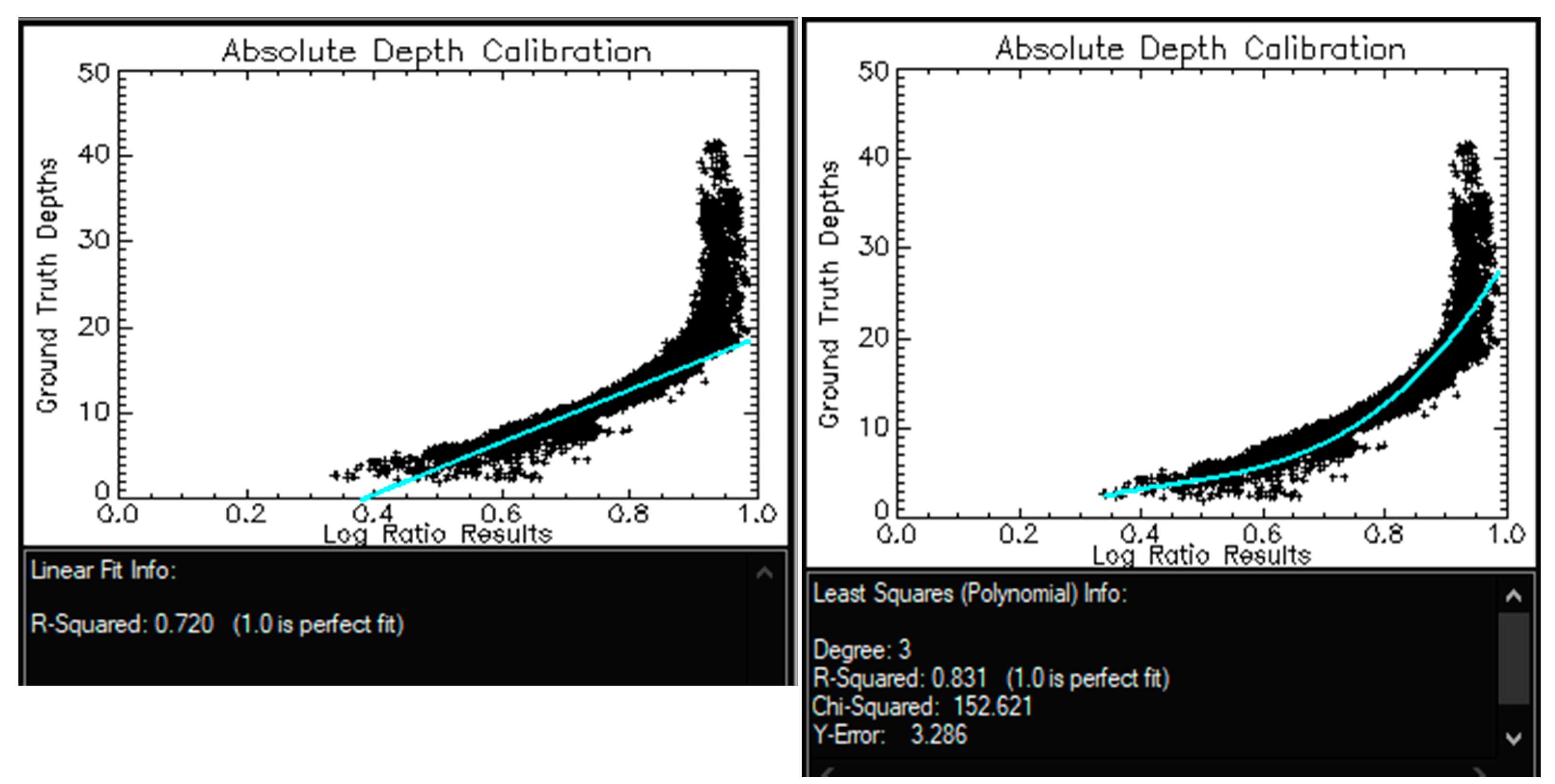
Appendix D

References
- Dierssen, H.M.; Thenberge, A.E., Jr. Bathymetry: Assessing methods. Encycl. Nat. Resour. 2014, 1–8. [Google Scholar] [CrossRef]
- Loveland, T.R.; Irons, J.R. Landsat 8: The plans, the reality, and the legacy. Remote Sens. Environ. 2016, 185, 1–6. [Google Scholar] [CrossRef]
- Clark, R.K.; Fay, T.H.; Walker, C.L. Bathymetry calculations with Landsat 4 TM imagery under a generalized ratio assumption. Appl. Opt. 1987, 26, 4036. [Google Scholar] [CrossRef] [PubMed]
- Mumby, P.J.; Green, E.P.; Edwards, A.J.; Clark, C.D. Coral reef habitat-mapping: How much detail can remote sensing provide? Mar. Biol. 1997, 130, 193–202. [Google Scholar] [CrossRef]
- Liceaga-Correa, M.A.; Euan-Avila, J.I. Assessment of coral reef bathymetric mapping using visible Landsat Thematic Mapper data. Int. J. Remote Sens. 2002, 23, 3–14. [Google Scholar] [CrossRef]
- Gao, J. Bathymetric mapping by means of remote sensing: Methods, accuracy and limitations. Prog. Phys. Geogr. 2009, 33, 103–116. [Google Scholar] [CrossRef]
- El-Askary, H.; Abd El-Mawla, S.H.; Li, J.; El-Hattab, M.M.; El-Raey, M. Change detection of coral reef habitat using Landsat-5 TM, Landsat 7 ETM+ and Landsat 8 OLI data in the Red Sea (Hurghada, Egypt). Int. J. Remote Sens. 2014, 35, 2327–2346. [Google Scholar] [CrossRef]
- Groeneveld, D.P.; Barz, D.D. Dixie Valley, Nevada playa bathymetry constructed from Landsat TM data. J. Hydrol. 2014, 512, 435–441. [Google Scholar] [CrossRef]
- Setiawan, K.T.; Osawa, T.; Nuarsa, I.W. Study of bathymetry map using Landsat ETM+ Data: A case study in Menjangan Island, Bali. Master’s Thesis, Udayana University, Bali, Indonesia, 2013. [Google Scholar]
- Zoffoli, M.L.; Frouin, R.; Kampel, M. Water column correction for coral reef studies by remote sensing. Sensors 2014, 14, 16881–16931. [Google Scholar] [CrossRef] [PubMed]
- Jawak, S.D.; Vadlamani, S.S.; Luis, A.J. A Synoptic Review on Deriving Bathymetry Information Using Remote Sensing Technologies: Models, Methods and Comparisons. Adv. Remote Sens. 2015, 4, 147–162. [Google Scholar] [CrossRef]
- Jerlov, N.G. Marine Optics; Elsevier: New York, NY, USA, 1976; Volume 14, ISBN 9780444414908. [Google Scholar]
- Kirk, J.T.O. Light and Photosynthesis in Aquatic Ecosystems; Kirk, J.T., Ed.; Cambridge University Press: Cambridge, UK, 2011; ISBN 978-0-521-15175-7. [Google Scholar]
- Simpson, J.J.; Dickey, T.D. Alternative parameterizations of downward irradiance and their dynamical significance. J. Phys. Oceanogr. 1981, 11, 876–882. [Google Scholar] [CrossRef]
- Morel, A.; Antoine, D. Heating rate within the upper ocean in relation to its Bio-optical State. J. Phys. Oceanogr. 1994, 24, 1652–1665. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Passive remote sensing techniques for mapping water depth and bottom features. Appl. Opt. 1978, 17, 379–383. [Google Scholar] [CrossRef] [PubMed]
- Lyzenga, D.R. Remote sensing of bottom reflectance and water attenuation parameters in shallow water using aircraft and Landsat data. Int. J. Remote Sens. 1981, 2, 71–82. [Google Scholar] [CrossRef]
- Tassan, S.; Ribera d’Alcalá, M. Water quality monitoring by thematic mapper in coastal environments. A performance analysis of local biooptical algorithms and atmospheric correction procedures. Remote Sens. Environ. 1993, 45, 177–191. [Google Scholar] [CrossRef]
- Sagawa, T.; Boisnier, E.; Komatsu, T.; Mustapha, K.B.; Hattour, A.; Kosaka, N.; Miyazaki, S. Using bottom surface reflectance to map coastal marine areas: A new application method for Lyzenga’s model. Int. J. Remote Sens. 2010, 31, 3051–3064. [Google Scholar] [CrossRef]
- Call, K.A.; Hardy, J.T.; Wallin, D.O. Coral reef habitat discrimination using multivariate spectral analysis and satellite remote sensing. Int. J. Remote Sens. 2003, 24, 2627–2639. [Google Scholar] [CrossRef]
- Lyzenga, D.R.; Malinas, N.P.; Tanis, F.J. Multispectral bathymetry using a simple physically based algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2251–2259. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Holderied, K.; Sinclair, M. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef]
- Morel, Y.G.; Favoretto, F. 4SM: A novel self-calibrated algebraic ratio method for satellite-derived bathymetry and water column correction. Sensors 2017, 17, 1682. [Google Scholar] [CrossRef] [PubMed]
- Morel, Y.G.; Lindell, L.T. Passive Multispectral bathymetry mapping of Negril shores, Jamaica. Presented at the Fifth International Conference on Remote Sensing for Marine and Coastal Environments, San Diego, California, CA, USA, 5–7 October 1998. [Google Scholar]
- Foster, M.S.R.; Riosmena-Rodriguez, R.; Steller, D.L.; Woelkerling, W.J. Living Rhodolith Beds in the Gulf of California and Their Implications; GSA Special Papers; Geological Society of America: Boulder, CO, USA, 1997. [Google Scholar]
- Halfar, J.; Godinez-Orta, L.; Ingle, J.C.J. Microfacies analysis of recent carbonate environments in the southern gulf of California, Mexico—A model for warm-temperate to subtropical carbonate formation. Palaios 2000, 15, 323–342. [Google Scholar] [CrossRef]
- Douglas, M.W.; Maddox, R.A.; Howard, K.; Reyes, S. The Mexican monsoon. J. Clim. 1993, 6, 1665–1677. [Google Scholar] [CrossRef]
- Obeso-Nieblas, M.; Gaviño-Rodríguez, J.H.; Obeso-Huerta, H.; Muñoz-Casillas, S.I. Variabilidad espacial termohalina, Masas de agua y circulaciòn geostrìfica en bahìa de La Paz, Golfo de california. Rev. Biol. Mar. Oceanogr. 2014, 49, 413–426. [Google Scholar] [CrossRef]
- Obeso-Nieblas, M.; Shirasago-Germán, B.; Gaviño-Rodríguez, J.H.; Obeso-Huerta, H.; Pérez-Lezama, E.L.; Jiménez-Illescas, A.R. Hidrografía en la Boca Norte de la Bahía de La Paz, Baja California Sur, México. Hydrogr. North Mouth La Paz Bay, Baja Calif. Sur Mex. 2007, 33, 281–291. (In Spanish) [Google Scholar]
- Salinas-González, F.; Zaytsev, O.; Makarov, V. Formation of the thermohaline structure of water in the Bahía de La Paz from summer to autumn. Ciencias Mar. 2003, 29, 51–65. [Google Scholar] [CrossRef]
- Gárate-Lizárraga, I.; Muñetón-Gómez, M.D.S.; Pérez-Cruz, B.; Díaz-Ortíz, J.A. Bloom of Gonyaulax spinifera (Dinophyceae: Gonyaulacales) in Ensenada de la Paz lagoon, Gulf of California. CICIMAR Oceánides 2014, 29, 11–18. [Google Scholar]
- Obeso-Nieblas, M.; Jimene-Illescas, A.; Troyo-Dieguez, S. Modelacion de la marea en la Bahia de La Paz, B.C.S. Inv. Mar CICIMAR 1993, 8, 14–22. [Google Scholar]
- Philpot, W.D. Bathymetric mapping with passive multispectral imagery. Appl. Opt. 1989, 28, 1569–1578. [Google Scholar] [CrossRef] [PubMed]
- Maritorena, S.; Morel, A.; Gentili, B. Diffuse reflectance of oceanic shallow waters: Influence of water depth and bottom albedo. Limnol. Oceanogr. 1994, 39, 1689–1703. [Google Scholar] [CrossRef]
- Hedley, J.D.; Harborne, A.R.; Mumby, P.J. Technical note: Simple and robust removal of sun glint for mapping shallow-water benthos. Int. J. Remote Sens. 2005, 26, 2107–2112. [Google Scholar] [CrossRef]
- Hijmans, R.J. Raster: Geographic data analysis and modeling. Available online: https://CRAN.R-project.org/package=raster (accessed on 15 September 2017).
- Baret, F.; Jacquemoud, S.; Hanocq, J.F. About the soil line concept in remote sensing. Adv. Sp. Res. 1993, 13, 281–284. [Google Scholar] [CrossRef]

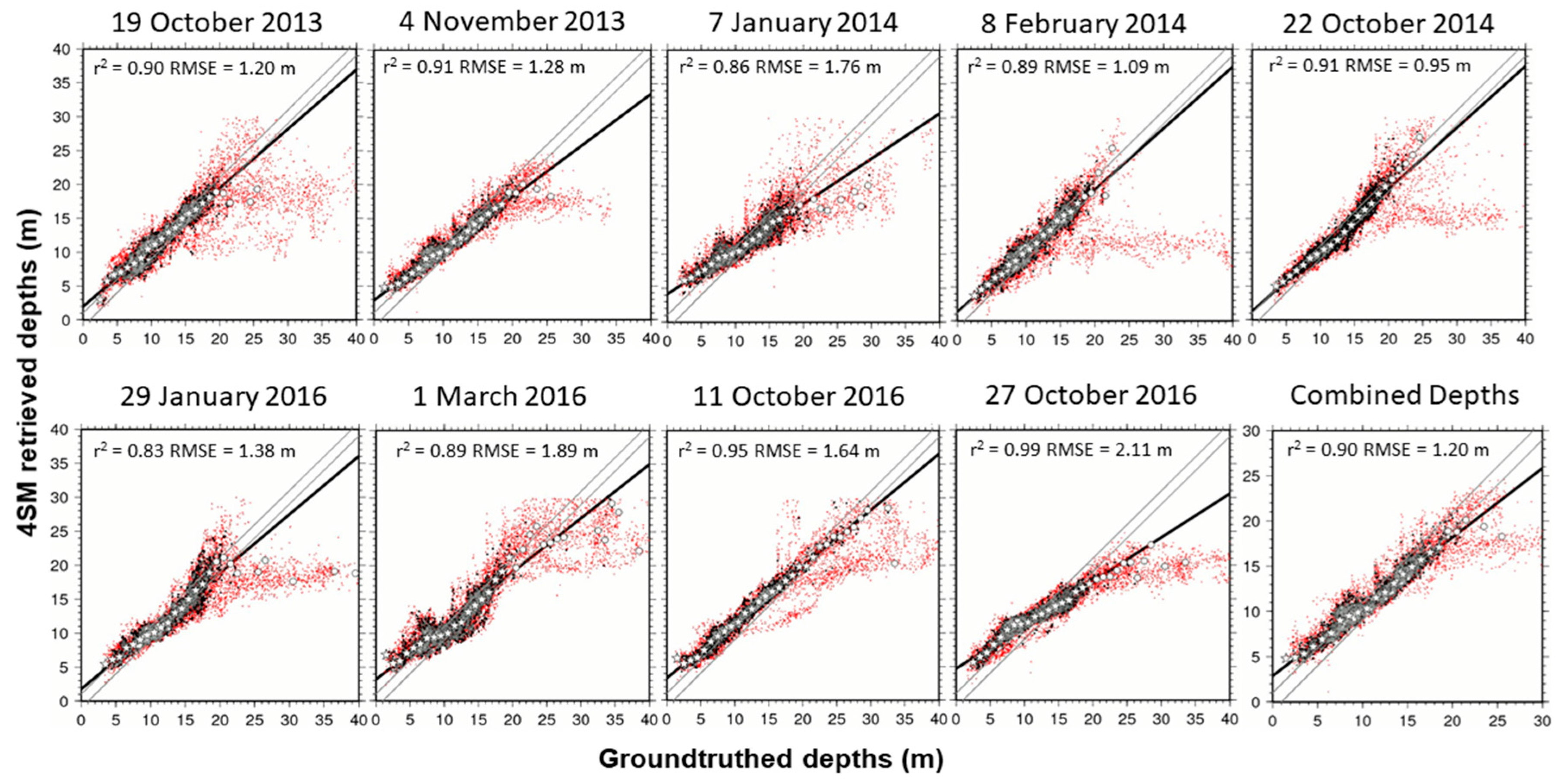

| Scene File Code | Date | Tide (m) | r2 |
|---|---|---|---|
| LC80340432013292LGN00 | 19 October 2013 | 0.0 | 0.90 |
| LC80340432013308LGN00 | 4 November 2013 | 0.6 | 0.91 |
| LC80340432014007LGN00 | 7 January 2014 | 0.0 | 0.86 |
| LC80340432014039LGN00 | 8 February 2014 | 0.6 | 0.89 |
| LC80340432014295LGN00 | 22 October 2014 | 1.6 | 0.91 |
| LC80340432016029LGN00 | 29 January 2016 | 1.7 | 0.83 |
| LC80340432016061LGN00 | 1 March 2016 | −0.3 | 0.89 |
| LC80340432016285LGN00 | 11 October 2016 | −0.2 | 0.95 |
| LC80340432016301LGN00 | 27 October 2016 | 0.0 | 0.99 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Favoretto, F.; Morel, Y.; Waddington, A.; Lopez-Calderon, J.; Cadena-Roa, M.; Blanco-Jarvio, A. Testing of the 4SM Method in the Gulf of California Suggests Field Data Are not Needed to Derive Satellite Bathymetry. Sensors 2017, 17, 2248. https://doi.org/10.3390/s17102248
Favoretto F, Morel Y, Waddington A, Lopez-Calderon J, Cadena-Roa M, Blanco-Jarvio A. Testing of the 4SM Method in the Gulf of California Suggests Field Data Are not Needed to Derive Satellite Bathymetry. Sensors. 2017; 17(10):2248. https://doi.org/10.3390/s17102248
Chicago/Turabian StyleFavoretto, Fabio, Yann Morel, Andrew Waddington, Jorge Lopez-Calderon, Marco Cadena-Roa, and Anidia Blanco-Jarvio. 2017. "Testing of the 4SM Method in the Gulf of California Suggests Field Data Are not Needed to Derive Satellite Bathymetry" Sensors 17, no. 10: 2248. https://doi.org/10.3390/s17102248
APA StyleFavoretto, F., Morel, Y., Waddington, A., Lopez-Calderon, J., Cadena-Roa, M., & Blanco-Jarvio, A. (2017). Testing of the 4SM Method in the Gulf of California Suggests Field Data Are not Needed to Derive Satellite Bathymetry. Sensors, 17(10), 2248. https://doi.org/10.3390/s17102248






