1. Introduction
The fluxgate sensor is a kind of sensor which can measure a weak magnetic field by using the nonlinear relationship between the magnetic flux density B and the magnetic field strength H [
1,
2]. In order to analyze, design and optimize fluxgate sensor, simulations are necessary. During the simulations, the accuracy of a mathematical model for magnetic core is significant. There have been numerous approaches to model the magnetic hysteresis loop, which can be roughly divided into three categories [
3]: (1) Macroscopic magnetization which ignores the underlying physics of the material behavior, such as tri-linear model, tangent function model, arctangent function model [
4], and Preisach model [
5] et al.; (2) Micro-magnetic theory which is derived from complex hysteresis theory but difficult to apply in real engineering materials; (3) Semi-macroscopic magnetization which combines the microstructural parameters of magnetic materials with the macroscopic magnetization curves, such as Globus model [
6] and Jiles-Atherton model [
7]. The Jiles-Atherton model is derived from the physical process of magnetic hysteresis and described by a first-order differential equation with five parameters. It is relatively simple in mathematical expressions and more accurate, which makes it a widely used hysteresis model in applications [
8].
However, the Jiles-Atherton model is a multi-parameter model which is sensitive to the variations of parameters, so the precise determination of the model parameters has become a focus of scholars. With the development of optimization algorithms, many intelligence optimization algorithms have been proposed to identify the parameters of the Jiles-Atherton model. At present, the most frequently used methods include Genetic Algorithm (GA) [
9,
10], Particle Swarm Optimization (PSO) algorithm [
11], Differential Evolution (DE) algorithm [
12] and Simulated Annealing (SA) algorithm [
13,
14].
Biogeography-Based optimization (BBO) [
15] is a new kind of swarm intelligence optimization algorithm, which is inspired by the study of the geographical distribution of the biological organisms. There are mainly three mechanisms in the algorithm: migration, mutation and elimination. The BBO algorithm and improved BBO algorithms have good convergence and stability, and they have been applied to solve many practical problems. Blended Biogeography-Based Optimization (B-BBO) has been applied on economic load dispatch (ELD) problem successfully [
16]. Li and Yin [
17] have proposed a multi-objective Biogeography-based Optimization to select the small subset of informative gene relevant to the classification. Hybridization of Biogeography-based Optimization and Ant Colony Optimization has been used to resolve mixed pixels [
18]. Simulation results have shown excellent performance of these methods.
In this paper, the IBBO algorithm is used to identify the parameters of Jiles-Atherton model for magnetic core. An improved BBO (IBBO) algorithm is proposed to enhance the global searching capability, convergence rate and accuracy of the algorithm: (1) the Arnold map generating uniform chaotic sequence as original populations to improve the algorithm in ergodicity, accuracy and global searching capability; (2) introducing mutation strategy DE/best/1 of DE algorithm as mutation operator to improve the diversity of solutions and global searching capability. Applying IBBO algorithm, BBO algorithm, GA algorithm, PSO algorithm and DE algorithm to identify the Jiles-Atherton model parameters of a magnetic core at the same time, the simulation results show that the IBBO algorithm has the advantages of high precision and fast convergence rate. According to magnetic hysteresis data of the selected permalloy by experiment, the IBBO algorithm is applied to identify the parameters of the Jiles-Atherton model for the selected material. The simulation hysteresis loop is in good agreement with experimental data; the output of fluxgate probe made of above selected material as magnetic core is consistent with the simulation output. The IBBO algorithm is a new method for parameters identification of the Jiles-Atherton model.
2. Materials and Equipment
2.1. Measurement of Dynamic Hysteresis Loop
In this paper, the oscilloscope method is applied to obtain the dynamic hysteresis loop of the selected permalloy. The permalloy sample is a ring with dimensions as following: outer diameter 24 mm, inner diameter 20 mm and thickness 0.15 mm. The magnetizing field is a sinusoidal signal with frequency of 30 kHz.
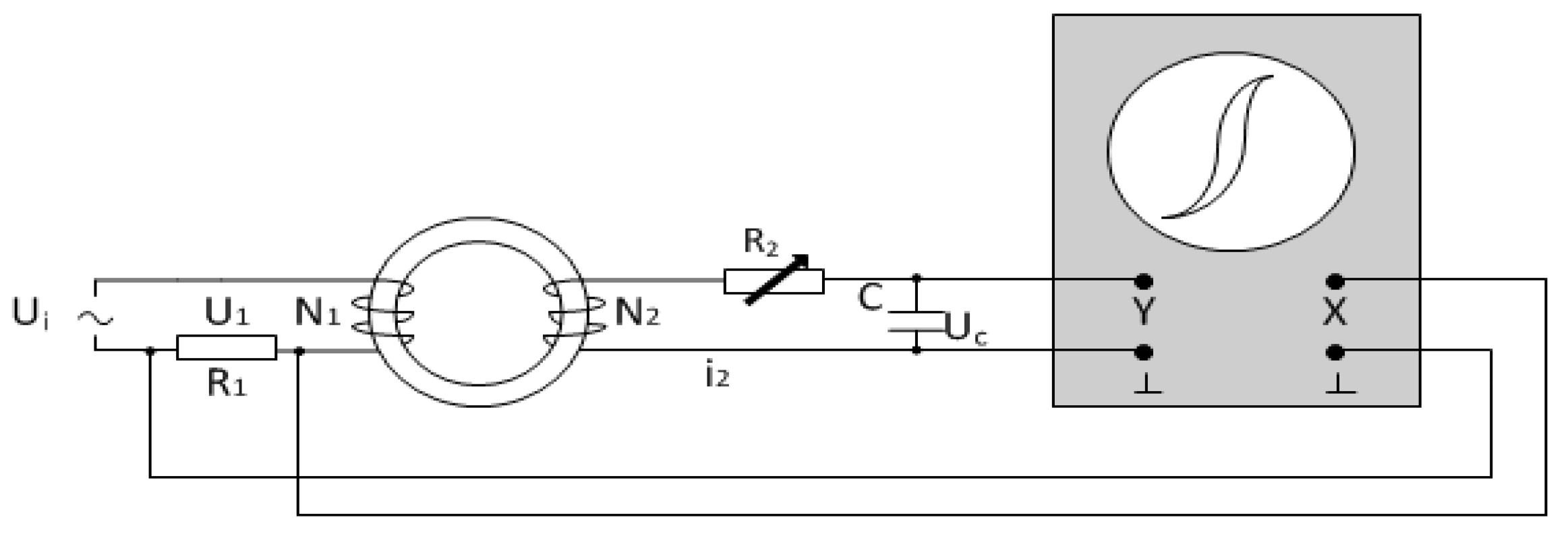
A dynamic hysteresis loop measurement system is established according to the diagram of the measurement system shown in
Figure 1 [
19].
Here, R1 = 2.6 Ω, C = 20 μF, R2 = 50 kΩ, the number of excitation coils and detection coils are both 600 turns. The excitation power supply is a signal generator (AFG 3021B, TEKTRONIX, Beaverton, OR, USA) together with a power amplifier, and the oscilloscope is a digital oscilloscope (DS1052E, RIGOL, Beijing, China).
The oscilloscope method is used to measure the dynamic hysteresis loop at the excitation voltage, which is big enough to make the sample saturate. The measurement data are transported through USB port on the oscilloscope. Then the magnetic field strength H and the magnetic flux density B can be calculated according to the following equations:
In Equation (2), parameter S is the cross-sectional area of the permalloy.
The B-H curve of the sample can be obtained in this way. In order to prevent the external magnetic field interfering with the sample, the measurement system is placed in a magnetic shielding cylinder (MD-10, JOZZON, Beijing, China) which is composed of six concentric cylinders. The outer layer is made of aluminum, and the other five layers are made of 1J85 permalloy.
2.2. Fluxgate Probe
A fluxgate probe is manufactured by the mentioned permalloy which is used as a magnetic core. The structure of fluxgate probe used in experiment is shown in
Figure 2. The excitation coils are the coils both on upper and bottom arms, and the detection coils are on the middle arm. The excitation coils are 1200 turns in sum and the detection coils are 600 turns. The material of the coils is copper wire coating polyimide with the diameter of 0.15 mm.
3. Description of the Jiles-Atherton Model
The Jiles-Atherton model is a widely used mathematical model, which can represent the nonlinear characteristics of magnetic core accurately. The model is described by a first-order differential equation [
7,
20]:
Here, Man denotes anhysteretic magnetization. k is pinning factor. c represents reversible magnetization coefficient. α is coupling factor between magnetic domains. δ is a direction parameter, which is defined as .
The anhysteretic magnetization
Man is provided by Langevin function and described in Equation (4):
Here,
Ms is saturation magnetization. Parameter
a is form factor.
He is effective magnetic field which is given by:
Combined Equations (3)–(5) can form a first order nonlinear differential equation. The numerical solution of the differential equation can be obtained when the five parameters (Ms, α, a, c, k) and the initial values are determined. Thus, the calculated M-H curve can be obtained.
The model used in this paper is the original Jiles-Atherton model which describes the relationship between M and H, while the inverse Jiles-Atherton model describes the relationship between B and H. The relationship between M, B and H is following:
Francesco and Alessandro [
21] have analyzed the effects of five parameters on the hysteresis loop: (1)
Ms mainly affects the slope dB/dH at coercive point and the maximum value of magnetization; (2) Parameter
a affects the knee region of the loop around the remanence magnetization value; (3)
α mainly controls the slope dB/dH in the region around the coercive point; (4) Parameters
k and
c control the amplitude of the loop area, the coercive field amplitude and the derivatives values on the points close to the coercive field.
Table 1 [
22] summarizes the influence of the parameters to the hysteresis loop. Symbols “↑” and “↓” represent increasing and decreasing respectively and symbol “--” indicates no influence or little influence.
The parameters identification of the Jiles-Atherton model is to determine the five coefficients from the experimental hysteresis loop. Utilizing appropriate optimization method, it is possible to obtain the mathematical model which has good agreement with the experimental hysteresis loop. The advantage of the Jiles-Atherton model is that the five parameters have physical meaning, which can be useful for further analysis.
4. The Principle of BBO Algorithm
4.1. Introduction of BBO Algorithm
The BBO algorithm is a new swarm intelligence optimization algorithm proposed by Simon in 2008 [
15]. It is designed according to the laws of the migration, mutation and extinction of the biological species in the habitat. If a habitat is suitable for species survival, the habitat has a high fitness index (Habitat Suitability Index, HSI). HSI is related to the factors such as rainfall, humidity, temperature, and plant coverage. These factors are called Suitability Index Variables (SIVs). HSI corresponds to the fitness value of the optimized problem and the number of SIVs in each solution corresponds to the number of optimized parameters. The algorithm uses the habitat migration operator, mutation operator and elimination operator to improve the optimization capability.
4.1.1. Migration Operator
BBO algorithm uses the migration operator to realize the information sharing between solutions. Each solution has its respective immigration rate and emigration rate to control the movement probabilities of solution information. The method to produce the next generation in BBO is by emigration solution features to other habitats and receiving solution features by immigration from other habitats. The algorithm assumes a high species count in habitats having high HSI, which encourages species to emigrate from the habitat, sharing their SIVs with other habitats. Hence, habitats with high HSI have high emigration rate and low immigration rate. Like other swarm based algorithms, the BBO algorithm replaces SIVs of emigration solution with SIVs of immigration solution in iterations to increase the diversity of swarms and the precision of solutions.
4.1.2. Mutation Operator
Affected by emergencies, some environmental indicators of habitat have changed suddenly, which can be simulated by the mutation operator.
Simon has reported that the mutation rate in the habitat is inversely proportional to the species count probability, which can be described as follows:
Here, ms is mutation rate of a habitat with s number of species, mmax is maximum mutation rate defined by user, ps is probability of a habitat with s number of species and pmax is the maximum of ps.
Mutation can increase the probability of the mutation of SIVs of low HSI, and improve the HSI, but the SIVs of high HSI may be destroyed at the same time. So the strategy of elite reservation is introduced in the iteration process.
4.1.3. Elimination Operator
In order to avoid the homogeneous solution and improve the diversity of population, Simon has designed elimination operator to clear the same solutions and replace the same solutions by randomly generated solutions.
4.2. Improved BBO Algorithm
In the process of iterations, BBO algorithm has poor global search capability, low accuracy and convergence rate [
23,
24]. The following improvements are made to the BBO algorithm to increase global search capability and improve the accuracy of solutions and convergence rate.
4.2.1. Generating Initial Populations by Arnold Map
Chaos is a kind of nonlinear phenomenon in nature. It has the characteristics of randomicity, ergodicity and regularity, which can improve the searching capability of the algorithm [
25].
In practice, the Logistic chaotic sequence is often introduced into the algorithms to improve the optimization capability. However, the distribution of the Logistic map is uneven, and has strong boundary search capability and low middle search probability. So it is poor in ergodicity [
26].
The sequence generated by the Arnold map is uniform and sensitive to initial value. So in this paper, the Arnold map is used to generate initial populations of BBO to improve the ergodicity and global searching capability of the algorithm. In this paper, the five parameters need to be determined, so the five-dimensional Arnold map is used to generate uniform chaotic sequence. The five-dimensional Arnold map equation is as follows [
27]:
Here, modN represents the fractional part, n is a positive integer, and the values of xn, yn...ln are all in [0, 1].
A uniform chaotic sequence generated by Arnold map is selected as initial populations of BBO algorithm, instead of Rand random function. The distribution of the initial populations is more uniform, which increases the accuracy of the solution and the searching capability of the algorithm.
4.2.2. Improving Migration Equation by DE Mutation Strategy
In the migration process, BBO algorithm replaces SIVs of emigration solution with SIVs of immigration solution. The migration equation of the conventional BBO algorithm is:
The migration Equation (9) is simple, which makes the new solution has only a small amount of information and affects the performance of the BBO algorithm. In order to solve this problem, the DE/best/1 mutation strategy of DE algorithm [
28] is introduced to the migration equation:
Here, Hbest is the best optimal solution, Hr1 and Hr2 are two different solutions randomly selected, and F is a scaling factor with the range of [0, 1].
Equation (10) shows that the solution preserves the information of the best optimal solution and absorbs the differential vector of the other solutions after migration. Scaling factor F balances the exploitation and exploration ability of the algorithm, which can avoid homogeneity of solution and increase the evolution rate of the excellent solutions.
4.3. Steps of Identification the Jiles-Atherton Model Parameters with IBBO
The steps of using IBBO to identify the parameters of Jiles-Atherton model are as follows:
Step 1: Set the initial values of IBBO algorithm and the range of the parameters of the Jiles-Atherton model.
Step 2: Apply the Arnold map to generate the initial solutions of the Jiles-Atherton model.
Step 3: Calculate the HSI values of the solutions, sort the HSI values in descending order (for minimum problems), and keep the optimal solutions. The fitness function is mentioned in
Section 5.
Step 4: According to the iteration termination conditions, determine whether the iteration is terminated. If the termination conditions are satisfied, output the optimal solution; if not, continue the following steps.
Step 5: Use the cosine model to calculate the immigration probability and the emigration probability of each habitat, and apply the mutation strategy of DE/best/1 to improve the migration equation.
Step 6: According to mutation probability, operate mutation of the population, which improves the diversity of the solution.
Step 7: Compare one solution with the others, find the same solutions, replace one of the same solutions with a randomly generated solution, and return to Step 3 to next generation iteration of the solutions.
The flow chart of IBBO algorithm to identify the parameters of Jiles-Atherton model is shown in
Figure 3.
5. Simulation Results and Analysis
5.1. Simulation Results for Theoretical Data
In this paper, a set of data is selected as the parameters of the Jiles-Atherton model. The hysteresis data can be obtained by solving the Equations (3)–(5) with 4th/5th Runge-Kutta method. In this case, the experimental data is replaced by numerical solutions. According to the numerical solutions, the parameters of the Jiles-Atherton model are determined by IBBO method. Also, the GA method, PSO method, DE method and BBO method are used to identify the parameters.
The simulation parameters of five algorithms are set as following:
- (1)
IBBO: population size is 20, iteration number is 50, initial mutation probability is 0.005 and scaling factor is 0.5.
- (2)
BBO: population size is 20, iteration number is 50, initial mutation probability is 0.005.
- (3)
GA: population size is 20, the maximum genetic algebra is 50, the binary number of variables is 20, mutation probability is 0.05, crossover probability is 0.9.
- (4)
PSO: particle swarm size is 20, the maximum number of iterations is 50, the inertia factor is 0.6, and the acceleration constants c1 = c2 = 2.
- (5)
DE: population size is 20, the maximum number of iterations is 50, mutation probability is 0.6, and crossover probability is 0.8.
The above algorithms are all optimization algorithms, so an optimized function (fitness function) must be defined. The optimized parameters are the five parameters (
Ms, α, a, c, k), so the fitness function must be described by the five parameters. Once the five parameters are determined, a set of solutions can be obtained by solving the Equations (3)–(5).The smaller the difference between the calculated B and experimental B at the same H is, the more accurate the parameters are. In this paper, the fitness function is defined as follows:
Here, Bexpi is experimental data, and Bi is calculated (simulation) data.
The five algorithms are run for 30 times respectively. The simulation results are listed in
Table 2. The results in
Table 2 are averaged. From
Table 2, it is found that: the fitness value of IBBO method is 0.0225 T which is the minimum fitness value of the five methods, and the simulation time of IBBO method is 197.25 s which is 25% faster than those of GA and PSO methods and more than 2 times faster than that of DE method. It is stated that the IBBO method runs faster and is more accurate compared with BBO, GA, PSO, and DE methods, due to the introduction of the Arnold map and DE mutation strategy.
Figure 4 shows the fitness values with iterations of five methods. IBBO method needs 7 iterations to converge to the best fitness value, which is faster than those of GA, PSO and BBO methods. The IBBO method has the smallest fitness value of the five methods. It can be seen that IBBO method has high accuracy and convergence rate in the identification of the parameters for the Jiles-Atherton model.
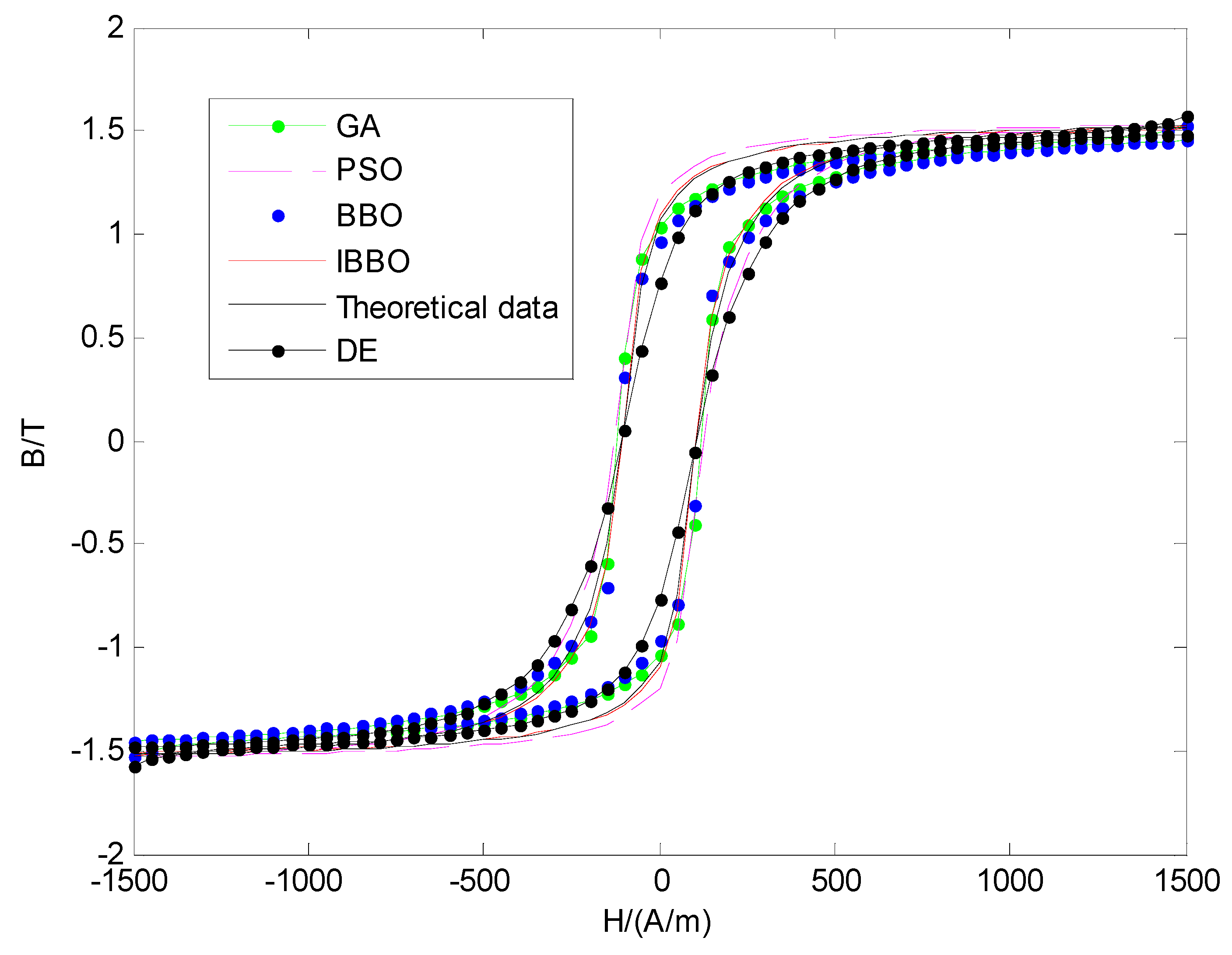
The five hysteresis loops obtained with the parameters in
Table 2 are shown in
Figure 5. It can be found that the hysteresis loop achieved by IBBO method is in high agreement with the theoretical data.
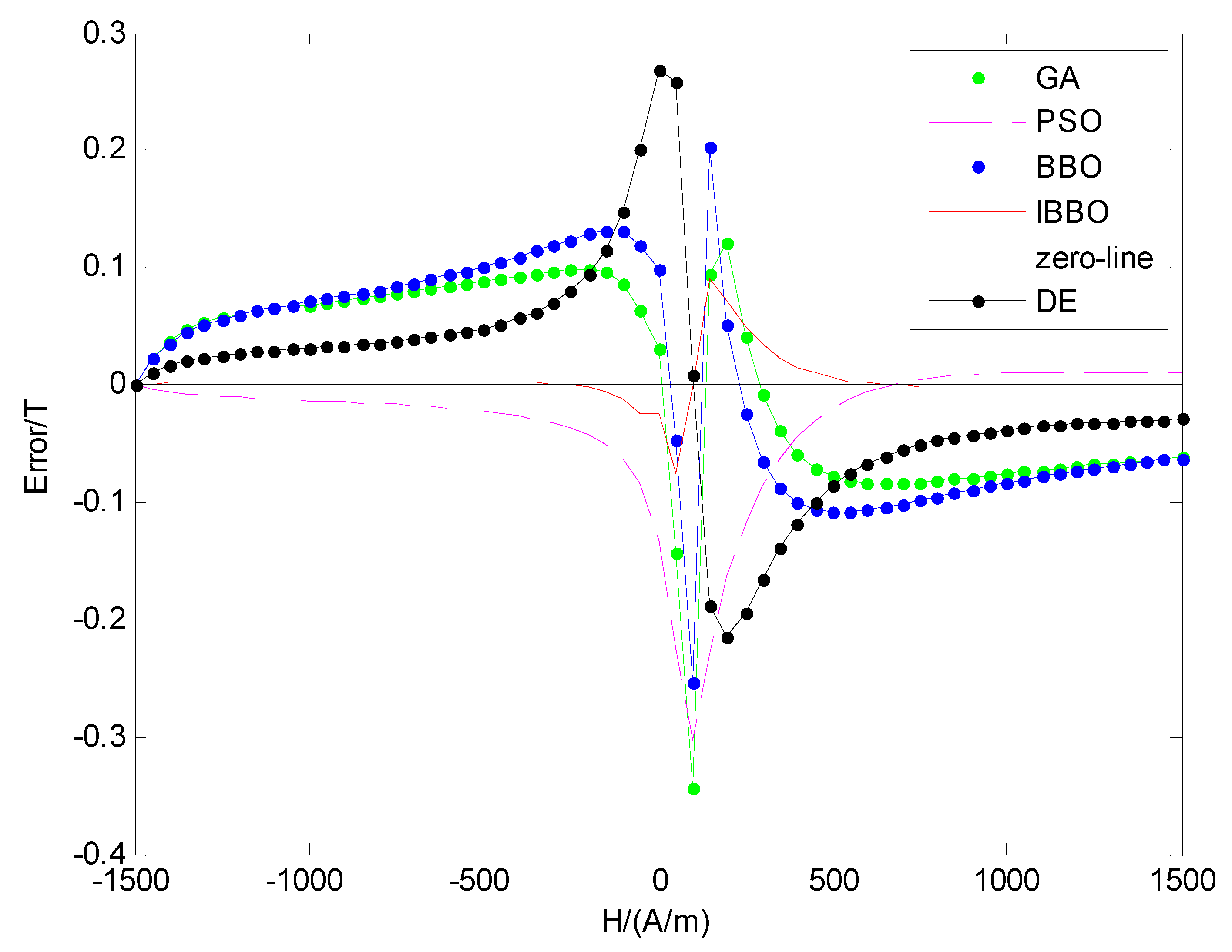
The errors between the simulation data and the theoretical data are shown in
Figure 6. From
Figure 6, it can be found that the maximum absolute error of the red line (obtained by IBBO) is 0.091 T at 150 A/m on the ascending part; the maximum absolute errors of the blue line (obtained by BBO) and the green line (obtained by GA) are 0.2535 T and 0.3443 T at 100 A/m respectively; the maximum absolute errors of PSO method and DE method are 0.3037 T and 0.2675 T; the errors are mainly concentrated on the middle part of H around coercive force point H
c. It is stated that the identification accuracy of IBBO method is the best. It can be used to determine the parameters of Jiles-Atherton model accurately.
5.2. Simulation Results for Experimental Data
According to the principle of dynamic hysteresis loop measurement, the experimental hysteresis loop is obtained, as shown in
Figure 7. Also the five methods are applied to identify the parameters of Jiles-Atherton model. Based on the influence of the parameters to hysteresis loop, the range of the parameters are determined, as seen in
Table 3 together with the identification results. From
Table 3, the smallest fitness value is 0.0544 T which is obtained by IBBO method; the biggest fitness value is 0.1707 T obtained by GA method; the fitness values of PSO, DE and BBO are in the middle. The simulation time of IBBO method is 199.03 s which is 25% faster than those of GA and PSO methods and 2.4 times faster than that of DE method. So the IBBO method has the advantage of fast convergence rate and good accuracy.
The simulation hysteresis loop obtained by IBBO is also depicted in
Figure 7, from which it can be found that the simulation hysteresis loop is in high agreement with the experimental one.
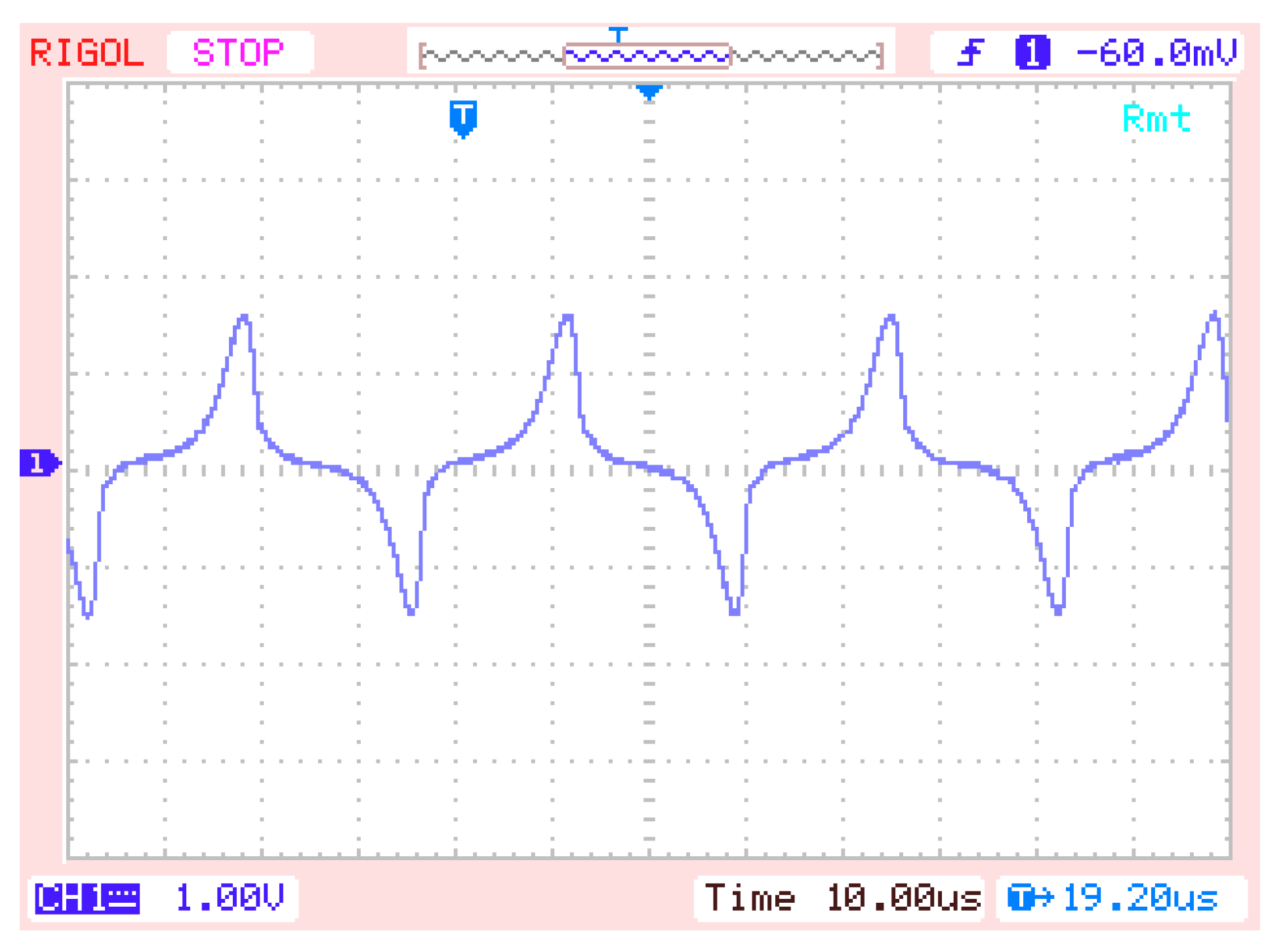
The experiment is carried out on fluxgate probe using the mentioned permalloy as the magnetic core. The structure of the magnetic fluxgate probe used in the experiment is depicted in
Figure 2, which is completely symmetrical in structure. When the external magnetic field is 30,000 nT, the experimental output of the magnetic fluxgate probe is shown in
Figure 8. The output waveform is a periodic signal with period T = 33.6 μs, the maximum value V
max = 1.52 V and the minimum value V
min = −1.6 V.
The fluxgate probe is a single-rod sensor in theory. A simulation model based on the Jiles-Atherton model is built in a MATLAB/Simulink environment.
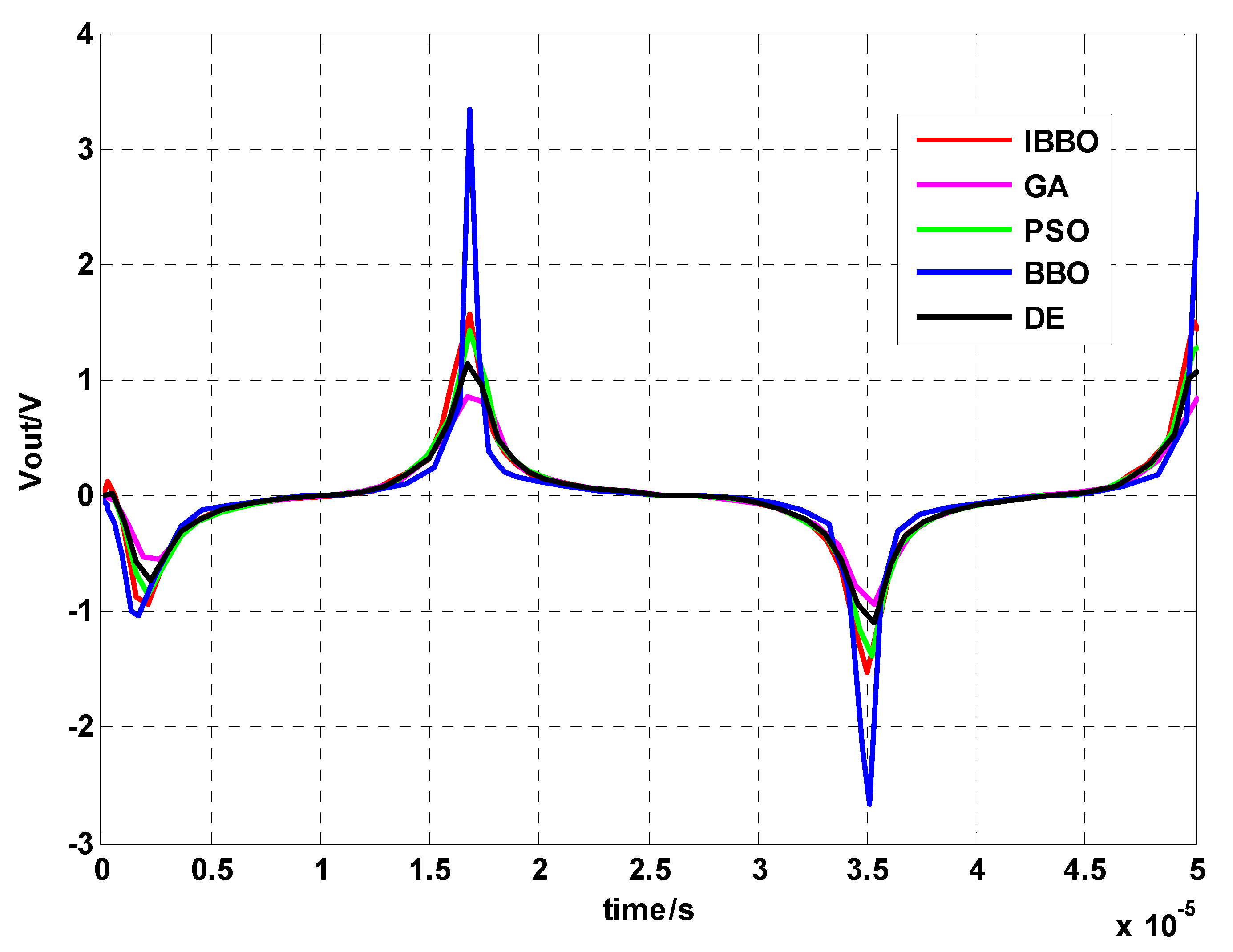
Figure 9 shows the simulation outputs of different parameters optimized by five methods. The output waveforms are periodic signals with period T = 33.38 μs. The maximum values V
max for IBBO method, BBO method, DE method, PSO method and GA method are 1.57 V, 3.33 V, 1.13 V, 1.41 V and 0.85 V respectively, and the minimum values V
min are −1.53 V, −2.65 V, −1.09 V, −1.39 V, and −0.94 V respectively. The simulation output of parameters optimized by IBBO method is consistent with the experimental output of the fluxgate probe.
6. Conclusions
In this paper, the BBO algorithm is applied to identify the five parameters of the Jiles-Atherton model. Through the improvement of the BBO algorithm, the convergence rate and the optimization accuracy are improved. Using the IBBO algorithm to identify the fixed parameters of the Jiles-Atherton model, simulation results have shown that IBBO algorithm has been improved significantly in terms of convergence rate and accuracy compared with GA, PSO, DE and BBO algorithms. For the permalloy Jiles-Atherton model parameters identification, the hysteresis loop of simulation and experiment are in high agreement. The simulation output of parameters optimized by IBBO method is consistent with the experimental output. IBBO method is a new approach for parameter identification of the Jiles-Atherton model, which provides a reference for further accurate analysis and design of the instruments and equipment with a magnetic core.
Acknowledgments
This research is supported by the National Natural Science Foundation of China (Grant No. 61501149), and the National Science and Technology Major Project of China (2013YQ170585).
Author Contributions
Yunbo Shi and Wenjie Zhao conceived and designed the experiments; Xiangxin Wang manufactured the sensor probe and performed the experiments; Wenjuan Jiang established the simulation platform, wrote simulation programs, performed data analysis and wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kaluza, F.; Grüger, A.; Grüger, H. New and future applications of fluxgate sensors. Sens. Actuators A Phys. 2003, 106, 48–51. [Google Scholar] [CrossRef]
- Ripka, P.; Janošek, M. Advances in Magnetic Field Sensors. IEEE Sens. J. 2010, 10, 1108–1116. [Google Scholar] [CrossRef]
- Liorzou, F.; Phelps, B.; Atherton, D.L. Macroscopic models of magnetization. IEEE Trans. Magn. 2000, 36, 418–428. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, S.; Zhou, Z.; Cheng, D.; Pang, N.; Wan, Y. Research on the Dynamic Hysteresis Loop Model of the Residence Times Difference (RTD)-Fluxgate. Sensors 2013, 13, 11539–11552. [Google Scholar] [CrossRef] [PubMed]
- Preisach, F. Über die magnetische nachwrikung. Zeitschrift für Physik 1935, 94, 277–302. (In German) [Google Scholar] [CrossRef]
- Globus, A.; Duplex, P.; Guyot, M. Determination of initial magnetization curve from crystallites size and effective anisotropy field. IEEE Trans. Magn. 1971, 7, 617–622. [Google Scholar] [CrossRef]
- Jiles, D.C.; Atherton, D.L. Theory of ferromagnetic hysteresis (invited). J. Magn. Magn. Mater. 1986, 61, 48–60. [Google Scholar] [CrossRef]
- Zaman, M.A.; Matin, M.A. Optimization of Jiles-Atherton Hysteresis Model Parameters Using Taguchi’s Method. IEEE Trans. Magn. 2015, 51, 1–5. [Google Scholar] [CrossRef]
- Leite, J.V.; Avila, S.L.; Batistela, N.J.; Carpes, W.P.; Sadowski, N.; Kuo-Peng, P.; Bastos, J.P.A. Real Coded Genetic Algorithm for Jiles-Atherton Model Parameters Identification. IEEE Trans. Magn. 2004, 40, 888–891. [Google Scholar] [CrossRef]
- Chwastek, K.; Szczyglowski, J. Identification of a hysteresis model parameters with genetic algorithms. Math. Comput. Simul. 2006, 71, 206–211. [Google Scholar] [CrossRef]
- Marion, R.; Scorretti, R.; Siauve, N.; Raulet, M.; Krähenbühl, L. Identification of Jiles-Atherton Model Parameters Using Particle Swarm Optimization. IEEE Trans. Magn. 2008, 44, 894–897. [Google Scholar] [CrossRef]
- Coelho, L.; Mariani, V.C.; Leite, J.V. Solution of Jiles-Atherton vector hysteresis parameters estimation by modified differential evolution approaches. Expert Syst. 2012, 39, 2021–2025. [Google Scholar] [CrossRef]
- Lederer, D.; Igarashi, H.; Kost, A.; Honma, T. On the parameter identification and application of the Jiles-Atherton hysteresis model for numerical modelling of measured characteristics. IEEE Trans. Magn. 1999, 35, 1211–1214. [Google Scholar] [CrossRef]
- Bai, B.; Wang, J.; Zhu, K. Identification of the Jiles-Atherton model parameters using simulated annealing method. In Proceedings of the International Conference on Electrical Machines and Systems (ICEMS), Beijing, China, 20–23 August 2011; pp. 1–4.
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Kanoongo, S.; Jain, P. Blended Biogeography Based Optimization for different economic load dispatch problem. In Proceedings of the 25th IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), Montreal, QC, Canada, 29 April–2 May 2012; pp. 1–5.
- Li, X.; Yin, M. Multiobjective Binary Biogeography Based Optimization for Feature Selection Using Gene Expression Data. IEEE Trans. NanoBiosci. 2013, 12, 343–353. [Google Scholar] [CrossRef]
- Sinha, S.; Bhola, A.; Panchal, V.K.; Singhal, S.; Abraham, A. Resolving mixed pixels by hybridization of biogeography based optimization and ant colony optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Brisbane, Austrilia, 10–15 June 2012; pp. 1–6.
- Lord, H.W. Dynamic hysteresis loop measuring equipment. Trans. Am. Inst. Electr. Eng. Part I Commun. Electron. 1952, 71, 269–272. [Google Scholar]
- Li, Z.; Li, Q.; Li, C.; Sun, Q.; Lou, J. Queries on the J-A modeling theory of the magnetization process in ferromagnets and proposed correction method. Proc. CSEE 2011, 31, 124–131. (In Chinese) [Google Scholar]
- Francesco, R.F.; Alessandro, S. Softcomputing for the identification of the Jiles-Atherton model parameters. IEEE Trans. Magn. 2005, 41, 1100–1108. [Google Scholar]
- Li, X.; Peng, Q.; Li, J.; Wen, X.; Lu, H. Parameter identification of hysteresis loop model for transformer core. Power Syst. Technol. 2012, 36, 200–205. (In Chinese) [Google Scholar]
- Bhattacharya, A.; Chattopadhyay, P.K. Hybrid Differential Evolution with Biogeography-Based Optimization for Solution of Economic Load Dispatch. IEEE Trans. Power Syst. 2010, 25, 1955–1964. [Google Scholar] [CrossRef]
- Lin, J. A hybrid biogeography-based optimization for the fuzzy flexible job-shop scheduling problem. Knowl. Based Syst. 2015, 78, 59–74. [Google Scholar] [CrossRef]
- Liu, B.; Wang, L.; Jin, Y.; Tang, F.; Huang, D. Improved particle swarm optimization combined with chaos. Chaos Solitons Fractals 2005, 25, 1261–1271. [Google Scholar] [CrossRef]
- Li, X.; Sun, L.; Yang, M. Research on ultrasonic signal processing based on improved FOA matching pursuit. Chin. J. Sci. Instrum. 2013, 34, 2068–2073. (In Chinese) [Google Scholar]
- Li, Y.; Ge, J.; Li, C.; Sun, Z. A new construction method for n-dimensional generalized Arnold matrixes and its application in image scrambling. J. Univ. Sci. Technol. Beijing 2010, 32, 1630–1636. (In Chinese) [Google Scholar]
- Price, K.V. Differential evolution: A fast and simple numerical optimizer. In Proceedings of the Biennial Conference of the North American, Berkeley, CA, USA, 19–22 June 1996; pp. 524–527.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).