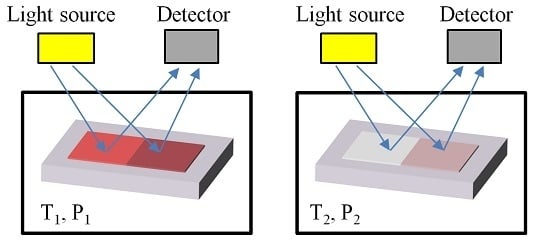
Pressure and Temperature Sensors Using Two Spin Crossover Materials
Abstract
:1. Introduction
2. Method and Tools
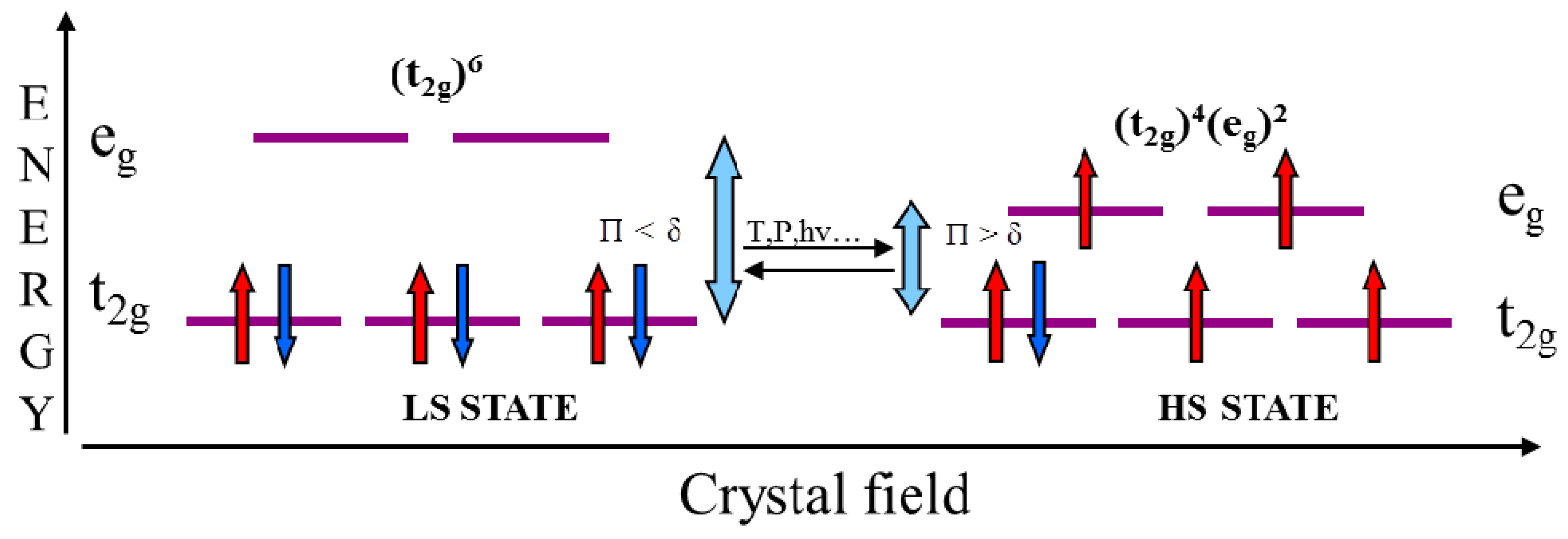
- In case where the energy gap is higher that the electron spin pairing energy, Δ >> Π, the electrons will occupy the orbitals with lowest energy with the total spin S = 0. This state is called low-spin (LS)
- In the second case when the energy gap is less that the electron spin pairing energy, Δ << Π, the electrons follow the Hund’s rule and will occupy the maximum possible number of orbitals. The total spin will be S = 2 and the state is called high-spin (HS).
- The transition occurs when Δ ≈ Π.
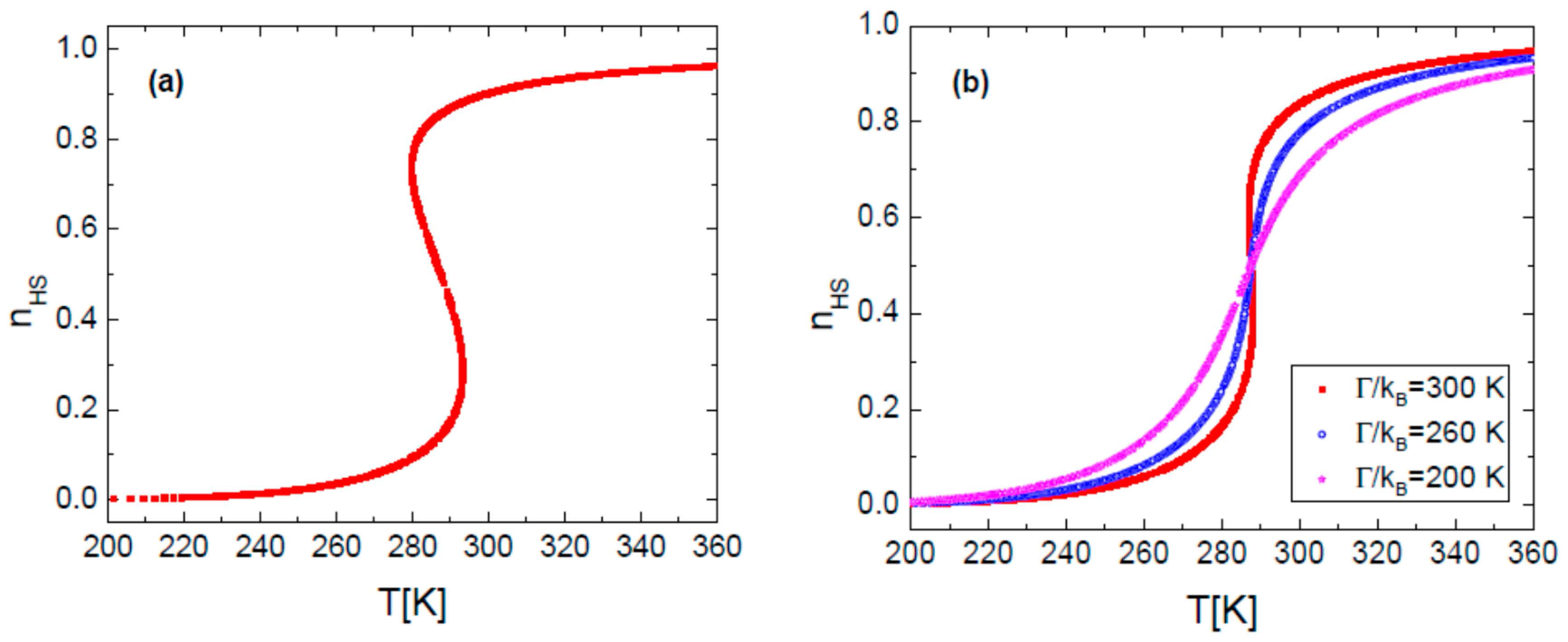
3. Results
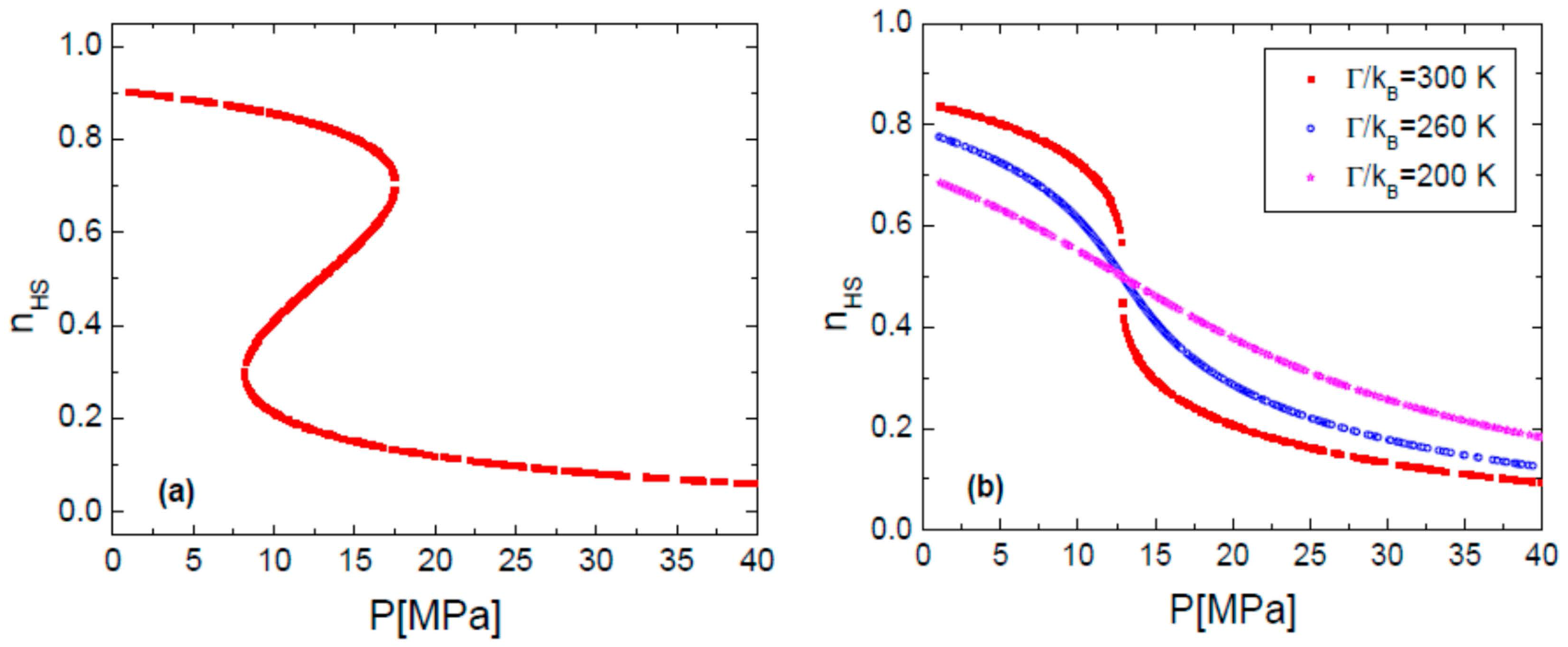
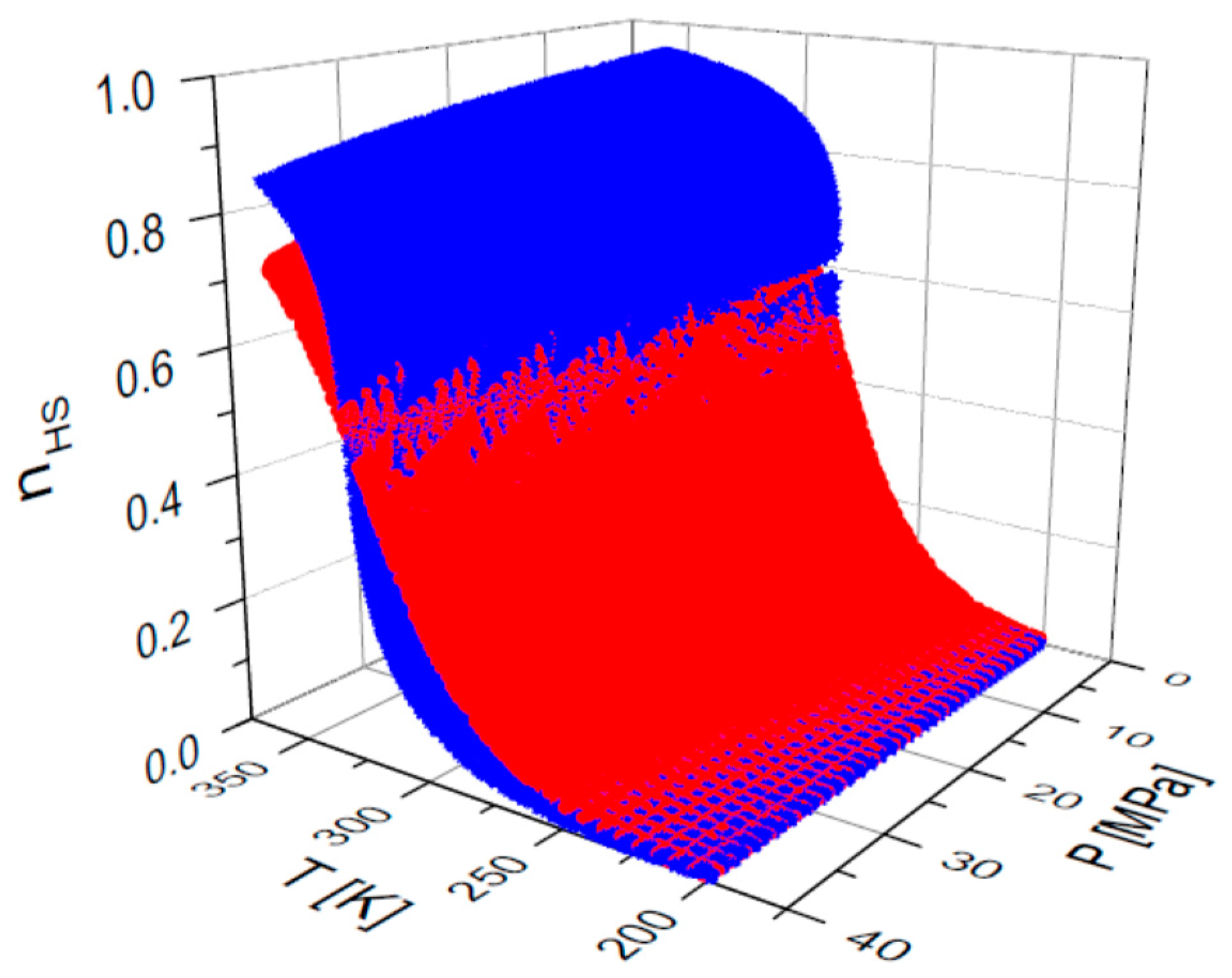

4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hashemian, H.M. Aging management of instrumentation & control sensors in nuclear power plants. Nucl. Eng. Des. 2010, 240, 3781–3790. [Google Scholar]
- Trots, D.M.; Kurnosov, A.; Ballaran, T.B.; Tkachev, S.; Zhuravlev, K.; Prakapenka, V.; Berkowski, M.; Frost, D.J. The Sm:YAG primary fluorescence pressure scale. J. Geophys. Res. 2013, 118, 5805–5813. [Google Scholar] [CrossRef]
- Jayasankar, C.K.; Babu, P.; Tröster, T.; Holzapfel, W.B. High-pressure fluorescence study of Sm3+: Lithium fluoroborate glass. J. Lum. 2000, 91, 33–39. [Google Scholar] [CrossRef]
- Jayasankar, C.K.; Venkatramu, V.; Babu, P.; Tröster, T.; Sievers, W.; Wortmann, G.; Holzapfel, W.B. High-pressure fluorescence study of Sm3+-doped borate and fluoroborate glasses. J. App. Phys. 2005, 97. [Google Scholar] [CrossRef]
- Jayasankar, C.K.; Balakrishnaiah, R.; Babu, P.; Tröster, T.; Sievers, W.; Wortmann, G. High pressure fluorescence studies of Sm3+-doped K-Ba-Al phosphate glass. High Press. Res. 2006, 26, 349–353. [Google Scholar] [CrossRef]
- Basavapoornima, C.; Jayasankar, C.K.; Tröster, T.; Sievers, W.; Wortmann, G. Pressure-dependent fluorescence studies of Sm3+-doped fluorophosphate glass. High Press. Res. 2011, 31, 121–125. [Google Scholar] [CrossRef]
- Barnett, J.D.; Block, S.; Piermarini, G.J. An optical fluorescence system for quantitative pressure measurement in the diamond-anvil cell. Rev. Sci. Instrum. 1973, 44, 1–9. [Google Scholar] [CrossRef]
- Forman, R.A.; Piermarini, C.J.; Barnett, J.D.; Block, S. Pressure measurement made by the utilization of ruby sharp-line luminescence. Science 1972, 176, 284–285. [Google Scholar] [CrossRef] [PubMed]
- Muraki, N.; Matoba, N.; Hirano, T.; Yoshikawa, M. Determination of thermal stress distribution in a model microelectronic device encapsulated with alumina filled epoxy resin using fluorescence spectroscopy. Polymer 2002, 43, 1277–1285. [Google Scholar] [CrossRef]
- Linares, J.; Codjovi, E.; Garcia, Y. Temperature and pressure sensors based on spin transition molecular materials. Sensors 2012, 12, 4479–4492. [Google Scholar] [CrossRef] [PubMed]
- Cavallini, M.; Bergenti, I.; Milita, S.; Kengne, J.C.; Gentili, D.; Ruani, G.; Salitros, I.; Meded, V.; Ruben, M. Thin deposits and patterning of room-temperature-switchable one-dimensional spin-crossover compounds. Langmuir 2011, 27, 4076–4081. [Google Scholar] [CrossRef] [PubMed]
- Molnár, G.; Cobo, S.; Real, J.A.; Carcenac, F.; Daran, E.; Vieu, C.; Bousseksou, A. A Combined Top-Down/Bottom-Up Approach for the Nanoscale Patterning of Spin-Crossover Coordination Polymers. Adv. Mater. 2007, 19, 2163–2167. [Google Scholar] [CrossRef]
- Thibault, C.; Molnar, G.; Salmon, L.; Bousseksou, A.; Vieu, C. Soft lithographic patterning of spin crossover nanoparticles. Langmuir 2010, 26, 1557–1560. [Google Scholar] [CrossRef] [PubMed]
- Naik, A.D.; Stappers, L.; Snauwaert, J.; Fransaer, J.; Garcia, Y. A biomembrane stencil for crystal growth and soft lithography of a thermochromic molecular sensor. Small 2010, 6, 2842–2846. [Google Scholar] [CrossRef] [PubMed]
- Cavallini, M. Status and perspectives in thin films and patterning of spin crossover compounds. Phys. Chem. Chem. Phys. 2012, 14, 11867–11876. [Google Scholar] [CrossRef] [PubMed]
- Quintero, C.M.; Gural’skiy, I.A.; Salmon, L.; Molnar, G.; Bergaud, C.; Bousseksou, A. Soft lithographic patterning of spin crossover complexes. Part 1: Fluorescent detection of the spin transition in single nanoobjects. J. Mater. Chem. 2012, 22, 3745–3751. [Google Scholar] [CrossRef]
- Akou, A.; Gural’skiy, I.A.; Salmon, L.; Bartual-Murgui, C.; Thibault, C.; Vieu, C.; Molnar, G.; Bousseksou, A. Soft lithographic patterning of spin crossover complexes. Part 2: Stimuli-responsive diffraction grating properties. J. Mater. Chem. 2012, 22, 3752–3757. [Google Scholar] [CrossRef]
- Naik, A.D.; Dîrtu, M.M.; Garcia, Y. Effect of texture alteration by thin film fabrication on the spin crossover of [Fe(3-Br-phen)2(NCS)2]∙0.5CH3OH. J. Phys. Conf. Ser. 2010, 217. [Google Scholar] [CrossRef]
- Tanaka, D.; Aketa, N.; Tanaka, H.; Tamaki, T.; Inose, T.; Akai, T.; Toyama, H.; Sakata, O.; Tajiri, H.; Ogawa, T. Thin films of spin-crossover coordination polymers with large thermal hysteresis loops prepared by nanoparticle spin coating. Chem. Commun. 2014, 50, 10074–10077. [Google Scholar] [CrossRef] [PubMed]
- Palamarciuc, T.; Oberg, J.C.; El-Hallak, F.; Hirjibehedin, C.F.; Serri, M.; Heutz, S.; Letard, J.-F.; Rosa, P. Spin crossover materials evaporated under clean high vacuum and ultra-high vacuum conditions: From thin films to single molecules. J. Mater. Chem. 2012, 22, 9690–9695. [Google Scholar] [CrossRef]
- Naggert, H.; Rudnik, J.; Kipgen, L.; Bernien, M.; Nickel, F.; Arruda, L.M.; Kuch, W.; Näther, C.; Tuczek, F. Vacuum-evaporable spin-crossover complexes: Physicochemical properties in the crystalline bulk and in thin films deposited from the gas phase. J. Mater. Chem. C 2015, 3, 7870–7877. [Google Scholar] [CrossRef]
- Cavallini, M.; Bergenti, I.; Milita, S.; Ruani, G.; Salitros, I.; Qu, Z.R.; Chandrasekar, R.; Ruben, M. Micro- and Nanopatterning of Spin-Transition Compounds into Logical Structures. Angew. Chem. Int. Ed. 2008, 47, 8596–8600. [Google Scholar] [CrossRef] [PubMed]
- Bartual-Murgui, C.; Akou, A.; Salmon, L.; Molnar, G.; Thibault, C.; Real, J.A.; Bousseksou, A. Guest Effect on Nanopatterned Spin-Crossover Thin Films. Small 2011, 7, 3385–3391. [Google Scholar] [CrossRef] [PubMed]
- Gütlich, P.; Garcia, Y.; Spiering, H. Spin Transition Phenomena, Magnetism. In Molecules to Materials IV—Nanosized Magnetic Materials; Miller, J.S., Drillon, M., Eds.; Wiley-VCH, Verlag GmbH: Weinheim, Germany, 2003; Chapter 8; pp. 271–344. [Google Scholar]
- Mishra, V.; Mukherjee, R.; Linares, J.; Balde, C.; Desplanches, C.; Letard, J.F.; Collet, E.; Toupet, L.; Castro, M.; Varret, F. Temperature-Dependent Interactions and Disorder in the Spin-Transition Compound [FeIIL2](ClO4)2·C7H8 Through Structural, Calorimetric, Magnetic, Photomagnetic, and Diffuse Reflectance Investigations. Inorg. Chem. 2008, 47, 7577. [Google Scholar] [CrossRef] [PubMed]
- Enachescu, C.; Tanasa, R.; Stancu, A.; Varret, F.; Linares, J.; Codjovi, E. First-order reversal curves analysis of rate-dependent hysteresis: The example of light-induced thermal hysteresis in a spin-crossover solid. Phys. Rev. B 2005, 72. [Google Scholar] [CrossRef]
- Gütlich, P.; Gaspar, A.B.; Garcia, Y. Spin state switching in iron coordination compoun. Beilstein J. Org. Chem. 2013, 9, 342–391. [Google Scholar] [CrossRef] [PubMed]
- Garcia, Y.; van Koningsbruggen, P.J.; Lapouyade, R.; Fournes, L.; Rabardel, L.; Kahn, O.; Ksenofontov, V.; Levchenko, G.; Gütlich, P. Influences of temperature, pressure, and lattice solvents on the spin transition regime of the polymeric compound [Fe(hyetrz)3]A2∙3H2O, with hyetrz = 4-(2’- hydroxyethyl)-1,2,4-triazole and A- = 3-nitrophenylsulfonate. Chem. Mater. 1998, 10, 2426–2433. [Google Scholar] [CrossRef]
- Real, J.A.; Gaspar, A.B.; Munoz, M.C.; Gütlich, P.; Ksenofontov, V.; Spiering, H. Bipyrimidine-Bridged Dinuclear Iron(II) Spin Crossover Compounds. In Spin Crossover in Transition Metal Compounds I; Springer Berlin Heidelberg: Berlin, Germay, 2004; Volume 233, pp. 167–193. [Google Scholar]
- Ohba, M.; Yoneda, K.; Agusti, G.; Munoz, M.C.; Gaspar, A.B.; Real, J.A.; Yamasaki, M.; Ando, H.; Nakao, Y.; Sakaki, S.; et al. Bidirectional chemo-switching of spin state in a microporous framework. Angew. Chem. Int. Ed. 2009, 48, 4767–4771. [Google Scholar] [CrossRef] [PubMed]
- Gütlich, P.; Hauser, A.; Spiering, H. Thermal and optical switching of iron(II) complexes. Angew. Chem. Int. Ed. Engl. 1994, 33, 2024–2054. [Google Scholar] [CrossRef]
- Gütlich, P.; Garcia, Y.; Goodwin, H.A. Spin crossover phenomena in Fe(II) complexes. Chem. Soc. Rev. 2000, 29, 419–427. [Google Scholar]
- Gütlich, P.; Goodwin, H.A. Spin Crossover—An Overall Perspective. In Spin Crossover in Transition Metal Compounds I; Springer Berlin Heidelberg: Berlin, Germay, 2004; Volume 233, pp. 1–47. [Google Scholar]
- Ksenofontov, V.; Spiering, H.; Reiman, S.; Garcia, Y.; Gaspar, A.B.; Moliner, N.; Real, J.A.; Gütlich, P. Direct monitoring of spin state in dinuclear iron(II) coordination compounds. Chem. Phys. Lett. 2001, 348, 381–386. [Google Scholar] [CrossRef]
- Dîrtu, M.M.; Schmit, F.; Naik, A.D.; Rotaru, A.; Marchand-Brynaert, J.; Garcia, Y. Spin transition sensors based on β-amino-acid 1,2,4-triazole derivative. Int. J. Mol. Sci. 2011, 12, 5339–5351. [Google Scholar] [CrossRef] [PubMed]
- Jureschi, C.-M.; Rusu, I.; Codjovi, E.; Linares, J.; Garcia, Y.; Rotaru, A. Thermo- and piezochromic properties of [Fe(hyptrz)]A2∙H2O spin crossover 1D coordination polymer: Towards spin crossover based temperature and pressure sensors. Phys. B 2014, 449, 47–51. [Google Scholar] [CrossRef]
- Lefter, C.; Gural’skiy, I.A.; Peng, H.; Molnár, G.; Salmon, L.; Rotaru, A.; Bousseksou, A.; Demont, P. Dielectric and charge transport properties of the spin crossover complex [Fe(Htrz)2(trz)]BF4. Phys. Status Solidi RRL 2014, 8, 191–193. [Google Scholar] [CrossRef]
- Lefter, C.; Tan, R.; Dugay, J.; Tricard, S.; Molnar, G.; Salmon, L.; Carrey, J.; Rotaru, A.; Bousseksou, A. Light induced modulation of charge transport phenomena across the bistability region in [Fe(Htrz)2(trz)]BF4 spin crossover micro-rods. Phys. Chem. Chem. Phys. 2015, 17, 5151–5154. [Google Scholar] [CrossRef] [PubMed]
- Chiruta, D.; Linares, J.; Dimian, M.; Alayli, Y.; Garcia, Y. Role of edge atoms on the hysteretic behavior of 3D spin crossover nanoparticles revealed by an Ising-like model. Eur. J. Inorg. Chem. 2013, 2013, 5086–5093. [Google Scholar] [CrossRef]
- Rotaru, A.; Dîrtu, M.M.; Enachescu, C.; Tanasa, R.; Linares, J.; Stancu, A.; Garcia, Y. Calorimetric measurements of diluted spin crossover complexes [FexM1-x(btr)2(NCS)2]∙H2O with MII = Zn and Ni. Polyhedron 2009, 28, 2531–2536. [Google Scholar] [CrossRef]
- Rotaru, A.; Linares, J.; Varret, F.; Codjovi, E.; Slimani, A.; Tanasa, R.; Enachescu, C.; Stancu, A.; Haasnoot, J. Pressure effect investigated with first-order reversal-curve method on the spin-transition compounds [FexZn1-x(btr)2(NCS)2]·H2O (x = 0.6, 1). Phys. Rev. B 2011, 83. [Google Scholar] [CrossRef]
- Chiruta, D.; Jureschi, C.-M.; Linares, J.; Garcia, Y.; Rotaru, A. Lattice architecture effect on the cooperativity of spin transition coordination polymers. J. Appl. Phys. 2014, 115. [Google Scholar] [CrossRef]
- Chiruta, D.; Linares, J.; Dahoo, P.R.; Dimian, M. Influence of pressure and interactions strength on hysteretic behavior in two-dimensional polymeric spin crossover compounds. Phys. B 2014, 435, 76–79. [Google Scholar] [CrossRef]
- Wajnsflasz, J.; Pick, R. Low-spin-high-spin transitions in Fe2+ complexes. J. Phys. Colloq. Fr. 1971, 32, C1. [Google Scholar]
- Linares, J.; Spiering, H.; Varret, F. Analytical solution of 1D Ising-like systems modified by weak long range interaction. Eur. Phys. J. B 1999, 10, 271–275. [Google Scholar] [CrossRef]
- Slichter, C.P.; Drickamer, H.G. Pressure-Induced Electronic Changes in Compounds of Iron. J. Chem. Phys. 1972, 56, 2142–2160. [Google Scholar] [CrossRef]
- Dîrtu, M.M.; Gillard, D.; Naik, A.; Rotaru, A.; Garcia, Y. Weak cooperativity in selected iron(II) 1D coordination polymers. Hyperfine Interact. 2012, 205, 75–79. [Google Scholar] [CrossRef]
- Mitsuoka, T.; Nakagawa, M.; Iyoda, T.; Einaga, Y. 57Fe Mössbauer, UV-visible, and FT-IR Study on Photoinduced Spin Transition of FeII-Triazole Complex. J. Nucl. Radiochem. Sci. 2007, 8, 1–3. [Google Scholar] [CrossRef]
- Dîrtu, M.M.; Schmit, F.; Naik, A.; Rotaru, A.; Marchand-Brynaert, J.; Garcia, Y. Impact of ligand spacer and counter-anion in selected 1D iron(II) spin crossover coordination polymers. Hyperfine Interact. 2012, 205, 69–73. [Google Scholar]
- Dîrtu, M.M.; Rotaru, A.; Gillard, D.; Linares, J.; Codjovi, E.; Tinant, B.; Garcia, Y. Prediction of the spin transition temperature in FeII 1D coordination polymers: An anion based database. Inorg. Chem. 2009, 48, 7838–7852. [Google Scholar] [CrossRef] [PubMed]
- Kröber, J.; Audière, J.P.; Claude, R.; Codjovi, E.; Kahn, O.; Haasnoot, J.G.; Grolière, F.; Jay, F.; Bousseksou, A.; Linares, J.; et al. Spin transitions and thermal hystereses in the molecular-based materials [Fe(Htrz)2(trz)]BF4 and [Fe(Htrz)3](BF4)2·H2O (Htrz = 1,2,4-4H-triazole; trz = 1,2,4 triazolato). Chem. Mater. 1994, 6, 1404–1412. [Google Scholar] [CrossRef]
- Jureschi, C.M.; Linares, J.; Rotaru, A.; Ritti, M.H.; Parlier, M.; Dîrtu, M.M.; Wolff, M.; Garcia, Y. Pressure sensor via optical detection based on a 1D spin transition coordinator polymer. Sensors 2015, 15, 2388–2398. [Google Scholar] [CrossRef] [PubMed]
- Ksenofontov, V.; Levchenko, G.; Spiering, H.; Gütlich, P.; Létard, J.-F.; Bouhedja, Y.; Kahn, O. Spin crossover behavior under pressure of [Fe(PM-L)2(NCS)2] compounds with substituted 2′-pyridylmethylene 4-anilino ligands. Chem. Phys. Lett. 1998, 294, 545–553. [Google Scholar] [CrossRef]
- Gaspar, A.B.; Ksenofontov, V.; Real, J.A.; Gütlich, P. Coexistence of spin-crossover and antiferromagnetic coupling phenomena in the novel dinuclear Fe(II) complex [Fe(dpa)(NCS)2]2bpym. Chem. Phys. Lett. 2003, 373, 385–391. [Google Scholar] [CrossRef]
- Seredyuk, M.; Gaspar, A.B.; Ksenofontov, V.; Reiman, S.; Galyametdinov, Y.; Haase, W.; Rentschler, E.; Gütlich, P. Room Temperature Operational Thermochromic Liquid Crystals. Chem. Mater. 2006, 18, 2513–2519. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jureschi, C.-M.; Linares, J.; Boulmaali, A.; Dahoo, P.R.; Rotaru, A.; Garcia, Y. Pressure and Temperature Sensors Using Two Spin Crossover Materials. Sensors 2016, 16, 187. https://doi.org/10.3390/s16020187
Jureschi C-M, Linares J, Boulmaali A, Dahoo PR, Rotaru A, Garcia Y. Pressure and Temperature Sensors Using Two Spin Crossover Materials. Sensors. 2016; 16(2):187. https://doi.org/10.3390/s16020187
Chicago/Turabian StyleJureschi, Catalin-Maricel, Jorge Linares, Ayoub Boulmaali, Pierre Richard Dahoo, Aurelian Rotaru, and Yann Garcia. 2016. "Pressure and Temperature Sensors Using Two Spin Crossover Materials" Sensors 16, no. 2: 187. https://doi.org/10.3390/s16020187
APA StyleJureschi, C.-M., Linares, J., Boulmaali, A., Dahoo, P. R., Rotaru, A., & Garcia, Y. (2016). Pressure and Temperature Sensors Using Two Spin Crossover Materials. Sensors, 16(2), 187. https://doi.org/10.3390/s16020187