Covariance-Based Direction-of-Arrival Estimation of Wideband Coherent Chirp Signals via Sparse Representation
Abstract
: This paper addresses the problem of direction-of-arrival (DOA) estimation of multiple wideband coherent chirp signals, and a new method is proposed. The new method is based on signal component analysis of the array output covariance, instead of the complicated time-frequency analysis used in previous literatures, and thus is more compact and effectively avoids possible signal energy loss during the hyper-processes. Moreover, the a priori information of signal number is no longer a necessity for DOA estimation in the new method. Simulation results demonstrate the performance superiority of the new method over previous ones.1. Introduction
Previous direction-of-arrival (DOA) estimation methods for wideband chirp signals are mostly based on the special time-frequency distribution of such signals. Ma and Goh separate the simultaneous chirp signals first according to their distinguishable auto- or cross-terms in the ambiguity function, and then use the secondary time-frequency data to estimate their directions [1]. Their methods are grounded on the assumption that the signals are separable in the time-frequency domain, so they are not usable for completely overlapped coherent chirp signals. Wang and Xia use the chirp rate and coarse DOA estimates to compensate the time-varying array manifold, and then introduce narrowband methods to refine the DOA estimates [2]. This process is repeated several times to obtain converged source directions, but our experiments and previous literature [1,3] show that such expected convergence is not guaranteed, especially when the signal-to-noise ratio (SNR) is low. Gershman and Amin focus the signal energy to a certain manifold in the time-frequency domain, and then use narrowband methods to estimate the directions of wideband chirp signals [3], but as the focusing process may loose some signal energy, the performance of this method at low SNR may deteriorate significantly. A maximum likelihood (ML) method has also proposed by Gershman et al. in [4] to address the parameter estimation of polynomial-phase signals generally, but it is computationally too intensive, thus is not suitable for practical applications.
This paper addresses the problem of DOA estimation of multiple wideband coherent chirp signals, which emerges due to various factors such as multi-path and echo signals [5]. The recently interest-attracting technique of sparse representation [6,7] is introduced to solve this problem. To simplify the analysis, we assume in this paper that the central frequency and chirp rate of the coherent signals are known, which is reasonable in cooperative applications or when it has been estimated using other methods. The new method significantly differs from previous ones, as it is based on the array output covariance matrix, and completely avoids time-frequency analysis, thus being much more compact and avoiding possible signal energy losses during the complicated hyper-processes. Furthermore, the new method transforms the problem of DOA estimation of wideband chirp signals to one of sparsely representing an observation vector, thus automatically concentrating the observation data energy on the signal directions, so it does not require the a priori information of incident signal number, and it achieves model-order selection simultaneously.
2. Problem Formulation
Suppose that the chirp rate of the incident coherent signals is α, the starting, ending and central frequencies are f1, f2 and f0, respectively, the chirp period is T, signal bandwidth is B, which satisfies. B= f2-f1= αT. The temporal waveform of the chirp signal is:
3. DOA Estimation of Wideband Coherent Chirp Signals
When K wideband coherent chirp signals impinge from directions θ1,…,θK simultaneously, the output of the mth sensor at time t is given by:
Equation (4) indicates that when K wideband coherent chirp signals impinge simultaneously, each covariance element consists of K2 “signal” components, including K auto-tems and K2−K cross-terms. For large, K the structure of the covariance is very complicated, and it is difficult to obtain the signal directions from it. Therefore, we set q=1 in Equation (4) to simplify their structure, i.e., we only extract the elements along the first column. The expressions of those elements are:
As, , the signal components are contaminated by the unknown noise power in R̂1,1, thus we extract the 2nd to Mth elements in the first column to form a new observation vector r̂= [R̂2,1, …, RM,1]T. Define , then r̂1 can be expressed as follows:
This sparse decomposition process can be implemented by solving the following convex optimization problem approximately [6,7]:
In order to solve Equation (9) for DOA estimation, one should first set β according to the perturbation level of r̂1. The variance of perturbation of r̂1 can be straightforwardly derived from Equation (6) as:
Thus the fitting error threshold in Equation (9) can be set according to [10] as:
In the above expression of Var(ε1), Rm,m and can be approximated by the corresponding elements in R̂, and is the unknown noise power. To estimate , we first separate the signal and noise subspaces of R̂ according to the model-order selection techniques, such as MDL [11], then we use the average of the eigenvalues corresponding to the noise subspace to approximate . Thus, the fitting error threshold β is uniquely determined by the weighting factor μ, which relies on the array geometry in use, and can be optimized empirically via sufficient simulations accordingly. In this paper, we choose an 8-element uniform linear array (ULA) for DOA estimation, and μ is set to 0.5.
After calculating the fitting error threshold according to Equation (12) and the above approximations, we can solve Equation (9) to reconstruct the signal components from r̂1, thus estimating the source directions. Various methods can be used for the solution of Equation (9) (see [7] and the references therein), so we do not go deeply into their details, and just turn to the toolbox of SeDuMi [12] for a satisfactory estimate. Finally, the signal directions can be determined according to the locations of the non-zero values in η̂. It should be noted that the sparsity constraint is an inner motivation for solving Equation (9), and this constraint helps to concentrate the data energy onto several dictionary atoms corresponding to the signal directions, thus the a priori information of signal number is not a necessity for the implementation of the new method. However, the goal of model-order selection is also achieved together with DOA estimation.
4. Simulation Results
Suppose two coherent chirp signals impinge onto an 8-element ULA from directions of 10° and 20°, respectively, the central frequency of the two signals is 2.5 MHz with a bandwidth of 40% (the starting and ending frequencies are 2 MHz and 3 MHz accordingly). The initial phases of the two signals are chosen independently and uniformly between 0 and in each trial. The ULA is inter-spaced by half-wavelength of a 2.5 MHz sinusoid, and 512 snapshots are collected at 10 MHz during a chirp period.
As the two signals are completely overlapped in the time-frequency domain, the method in [1] is not able to separate them, thus we choose the conventional coherent signals subspace method (CSM) [13], the iterative method in [2] (denoted as the Wang Method), the focusing method in [3] (denoted as the Gershman Method) and the proposed method to estimate their directions. The central frequency and chirp rate of the incident signals are assumed to be known exactly, the snapshots are divided into sections of 64 snapshots each in CSM, and the iteration number is set to 3 in the Wang Method. The a priori signal number information is not used in the proposed method, but is used in the other three methods. As too dense a dictionary may cause an increased estimation bias in the sparse representation techniques [14], we divide the [−90°, 90° ] space into 1° intervals and set the angular samples on the grids to form the dictionary (the searching grid is set identically in the other three methods). If such spatial sampling does not provide the required precision, further grid refinement process [6] or the ML method [4] can be introduced to improve it. The selected model order and coarse DOA estimates can be used to restrict the parameter scope in those further processes to save computational load. In this paper, we skip over those further processes, and concentrate on the performance of adaptability and superresolution in demanding scenarios.
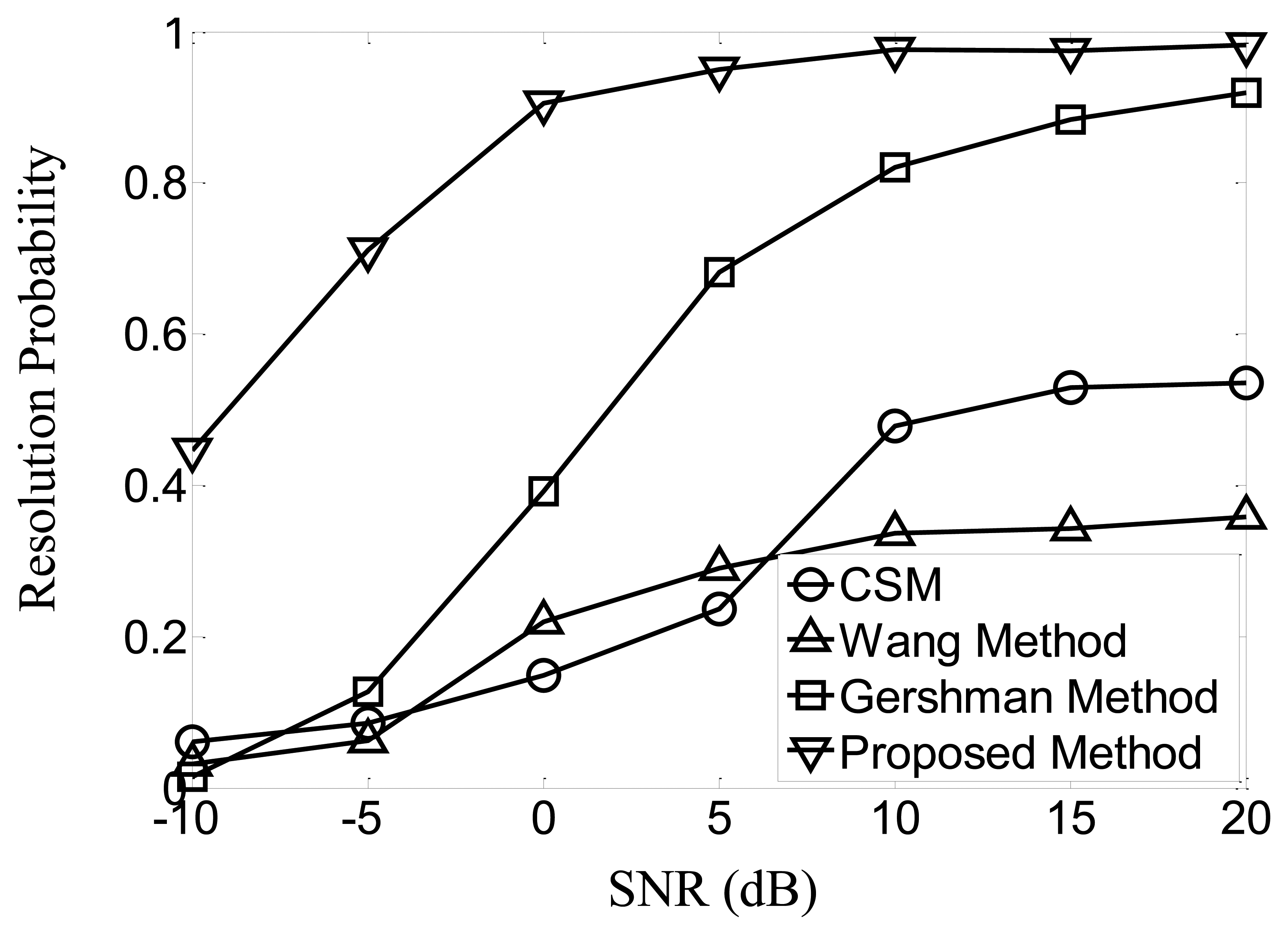
Firstly, suppose that the SNR of both signals is identical and varies from −10 dB to 20 dB, 1,000 trials are carried out at each SNR. Successful resolution is defined when the two most significant spectrum peaks are located near the true signal directions, and the biases are no larger than 3°. The resolution probabilities of the four methods at various SNR are given in Figure 1. The results indicate that, the proposed method greatly surpasses the other three methods in the given scenarios, and Gershman Method obtains the second best performance, while CSM and the Wang Method fail to achieve satisfying resolution probability, even when the SNR is as high as 20 dB.
Then we fix the SNR of the first signal at 10 dB, and attenuate that of the second signal from 10 dB to 0 dB (i.e., the SNR diversity increases from 0 dB to 10 dB) to simulate more vividly the multi-path and echo scenarios. The resolution probabilities of the four methods derived from 1,000 trials are given in Figure 2. The results show that the proposed method is less significantly influenced by the power diversity. It still retains a higher than 80% resolution probability when the SNR diversity is as large as 10 dB. Contrarily, the resolution probabilities of CSM and the Wang Method decrease to 0, and that of the Gershman Method decreases to about 40%.
6. Conclusions
The technique of sparse representation to estimate the directions of simultaneous wideband coherent chirp signals is introduced in this paper. The covariance matrix, instead of the time-frequency distribution, is exploited in the new method, and the a priori information of signal number is no longer a necessity. Simulation results show that the proposed method greatly surpasses its existing counterparts, especially when the SNR is low or the incident signals are very diverse in amplitude. Moreover, it simultaneously achieves model-order selection.
Acknowledgments
This work was supported by the program for New Century Excellent Talents in University (NCET).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ma, N.; Goh, J.T. Ambiguity-function-based techniques to estimate DOA of broadband chirp signals. IEEE Trans. Signal Proc. 2006, 54, 1826–1839. [Google Scholar]
- Wang, G.; Xia, X.G. Iterative algorithm for direction of arrival estimation with wideband chirp signals. IEE Proc. Radar Sonar Navig. 2000, 147, 233–238. [Google Scholar]
- Gershman, A.B.; Amin, M.G. Wideband direction-of-arrival estimation of multiple chirp signals using spatial time-frequency distributions. IEEE Signal Proc. Lett. 2000, 7, 152–155. [Google Scholar]
- Gershman, A.B.; Pesavento, M.; Amin, M.G. Estimating parameters of multiple wideband polynomial-phase sources in sensor arrays. IEEE Trans. Signal Proc. 2001, 49, 2924–2934. [Google Scholar]
- Cowell, D.M.J.; Freear, S. Separation of overlapping linear frequency modulated (LFM) signals using the fractional Fourier transform. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 2324–2333. [Google Scholar]
- Malioutov, D.; Cetin, M.; Willsky, A.S. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Proc. 2005, 53, 3010–3022. [Google Scholar]
- Tropp, J.A.; Wright, S.J. Computational methods for sparse solution of linear inverse problems. Proc. IEEE 2010, 98, 948–958. [Google Scholar]
- Fuchs, J.J. Multipath time-delay detection and estimation. IEEE Trans. Signal Proc. 1999, 47, 237–243. [Google Scholar]
- Chen, J.; Huo, X. Theoretical results on sparse representations of multiple-measurement vectors. IEEE Trans. Signal Proc. 2006, 54, 4634–4643. [Google Scholar]
- Donoho, D.L.; Mallat, S.; Sachs, R.; Samuelides, Y. Locally stationary covariance and signal estimation with macrotiles. IEEE Trans. Signal Proc. 2003, 51, 614–627. [Google Scholar]
- Stoica, P.; Selen, Y. Model-order selection: A review of information criterion rules. IEEE Signal Proc. Mag. 2004, 21, 36–47. [Google Scholar]
- Sturm, J.F. Using SeDuMi 1.02, a Matlab Toolbox for Optimization over Symmetric Cones. Optim. Methods softw. 1999, 11, 625–653. [Google Scholar]
- Wang, H.; Kaveh, M. Coherent signal-subspace processing for the detection and estimation of angles of arrival of multiple wide-band sources. IEEE Trans. Acoust. Speech Signal Proc. 1985, 33, 823–831. [Google Scholar]
- Sustin, C.D.; Moses, R.L.; Ash, J.N.; Ertin, E. On the relation between sparse reconstruction and parameter estimation with model order selection. IEEE J. Sel. Top. Signal Proc. 2010, 4, 560–570. [Google Scholar]

© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sha, Z.; Liu, Z.; Huang, Z.; Zhou, Y. Covariance-Based Direction-of-Arrival Estimation of Wideband Coherent Chirp Signals via Sparse Representation. Sensors 2013, 13, 11490-11497. https://doi.org/10.3390/s130911490
Sha Z, Liu Z, Huang Z, Zhou Y. Covariance-Based Direction-of-Arrival Estimation of Wideband Coherent Chirp Signals via Sparse Representation. Sensors. 2013; 13(9):11490-11497. https://doi.org/10.3390/s130911490
Chicago/Turabian StyleSha, Zhichao, Zhengmeng Liu, Zhitao Huang, and Yiyu Zhou. 2013. "Covariance-Based Direction-of-Arrival Estimation of Wideband Coherent Chirp Signals via Sparse Representation" Sensors 13, no. 9: 11490-11497. https://doi.org/10.3390/s130911490



