A Table-Shaped Tactile Sensor for Detecting Triaxial Force on the Basis of Strain Distribution
Abstract
: A slim and flexible tactile sensor applicable to the interaction of human and intelligent robots is presented. In particular, a simple sensing principle for decoupling of three-dimensional force is proposed. Sensitivity of the proposed tactile sensor is tested experimentally. To improve the sensitivity of the sensor, a table-shaped sensing element was designed. Table-shaped structure can convert an external acting force into concentrated internal stress. A “triaxial force decoupling algorithm” was developed by combining two-dimensional mapping data calculated by finite element analysis. The sensor was calibrated under normal and tangential forces. The external loads applied to the sensor could be decoupled independently as a function of the strain-gauge responses.1. Introduction
In recent years, studies on human–robot interaction have needed to utilize tactile sensors to physically interact with people and their environment in contexts such as rehabilitation, home/hospital care, education, and entertainment. In regard to human communication, physical touch is essential for an infant or child's social, cognitive, and physical development [1]. Touch also plays an important role in adulthood, when a person is soothing, playing, and maintaining proximity between a child and caretaker [2]. Similarly, physical interaction with robots (such as hugging and hand shaking) builds closer relationships between a human and a robot from the perspective of spatial distance [3]. The ROBOSKIN project shows another application domain of tactile interaction, namely, that between robots and autistic children to improve social-interaction capabilities of the children [4]. Furthermore, physical therapy for stroke rehabilitation by robotic manipulators is a promising application of tactile sensors [5].
In work on the human–robot collaboration, researchers have been developing tactile sensors [6,7]. Manipulating objects by a robotic hand requires flexible tactile sensors mounted on the curved surface of the robot's fingertip to detect the forces acting on it. To dexterously manipulate and grasp an object while maintaining physical contact between the object and the robot's finger tips, it must be possible to measure normal and tangential forces acting on the object. To enable that measurement, two studies applied displacement control by robot-vision systems [8,9] and another used a force-toque sensor on the fingertips of the robotic hand [10]. In consideration of the role of tactile sensors in the domain of human–robot interaction, it is necessary to ensure that the sensors are small and flexible enough to fit onto various surfaces of machinery components as well as have sufficient accuracy to allow precise manipulation of the robotic hand.
Researchers have been developing several types of tactile sensor based on “microelectromechanical systems” (MEMS) composed of different materials (e.g., silicon and polymers) because MEMS can be applied to tiny integrated sensing units. In the early stage of developing tactile sensors, Kane et al. and Mei et al. used micromachining to fabricate diaphragm-style tactile sensors composed of triaxial force sensors [11,12]. Although these silicon micro-machined tactile sensors have high sensitivity, they are not flexible or durable. Silicon is mechanically brittle, so it cannot sustain large deformations and sudden shocks. Additionally, a rigid silicon substrate makes it difficult to cover contoured surfaces [13,14]. The characteristics of silicon-based tactile sensors makes it difficult to apply them in wide variety of domains and, at the same time, increases development cost. Meanwhile, other approaches are using change of capacitance or conductive polymer films [15–17]. Even if these types of tactile sensors are beneficial in terms of low development cost and higher flexibility, they still have two drawbacks: low sensitivity and poor spatial resolution. To create a tactile sensor with both small size and high flexibility, polymer micromachining (which makes it possible to integrate MEMS devices on a flexible polymer substrate) has been introduced. Engel et al. have proposed a “flexible tactile-sensor skin” that has an expandable sensor array [14]. However, this sensor (skin) is can only measure a normal force component. To overcome these drawbacks of the silicon-based and polymer-based approaches, “hybrid tactile sensors”—combining silicon and polymers—have recently been developed [18–20]. Various other types of tactile sensor, including optical ones, have been developed [6,21]. Although flexible polymer-based tactile sensors are being increasingly reported, it is still a great challenge to implement three-axial force detection with a small tactile sensor. In a previous study, the authors demonstrated a prototype flexible tactile sensor with a three-dimensional table-shaped structure [22]. However, we did not present a solution to the problem of simultaneously applying a three-dimensional resultant force; that is, our previous work presented measurement results under the restriction of independently separated normal and tangential forces [22]. Generally, if the resultant force is applied at a point on the contact surface, it is possible to apply torque to the contact surface. In the present study, this difficulty is irrelevant since the target of the sensor is assumed to be manipulated by the robot's finger. In other words, torque does not occur because loading applied to the contact surface is a uniformly distributed load (i.e., not a point). However, we plan to improve the algorithm for decoupling the applied three-dimensional force by assuming that torque is exerted by the applied force. In the present study, a new approach for decoupling the applied three-dimensional force by using normalized force components is therefore proposed. In particular, the mechanism of force detection was identified, and a decoupling algorithm for a tactile sensor was devised and applied to the dexterous manipulation by a robotic hand.
2. Triaxial Force Decoupling
2.1. Sensor Body and Circuit Design
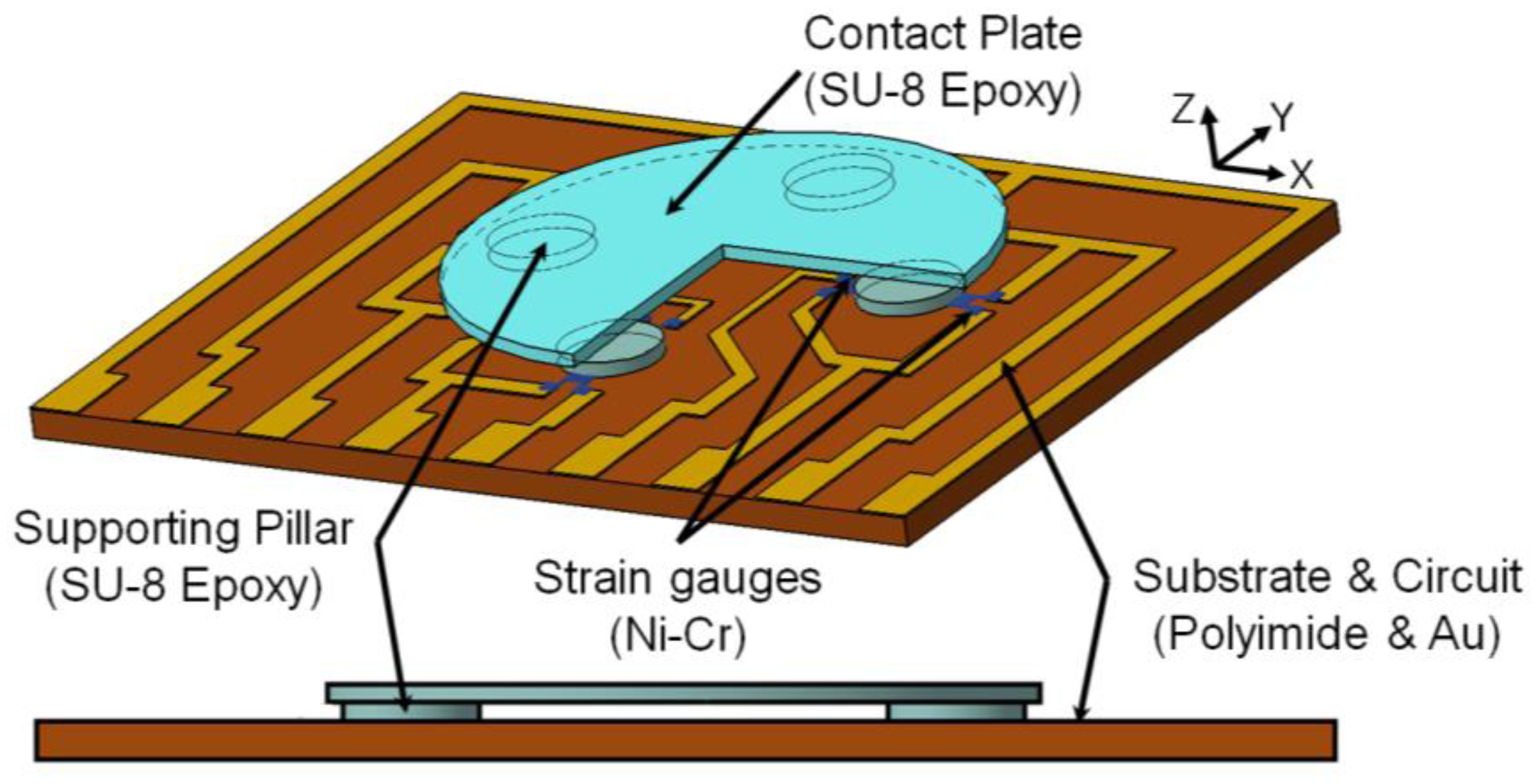
In this study, a resistance-type tactile sensor is used. A strain gauge can convert an external force to change of resistance as an internal strain. To amplify a contact stress, a tactile-sensing pad has a three-dimensional, small and thin structure with a table-shaped top-head. A schematic diagram and cross-sectional view of the table-shaped sensing pad is shown in Figure 1. A polymer material (SU-8 epoxy) was used as the three-dimensional structure of the contact plate and force-transfer pillars.
To maximize the sensitivity of the sensor, the optimal locations of the strain gauges were determined by the strain distribution obtained by finite element analysis. The strain distribution was then used to determine the shape of the strain gauge and its size. Configuration of strain gauges is carefully investigated to set the area of highest strain. The conceptual design of the sensor was determined by a commercial finite element analysis (FEA) program, i.e., ABAQUS Ver. 6.10.
Since the external force applied to the sensing plate is transmitted to the substrate through the force-transfer columns, most strain changes on the substrate appear on the bottom of the strained columns. From the FEA analysis results, it is clear that the strain-sensing elements in the tactile sensor must be placed at the periphery of the columns. The designed tactile sensor consists of a 60-μm-thick, 1,870-μm-diameter upper plate as a sensing element and four 60-μm-high, 440-μm-diameter force-transfer columns on a 125-μm-thick, 4.18 × 2.91-mm rectangular membrane (see Figure 1). The membrane material is a polyimide film (with Young's modulus of 2.5 GPa and Poisson's ratio of 0.34). For the column and upper-plate materials, SU-8, with Young's modulus of 4.4 GPa and Poisson's ratio of 0.22, is used [23].
As shown in Figure 2, four strain gauges (R2, R1, R5, and R6) along the x-axis and four more strain gauges (R4, R3, R7, and R8) along the y-axis are arranged as pairs under the four force-transfer columns. The resistance of the strain gauges is changed symmetrically as they are physically deformed according to the applied direction of external force. Put simply, to measure the direction and magnitude of the applied external force, just four strain gauges (R1, R3, R5, and R7) inside of the contact plate are needed. The direction and magnitude of applied force could therefore be measured by combination of either increasing or decreasing the output resistance.
2.2. Superposition Principle of Vector Force
Force applied to a monolithic sensor is a vector combination of normal and tangential forces. The mixed components of normal and tangential forces must be decoupled. However, it is a problem that the decoupling cannot be done directly. To solve this problem, output resistance can be related to applied loading. A distribution map of the strain gauges (which depends on the configuration of the gauges) can then be drawn. It is therefore possible to approximately calculate the direction and magnitude of the applied loading through the reconstruction of the contributing directional forces (which are combined by using calibration data).
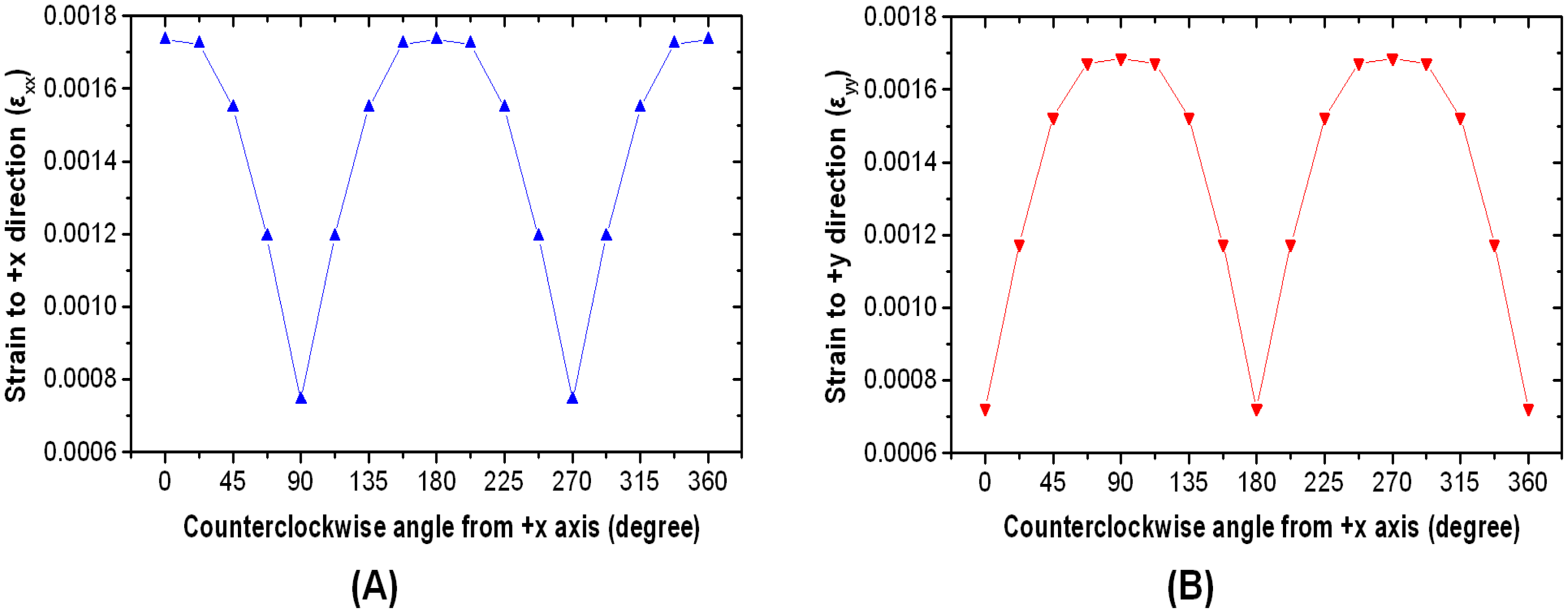
A schematic representation of the design of loading simulations for each directional tangential loading is shown in Figure 3. Maximum strain change under 1-N directional tangential loading is plotted against principal strain variation in the +x direction (εxx) in Figure 4A, and principal strain variation in the +y direction (εyy) is plotted in Figure 4B. These data are measured every 22.5° from 0° to 360° parallel to the +x-axis. These asymmetric sinusoidal results caused by the configuration of the support pillar could be expandable in two-dimensional mapping shown as Figure 5. We are able to produce a two-dimensional strain distribution map to directional loading divided into five cases.
The results of FEA loading simulations, namely, displacement contour (U) and strain distribution due to application of 1-N directional tangential loading [(εxx) and (εyy)] at 0°, 22.5°, 45°, 67.5°, and 90° against the +x-axis, are plotted in Figure 5A–E, respectively. A displacement contour (U) and strain distribution due to application of 1-N normal loading [(εxx) and (εyy)] are plotted in Figure 5F. A displacement contour (U) and strain distribution due to application of normal and tangential loading ((εxx) and (εyy)) at 0° against the +x-axis are plotted in Figure 5G. To find the origin of the applied force, we are able to use two-dimensional mapping data obtained from the directional force contribution of the strain distribution. Direction and magnitude of the applied loading can therefore be back-calculated by reconstructing an image of the total-axial-force components. This superposition principle is theoretically right (at least in the elastic region).
2.3. Decoupling Method
Increases and decreases in change of resistance according to direction of applied external force are listed in Table 1. In the table, “(+)” and “(−)” signs indicate increase and decrease in resistance against the initial value, respectively. For example, when an external force is applied in the +x-axis direction, strain gauges R1 and R5 adopt compressive and tensile states, respectively. The resistances therefore decrease (−, R1) and increase (+, R5), respectively. Meanwhile, when an external force is applied in the −x-axis direction, strain gauges R1 and R5 adopt tensile and compressive states, respectively. These resistance changes are opposite to those in the case that the external force is applied in the +x-axis direction. Note here that R3 and R7 lie along the y-axis and the change of resistance is negligibly small (see strain distribution (εyy) in Figure 5A). When an external force is applied in either the ±x or ±y-axis direction, the other axial change of resistance should be designed to be as small as possible. When an external force is applied in the +y-axis direction, the resistance changes of R3 and R7 are decreased and increased, respectively. Here, R1 and R5 (lying along the x-axis) are also not physically changed (see strain distribution (εxx) in Figure 5E). On the other hand, when an external force is applied in the normal direction (i.e., the −z-axis direction) relative to the contact plate surface, the resistances of all the strain gauges (R1, R3, R5, and R7) increase (see Figure 5F).
The strain distributions due to the configuration of the strain gauges give the decoupling solution derived from the directional force components in the following equations. Generally, this decoupling solution has been widely applied to resistance-type tactile sensors [24–27]; for −Fz loading; from strain gauge signals of R1, R3, R5 and R7:
Here, ΔR means the change of resistance of the strain gauge. The positive sign represents a tensile state, and the negative sign represents a compressive state. From Equations (1) to (3), the magnitude of loadings can be calculated. Applied loadings along the x-, y-, and z-axes can be estimated through calculation of the resistance change from the output signals of the four strain gauges arranged inside contact plate. In Figure 2, the four extra strain gauges (R2, R4, R6, and R8) arranged outside of the contact plate (which are candidates for a quarter-bridge or moment-compensation circuit) are also shown. However, these extra strain gauges are not considered in this study.
2.4. Application of Decoupling Method to Loading Simulations
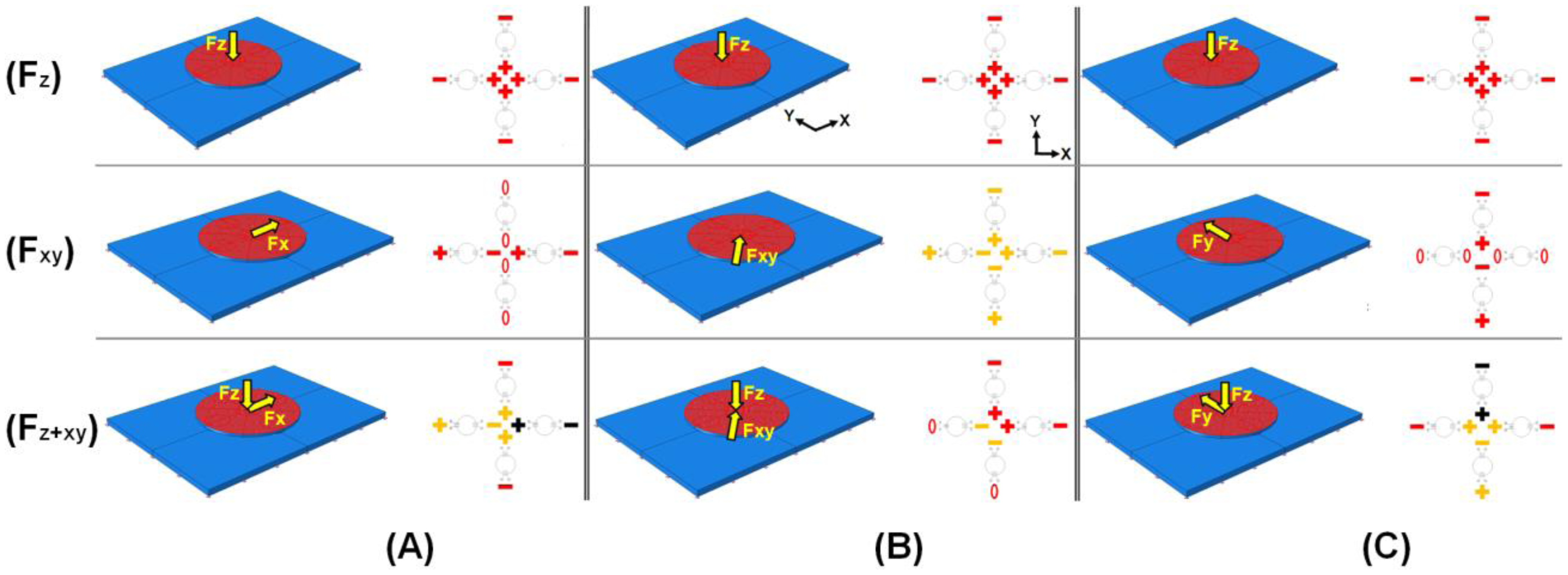
The combined results of Figures 4 to 5 and Table 1 are shown in Figure 6A–C. The FEA simulation result for superposition of normal force and tangential force at 0° parallel to the +x-axis is shown in Figure 6A. When a normal load is uniformly applied to the top surface of the contact plate, the simulation result shows a symmetrical feature under the support column. Four strain gauges inside the contact plate undergo tensile state (see Figure 6Fz). However, the state of the four strain gauges arranged outside the contact plate becomes compressive. Meanwhile, in the case that a tangential load is uniformly applied to the contact plate, the simulation result shows two different results. The state of the strain gauges arranged in the forward direction of the columns parallel to the loading direction becomes compressive, while the state of the strain gauges arranged in the backward direction of the columns parallel to the loading direction becomes tensile. Notice that the four strain gauges at a right angle to the loading direction do not change state (see Figure 6Fxy). Therefore, superposition of normal force and tangential force at 0° parallel to the +x-axis shows the sum of the strain change at each strain gauge. However, tangential variation is more dominant compared to normal variation in the case of the resultant force, if the magnitudes of the applied normal and tangential forces are the same.
Accordingly, when the positive sign of a tangential force meets the negative sign of a normal force, it does not give zero (see Figure 6Fz+xy). In the figure, red indicates the strain change values under applied loading of 1 N. Black indicates duplicated red. Yellow indicates counterbalanced value when (+) and (−) red meet each other. Similarly, results for the superposition of normal force and tangential force at 45° and 90° parallel to the +x-axis are shown in Figure 6B,Crespectively. The signal combinations of all possible arrangements of the strain gauges and the predicted direction are listed in Table 2. The directions of applied tangential force can be predicted by comparing the configuration of settled standard feature using Figure 6 due to Table 1 and Figures 4 and 5. Prediction resolution is shown as three levels of color (i.e., black, red, and yellow). Note that the prediction resolution can be increased by increasing the number of color levels.
3. Sensor Fabrication
A tactile sensor was fabricated (inside a clean room) by the following process: first, nickel-chrome-alloy (Ni-Cr; 80:20) strain gauges were made by sputtering and lift-off techniques. In detail, a 400-Å-thick Ni-Cr layer was patterned on a 100-Å-thick chromium adhesion layer on a 125-μm-thick polyimide substrate. Then, 2,000-Å-thick gold interconnects were deposited on a 200-Å-thick chromium adhesion layer by sputtering and lift-off on the top surface of the polyimide film. A sacrificial layer was used to make a table-shaped three-dimensional structure as a sensing element. As a contact plate and support column respectively, SU-8 epoxy was deposited by using a photo-definable lithography process on the surface of the film. After all micromachining process was completed, the fabricated sensor (with a total thickness of 250 μm) has a radius of curvature of less than 8 mm. This curvature coincides with the expected flexibility of this study. The fabricated sensor body and table-shaped pad are shown in Figure 7A. Finally, the tactile sensor was connected to an electric cord and packaged (see Figure 7B).
4. Force Detection
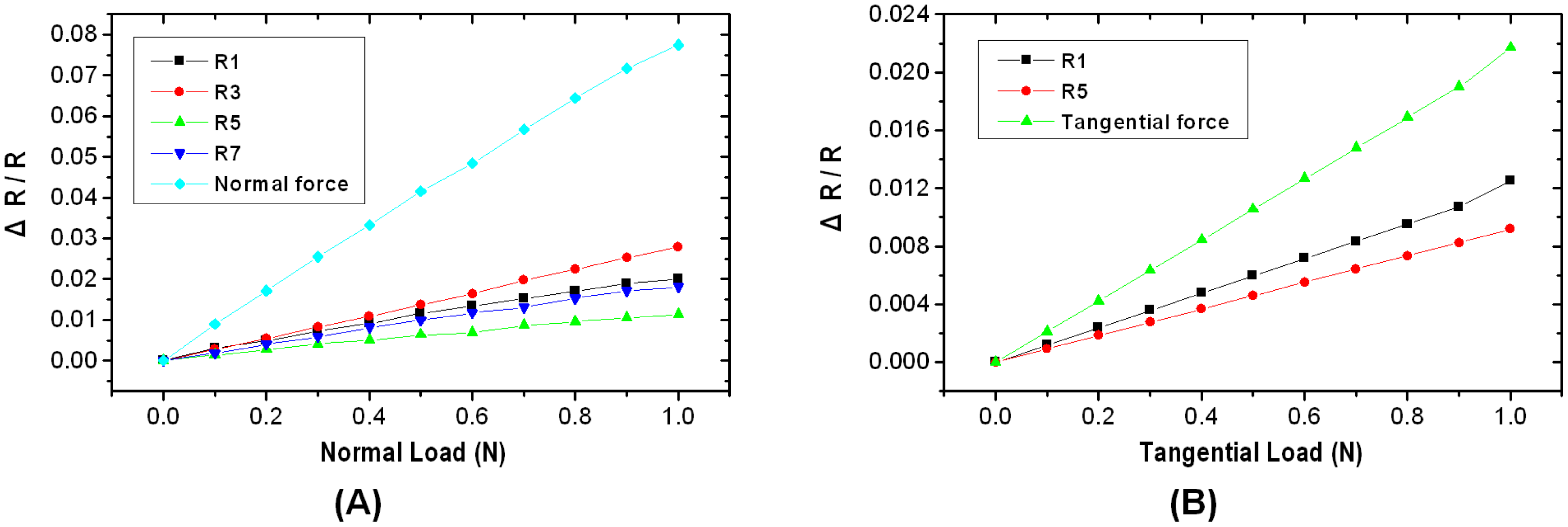
The fabricated tactile sensor was evaluated by using a three-component load cell to apply normal and tangential forces between zero and 1 N, respectively. For the signal processing, a PCI-type 12-bit/16-channel data-acquisition board (PCI-3174, Interface. Co., Hiroshima, Japan) and I/O interface (TRM-7101, Interface. Co) were connected to the sensor with a power supply (IPS-3610D, ISO-tech. Co., Corby, UK), and a constant force was applied to the sensor. The voltage change of each strain gauge was converted to a resistance through the data-acquisition board, and the load was calculated from that resistance. While force was applied to the sensor along the z- and x-axes, the change in force on the four strain gauges, R1, R3, R5 and R7, was measured. The measured increases and decreases in resistances were found to be equal to the theoretically expected values listed in Table 1.
When Fz loading increasing from 0 to 1 N was applied to the sensor, the output signal due to the resistance change with respect to the Fz loading (which is normalized by resistors R1, R3, R5, and R7) is shown in Figure 8A. Ideally, strain gauges made by the same process will have equal resistances. Although the experimental setup is perfect, fabrication errors due to the uncontrollable factors are inevitable. If the fabrication process is improved in the future, we believe that it will be possible to provide a simpler algorithm. The resolution of resistance with respect to force is measured at 77,465 ppm/N in terms of ΔR/R. In the case of applied Fx loading (which is normalized by resistors R1 and R5), the resolution of resistance with respect to force is measured at 21,693 ppm/N, see Figure 8B. To verify the proposed decoupling method, we plan to develop an experimental setup for applying normal and tangential loadings simultaneously.
5. Concluding Remarks
A new type of slim, flexible tactile sensor and an analytical approach for a decoupling method for obtaining directional three-dimensional force components were proposed. A table-shaped epoxy sensing plate with four legs was built on the top of a flexible polymer substrate to enhance sensor sensitivity. The applied forces could be calculated by combining the signal responses from the strain gauges. To calculate the applied loading, two-dimensional mapping results derived from finite element analysis was developed. The tactile sensor was calibrated to normal and tangential loadings from 0 to 1 N by the evaluation apparatus. The proposed sensing and decoupling algorithm are able to measure the triaxial forces only using four strain gauges. In the future, the sensing and decoupling algorithm will be improved to measure not only force, but also torque, by using all eight strain gauges and to solve a moment interference problem when a sensing pad meets the inclined force. It is hoped that the improved sensor will find many applications in the fields of not only intelligent robotic hand manipulation, but also physical human–robot interaction and human–robot collaborative tasks such as dependable force feedback control.
Acknowledgments
This work was partially supported by the 18th Research Promotion Program for Foreign Researchers in the HORI Information Science Promotion Foundation, Japan and Global Center of Excellence (GCOE) program (Micro- and Nano-Mechatronics for Information-Based Society) of the Ministry of Education, Culture, Sports, Science and Technology, Japan. We would like to thank Jong Ho Kim and Hyun Joon Kwon of the Korea Research Institute of Standards and Science (KRISS) for their technical assistance of calibration.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Field, T. Touch in Development. In Touch; MIT Press: Cambridge, MA, USA, 2001; pp. 37–57. [Google Scholar]
- Eibl-Eibesfeldt, I. Tactile Communication. In Human Ethology; Aldine de Gruyter: Hawthorne, NY, USA, 2001; pp. 430–437. [Google Scholar]
- Yamaoka, F.; Kanda, T.; Ishiguro, H.; Hagita, N. How contingent should a lifelike robot be? The relationship between contingency and complexity. Connect. Sci. 2007, 19, 143–162. [Google Scholar]
- Wainer, J.; Dautenhahn, K.; Robins, B.; Amirabdollahian, F. A pilot study with a novel setup for collaborative play of the humanoid robot KASPAR with children with autism. Int. J. Soc. Rob. 2013. [Google Scholar] [CrossRef]
- Lum, P.S.; Burgar, C.G.; Shor, P.C.; Majmundar, M.; Loos, M.V. Robot-assisted movement training compared with conventional therapy techniques for the rehabilitation of upper-limb motor function after stroke. Arch. Phys. Med. Rehabil. 2002, 83, 952–959. [Google Scholar]
- Yussof, H.; Ohka, M.; Suzuki, H.; Morisawa, N.; Takata, J. Tactile sensing-based control architecture in multi-fingered arm for object manipulation. Eng. Lett. 2008, 16, 236–247. [Google Scholar]
- Fritzsche, M.; Elkmann, N.; Schulenburg, E. Tactile Sensing: A Key Technology for Safe Physical Human Robot Interaction. Proceedings of International Conference on Human-Robot Interaction, Lausanne, Switzerland, 8–11 March 2011; pp. 139–140.
- Hager, G.D. A modular system for robust positioning using feedback from stereo vision. Trans. Rob. Autom. 1997, 13-14, 582–595. [Google Scholar]
- Prats, M.; Martinet, P.; Pobil, A.P.; Lee, S. Vision/Force Control in Task-Oriented Grasping and Manipulation. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 1320–1325.
- Wen, S.; Jia, B.; Wu, T.; Liu, S. Unknown objects grasp planning using force/torque measurements. Adv. Int. Soft Comput. 2012, 125, 741–749. [Google Scholar]
- Kane, B.J.; Cutkosky, M.R.; Kovacs, G.T.A. A traction stress sensor array for use in high-resolution robotic tactile imaging. JMEMS 2000, 9, 425–434. [Google Scholar]
- Mei, T.; Li, W.J.; Ge, Y.; Chen, Y.; Ni, L.; Chan, M.H. An integrated MEMS three-dimensional tactile sensor with large force range. Sens. Actuators A 2000, 80, 155–162. [Google Scholar]
- Lee, M.H.; Nicholls, H.R. Tactile sensing for mechatronics—A state of the art survey. Mechatronics 1999, 9, 1–31. [Google Scholar]
- Engel, J.; Chen, J.; Liu, C. Development of polyimide flexible tactile sensor skin. J. Micromech. Microeng. 2003, 13, 359–366. [Google Scholar]
- Cheng, M.Y.; Huang, X.H.; Ma, C.W.; Yang, Y.J. A flexible capacitive tactile sensing array with floating electrodes. J. Micromech. Microeng. 2009, 19, 115001. [Google Scholar]
- Lee, H.K.; Chang, S.I.; Yoon, E. A flexible polymer tactile sensor: Fabrication and modular expandability for large area deployment. JMEMS 2006, 15, 1681–1686. [Google Scholar]
- Yang, Y.J.; Cheng, M.Y.; Chang, W.Y.; Tsao, L.C.; Yang, S.A.; Shih, W.P.; Chang, F.Y.; Chang, S.H.; Fan, K.C. An integrated flexible temperature and tactile sensing array using PI-copper films. Sens. Actuators A 2008, 143, 143–153. [Google Scholar]
- Jiang, F.; Lee, G.B.; Tai, Y.C.; Ho, C.M. A flexible micromachine-based shear-stress sensor array and its application to separation-point detection. Sens. Actuators A 2000, 79, 194–203. [Google Scholar]
- Noda, K.; Hoshino, K.; Matsumoto, K.; Shimoyama, I. A shear stress sensor for tactile sensing with the piezoresistive cantilever standing in elastic material. Sens. Actuators A. 2006, 127, 295–301. [Google Scholar]
- Sohgawa, M.; Hirashima, D.; Moriguchi, Y.; Uematsu, T.; Mito, W.; Kanashima, T.; Okuyama, M.; Noma, H. Tactile sensor array using microcantilever with nickel-chromium alloy thin film of low temperature coefficient of resistance and its application to slippage detection. Sens. Actuators A 2012, 186, 32–37. [Google Scholar]
- Hasegawa, Y.; Shikida, M.; Shimizu, T.; Miyaji, T.; Sasaki, H.; Sato, K.; Itoigawa, K. A micromachined active tactile sensor for hardness detection. Sens. Actuators A 2004, 114, 141–146. [Google Scholar]
- Lee, J.I.; Hida, H.; Shikida, M.; Sato, K. Microfabricated 3D Flexible Tactile Sensor with Table-Shaped Structure for Intelligent Robot Fingers. Proceedings of the IEEE International Symposium on Micro-Nano Mechatronics and Human Science, Nagoya, Japan; 2010; pp. 417–419. [Google Scholar]
- Mark, J.E. Polymer Data Handbook; Oxford University Press Inc.: New York, NY, USA, 1999. [Google Scholar]
- Kim, J.H.; Lee, J.I.; Lee, H.J.; Park, Y.K.; Kim, M.S.; Kang, D.I. Design of Flexible Tactile Sensor Based on Three-Component Force and its Fabrication. Proceedings of the IEEE International Conference on Robotics and Automation, Barcelona, Spain; 2005; pp. 2589–2592. [Google Scholar]
- Lee, J.I.; Kim, J.H.; Choi, W.C.; Park, Y.K.; Kang, D.I. Design of a Flexible Tactile Sensor Based on Polymer Micromachining and Its Fabrication. Proceedings of the Asia-Pacific Symposium on Mass, Force and Torque, Jeju, Korea, 18–22 April 2005; pp. 269–274.
- Kwon, H.J.; Choi, W.C. Design and fabrication of a flexible three-axial tactile sensor array based on polyimide micromachining. J. Microsyst. Technol. 2010, 16, 2029–2035. [Google Scholar]
- Kwon, H.J.; Kim, J.H.; Choi, W.C. Development of a flexible three-axial tactile sensor array for a robotic finger. J. Microsyst. Technol. 2011, 17, 1721–1726. [Google Scholar]




| Sign of the Strain Gauges by Applying Direction | ||||||
|---|---|---|---|---|---|---|
| +x | −x | +y | −y | −z | ||
| Strain gauges on the axis along the x-direction | R2 | (+) | (−) | 0 | 0 | (−) |
| R1 | (−) | (+) | 0 | 0 | (+) | |
| R5 | (+) | (−) | 0 | 0 | (+) | |
| R6 | (−) | (+) | 0 | 0 | (−) | |
| Strain gauges on the axis along the y-direction | R8 | 0 | 0 | (−) | (+) | (−) |
| R7 | 0 | 0 | (+) | (−) | (+) | |
| R3 | 0 | 0 | (−) | (+) | (+) | |
| R4 | 0 | 0 | (+) | (−) | (−) | |
| Signals and Decisions | |||||
|---|---|---|---|---|---|
| R1 | R3 | R5 | R7 | Decision | |
| 1 | + | + | + | + | F−z |
| 2 | − | 0 | + | 0 | F+x |
| 3 | + | 0 | − | 0 | F−x |
| 4 | 0 | − | 0 | + | F+y |
| 5 | 0 | + | 0 | − | F−y |
| 6 | − | − | + | + | F+x+y |
| 7 | + | − | − | + | F−x+y |
| 8 | + | + | − | − | F−x−y |
| 9 | − | + | + | − | F+x−y |
| 10 | − | + | + | + | F−z+ F+x |
| 11 | + | + | − | + | F−z+ F−x |
| 12 | + | − | + | + | F−z+ F+y |
| 13 | + | + | + | − | F−z+ F−y |
| 14 | − | − | + | + | F−z+ F+x+y |
| 15 | + | − | − | + | F−z+ F−x+y |
| 16 | + | + | − | − | F−z+ F−x−y |
| 17 | − | + | + | − | F−z+ F+x−y |
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lee, J.I.; Kim, M.-G.; Shikida, M.; Sato, K. A Table-Shaped Tactile Sensor for Detecting Triaxial Force on the Basis of Strain Distribution. Sensors 2013, 13, 16347-16359. https://doi.org/10.3390/s131216347
Lee JI, Kim M-G, Shikida M, Sato K. A Table-Shaped Tactile Sensor for Detecting Triaxial Force on the Basis of Strain Distribution. Sensors. 2013; 13(12):16347-16359. https://doi.org/10.3390/s131216347
Chicago/Turabian StyleLee, Jeong Il, Min-Gyu Kim, Mitsuhiro Shikida, and Kazuo Sato. 2013. "A Table-Shaped Tactile Sensor for Detecting Triaxial Force on the Basis of Strain Distribution" Sensors 13, no. 12: 16347-16359. https://doi.org/10.3390/s131216347




