A Highly Sensitive Refractometric Sensor Based on Cascaded SiN Microring Resonators
Abstract
: We investigate a highly sensitive optical sensor based on two cascaded microring resonators exploiting the Vernier effect. The architecture consists of two microrings with a slight difference in their free spectral ranges. This allows the generation of the Vernier effect for achieving ultra-high sensitivities. The sensor chip was fabricated using a silicon nitride platform and characterized with isopropanol/ethanol mixtures. A sensitivity of 0.95 nm/% was found for isopropanol concentrations in ethanol ranging from 0% to 10%. Furthermore, a collection of measurements was carried out using aqueous sodium chloride (NaCl) in solutions of different concentrations, confirming a high sensitivity of 10.3 nm/% and a bulk refractive index sensitivity of 6,317 nm/RIU. A limit of detection of 3.16 × 10−6 RIU was determined. These preliminary results show the potential features of cascaded silicon nitride microring resonators for real-time and free-label monitoring of biomolecules for a broad range of applications.1. Introduction
The development of integrated optical sensors with high precision and fast response times allows the elaboration of reliable and portable lab-on-a-chip (LOC) optical devices for sensing applications. The sensor elements exhibit remarkable features such as high sensitivity, electromagnetic immunity, the potential for high volume production, as well as hybrid integration with fluidic and electronic microsystems. Most of them are sensitive enough to identify biomolecules without fluorescent markers, thus enabling reduced preparation efforts and costs. The selectivity of such sensors to diverse target molecules by probe surface functionalization has been already demonstrated. Fields of application of LOC-based sensors may encompass the areas of medical research, healthcare, biological recognition, process control including food technology, environment monitoring, as well as safety and security purposes.
In particular, resonance-based optical sensors have been widely studied due to their positive features regarding miniaturization and multiplexing potential. Their work principle is based on the change of the refractive index by capturing analyte molecules. This induces a perturbation in the resonance condition causing a wavelength shift which is monitored as a function of the analyte deposition. Several types of sensor elements have been investigated for this purpose, such as microdisk resonators [1], microring resonators (MRRs) [2–4], and photonic crystals cavities [5]. MRRs have become a favorite structure of resonance-based sensors because of their performance and potential for high volume fabrication. The high quality (Q) factor of MRRs results in low limits of detection (LODs) ranging from 10−4 refractive index units (RIU) to 10−6 RIU [2–4]. In addition, arrays of MRRs for the detection of multiple species at bulk refractive index sensitivities (BRISs) ranging from 190 nm/RIU to 248 nm/RIU were reported using slot waveguide MRRs [6] and a technique based on the frequency modulation for read-out of a sequence of individual MRRs fed by a common bus waveguide [7]. However, the reported sensitivities and LODs are still not sufficient to detect and analyze low concentrations of molecules.
Recently, cascaded microring resonators (CMRRs) exploiting the Vernier effect have been proposed as a highly sensitive optical sensor. This novel architecture was firstly analyzed as a digital sensor [8]. Later, the structure was fabricated on a silicon-on-insulator (SOI) platform and characterized in aqueous medium, reaching a BRIS of 2,169 nm/RIU [9]. This value was improved by two orders of magnitude by using suspended Si-nanowires in this type of architecture [10]. A low-cost intensity interrogation method of CMRRs using a broadband source also was reported [11]. All of them operate in TE mode. In addition, cascaded SOI MRRs were designed and fabricated for operating in TM mode, where a BRIS of 24,300 nm/RIU was demonstrated [12].
In this paper, we present an optical sensor that consists of two cascaded silicon nitride (SiN) MRRs for sensing applications. The theoretical analysis and the fabrication of CMRRs on a SiN platform were reported previously [13,14]. Two types of analyte-isopropanol/ethanol mixtures and sodium chloride (NaCl) in aqueous solutions–were used for the characterization of the sensor in TE mode. Here, real-time measurements were performed resulting in a BRIS of 6,317 nm/RIU for NaCl solutions. Moreover, SiN waveguides can spectrally be tuned via integrated microheater elements due to the thermo-optic dependency of the SiN material. The waveguides have low optical losses over a wide wavelength range. Thereby, sensors based on cascaded SiN MRRs show a high grade of flexibility to operate in different wavelength windows, even at visible wavelengths.
2. Sensor Structure
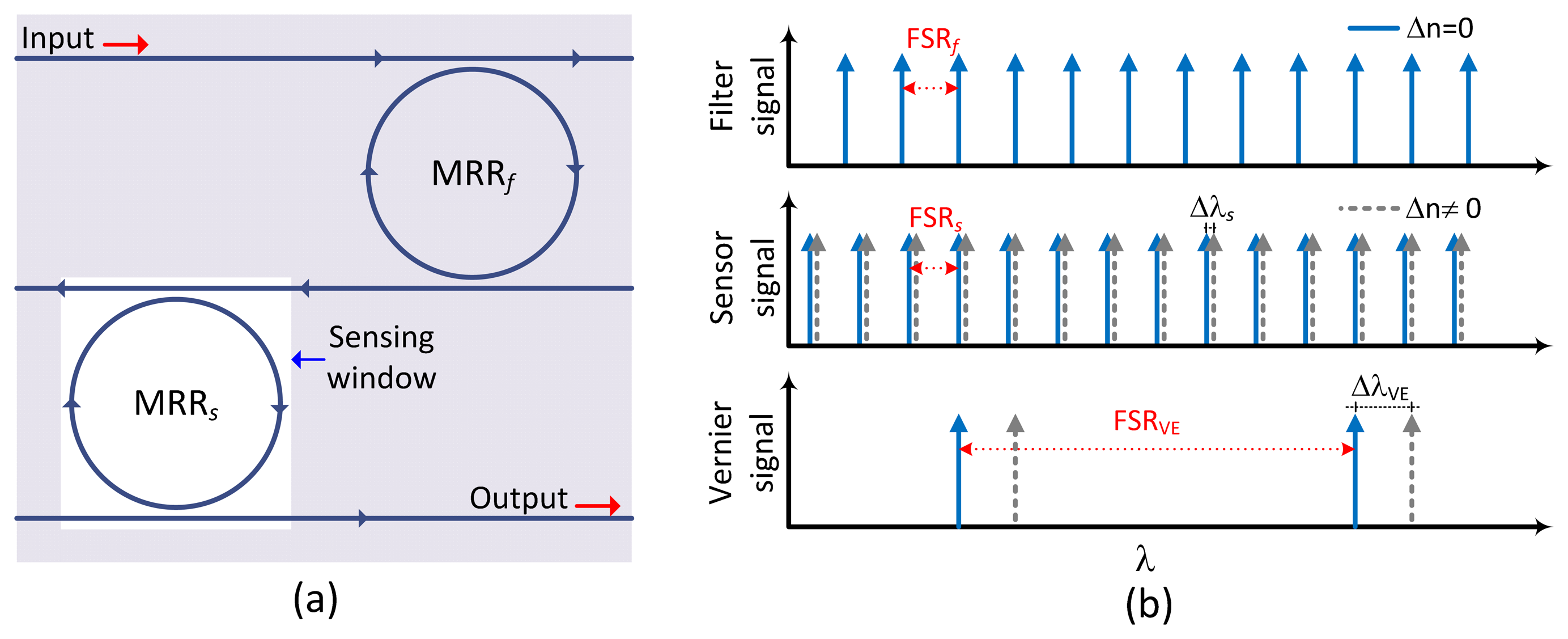
The sensor architecture shown in Figure 1a consists of two cascaded MRRs in an add/drop configuration. The filter element (MRRf) and the sensor element (MRRs) are connected via a common bus waveguide, defining the output drop port of the MRRf as the input port of the MRRs. A top cladding layer covers the complete structure for the interaction with the analyte sample except the MRRs. The Vernier operation in two cascaded systems is due to the difference in the free spectral range (FSR) as illustrated in Figure 1b, resulting in a large period (FSRVE) between two consecutive maximum peaks. An index change (Δn ≠ 0) in the sensor element (dashed gray arrows) causes a large wavelength shift (ΔλVE) compared to the wavelength shift (Δλs) for the individual sensor element.
For optical interfacing between the sensor chip and the feeding optical fibers, tapered grating couplers have been integrated at the ends of the waveguides for efficient optical interfacing at moderate alignment tolerances. A coupling efficiency of up to 60% in [15] has been reported using grating couplers integrated on SiN waveguides.
The transmission spectrum of CMRRs is the spectral product of the transmitted light by each individual MRR. It consists of a periodicity of resonances peaks whose maximum amplitude occurs by the complete overlap of peaks of the MRRf and the MRRs. The resulting transmission peaks have a series of envelopes where each one of them is fitted with a Lorentzian function. The spectral distance (FSRVE) between two consecutive Vernier peaks at the center of the envelope is defined by [9]:
Here, the FSRVE is inversely proportional to the difference of individual FSRs calculated from FSR = λ2/ngL, where ng is the group index of the waveguide and L is the perimeter of the MRR.
The sensitivity of the individual MRRs, which is related to the sensitivity of the waveguide, can be obtained by S = λ/ng,s·δns/δnmedium, where δns is the effective index change and δnmedium is the index change caused by the analyte amount. According to the Vernier effect, the sensitivity (SVE) of CMRRs is simply the sensitivity of the sensor element increased by an amplification factor (M) [9]:
Note that the factor M is directly related to the difference of the individual FSRs. In this context, small amounts of analyte on the sensor element surface can be detected via CMRRs fabricated with a small difference in FSRs.
3. Fabrication
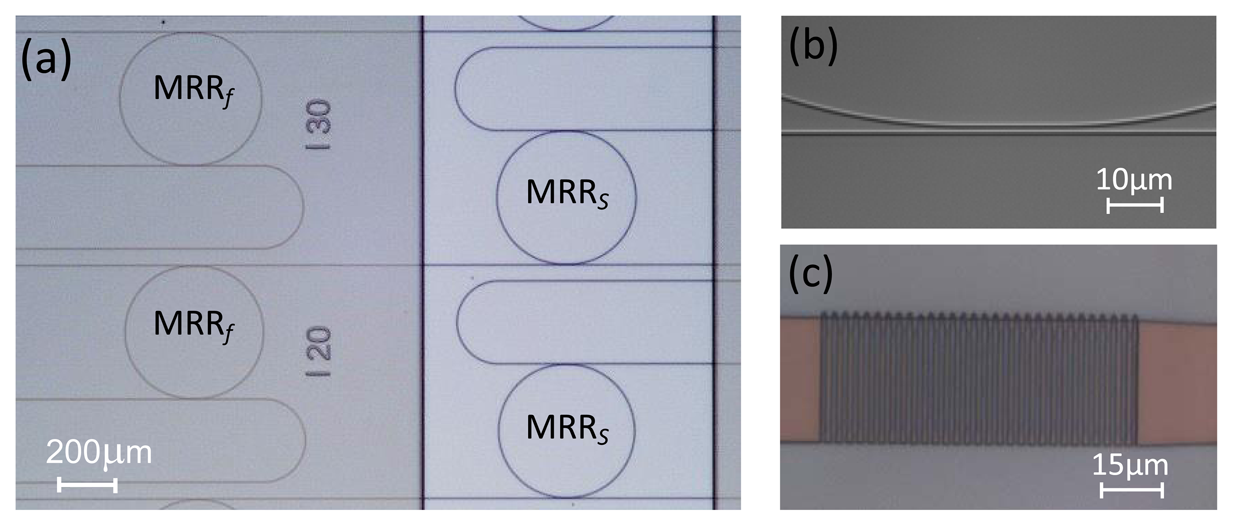
The sensor was designed on the SiN material platform and fabricated via a mask-based UV patterning process followed by an RIE etching process [7]. The ridge SiN waveguides (nSiN = 1.99) of 1.25 μm width that form the sensor were etched at a depth of 80 nm, starting from an initial SiN layer of 250 nm thickness deposited on a thermal SiOx layer (nSiOx = 1.45) of 8 μm thickness. The designed waveguide only supports the fundamental TE mode at 1,500 nm. The final MRRs had a racetrack shape with a coupler gap (g) of 1 μm and different straight section lengths (l) between 10 μm and 50 μm. The MRRs had radii of Rs = 199 μm and Rf = 200 μm, respectively. Finally, the complete structure was covered with a 4 μm-thick benzocyclobutene (BCB) layer (nBCB = 1.56), which was only opened on MRRss by using an extra photolithography step. Figure 2 shows optical microscope images of fabricated CMRR structures. The coupling region of waveguides for l = 20 μm and the tapered grating coupler with a period of 1.2 μm, a grating width of 0.6 μm, a spacing of 0.6 μm, and an initial width of 30 μm are also shown in Figures 2b,c, respectively.
Individual FSRs were designed at 1,550 nm that correspond to values of FSRf = 1.006 nm and FSRs = 0.986 nm, respectively. The MRRf had a group index of ng,f = 1.8215 and a perimeter of Lf = 1310.3 μm. The MRRs had values of ng,s = 1.849 and Ls = 1316.6 μm for operation in water (nmedium = 1.33). From Equation (1), the theoretical FSRVE of 49.6 nm was estimated resulting from a difference of FSRs of about 0.02 nm. As for the Vernier sensitivity of the sensor, an amplification factor of M = 50.3 over the sensitivity of the single sensor element was found from Equation (2).
4. Results and Discussion
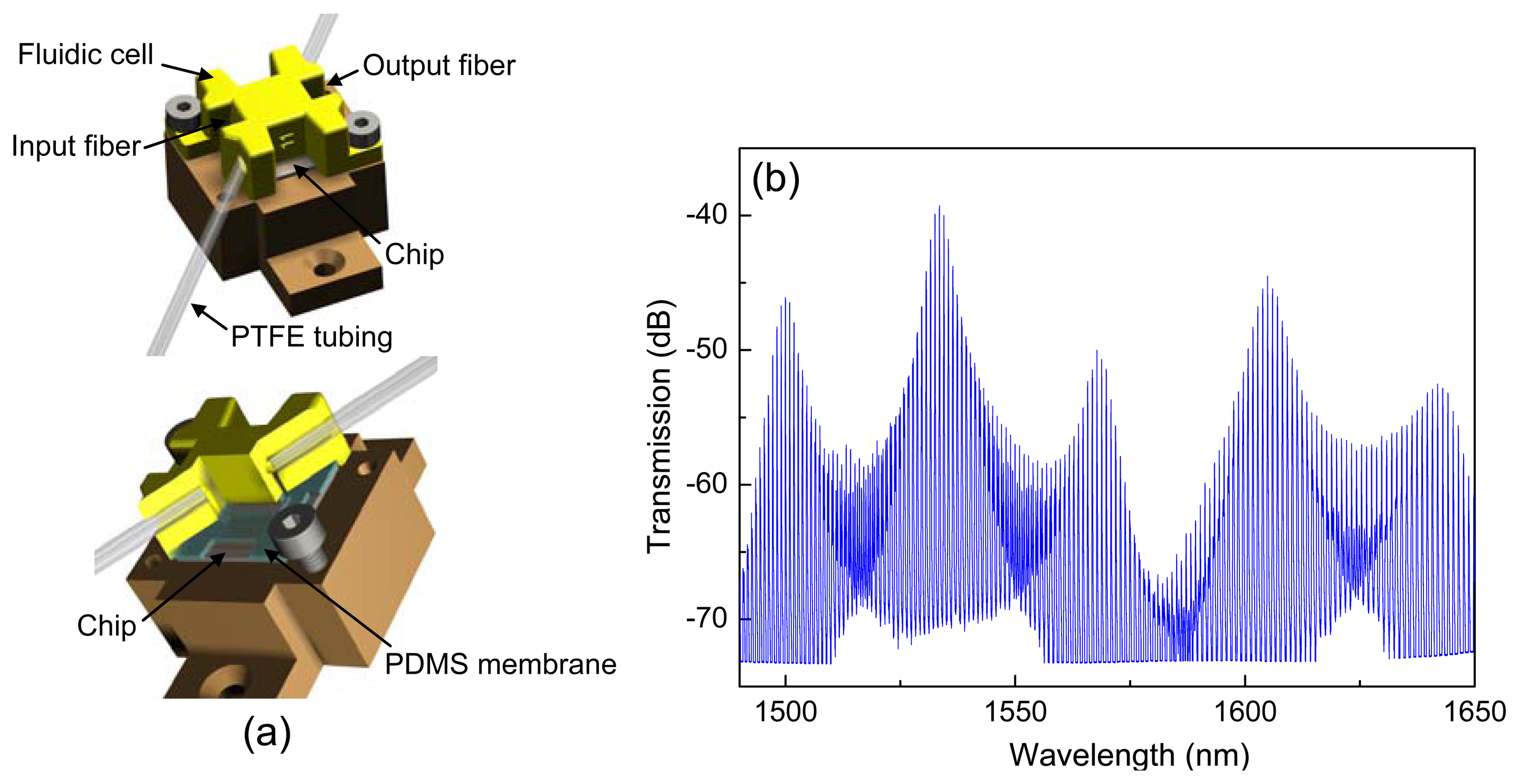
To measure the transmission spectrum of the sensor chip, a tunable laser source (TLS)–with an internal piezoelectric element for operation in a dynamic sweep mode or for operation in “digital” wavelength steps of 1 pm–an optical fiber controller for polarization adjustment, and a photodetector were used. The optical interfacing was done by using cleaved optical fibers aligned to tapered grating couplers, which were localized at the ends of the waveguides. A fluidic cell made of acrylate material was fabricated via 3D printing technique (ProJet HD 3000 from 3D Systems, Inc., Rock Hill, SC, USA) and was deposited on top of the 10 × 10 mm2 sensor chip in order to allow the measurements of different liquid solutions. A PDMS soft membrane was inserted for a better sealing to the sensor chip. The 1/16″ PTFE tubing with an inner diameter of 250 μm was connected to the inlet and the outlet of the fluidic cell, respectively. The solution transport was realized using a syringe pump connected to the end of the outlet tubing. The analyte flowed through inlet tubing with a velocity of 10 μL/min. Figure 3a shows a diagram of the device.
Figure 3b shows the transmission spectrum of the sensor when deionized (DI) water covers the sensing window. Here, five Vernier peaks were measured between 1,490 nm and 1,650 nm. The single Vernier peak, composed by a series of resonance peaks, exhibits an envelope as mentioned above. The analysis of the Vernier peak is based on a Lorentzian fit of the envelope, which is calculated from the maxima of the resonance peaks. The fitted envelopes of two Vernier peaks centered at 1,533.52 nm and 1,568.06 nm showed full-widths at half-maximum (FWHMs) of 4.08 nm and 5.28 nm, respectively. The corresponding FRSVE was found to be of 34.54 nm. The MRRs showed experimentally a Q factor of 1.8 × 104 and an FSRs of 0.93 nm, whereas the MRRf exhibited a Q factor of 2.1 × 104 and an FSRf of 0.95 nm. According to Equation (1), the FRSVE can be calculated by using individual FSRs; the difference of individual FSRs was 0.02 nm. Consequently, a theoretical FRSVE of 44.17 nm was obtained by using the experimental FSRs. The difference between the theoretical FSRVE and the experimental FSRVE can be related to the waveguide dispersion, which was not taken into account in Equation (1). Note that the amplitude of the Vernier peaks also varies in Figure 3 due to the wavelength dependency on the efficient coupling of the grating couplers.
4.1. Isopropanol/Ethanol Measurements
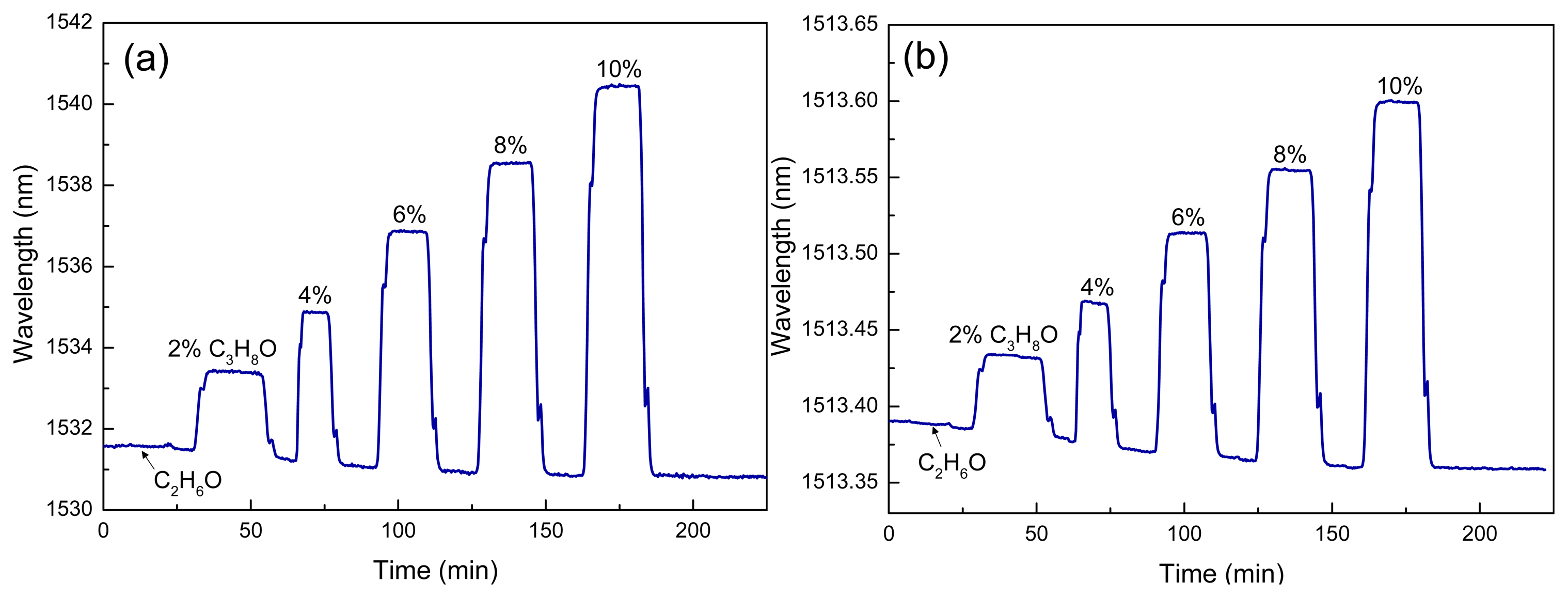
Firstly, the sensor chip was investigated in terms of its sensitivity with different isopropanol/ethanol mixtures. Figure 4a shows the real-time measurement of the wavelength shift for one Vernier envelope as a function of the isopropanol concentrations in ethanol at room temperature. The isopropanol amount increases in steps of 2% from 0% up to 10%. The next Vernier peak was initially centered at 1,531.59 nm for ethanol solution. As expected, the Vernier peak was displaced to longer wavelengths when the isopropanol amount increases. A wavelength shift of 9.56 nm was demonstrated for the highest isopropanol concentration. From this, a sensitivity of 0.95 nm/% was calculated. Ethanol was drained over the sensor element approximately 20 min between two analyte samples in order to avoid false wavelength shifts. The baseline drift in Figure 4a is mainly due to temperature effects and could be eliminated by employing a temperature reference on chip (for instance an additional MRR).
A study on the sensitivity was performed by tracking a resonance peak of the single MRRs. The wavelength shift monitoring of the resonance in Figure 4b is shown for the previous isopropanol/ethanol mixtures. A wavelength resonance shift of 240 pm was found for 10% isopropanol in ethanol. This results into a sensitivity of 0.02 nm/%. The Vernier sensitivity of the sensor can be estimated from Equation (2) and to be compared to the experimental value. An M factor of 47.5 was calculated. The resulting SVE reached 0.95 nm/%, corresponding very well to the experimental value. The temperature effect on the measurement of isopropanol/ethanol mixtures has been observed as well.
4.2. Sodium Chloride (NaCl) Measurements
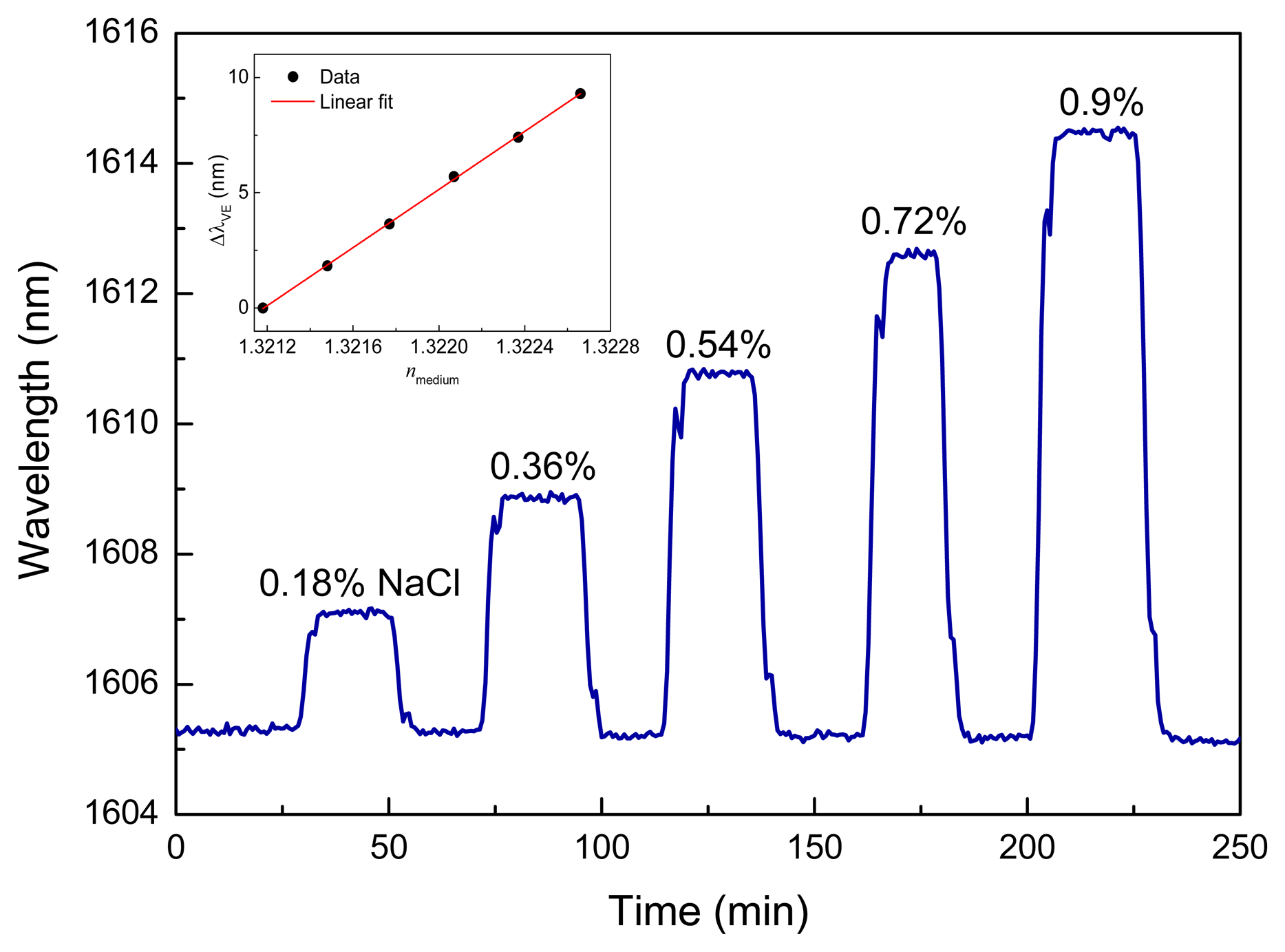
In addition, the sensor chip has been used to measure different NaCl solutions in DI water ranging in concentration from 0% to 0.9% in steps of 0.18%. The corresponding refractive index range was between 1.32118 and 1.32266 with a step of about 3 × 10−4 at 25 °C [16]. The wavelength shift of the Vernier envelope centered at 1,605.29 nm was tracked using the respective NaCl solutions, as shown in Figure 5. The NaCl concentration increases up to 0.9%, reaching a maximum wavelength shift of 9.3 nm. After each measurement at a distinct NaCl concentration, the sensor was wiped flowing DI water through the fluidic cell. The sensitivity was of 10.3 nm/%, which is clearly a higher value than the previous one obtained for isopropanol/ethanol mixtures due to the significantly higher refractive index difference between water and NaCl. By using the index change of NaCl solutions, an BRIS of 6,317 nm/RIU was calculated via the slope of the data shown in inset of Figure 5. In contrast to isopropanol/ethanol measurements, the influence of the temperature to the sensor chip was much lower for aqueous solutions. This effect can be caused by the low boiling point of alcohol solutions to temperature changes.
The LOD has been defined as the ratio of the minimum detectable wavelength shift of our system and the sensitivity of the sensor chip. For the minimum detectable wavelength shift, a value of 0.02 nm was found taking into account the noise level of our system as described in [17]. This results in a LOD of 3.16 × 10−6 RIU for the proposed sensor.
Finally, Table 1 gives an overview of sensing data for different cascaded optical structures. The Vernier principle has been demonstrated in structures such as MRRs, Mach-Zenhder interferometers (MZIs), and capillary optofluidic rings (OFRRs). All of them show sensitivities up to three orders of magnitude higher than the sensitivity for a single structure. Integrated MZIs are architectures based on a sensing arm and a reference arm connected to Y-junctions for the optical interrogation. The high efficiency of MZIs using an intensity interrogation method is related to the length of their arms. Cascaded MZIs with arms of about millimeters in length become less appropriate for the complete integration of the sensor. However, a single MZI presents high sensitivities and low LODs. Concerning the OFRRs, an effort is being widely performed for their compatibility with integrated waveguide systems. The Vernier operation in this type of structures is achieved by using a reference active fiber and an OFRR. For sensing operation, the modal interaction of the OFRR with the analyte requires a wall thickness of about 1 μm, which is too fragile for practical handling. The advantages of OFRRs are such as a high Q factor and their natural fluidic channel that avoids the microfluidic cell integration as in the case of LOC optical devices. Finally, focusing on CMRRs, all of them have been fabricated on SOI platforms and optically characterized in aqueous medium. SOI material permits a CMOS compatible process, which reduces the cost per chip. High sensitivities have been successfully demonstrated using cascaded SOI MRRs. However, the reported LODs are still insufficient compared to, e.g., LODs between 10−5 RIU and 10−8 RIU obtained via superficial plasmon resonance (SPR) sensors [21,22]. LODs in CMRRs can be improved decreasing the difference of individual FSRs [8], consequently, CMRRs should be performed on a technique with low fabrication tolerances as, e.g., the e-beam direct writing process. However, they are still structures in stage of development and improvement.
We conclude by proposing cascaded SiN MRRs as sensor structures equal to SOI MRRs for sensitive biochemical sensing, due to their overall performance in real-time monitoring and sensitivity, e.g., for alcohol and aqueous solutions. SiN MRRs sensors operate over a wide wavelength range [23] and also can be moderately tuned by using integrated microheater elements [7], i.e., the Vernier peak can be centered at any required SiN MRRs wavelength.
5. Conclusions
An optical sensor chip based on two cascaded SiN MRRs was experimentally investigated. The sensor was characterized with two types of analyte: isopropanol/ethanol mixtures and aqueous NaCl solutions. A sensitivity of 0.95 nm/% was found for isopropanol/ethanol mixtures compared to the sensitivity of 0.02 nm/% for a single sensor element. Here, an amplification factor of M = 47.5 was reported for the actual sensor. Furthermore, the sensing operation was carried out in aqueous solutions of NaCl concentration resulting in a sensitivity of 10.3 nm/% and a BRIS of 6,317 nm/RIU, respectively. In addition, an LOD of 3.16 × 10−6 RIU was demonstrated for the proposed sensor. CMRRs based on SiN material are promising candidates for highly sensitive optical sensors at real-time monitoring of biomolecules in wide wavelength range.
Acknowledgments
The authors thank André Lehmann from Fraunhofer Institute for Biomedical Engineering for the fabrication of the fluidic cell. The authors acknowledge helpful discussions with Helmut Heidrich from Fraunhofer Institute for Telecommunications, Heinrich Hertz Institute (HHI).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cho, S.-Y.; Jokerst, N.M. A polymer microdisk photonic sensor integrated onto silicon. IEEE Photon. Technol. Lett. 2006, 18, 2096–2098. [Google Scholar]
- De Vos, K.; Bartolozzi, I.; Schacht, E.; Bienstman, P.; Baets, R. Silicon-On-Insulator microring resonator for sensitive and label-free biosensing. Opt. Express 2007, 15, 7610–7615. [Google Scholar]
- Chao, C.-Y.; Fung, W.; Guo, L.J. Polymer microring resonators for biochemical sensing applications. IEEE J. Sel. Top. Quant. Electron. 2006, 12, 134–142. [Google Scholar]
- Ksendsov, A.; Lin, Y. Integrated optics ring-resonator sensors for protein detection. Opt. Lett. 2005, 30, 3344–3346. [Google Scholar]
- Lee, M.; Fauchet, P.M. Two-Dimensional silicon photonic crystal based biosensing platform for protein detection. Opt. Express 2007, 15, 4530–4535. [Google Scholar]
- Carlborg, C.F.; Gylfason, K.B.; Kaźmierczak, A.; Dortu, F.; Bañuls Polo, M.J.; Maquieira Catala, A.; Kresbach, G.M.; Sohlström, H.; Moh, T.; Vivien, L.; et al. A packaged optical slot-waveguide ring resonator sensor array for multiplex label-free assays in labs-on-chips. Lab. Chip 2010, 10, 281–290. [Google Scholar]
- Lützow, P.; Pergande, D.; Heidrich, H. Integrated optical sensor platform for multiparameter biochemical analysis. Opt. Express 2011, 19, 13277–13284. [Google Scholar]
- Dai, D. Highly sensitive digital optical sensor based on cascaded high-Q ring-resonators. Opt. Express 2009, 17, 23817–23822. [Google Scholar]
- Claes, T.; Bogaerts, W.; Bienstman, P. Experimental characterization of a silicon photonic biosensor consisting of two cascaded ring resonators based on the vernier-effect and introduction of a curve fitting method for an improved detect limit. Opt. Express 2010, 18, 22747–22761. [Google Scholar]
- Hu, J.; Dai, D. Cascaded-Ring optical sensor with enhanced sensitivity by using suspended Si-nanowires. IEEE Photon. Technol. Lett. 2011, 23, 842–844. [Google Scholar]
- Jin, L.; Li, M.; He, J.-J. Optical waveguide double-ring sensor using intensity interrogation with a low-cost broadband source. Opt. Lett. 2011, 36, 1128–1130. [Google Scholar]
- Jiang, X.; Ye, J.; Zou, J.; Li, M.; He, J.-J. Cascaded silicon-on-insulator double-ring sensors operating in high-sensitivity transverse-magnetic mode. Opt. Lett. 2013, 38, 1349–1351. [Google Scholar]
- Zamora, V.; Lützow, P.; Pergande, D.; Heidrich, H. Cascaded Microring Resonators for Biomedical Applications: Improved Sensitivity at Large Tuning Range. Proceedings of the SPIE Photonics West Conference, San Francisco, CA, USA, 2–7 February 2013; p. p. 857002.
- Zamora, V.; Lützow, P.; Weiland, M.; Pergande, D. Investigation of cascaded SiN microring resonators at 1.3 μm and 1.5 μm. Opt. Express 2013. (accepted). [Google Scholar]
- Maire, G.; Vivien, L.; Sattler, G.; Kazmierczak, A.; Sanchez, B.; Gylfason, K.B.; Griol, A.; Marris-Morini, D.; Cassan, E.; Giannone, D.; et al. High efficiency silicon nitride surface grating couplers. Opt. Express 2008, 16, 328–333. [Google Scholar]
- Quan, X.; Fry, E.S. Empirical equation for the index of refraction of seawater. Appl. Opt. 1995, 34, 3477–3480. [Google Scholar]
- White, I.M.; Fan, X. On the performance quantification of resonant refractive index sensors. Opt. Express 2008, 16, 1020–1028. [Google Scholar]
- Jin, L.; Li, M.; He, J.-J. Highly-Sensitive silicon-on insulator sensor based on two cascaded-microring resonators with Vernier effect. Opt. Commun. 2011, 284, 156–159. [Google Scholar]
- Tu, X.; Song, J.; Liow, T.-Y.; Park, M.K.; Yiying, J.Q.; Kee, J.S.; Yu, M.; Lo, G.-Q. Thermal independent silicon-nitride slot waveguide biosensor with high sensitivity. Opt. Express 2012, 20, 2640–2648. [Google Scholar]
- Ren, L.; Wu, X.; Li, M.; Zhang, X.; Liu, L.; Xu, L. Ultrasensitive label-free coupled optofluidic ring laser sensor. Opt. Lett. 2012, 37, 3873–3875. [Google Scholar]
- Homola, J.; Yee, S.S.; Gauglitz, G. Surface plasmon resonance sensors: Review. Sens. Actuators B Chem. 1999, 54, 3–15. [Google Scholar]
- Nenninger, G.G.; Tobiška, P.; Homola, J.; Yee, S.S. Long-Range surface plasmons for high-resolution surface plasmon resonance sensors. Sens. Actuators B Chem. 2001, 74, 145–151. [Google Scholar]
- Ghasemi, F.; Eftekahr, A.A.; Gottfried, D.S.; Song, X.; Cummings, R.D.; Adibi, A. Self-Referenced Silicon Nitride Array Microring Biosensor for Toxic Detection Using Glycans at Visible Wavelength. Proceedings of the SPIE Photonics West Conference, San Francisco, CA, USA, 2–7 February 2013; p. p. 85940A.
| Cascaded Structures | Analyte | SVE(nm/RIU) | LOD (RIU) | Ref. |
|---|---|---|---|---|
| SOI MRRs | NaCl | 2,169 | 8.3 × 10−6 | [9] |
| Ethanol | 1,300 | 2.2 × 10−4 | [18] | |
| SOI MRRs * | NaCl | 24,300 | 4.8 × 10−6 | [12] |
| SOI MRRs ** | Salt | 460,000 | [10] | |
| SiN MZIs | NaCl | 14,500 (2π)/RIU | 1.08 × 10−6 | [19] |
| SiO2 OFRRs | Glucose | 2,510 | 1.6 × 10−5 | [20] |
| SiN MRRs | NaCl | 6,317 | 3.16 × 10−6 | This paper |
*The fabricated structure operating in TM mode. All of them operate in TE mode.**CMRRs with a suspended Si-nanowire.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zamora, V.; Lützow, P.; Weiland, M.; Pergande, D. A Highly Sensitive Refractometric Sensor Based on Cascaded SiN Microring Resonators. Sensors 2013, 13, 14601-14610. https://doi.org/10.3390/s131114601
Zamora V, Lützow P, Weiland M, Pergande D. A Highly Sensitive Refractometric Sensor Based on Cascaded SiN Microring Resonators. Sensors. 2013; 13(11):14601-14610. https://doi.org/10.3390/s131114601
Chicago/Turabian StyleZamora, Vanessa, Peter Lützow, Martin Weiland, and Daniel Pergande. 2013. "A Highly Sensitive Refractometric Sensor Based on Cascaded SiN Microring Resonators" Sensors 13, no. 11: 14601-14610. https://doi.org/10.3390/s131114601
APA StyleZamora, V., Lützow, P., Weiland, M., & Pergande, D. (2013). A Highly Sensitive Refractometric Sensor Based on Cascaded SiN Microring Resonators. Sensors, 13(11), 14601-14610. https://doi.org/10.3390/s131114601




