A Novel INS and Doppler Sensors Calibration Method for Long Range Underwater Vehicle Navigation
Abstract
: Since the drifts of Inertial Navigation System (INS) solutions are inevitable and also grow over time, a Doppler Velocity Log (DVL) is used to aid the INS to restrain its error growth. Therefore, INS/DVL integration is a common approach for Autonomous Underwater Vehicle (AUV) navigation. The parameters including the scale factor of DVL and misalignments between INS and DVL are key factors which limit the accuracy of the INS/DVL integration. In this paper, a novel parameter calibration method is proposed. An iterative implementation of the method is designed to reduce the error caused by INS initial alignment. Furthermore, a simplified INS/DVL integration scheme is employed. The proposed method is evaluated with both river trial and sea trial data sets. Using 0.03°/h(1σ) ring laser gyroscopes, 5 × 10−5 g(1σ) quartz accelerometers and DVL with accuracy 0.5% V ± 0.5 cm/s, INS/DVL integrated navigation can reach an accuracy of about 1‰ of distance travelled (CEP) in a river trial and 2‰ of distance travelled (CEP) in a sea trial.1. Introduction
Autonomous Underwater Vehicles (AUV) present a uniquely challenging navigational problem because they operate autonomously in a highly unstructured environment [1]. Autonomous operations in deep water or covert military operations require the AUV to handle submerged operation for long periods of time. Currently, few techniques exist for reliable navigation for long range AUVs. Ultra-short baseline (USBL) acoustic navigation systems are employed on industrial, military, and scientific underwater vehicles and are preferred for the task of docking a vehicle to a transponder-equipped docking station [2–6]. Terrain- or landmark-based navigation methods use real-time sensing and a terrain or landmark map (e.g., topographic, magnetic, gravitational, or other geodetic data) to determine the vehicle's position [2]. But an a priori map is seldom available in AUV terrain- or landmark-based navigation. The standard method for full ocean depth XYZ acoustic navigation is 12-kHz-long baseline (LBL) acoustic navigation [2,7], but the precision and update rate of LBL position fixes vary over several orders of magnitude depending on the acoustic frequency, range, and acoustic path geometry [2]. Global Navigation Satellite System (GNSS) provides superior three-dimensional navigation capability for both surface and air vehicles but its signal cannot be directly received by deeply submerged ocean vehicles. A strapdown inertial navigation system (INS) is a good choice for self-contained localization and navigation of AUVs, but its position error accumulates with time elapse due to the inherent bias errors of gyros and accelerometers. Hence a navigation system based on INS will have an unacceptable position error drift without sufficient aiding. INS/DVL integrated navigation system using the high accurate velocity offered by DVL to restrain the error accumulation of INS is a widely-used under-water integrated navigation technology [8–18]. Even when a DVL is included, the accuracy of INS/DVL integration will be reduced because of the scale factor error of DVL and the misalignments between INS and DVL.
Because the scale factor error of DVL and the misalignments between INS and DVL are the key factors which limit the accuracy of INS/DVL integration, calibration and compensation of these parameters must be done before a mission is conducted. This calibration is necessary to account for mechanical misalignments in the installations of the INS and DVL, as well as for potential errors in the velocity estimates of the units [7]. In practical engineering applications, the first adapted method is based on the assumptions: (a) both INS and DVL are mounted onto the same rigid structure throughout a mission; (b) the lever arms and misalignments between these devices remain constant and small. However, such assumptions are not realistic in the real world. The second adapted method is to treat the misalignments between INS and DVL as unknown and then GNSS is used to estimate misalignment parameters in three dimensions. However, only yaw misalignment parameter between INS and DVL was considered in some early work. For example, in [19], Joyce proposed a method to estimated yaw misalignment error by using least squares (LS) method. In [20,21], the heading accuracy was further considered as one of the key factors which limit the calibration accuracy. In [2,22,23], James and his colleagues improved the calibration method, with precise position of acoustic navigation sensors such as LBL, three dimensional misalignments between INS and DVL can then be estimated simultaneously. But this method is difficult to implement that it might cause some inconvenience for real applications. In [24], an online estimation method of DVL misalignment angle in SINS/DVL was presented. However, it requires the AUV to be operated with complex maneuvers to enhance observability of the unknown states. The paper proposes a novel alignment calibration method with external GNSS signals. However, there is no need to receive the GNSS signals continuously which make it suitable for AUV platforms. Furthermore, a recursive implementation which can eliminate the effects of the INS initial alignment is proposed. The accuracy of the calibration is further improved.
This paper is organized as follows: Section 2 introduces the navigation equations, including INS/DVL system equations and observation equations. The parameter calibration method is proposed in Section 3, followed by an iterative implementation to reduce the effects of the INS initial alignment. After the scale factor of DVL and misalignments between INS and DVL are fixed, the simplified INS/DVL integrated navigation system is designed in Section 4. An experimental evaluation of the proposed navigation system is presented in Section 5, where in particular, the performance of the navigation system both in the river trial and the sea trial is discussed. Finally, conclusions are drawn in Section 6.
3. Parameter Calibration Algorithm
The main advantage of the online calibration method proposed in [24] is that no external sensors are required. However, it requires the AUV to operate complex maneuvers. Generally, AUVs travel in a straight path at a constant velocity. Although the scale factor error and the misalignments can be chosen as the Kalman filter states for the INS/DVL integrated navigation system and hence estimated on line, it should be noted from the observability analysis that not all of the states are observable under that sailing condition [25–29]. Therefore, a novel parameter calibration method is proposed.
3.1. Formulas of the Proposed Method
It can be guaranteed that the misalignments ε are reduced to a small value during manufacture. Since the velocity of DVL in the lateral direction and the up direction are miniature, ignore the influence of the roll error εx of the misalignments. Therefore, only the scale factor error k, the yaw misalignment error εy, the pitch misalignment error εz are considered.
Applying Equation (4), the DVL measurements can be expressed as:
Rearranging gives:
Ignoring the influence of the small products, so:
Rearranging Equation (7) gives:
During the process of calibration voyage, the AUV travels in a straight path at a constant velocity. Therefore, the roll γ and the pitch θ remain small:
Substituting Equation (9) into Equation (8) gives:
Ignoring the influence of , and small products gives:
Rearranging gives:
The misalignments ε can be regarded as small values, so:
From Equation (13), the following equation can be obtained:
Both parts of the Equation (14) are integrated to yield:
From Equation (13):
Both parts are integrated to yield:
Dot-multiplying both of its parts by gives:
Since:
Substituting this into Equation (18) gives:
Dot-multiplying both parts of Equation (17) by gives:
Since:
Substituting this into Equation (21), the scale factor can be calculated as follows:
Supposing the AUV travels in a straight path at a constant speed during [t0, t1], then:
3.2. An Iterative Implementation
The attitude error caused by INS initial alignment is a key factor which limits the accuracy of the calibration. In [30,31], the methods of INS initial alignment for AUV are presented. In order to reduce the effects of the INS initial alignment, an iterative implementation is proposed as follows (shown in Figure 2):
- (1)
Update the position of INS/DVL integrated navigation by GNSS when the initial INS alignment is finished and record the positions (LD(t0),λD(t0),hD(t0)) and (LG(t0),λG(t0),hG(t0)).
- (2)
After the AUV has travelled over a distance, for example, 8 km, record the INS/DVL integrated navigation and GNSS positions as: (LD(t1),λD(t1),hD(t1)) and (LG(t1),λG(t1),hG(t1)).
- (3)
With the recorded position information from steps (1) and (2), the scale factor error k0, misalignment yaw error εy0 and pitch misalignment error εz0 can be obtained according to Equations (15), (20) and (23).
- (4)
The estimated scale factor and misalignment parameters are used in the subsequent navigation. Record the current position: (LD(t2),λD(t2),hD(t2)), (LG(t2),λG(t2),hG(t2)). Then the AUV takes a 180° turn. After the AUV has travelled over a distance, for example, 8 km, record more positions: (LD(t3),λD(t3),hD(t3)) and (LG(t3),λG(t3),hG(t3)).
- (5)
New parameter estimates (scale factor error k1, misalignment yaw error εy1 and pitch misalignment error εz1) can be obtained by the newly recorded positions above. Therefore, the parameter estimates can be calculated as follows:
- (6)
Repeat Step (4) and (5) until the accuracy of the INS/DVL integrated navigation system meets the requirement(about 1.5‰ of the distance travelled (CEP)).
5. Experimental Results and Discussions
Both river trials and sea trials were carried out to evaluate the performance of the proposed method. For this, an high performance INS Kit is designed. The INS Kit is a fully qualified inertial navigator that is based on three Ring Laser Gyros(RLG) produced by Huatian Photoelectron and INS Technology Co., Ltd., Changsha, China and three quartz accelerometers offered by Beijing StarNeto Technology Co., Ltd., Beijing, China. Inertial sensors specifications are shown Table 1.
The INS Kit modular architecture allows for various on board aiding devices such as GNSS, Doppler Velocity Log and Depth Sensor. The primary navigation aiding sensors are shown in Table 2.
The bottom-locked Doppler sensor HEU DVL produced by Harbin Engineering University could provide three-axis transformation velocities. The INS Kit and DVL modular are shown in Figure 3.
5.1. The River Trial
In the river trial, the devices were fixed on a ship. DGPS positioning results were employed as the benchmark. Four suiets of INS were fixed on the deck of a ship. They were marked with N1, N2, N3 and N4 respectively. The DVL modules were put 1 m underwater.
5.1.1. River Trial Experimental Results
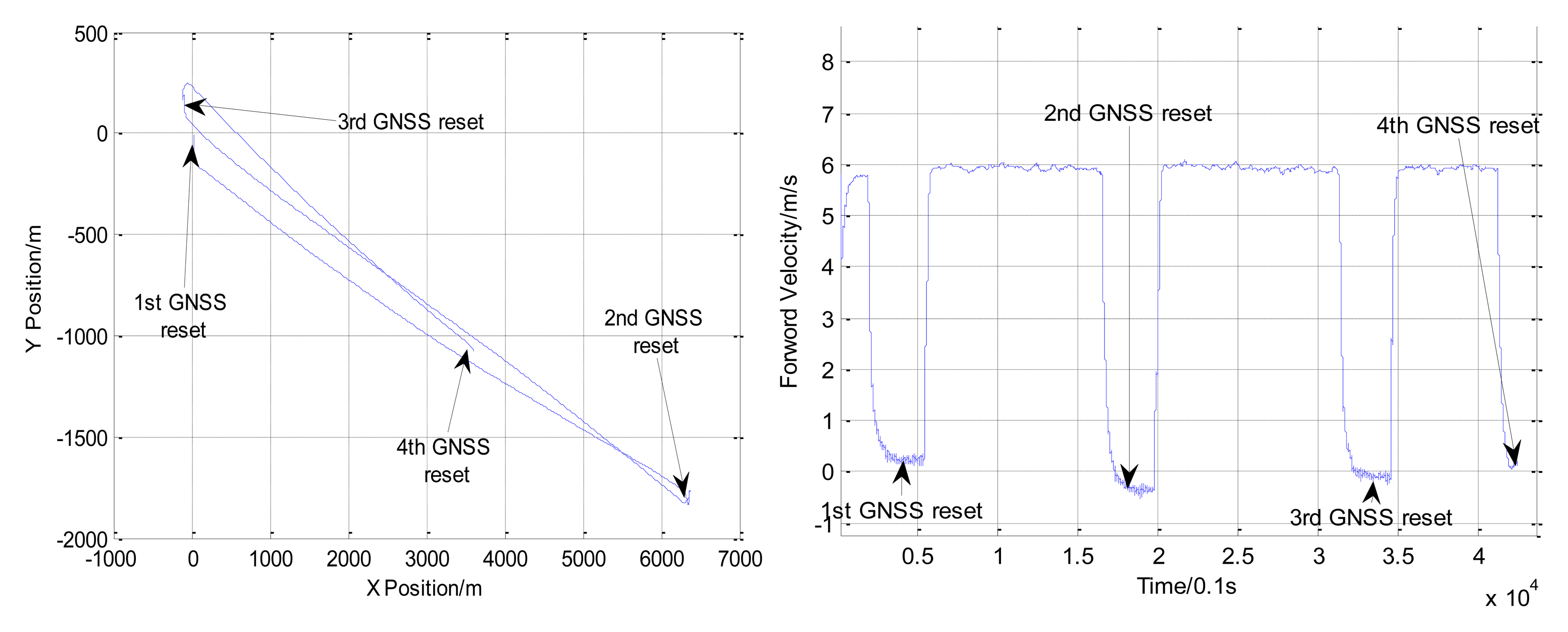
A near straight trajectory which is about 8 km was chosen for parameter calibration. The trajectory and forward velocity of the vessel in the river trial are shown in Figure 4.
With the positions of the first and the second dot (shown in Figure 3) obtained from GNSS positions and INS/DVL positions, an initial scale factor of DVL and misalignments parameters were calculated. With the positions of the second and the third dot, the calibration parameters were updated with the proposed iterative implementation. These estimates are shown in Table 3.
With calibrated parameter estimates from Table 3 and the positions of the forth dot (shown in Figure 4), the final position errors are calculated in Table 4.
From Table 4, with calibrated parameter estimates, the final position errors of INS/DVL integrated navigation are within 5 m in the 7 km distance travelled. The accuracy of INS/DVL integrated navigation system is better than 1‰D (distance travelled). If the accuracy of INS/DVL integrated navigation system is bigger than 1.5‰D, with the positions of the third and the forth dot, the calibration parameters were updated with the iterative implementation.
5.1.2. Validation of the Calibrated Parameters Estimates in the River Trial
In order to evaluate the performance of the calibrated parameter estimates, another test was done. The calibrated parameter estimates were employed in the INS/DVL integrated navigation. During the experiment, the simplified INS/DVL integrated navigation scheme proposed in Section 4 is used. The trajectory of the vessel is shown in Figure 5. Comparing with the positions obtained from GNSS, the on-line experimental results are shown in Table 5.
As shown in Table 5, the accuracy of the INS/DVL integrated navigation system is about 1‰D(CEP). Furthermore, the accuracy of INS/DVL integrated navigation system is improved with the increase of distance travelled.
5.2. The Sea Trial
These experiments were done in the South Sea, China. During the sea trial, the INS and DVL were assembled as a single mechanical unit, and placed in the AUV. The scale factor and misalignments were calibrated in the river trial. In the sea trial, the experiment process of is as follows:
- (1)
INS initial alignment.
- (2)
The AUV is launched, and running an autonomous type of mission navigating with DVL aided INS and GNSS surface fixes at regular intervals. Once the DVL measurements are available, the navigation system is working at the mode of INS/DVL integrated navigation.
- (3)
After the AUV has travelled for a certain distance, it surfaces to receive the GNSS signals. By comparing the INS/DVL integrated navigation positioning data with independent DGNSS data, position error of the INS/DVL integrated navigation system can be obtained. Then the AUV submerges until the mission is finished.
Three experiments were carried out in the sea trial.
5.2.1. Experiment 1
In Experiment 1, after initial alignment, the AUV surfaced to receive DGPS measurements at the surface for a short period of time to calibrate the position error of INS/DVL integrated navigation system. Then the AUV submerged to travel a straight line approximately 17 Km in length, equivalent to about 2 h at nominal speed. The depth varies from 60 to 180 m. The trajectory obtained by INS/DVL integrated navigation system is shown in Figure 6. During the process of the experiment, the AUV surfaced twice to receive the GNSS signals.
Comparing with the positions obtained from GNSS, the accuracy of the INS/DVL integrated navigation system is shown in Table 6. The accuracy of the INS/DVL integration is about 1.76‰D.
5.2.2. Experiment 2
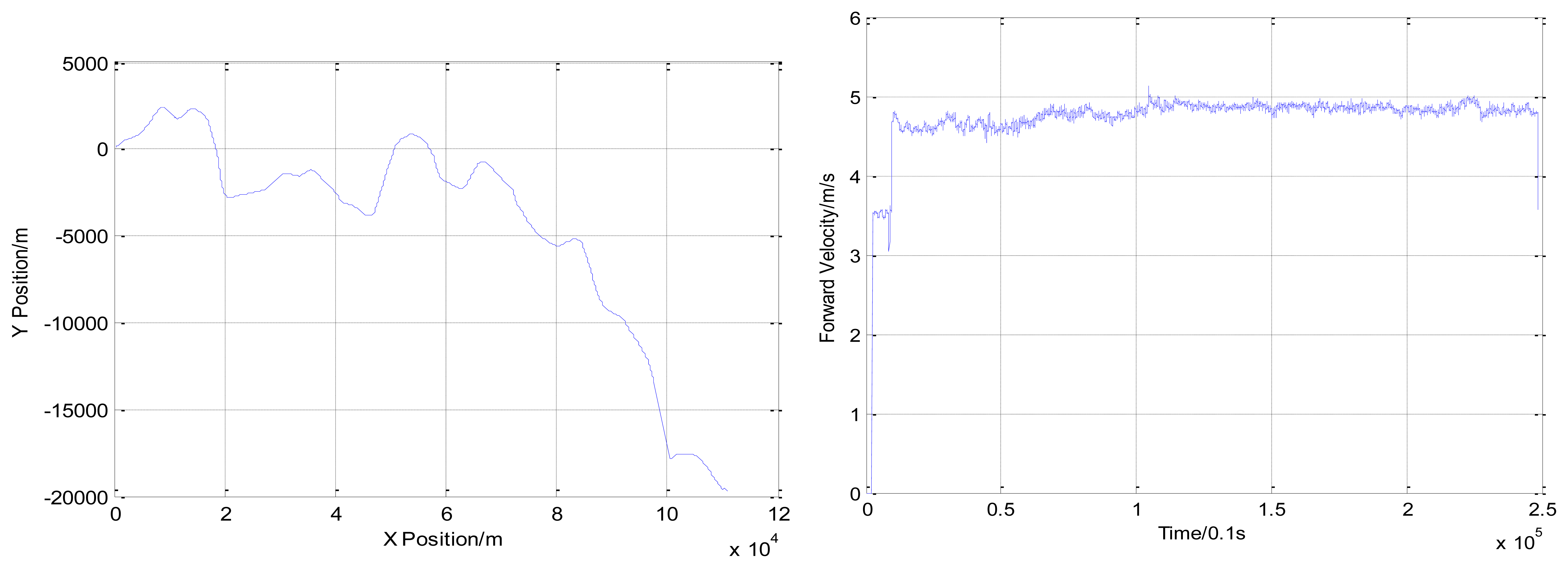
In Experiment 2, the AUV travelled for about 120 km. The depth varies from 60 to 180 m. The trajectory obtained by INS/DVL integrated navigation system is shown in Figure 7. During the process of the experiment, the AUV surfaced five times to receive the GNSS signals.
Comparing the positions obtained from GNSS, the accuracy of the INS/DVL integrated navigation system is shown in Table 7. The accuracy of the INS/DVL integrated navigation system is within 3‰D.
5.2.3. Experiment 3
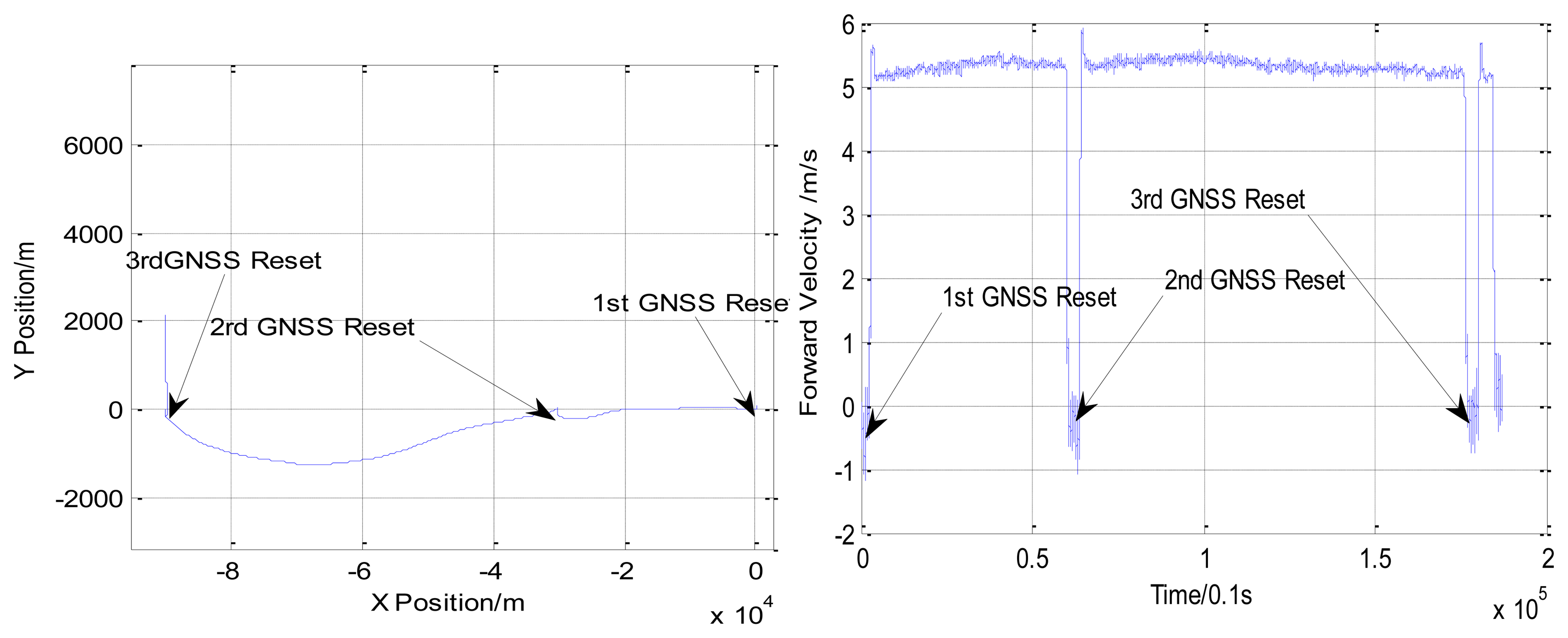
In Experiment 3, the AUV travelled for about 90 km. The depth varies from 60 to 180 m. The trajectory obtained by INS/DVL integrated navigation system is shown in Figure 8. During the process of the experiment, the AUV surfaced three times to receive the GNSS signals.
Comparing the position obtained from DGNSS, the accuracy of the INS/DVL integrated navigation system is shown in Table 8. The accuracy of the INS/DVL integrated navigation system is within 3‰D.
According to the experimental results in Table 6, 7 and 8, the INS/DVL integrated navigation system has reached the accuracy of about 2‰D (CEP) with the calibrated parameter estimates obtained by the proposed method.
6. Conclusions
In order to meet the requirements of the AUV, an INS/DVL integrated navigation method has been designed. As the scale factor of DVL and misalignments between INS and DVL are the key factors which limit the accuracy of the INS/DVL integrated navigation, a novel parameter calibration method has been proposed. With this method, it is needless to receive GNSS signals continuously, making this method suitable for AUV platforms. The proposed method has been evaluated with both river trial and sea trial data sets. With the calibrated parameter estimates, INS/DVL integrated navigation can reach the accuracy of about 1‰ of the distance travelled (CEP) in the river trial and 2‰ of the distance travelled (CEP) in the sea trials.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant No. 61104201). The authors are grateful to Hua Mu and Ancheng Wang for his valuable suggestions for the manuscript revisions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Stutters, L.; Liu, H.; Tiltman, C.; Brown, D.J. Navigation technologies for autonomous underwater vehicles. IEEE Trans. Syst. Man Cybern. C 2008, 38, 581–589. [Google Scholar]
- James, C.K.; Louis, L.W. In Situ alignment calibration of attitude and doppler sensors for precision underwater vehicle navigation: Theory and experiment. IEEE J. Ocean. Eng. 2007, 32, 286–299. [Google Scholar]
- Jalving, B.; Gade, K.; Hagen, O.K.; Vestgard, K. A toolbox of aiding techniques for the HUGIN AUV integrated inertial navigation system. Model. Identif. Control 2004, 25, 173–190. [Google Scholar]
- Peyronne, J.P.; Person, R.; Rybicki, F. POSIDONIA 6000-A New Long Range Higly Accurate Ultra Short Base Longe Positioning System. Proceedings of the IEEE /MTS OCEANS, Nice, France, 28 Sepember–1 October 1998; Volume 3, pp. 1721–1727.
- Singh, H.; Catipovic, H.; Eastwood, R.; Freitag, L.; Hericksen, H.; Yoerger, D.; Bellingham, J.G.; Moran, B.A. An Integrated Approach to Multiple AUV Communications, Navigation and Docking. Proceedings of the IEEE /MTS OCEANS, Fort Lauderdale, FL, USA, 23–26 September 1996; pp. 59–64.
- Smith, S.M.; Kronen, D. Experimental Results of an Inexpensive Short Baseline Acoustic Positioning System for AUV Navigation. Proceedings of the IEEE /MTS OCEANS, Halifax, NS, Canada, 6–9 October 1997; pp. 714–720.
- Panish, R.; Taylor, M. Achieving High Navigation Accuracy Using Inertial Navigation Systems in Autonomous Underwater Vehicles. Proceedings of the OCEANS'11 IEEE, Santander, Spain, 6–9 June 2011.
- Kearfott Corporation. Seaborne Navigation System (SEANAV). KN-5050 Family. Data Sheet. 2010. [Google Scholar]
- IXSEA. PHINS User Guide. Available online http://www.ixsea.com/en/subsea_positioning/6/phins.html (accessed on 22 October 2013).
- Troni, G.; Whitcomb, L. New Methods for In-Situ Calibration of Attitude and Doppler Sensors for Underwater Vehicle Navigation: Preliminary Results. Proceedings of the IEEE International Conference of Robotics and Automation, Seattle, WA, USA, 20–23 September 2010.
- Jalving, B.; Gade, K.; Svartveit, K.; Yillumsen, A.; Sørhagen, R. DVL velocity aiding in the HUGIN 1000 integrated inertial navigation system. Model. Identif. Control 2004, 25, 223–235. [Google Scholar]
- Yun, X.E.R.; Bachmann, R.B.; Mcghee, R.B.; Whalen, R.H.; Roberts, R.L.; Knapp, R.G.; Healey, A.J.; Zyda, M.J. Testing and evaluation of an integrated GPS/INS system for small AUV navigation. IEEE J. Ocean. Eng. 1999, 24, 396–404. [Google Scholar]
- Marco, D.B.; Healey, A.J. Command, control, and navigation experimental results with the NPS ARIES AUV. J. Ocean. Eng. 2001, 26, 466–476. [Google Scholar]
- Kinsey, J.C.; Whitcomb, L.L. Preliminary field experience with the DVLNAV integrated navigation system for oceanographic submersibles. Control Eng. Pract. 2004, 12, 1541–1549. [Google Scholar]
- Jalving, B.; Gade, K. Positioning Accuracy for the HUGIN Detailed Seabed Mapping UUV. Proceedings of the OCEANS'98 Conference, Defence Research Establishment, Kjeller, Norway, 28 September–1 October 1998; pp. 108–112.
- Grenon, G.; An, P.E.; Smith, S.M.; Healey, A.J. Enhancement of the inertial navigation system for the morpheus autonomous underwater vehicles. J. Ocean. Eng. 2001, 26, 548–560. [Google Scholar]
- Li, Y.; Xu, X.-S.; Wu, B.-X. Observable degree information matching in AUV integrated navigation. J. Chin. Inert. Technol. 2008, 16, 589–594. [Google Scholar]
- Bingham, B. Predicting the Navigation Performance of Underwater Vehicles. Proceedings of the 2009 IEEE/RSJ International Conference on Integrated Robots and Systems, St Louis, MO, USA, 11–15 October 2009.
- Joyce, T. On in situ “calibration” of shipboard ADCPs. J. Atmos. Ocean. Technol. 1989, 6, 169–172. [Google Scholar]
- Pollary, R.; Read, J. A method for calibrating shipmounted acoustic doppler profilers and the limitations of gyro compass. J. Atmos. Ocean. Technol. 1989, 6, 859–865. [Google Scholar]
- Münchow, T.; Coughran, C.; Hendershott, M.; Winant, C. Performance and calibration of an acoustic doppler current profiler towed below the surface. J. Atmos. Ocean. Technol. 1995, 12, 435–444. [Google Scholar]
- Kinsey, J.; Whitcomb, L. Adaptive identification on the group of rigid-body rotations and its application to underwater vehicle navigation. IEEE Trans. Rob. 2007, 23, 124–136. [Google Scholar]
- Kinsey, J.; Whitcomb, L. Towards In-Situ Calibration of Gyro and Doppler Navigation Sensors for Precision Underwater Vehicle Navigation. Proceedings of the 2002 IEEE International Conference Robotics and Automation (ICRA), Washington, DC, USA, 11–15 May 2002.
- Lv, Z.; Tang, K.H.; Wu, M. Online Estimation of DVL Misalignment Angle in SINS/DVL Integrated Navigation System. Proceedings of the 10th International Conference on Electronic Measurement & Instruments, Chengdu, China, 16–19 August 2011.
- Wu, Y.X.; Wu, M.P.; Hu, X.P.; Hu, D.W. Self-calibration for Land Navigation Using Inertial Sensors and Odometer: Observability Analysis. Proceedings of the AIAA Guidance, Navigation and Control Conference, Chicago, IL, USA, 10–13 August 2009.
- Wu, Y.X.; Goodall, C.; El-sheimy, N. Self-calibration for IMU/Odometer Land Navigation: Simulation and Test Results. Proceedings of the ION International Technical Meeting, San Diego, CA, USA, 25–27 January 2010.
- Wu, Y.X.; Hu, D.W.; Wu, M.P.; Hu, X.P.; Wu, T. Observability analysis of rotation estimation by fusing inertial and line-based visual information: A revisit. Automatica 2006, 42, 1809–1812. [Google Scholar]
- Hong, S.; Chang, Y.-S.; Ha, S.-K.; Lee, M.-H. Estimation of Alignment Errors in GPS/INS Integration. Proceedings of the ION GPS, Portland, OR, USA, 24–27 September 2002.
- Wu, Y.X.; Zhang, H.L.; Wu, M.P.; Hu, X.P.; Hu, D.W. Observability of SINS alignment: A global perspective. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 78–102. [Google Scholar]
- Li, W.L.; Wu, W.Q.; Wang, J.; Lu, L.Q. A fast SINS initial alignment scheme for underwater vehicle applications. J. Navig. 2013, 66, 181–189. [Google Scholar]
- Li, W.L.; Wang, J.; Lu, L.Q.; Wu, W.Q. A novel scheme for DVL-aided SINS in-motion alignment using UKF techniques. Sensors 2013, 13, 1046–1063. [Google Scholar]
- Petovello, M.G.; Cannon, M.E.; Lachapelle, G. Kalman Filter Reliability Analysis Using Different Update Strategies. Proceedings of the CASI Annual General Meeting, Montreal, QC, Canada, 28–30 April 2003.
- Angrisano, A.; Petovello, M.; Pugliano, G. Benefits of combined GPS/GLONASS with low-cost MEMS IMUs for vehicular urban navigation. Sensors 2012, 12, 5134–5158. [Google Scholar]





| Bias | Scale Factor | Rate | ||
|---|---|---|---|---|
| Gyro | Acc | Gyro | Acc | |
| 0.03 deg/h | 50 μg | 10 PPM | 50 PPM | 200 Hz |
| Variable | Sensors | Precision | Rate |
|---|---|---|---|
| Position | NovAtel DGPS | 1 m | 1 Hz |
| Velocity | HEU DVL | ± 0.5% ± 0.5 cm/s | >=1 Hz |
| N1 | N2 | N3 | N4 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 + k | α | β | 1 + k | α | β | 1 + k | α | β | 1 + k | α | β | |
| Initial estimates | 0.9935 | 0.075 | 0.256 | 0.9988 | 0.287 | 0.363 | 0.9954 | 0.265 | 0.267 | 0.9958 | 0.423 | 0.207 |
| iterative estimates | 0.9944 | 0.123 | 0.248 | 0.9936 | 0.134 | 0.365 | 0.9972 | 0.271 | 0.244 | 0.9960 | 0.390 | 0.214 |
| N1 | N2 | N3 | N4 | |||||
|---|---|---|---|---|---|---|---|---|
| D(m) | Position Error(m) | Accuracy (‰D) | Position Error(m) | Accuracy (‰D) | Position Error(m) | Accuracy (‰D) | Position Error(m) | Accuracy (‰D) |
| 7,140 | 3.0 | 0.40 | 4.0 | 0.56 | 5.0 | 0.70 | 3.0 | 0.40 |
| N1 | N2 | N3 | N4 | |||||
|---|---|---|---|---|---|---|---|---|
| D(km) | Position Error (m) | Accuracy (‰D) | Position Error(m) | Accuracy (‰D) | Position Error(m) | Accuracy (‰D) | Position Error(m) | Accuracy (‰D) |
| 20 | 34.7 | 1.73 | 34.9 | 1.74 | 35.9 | 1.79 | 36.2 | 1.81 |
| 40 | 31.7 | 0.79 | 58.3 | 1.45 | 41.4 | 1.03 | 52.7 | 1.32 |
| 60 | 18.2 | 0.3 | 66.8 | 1.11 | 30.8 | 0.5 | 54.9 | 0.91 |
| 80 | 37.3 | 0.46 | 70.8 | 0.88 | 46.8 | 0.58 | 62.6 | 0.78 |
| 100 | 42.3 | 0.47 | 88.6 | 0.98 | 53.1 | 0.58 | 80.7 | 0.89 |
| Distance (m) | Error (m) | Accuracy (‰D) |
|---|---|---|
| 17,614 | 31.0 | 1.76 |
| Distance (m) | Error (m) | Accuracy (‰D) |
|---|---|---|
| 31,467 | 53.3 | 1.7 |
| 29,772 | 90.4 | 3.0 |
| 31,102 | 68.5 | 2.2 |
| 31,870 | 56.0 | 1.7 |
| Distance (m) | Error (m) | Accuracy (‰D) |
|---|---|---|
| 30,836 | 90.3 | 2.9 |
| 60,341 | 27.0 | 0.5 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Tang, K.; Wang, J.; Li, W.; Wu, W. A Novel INS and Doppler Sensors Calibration Method for Long Range Underwater Vehicle Navigation. Sensors 2013, 13, 14583-14600. https://doi.org/10.3390/s131114583
Tang K, Wang J, Li W, Wu W. A Novel INS and Doppler Sensors Calibration Method for Long Range Underwater Vehicle Navigation. Sensors. 2013; 13(11):14583-14600. https://doi.org/10.3390/s131114583
Chicago/Turabian StyleTang, Kanghua, Jinling Wang, Wanli Li, and Wenqi Wu. 2013. "A Novel INS and Doppler Sensors Calibration Method for Long Range Underwater Vehicle Navigation" Sensors 13, no. 11: 14583-14600. https://doi.org/10.3390/s131114583




