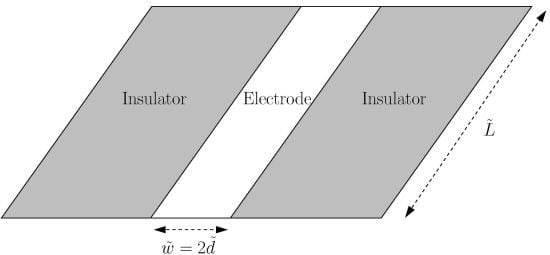
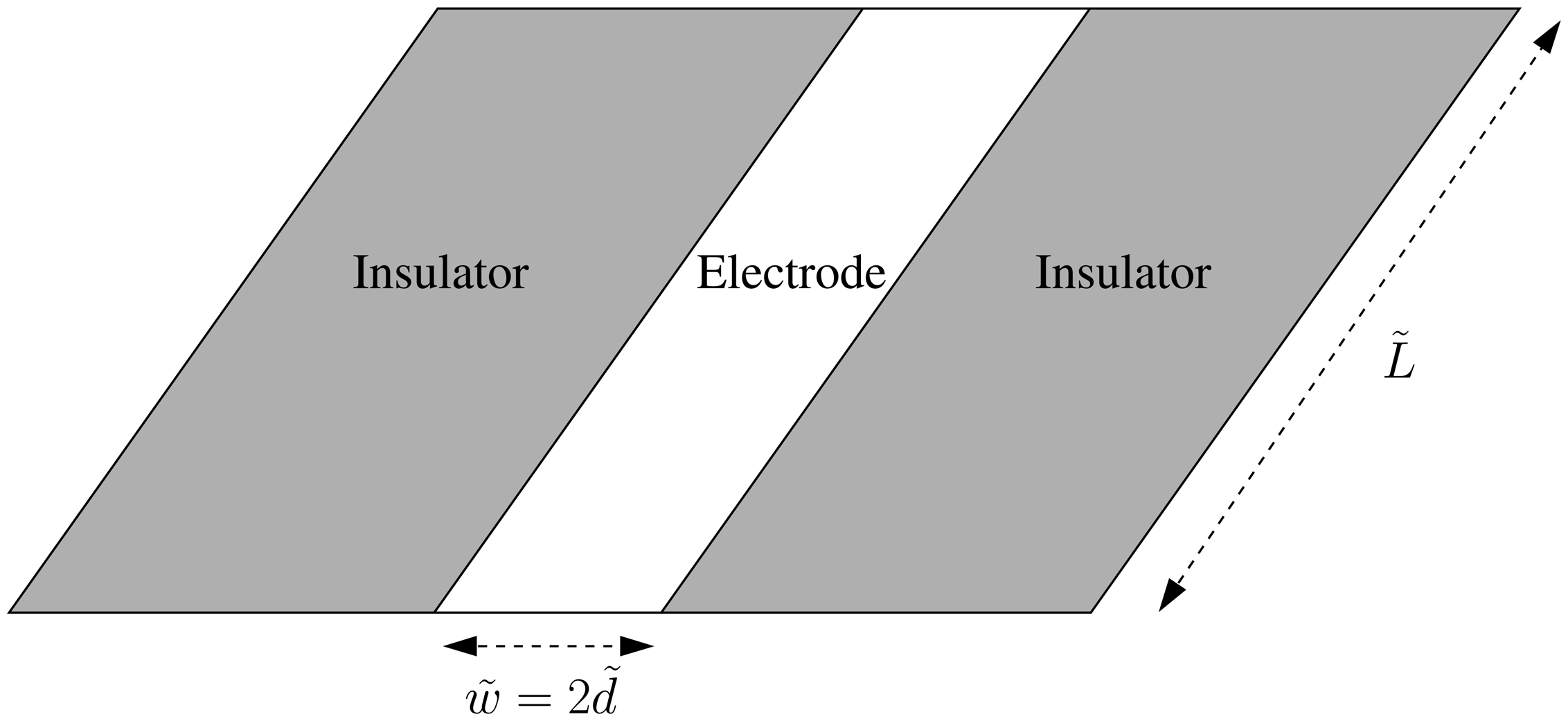
The Long-Time Chronoamperometric Current at an Inlaid Microband (or Laminar) Electrode
Abstract
:1. Introduction
2. Theory
2.1. Asymptotic Solution for the Long-time Transient Behaviour
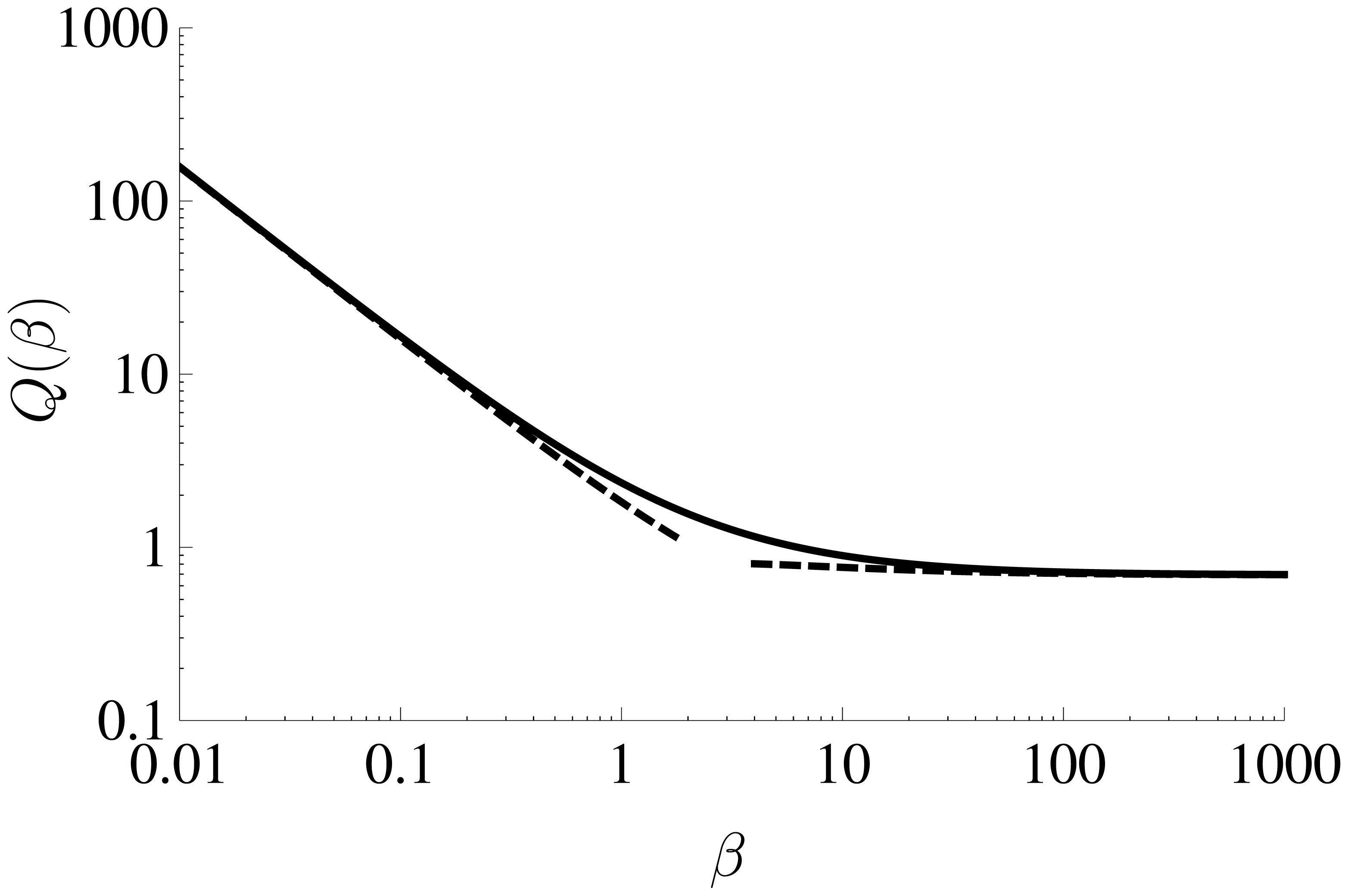
2.2. Calculation of Q(β)
3. Results and Discussion
3.1. Diffusion-limited Currents due to Extreme Polarization
3.2. Reversible Reactions
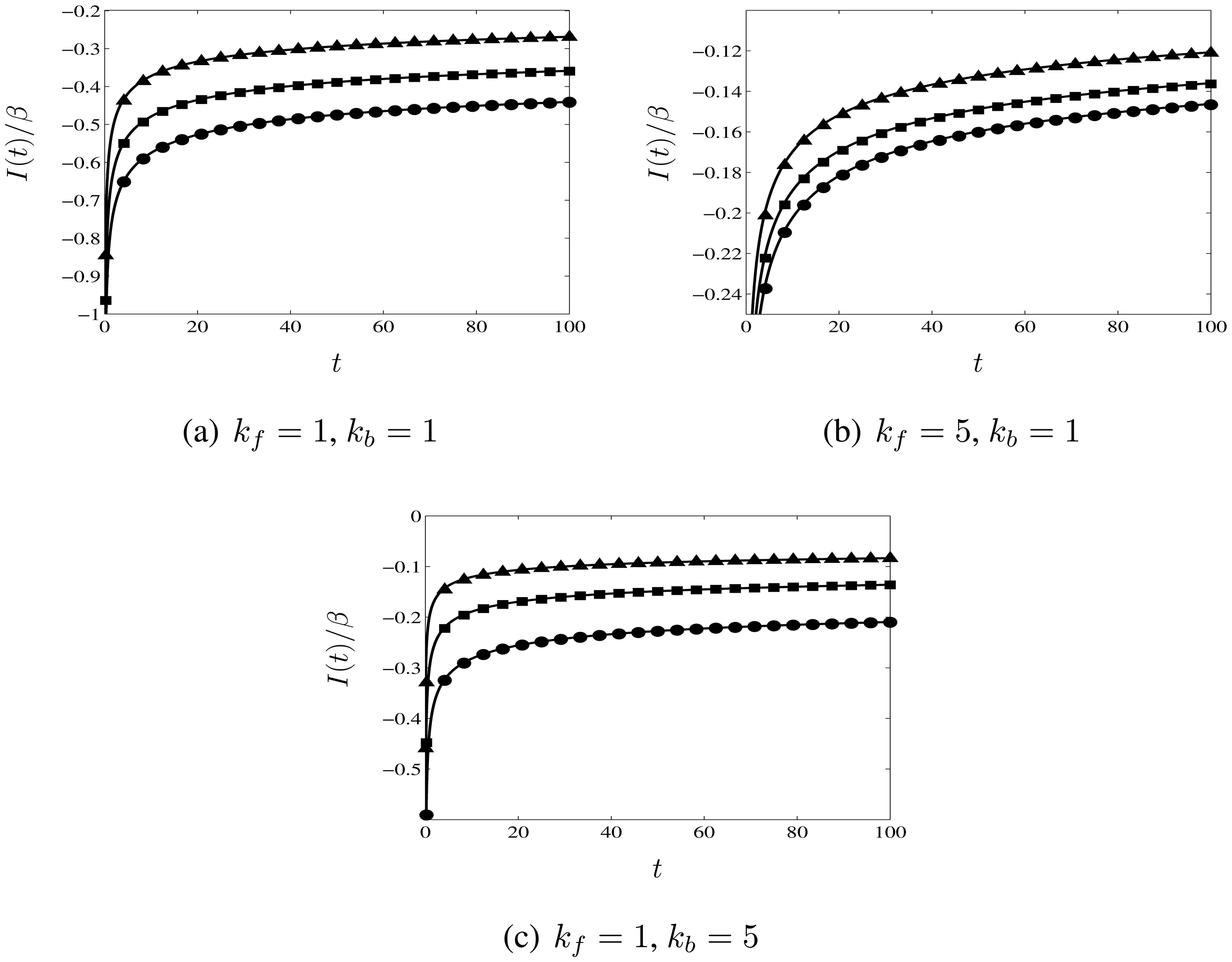
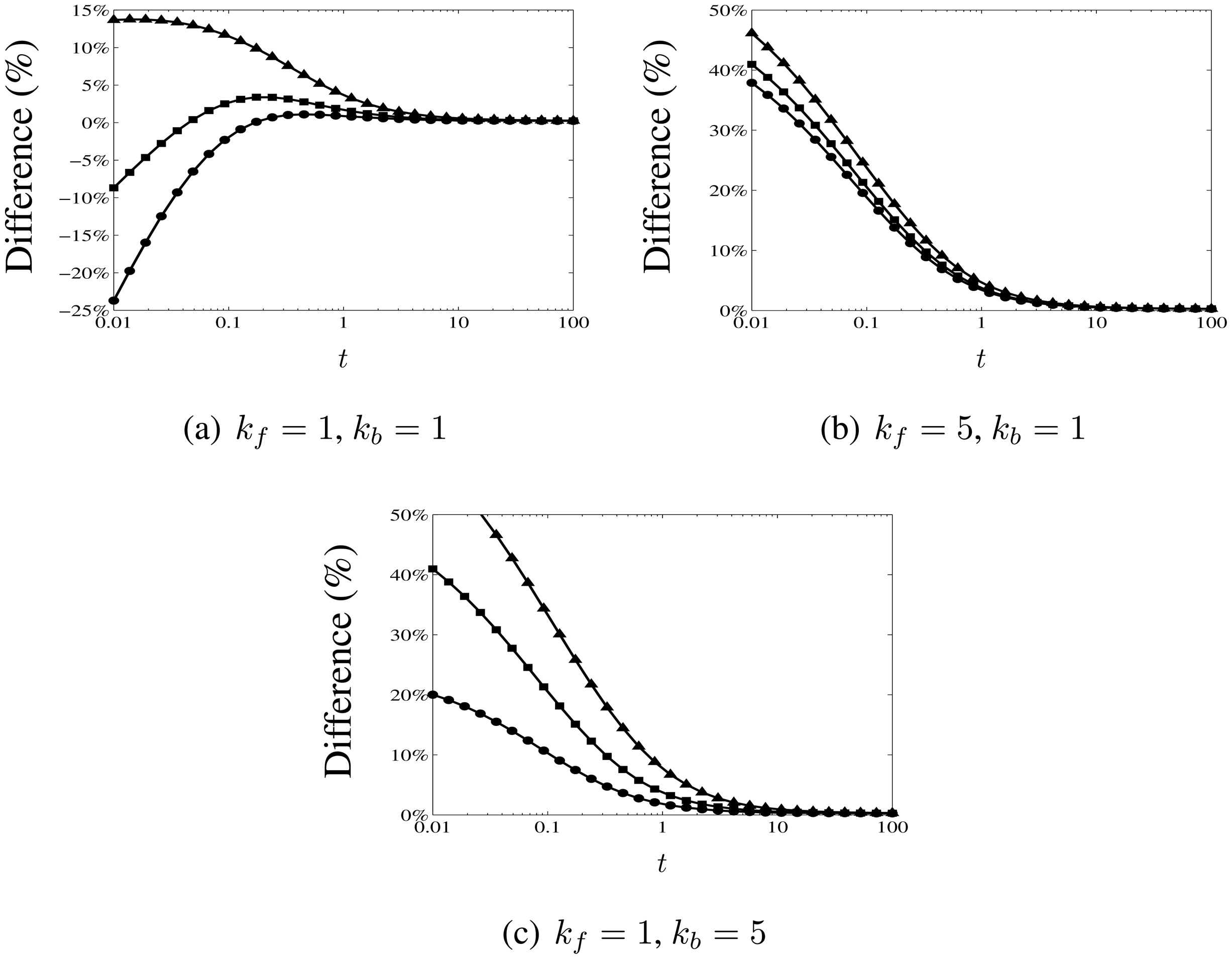
3.3. Comparison with Numerical Calculations
3.4. Long-time Current Response for a One-step, One-electron Redox Reaction Modelled in the Butler–Volmer Framework
4. Conclusions
Appendix
A. Large-β Asymptotic Solution for Q(β)
References
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods: Fundamentals and Applications; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Aoki, K. Theory of ultramicroelectrodes. Electroanalytical 1993, 5, 627–639. [Google Scholar]
- Amatore, C. Electrochemistry at Ultramicroelectrodes. In Physical Electrochemistry: Principles, Methods and Applications; Rubinstein, I., Ed.; Marcel Dekker: New York, NY, USA, 1995; pp. 131–208. [Google Scholar]
- Bond, A.M.; Oldham, K.B.; Zoski, C.G. Theory of electrochemical processes at an inlaid disc microelectrode under steady-state conditions. J. Electroanal. Chem. 1988, 245, 71–104. [Google Scholar]
- Kovach, P.M.; Caudill, W.L.; Peters, D.G.; Wightman, R.M. Faradaic electrochemistry at microcylinder, band, and tubular band electrodes. J. Electroanal. Chem. 1985, 185, 285–295. [Google Scholar]
- Wehmeyer, K.R.; Deakin, M.R.; Wightman, R.M. Electroanalytical properties of band electrodes of submicrometer width. Anal. Chem. 1985, 57, 1913–1916. [Google Scholar]
- Coen, S.; Cope, D.K.; Tallman, D.E. Diffusion current at a band electrode by an integral equation method. J. Electroanal. Chem. 1986, 215, 29–48. [Google Scholar]
- Deakin, M.R.; Wightman, R.M.; Amatore, C.A. Electrochemical kinetics at microelectrodes: Part II. Cyclic voltammetry at band electrodes. J. Electroanal. Chem. 1986, 215, 49–61. [Google Scholar]
- Cope, D.K.; Scott, C.H.; Kalapathy, V.; Tallman, D.E. Transient behavior at planar microelectrodes:: Diffusion current at a band electrode by an integral equation method. Part II. J. Electroanal. Chem. 1990, 280, 27–35. [Google Scholar]
- Alden, J.A.; Compton, R.G.; Dryfe, R.A.W. Theory of ECE processes at hemicylinder and band microelectrodes. J. Electroanal. Chem. 1995, 397, 11–17. [Google Scholar]
- Alden, J.A.; Booth, J.; Compton, R.G.; Dryfe, R.A.W.; Sanders, G.H.W. Diffusional mass transport to microband electrodes of practical geometries: A simulation study using the strongly implicit procedure. J. Electroanal. Chem. 1995, 389, 45–54. [Google Scholar]
- Alden, J.A.; Compton, R.G.; Dryfe, R.A.W. Modelling electrode transients: The strongly implicit procedure. J. Appl. Electrochem. 1996, 26, 865–872. [Google Scholar]
- Alden, J.A.; Compton, R.G. A comparison of finite difference algorithms for the simulation of microband electrode problems with and without convective flow. J. Electroanal. Chem. 1996, 402, 1–10. [Google Scholar]
- Jin, B.; Qian, W.; Zhang, Z.; Shi, H. Finite analytic numerical method-a new numerical simulation method for electrochemical problems. J. Electroanal. Chem. 1996, 411, 19–27. [Google Scholar]
- Qiu, F.L.; Fisher, A.C. The dual reciprocity method: Simulation of potential step voltammetry at microelectrodes. Electrochem. Comm. 2000, 2, 738–742. [Google Scholar]
- Qiu, F.L.; Fisher, A.C. The boundary element method: Chronoamperometric simulations at microelectrodes. Electrochem. Comm. 2003, 5, 87–93. [Google Scholar]
- Britz, D. Digital Simulation in Electrochemistry; Springer-Verlag: Berlin, Germany, 2005. [Google Scholar]
- Britz, D.; Poulsen, K.; Strutwolf, J. Reference values of the diffusion-limited chronoamperometric current at a microband electrode. Electrochim. Acta 2005, 51, 333–339. [Google Scholar]
- Strutwolf, J. Computational study of chronoamperometry at rectangular microelectrodes. Electroanalytical 2005, 17, 1547–1554. [Google Scholar]
- Cutress, I.J.; Compton, R.G. Theory of square, rectangular, and microband electrodes through explicit GPU simulation. J. Electroanal. Chem. 2010, 645, 159–166. [Google Scholar]
- Amatore, C.; Pebay, C.; Sella, C.; Thouin, L. Mass transport at microband electrodes: Transient, quasi-steady-state, and convective regimes. Chem. Phys. Chem. 2012, 13, 1562–1568. [Google Scholar]
- Oldham, K.B. Edge effects in semiinfinite diffusion. J. Electroanal. Chem. 1981, 122, 1–17. [Google Scholar]
- Aoki, K.; Tokuda, K.; Matsuda, H. Theory of chronoamperometric curves for a short time at microband electrodes. Denki Kagaku (J. Electrochem. Soc. Jpn.) 1986, 54, 1010–1017. [Google Scholar]
- Aoki, K.; Tokuda, K.; Matsuda, H. Theory of chronoamperometric curves at microband electrodes. J. Electroanal. Chem. 1987, 225, 19–32. [Google Scholar]
- Phillips, C.G.; Jansons, K.M. The short-time transient of diffusion outside a conducting body. Proc. R. Soc. Lon. Ser.-A 1990, 428, 431–449. [Google Scholar]
- Phillips, C.G. The long-time transient of two-and three-dimensional diffusion in microelectrode chronoamperometry. J. Electroanal. Chem. 1992, 333, 11–32. [Google Scholar]
- Szabo, A.; Cope, D.K.; Tallman, D.E.; Kovachi, P.M.; Wightman, R.M. Chronoamperometric current at hemicylinder and band microelectrodes: Theory and experiment. J. Electroanal. Chem. 1987, 217, 417–423. [Google Scholar]
- Aoki, K.; Tokuda, K.; Matsuda, H. Derivation of an approximate equation for chronoamperometric curves at microband electrodes and its experimental verification. J. Electroanal. Chem. 1987, 230, 61–67. [Google Scholar]
- Wang, Y.; Limon-Petersen, J.G.; Compton, R.G. Measurement of the diffusion coefficients of [Ru (NH3)6]3+ and [Ru (NH3)6]2+ in aqueous solution using microelectrode double potential step chronoamperometry. J. Electroanal. Chem. 2011, 652, 13–17. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; National Bureau of Standards Applied Mathematics Series, 55, US Goverment Printing Office: Washington, DC, USA, 1964.
- Hinch, E.J. Perturbation Methods; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Delves, L.M.; Mohamed, J.L. Computational Methods for Integral Equations; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Gavaghan, D.J. An exponentially expanding mesh ideally suited to the fast and efficient simulation of diffusion processes at microdisc electrodes 1. Derivation of the mesh. J. Electroanal. Chem. 1998, 456, 1–12. [Google Scholar]
- Gavaghan, D.J. An exponentially expanding mesh ideally suited to the fast and efficient simulation of diffusion processes at microdisc electrodes 2. Application to chronoamperometry. J. Electroanal. Chem. 1998, 456, 13–23. [Google Scholar]
- Phillips, C.G. The steady-state current for a microelectrode near diffusion-limited conditions. J. Electroanal. Chem. 1990, 291, 251–256. [Google Scholar]
- Classification: PACS 82.45.Fk, 82.45.Rr, 82.80.Fk, 82.47.Rs

Supplementary Files
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bell, C.G. The Long-Time Chronoamperometric Current at an Inlaid Microband (or Laminar) Electrode. Sensors 2013, 13, 626-647. https://doi.org/10.3390/s130100626
Bell CG. The Long-Time Chronoamperometric Current at an Inlaid Microband (or Laminar) Electrode. Sensors. 2013; 13(1):626-647. https://doi.org/10.3390/s130100626
Chicago/Turabian StyleBell, Christopher G. 2013. "The Long-Time Chronoamperometric Current at an Inlaid Microband (or Laminar) Electrode" Sensors 13, no. 1: 626-647. https://doi.org/10.3390/s130100626