Health Assessment of Cooling Fan Bearings Using Wavelet-Based Filtering
Abstract
:1. Introduction
2. Principle of Comblet Filtering
2.1. Time-Domain Synchronous Averaging
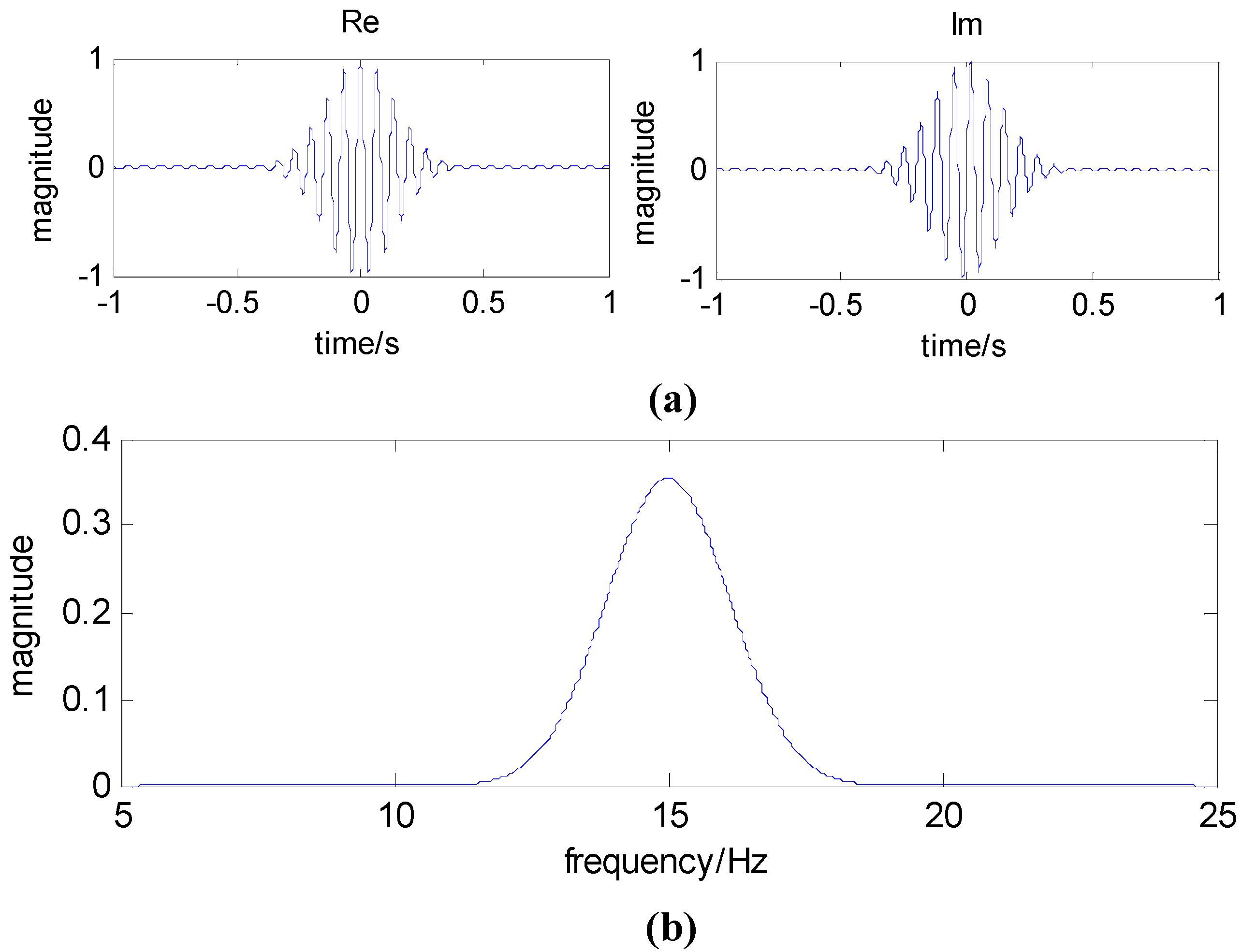
2.2. Wavelet Filtering
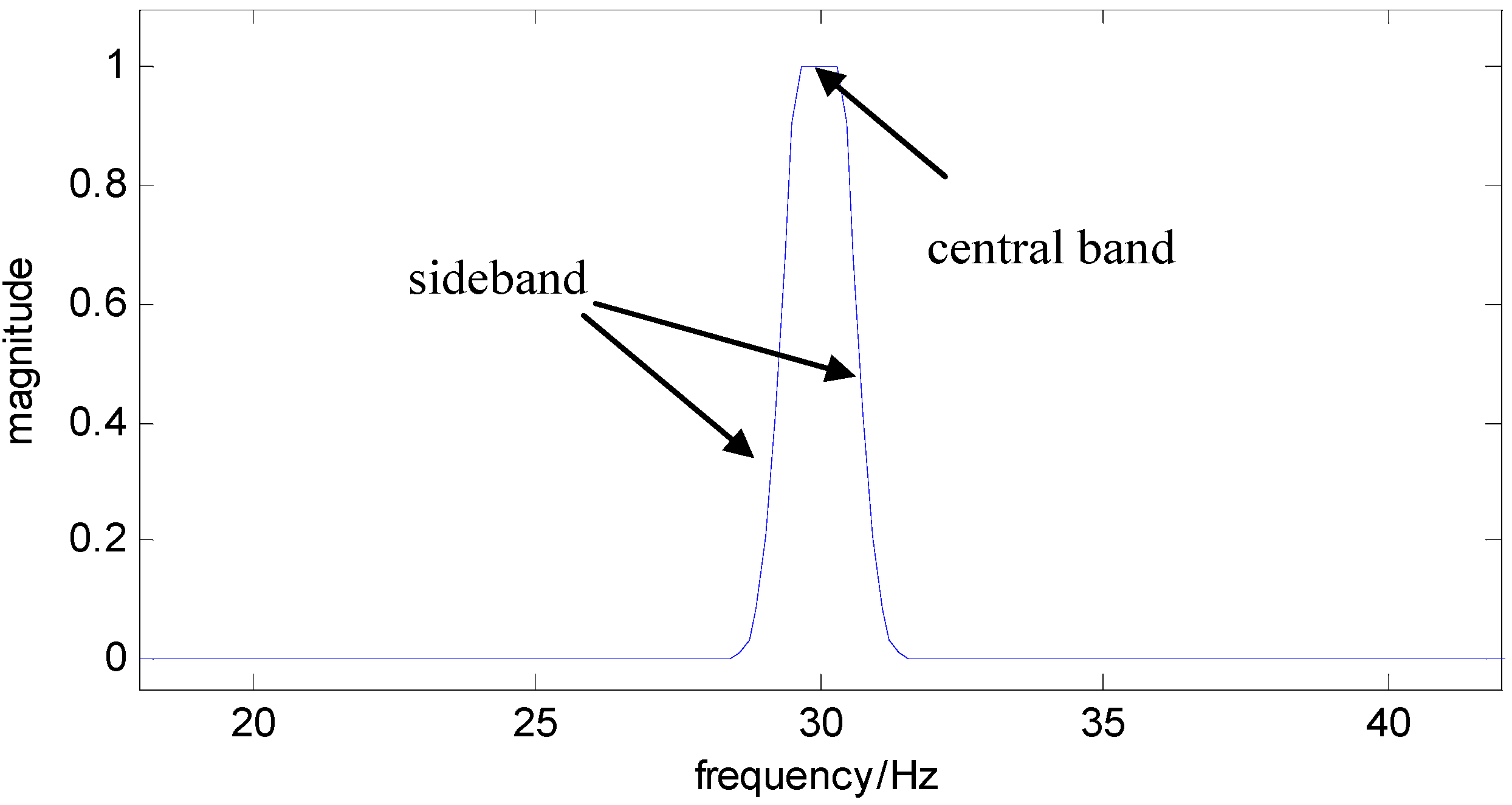
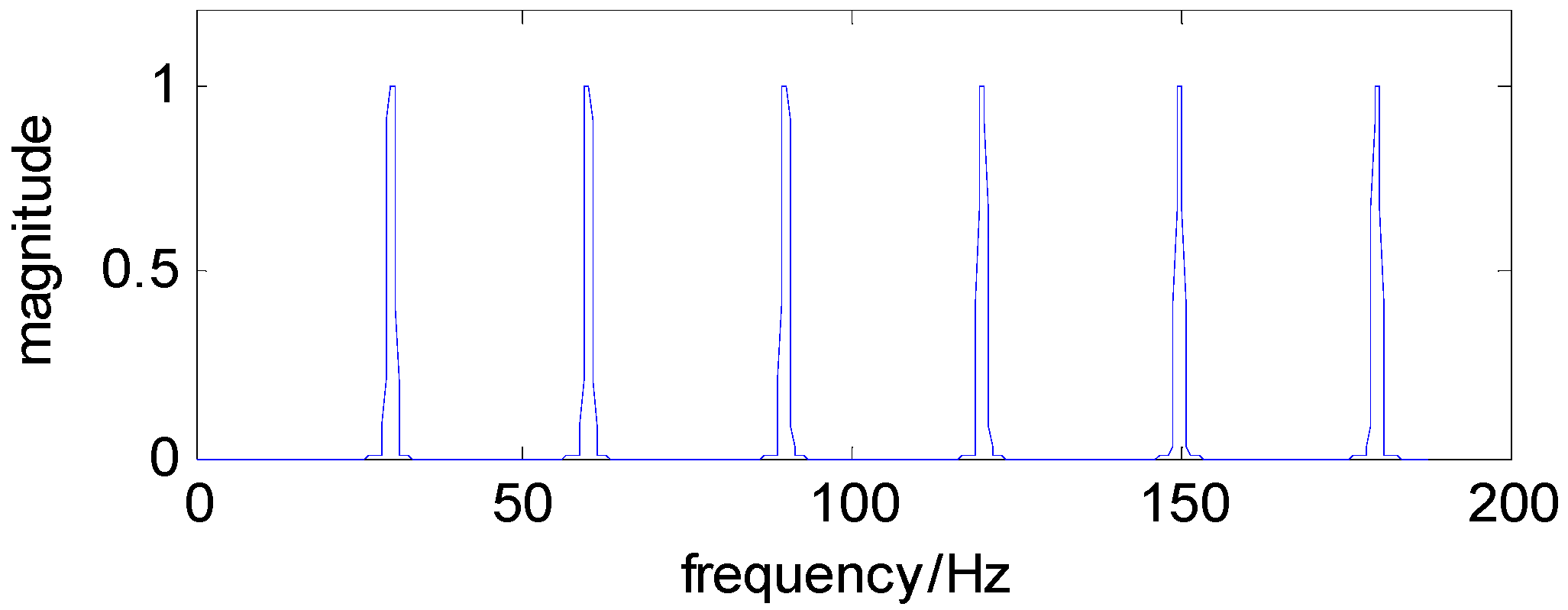
2.3. Comblet Filter Design
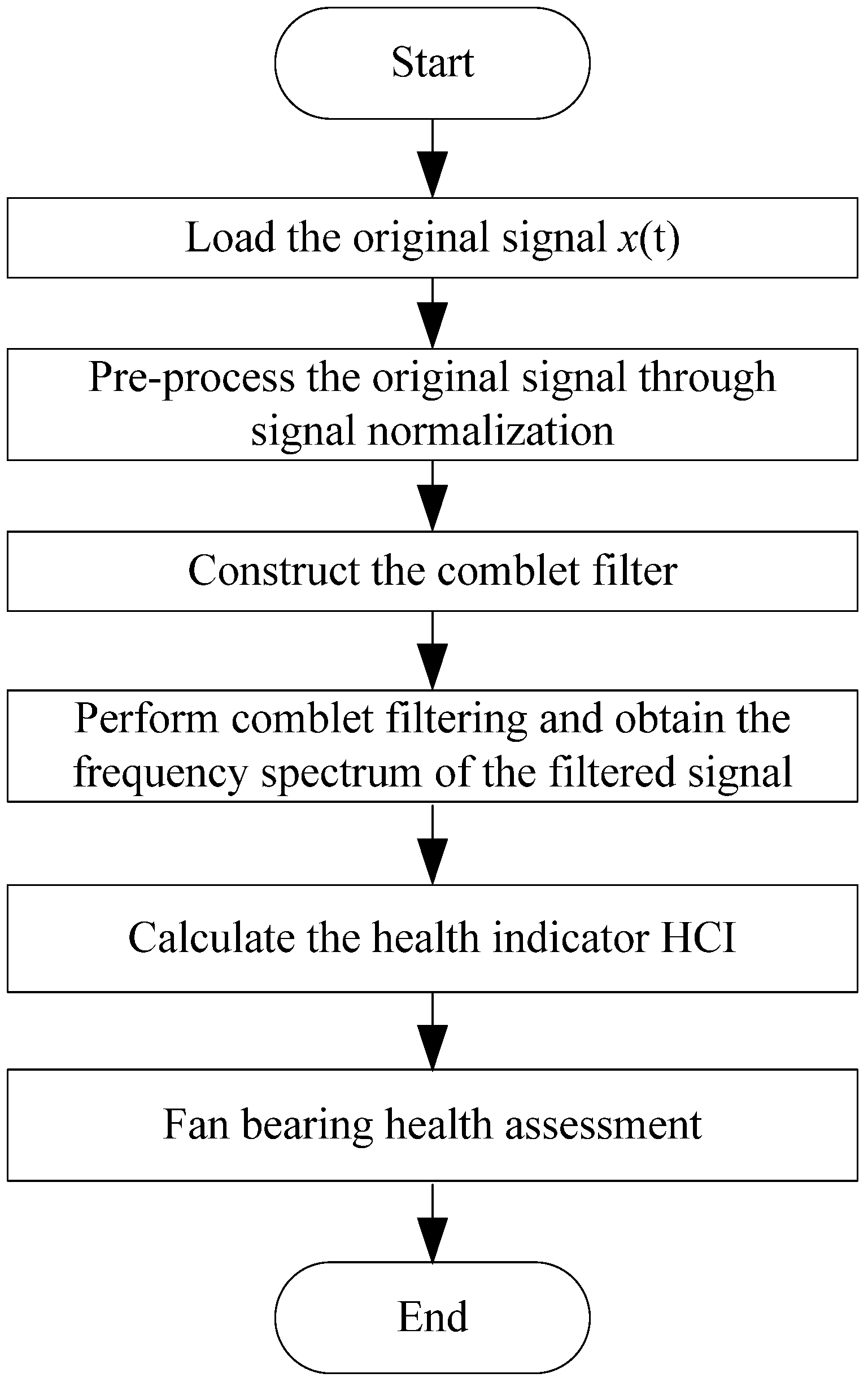
3. Proposed Fan Bearing Health Assessment Method
3.1. Fan Bearing Vibration Characteristics
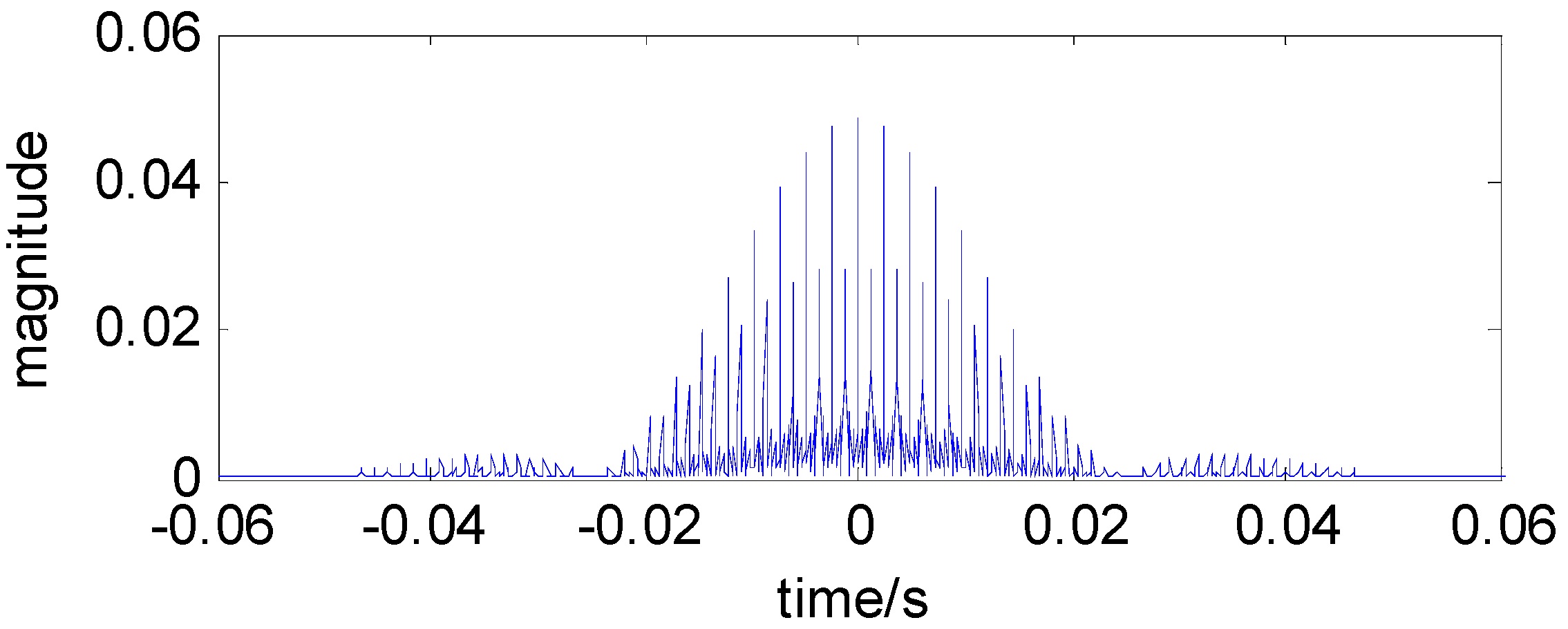
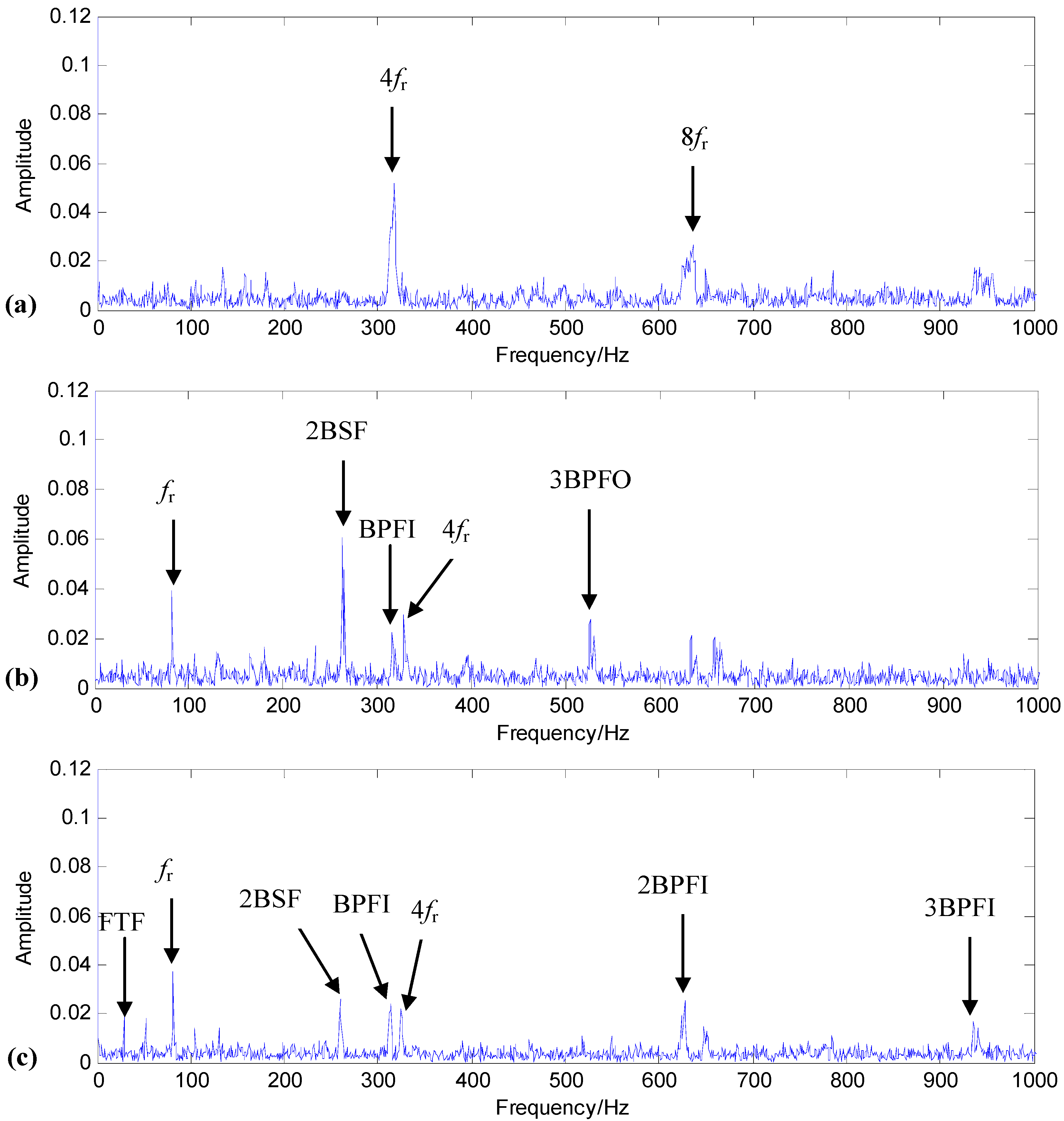
3.2. Implementation of Comblet Filtering
3.3. Fan Bearing Degradation Assessment
4. Case Study with Fan Bearing
4.1. Description of Experimental Setup
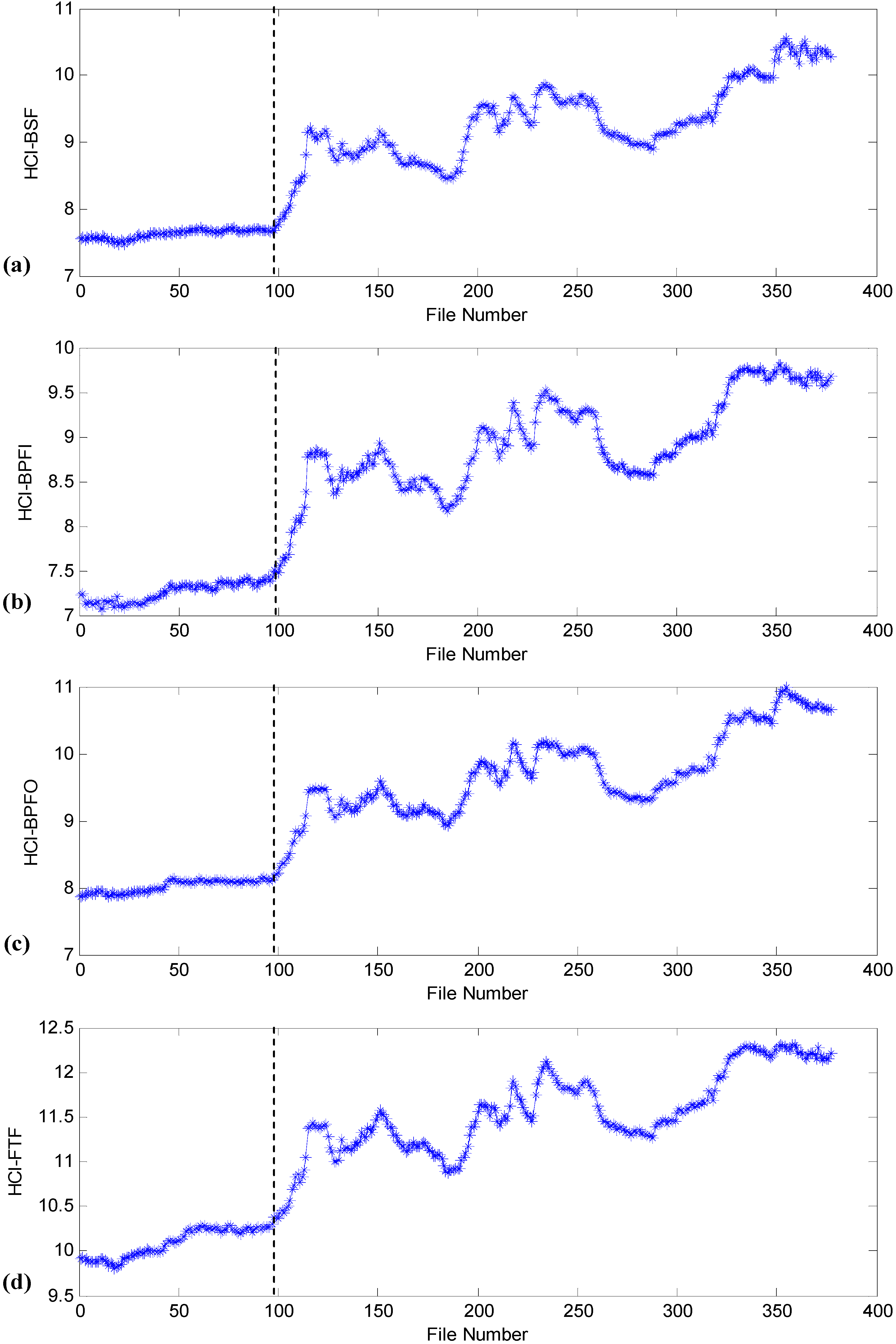
4.2. Evaluation of the Proposed Health Indicator
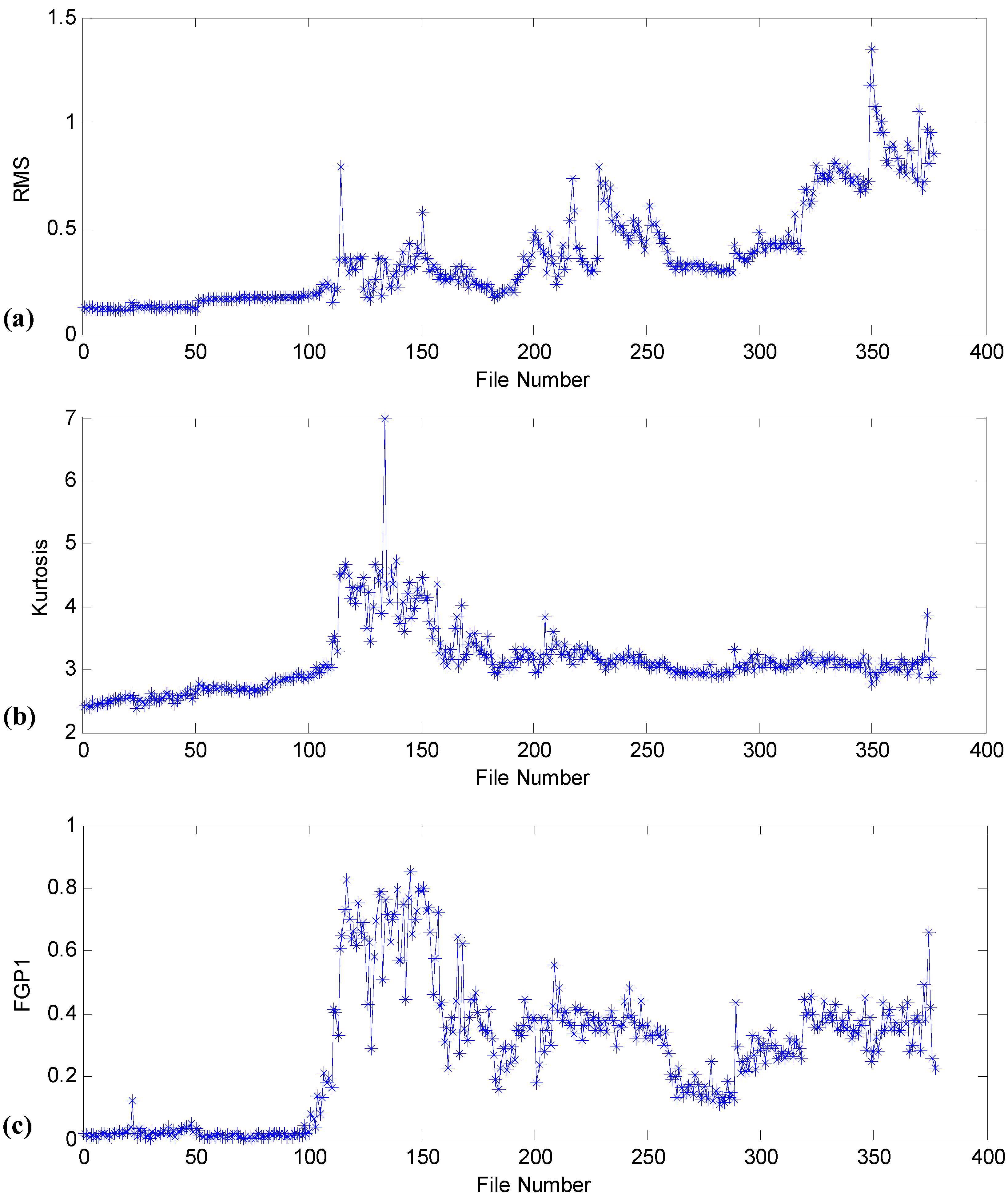
4.3. Comparison with Other Health Indicators
5. Conclusions
Acknowledgments
References
- Pecht, M. Prognostics and Health Management of Electronics, 1 ed.; Wiley-Interscience: London, UK, 2008. [Google Scholar]
- Tian, X. Cooling fan reliability: failure criteria, accelerated life testing, modeling and qualification. Proceedings of 2006 Reliability and Maintainability Symposium, Newport Beach, CA, USA, 23-26 January 2006; pp. 380–384.
- Miao, Q.; Azarian, M.; Pecht, M. Cooling fan bearing fault identification using vibration measurement. Proceedings of 2011 IEEE International Conference on Prognostics and Health Management, Montreal, QC, Canada, 20- 23 June 2011; pp. 1–5.
- He, W.; Jiang, Z.-N.; Feng, K. Bearing fault detection based on optimal wavelet filter and sparse code shrinkage. Measurement 2009, 42, 1092–1102. [Google Scholar]
- Rai, V.K.; Mohanty, A.R. Bearing fault diagnosis using FFT of intrinsic mode functions in Hilbert–Huang transform. Mech. Syst. Signal. Process 2007, 21, 2607–2615. [Google Scholar]
- Qiu, H.; Lee, J.; Lin, J.; Yu, G. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics. J. Sound. Vib. 2006, 289, 1066–1090. [Google Scholar]
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal. Process 2011, 25, 485–520. [Google Scholar]
- Yang, Z.; Cai, L.; Gao, L.; Wang, H. Adaptive redundant lifting wavelet transform based on fitting for fault feature extraction of roller bearings. Sensors 2012, 12, 4381–4398. [Google Scholar]
- Li, K.; Chen, P.; Wang, S. An Intelligent diagnosis method for rotating machinery using least squares mapping and a fuzzy neural network. Sensors 2012, 12, 5919–5939. [Google Scholar]
- Wang, D.; Tse, P.W.; Tse, Y.L. A morphogram with the optimal selection of parameters used in morphological analysis for enhancing the ability in bearing fault diagnosis. Meas. Sci. Technol. 2012, 23, 065001. [Google Scholar]
- Gao, L.; Yang, Z.; Cai, L.; Wang, H.; Chen, P. Roller bearing fault diagnosis based on nonlinear redundant lifting wavelet packet analysis. Sensors 2010, 11, 260–277. [Google Scholar]
- Wang, D.; Miao, Q.; Fan, X.; Huang, H.-Z. Rolling element bearing fault detection using an improved combination of Hilbert and wavelet transforms. J. Mech. Sci. Technol. 2009, 23, 3292–3301. [Google Scholar]
- Miao, Q.; Wang, D.; Pecht, M. A probabilistic description scheme for rotating machinery health evaluation. J. Mech. Sci. Technol. 2010, 24, 2421–2430. [Google Scholar]
- Wang, D.; Miao, Q.; Kang, R. Robust health evaluation of gearbox subject to tooth failure with wavelet decomposition. J. Sound. Vib. 2009, 324, 1141–1157. [Google Scholar]
- Wang, D.; Tse, P.W.; Guo, W.; Miao, Q. Support vector data description for fusion of multiple health indicators for enhancing gearbox fault diagnosis and prognosis. Meas. Sci. Technol. 2011, 22, 025102. [Google Scholar]
- Yang, M.; Makis, V. ARX model-based gearbox fault detection and localization under varying load conditions. J. Sound. Vib. 2010, 329, 5209–5221. [Google Scholar]
- Lin, D.; Wiseman, M.; Banjevic, D.; Jardine, A.K.S. An approach to signal processing and condition-based maintenance for gearboxes subject to tooth failure. Mech. Syst. Signal. Process 2004, 18, 993–1007. [Google Scholar]
- Qiu, H.; Lee, J.; Lin, J.; Yu, G. Robust performance degradation assessment methods for enhanced rolling element bearing prognostics. Adv. Eng. Inform. 2003, 17, 127–140. [Google Scholar]
- Ocak, H.; Loparo, K.A.; Discenzo, F.M. Online tracking of bearing wear using wavelet packet decomposition and probabilistic modeling: A method for bearing prognostics. J. Sound. Vib. 2007, 302, 951–961. [Google Scholar]
- Pan, Y.; Chen, J.; Li, X. Bearing performance degradation assessment based on lifting wavelet packet decomposition and fuzzy c-means. Mech. Syst. Signal. Process 2010, 24, 559–566. [Google Scholar]
- Pan, Y.; Chen, J.; Guo, L. Robust bearing performance degradation assessment method based on improved wavelet packet–support vector data description. Mech. Syst. Signal. Process 2009, 23, 669–681. [Google Scholar]
- Pan, Y.N.; Chen, J.; Dong, G.M. A hybrid model for bearing performance degradation assessment based on support vector data description and fuzzy c-means. Proc. IME. C J. Mech. Eng. Sci. 2009, 223, 2687–2695. [Google Scholar]
- Jiang, L.; Liu, Y.; Li, X.; Chen, A. Degradation assessment and fault diagnosis for roller bearing based on AR model and fuzzy cluster analysis. Shock Vibration 2011, 18, 127–137. [Google Scholar]
- Shen, Z.; He, Z.; Chen, X.; Sun, C.; Liu, Z. A Monotonic degradation assessment index of rolling bearings using fuzzy support vector data description and running time. Sensors 2012, 12, 10109–10135. [Google Scholar]
- Lei, Y.; Kong, D.; Lin, J.; Zuo, M.J. Fault detection of planetary gearboxes using new diagnostic parameters. Meas. Sci. Technol. 2012, 23, 055605. [Google Scholar]
- Oh, H.; Azarian, M.H.; Pecht, M.; White, C.H.; Sohaney, R.C.; Rhem, E. Physics-of-failure approach for fan PHM in electronics applications. Proceedings of the IEEE Prognostics and System Health Management Conference 2010, Macao, China, 12- 14 January 2010; pp. 1–6.
- Oh, H.; Shibutani, T.; Pecht, M. Precursor monitoring approach for reliability assessment of cooling fans. J. Intell. Manuf. 2012, 23, 173–178. [Google Scholar]
- Oh, H.; Azarian, M.H.; Pecht, M. Estimation of fan bearing degradation using acoustic emission analysis and Mahalanobis distance. Proceedings of the Applied Systems Health Management Conference, Virginia Beach, VA, USA, 10-12 May 2011; pp. 1–12.
- Miller, A.J. A New Wavelet Basis for the Decomposition of Gear Motion Error Signals and its Application to Gearbox Diagnostics. M.Sc. Thesis, The Pennsylvania State University, Pennsylvania, PA, USA, 1999. [Google Scholar]
- Liang, W.; Que, P.-W. Optimal scale wavelet transform for the identification of weak ultrasonic signals. Measurement 2009, 42, 164–169. [Google Scholar]
- Liu, C.S. Fault Detection of Rolling Element Bearings. Ph.D. Thesis, University of Washington, Seattle, WA, USA, 2005. [Google Scholar]
- Lucas, J.M.; Saccucci, M.S. Exponentially weighted moving average control schemes: Properties and enhancements. Technometrics 1990, 32, 1–29. [Google Scholar]
- Performance parameters (mechanical, electrical, environmental and quality/reliability) for air moving devices IPC-9591. 2006.

| Number of rolling elements, n | 6 |
| Mean diameter of rolling element, d | 1.59 mm |
| Pitch diameter of bearing, D | 5.5 mm |
| Contact angle, γ | 10.4° |
| Ball spin frequency (BSF) | 127.178 Hz |
| Ball pass frequency, inner race (BPFI) | 308.242 Hz |
| Ball pass frequency, outer race (BPFO) | 171.758 Hz |
| Fundamental train frequency (FTF) | 28.626 Hz |
| Filter type | Central Frequency,f0 | Rotation Variation Parameter,c | Half Central Bandwidth, bw | Number of Comb Teeth,n |
|---|---|---|---|---|
| Comblet filter: BSF | 127.178 Hz | 2% | 1.272 Hz | 100 |
| Comblet filter: BPFI | 308.242 Hz | 2% | 3.082 Hz | 41 |
| Comblet filter: BPFO | 171.758 Hz | 2% | 1.718 Hz | 74 |
| Comblet filter: FTF | 28.626 Hz | 2% | 0.286 Hz | 447 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Miao, Q.; Tang, C.; Liang, W.; Pecht, M. Health Assessment of Cooling Fan Bearings Using Wavelet-Based Filtering. Sensors 2013, 13, 274-291. https://doi.org/10.3390/s130100274
Miao Q, Tang C, Liang W, Pecht M. Health Assessment of Cooling Fan Bearings Using Wavelet-Based Filtering. Sensors. 2013; 13(1):274-291. https://doi.org/10.3390/s130100274
Chicago/Turabian StyleMiao, Qiang, Chao Tang, Wei Liang, and Michael Pecht. 2013. "Health Assessment of Cooling Fan Bearings Using Wavelet-Based Filtering" Sensors 13, no. 1: 274-291. https://doi.org/10.3390/s130100274






