Implantation of a total hip replacement (THR) has become a standard procedure for the treatment of degenerated or fractured hip joints. After resection of the femoral head, a stem is impacted or cemented into the femur. The acetabulum is reamed and a cup is placed into the cavity. The artificial joint is realized by connecting a ball-head to the stem and a liner into the cup. The modular design of modern total hip replacements allows choice of different materials as bearing surfaces in combination with materials of high biocompatibility and enhanced bone ingrowth. Despite more than forty years of clinical experience, complications can still occur which require an exchange (revision) of the THR or some of its components. The main reason for failure is loosening of the stem or the cup [
1]. Acute pain requires clarification as to whether the THR is mechanically loose and has to be revised [
2]. In orthopedic surgery, each revision of a THR leads to subsequent tissue defects and functional deficits. The sooner the loosening is detected, the better the prognosis for the new implant. However, clinically applied methods of assessing implant fixation with respect to implant loosening are of suboptimal precision, leading to uncertain indication of revision surgery and late recognition of bone defects. In clinical practice, imaging methods, especially radiography, are used to identify the actual condition of fixation, but fail in the aim of achieving 100% accuracy in the diagnosis of slight loosening [
3,
4]. Thus, vibration techniques were investigated experimentally to assess the structural integrity of endoprosthetic implant systems by evaluating acoustic and structural vibration parameters e.g., damping and resonant frequency [
5–
12]. Different research studies, including animal experiments, demonstrated a positive correlation between a decrease in the resonant frequency and a decrease of the system stiffness, and therefore an increase in implant loosening [
13–
16]. The focus of past studies was to obtain vibrational output by exciting the bone-implant-system using an external electrodynamic shaker at the femoral condyles [
17–
19]. The output signal could be measured with an accelerometer attached to the skin at the prominence of the greater trochanter. Resonant frequencies in the highly sensitive band starting at 2,500 Hz are most sensitive to changes in the biological structure and thus the condition of fixation of the THR [
20]. This frequency range is difficult to reach using the shaker, since higher frequencies are reported to provoke pain. Currently, researchers are striving to replace
ex vivo techniques with novel
in vivo sensors, such as accelerometers in vibration analysis [
21]. For any measurement system that uses electronics integrated in the THR, loss of functionality and degradation during sterilization presents a significant challenge. Besides miniaturized design and biocompatibility, a reliable power supply is an issue in development of
in vivo sensors. The technology of choice for vibrometry in most studies is wireless powering and data telemetry. Hence, energy can be provided extracorporeally by a primary coil and an
in vivo secondary coil integrated in the endoprosthetic implant. In order to ensure long-term performance of the
in vivo electronics, inductivities and capacities have to be chosen carefully. During the design of application specific electric circuits, low operating voltages and extremely low input signal levels appear, resulting in offset voltages and crosstalk from digital to analogue wires [
22]. A study with an artificial thigh and a THR equipped with an integrated accelerometer showed damping of frequencies in the highly sensitive band, even though an optimized amplification was applied [
23].
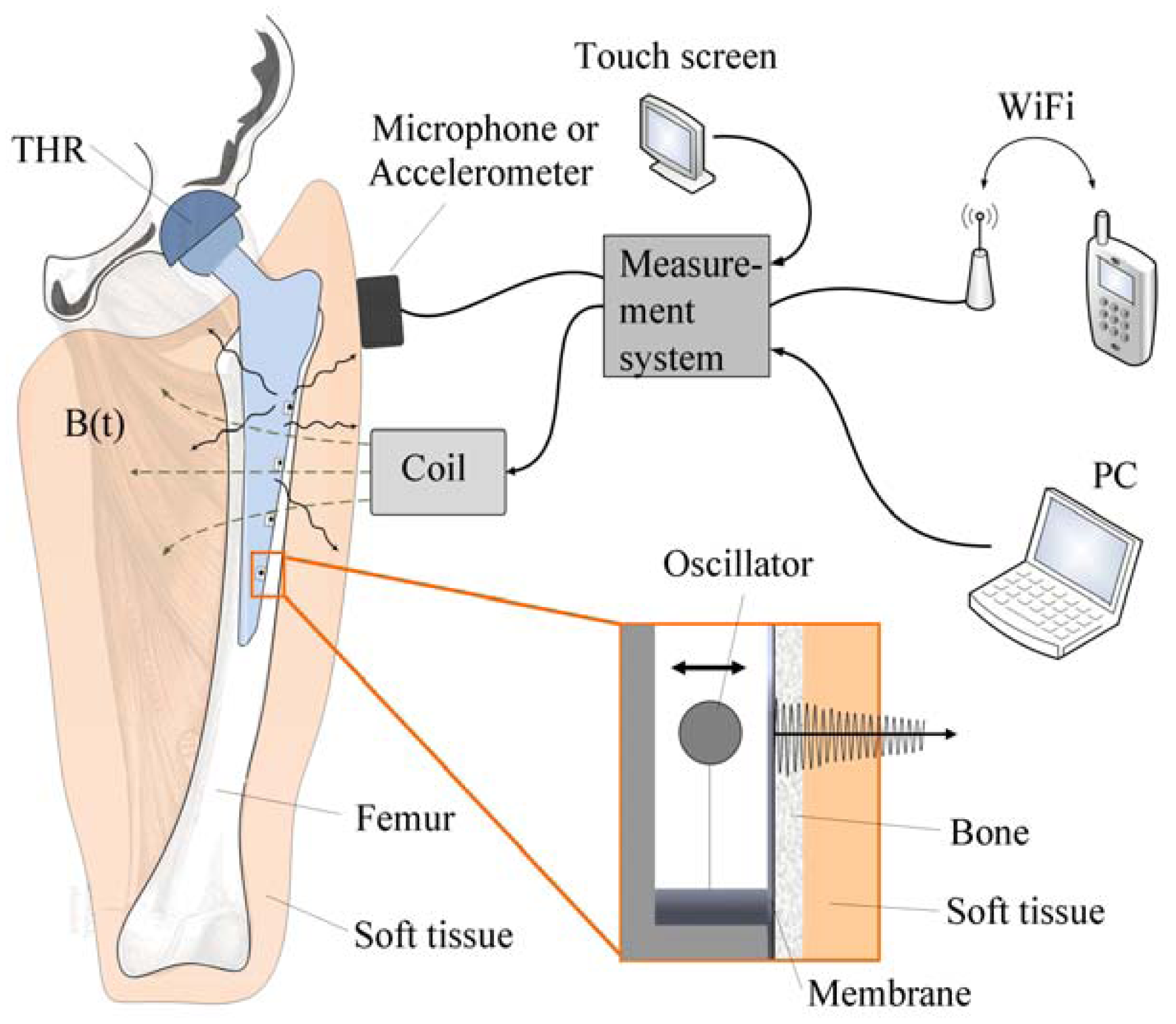
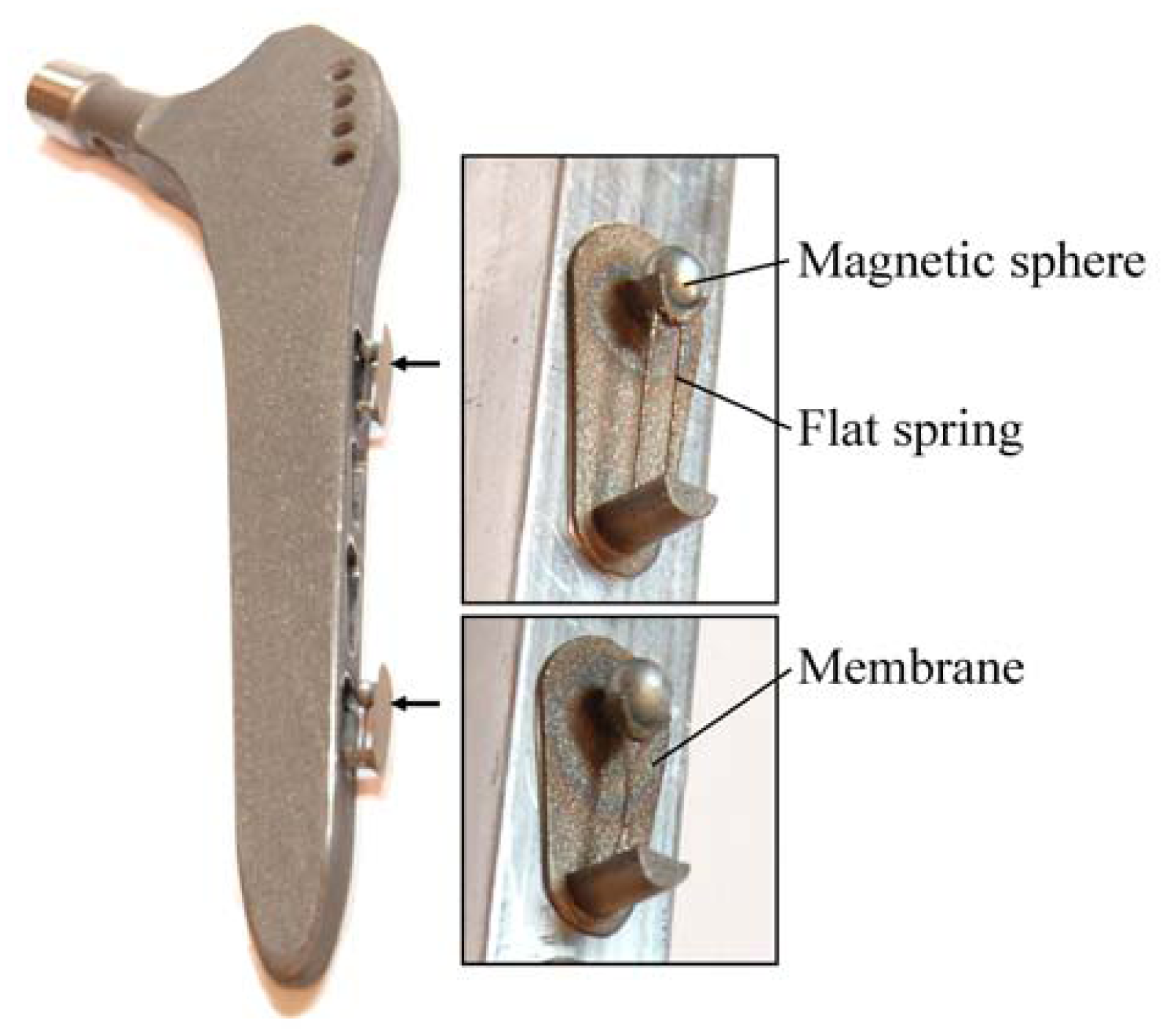
Due to the aforementioned challenges of implementation of an integrated active system to identify implant loosening, we proposed a passive sensor concept based on magnetic induction [
24]. The concept is characterized by an extracorporeal coil, which excites several magnetic oscillators inside the THR to impinge on thin membranes and thus producing a sound and vibration signal (
Figure 1). The proposed passive concept consists of several spring-mass-oscillators, which are assembled by a flat spring and a permanent magnetic sphere. This kind of oscillating system can be excited using an excitation coil, due to the polarization of the sphere. The external magnetic field effects the displacement of the oscillator from its neutral position. Hence, the oscillator moves back and impinges on the membrane dependent on its back-spring force. From this central point, sound emission originates due to the excitation of a free oscillation of the membrane-bone system in its bending modes. The resultant structure-borne sound waves propagate as transient elastic sound waves through the adjacent tissue. At the border of the bone-membrane system, changes in the sound characteristics appear dependent on the condition of implant fixation.
The sound emission and vibration of the system can be detected using a structure-borne sound sensor, e.g., an accelerometer or a microphone. To identify loosening at different locations of the hip stem, several integrated oscillators are necessary.
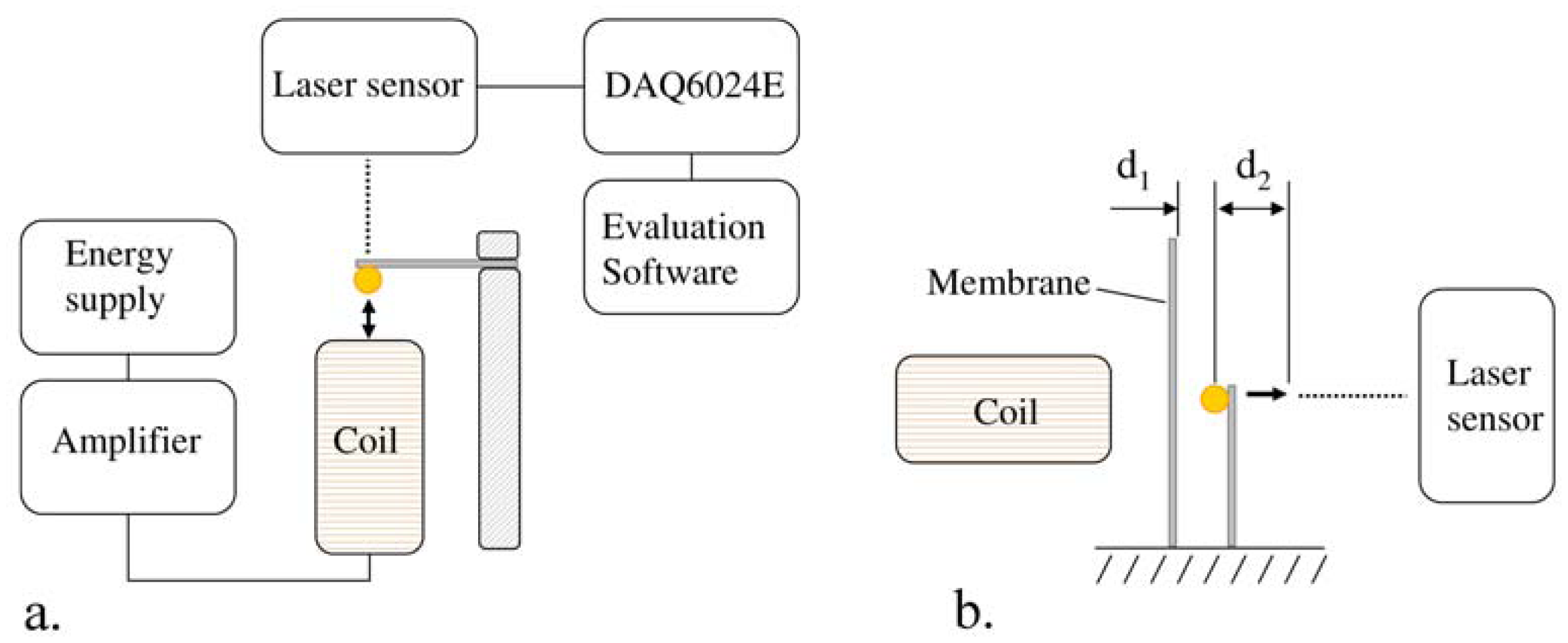
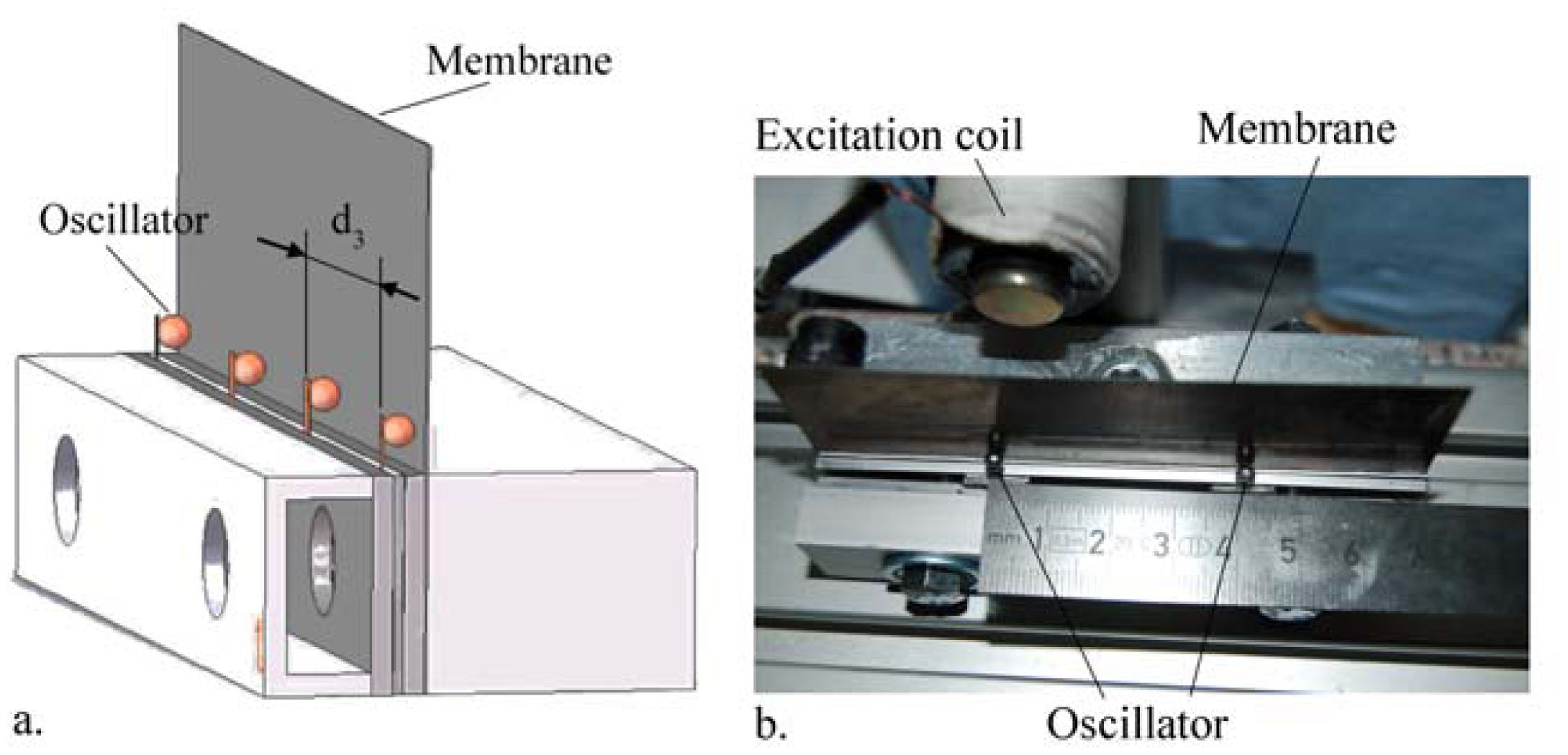
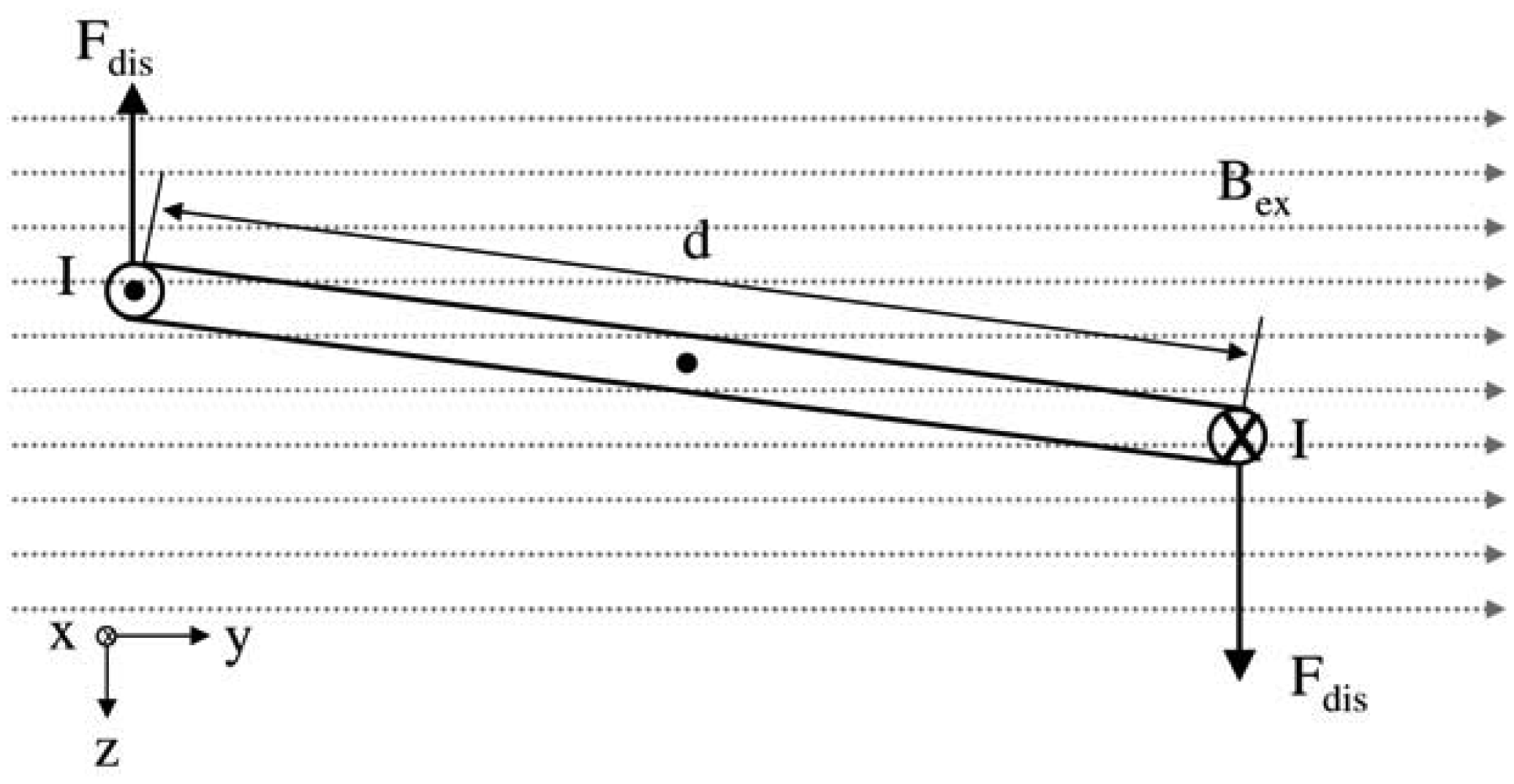
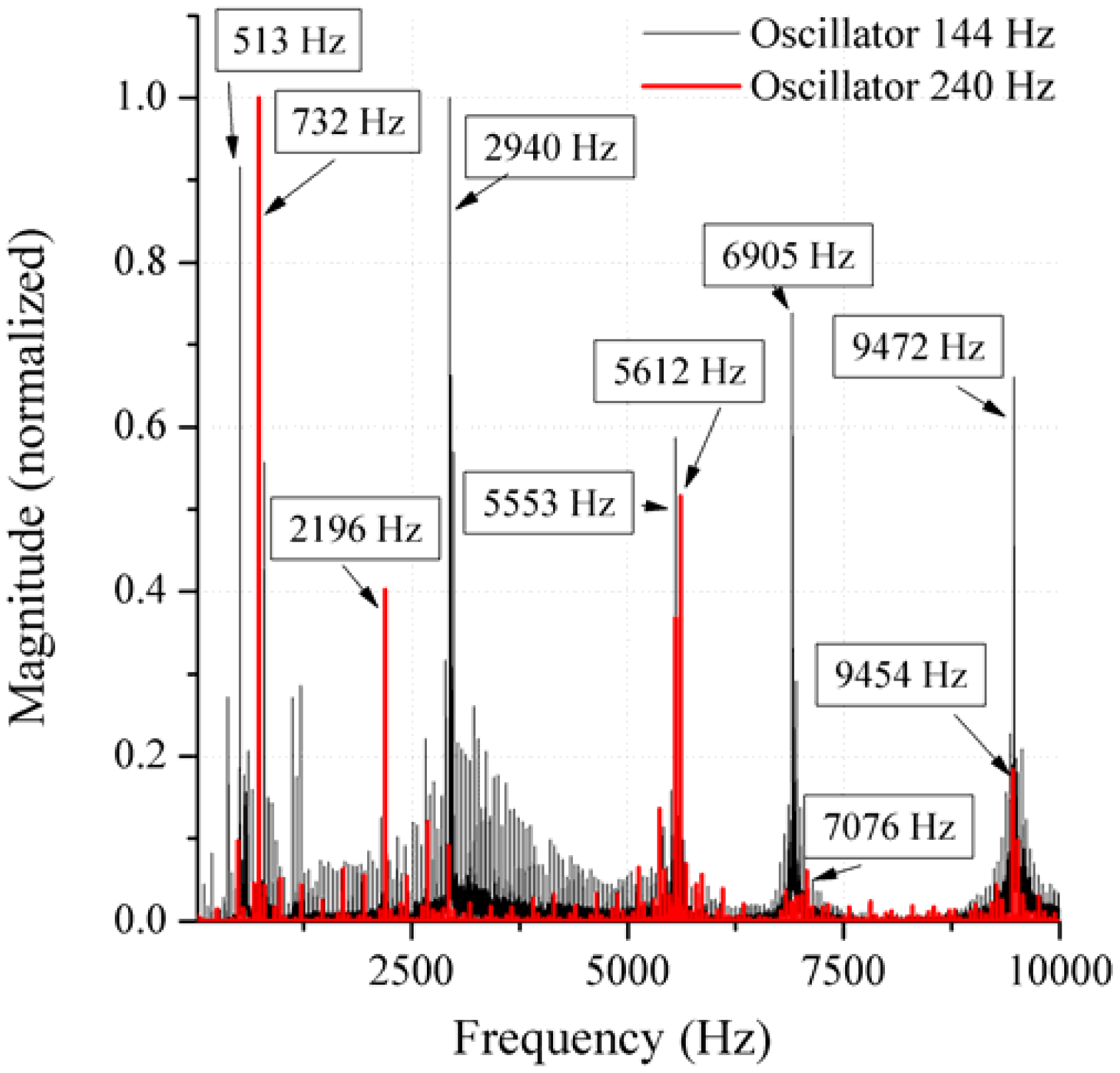
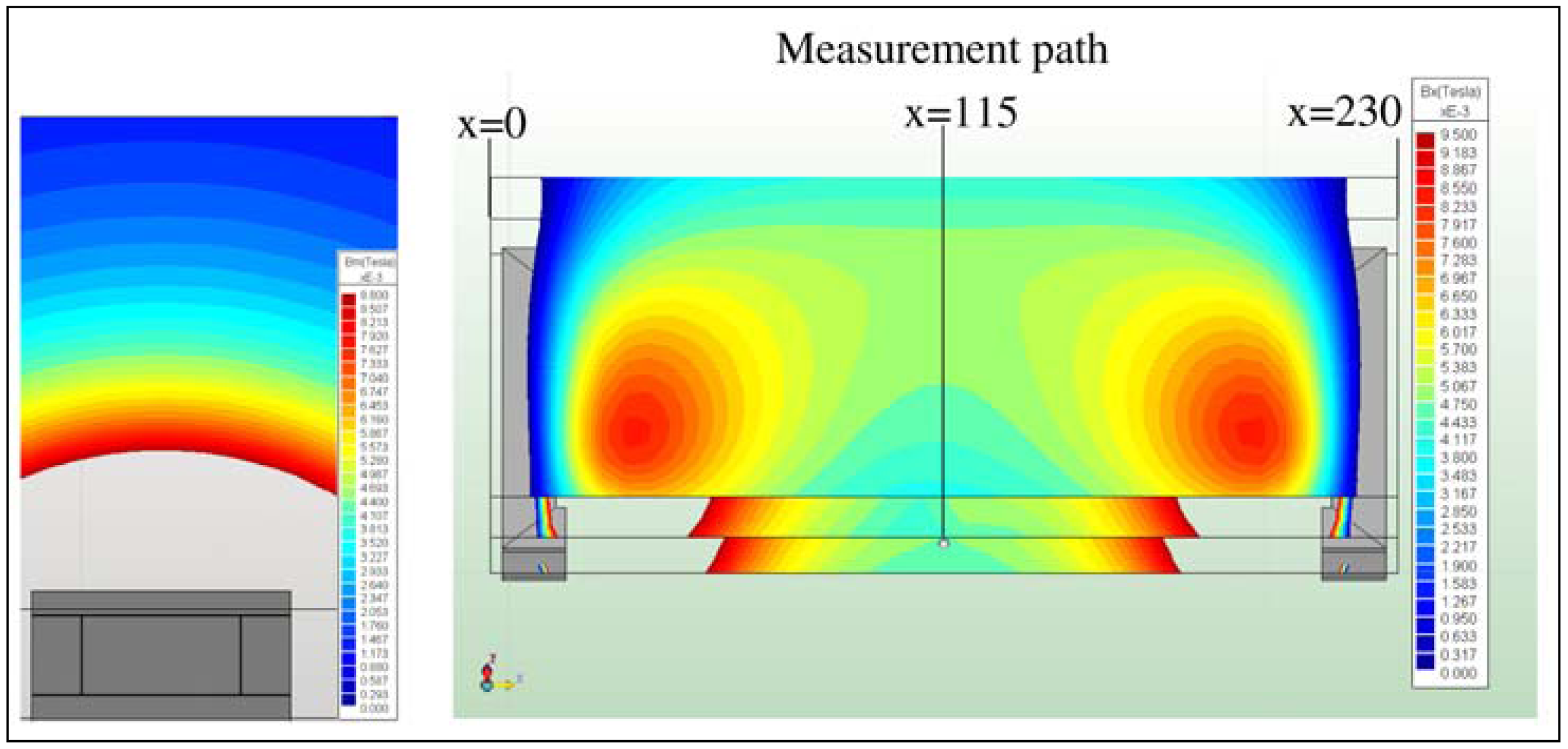
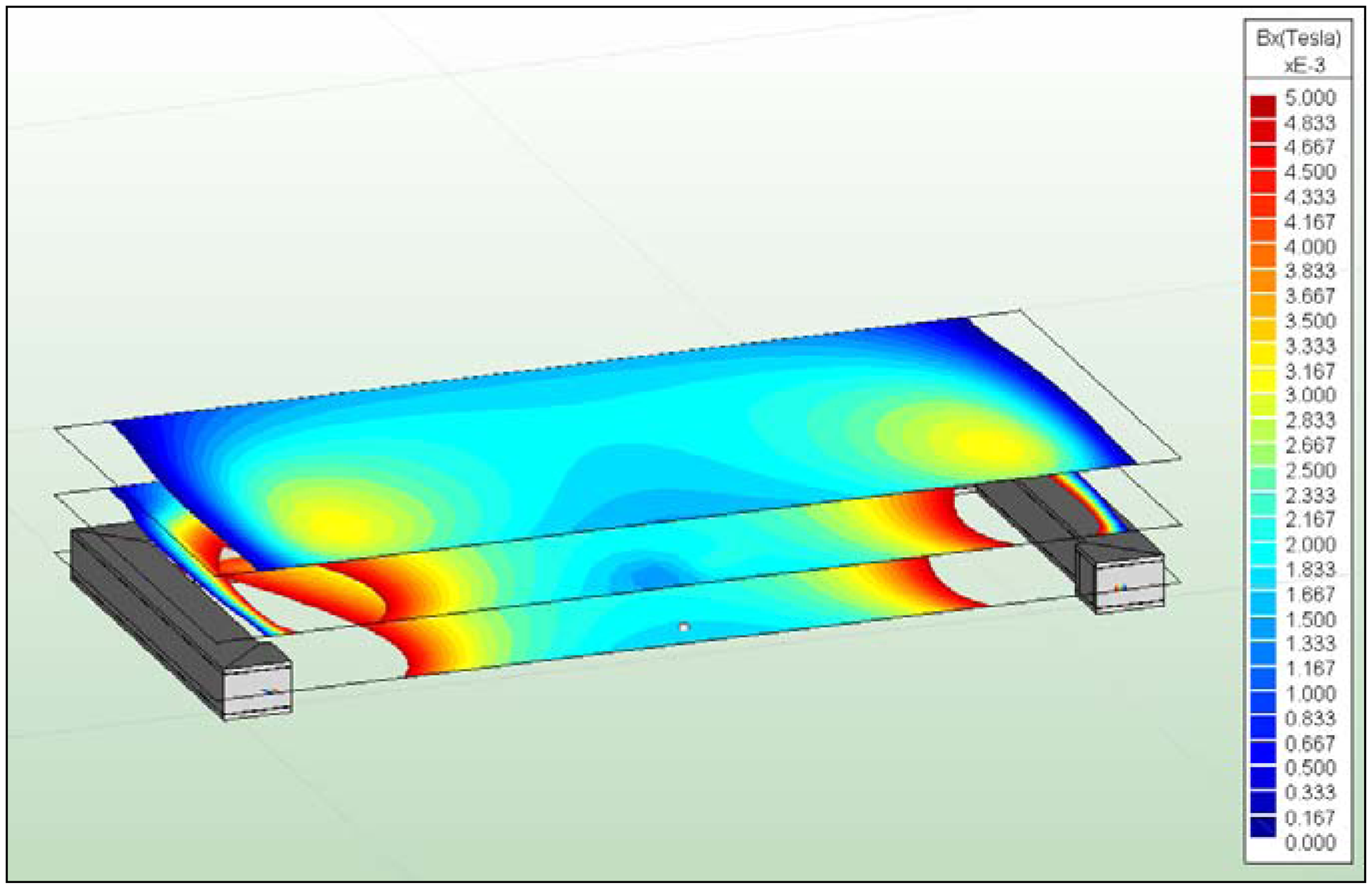
In the present work, the passive sensor array was investigated to guarantee the reproducible and selective excitation of sound emission inside the THR. In the study, one of the most important considerations is how to excite each individual oscillator without influencing oscillators proximal to the excited one, and therefore achieve the highest possible selectivity. In particular, we addressed the question of which parameter adjustments of the extracorporeal coil are most appropriate for the selective excitation of the oscillators. A numerical simulation of two different excitation coil designs, applying the boundary element method, was carried out.